Aerodynamic Investigation on a Coaxial-Rotors Unmanned Aerial Vehicle of Bionic Chinese Parasol Seed
Abstract
:1. Introduction
- (1)
- There is still relatively limited research on coaxial-rotor configuration optimization and overall aerodynamic performance analysis [16];
- (2)
- The results are unitary, and less attention is paid to designing and analyzing new efficient bionics that emulate nature.
- (3)
- Due to limited experimental and computational resources, it is necessary to conduct comparative validation between calculations and experiments based on design requirements to reflect the accuracy and practicality of simulation results. The MRF (Moving Reference Frame) model used is suitable for steady-state calculations, employing a fixed rotating reference frame to handle the flow in rotating regions.
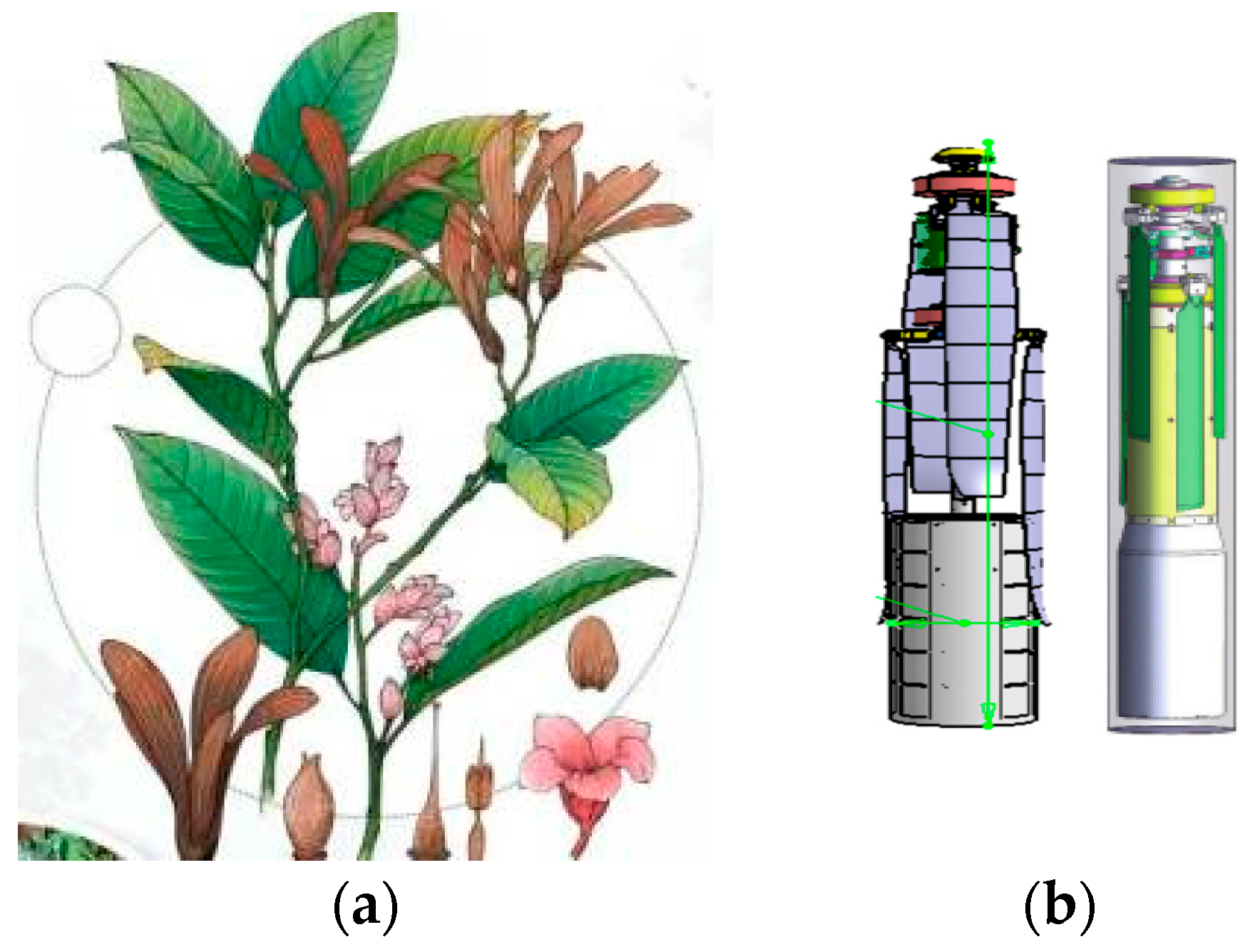
2. Conceptual Bionic Design of UAVs
2.1. The Design Requirement of a Coaxial-Rotor UAV
- (1)
- In terms of efficiency, a coaxial-rotor power system is adopted to enhance lift and power payload efficiency. It results in higher cruise efficiency within a specific altitude range of 0–5 km.
- (2)
- Regarding stability, the coaxial rotors’ power system, consisting of upper and lower motors and folding rotors, should achieve balanced torque and variable pitch control during a flight in the 0–5 km altitude range, despite the yaw-torque authority being less than that of a conventional single main rotor helicopter.
- (3)
- In terms of mission payload, a downward-mounted spherical package payload compartment is employed as far as possible. It allows the center of mass to move down for UAV stability and provides partial buoyancy to achieve omnidirectional detection and surveillance.
2.2. Bionic Design Modeling of the Coaxial-Rotors UAV
2.2.1. Three-Dimensional Tube Folding Design
2.2.2. Initiated Flyby Configuration Design
2.2.3. Variable Altitude Variable Speed Flight Configuration Design
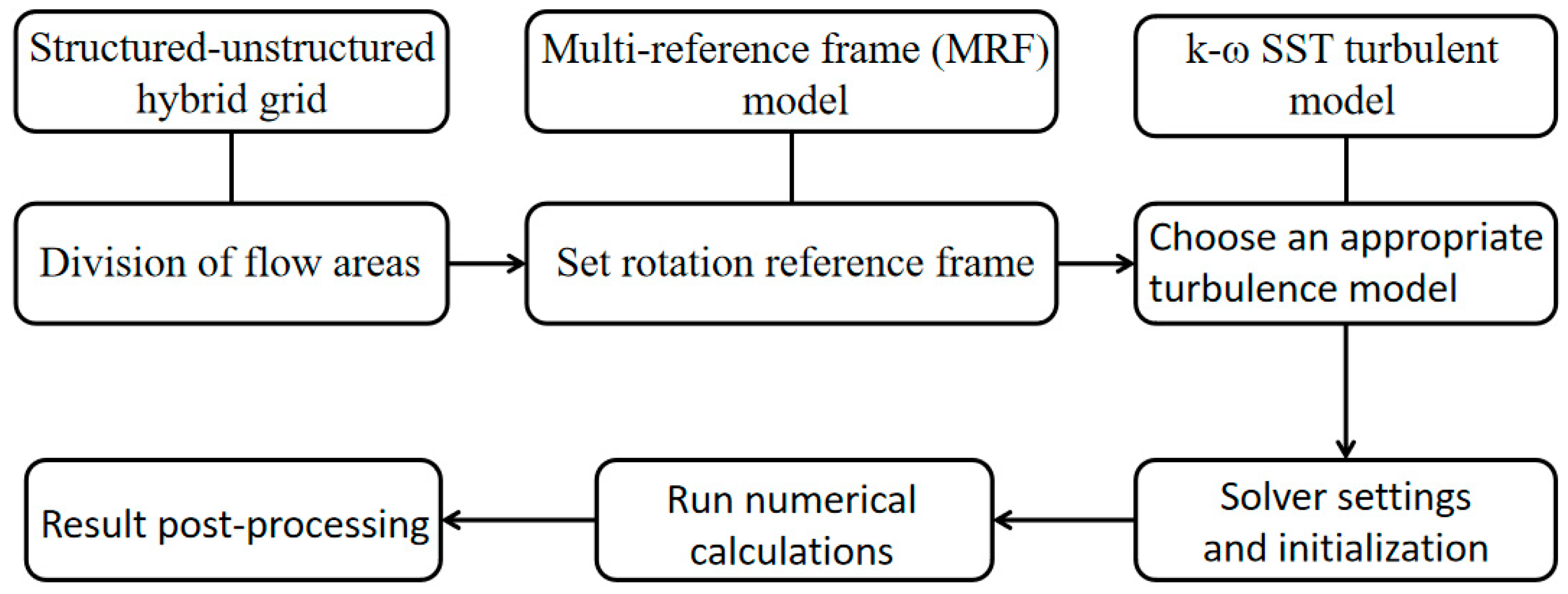
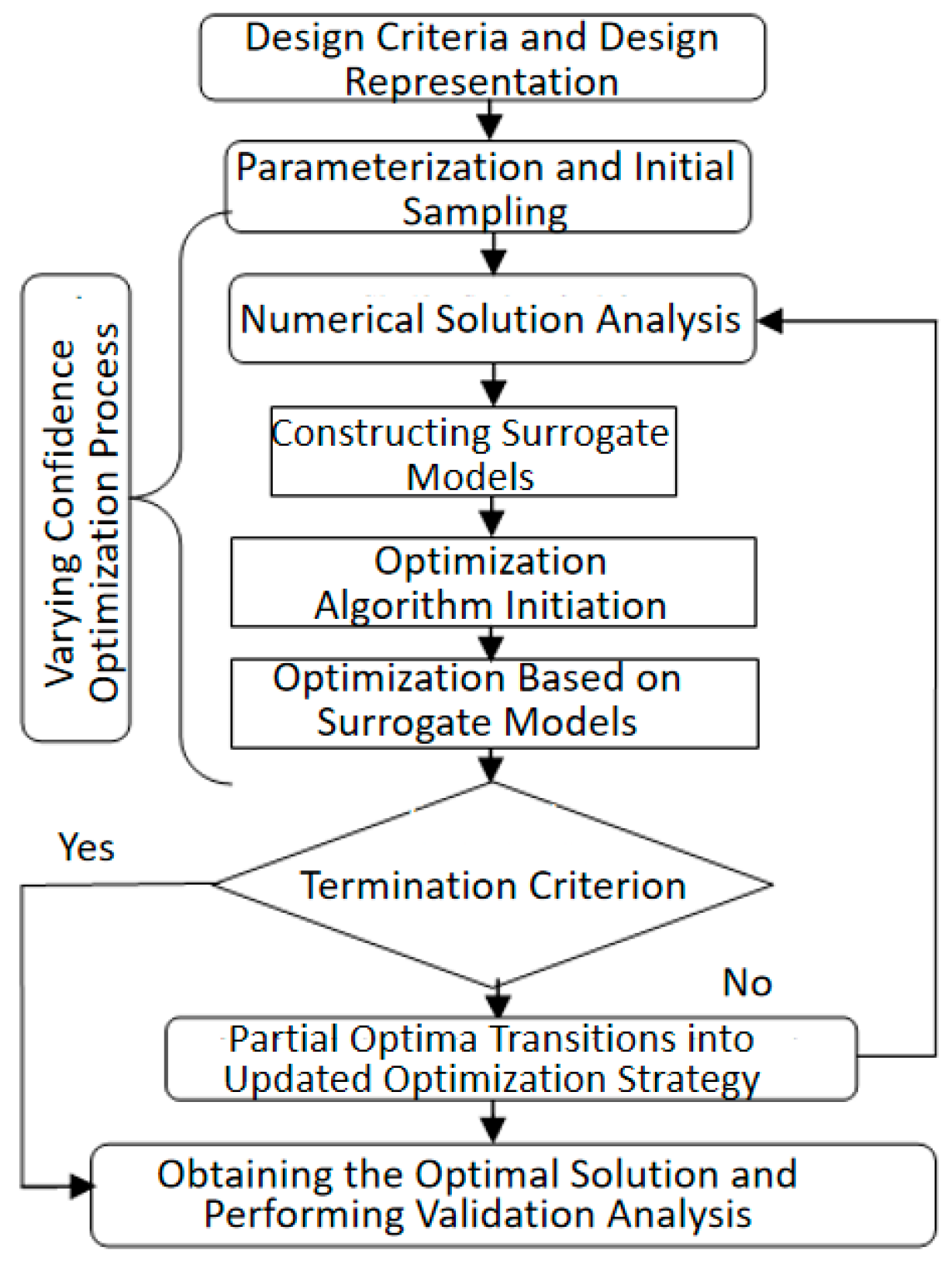
3. The Numerical Method
3.1. The Numerical Method
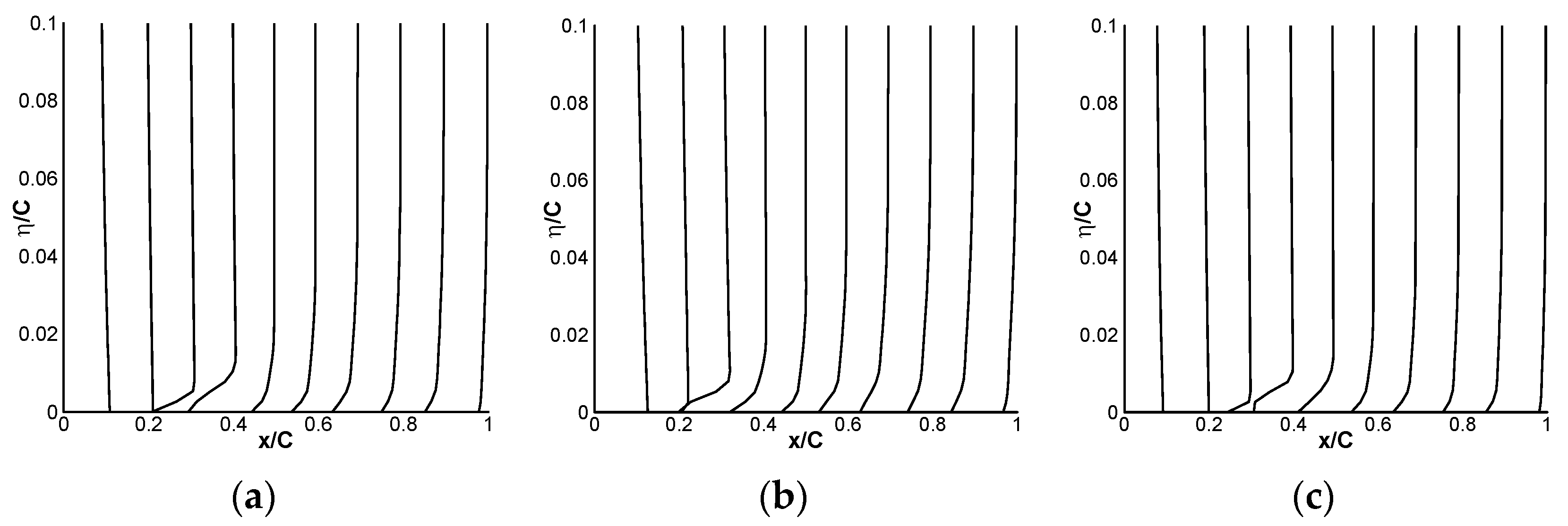
3.2. The Numerical Verification
4. The Aerodynamic Design of a Coaxial-Rotor UAV
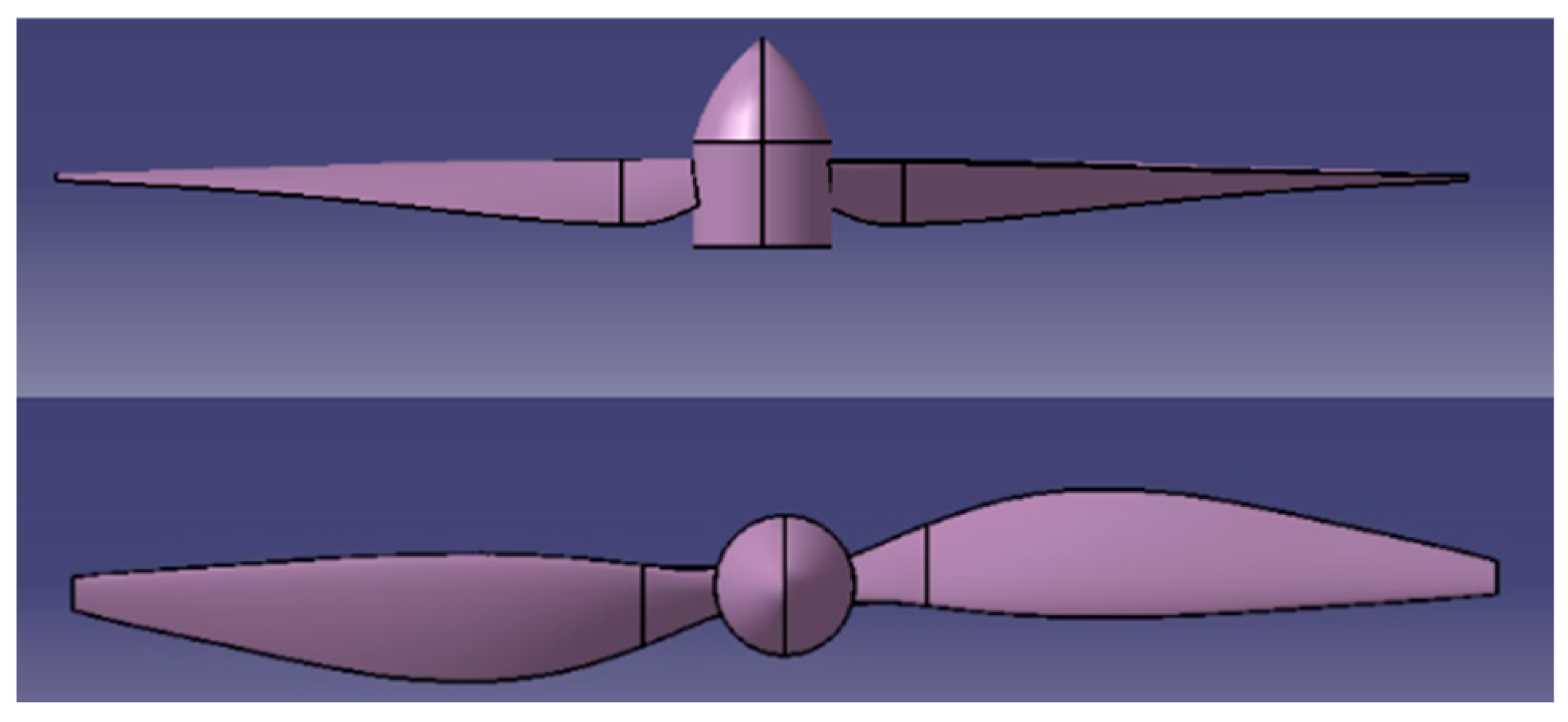
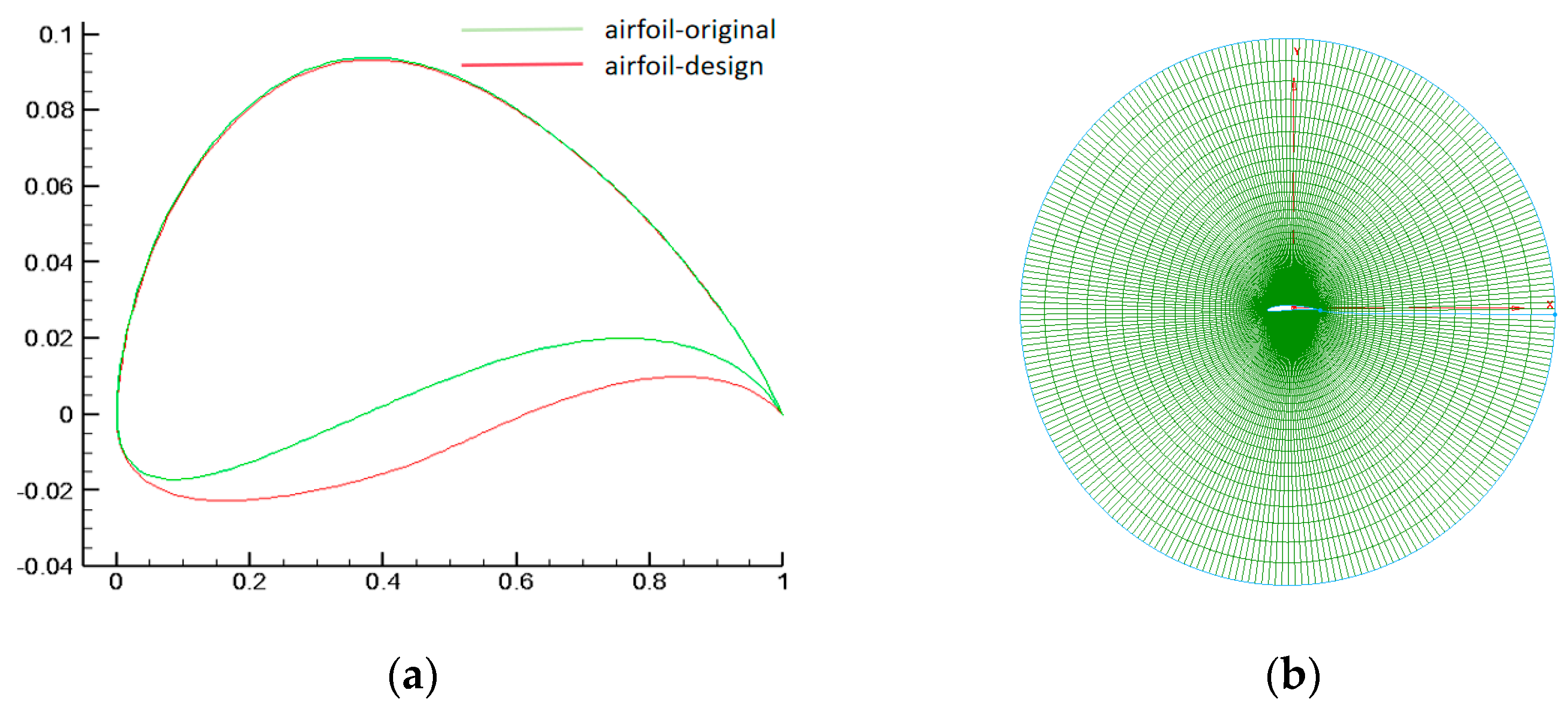
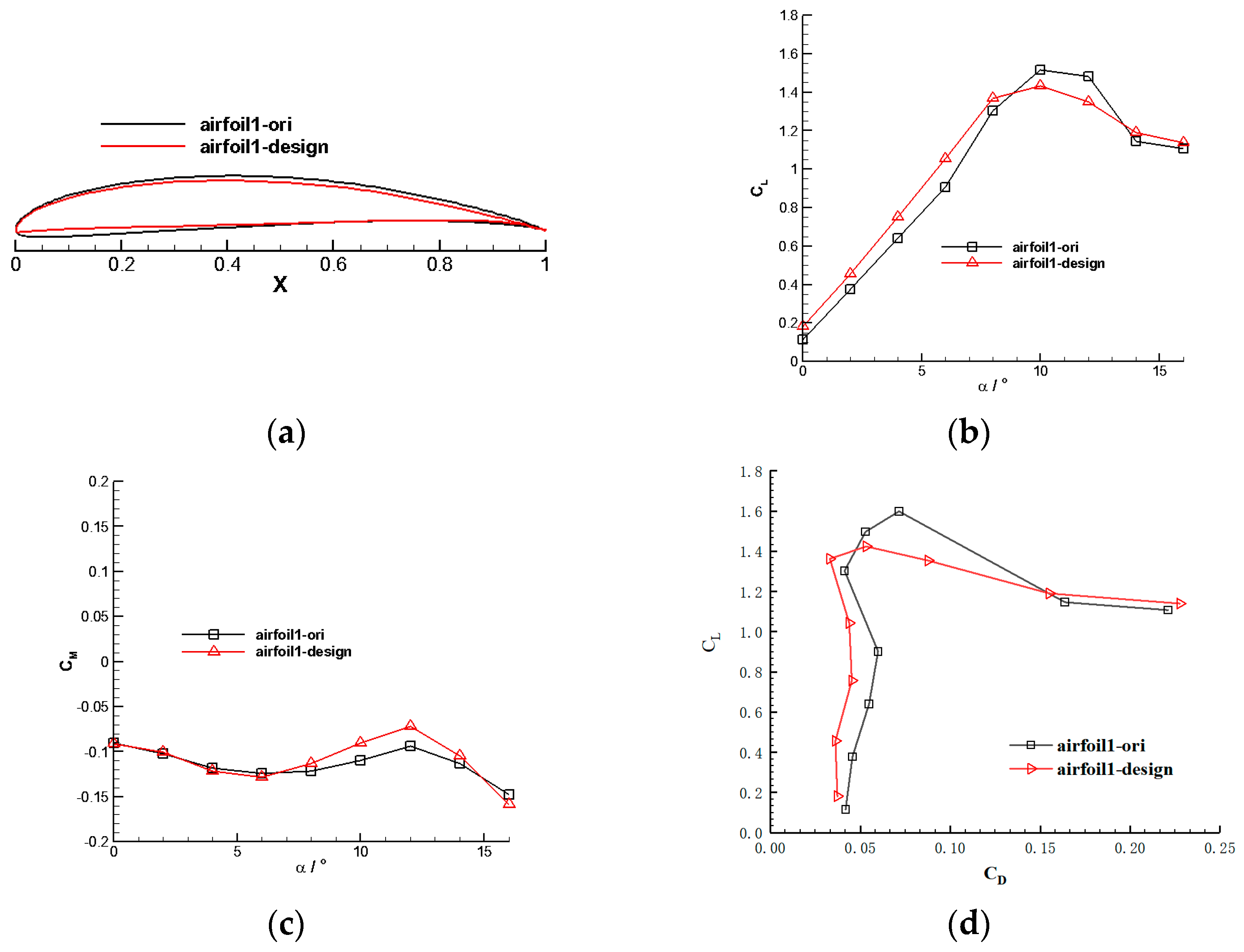
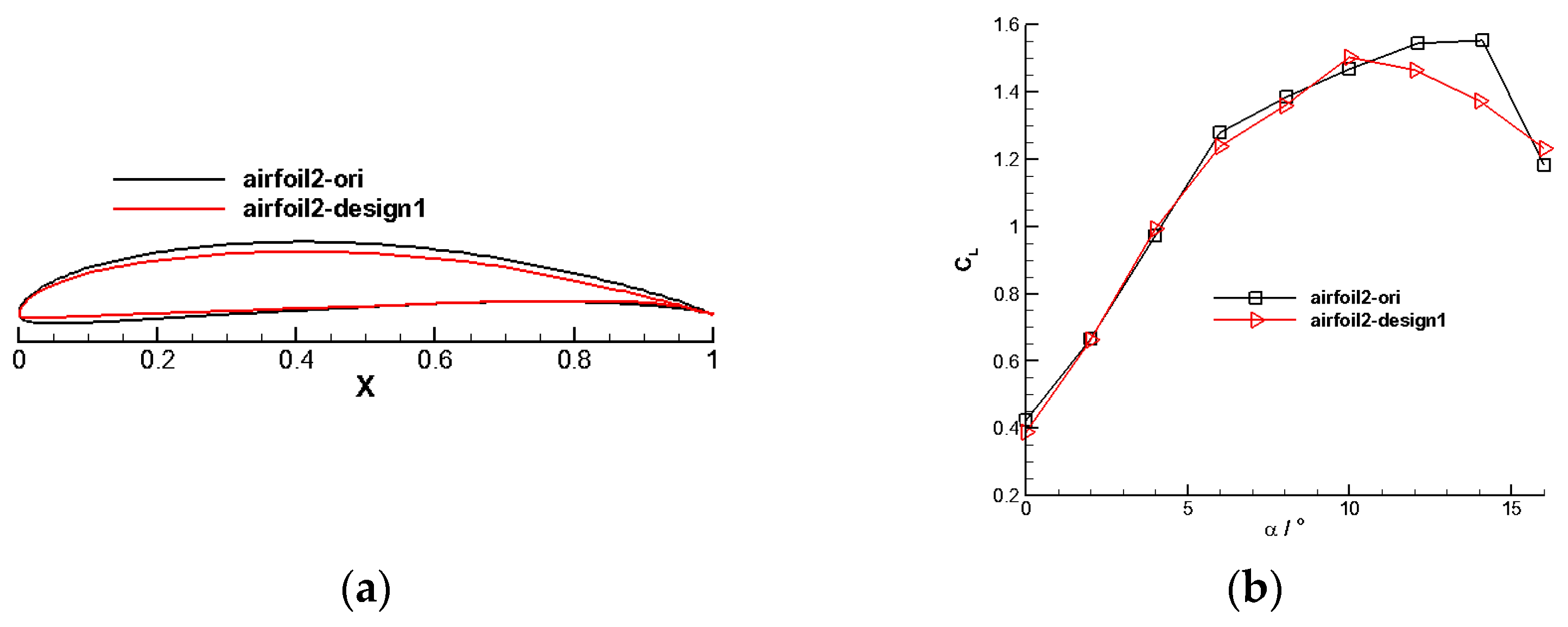
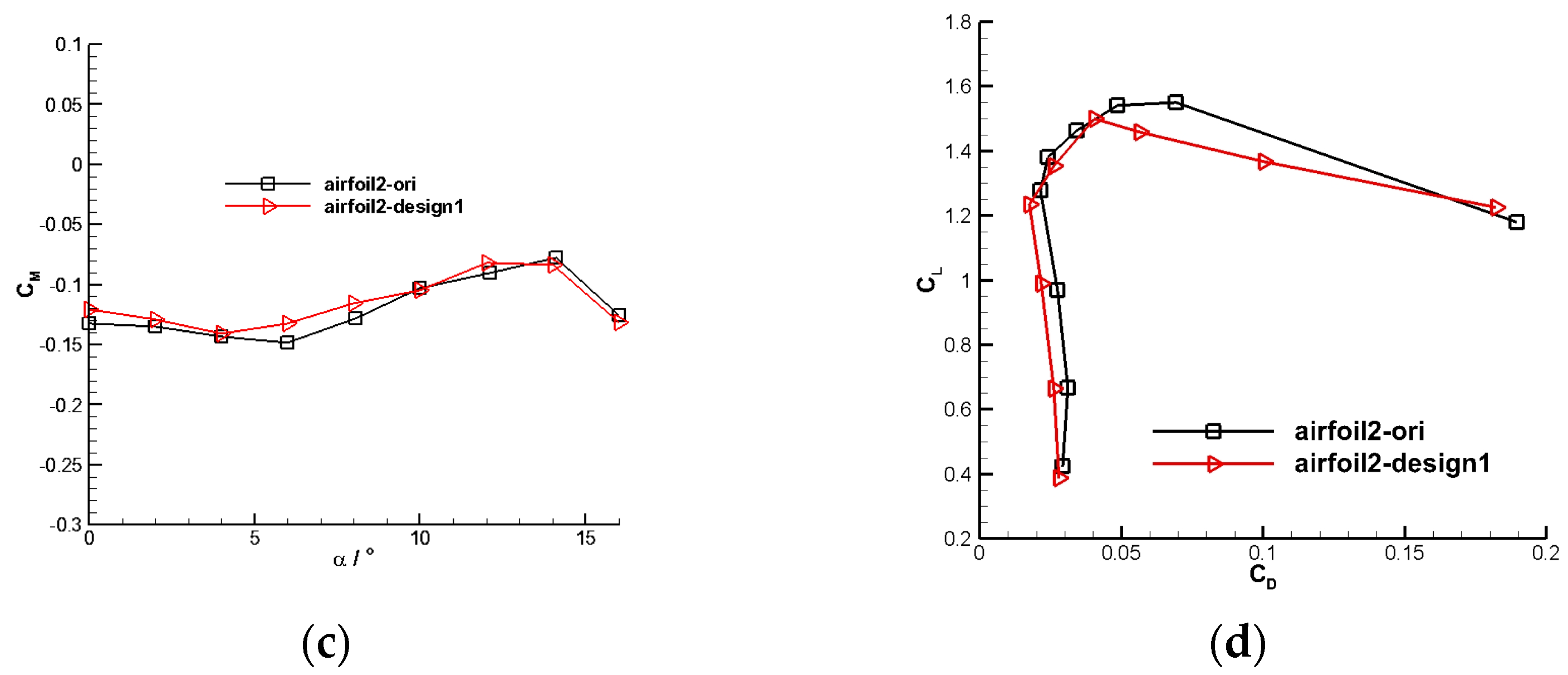
4.1. Rotor Airfoil Design
4.1.1. Inner Section Airfoil
4.1.2. Outer Section Airfoil
4.2. The Coaxial Rotors Design
4.2.1. Aerodynamic Performance of a Single Rotor
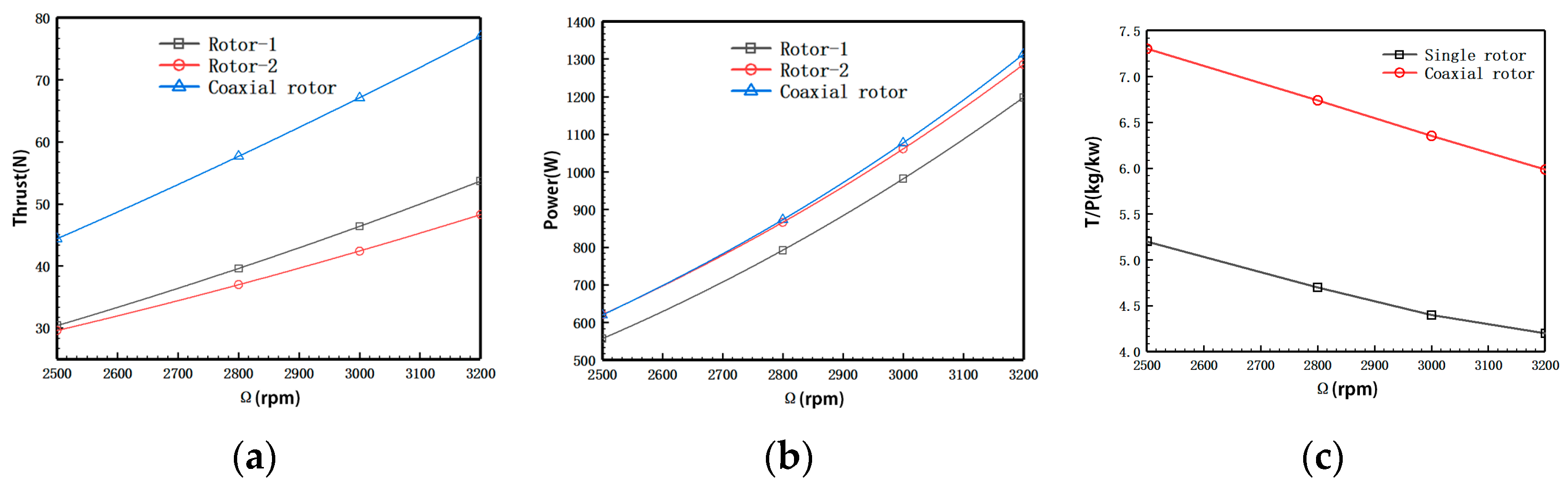
4.2.2. Aerodynamic Performance of Coaxial Rotors
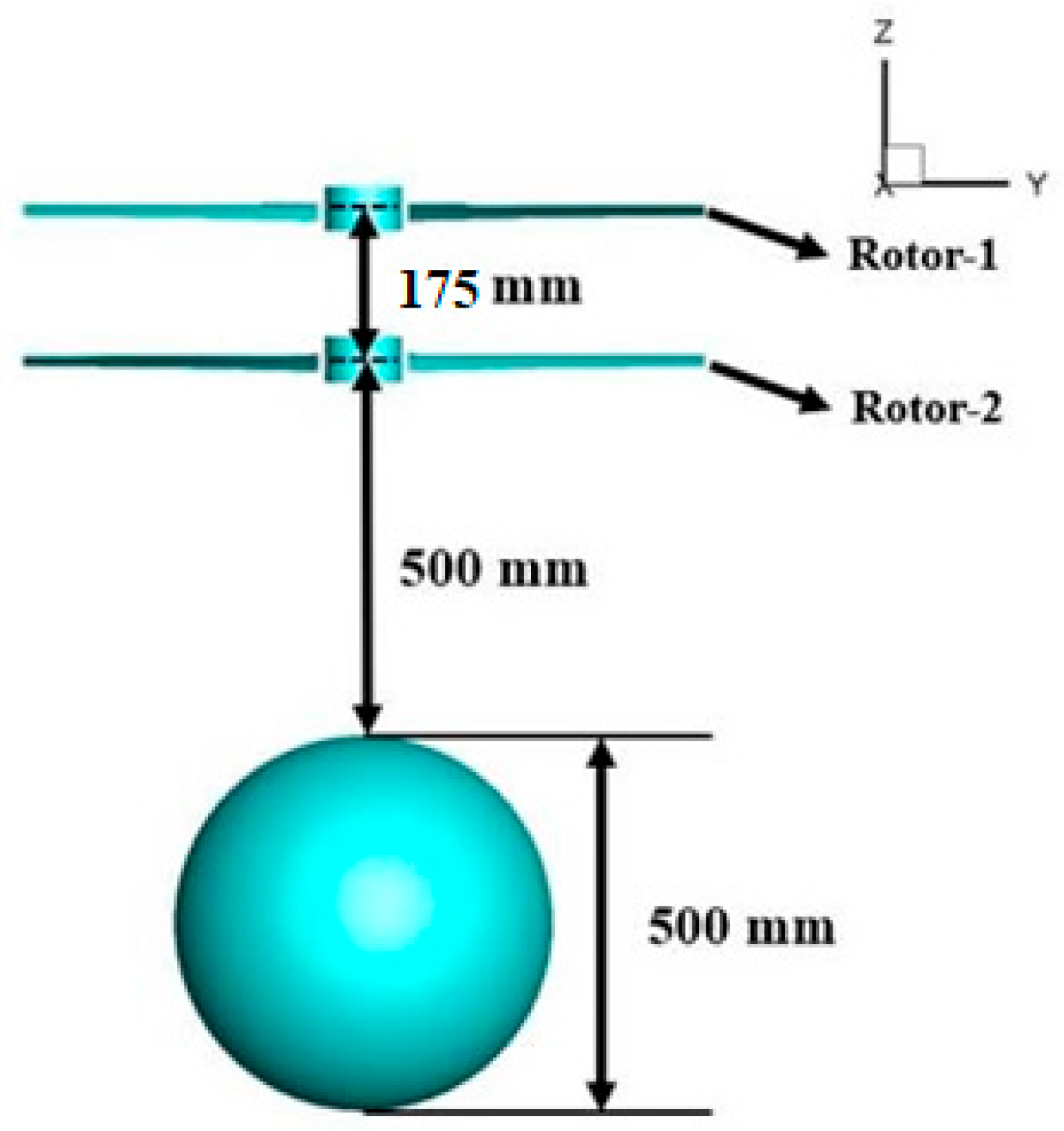
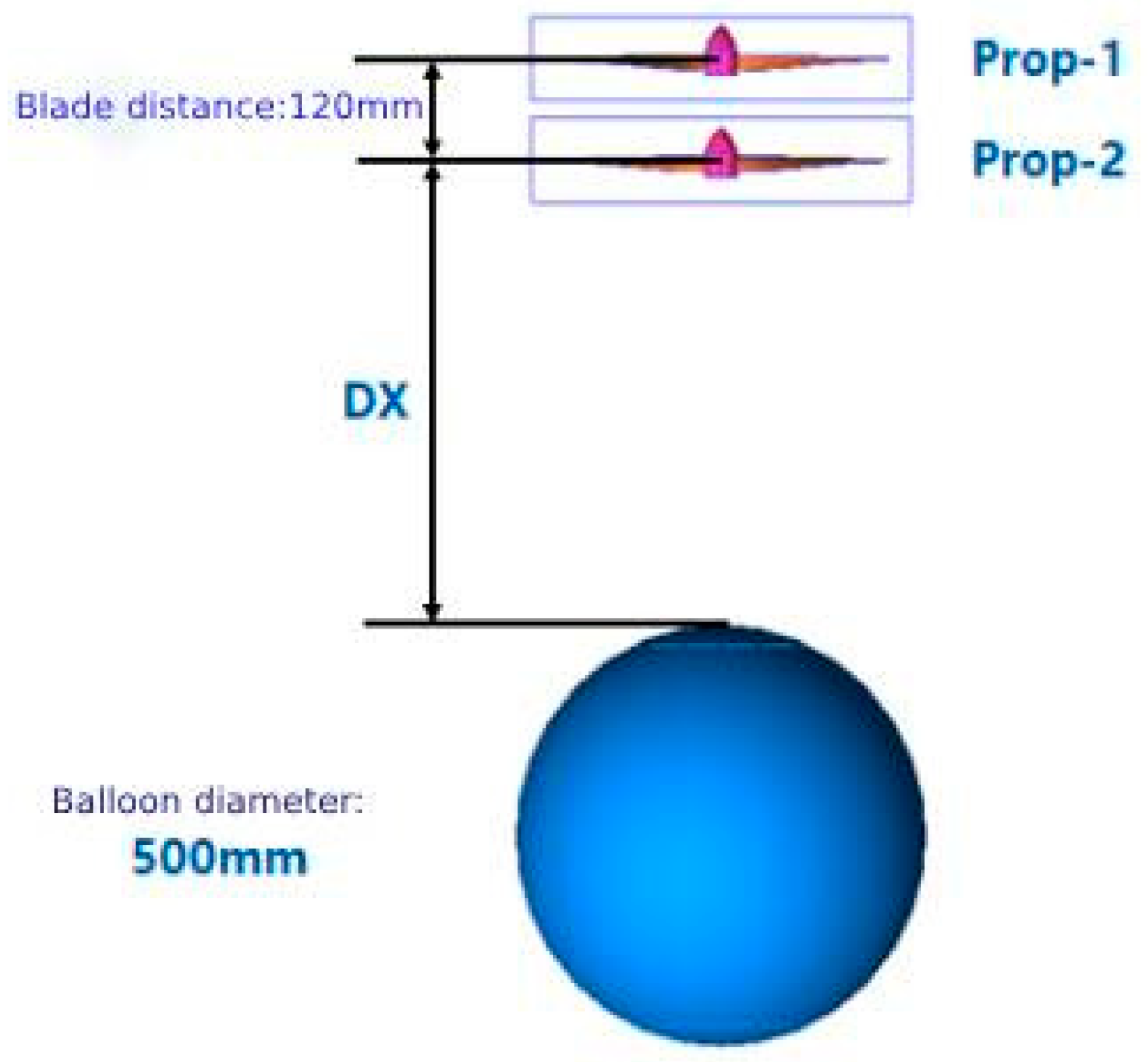
4.2.3. Space Ratio Effects
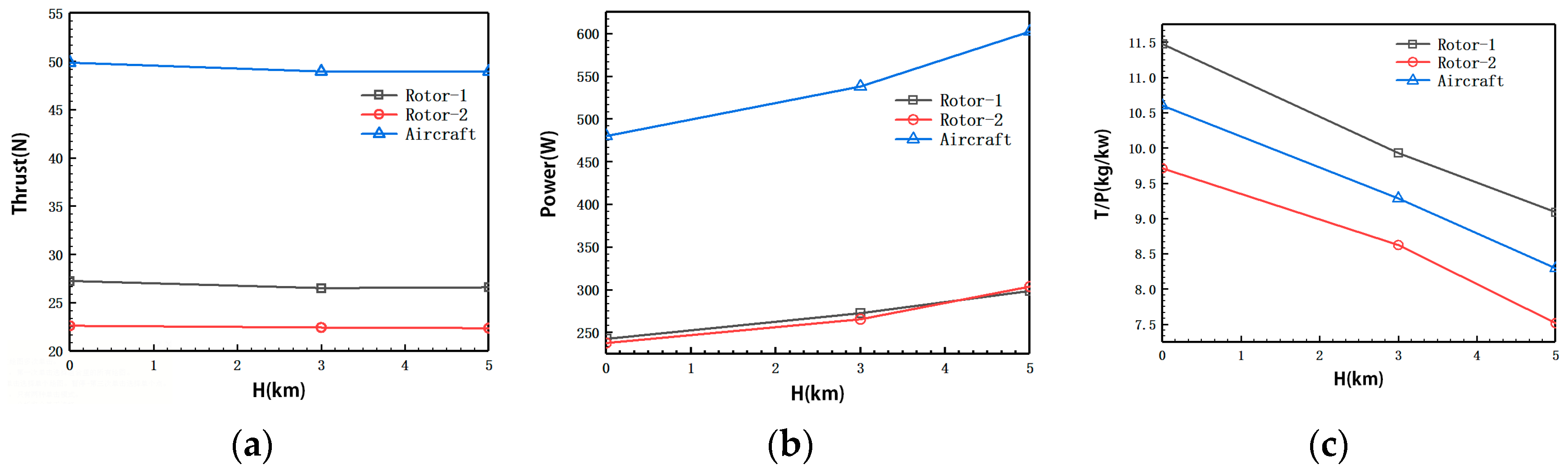
4.2.4. Design Results of the Whole Aircraft
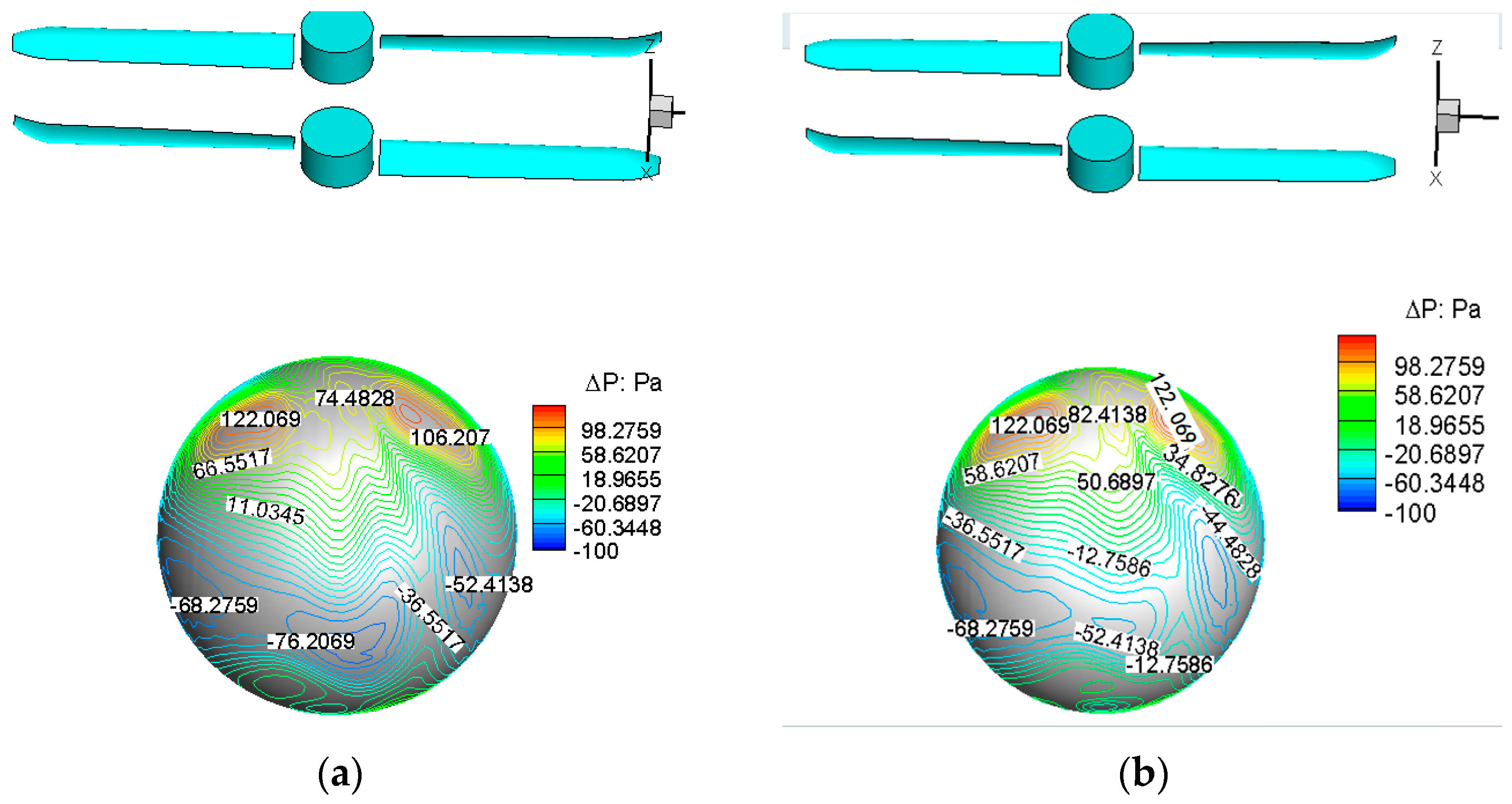
5. Aerodynamic Analysis of Coaxial-Rotors UAV
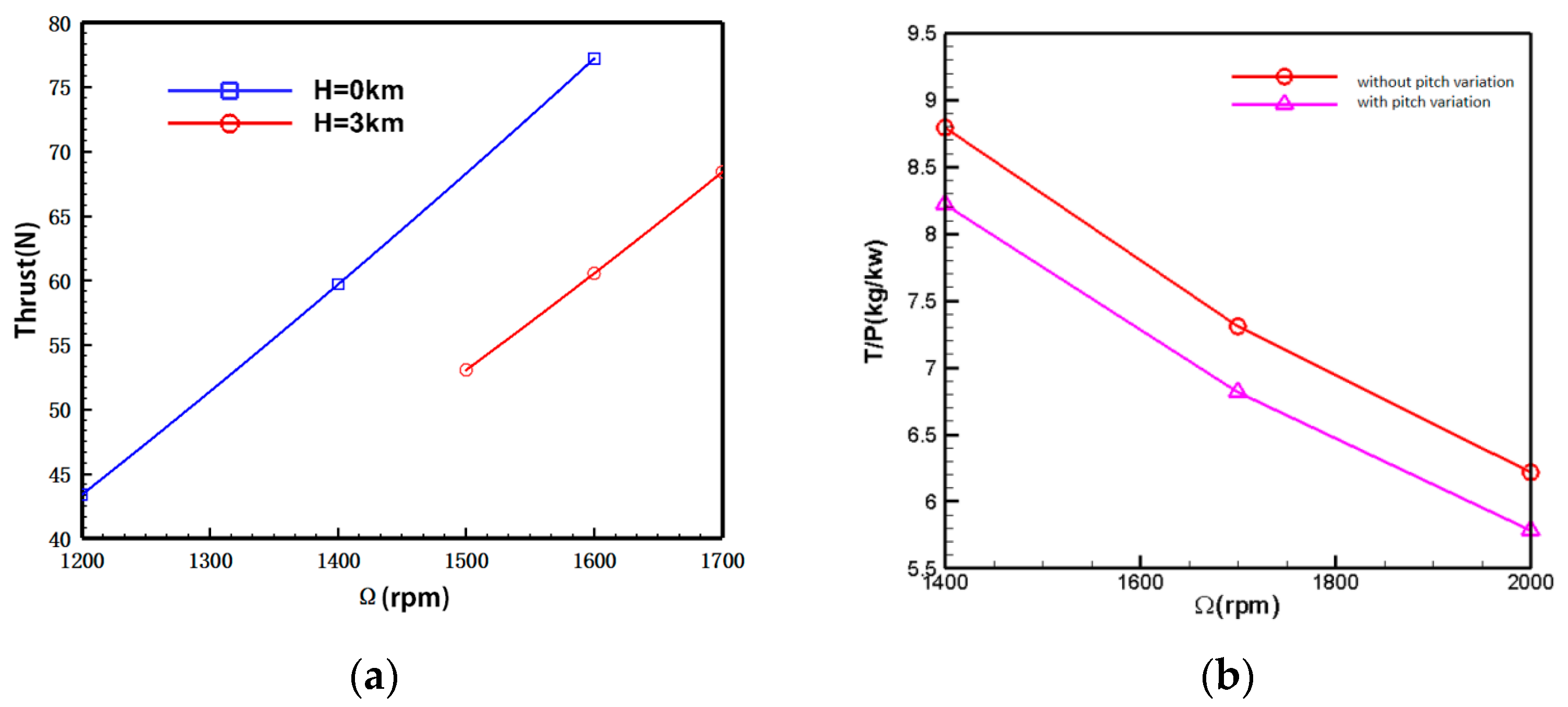
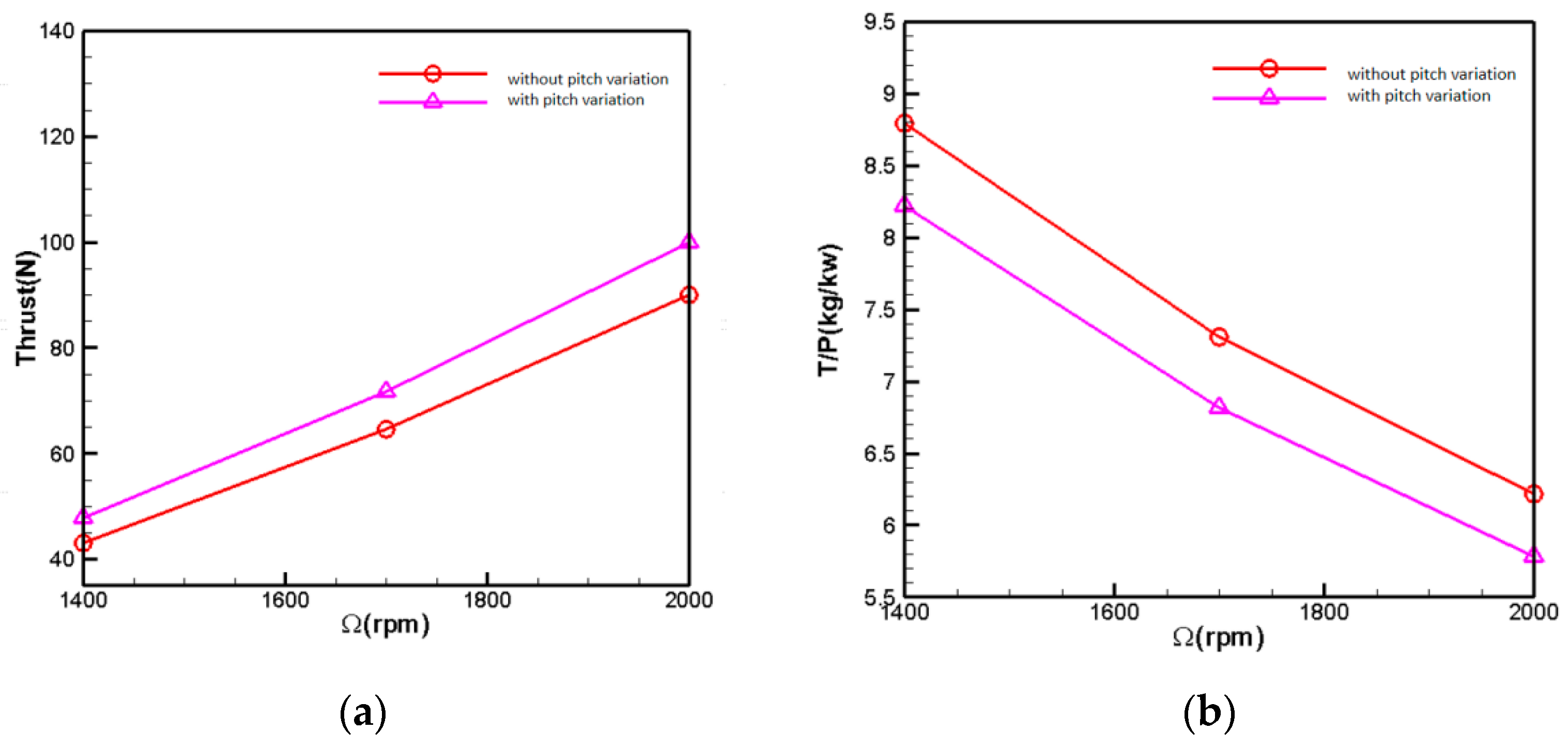
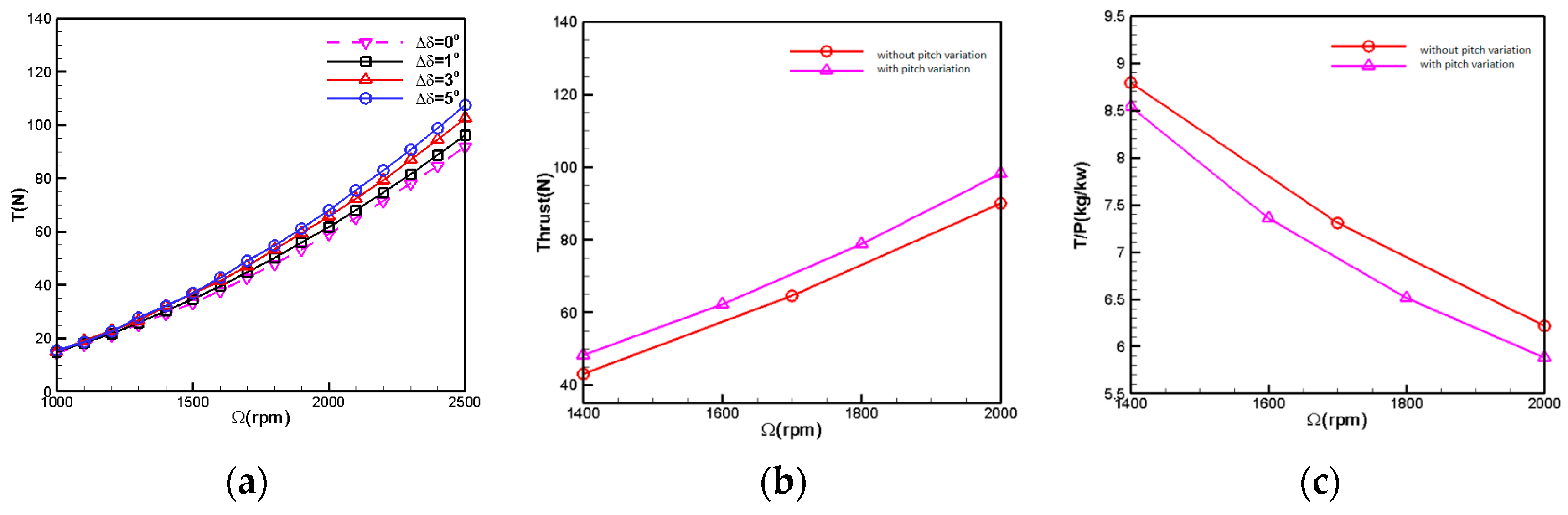
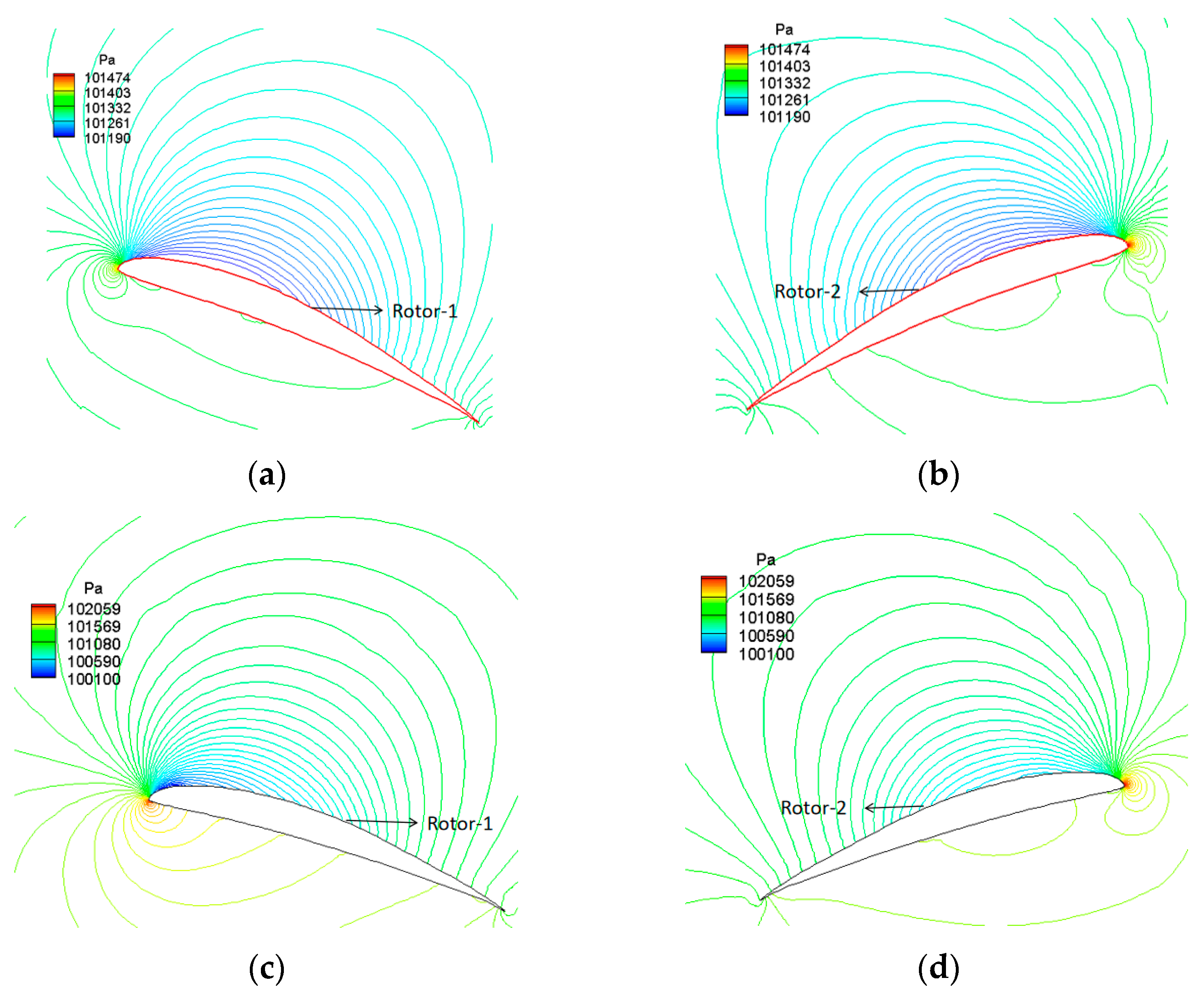
5.1. Variable Pitch Analysis
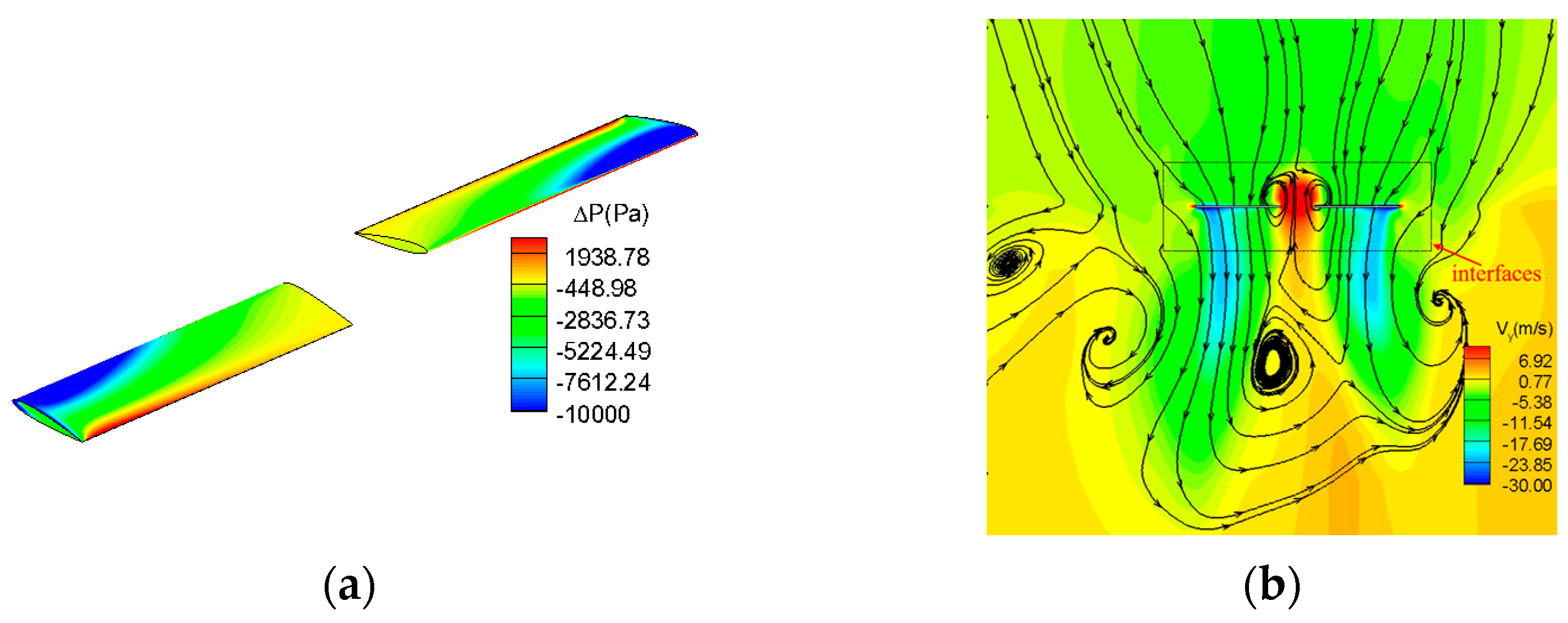
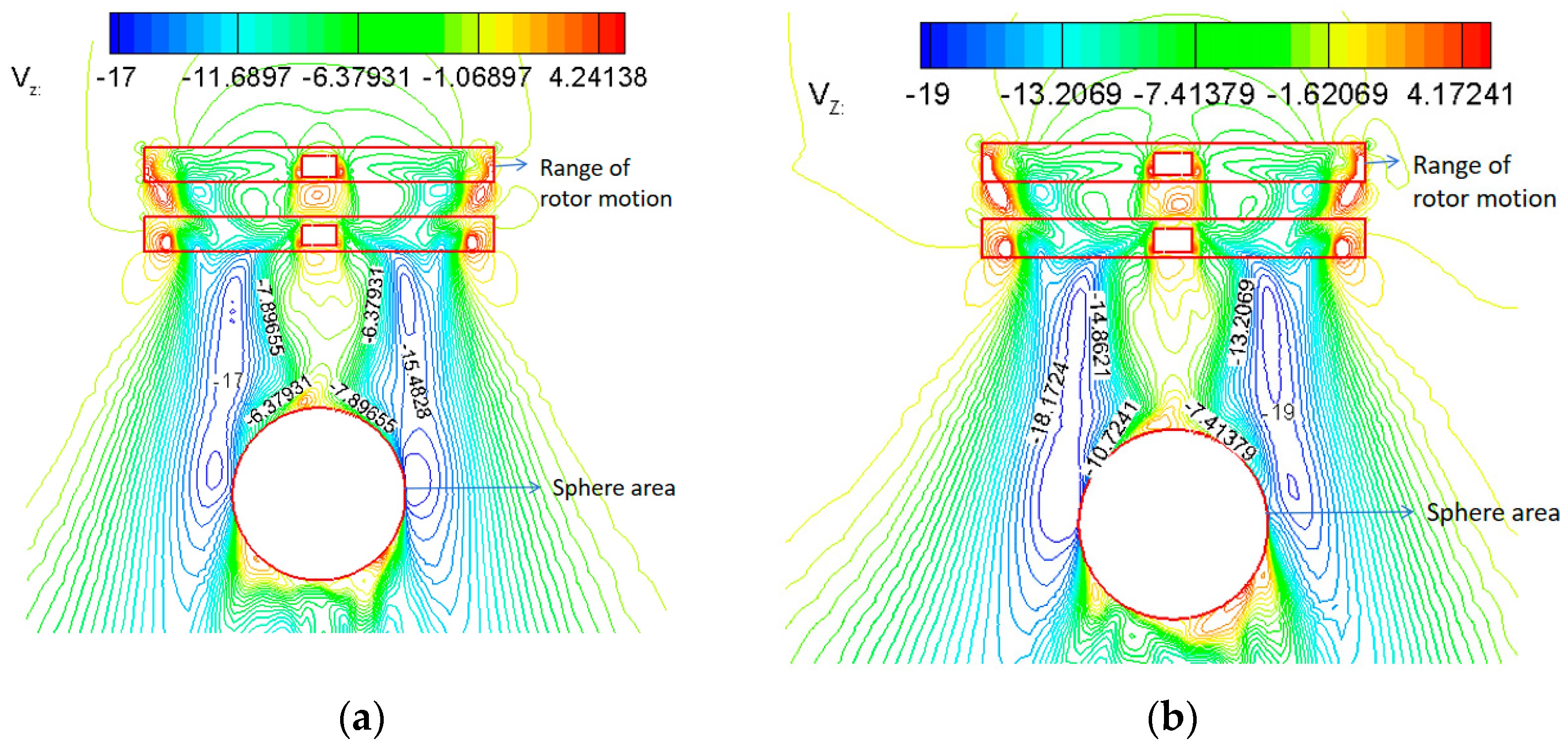
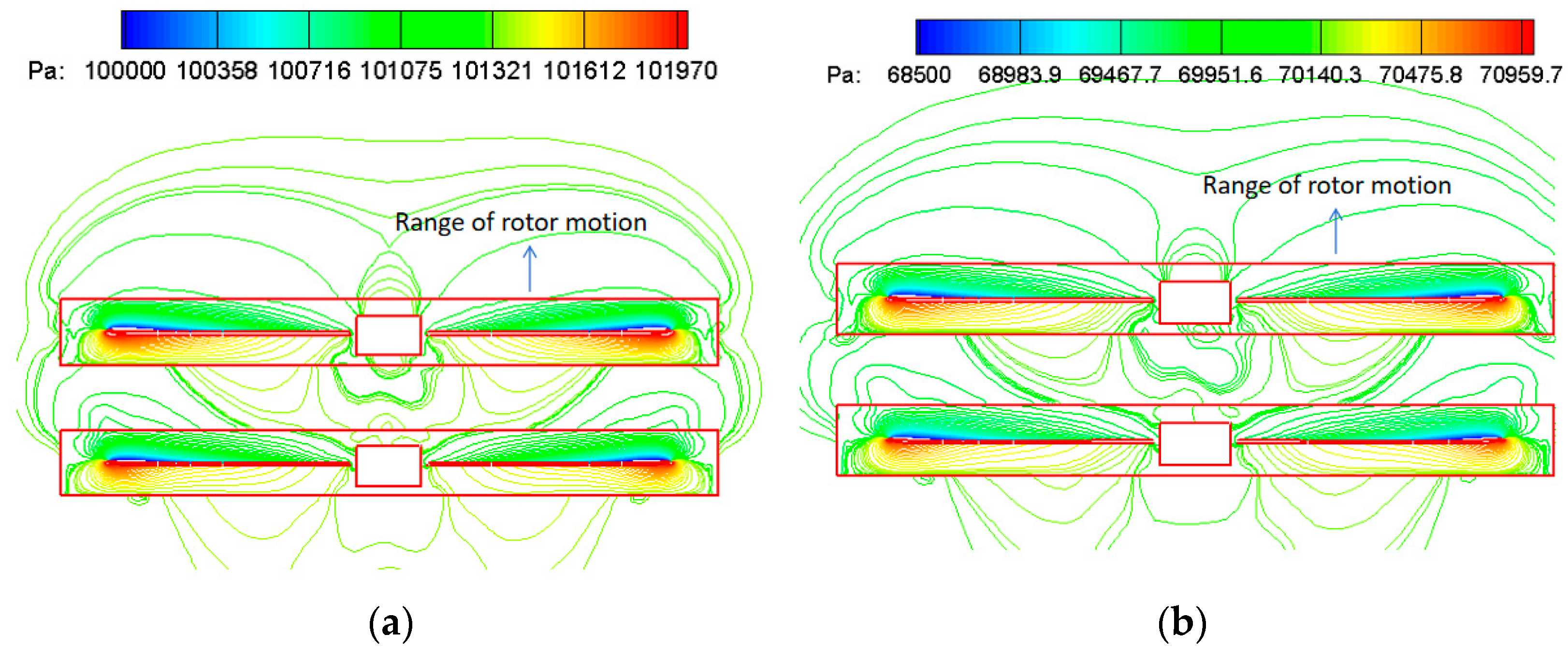
5.2. Flow Field Analysis
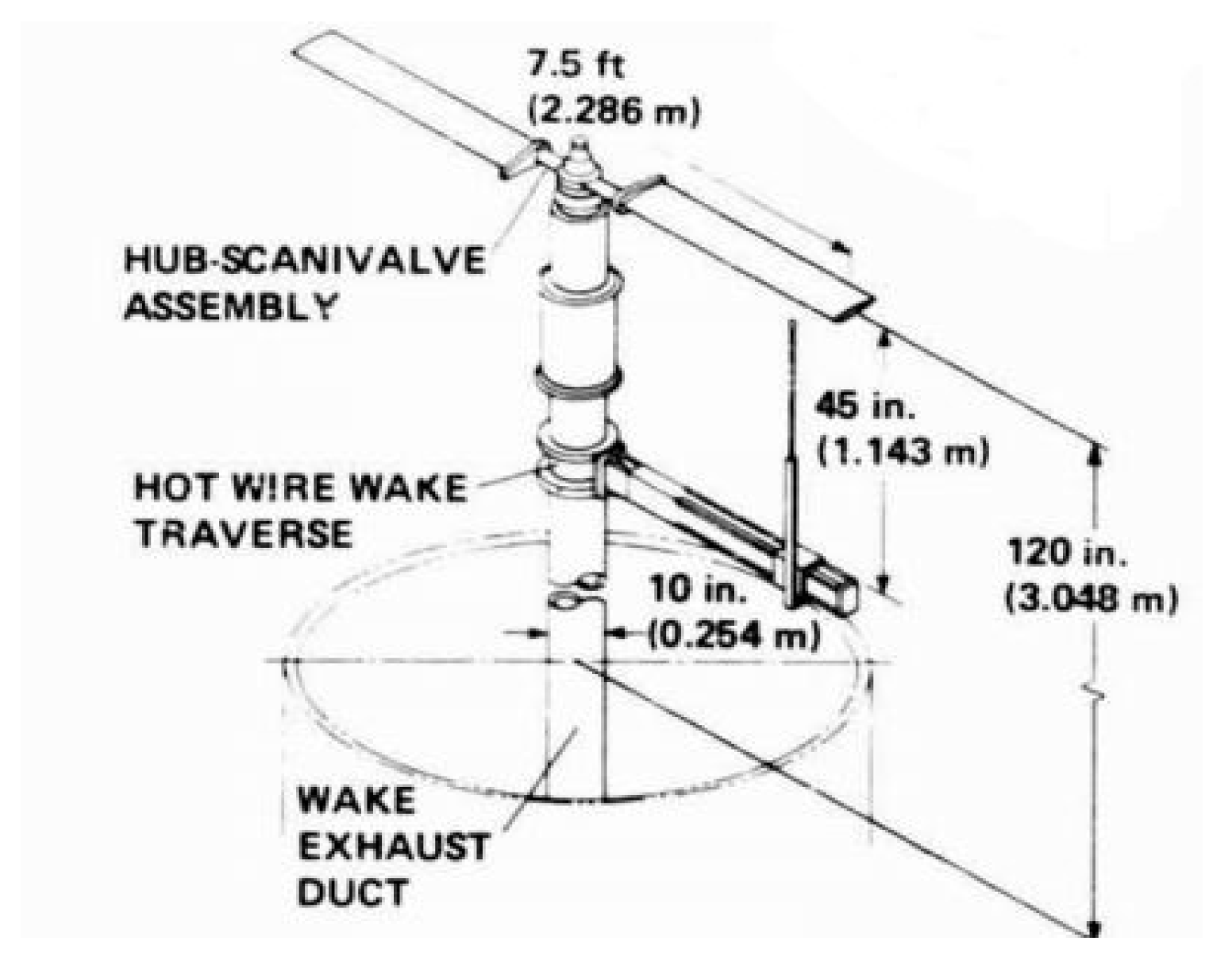
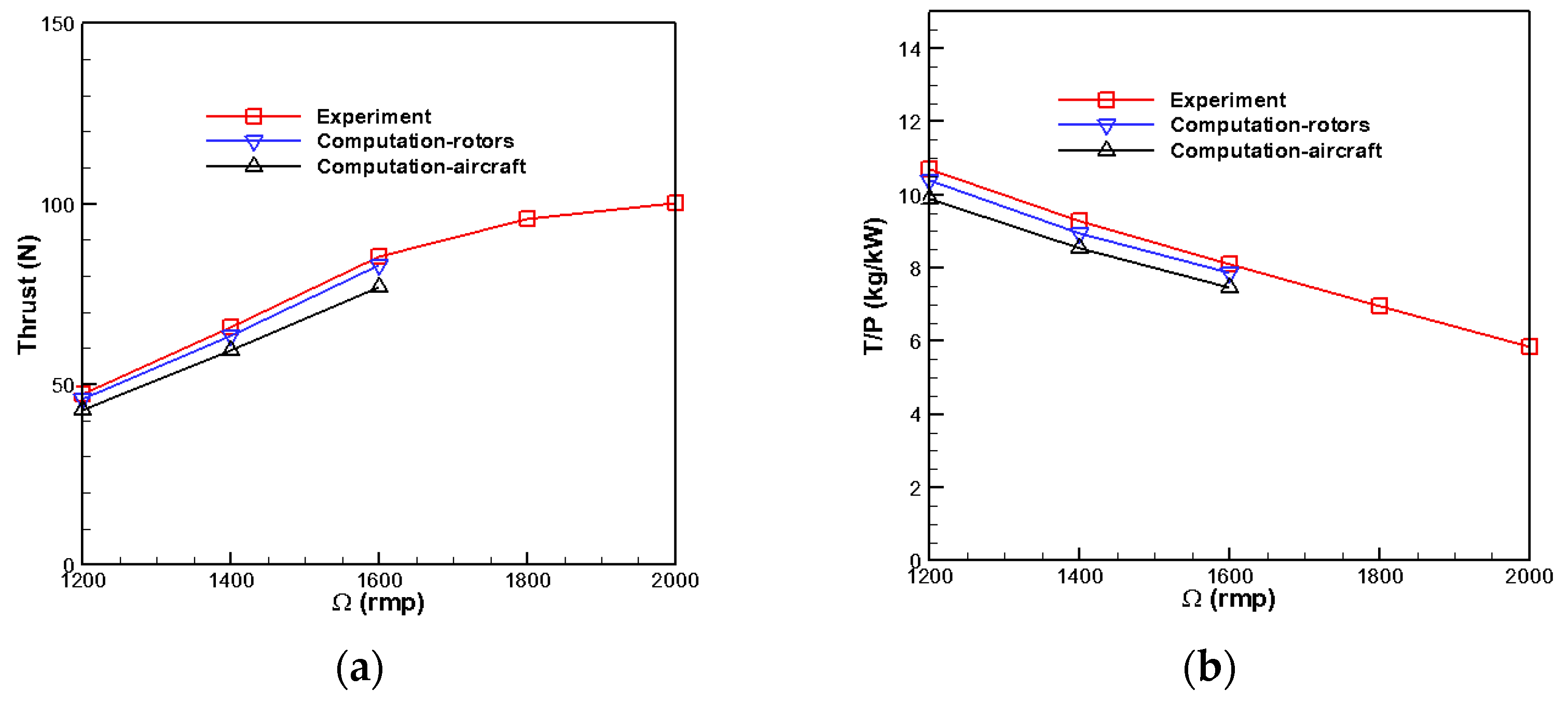
5.3. Verification Measurement
6. Conclusions
- (1)
- The bionic conceptual design is excellent. It can fully integrate Chinese parasol seed flight features and UAV flight requirements.
- (2)
- The UAV, bionically modeled as a Chinese parasol seed, has high essential aerodynamic performance. Its navigation stability and variable pitch flight capability are good. The cruise power load reaches 8.36 kg/kw, and the cruise flying thrust force is not less than 78 N at coaxial-rotor and rotor-balloon distance ratios of 0.39 and 1.12, respectively. Despite achieving a cruise power loading of 10.61 kg/kw, the cruise flying thrust force of the single rotor is only 39 N under these conditions. Therefore, the bionic simulation of the coaxial-rotor configuration is superior to the single rotor configuration.
- (3)
- The UAV has the “blocks stability phenomenon” formed by decreased rotor downwash speed and the balloon’s additional negative pressure. However, it can provide space for omnidirectional detection and reconnaissance missions.
- (4)
- The efficiency experiment and simulation of the coaxial rotors/motor can be agreed upon. The present method and the bionic configuration provide a feasible design and analysis strategy for coaxial-rotor UAVs.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Nonami, K. Prospect and Recent Research & Development for Civil Use Autonomous Unmanned Aircraft as UAV and MAV. J. Syst. Des. Dyn. 2007, 1, 120–128. [Google Scholar]
- Zhu, Z.; Zhao, Q.J.; Li, P. Unsteady flow interaction mechanism of coaxial rigid rotors in hover. Acta Aeronaut. Astronaut. Sin. 2016, 37, 568–578. [Google Scholar]
- Yoon, S.; Lee, H.C.; Pulliam, T.H. Computational study of flow interactions in coaxial rotors. In Proceedings of the AHS Technical Meeting on Aeromechanics Design for Vertical Lift, San Francisco, CA, USA, 20–22 January 2016; pp. 1–8. [Google Scholar]
- Yuan, M.; Liu, P.A.; Fan, F.; Jiang, L.; Lin, Y. Wind tunnel test investigation of coaxial rigid rotor aerodynamic interaction. J. Nanjing Univ. Aeronaut. Astronaut. 2019, 51, 257–262. [Google Scholar]
- Lakshminarayan, V.K. Computational investigation of micro-scale coaxial rotor aerodynamics in hover. J. Aircr. 2010, 47, 940–955. [Google Scholar] [CrossRef]
- Passe, B.; Sridharan, A.; Baeder, J. Computational investigation of coaxial rotor interactional aerodynamics in steady forward flight. In Proceedings of the 33rd AIAA Applied Aerodynamics Conference, Dallas, TX, USA, 22–26 June 2015; pp. 1–29. [Google Scholar]
- Lu, C.L.; Qi, H.T.; Xu, G.H. Unsteady flow field interaction of coaxial rotor. J. Aerosp. Power 2019, 34, 1459–1470. [Google Scholar]
- Ye, Z.; Shi, Y.J.; Xu, G.H. Analytical method of rotor aerodynamic characteristics by coupling a high-efficiency trim strategy. J. Aerosp. Power 2017, 32, 882–889. [Google Scholar]
- Qin, Y.H.; Zhu, Q.H.; Shao, S. Aerodynamic characteristics analysis for hovering coaxial rotors in ground effect. J. Nanjing Univ. Aeronaut. Astronaut. 2015, 47, 266–274. [Google Scholar]
- Lei, Y.; Ji, Y.X.; Wang, C.W. Numerical simulation and experimental study on aerodynamics of the micro coaxial rotors. J. Exp. Fluid Mech. 2017, 31, 67–73. [Google Scholar]
- Ramasamy, M. Hover performance measurements toward understanding aerodynamic interference in coaxial, tandem, and tilt rotors. J. Am. Helicopter Soc. 2015, 60, 1–17. [Google Scholar] [CrossRef]
- Yan, X.; Zhao, X.; Guo, H.Q.; Li, X.D.; Wang, N.H. Force measurement and CFD validation of coaxial rotor in hover. Aeronaut. Comput. Tech. 2015, 45, 65–67+71. [Google Scholar]
- Lu, T.Y.; Chen, R.L.; Ji, H.L.; Xin, J. Performance analysis of coaxial-rotor for hovering in ground effect. J. Harbin Inst. Technol. 2017, 49, 45–52. [Google Scholar]
- Ma, Y.M.; Chen, M.; Wang, Q.; Xu, G. PIV measurements of model-scale coaxial rotors flow features. J. Nanjing Univ. Aeronaut. Astronaut. 2015, 47, 220–227. [Google Scholar]
- Lei, Y.; Bai, Y.; Xu, Z.J.; Gao, Q.J.; Zhao, C.G. An experimental investigation on aerodynamic performance of a coaxial rotors system with different rotor spacing and wind speed. Exp. Therm. Fluid Sci. 2013, 44, 779–785. [Google Scholar] [CrossRef]
- Cornelius, J.; Schmitz, S. Dragonfly Rotor Optimization using Machine Learning Applied to an OVERFLOW Generated Airfoil Database. In Proceedings of the 80th Annual Vertical Flight Society Forum & Technology Display, Montreal, QC, Canada, 7–9 May 2024. [Google Scholar]
- Nave, G.K., Jr.; Hall, N.; Somers, K.; Davis, B.; Gruszewski, H.; Powers, C.; Collver, M.; Schmale, D.G., III; Ross, S.D. Wind Dispersal of Natural and Biomimetic Maple Samaras. Biomimetics 2021, 6, 23. [Google Scholar] [CrossRef] [PubMed]
- Lentink, D.; Dickson, W.B.; Van Leeuwen, J.L.; Dickinson, M.H. Leading-edge vortices elevate lift of autorotating plant seeds. Science 2009, 324, 1438–1440. [Google Scholar] [CrossRef] [PubMed]
- Azuma, A.; Yasuda, K. Flight performance of rotary seeds. J. Theor. Biol. 1989, 138, 23–53. [Google Scholar] [CrossRef]
- Greene, D.F.; Johnson, E.A. A model of wind dispersal of winged or plumed seeds. Ecology 1989, 70, 339–347. [Google Scholar] [CrossRef]
- Fauli, R.A.; Rabault, J.; Carlson, A. Effect of wing fold angles on the terminal descent velocity of double-winged autorotating seeds, fruits, and other diaspores. Phys. Rev. E 2019, 100, 013108. [Google Scholar] [CrossRef] [PubMed]
- Norberg, R.A. Autorotation, self-stability, and structure of single-winged fruits and seeds (samaras) with comparative remarks on animal flight. Biol. Rev. 1973, 48, 561–596. [Google Scholar] [CrossRef]
- Yeh, S.I.; Hsu, C.Y. The Aerodynamic Effect of Biomimetic Pigeon Feathered Wing on a 1-DoF Flapping Mechanism. Biomimetics 2024, 9, 36. [Google Scholar] [CrossRef] [PubMed]
- Russo, N.; Marano, A.D.; Gagliardi, G.M.; Guida, M.; Polito, T.; Marulo, F. Thrust and Noise Experimental Assessment on Counter-Rotating coaxial rotors. Aerospace 2023, 10, 535. [Google Scholar] [CrossRef]
- Field, S.B.; Klaus, M.; Moore, M.; Nori, F. Chaotic dynamics of falling disks. Nature 1997, 388, 252–254. [Google Scholar] [CrossRef]
- Ern, P.; Risso, F.; Fabre, D.; Magnaudet, J. Wake-induced oscillatory paths of bodies freely rising or falling in fluids. Ann. Rev. Fluid Mech. 2012, 44, 97–121. [Google Scholar] [CrossRef]
- Varshney, K.; Chang, S.; Wang, Z. The kinematics of falling maple seeds and the initial transition to a helical motion. Nonlinearity 2011, 25, C1–C8. [Google Scholar] [CrossRef]
- Yasuda, K.; Azuma, A. The autorotation boundary in the flight of samaras. J. Theor. Biol. 1997, 185, 313–320. [Google Scholar] [CrossRef]
- Bullock, J.M.; Clarke, R.T. Long distance seed dispersal by wind: Measuring and modelling the tail of the curve. Oecologia 2000, 124, 506–521. [Google Scholar] [CrossRef] [PubMed]
- Giljarhus, K.E.T.; Porcarelli, A.; Apeland, J. Investigation of Rotor Efficiency with Varying Rotor Pitch Angle for a Coaxial Drone. Drones 2022, 6, 91. [Google Scholar] [CrossRef]
- Basri, E.I.; Basri, A.A.; Ahmad, K.A. Computational Fluid Dynamics Analysis in Biomimetics Applications: A Review from Aerospace Engineering Perspective. Biomimetics 2023, 8, 319. [Google Scholar] [CrossRef] [PubMed]
- Caradonna, F.X.; Tung, C. Experimental and Analytical Studies of a Model Helicopter Rotor in Hover; NASA TM-81232; NASA: Washington, DC, USA, 1981. [Google Scholar]
- Leishman, J.G.; Shreyas, A. An optimum coaxial rotor system for axial flight. J. Am. Helicopter Soc. 2008, 53, 366–381. [Google Scholar] [CrossRef]
- Gan, W.B. General Design Report of Coaxial Rotor Unmanned System; Beihang University: Beijing, China, 2020. [Google Scholar]
- Lei, Y.; Ji, Y.; Wang, C. Optimization of aerodynamic performance for co-axial rotors with different rotor spacings. Int. J. Micro Air Veh. 2018, 10, 362–369. [Google Scholar] [CrossRef]
- Gan, W.B. The Report on the Overall Design of Coaxial-Rotors Unmanned System; Beihang University: Beijing, China, 2021. [Google Scholar]
- Lei, Y.; Ye, Y.; Wang, H.; Huang, Y. Study on Aerodynamic Characteristics of coaxial-rotors UAV with Different Rotor Spacing. Mech. Sci. Technol. Aerosp. Eng. 2022, 3, 487–492. [Google Scholar]


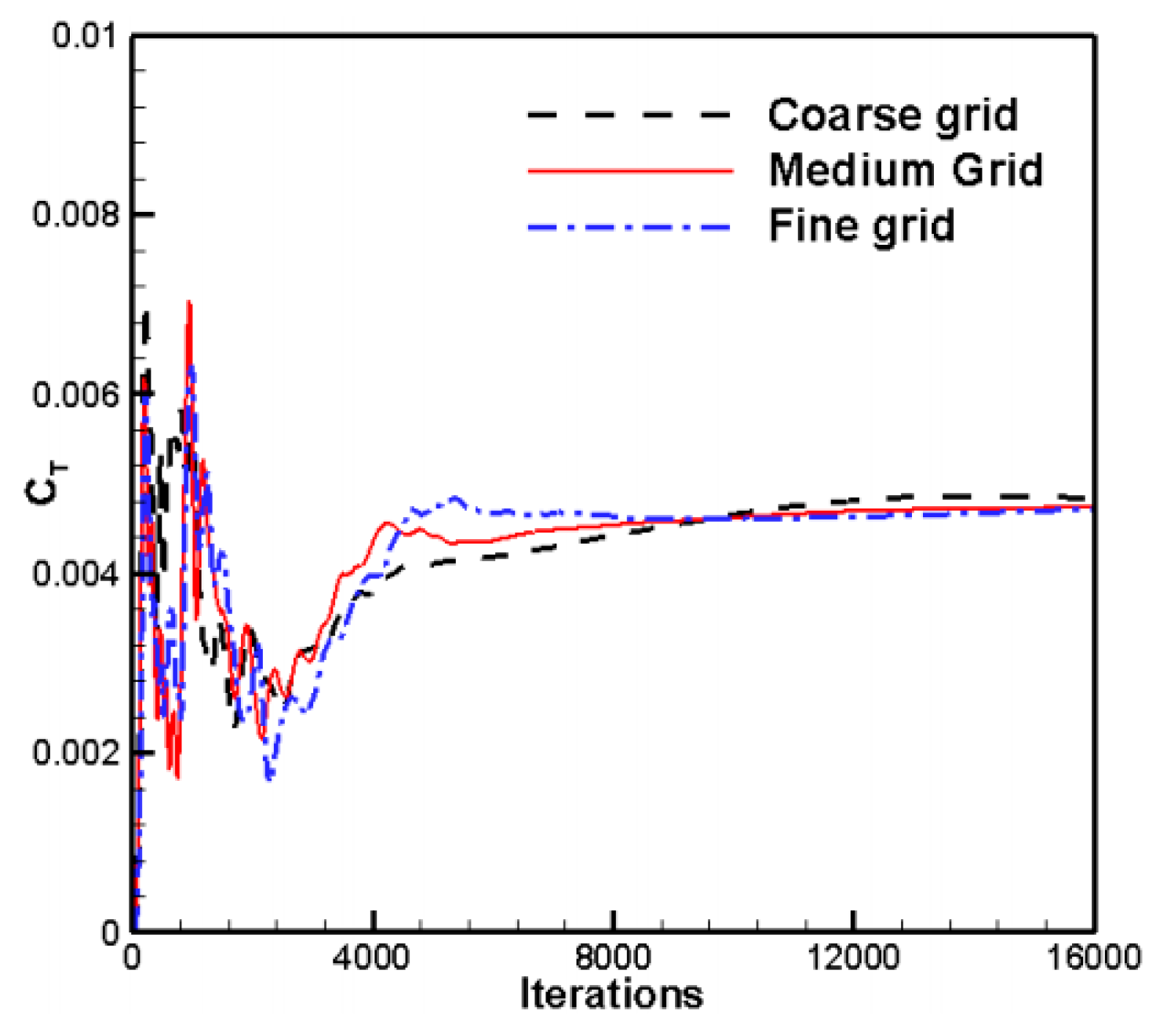
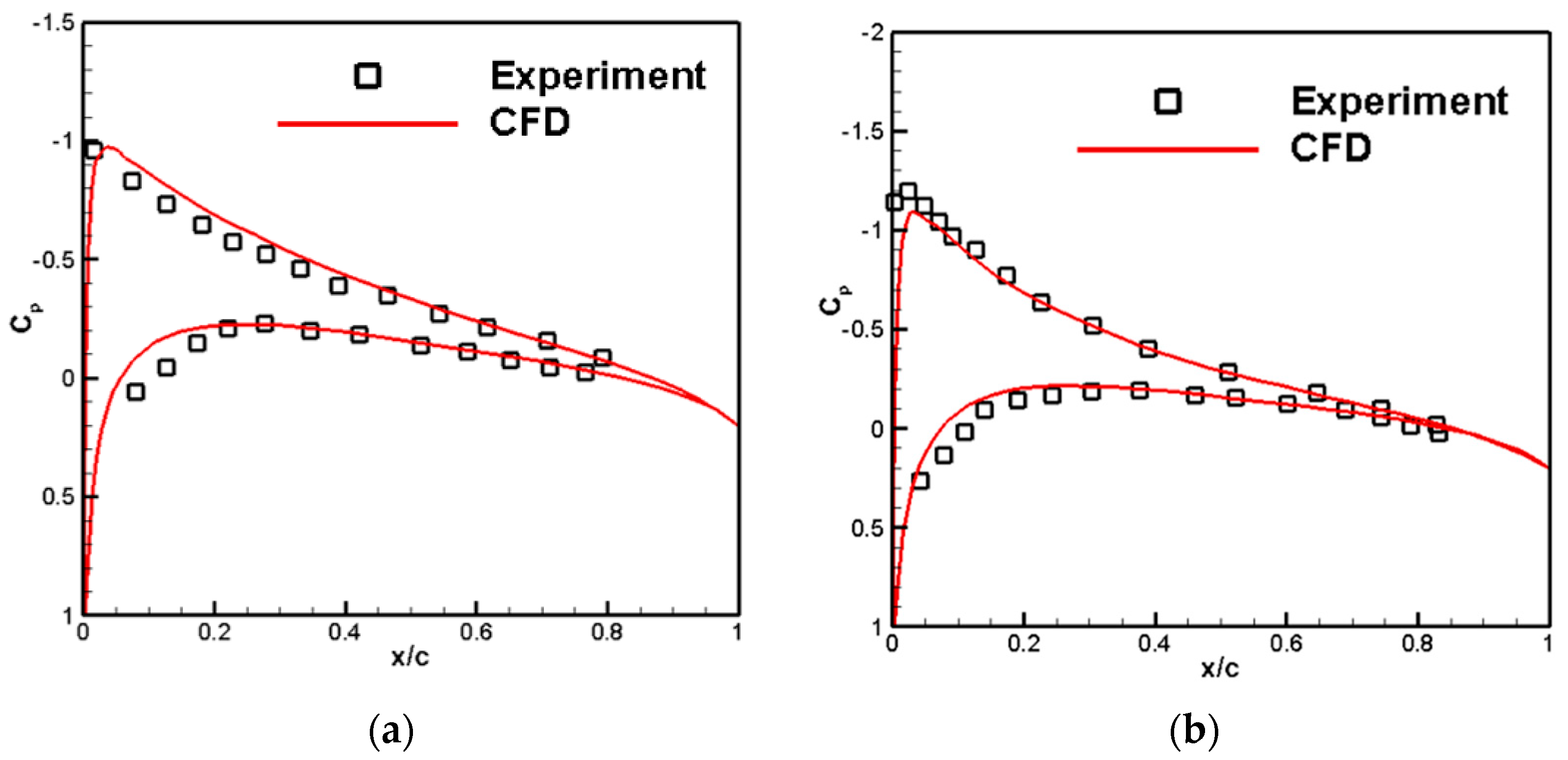



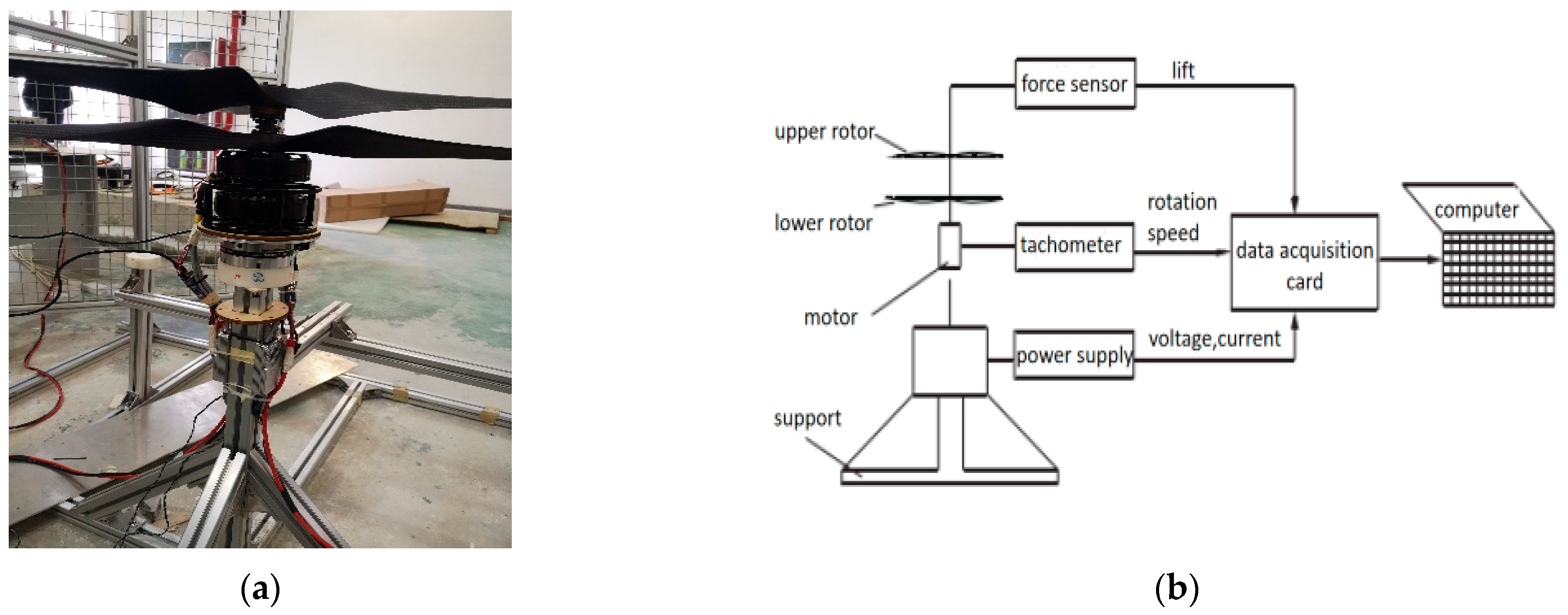

| Rotation Speed (RMP) | Experiment | CFD | ||
|---|---|---|---|---|
| Coarse | Middle | Fine | ||
| 1750 | 0.00455 | 0.004857 | 0.00474 | 0.00469 |
| 2250 | 0.00462 | 0.004998 | 0.00491 | 0.00487 |
| Height | Rotation Speed | Single Rotor Thrust | Upper Rotor Thrust | Lower Rotor Thrust | Single Rotor Efficiency | Coaxial Rotors Efficiency |
|---|---|---|---|---|---|---|
| 3 km | 1600 rpm | 39.34 N | 32.70 N | 27.49 N | 10.61 kg/kw | 8.36 kg/kw |
| Ω (RPM) | Thrust (N) | (g/W) |
|---|---|---|
| 1200 | 42.91 | 9.88 |
| 1400 | 59.32 | 8.55 |
| 1600 | 76.99 | 7.46 |
| 3505 | 172.38 | 6.71 |
| 3700 | 185.02 | 6.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gan, W.; Wang, Y.; Wang, H.; Zhuang, J. Aerodynamic Investigation on a Coaxial-Rotors Unmanned Aerial Vehicle of Bionic Chinese Parasol Seed. Biomimetics 2024, 9, 403. https://doi.org/10.3390/biomimetics9070403
Gan W, Wang Y, Wang H, Zhuang J. Aerodynamic Investigation on a Coaxial-Rotors Unmanned Aerial Vehicle of Bionic Chinese Parasol Seed. Biomimetics. 2024; 9(7):403. https://doi.org/10.3390/biomimetics9070403
Chicago/Turabian StyleGan, Wenbiao, Yunpeng Wang, Hongbo Wang, and Junjie Zhuang. 2024. "Aerodynamic Investigation on a Coaxial-Rotors Unmanned Aerial Vehicle of Bionic Chinese Parasol Seed" Biomimetics 9, no. 7: 403. https://doi.org/10.3390/biomimetics9070403
APA StyleGan, W., Wang, Y., Wang, H., & Zhuang, J. (2024). Aerodynamic Investigation on a Coaxial-Rotors Unmanned Aerial Vehicle of Bionic Chinese Parasol Seed. Biomimetics, 9(7), 403. https://doi.org/10.3390/biomimetics9070403






