Laser Ablating Biomimetic Periodic Array Fish Scale Surface for Drag Reduction
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
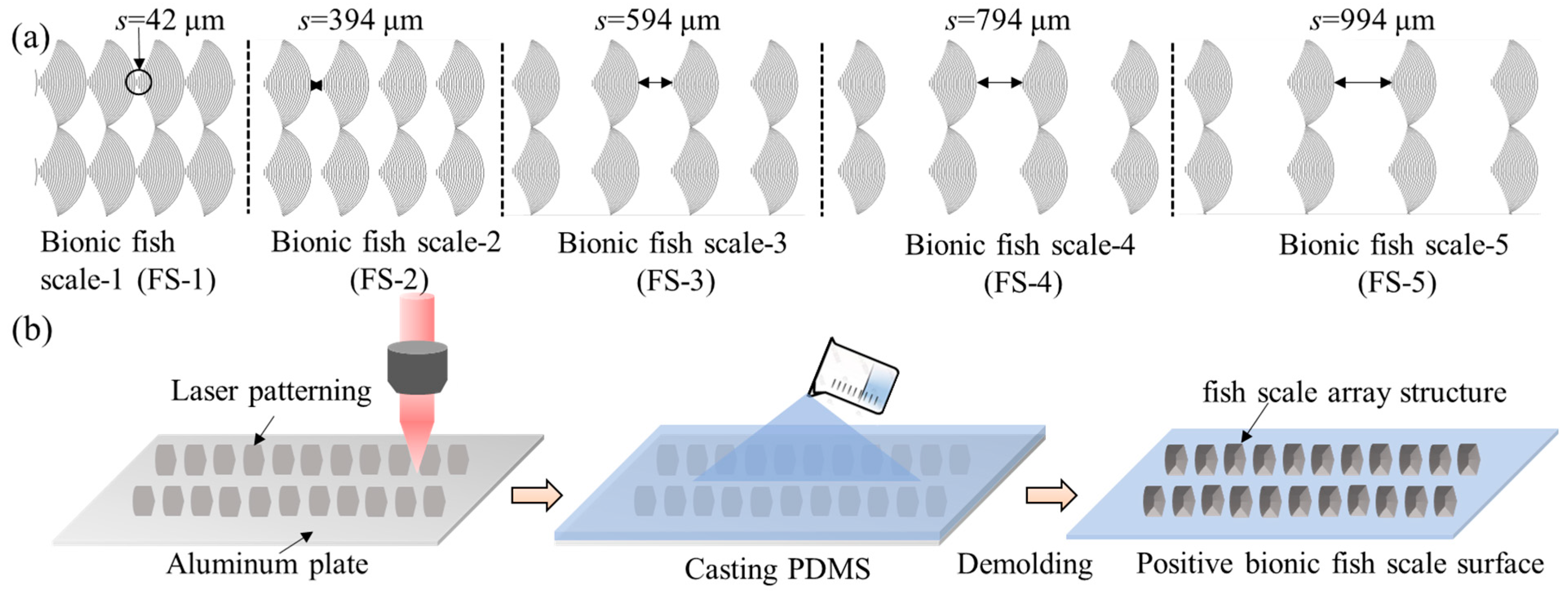
2.2. Biomimetic Prototype and Model Extraction
2.3. Sample Preparation
2.4. Sample Characterization
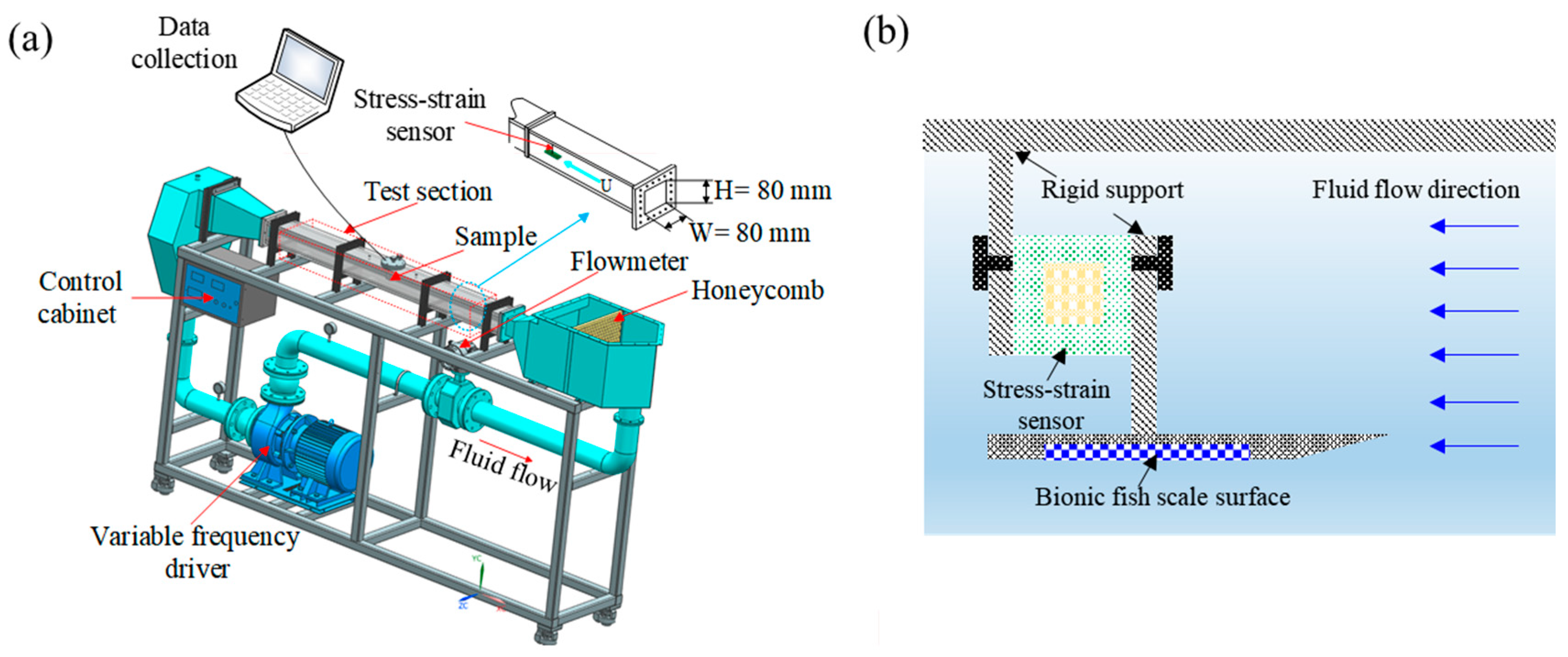
2.5. Drag Measurement
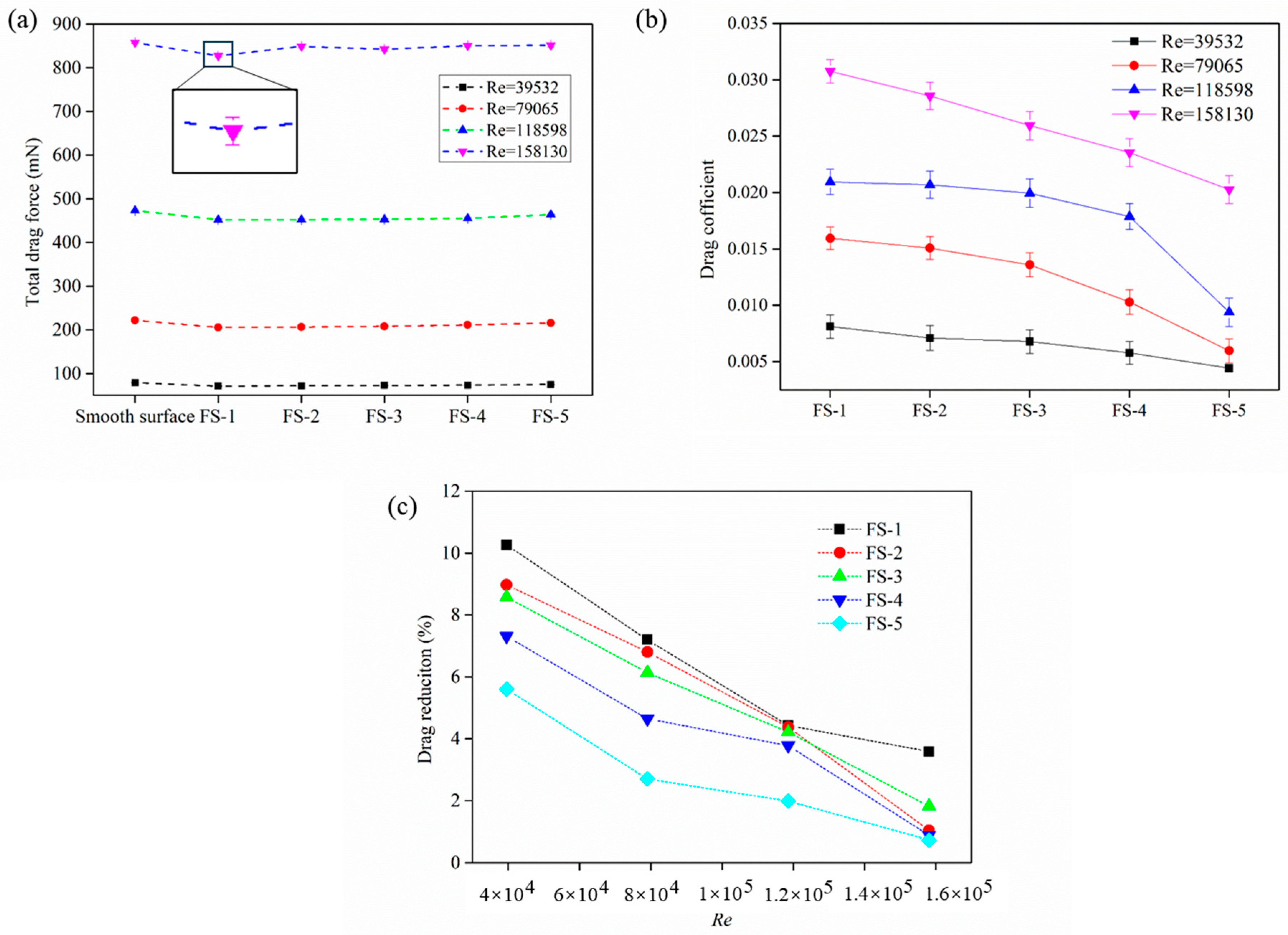
3. Drag Reduction
4. Mechanism
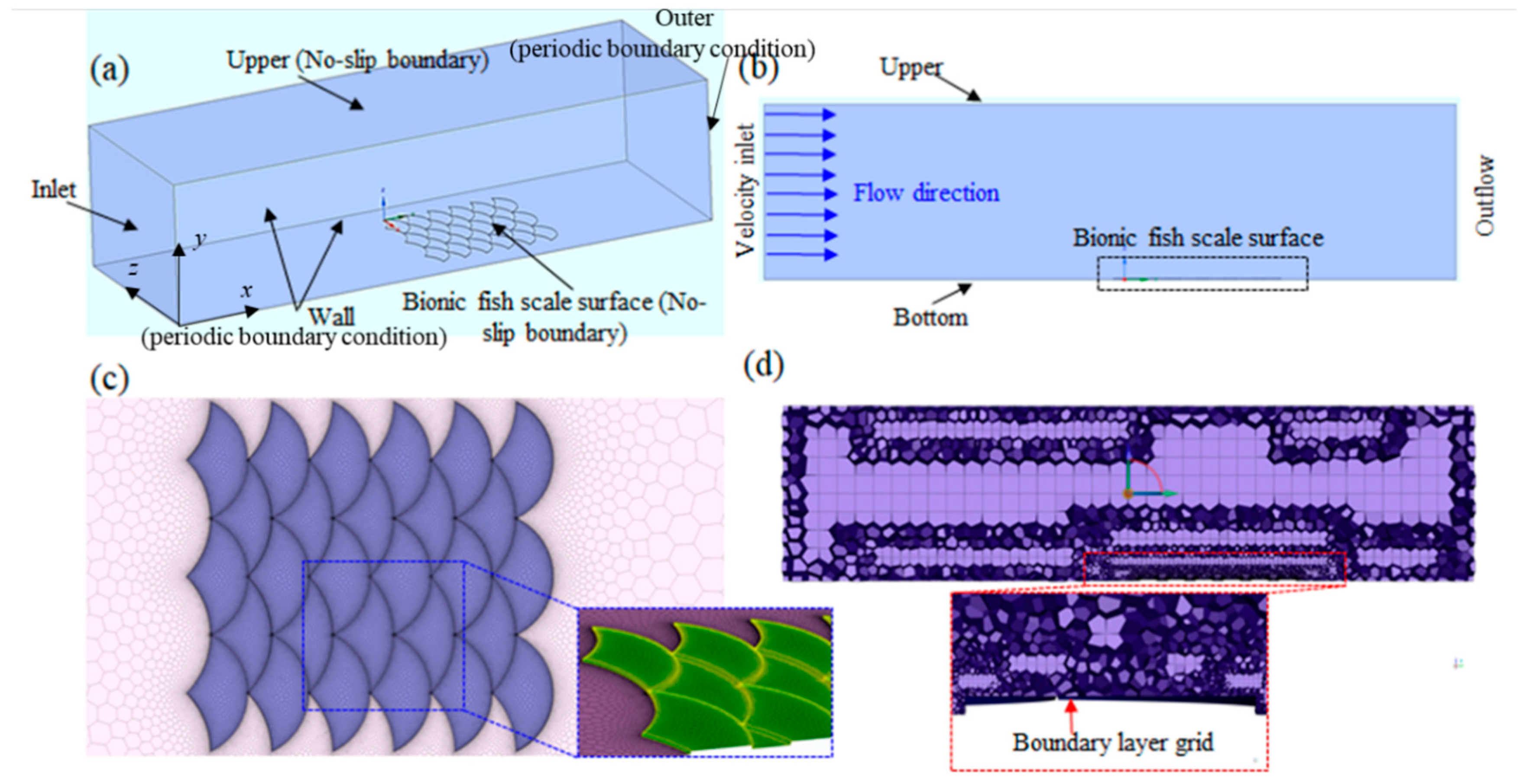
4.1. Simulation Model
4.2. Flow Characteristics
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, T.; Chen, W.; Zhao, A.; He, P.; Chen, H. A comprehensive investigation on micro-structured surfaces for underwater drag reduction. Ocean Eng. 2020, 218, 107902. [Google Scholar] [CrossRef]
- Ricco, P.; Skote, M.; Leschziner, M.A. A review of turbulent skin-friction drag reduction by near-wall transverse forcing. Prog. Aerosp. Sci. 2021, 123, 100713. [Google Scholar] [CrossRef]
- Liu, G.; Yuan, Z.; Qiu, Z.; Feng, S.; Xie, Y.; Leng, D.; Tian, X. A brief review of bio-inspired surface technology and application toward underwater drag reduction. Ocean Eng. 2020, 199, 106962. [Google Scholar] [CrossRef]
- Chen, D.; Liu, X.; Cui, X.; Zhang, L.; Chen, H. Research progress and development trend of the drag reduction inspired by fish skin. Prog. Org. Coat. 2023, 182, 107613. [Google Scholar] [CrossRef]
- Zhang, L.; Shan, X.; Xie, T. Active control for wall drag reduction: Methods, mechanisms and performance. IEEE Access 2020, 8, 7039–7057. [Google Scholar] [CrossRef]
- Perlin, M.; Dowling, D.R.; Ceccio, S.L. Freeman scholar review: Passive and active skin-friction drag reduction in turbulent boundary layers. J. Fluids Eng.-Trans. ASME 2016, 138, 091104. [Google Scholar] [CrossRef]
- Fish, F.E.; Lauder, G.V. Passive and active flow control by swimming fishes and mammals. Annu. Rev. Fluid Mech. 2006, 38, 193–224. [Google Scholar] [CrossRef]
- Tong, J.; Wu, B.; Song, Z.; Gao, Z.; Sun, J.; Ma, Y.; Zhuang, J. Research on the drag reduction mechanism of antlion (Myrmeleon sagax) larvae nonsmooth structural surface. Microsc. Res. Technol. 2019, 83, 338–344. [Google Scholar] [CrossRef] [PubMed]
- Drelich, A.J.; Monteiro, S.N.; Brookins, J.; Drelich, J.W. Fish Skin: A Natural Inspiration for Innovation. Adv. Biosyst. 2018, 2, 1800055. [Google Scholar] [CrossRef]
- Funk, N.; Vera, M.; Szewciw, L.J.; Barthelat, F.; Stoykovich, M.P.; Vernerey, F.J. Bioinspired Fabrication and Characterization of a Synthetic Fish Skin for the Protection of Soft Materials. Acs Appl. Mater. Interfaces 2015, 7, 5972–5983. [Google Scholar] [CrossRef]
- Yang, W.; Chen, I.H.; Gludovatz, B.; Zimmermann, E.A.; Ritchie, R.O.; Meyers, M.A. Natural Flexible Dermal Armor. Adv. Mater. 2013, 25, 31–48. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Sherman, V.R.; Gludovatz, B.; Mackey, M.; Zimmermann, E.A.; Chang, E.H.; Schaible, E.; Qin, Z.; Buehler, M.J.; Ritchie, R.O.; et al. Protective role of Arapaima gigas fish scales: Structure and mechanical behavior. Acta Biomater. 2014, 10, 3599–3614. [Google Scholar] [CrossRef]
- Sun, Z.; Liao, T.; Li, W.; Dou, Y.; Liu, K.; Jiang, L.; Kim, S.-W.; Kim, J.H.; Dou, S.X. Fish-scale bio-inspired multifunctional ZnO nanostructures. NPG Asia Mater. 2015, 7, e232. [Google Scholar] [CrossRef]
- Lauder, G.V.; Wainwright, D.K.; Domel, A.G.; Weaver, J.C.; Wen, L.; Bertoldi, K. Structure, biomimetics, and fluid dynamics of fish skin surfaces. Phys. Rev. Fluids 2016, 1, 060502. [Google Scholar] [CrossRef]
- Wen, L.; Weaver, J.C.; Lauder, G.V. Biomimetic shark skin: Design, fabrication and hydrodynamic function. J. Exp. Biol. 2014, 217, 1656–1666. [Google Scholar] [CrossRef] [PubMed]
- Muthuramalingam, M.; Villemin, L.S.; Bruecker, C. Streak formation in flow over biomimetic fish scale arrays. J. Exp. Biol. 2019, 222, jeb205963. [Google Scholar] [CrossRef] [PubMed]
- Muthuramalingam, M.; Puckert, D.K.; Rist, U.; Bruecker, C. Transition delay using biomimetic fish scale arrays. Sci. Rep. 2020, 10, 14534. [Google Scholar] [CrossRef]
- Zhu, D.; Zhang, C.; Liu, P.; Jawad, L.A. Comparison of the Morphology, Structures and Mechanical Properties of Teleost Fish Scales Collected from New Zealand. J. Biomim. Eng. 2019, 16, 328–336. [Google Scholar] [CrossRef]
- Vernerey, F.J.; Barthelat, F. Skin and scales of teleost fish: Simple structure but high performance and multiple functions. J. Mech. Phys. Solids 2014, 68, 66–76. [Google Scholar] [CrossRef]
- Wu, L.; Jiao, Z.; Song, Y.; Ren, W.; Niu, S.; Han, Z. Water-trapping and drag-reduction effects of fish Ctenopharyngodon idellus scales and their simulations. Sci. China-Technol. Sci. 2017, 60, 1111–1117. [Google Scholar] [CrossRef]
- Dou, Z.; Wang, J.; Chen, D. Biomimetic research on fish scales for drag reduction. J. Biomim. Eng. 2012, 9, 457–464. [Google Scholar]
- Wang, Y.; Zhang, Z.; Xu, J.; Yu, H. One-step method using laser for large-scale preparation of biomimetic superhydrophobic & drag-reducing fish-scale surface. Surf. Coat. Technol. 2021, 409, 126801. [Google Scholar]
- Rong, W.; Zhang, H.; Mao, Z.; Chen, L.; Liu, X. Stable drag reduction of anisotropic superhydrophobic/hydrophilic surfaces containing bioinspired micro/nanostructured arrays by laser ablation. Colloids Surf. A Physicochem. Eng. Asp. 2021, 622, 126712. [Google Scholar] [CrossRef]
- Rong, W.; Zhang, H.; Zhang, T.; Mao, Z.; Liu, X.; Song, K. Drag Reduction Using Lubricant-Impregnated Anisotropic Slippery Surfaces Inspired by Biomimetic Fish Scale Surfaces Containing Micro-/Nanostructured Arrays. Adv. Eng. Mater. 2021, 23, 2000821. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, L.; Wang, R.; Liu, J.; Lin, Z.; Li, G.; Liu, H.; Lei, Y.; Xiong, Y.; Zhao, Y.; et al. Fish Skin-Inspired Janus Hydrogel Coating for Drag Reduction. Chin. J. Chem. 2024, 42, 867–872. [Google Scholar] [CrossRef]
- Chen, D.; Cui, X.; Liu, X.; Chen, H. Biomimetic gradient flexible fish skin acts as a passive dynamic micro-roughness to drag reduction. Surf. Coat. Technol. 2023, 457, 12933. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, C.; Cai, Y.; Luo, X.; Wang, B.; Song, Q.; Liu, Z. Periodically oriented superhydrophobic microstructures prepared by laser ablation-chemical etching process for drag reduction. Appl. Surf. Sci. 2023, 615, 15640. [Google Scholar] [CrossRef]
- Gleiss, A.C.; Schallert, R.J.; Dale, J.J.; Wilson, S.G.; Block, B.A. Direct measurement of swimming and diving kinematics of giant Atlantic bluefin tuna (Thunnus thynnus). R. Soc. Open Sci. 2019, 6, 190203. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Liu, B.; Yan, X. Drag Reduction Properties of Polyurethane-Poly (acrylate) Hybrid Emulsions. Polym. Mater. Sci. Eng. 2017, 33, 59–64. [Google Scholar]
- Wang, Y.; Sun, Z.; Ju, S.; Guo, D.; Yin, B.; Pan, B.; Nan, K.; Yang, G. Drag reduction using riblets downstream of a high Reynolds number inclined forward step flow. Phys. Fluids 2024, 35, 125151. [Google Scholar] [CrossRef]
- İlter, Y.K.; Çetinkaya, A.; Ünal, U.O. Large eddy simulations of the turbulent channel flow over dimpled surfaces. J. Turbul. 2023, 24, 3. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, Y.; Zhang, L.W. Effective Underwater Drag Reduction: A Butterfly Wing Scale-Inspired Superhydrophobic Surface. ACS Appl. Mater. Interfaces 2024, 16, 26954–26964. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Zhu, D.; Feng, X.; Chen, B.; Tian, G.; Wei, K.; Song, Z. Numerical investigation into turbulent drag reduction via the application of pufferfish spine-inspired cone microstructures in Suboff models. Phys. Scr. 2024, 99, 5. [Google Scholar] [CrossRef]
- Inasawa, A.; Taniguchi, R.; Asai, M.; Sasamori, M.; Kurita, M. Experimental investigation of yaw-angle effects on drag reduction rate for trapezoidal riblets. Exp. Fluids 2024, 65, 3. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Zhang, B.; Zhang, H.; Shangguan, Z.; Sun, C.; Cui, X.; Liu, X.; Zhao, Z.; Liu, G.; Chen, H. Laser Ablating Biomimetic Periodic Array Fish Scale Surface for Drag Reduction. Biomimetics 2024, 9, 415. https://doi.org/10.3390/biomimetics9070415
Chen D, Zhang B, Zhang H, Shangguan Z, Sun C, Cui X, Liu X, Zhao Z, Liu G, Chen H. Laser Ablating Biomimetic Periodic Array Fish Scale Surface for Drag Reduction. Biomimetics. 2024; 9(7):415. https://doi.org/10.3390/biomimetics9070415
Chicago/Turabian StyleChen, Dengke, Bowen Zhang, Haifeng Zhang, Zheng Shangguan, Chenggang Sun, Xianxian Cui, Xiaolin Liu, Zehui Zhao, Guang Liu, and Huawei Chen. 2024. "Laser Ablating Biomimetic Periodic Array Fish Scale Surface for Drag Reduction" Biomimetics 9, no. 7: 415. https://doi.org/10.3390/biomimetics9070415
APA StyleChen, D., Zhang, B., Zhang, H., Shangguan, Z., Sun, C., Cui, X., Liu, X., Zhao, Z., Liu, G., & Chen, H. (2024). Laser Ablating Biomimetic Periodic Array Fish Scale Surface for Drag Reduction. Biomimetics, 9(7), 415. https://doi.org/10.3390/biomimetics9070415







