Numerical Study on the Hydrodynamic Performance of a Flexible Caudal Fin with Different Trailing-Edge Shapes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Geometric Model
2.2. Governing Equations
2.3. Numerical Setup
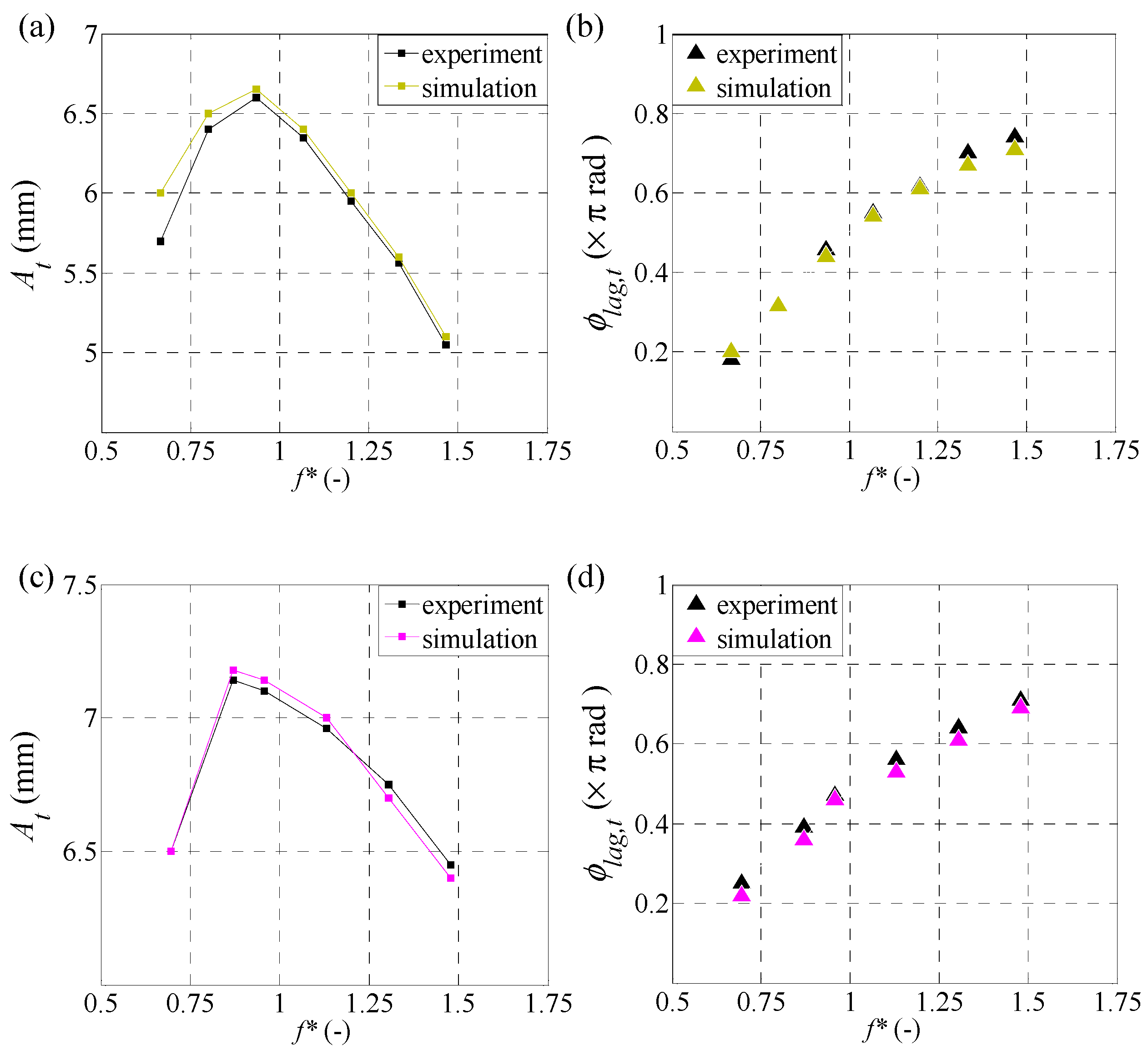
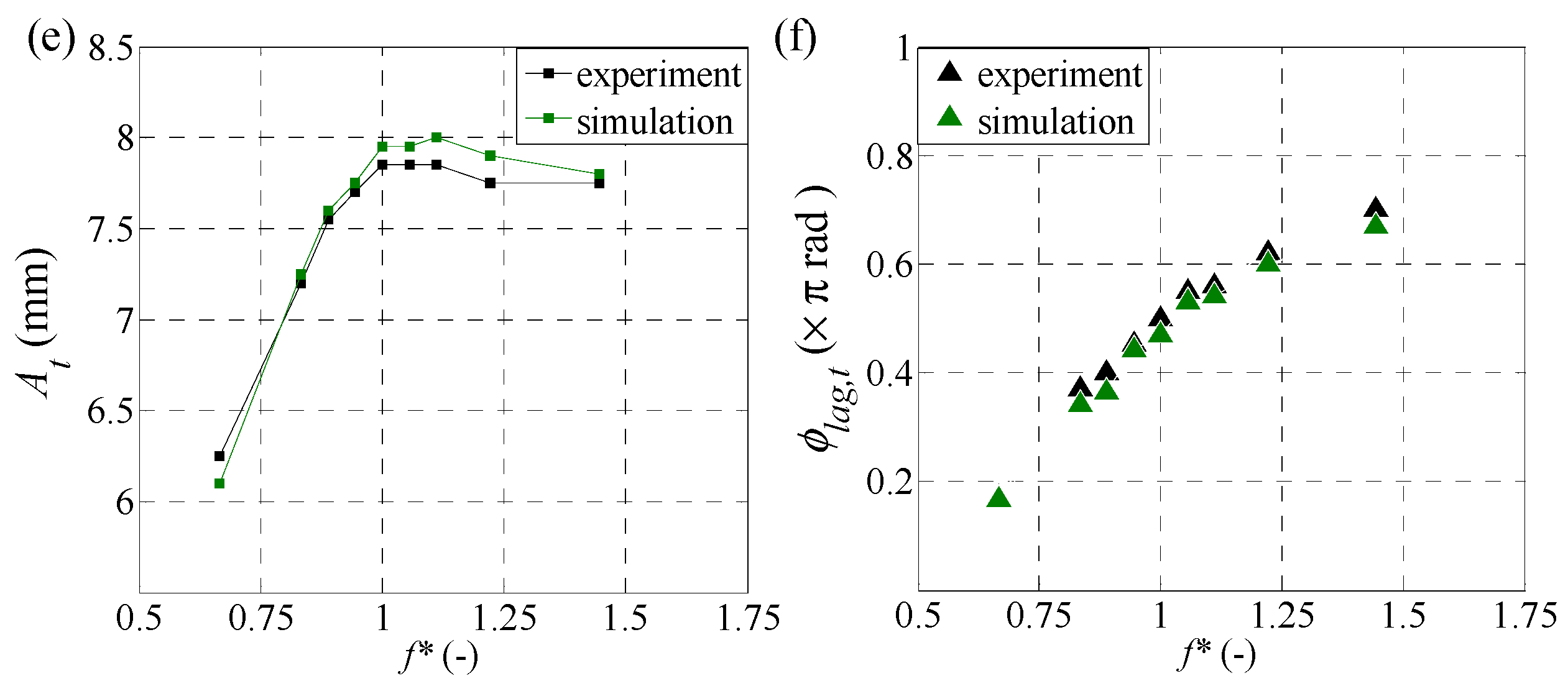
2.4. Validation and Grid Independence Study
3. Results and Discussion
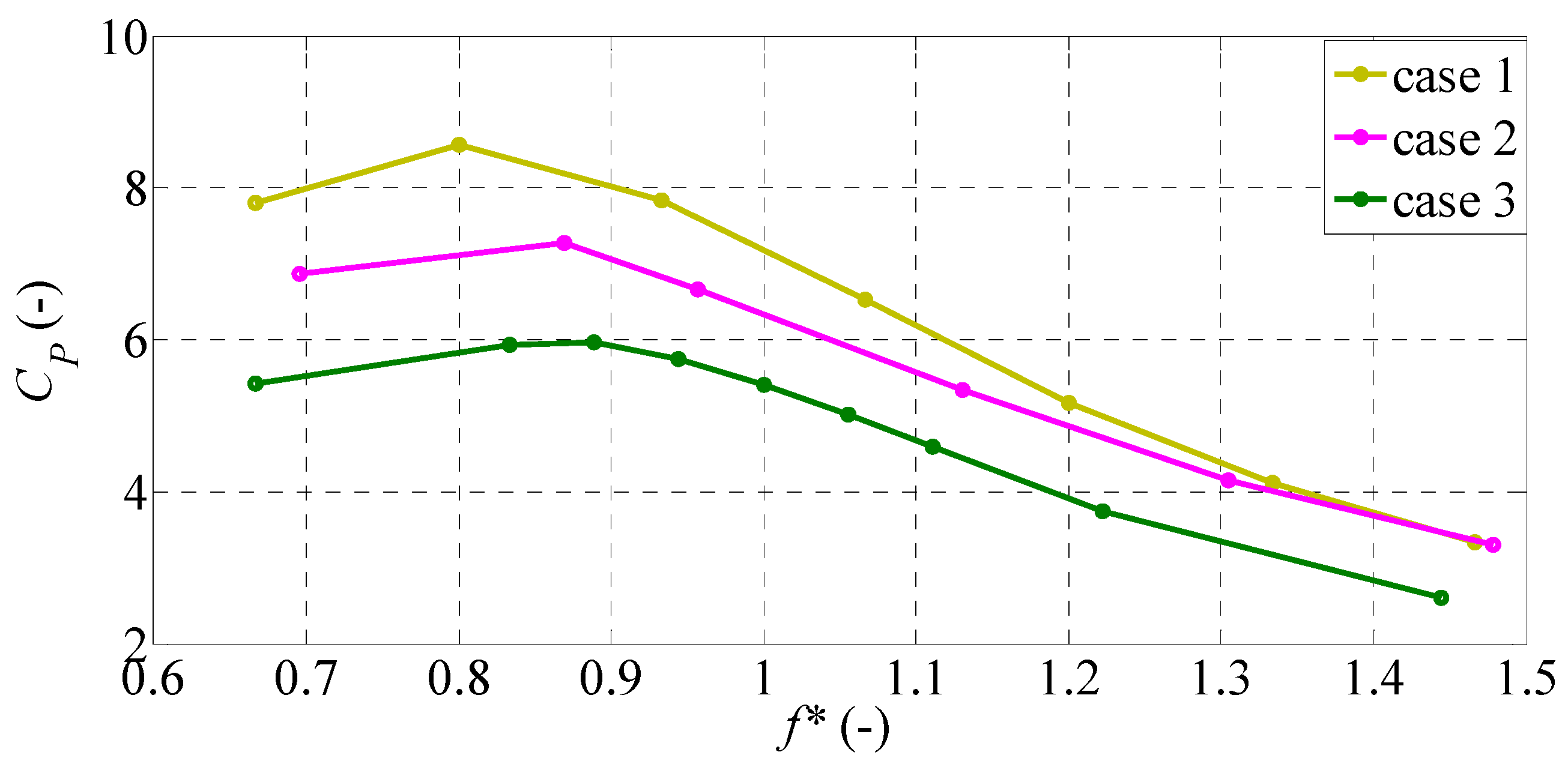
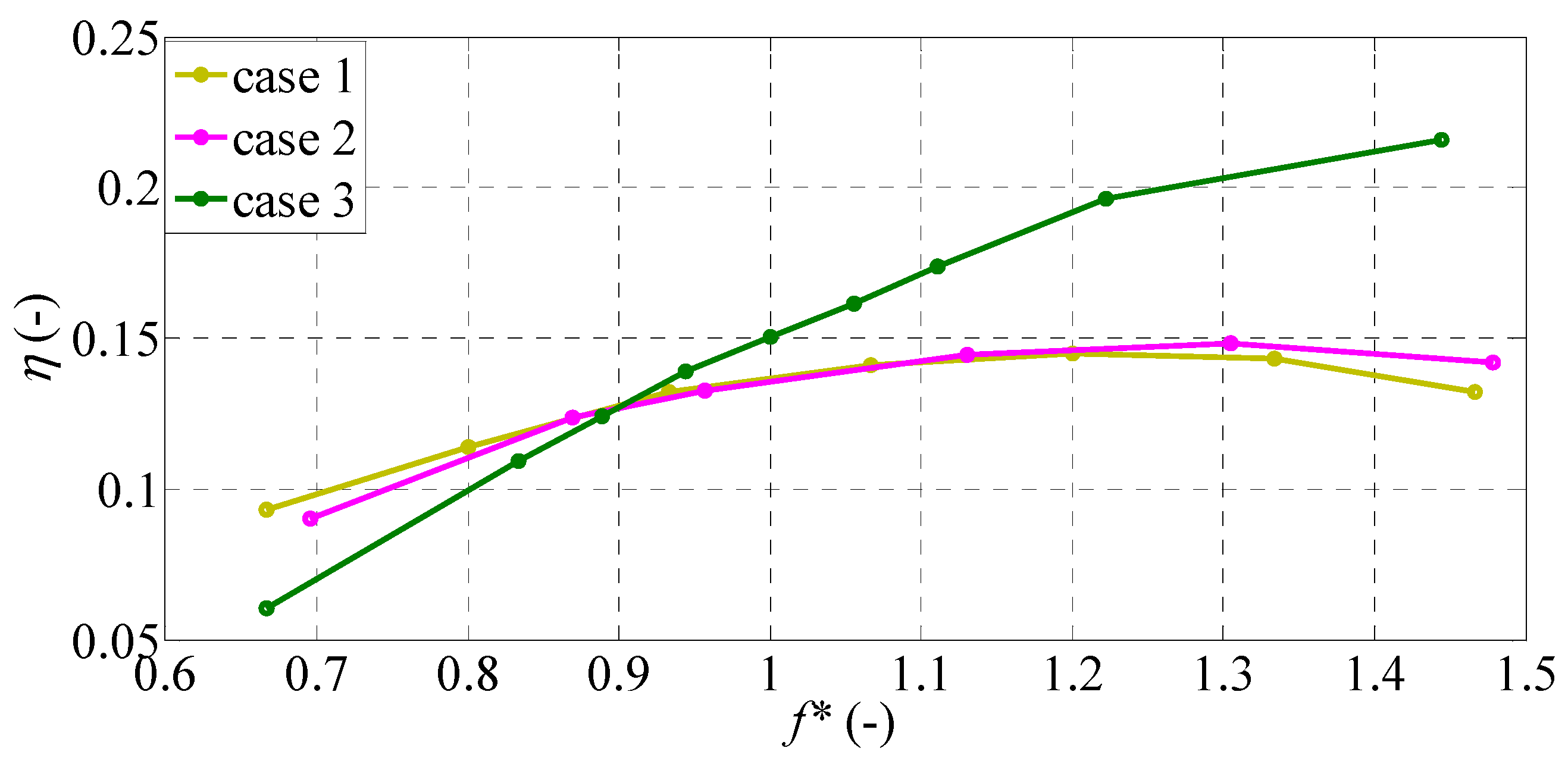
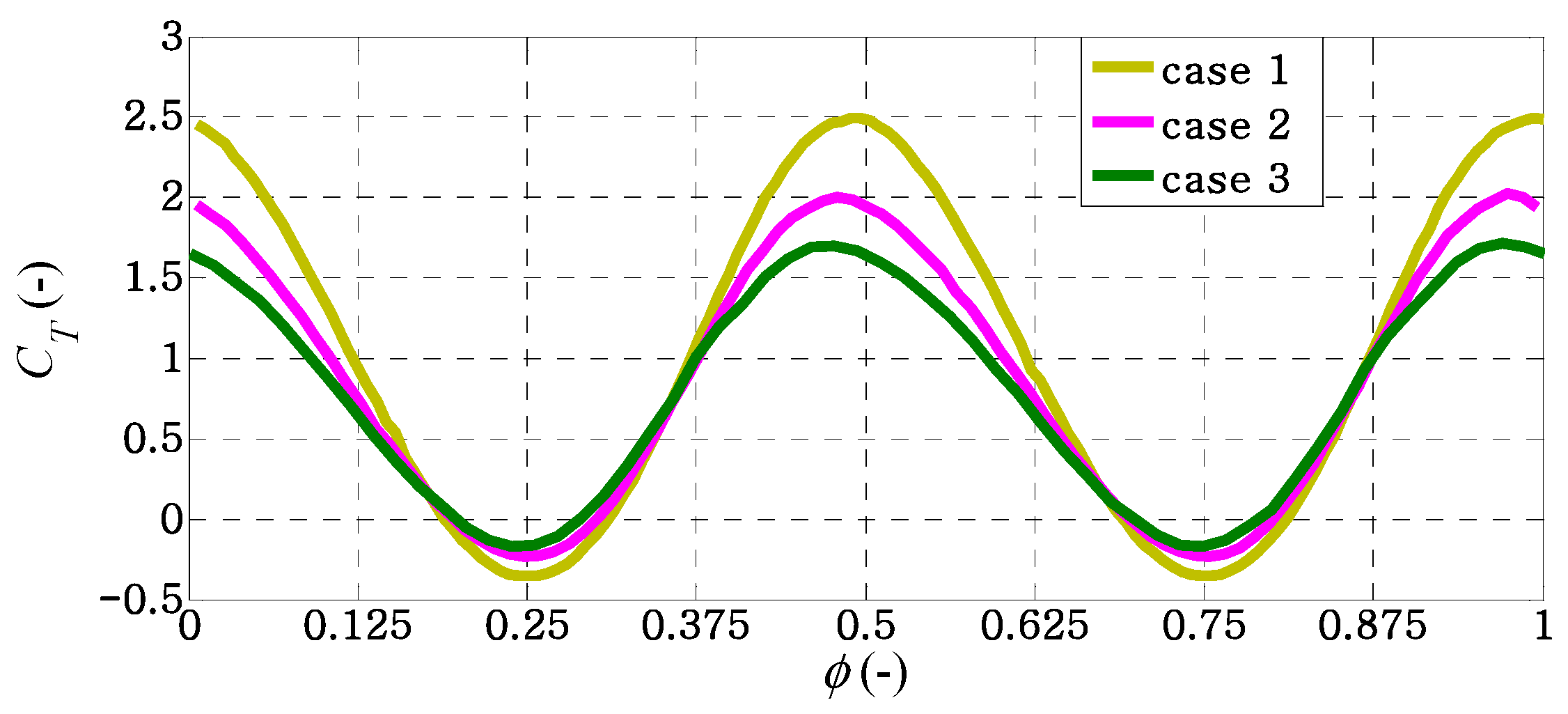
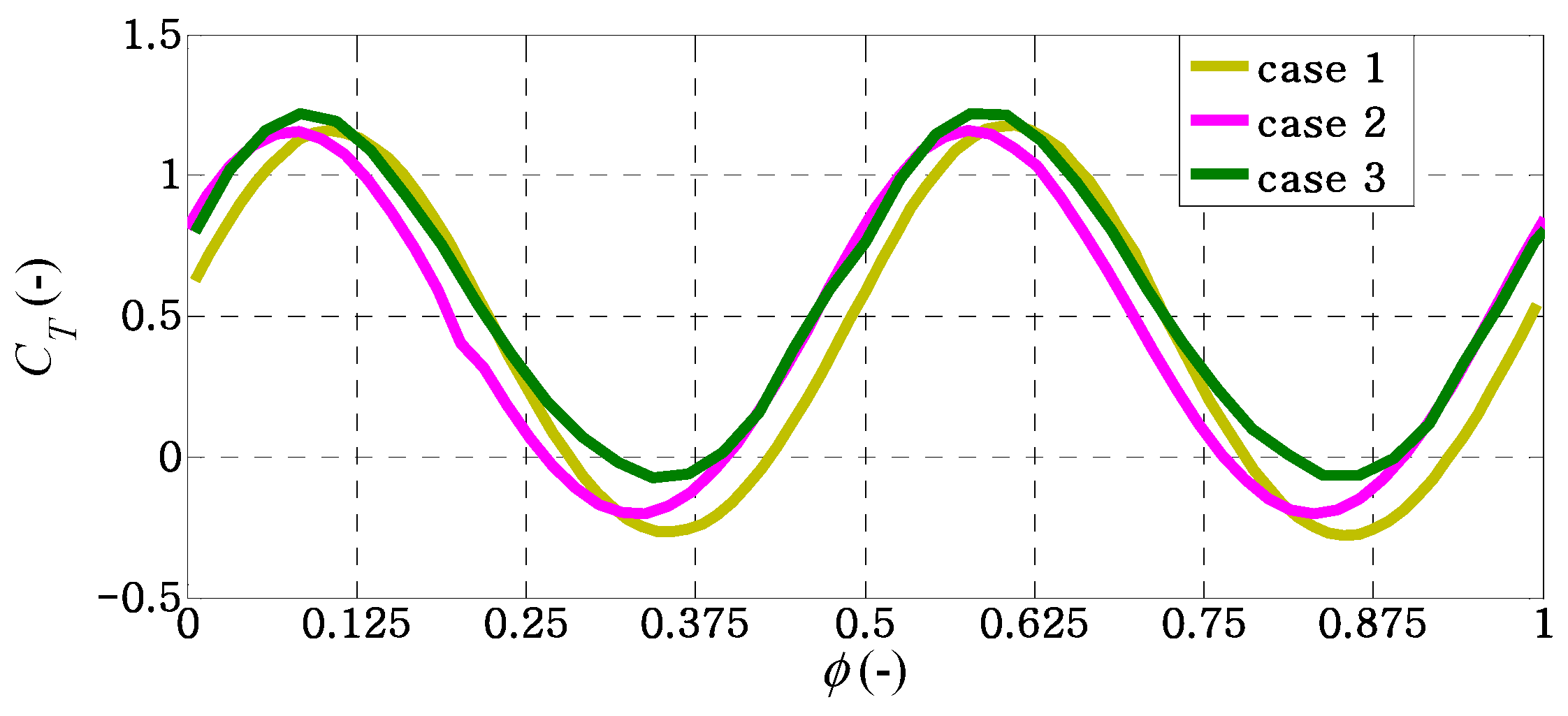
3.1. Hydrodynamic Performance
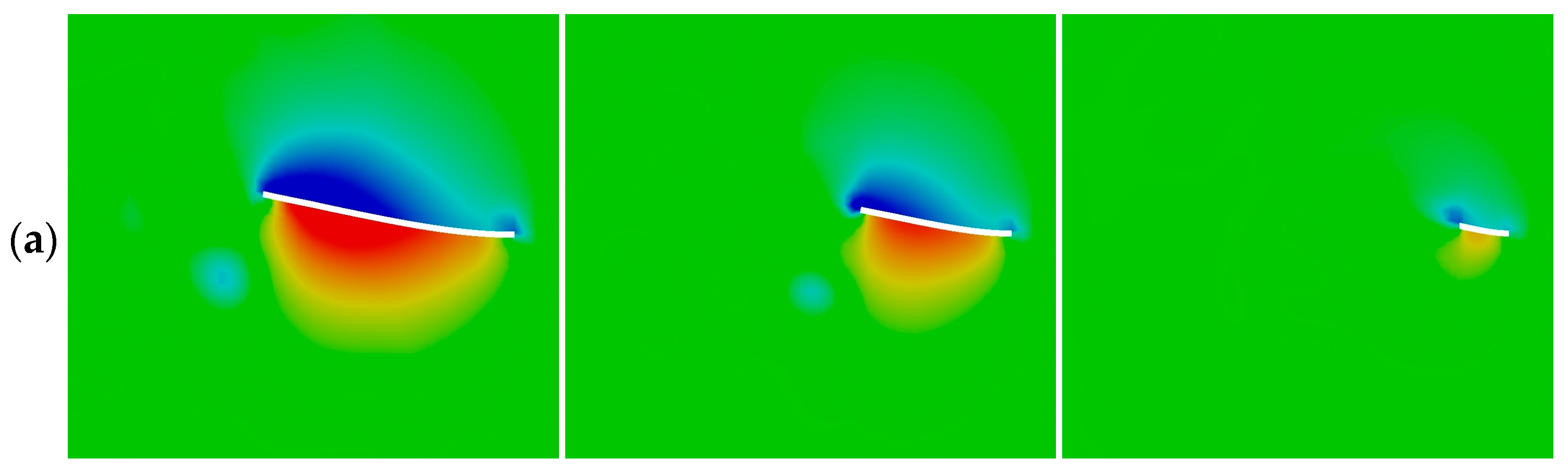
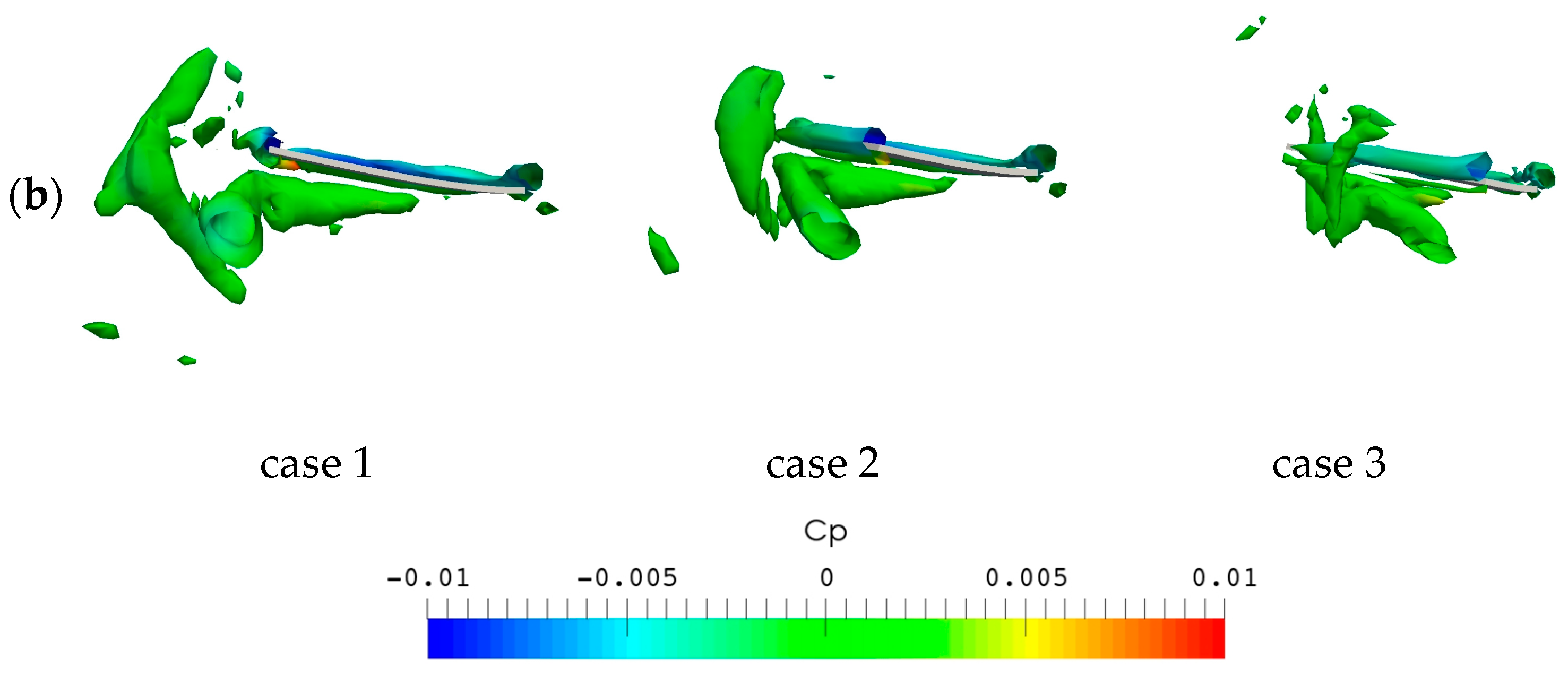
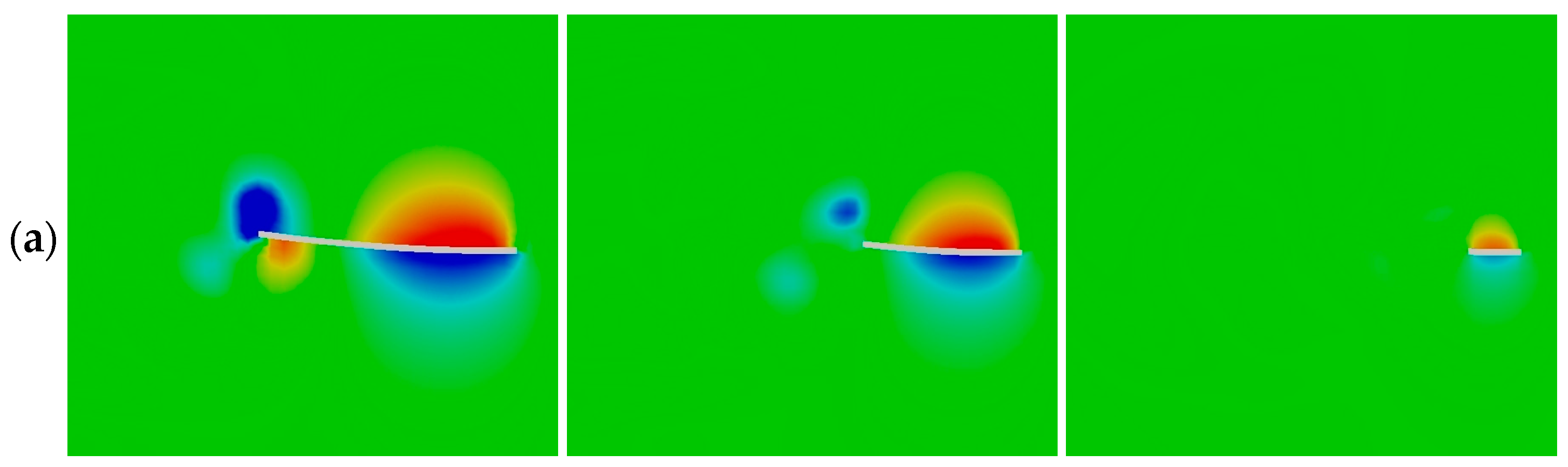
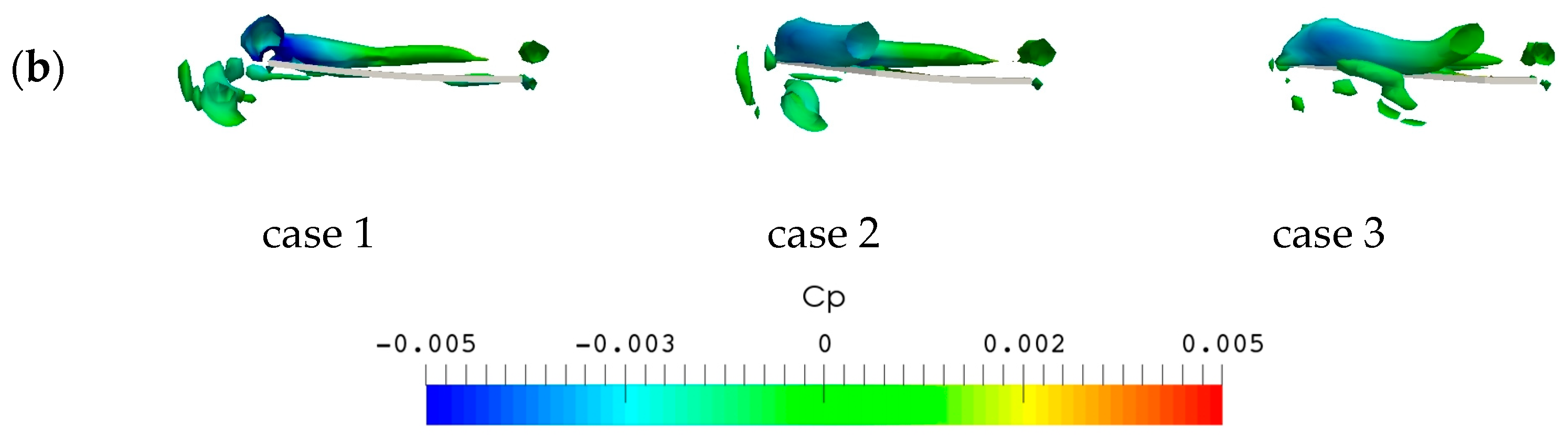
3.2. Flow Structures
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhu, Q.; Wolfgang, M.J.; Yue, D.K.P.; Triantafyllou, M.S. Three-dimensional flow structures and vorticity control in fish-like swimming. J. Fluid Mech. 2002, 468, 1–28. [Google Scholar] [CrossRef]
- Wen, L.; Liang, J.; Wu, G.; Li, J. Hydrodynamic experimental investigation on efficient swimming of robotic fish using self-propelled method. In Proceedings of the Twentieth International Offshore and Polar Engineering Conference, Beijing, China, 20–25 June 2010. [Google Scholar]
- Zhou, K.; Liu, J.; Chen, W. Numerical study on hydrodynamic performance of bionic caudal fin. Appl. Sci. 2016, 6, 15. [Google Scholar] [CrossRef]
- Li, N.; Liu, H.; Su, Y. Numerical study on the hydrodynamics of thunniform bio-inspired swimming under self-propulsion. PLoS ONE 2017, 12, e0174740. [Google Scholar] [CrossRef] [PubMed]
- Mannam, N.P.B.; Krishnankutty, P. Hydrodynamic study of flapping foil propulsion system fitted to surface and underwater vehicles. Ships Offshore Struct. 2018, 13, 575–583. [Google Scholar] [CrossRef]
- Huang, Q.; Zhang, D.; Pan, G. Computational model construction and analysis of the hydrodynamics of a Rhinoptera Javanica. IEEE Access 2020, 8, 30410–30420. [Google Scholar] [CrossRef]
- Liu, G.; Liu, S.; Xie, Y.; Leng, D.; Li, G. The analysis of biomimetic caudal fin propulsion mechanism with CFD. Appl. Bionics Biomech. 2020, 2020, 7839049. [Google Scholar] [CrossRef] [PubMed]
- Lauder, G.V.; Anderson, E.J.; Tangorra, J.; Madden, P.G. Fish biorobotics: Kinematics and hydrodynamics of self-propulsion. J. Exp. Biol. 2007, 210, 2767–2780. [Google Scholar] [CrossRef] [PubMed]
- Tangorra, J.L.; Lauder, G.V.; Hunter, I.W.; Mittal, R.; Madden, P.G.; Bozkurttas, M. The effect of fin ray flexural rigidity on the propulsive forces generated by a biorobotic fish pectoral fin. J. Exp. Biol. 2010, 213, 4043–4054. [Google Scholar] [CrossRef] [PubMed]
- Esposito, C.J.; Tangorra, J.L.; Flammang, B.E.; Lauder, G.V. A robotic fish caudal fin: Effects of stiffness and motor program on locomotor performance. J. Exp. Biol. 2012, 215, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.; Hu, K.; Wang, T.; Wen, L. Investigation of fish caudal fin locomotion using a bio-inspired robotic model. Int. J. Adv. Robot. Syst. 2016, 13, 87. [Google Scholar] [CrossRef]
- Li, R.; Xiao, Q.; Liu, Y.; Li, L.; Liu, H. Computational investigation on a self-propelled pufferfish driven by multiple fins. Ocean Eng. 2020, 197, 106908. [Google Scholar] [CrossRef]
- Han, P.; Lauder, G.V.; Dong, H. Hydrodynamics of median-fin interactions in fish-like locomotion: Effects of fin shape and movement. Phys. Fluids 2020, 32, 011902. [Google Scholar] [CrossRef]
- Luo, Y.; Xiao, Q.; Shi, G.; Pan, G.; Chen, D. The effect of variable stiffness of tuna-like fish body and fin on swimming performance. Bioinspiration Biomim. 2020, 16, 016003. [Google Scholar] [CrossRef] [PubMed]
- Kikuchi, K.; Uehara, Y.; Kubota, Y.; Mochizuki, O. Morphological considerations of fish fin shape on thrust generation. J. Appl. Fluid Mech. 2014, 7, 625–632. [Google Scholar]
- Matta, A.; Bayandor, J.; Battaglia, F.; Pendar, H. Effects of fish caudal fin sweep angle and kinematics on thrust production during low-speed thunniform swimming. Biol. Open 2019, 8, bio040626. [Google Scholar] [CrossRef] [PubMed]
- Berlinger, F.; Saadat, M.; Haj-Hariri, H.; Lauder, G.V.; Nagpal, R. Fish-like three-dimensional swimming with an autonomous, multi-fin, and biomimetic robot. Bioinspiration Biomim. 2021, 16, 026018. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Ma, S.; Lin, Z.; Zhu, K.; Wang, P.; Ahmed, R.; Ren, C.; Marvi, H. Impact of caudal fin geometry on the swimming performance of a snake-like robot. Ocean Eng. 2022, 245, 110372. [Google Scholar] [CrossRef]
- Lee, J.; Park, Y.J.; Cho, K.J.; Kim, D.; Kim, H.Y. Hydrodynamic advantages of a low aspect-ratio flapping foil. J. Fluids Struct. 2017, 71, 70–77. [Google Scholar] [CrossRef]
- Li, G.J.; Lu, X.Y. Force and power of flapping plates in a fluid. J. Fluid Mech. 2012, 712, 598–613. [Google Scholar] [CrossRef]
- Song, J.; Zhong, Y.; Du, R.; Yin, L.; Ding, Y. Tail shapes lead to different propulsive mechanisms in the body/caudal fin undulation of fish. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 351–364. [Google Scholar] [CrossRef]
- Lauder, G.V.; Lim, J.; Shelton, R.; Witt, C.; Anderson, E.; Tangorra, J.L. Robotic models for studying undulatory locomotion in fishes. Mar. Technol. Soc. J. 2011, 45, 41–55. [Google Scholar]
- Liu, G.; Dong, H. Effects of tail geometries on the performance and wake pattern in flapping propulsion. In Fluids Engineering Division Summer Meeting; American Society of Mechanical Engineers: New York City, NY, USA, 2016; Volume 50299, p. V01BT30A002. [Google Scholar]
- Matta, A.; Pendar, H.; Battaglia, F.; Bayandor, J. Impact of caudal fin shape on thrust production of a Thunniform swimmer. J. Bionic Eng. 2020, 17, 254–269. [Google Scholar] [CrossRef]
- Li, G.J.; Luodin, Z.H.U.; Lu, X.Y. Numerical studies on locomotion perfromance of fish-like tail fins. J. Hydrodyn. Ser. B 2012, 24, 488–495. [Google Scholar] [CrossRef]
- Van Buren, T.; Floryan, D.; Brunner, D.; Senturk, U.; Smits, A.J. Impact of trailing edge shape on the wake and propulsive performance of pitching panels. Phys. Rev. Fluids 2017, 2, 014702. [Google Scholar] [CrossRef]
- Baba, N.; Obi, S. Experimental study on modeled caudal fins propelling by elastic deformation. In Fluids Engineering Division Summer Meeting; American Society of Mechanical Engineers: New York City, NY, USA, 2018; Volume 51555, p. V001T02A007. [Google Scholar]
- Rosic, M.N.; Thornycroft, P.J.M.; Feilich, K.L.; Lucas, K.N.; Lauder, G.V. Performance variation due to stiffness in a tuna-inspired flexible foil model. Bioinspiration Biomim. 2017, 12, 016011. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Huang, H.; Lu, X.Y. Effect of trailing-edge shape on the self-propulsive performance of heaving flexible plates. J. Fluid Mech. 2020, 887, A7. [Google Scholar] [CrossRef]
- Feilich, K.L.; Lauder, G.V. Passive mechanical models of fish caudal fins: Effects of shape and stiffness on self-propulsion. Bioinspiration Biomim. 2015, 10, 036002. [Google Scholar] [CrossRef] [PubMed]
- Khin, M.H.W.; Kato, K.; Sung, H.J.; Obi, S. Fluid flow induced by an elastic plate in heaving motion. ASEAN Eng. J. 2022, 12, 1–9. [Google Scholar] [CrossRef]
- Donea, J.; Huerta, A.; Ponthot, J.-P.; Rodriguez-Ferran, A. Arbitrary Lagrangian–Eulerian Methods. Encycl. Comput. Mech. 2004, 1, 413–437. [Google Scholar]
- Tuković, Ž.; Karač, A.; Cardiff, P.; Jasak, H.; Ivanković, A. OpenFOAM Finite Volume Solver for Fluid-Solid Interaction. Trans. Famena 2018, 42, 1–31. [Google Scholar] [CrossRef]
- Khin, M.H.W.; Obi, S. Three-Dimensional Hydrodynamic Analysis of a Flexible Caudal Fin. Appl. Sci. 2022, 12, 12693. [Google Scholar] [CrossRef]
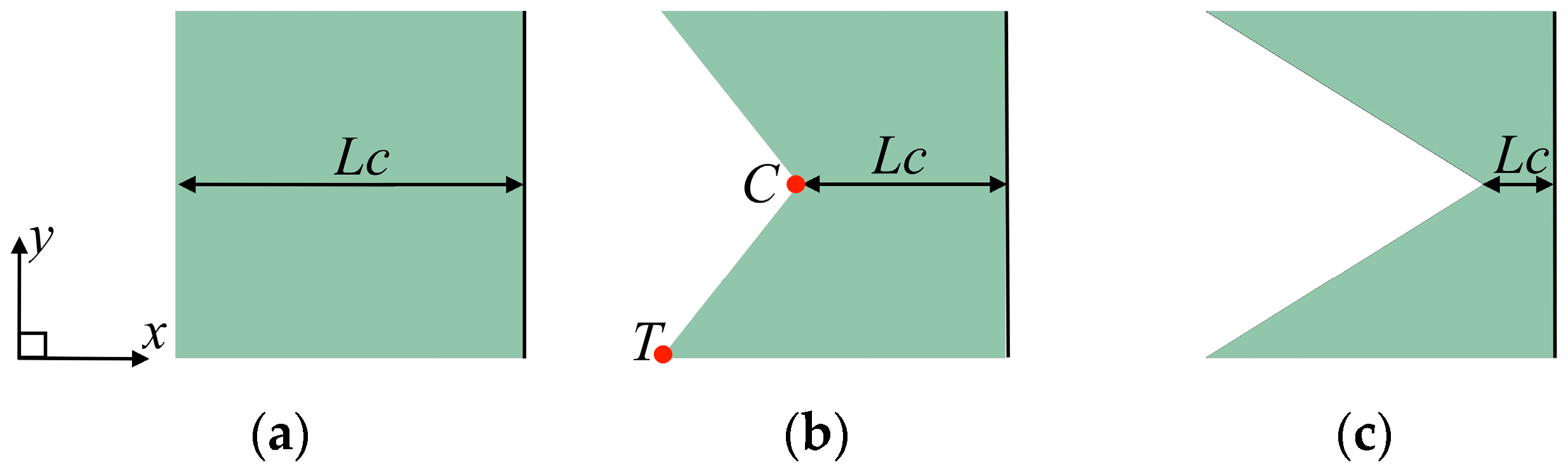
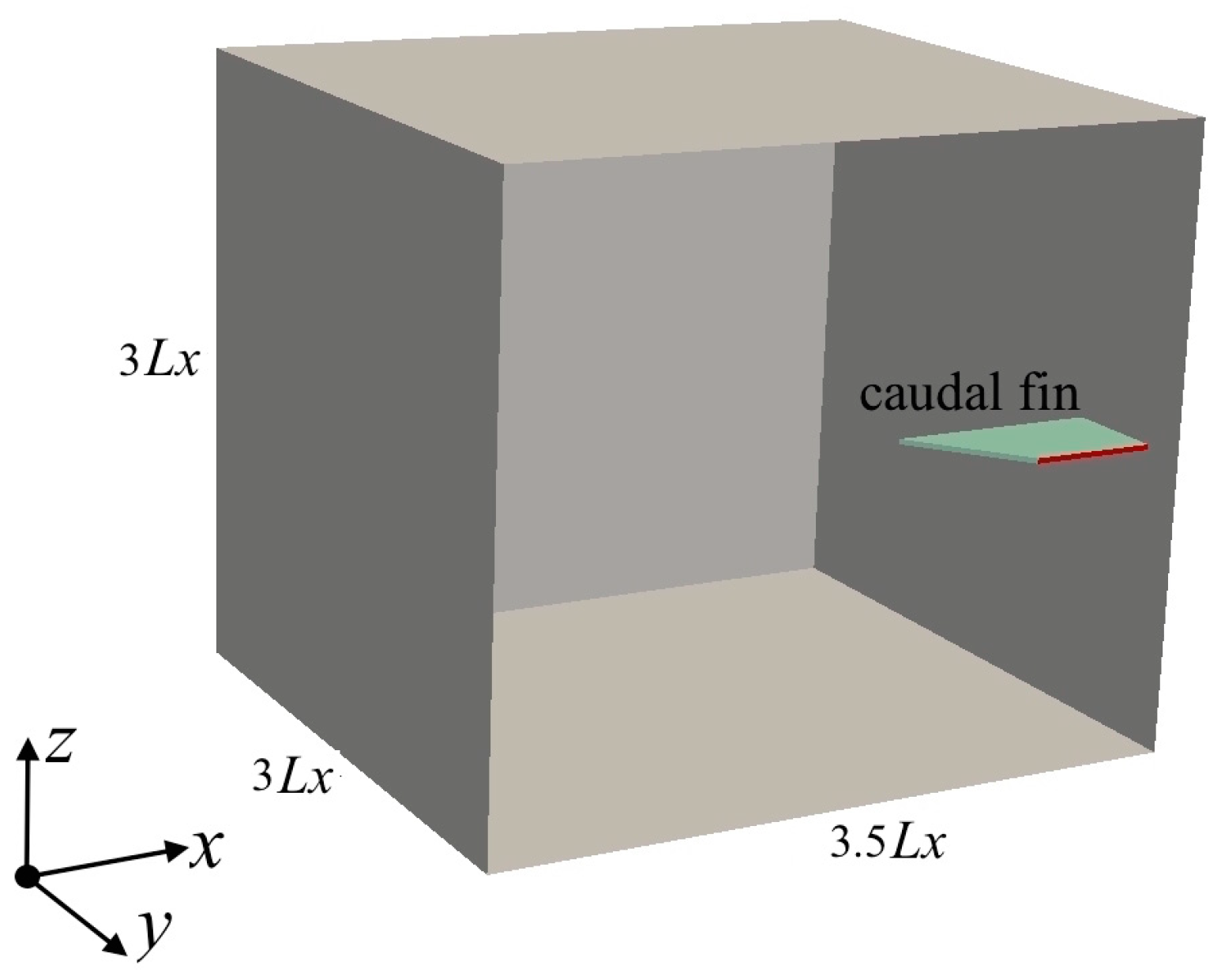

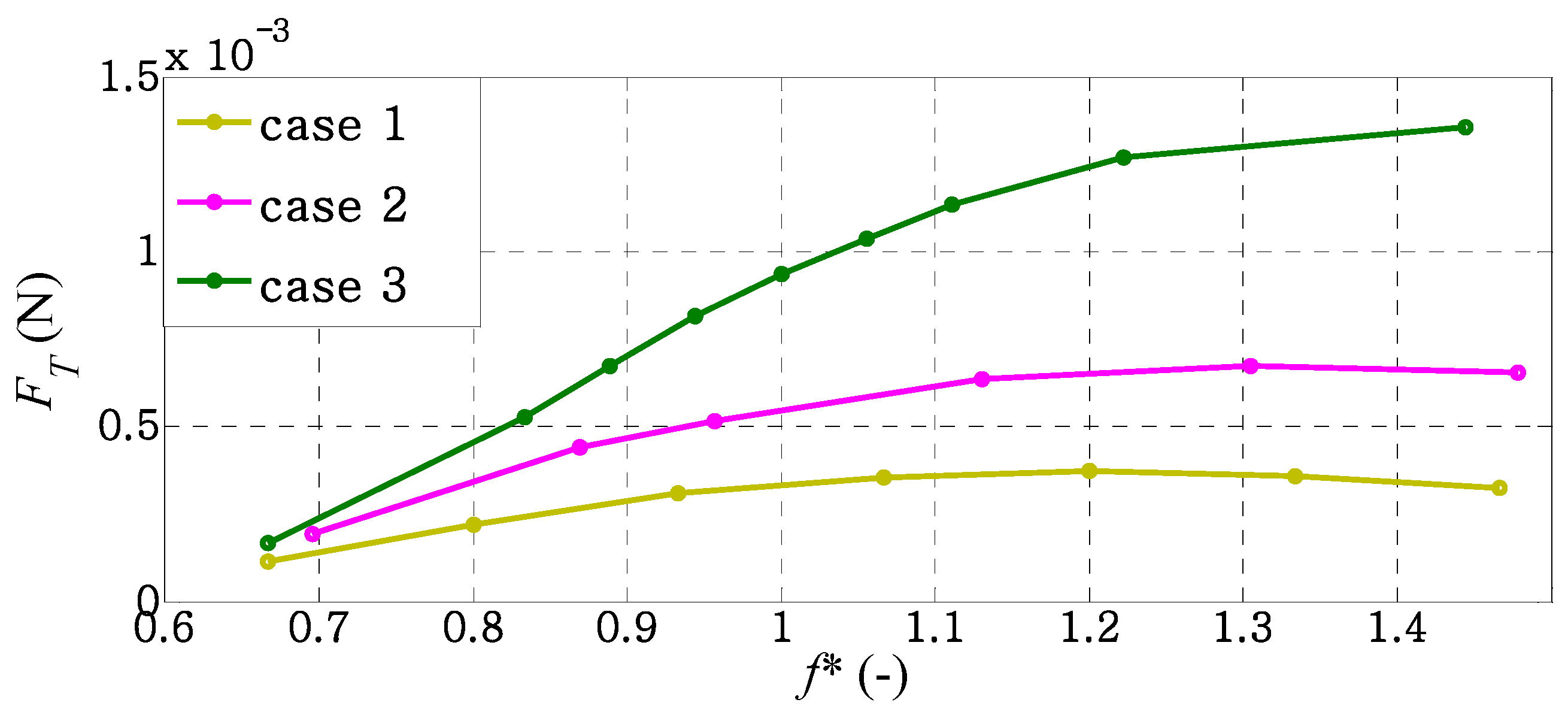


| Type | Lx [m] | Lc [m] | S [m2] | AR [-] |
|---|---|---|---|---|
| case 1 | 0.04 | 0.040 | 0.00160 | 1.00 |
| case 2 | 0.04 | 0.024 | 0.00128 | 1.25 |
| case 3 | 0.04 | 0.008 | 0.00096 | 1.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khin, M.H.W.; Obi, S. Numerical Study on the Hydrodynamic Performance of a Flexible Caudal Fin with Different Trailing-Edge Shapes. Biomimetics 2024, 9, 445. https://doi.org/10.3390/biomimetics9070445
Khin MHW, Obi S. Numerical Study on the Hydrodynamic Performance of a Flexible Caudal Fin with Different Trailing-Edge Shapes. Biomimetics. 2024; 9(7):445. https://doi.org/10.3390/biomimetics9070445
Chicago/Turabian StyleKhin, May Hlaing Win, and Shinnosuke Obi. 2024. "Numerical Study on the Hydrodynamic Performance of a Flexible Caudal Fin with Different Trailing-Edge Shapes" Biomimetics 9, no. 7: 445. https://doi.org/10.3390/biomimetics9070445
APA StyleKhin, M. H. W., & Obi, S. (2024). Numerical Study on the Hydrodynamic Performance of a Flexible Caudal Fin with Different Trailing-Edge Shapes. Biomimetics, 9(7), 445. https://doi.org/10.3390/biomimetics9070445







