A Mathematical Model of Pressure Ulcer Formation to Facilitate Prevention and Management
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Formalism
- : there exists an open set such that
- , , X is surjective.
- X is on
- X is a homeomorphism.
- , is injective.
2.2. Cellular Death Model
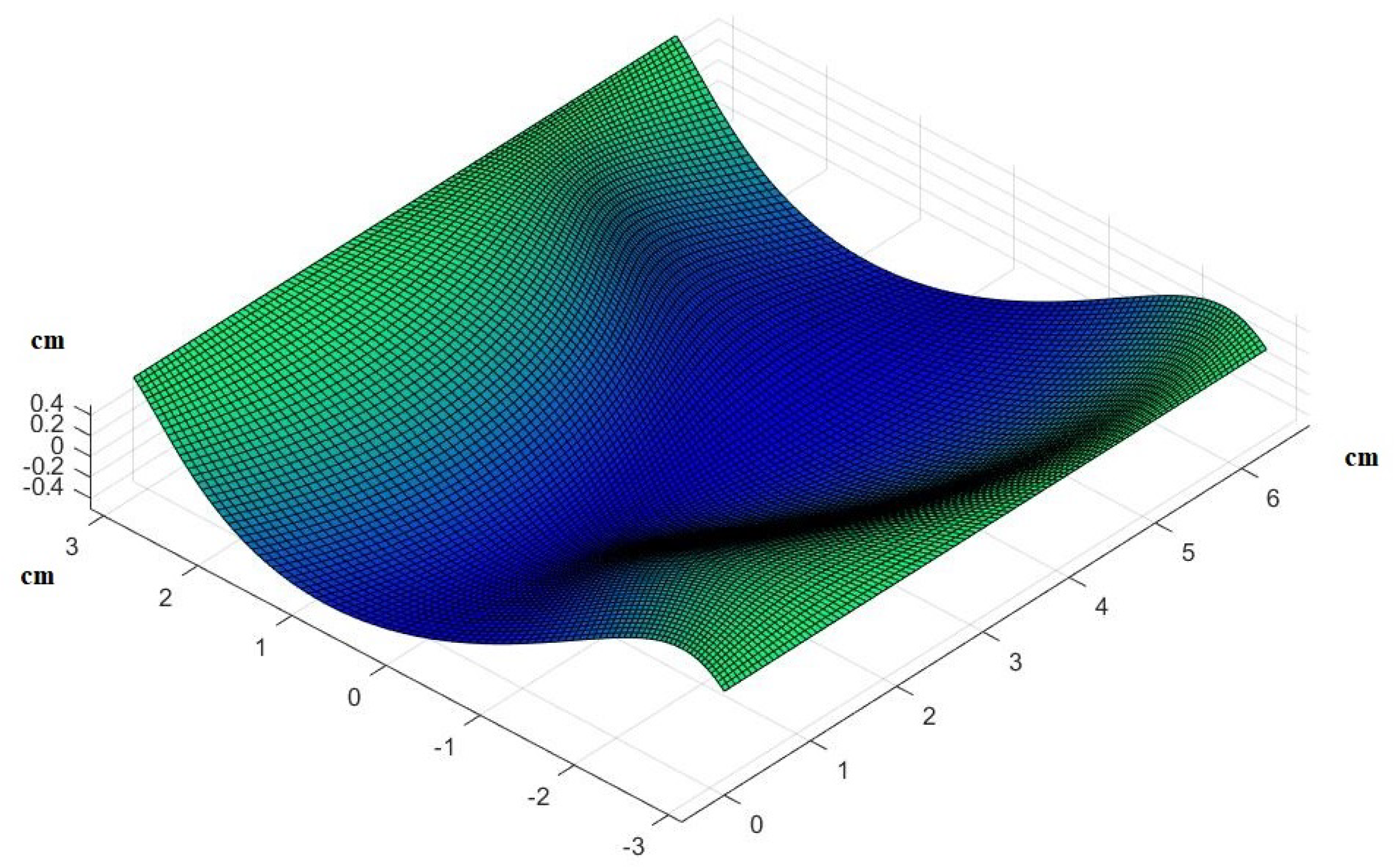
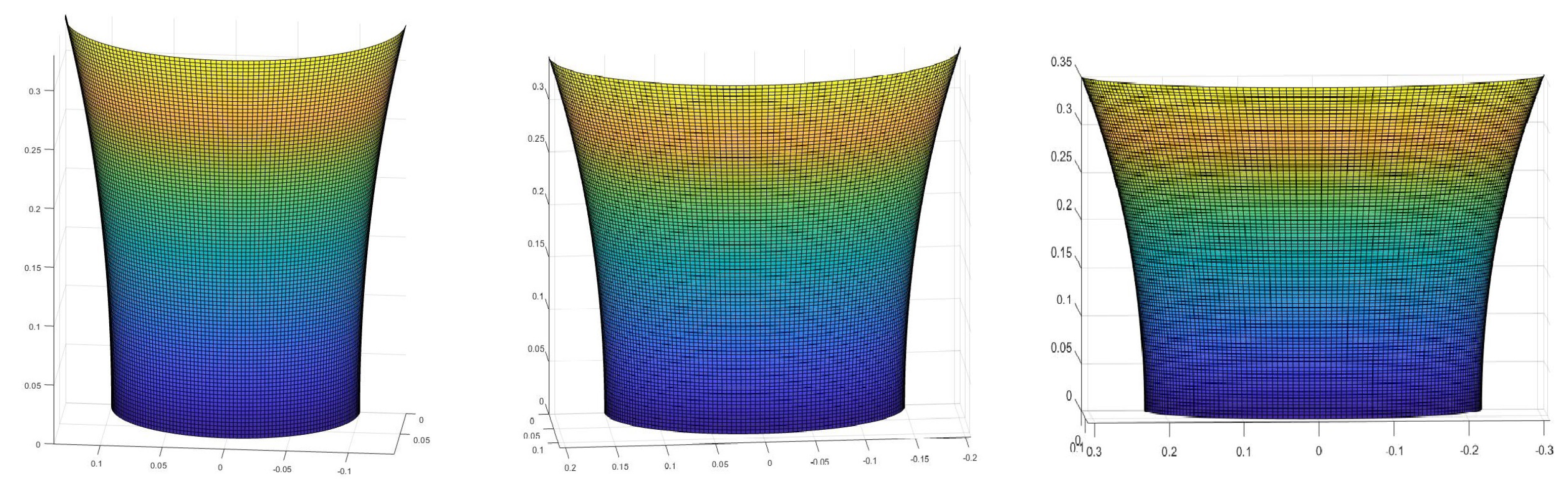
2.3. Surfaces of Interest
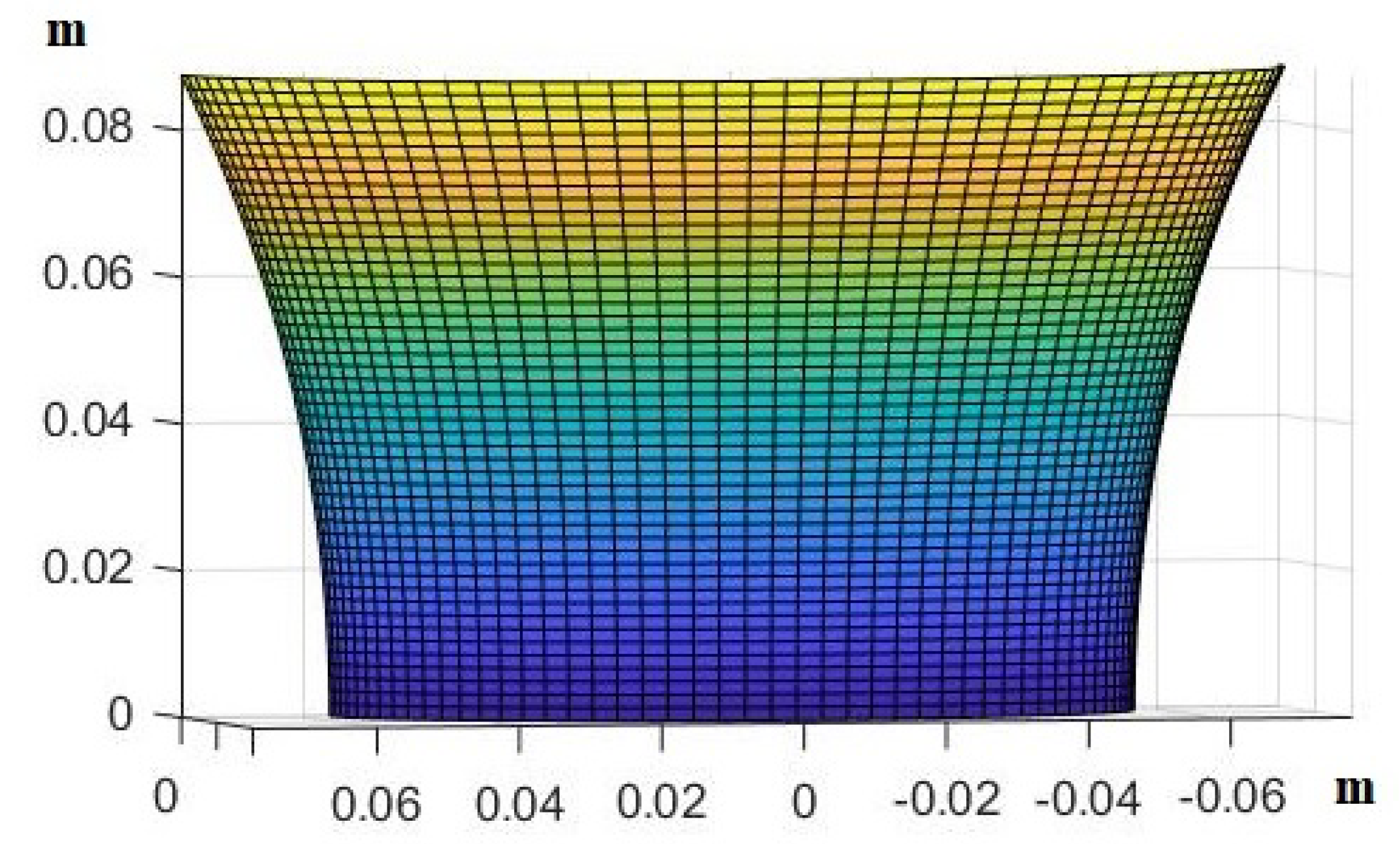
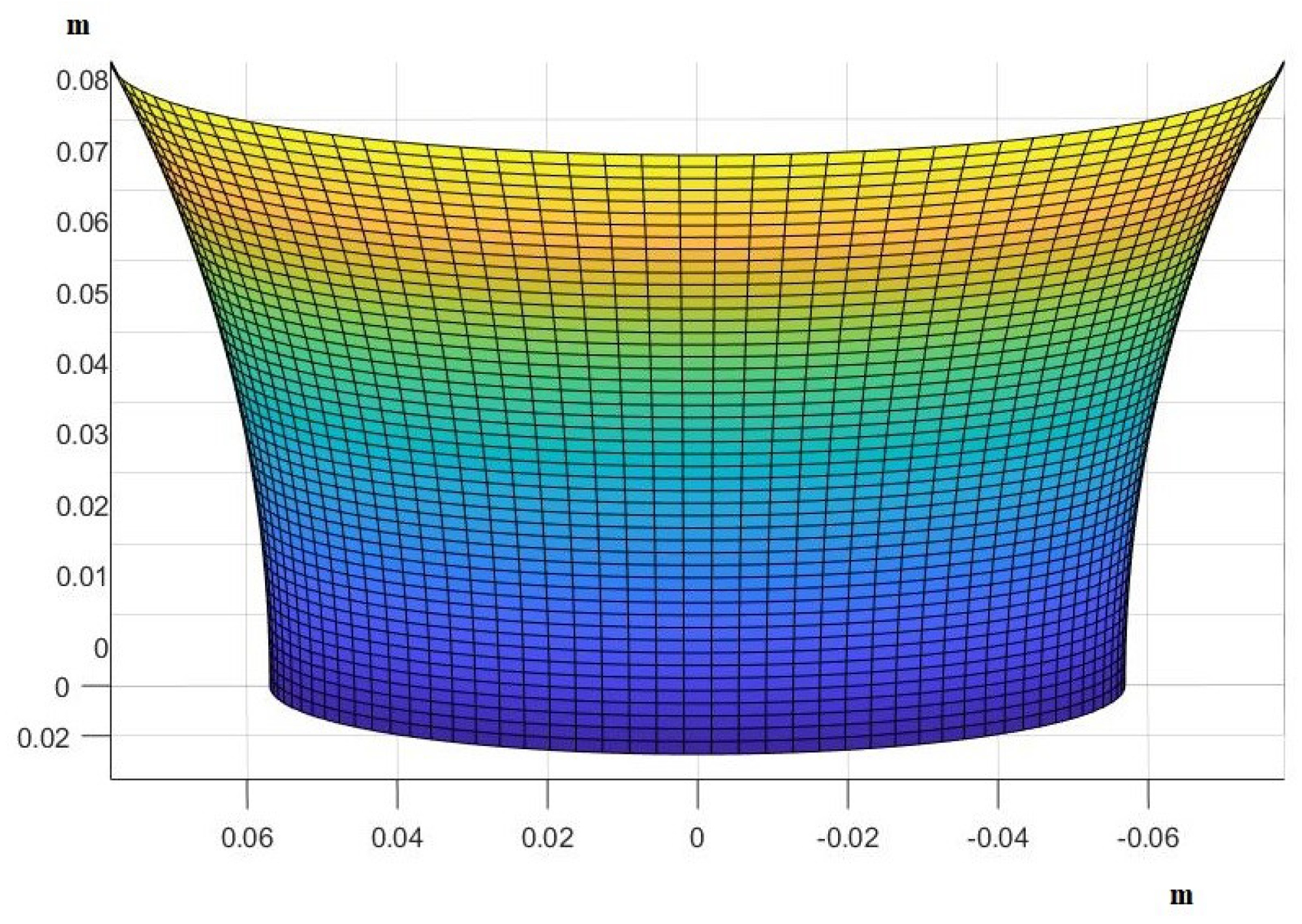
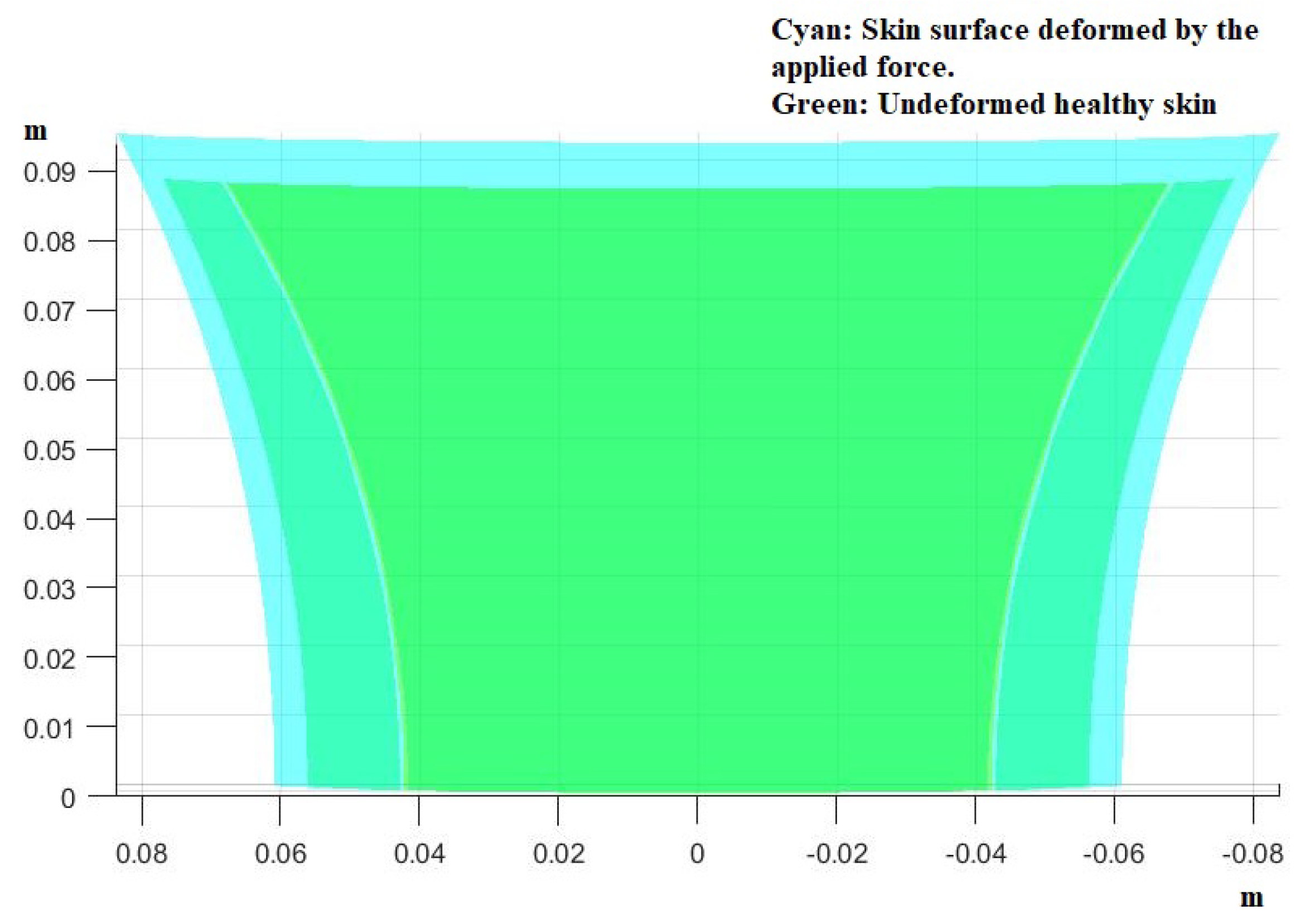
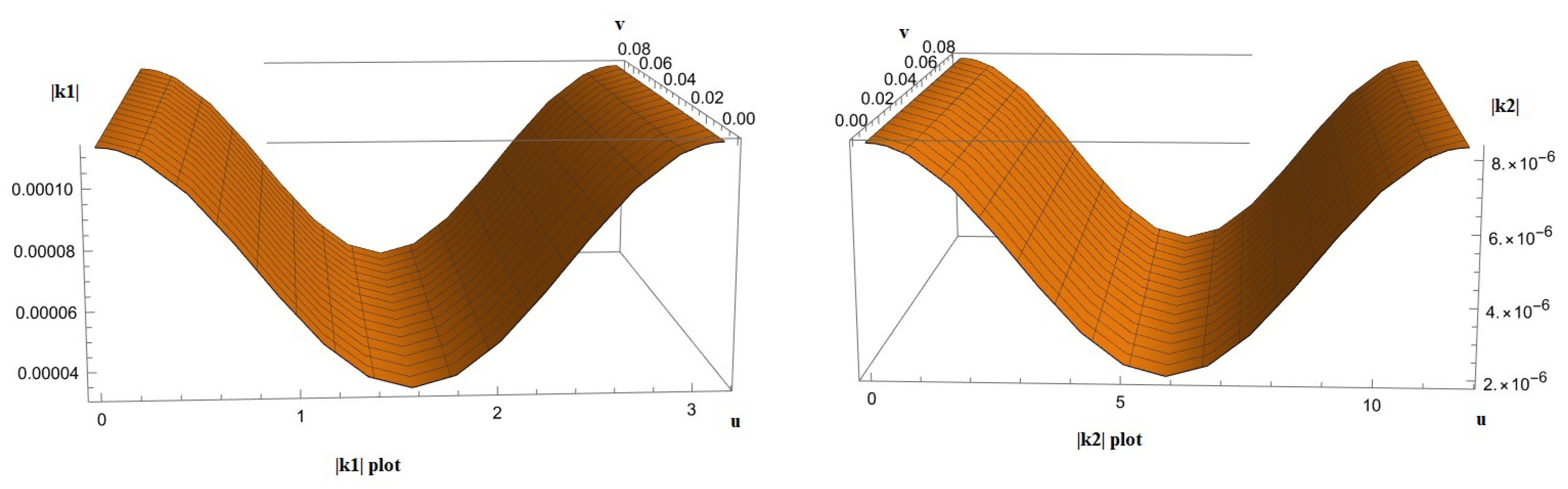
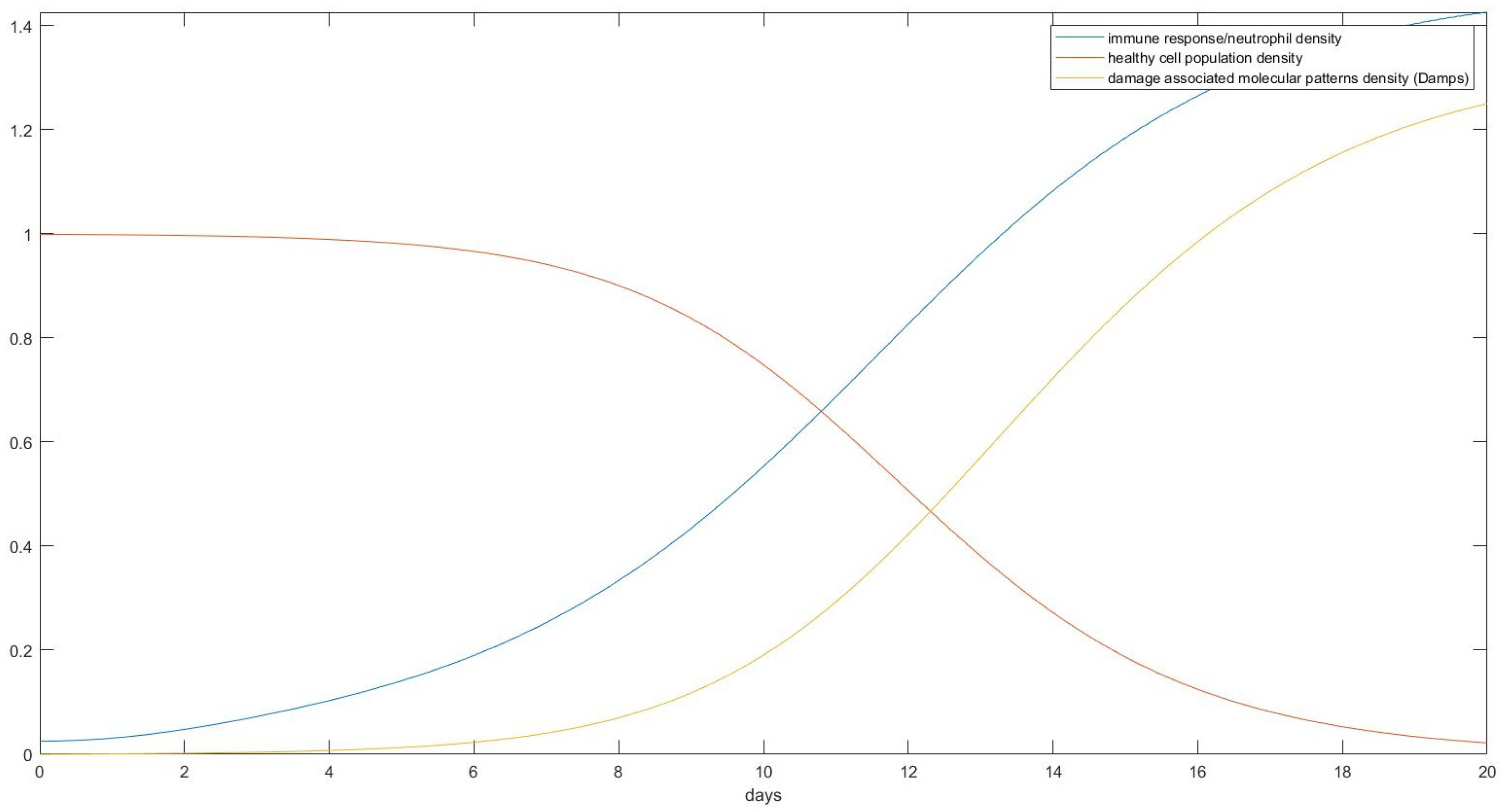
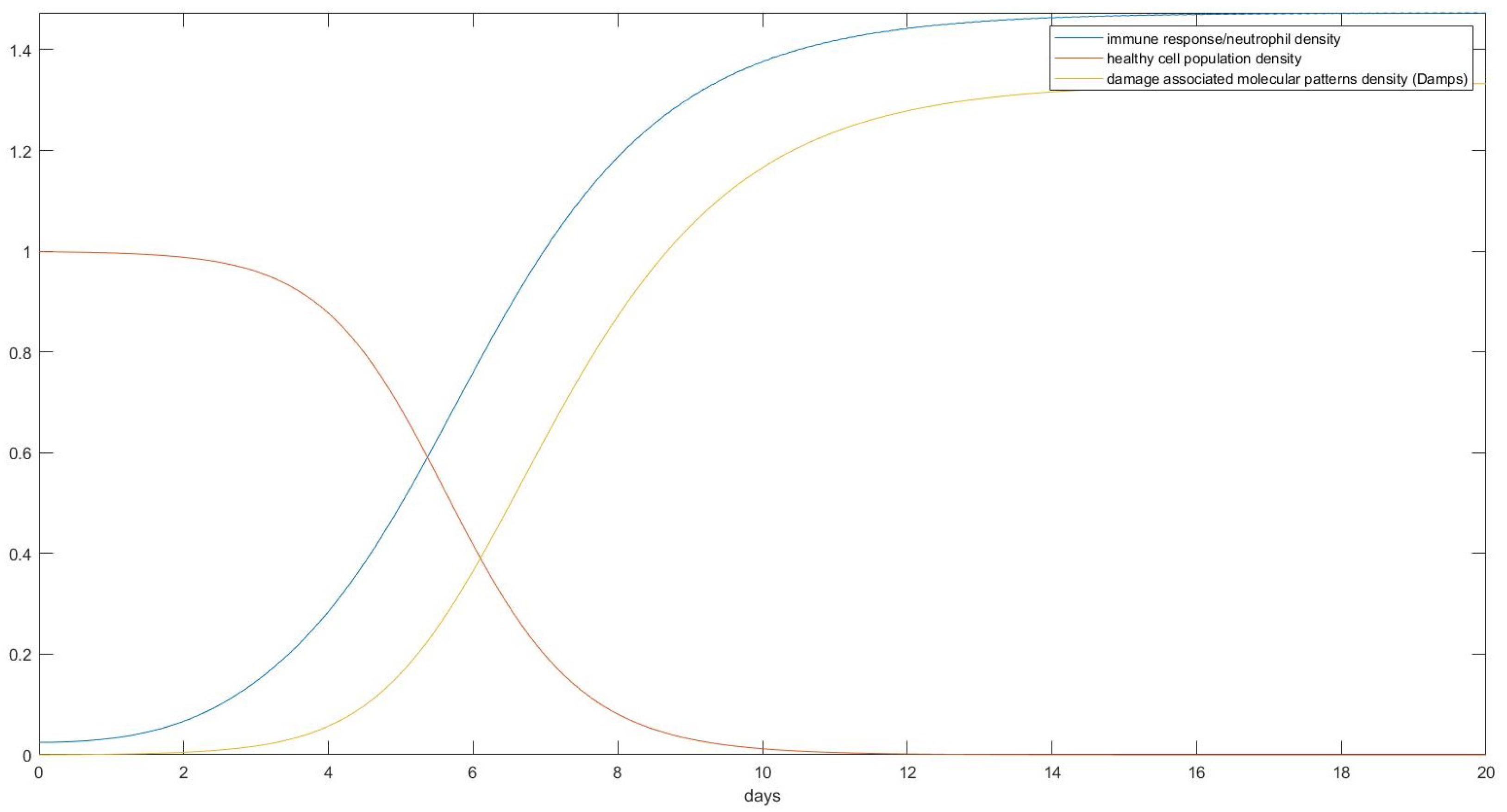
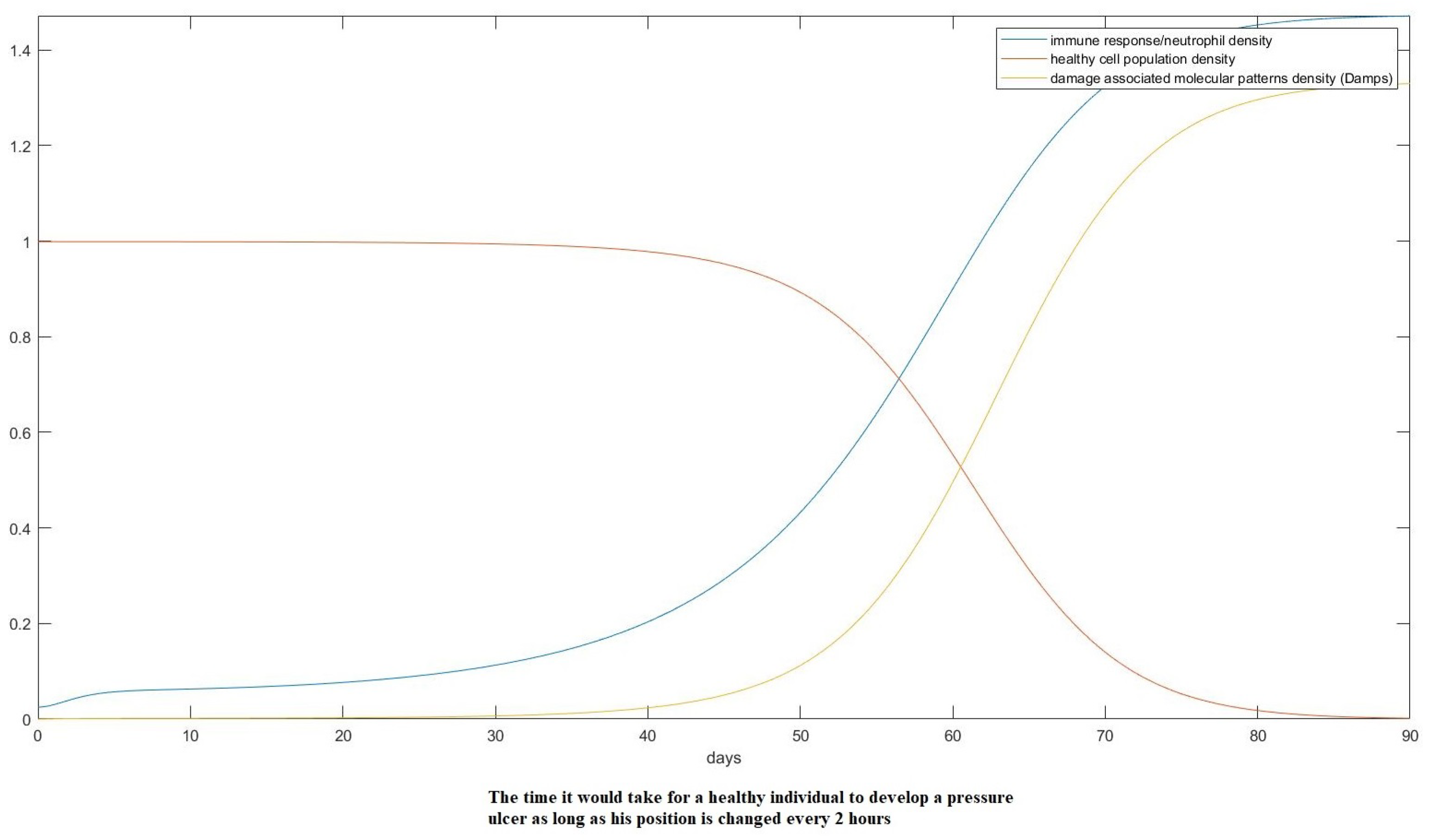
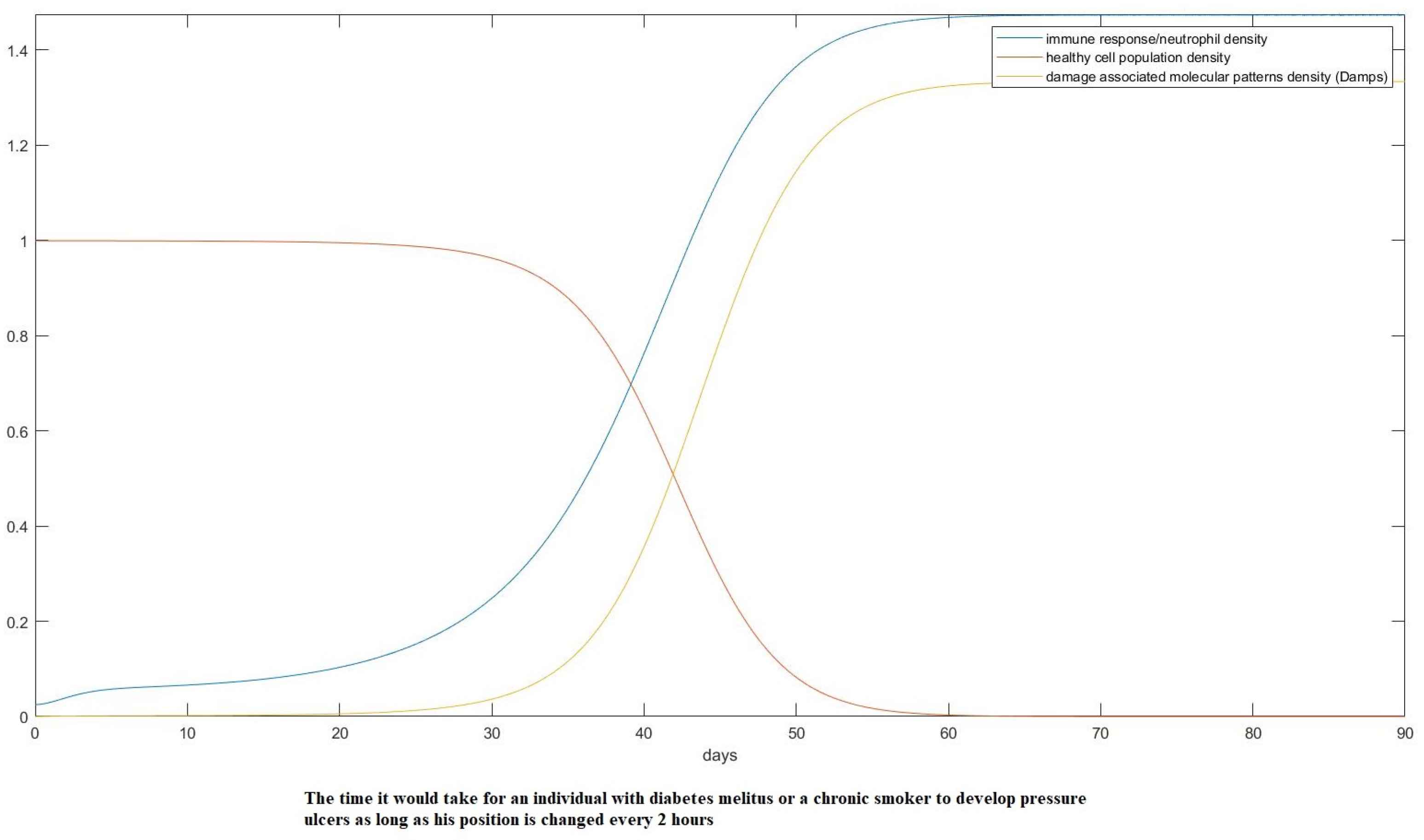
3. Results
- Estimate the area of the surface of an average human body touching the plane of the bed.
- Use the theory we established in the Materials and Methods to calculate how the skin in these areas would be deformed after receiving the pressure from its own weight and finding the new post-deformation area and Gaussian curvature.
- Calculate the capillary density of the new deformed surface as well as the reduction in blood flow due to the new curvature.
- Use our proposed model of ODEs to predict the effect of that deformation on the cells of the epidermis over time over the areas in question.
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
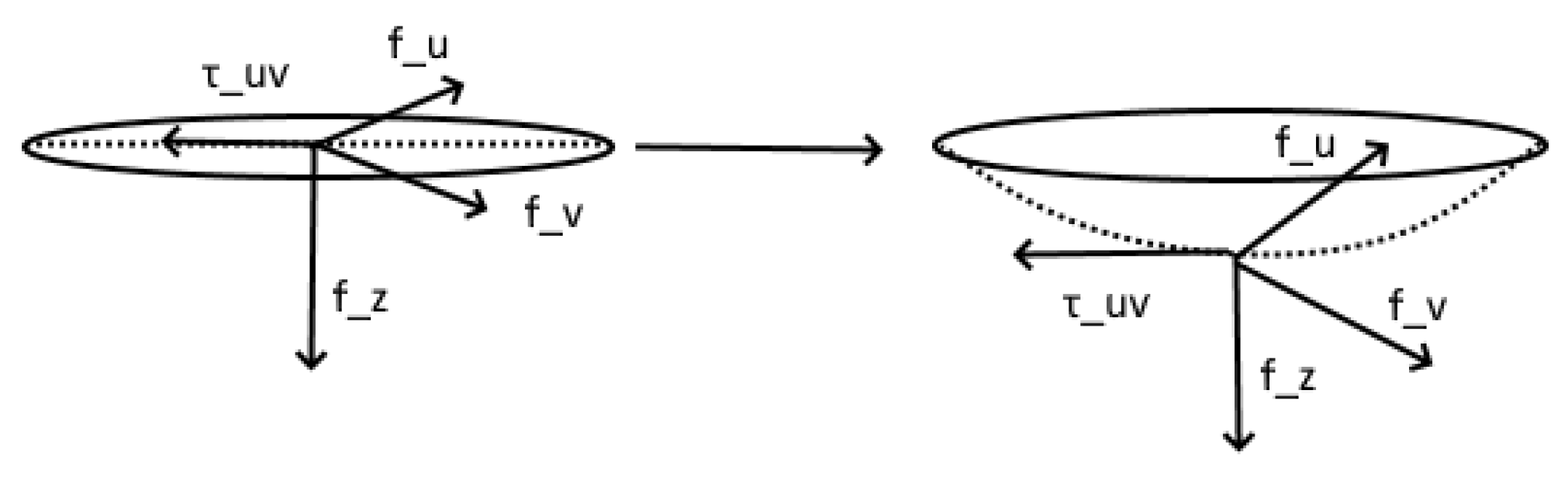
Appendix A. Stress Tensor
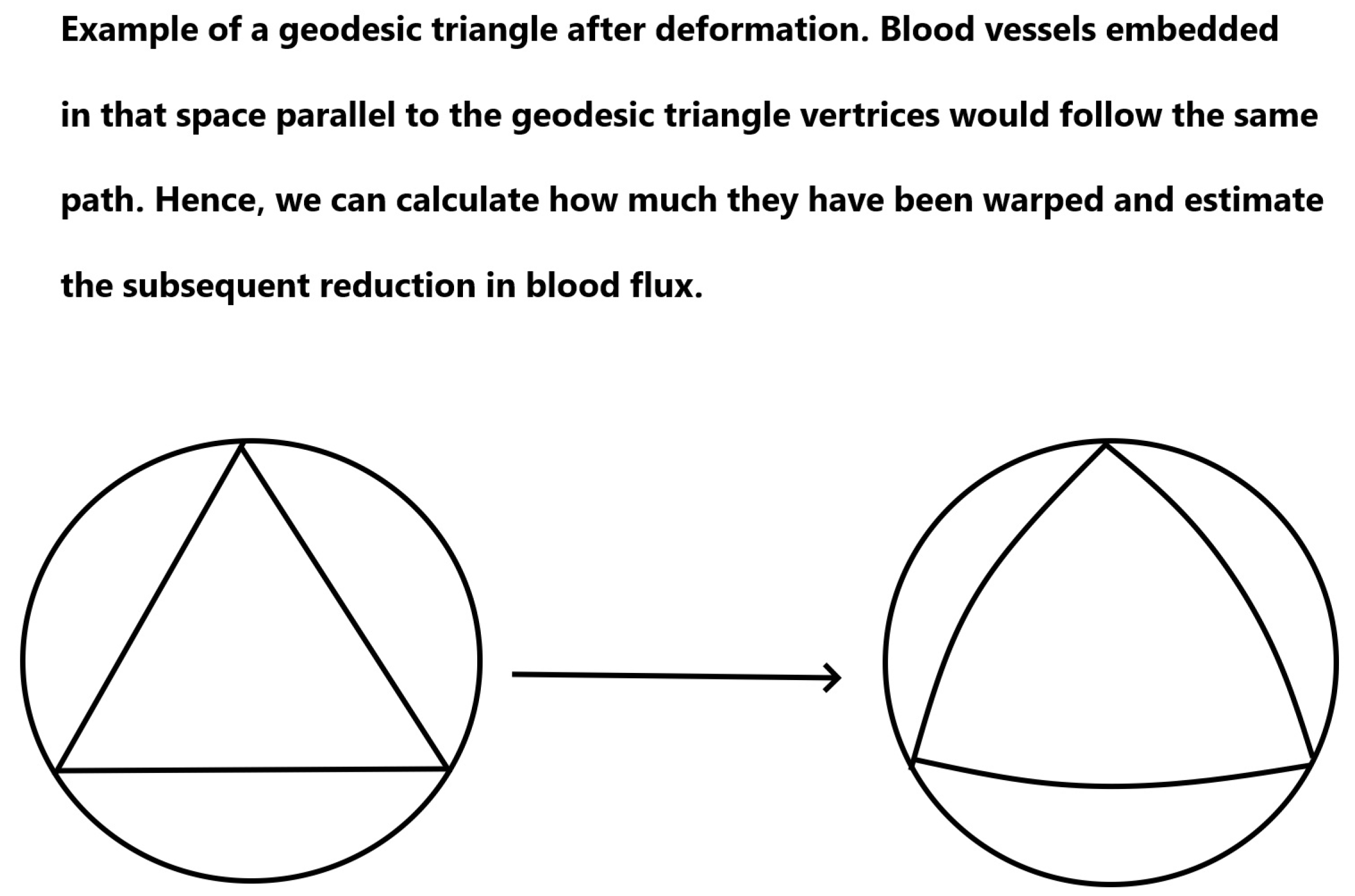
Appendix B. Euler–Lagrange Equations
Appendix C
Appendix D
Appendix E. Changes in Flow Due to Deformation
Appendix F. Model Normalization
References
- Timoshenko, S.; Goodier, J.N. Theory of Elasticity, 3rd ed.; McGraw-Hill: New York, NY, USA, 1976. [Google Scholar]
- Washizu, K. Variational Methods in Elasticity and Plasticity; International Series of Monographs in Aeronautics and Astronautics; Pergamon Press: Oxford, UK, 1968. [Google Scholar]
- Do Carmo, M.P. Differential Geometry of Curves and Surfaces; Prentice-Hall: New York, NY, USA, 1970. [Google Scholar]
- Verkaik, A.C.; Beulen, B.W.A.M.M.; Bogaerds, A.C.B.; Rutten, M.C.M.; van de Vosse, F.N. Estimation of volume flow in curved tubes based on analytical and computational analysis of axial velocity profiles. Phys. Fluids 2009, 21, 023602. [Google Scholar] [CrossRef]
- Sree, V.D.; Rausch, M.K.; Tepole, A.B. Towards understanding pressure ulcer formation: Coupling an inflammation regulatory network to a tissue scale finite element model. Mech. Res. Commun. 2019, 97, 80–88. [Google Scholar] [CrossRef]
- Wang, W. Oxygen Partial Pressure in Outer Layers of Skin: Simulation Using Three-Dimensional Multilayered Models. Microcirculation 2005, 12, 195–207. [Google Scholar] [CrossRef] [PubMed]
- Tikuisis, P.; Meunier, P.; Jubenville, C.E. Human body surface area: Measurement and prediction using three dimensional body scans. Eur. J. Appl. Physiol. 2001, 85, 264–271. [Google Scholar] [CrossRef] [PubMed]
- Delalleau, A.; Josse, G.; Lagarde, J.-M.; Zahouani, H.; Bergheau, J.-M. A nonlinear elastic behavior to identify the mechanical parameters of human skin in vivo. Ski. Res. Technol. 2008, 14, 152–164. [Google Scholar] [CrossRef] [PubMed]
- Benítez, J.M.; Montáns, F.J. The mechanical behavior of skin: Structures and models for the finite element analysis. Comput. Struct. 2017, 190, 75–107. [Google Scholar] [CrossRef]
- Polyanin, A.D. Handbook of Linear Partial Differential Equations for Engineers and Scientists; CHAPMAN and HALL/CRC: Boca Raton, FL, USA, 2002. [Google Scholar]
- Secomb, T.W. Blood Flow in the Microcirculation. Annu. Rev. Fluid Mech. 2017, 49, 443–461. [Google Scholar] [CrossRef]
- Richardson, D. Effects of tobacco smoke inhalation on capillary blood flow in human skin. Arch. Environ. Heal. Int. J. 1987, 42, 19–25. [Google Scholar] [CrossRef] [PubMed]
- Rayman, G.; Wiliams, S.A.; Spencer, P.D.; Smaje, L.H.; Wise, P.H.; Tooke, J.E. Impaired microvascular hyperaemic response to minor skin trauma in type I diabetes. Br. Med. J. (Clin. Res. Ed.) 1986, 292, 1295–1298. [Google Scholar] [CrossRef] [PubMed]
- Schoonhoven, L.; Bousema, M.T.; Buskens, E. prePURSE-Study Group The prevalence and incidence of pressure ulcers in hospitalised patients in the Netherlands: A prospective inception cohort study. Int. J. Nurs. Stud. 2007, 44, 927–935. [Google Scholar] [CrossRef] [PubMed]
- Bours, G.J.; Halfens, R.J.; Abu-Saad, H.H.; Grol, R.T. Prevalence, prevention, and treatment of pressure ulcers: Descriptive study in 89 institutions in the Netherlands. Res. Nurs. Health 2002, 25, 99–110. [Google Scholar] [CrossRef] [PubMed]
- Padula, W.V.; Delarmente, B.A. The national cost of hospital-acquired pressure injuries in the United States. Int. Wound J. 2019, 16, 634–640. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Lin, F.; Thalib, L.; Chaboyer, W. Global prevalence and incidence of pressure injuries in hospitalised adult patients: A systematic review and meta-analysis. Int. J. Nurs. Stud. 2020, 105, 103546. [Google Scholar] [CrossRef] [PubMed]
- Mishu, M.C.; Schroeder, J.W. Modelling of pressure ulcer (PU) risk prediction system. In Proceedings of the 2015 Science and Information Conference (SAI), London, UK, 28–30 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 650–656. [Google Scholar] [CrossRef]
- Ziraldo, C.; Solovyev, A.; Allegretti, A.; Krishnan, S.; Henzel, M.K.; Sowa, G.A.; Vodovotz, Y. A computational, tissue-realistic model of pressure ulcer formation in individuals with spinal cord injury. PLoS Comput. Biol. 2015, 11, e1004309. [Google Scholar] [CrossRef] [PubMed]
- Makhsous, M.; Lim, D.; Hendrix, R.; Bankard, J.; Rymer, W.Z.; Lin, F. Finite element analysis for evaluation of pressure ulcer on the buttock: Development and validation. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 517–525. [Google Scholar] [CrossRef] [PubMed]
- Limbert, G. Mathematical and computational modelling of skin biophysics: A review. Proc. Math. Phys. Eng. Sci. 2017, 473, 20170257. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Utyuzhnikov, S. Tensor Train-Based Higher-Order Dynamic Mode decomposition for dynamical systems. Mathematics 2023, 11, 1809. [Google Scholar] [CrossRef]
- Yu, D.; Zhou, Y.; Zhang, S.; Li, W.; Small, M.; Shang, K. Information Cascade Prediction of complex networks based on Physics-informed Graph Convolutional Network. New J. Phys. 2024, 26, 013031. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Violaris, I.G.; Kalafatakis, K.; Giannakeas, N.; Tzallas, A.T.; Tsipouras, M. A Mathematical Model of Pressure Ulcer Formation to Facilitate Prevention and Management. Methods Protoc. 2024, 7, 62. https://doi.org/10.3390/mps7040062
Violaris IG, Kalafatakis K, Giannakeas N, Tzallas AT, Tsipouras M. A Mathematical Model of Pressure Ulcer Formation to Facilitate Prevention and Management. Methods and Protocols. 2024; 7(4):62. https://doi.org/10.3390/mps7040062
Chicago/Turabian StyleViolaris, Ioannis G., Konstantinos Kalafatakis, Nikolaos Giannakeas, Alexandros T. Tzallas, and Markos Tsipouras. 2024. "A Mathematical Model of Pressure Ulcer Formation to Facilitate Prevention and Management" Methods and Protocols 7, no. 4: 62. https://doi.org/10.3390/mps7040062
APA StyleViolaris, I. G., Kalafatakis, K., Giannakeas, N., Tzallas, A. T., & Tsipouras, M. (2024). A Mathematical Model of Pressure Ulcer Formation to Facilitate Prevention and Management. Methods and Protocols, 7(4), 62. https://doi.org/10.3390/mps7040062









