Aristotle’s Political Justice and the Golden Ratio between the Three Opposing Criteria for the Distribution of Public Goods among Citizens: Freedom, Wealth and Virtue
Abstract
:1. Introduction: The Ethical Problem of Political Justice Revolves around the Dispute over Who Should Govern
2. In Search of the Mean Term of Distributive Justice
«All are agreed that justice in distributions must be based on desert of some sort, although they do not all mean the same sort of desert; democrats make the criterion free birth; those of oligarchical sympathies wealth, or in other cases birth; upholders of aristocracy make it virtue. Justice is therefore a sort of proportion» [2] (Book V, 3).
2.1. Theorem: The Theory of the Mean Is Necessary to Find the Mean Term of Distributive Justice
«Now of everything that is continuous and divisible, it is possible to take the larger part, or the smaller part, or an equal part, and these parts may be larger, smaller, and equal either whit respect to the thing itself or relatively to us; the equal part being a mean between excess and deficiency» [2] (Book II, 1106a 25–29).
«Justice is a mode of observing the mean, though not in the same way as the other virtues are, but because it is related to a mean, while Injustice is related to the extremes. Also, Justice is that quality in virtue of which a man is said to be disposed to do by deliberate choice that which is just, and, when distributing things between himself and another, or between two others, not to give too much to himself and too little to his neighbor of what is desirable, and too little to himself and too much to his neighbor of what is harmful, but to each what is proportionately equal; and similarly, when he is distributing between two other persons» [2] (Book V, 5, 1134a1–18).
«For when deliberating one seems in the procedure described to be pursuing an investigation or analysis that resembles the analysis of a figure in geometry—indeed it appears that though not all investigation is deliberation, for example, mathematical investigation is not, yet all deliberation is investigation—and the last step in the analysis seems to be the first step in the execution of the design» [2] (Book III, 1112b 20–24).
«All are agreed that justice in distributions must be based on desert of some sort, although they do not all mean the same sort of desert; democrats make the criterion free birth; those of oligarchical sympathies wealth, or in other cases birth; upholders of aristocracy make it virtue. Justice is therefore a sort of proportion; for proportion is not a specific characteristic of the monadic number6, but of the number as a whole. For proportion is equality of ratios and involves four terms at least. That discrete proportion involves four terms is plain, but so too does continuous proportion, for it uses one term as two and mentions it twice; e.g., as the line A is to the line B, so is the line B to the line Γ; the line B, then, has be mentioned twice, so that if the line B be assumed twice, the proportional terms will be four. And the just, too, involves at least four terms, and the ratio is the same because it joins the terms in the same way7. As the term A, then, is to B, so will Γ be to Δ, and therefore, alternando, as A is to Γ, B will be to Δ. Therefore, also the whole is in the same ratio to the whole. If the division joins the terms in this way, then it joins rightly. In fact, the conjunction between the lines AΓ and BΔ is what is just in distribution, and this species of the just is a mean proportional, and the unjust is what violates the proportion; in fact, this mean proportional is the just proportion. Mathematicians call this kind of proportion geometrical; for it is in geometrical proportion that it follows that the whole is to the whole as either part is to the corresponding part. But this proportion is not continuous: for it does not arise from a single dimension ad infinitum8. This, then, is what the just is—the proportional; the unjust is what violates the proportion».9
- The Mean Term of Distributive Justice is relative to a Proportional Equality between the three opposing Criteria of Distribution—Freedom, Wealth, and Virtue—, and unjust distribution is that which violates this Proportional Equality. The corresponding justice and injustice are a special Ethical Virtue and Vice: the ethical motive of just action is the πλεονεξία, covetousness or love for gain, the desire to secure more than the agent’s share of honor, wealth or bodily safety. The rights and the wrongs in this case are always rights of one individual against another, wrong done by one private individual to another. So, the Geometric Mean of Distributive Justice is relative to a Proportion which is composed of Four terms (i.e., the Three Criteria of Distribution and their Mean Proportional): A/B = C/D.
- Moreover, this Proportion is not discrete but Continuous, i.e., divisible ad infinitum. Aristotle explains that Proportion is equivalent to analogia, equality of ratios, i.e., A/B = C/D if the proportion is Discrete, and A/B = B/C if is Continuous; «and the just too involves at least four terms, and the ratio is the same because it joins the terms in the same way. As the term A, then, is to B, so will C be to D, and therefore, alternando, as A is to C, B will be to D. Therefore, also the whole is in the same ratio to the whole. If the division joins the terms in this way, then it joins rightly». That is, the Geometric Mean is relative to a Proportion that is also Continuous because it joins the terms so that the ratio between the whole and its parts is the same: A/C = B/D.
- However, this Proportion is Continuous, i.e., divisible ad infinitum, in several dimensions and not only in one, which means that we do not have to draw a one-dimensional Geometric Figure (i.e., the Line that possesses only the dimension of length). In fact, since we have to calculate the Geometric Mean relative to a Proportional Equality between the three opposing Criteria of Distribution, we have to construct a Triangle ABC, which, in effect, is a two-dimensional (length and width) Geometric Figure.
- Thus, in the Triangle ABC, the Point of Conjunction or Intersection between line AC and line BD determines what is just in the distribution: «In fact, the conjunction between the lines AC and BD is what is just in distribution, and this species of the just is a mean proportional, and the unjust is what violates the proportion; in fact, this mean proportional is the just proportion». In other words, the Mean Term of Distributive Justice is determined by the point of conjunction between lines AC and BD of a triangle ABC.
- Finally, Aristotle gives us the definition of the Rational Principle that underlies the Geometrical Proportion that we need to identify in order to be able to construct the Geometric Figure or διάγραμμα required by Aristotle, knowing that the ‘last step in the analysis seems to be the first step in the execution of the design’: «Mathematicians call this kind of proportion geometrical; for it is in geometrical proportion that it follows that the whole is to the whole as either part is to the corresponding part».
2.2. Proof of the Theorem: The Mean Term of Distributive Justice Is the Golden Ratio between the Three Opposite Criteria of Distribution
3. Demonstration
4. Discussion: How to Know the First Principles of Political Justice through the Dialectical Method
- I.
- The Efficient Cause of Political Justice. The efficient or promoting agent (κινέω) of the Just Distribution is love of Freedom, which means that only freemen can prudently choose the Rational Principle underlying the Golden Ratio, i.e., Geometrical Equality. Freemen like the Greeks, whose character blends courage and intelligence, i.e., capacities for self-government and for empire, while the people of «other nations inhabiting the cold places and those of Europe are full of spirit but somewhat deficient in intelligence and skill, so that they continue comparatively free, but lacking in political organization and capacity to rule their neighbors. The peoples of Asia on the other hand are intelligent and skillful in temperament, but lack spirit, so that they are in continuous subjection and slavery. But the Greek race participates in both characters, just as it occupies the middle position geographically, for it is both spirited and intelligent; hence it continues to be free and to have very good political institutions, and to be capable of ruling all mankind if it attains constitutional unity. The same diversity also exists among the Greek races compared with one another: some have a one-sided nature; others are happily blended in regard to both these capacities. It is clear therefore that people that are to be easily guided to virtue by the lawgiver must be both intellectual and spirited in their nature (…). Moreover, it is from this faculty that power to command and love of freedom are in all cases derived; for spirit is a commanding and indomitable element» [19]. Thus, Aristotle architecturally designs the internal structure of the Best Constitution (its social and political institutions) by applying the Distributive Principle of Geometrical Equality: citizens are divided into six classes with different functions, since it is necessary for the self-sufficient State to have the classes of (1) husbandmen (slaves or foreign servants), (2) artisans, (3) war-like class, (4) a well-to-do class, (5) priests and (6) judges of what is just and expedient. Having said this, the citizens who are to perform the constitutional functions must be absolutely free, i.e., they should not lead a mechanical or mercantile life (because such a life is ignoble and contrary to virtue), nor should they be cultivators of the land (for leisure is needed both for the development of virtue and for active participation in politics); that is why Aristotle (Politics VII, 8) limits the Citizenship to two classes—war-like class and judges—which will exercise power in turn according to their age and their virtues: courage, and theoretical and practical wisdom.
- II.
- The Material Cause of Political Justice. The material element (ὕλη) of the Just Distribution is Wealth. In the Nicomachean Ethics Aristotle refers primarily to property rights, using property to cover possessions, honor and bodily security, i.e., all those things to which an individual citizen may be entitled to the exclusion of all other citizens. In agreement with Joachim’s commentary, there is no doubt that Aristotle may be thinking partly of distributions of surplus revenue (e.g., from the silver mines), or of windfalls of public money (e.g., of gifts of corn from foreign potentates, or goods escheated of the State) [6] (p. 139–140). However, in the Politics and with reference to the Best Constitution, Aristotle opposes the Platonic idea that land ownerships should be common to all citizens, stating on the contrary that it should belong to those who possess arms and share political rights—i.e., war-like class and judges—, and that only the use of part of it should be in common to all in a spirit of friendship, so that no citizen should lack food: «It has been stated before that the land ought to be owned by those who possess arms and those who share the rights of the constitution, and why the cultivators ought to be a different caste from these, and what is the proper extent and conformation of the country. We have now to discuss first the allotment of the land, and the proper class and character of its cultivators; since we advocate not common ownership of land, as some have done, but community in it brought about in a friendly way by the use of it, and we hold that no citizen should be ill supplied with means of subsistence» [19] (Book VII, 9, 1329b 36–1330a 10). Consequently and applying the Distributive Principle of Geometrical Equality, Aristotle states that it is necessary to divide the land of the better State into two parts, of which one part shall be for common use and the other for private use. And each of these two parts shall again be divided into two: of the common lands, one part shall be used for religious functions, and the other for common meals; of the private lands, one part shall be situated in the district near the frontiers, and the other in the district near the city; after which, two lots of land shall be allotted to each citizen, so that each shall have a part of land in both districts. In this way and with this fair distribution of wealth, according to Aristotle, the demands of equality and justice would be fulfilled.
- III.
- The Final Cause of Political Justice. The end (τέλος), or the goal of the Just Distribution, is Virtue, which indicates that its purpose is not only the prevention of mutual crime or economic exchange but above all the Happy and Self-Sufficient Life in accordance with Virtue. Indeed, Aristotle explains that the difference between the Absolute Best Constitution and the Best Constitution in certain Circumstances lies in virtue, since Happiness is necessarily different from Prosperity. Actually: «The goal of the polis is the good life, and these things are means to that end. And a polis is an association of clans and villages in a perfect and self-sufficient existence, which in our view constitutes a happy and noble life. Therefore, the political communities must be considered to exist for the sake of good actions, and not for the sake of bare social life. Hence, those who contribute most to such an association have a greater share in the polis then those who are their equals or superiors in freedom or decent but not their equals in political virtue, or than those who surpass them in wealth but are surpassed by them in virtue» [19] (Book III, 9, 1281a 1–10). In fact, Aristotle explains that men have the same end both collectively and individually, and this end is Peace and Leisure, which are essential because peace is the end of war, while leisure is the end of business. Indeed, «courage and fortitude are necessary for business, love of wisdom for leisure, temperance and justice for both times, and more especially when men are at peace and have leisure» [19] (Book VII, 15, 1334a 24–26). Therefore, men should prefer to carry out theoretical and practical activity of the soul, trying to accumulate as many virtues as possible both intellectual and ethical, rather than preferring the accumulation of wealth, and external goods. In fact, accumulating great wealth cannot be the goal of the happy life, although most people today think it is. That is why Aristotle devotes the last Book of Politics to the Education of the Young, which in the Absolute Best Constitution must be public, unique and equal for all citizens.
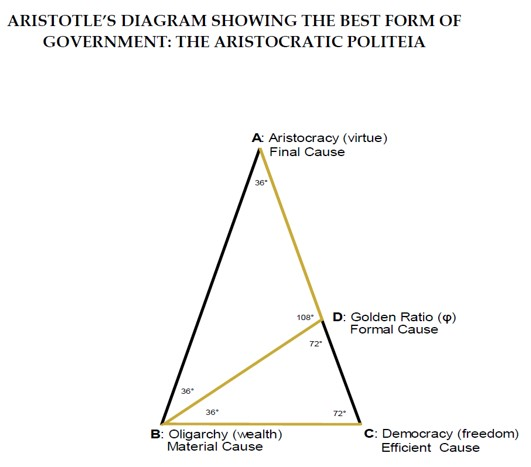
- IV.
- The Formal Cause of Political Justice. The form (μορφή), or the geometric figure of the Just Distribution, is determined by the Rational Principle underlying the Mean Term of Distributive Justice, that is, as we have seen, the Golden Ratio (Φ). And the Rational Principle underlying the Golden Ratio is Geometrical Equality, which is opposed to Arithmetical Equality, since it achieves the Unity or Harmony of Opposite Elements of the Polis, namely the Democratic, Oligarchic and Aristocratic classes. In fact, Geometrical Equality preserves harmony among citizens by preventing them from falling into the vice of πλεονεξία, greed or love of gain. Thus, the geometrical figure required by Aristotle, the Golden Triangle, indicates that the Geometric Mean of Aristotle’s Distributive Justice is relative to a Proportional Equality (the Golden Ratio) between the three opposing Criteria of distribution, so that none of them is more powerful than the others; therefore, Freedom is balanced by Wealth, Wealth by Virtue, and Virtue by Freedom. Moreover, the Aristotelian διάγραμμα also allows us to highlight Aristotle’s preferred criterion of distribution, ordering the three in a hierarchical manner. In fact, if the aim of the Absolute Best Constitution is the Happy and Self-Sufficient Life in accordance with Virtue, the first criterion of distribution to be considered must necessarily be Virtue (this is why I have placed Virtue at the apex of the Triangle). In this way the Aristotelian ideal would be realized, according to which those who are superior in political Virtue should deserve a greater share of economic and political rights than those who are equal or superior in Wealth or Freedom. From a purely mathematical point of view, finally, it is confirmed that in the bi-dimensional geometric figure of the Golden Triangle the Proportion is Continuous, i.e., divisible ad infinitum, as Aristotle had said; in fact, in the Golden Triangle the process of division can be repeated ad infinitum since, by sectioning the longest side with the shortest side, infinite isosceles triangles are formed that replicate the Golden Ratio. The rule in fact is that: «Golden triangles and gnomons can be sectioned into smaller triangles that are golden gnomons and triangles» [15] (p. 79). Additionally, in my opinion, Plato had already referred to the Golden Ratio, or Divine Proportion, when explaining his preference for Geometrical Equality over Arithmetical Equality. For Plato, Geometrical Equality is the best form of Equality because it refers to a ‘Small Measure’ that comes from the ‘Judgment of Zeus’. And this Divine Measure, though small, always produces good things when applied to Political Justice:«For there are two kinds of equality which, though identical in name, are often almost opposites in their practical results. The one of these any State or lawgiver is competent to apply in the assignment of honors—namely, the equality determined by measure, weight and number—by simply employing the lot to give even results in the distributions; but the truest and best form of equality is not an easy thing for everyone to discern. It is the judgment of Zeus, and men it never assists save in small measure, but in so far as it does assist either States or individuals, it produces all things good; for it dispenses more to the greater and less to the smaller, giving due measure to each according to nature; and with regard to honors also, by granting the greater to those that are greater in goodness, and the less to those of the opposite character in respect of goodness and education, it assigns in proportion what is fitting to each» [20,21].
5. Conclusions: If Happiness Is Necessarily Different from Prosperity, the Best Constitution Will Be the Aristocratic Politeia
«Let us then take it as agreed between us that to each man there falls just so large a measure of happiness as he achieves of virtue and wisdom or virtuous and wise action: in evidence of this we have the case of God, who is happy and blessed, but is so on account of no external goods, but on account of himself, and by being of a certain quality in his nature; since it is also for this reason that prosperity is necessarily different from happiness—for the cause of goods external to the soul is the spontaneous and fortune, but nobody is just or temperate as a result of or owing to the action of fortune. And connected is a truth requiring the same arguments to prove it, that it is also the best state, and the one that does well, that is happy» [19] Book VII, 1, 1323 b 20–30.
«In most states then the name of aristocracy is given to that form of constitutional government, for the combination aims only at the well-off and the poor, wealth and freedom (since in almost the largest number of states the rich seem to occupy the place of the gentry); but as there are three things that claim equal participation in the constitution, freedom, wealth and virtue (for the fourth, what is called nobility, accompanies the two latter—nobility means ancient wealth and virtue), it is manifest that the mixture of the two factors, the rich and the poor, ought to be termed πολιτεία, while the mixture of the three factors deserves the name of aristocratic most of all the various forms of aristocracy beside the true and best form» [19] Book IV, 8, 1294 a 10–25.
«But the actual overthrow of both πολιτεῖαι and aristocracies is mostly due to a deviation from justice in the actual framework of the constitution. For what starts it in the case of a πολιτείᾳ is that it does not contain a good blend of democracy and oligarchy; and in the case of an aristocracy, it is the lack of a good blend of those two elements and of virtue, but chiefly of the two elements (I mean popular government and oligarchy), for both πολιτεῖαί and most of the constitutions that are called aristocracies aim at blending these. For this is the point of distinction between aristocracies and what are called πολιτειῶν, and it is owing to this that some of them are less and others more stable. (…) Small reforms lead to revolution. And aristocracies are most liable to undergo revolution unobserved, through gradual relaxation, just as it has been said in what has gone before about all forms of constitution in general, that even a small change may cause a revolution. For when they give up one of the details of the constitution, afterwards they also make another slightly bigger change more readily, until they alter the whole system» [19] Book V, 1307a 7–1307b 8.
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
| 1 | Area ABC = 100 × 153.88/2 = 7694.0; Area BDA = 161.8 × 58.78/2 = 4755.4; Area CBD = 61.8 × 95.11/2 = 2938.8. |
| 2 | [11], In agreement with Burnet, who explains that the Greek word μεσότης does not mean “only or even primarily the arithmetical mean” but is “the oldest word for a proportion of any kind however determined”, that is, also or even mainly the geometrical mean. |
| 3 | [6] (p. 90), For a συνεχής (continuum) is essentially divisible into parts themselves continuous and therefore divisible, and so on ad infinitum. A continuous quantum -e.g., an extensive continuous quantum like a line, or an intensive continuous quantum like a feeling—is such that it can always be divided into smaller parts or lesser degrees, but never into smallest parts or least degrees. Within any continuum you can always take a length or a degree exactly so long or intense as you require (the length or intensity being, of course, less than the whole). |
| 4 | [4] (p. 131), Quantity which is continuous is not merely divisible, but divisible ad infinitum: it has no indivisible, atomic, parts. This is the definition of continuous in De Caelo 268a6 and Physics 231b16. Thus, the sense conveyed by the whole phrase is that of ‘continuous, i.e., divisible ad infinitum’. |
| 5 | [3] Note to 1112 b21: Aristotle has in mind the method of discovering the solution of a geometrical problem. The problem being to construct a figure of a certain kind, we suppose it constructed and then analyze it to see if there is some figure by constructing which we can construct the required figure, and so on till we come to a figure which our existing knowledge enables us to construct. |
| 6 | [12], Book I, Definition 1: “A point is that which hath no part, or which hath no magnitude”). According to Pythagoras, the number one (μοναδικοῦ ἀριθμοῦ) or the Pythagorean unitary point is indivisible, and this constitutes the first axiom of the mathematical sciences. What Aristotle probably means here is that no proportion can be constructed on the basis of a single term because the number one is indivisible. As we know, according to Euclid, at least three terms are needed to construct a proportion (continuous proportion). |
| 7 | [13], According to the Arabic version of the Nicomachean Ethics, the relative pronouns “οἷς τε καὶ ἅ” clearly refer to the terms of the Continuous proportion that Aristotle has just finished explaining: A/B= B/C. Unfortunately, these relative pronouns have been translated and interpreted as if they referred to the ‘persons and things’ Aristotle spoke of in the previous paragraph, when he introduced the Discrete proportion A/B= C/D. Nothing could be further from the interpretative truth. |
| 8 | This sentence of the geometric problem is the most difficult to translate and understand. It is probably the reason why scholars have made very serious mistakes in interpreting it and have not been able to solve the theorem. It is a double negative, and the meaning of the sentence should be as follows: “This proportion is continuous in several dimensions ad infinitum, and not only in one”. Double negatives are perfectly correct in ancient Greek; and we can be sure that Aristotle, as the father of formal logic, knew how to use them very well. |
| 9 | [2], EN, Book V, 1131 a 25–1131 b-14: «Τὸ γὰρ δίκαιον ἐν ταῖς διανομαῖς ὁμολογοῦσι πάντες κατ᾿ ἀξίαν τινὰ δεῖν εἶναι, τὴν μέντοι ἀξίαν οὐ τὴν αὐτὴν λέγουσι πάντες [ὑπάρχειν], ἀλλ᾿ οἱ μὲν δημοκρατικοὶ ἐλευθερίαν, οἱ δ᾿ ὀλιγαρχικοὶ πλοῦτον, οἱ δ᾿ εὐγένειαν, οἱ δ᾿ ἀριστοκρατικοὶ ἀρετήν. ἔστιν ἄρα τὸ δίκαιον ἀνάλογόν τι. Τὸ γὰρ ἀνάλογον οὐ μόνον ἐστὶ μοναδικοῦ ἀριθμοῦ ἴδιον, ἀλλ᾽ ὅλως ἀριθμοῦ: ἡ γὰρ ἀναλογία ἰσότης ἐστὶ λόγων, καὶ ἐν τέτταρσιν ἐλαχίστοις. ἡ μὲν οὖν διῃρημένη ὅτι ἐν τέτταρσι, δῆλον. ἀλλὰ καὶ ἡ συνεχής: τῷ γὰρ ἑνὶ ὡς δυσὶ χρῆται καὶ δὶς λέγει, οἷον ὡς ἡ τοῦ α πρὸς τὴν τοῦ β, οὕτως ἡ τοῦ β πρὸς τὴν τοῦ γ. Δὶς οὖν ἡ τοῦ β εἴρηται: ὥστ᾽ ἐὰν ἡ τοῦ β τεθῇ δίς, τέτταρα ἔσται τὰ ἀνάλογα. ἔστι δὲ καὶ τὸ δίκαιον ἐν τέτταρσιν ἐλαχίστοις, καὶ ὁ λόγος ὁ αὐτός: διῄρηται γὰρ ὁμοίως οἷς τε καὶ ἅ. ἔσται ἄρα ὡς ὁ α ὅρος πρὸς τὸν β, οὕτως ὁ γ πρὸς τὸν δ, καὶ ἐναλλὰξ ἄρα, ὡς ὁ α πρὸς τὸν γ, ὁ β πρὸς τὸν δ. ὥστε καὶ τὸ ὅλον πρὸς τὸ ὅλον: ὅπερ ἡ νομὴ συνδυάζει, κἂν οὕτω συντεθῇ, δικαίως συνδυάζει. ἡ ἄρα τοῦ α ὅρου τῷ γ καὶ ἡ τοῦ β τῷ δ σύζευξις τὸ ἐν διανομῇ δίκαιόν ἐστι, καὶ μέσον τὸ δίκαιον τοῦτ᾽ ἐστί, τὸ δ᾽ ἄδικον τὸ παρὰ τὸ ἀνάλογον: τὸ γὰρ ἀνάλογον μέσον, τὸ δὲ δίκαιον ἀνάλογον. Καλοῦσι δὲ τὴν τοιαύτην ἀναλογίαν γεωμετρικὴν οἱ μαθηματικοί: ἐν γὰρ τῇ γεωμετρικῇ συμβαίνει καὶ τὸ ὅλον πρὸς τὸ ὅλον ὅπερ ἑκάτερον πρὸς ἑκάτερον. ἔστι δ᾽ οὐ συνεχὴς αὕτη ἡ ἀναλογία: οὐ γὰρ γίνεται εἷς ἀριθμῷ ὅρος, ᾧ καὶ ὅ. Τὸ μὲν οὖν δίκαιον τοῦτο, τὸ ἀνάλογον: τὸ δ᾽ ἄδικον τὸ παρὰ τὸ ἀνάλογον». |
| 10 | [4] (p. 189), There is no question here of arriving at a knowledge of the mean by a mathematical calculation, or quasi-calculation, which starts from a knowledge of extremes. The data required for pin-pointing the mean, the right size of the share to be assigned, are the relative merit of the recipients and the amount to be distributed. |
| 11 | [14], By distribution of honour, Aristotle means the distribution of office in accordance with the underlying hypotheses of the particular state that free status, wealth, noble birth, or virtue is to be the standard. This conception plays a large part in the Politics. |
| 12 | [6] (p. 138), Aristotle was thinking of the fundamental legislative acts by which privileges, powers and places were assigned to the constituent members or estates of the political community. But such distribution would require practical wisdom, which is an intellectual virtue, in its highest form, like the legislative genius of the architectural statesman. |
| 13 | [12], Book VI, Definition 3: A straight line is said to be cut into extreme and mean ratio, when the whole is to the greater segment, as the greater is to the lesser. |
| 14 | [12], (Book IV, Preposition 10): «To describe an isosceles triangle, having each of the angles at the base double of the third angle». |
| 15 | [15], The first definition of the Golden Ratio, in relation to areas, is given somewhat obliquely in Book II. A second, clearer definition, in relation to proportion, appears in Book VI. Euclid then uses the Golden Ratio, especially in the construction of the pentagon (in Book IV) and in the construction of the icosahedron and dodecahedron (in Book XIII). |
| 16 | |
| 17 | [18], Aristotle describes two methods of inquiry that begin from our initial beliefs and the things we intuitively recognise, the ‘things known to us’, and claim to reach principles ‘known by nature’. Empirical inquiry begins from perception, proceeds by induction and generalisation, and tests theories by appeal to experience. Dialectic inquiry begins from common beliefs, proceeds by raising and solving puzzles, and tests theories against common beliefs. Distinguishing these two methods is useful since they suggest two ways of passing the metaphysical realist test for genuine first principles. |
| 18 | [22], «Finally, in Book Seven of the Politics, where Aristotle outlines the characteristics of the optimal constitution in the absolute sense (Aristocratic Politeia), pausing to illustrate the ideal number of citizens of which a city should be formed, the ideal region in which it should be located, the ideal qualities that the citizens should possess, and other such particulars, he returns to the problem of who is to exercise power, and observes that, as the citizens of such a city are of course all equal, government among equal persons can only be exercised in turn, so that all, first or second, command and all, first or second, obey. He even goes so far as to indicate when the citizens themselves must govern and when they must obey, and states that when young, having above all strength, they must obey, and in particular serve the city with arms, while when old, having above all wisdom, they must govern. The important thing is that all of them, being equal, should obey at one time of their lives, for example by waging war or doing business, and at another time rule. On the contrary, the important thing is to remember that, since the polis has as its end the good life, that is, happiness, instrumental activities, such as war and business, are means oriented towards activities that are ends in themselves, such as, respectively, peace and the good use of leisure time». |
References
- Gauthier, R.A.; Jolif, J.Y. Aristotle: L’Éthique, À Nicomaque; Vol. I, Introduction and Translation; Vol. II, Commentary; Nauwelaerts: Louvain, Belgium, 1959. [Google Scholar]
- Rackham, H. Aristotle. In Nicomachean Ethics; Harvard University Press: Cambridge, MA, USA, 1934. [Google Scholar]
- Ross, W.D. The Works of Aristotle Translated into English; Volume IX, Ethica Nicomachea; Oxford University Press: Oxford, UK, 1925. [Google Scholar]
- Hardie, W.F.R. Aristotle’s Ethical Theory; Oxford University Press: Oxford, UK, 1980. [Google Scholar]
- Tricot, J. Aristote. In Étique à Nícomaque; Vrin: Paris, France, 1987. [Google Scholar]
- Joachim, H.H. The Nicomachean Ethics. In A Commentary by the Late; Rees, D.A., Ed.; Clarendon Press: Oxford, UK, 1951; p. 141. [Google Scholar]
- Salamone, M.A. The Aristotelian paradigm of distributive justice: The golden triangle. In Philosophy, Politics and Economics, Proceeding of the 23rd International Conference of Philosophy, Politics and Economics in the Global Era, Athens, Greece, 17–22 July 2011; Adam, M., Boudouris, K., Eds.; Iona Publications: Athens, Greece, 2014; pp. 207–221. [Google Scholar]
- Salamone, M.A. Equality and Justice in Early Greek Cosmologies: The Paradigm of the Line of the Horizon. Philos. Cosmol. 2017, 18, 22–31. [Google Scholar]
- Sen, A. The Idea of Justice; Harvard University Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Knoll, M.; Snyder, S.; Şimsek, N. New Perspectives on Distributive Justice: Deep Disagreements, Pluralism, and the Problem of Consensus; De Gruyter: Berlin, Germany; Boston, MA, USA, 2019. [Google Scholar]
- Burnet, J. The Ethics of Aristotle; Metheuen: London, UK, 1900; p. 70. [Google Scholar]
- Euclid-Heath, T. The Thirteen Books of Euclid’s Elements, 2nd ed.; Heath, T., Ed.; Cambridge University Press: Cambridge, UK; New York, NY, USA; Dover, UK, 1956. [Google Scholar]
- Fidora, A.; Akasoy, A. The Arabian Version of Nicomachean Ethics, 1st ed.; Brill: Leiden, The Netherlands, 2005; p. 32. [Google Scholar]
- Ross, W.D. Aristotle; Routledge: London, UK; New York, NY, USA, 1995. [Google Scholar]
- Livio, M. The Golden Ratio: The Story of PHI, the World’s Most Astonishing Number; Broadway Books: New York, NY, USA, 2002. [Google Scholar]
- Aristotle. Metaphysics, Volume I: Books 1–9; Tredennick, H., Ed.; Harvard University Press: Cambridge, MA, USA, 1933; Book VIII. [Google Scholar]
- Aristotle. On the Cosmos; Forster, E.S., Furley, D.J., Eds.; Harvard University Press: Cambridge, MA, USA, 1955; Chapter V. [Google Scholar]
- Irwin, T. Aristotle’s First Principles; Oxford University Press: Oxford, UK, 1988. [Google Scholar]
- Aristotle. Politics; Rackham, H., Ed.; Harvard University Press: Cambridge, MA, USA, 1932. [Google Scholar]
- Plato. Laws, Volume I: Books 1–6; Bury, R.G., Ed.; Harvard University Press: Cambridge, MA, USA, 1926. [Google Scholar]
- Salamone, M.A. The Two Supreme Principles of Plato’s Cosmos—The One and the Indefinite Dyad—The Division of a Straight Line into Extreme and Mean Ratio, and Pingala’s Mātrāmeru. Symmetry 2019, 11, 98. [Google Scholar] [CrossRef] [Green Version]
- Berti, E. Aristotele e la democrazia. In Aristotele e la storia; Rossitto, C., Coppola, A., Biasutti, F., Eds.; CLEUP: Padova, Italy, 2013; pp. 32–52. [Google Scholar]
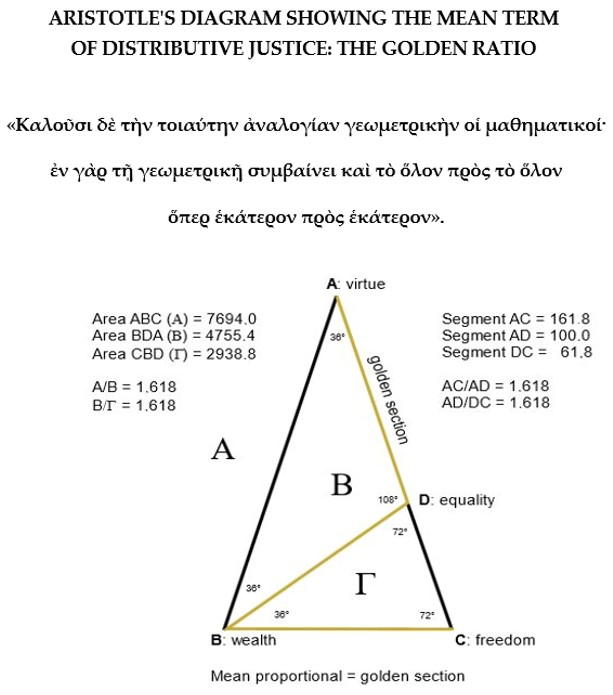
| A/B = B/Γ1 (τὸ ὅλον πρὸς τὸ ὅλον) |
| 7694.0/4755.4 = 4755.4/2938.8 = Φ = 1.618 |
| AC/AD = AD/DC (ὅπερ ἑκάτερον πρὸς ἑκάτερον) |
| 161.8/100 = 100/61.8 = Φ = 1.618 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salamone, M.A. Aristotle’s Political Justice and the Golden Ratio between the Three Opposing Criteria for the Distribution of Public Goods among Citizens: Freedom, Wealth and Virtue. Philosophies 2021, 6, 96. https://doi.org/10.3390/philosophies6040096
Salamone MA. Aristotle’s Political Justice and the Golden Ratio between the Three Opposing Criteria for the Distribution of Public Goods among Citizens: Freedom, Wealth and Virtue. Philosophies. 2021; 6(4):96. https://doi.org/10.3390/philosophies6040096
Chicago/Turabian StyleSalamone, Maria Antonietta. 2021. "Aristotle’s Political Justice and the Golden Ratio between the Three Opposing Criteria for the Distribution of Public Goods among Citizens: Freedom, Wealth and Virtue" Philosophies 6, no. 4: 96. https://doi.org/10.3390/philosophies6040096
APA StyleSalamone, M. A. (2021). Aristotle’s Political Justice and the Golden Ratio between the Three Opposing Criteria for the Distribution of Public Goods among Citizens: Freedom, Wealth and Virtue. Philosophies, 6(4), 96. https://doi.org/10.3390/philosophies6040096





