Neural Crypto-Coding Based Approach to Enhance the Security of Images over the Untrusted Cloud Environment
Abstract
1. Introduction
- Sharing the secret key between two parties.
- Keeping the secret key secure from the intruder so that communication is not compromised.
- A new key generation technique for securing the shared key of AES and a new subkey generation technique to strengthen the KSA.
- Instead of treating encryption and encoding as two separate steps, our approach combines them into a single step. This helps to achieve the security and reliability of image data over the internet.
- The new technique successfully passes the key strength analysis tests, such as frequency test, bit independence test, and bitwise uncorrelation test.
2. Related Work, Research Gap, and Problem Formulation
- Most of the approaches involve chaos-based and/or hybrid techniques for key generation and encryption. However, of the approaches are limited to academic interest rather than real-world application, because of problems such as insufficient security analysis, flawed design methodology, and low efficiency.
- Few research papers focus on key generation with minimal or no key strength analysis.
- None of the researchers provided a holistic end-to-end solution ensuring the security and reliability of data at rest and during transmission.
- The scope of our work focuses on AES, since it is widely used in the industry because of its versatility and ease of use.
- Multi-layered architecture comprising key generation using neural key exchange protocol from the shared secret key.
- Improving nonlinearity of subkey using the Khazad function.
- Combining encryption and encoding in a single step to provide secure and reliable data transfer.
- Detailed analysis comprising statistical, differential, and key strength analysis.
3. System Architecture
- (1)
- The data owner has sensitive data/files (personally identifiable information) that needs to be stored in the cloud in encrypted form (detailed in the proposed system architecture: steps 1 through 4).
- (2)
- Data owners and authorized users share a single secret key. On both sides, a new key is generated for encryption/decryption using the neural key exchange protocol. The user can be an owner as well (detailed in the proposed system architecture: steps 8 and 9).
- (3)
- When an authorized user wants to recover the original data/file, he/she downloads the encrypted files from the cloud, generates the key and executes the decryption algorithm, and gets back the corresponding original data/files (detailed in the proposed system architecture: steps 5, 6 and 7).
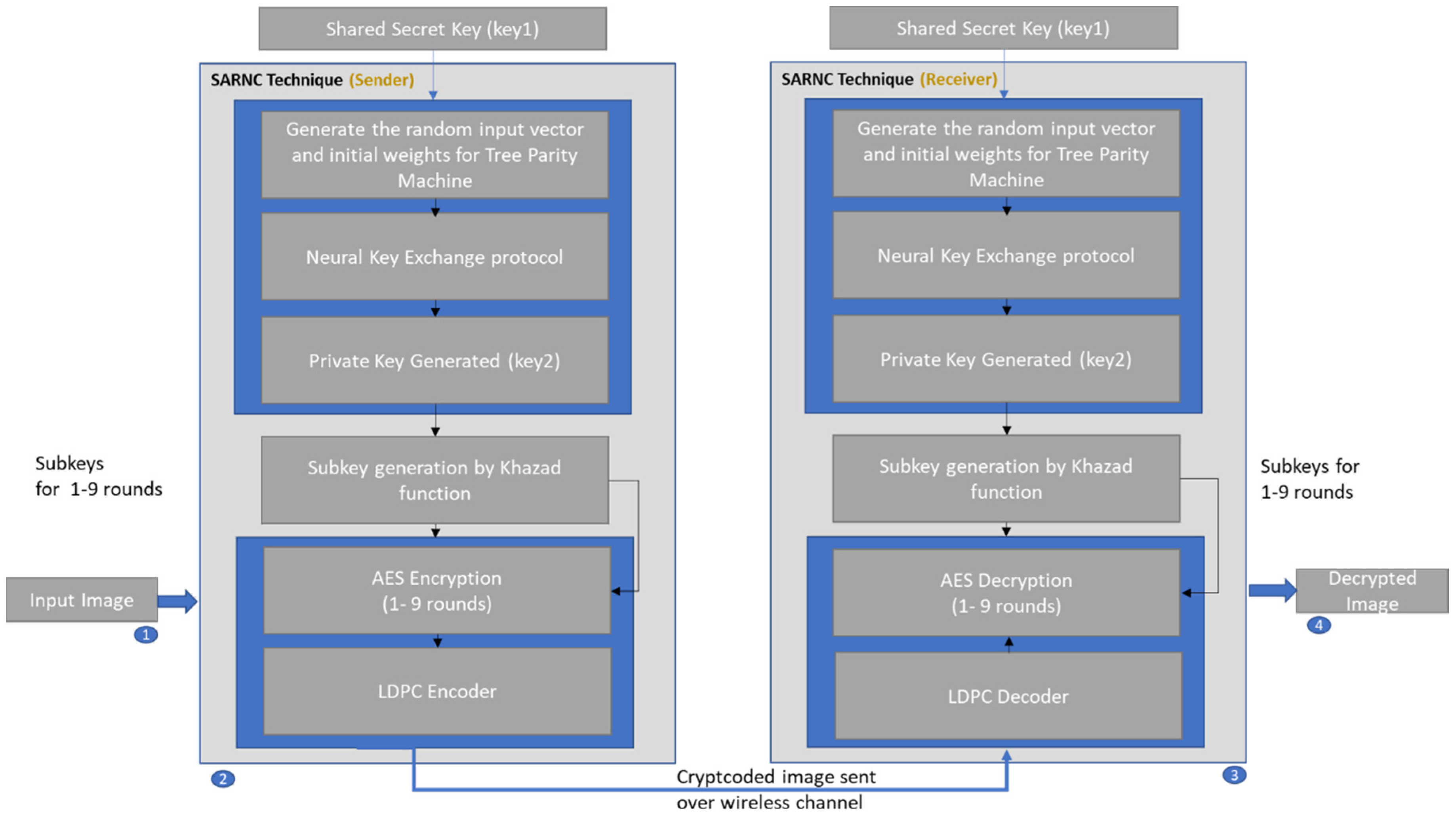
4. Methodology
4.1. Key Generation by Neural Key Exchange Protocol
| Algorithm 1: Tree Parity Machine | |
| Given I[n] | |
| I is the input vector of size n. | |
| Given H, M, L | |
| H—The number of hidden neurons. | |
| M—The number of input neurons connected to hidden neurons. | |
| L—Defines the range of each weight {−L, 0, +L} | |
| Weights Wij = {−L, ….., 0,….., L} | |
| (1) | |
| is the activation function. | |
| τ | (2) |
| Algorithm 2: Hebbian Rule | |
| , τ1, τ2, l} | |
| for each (i, j) in W do, | |
| (3) | |
| (4) | |
| end for | |
| where, | |
4.2. Subkey Generation
4.3. Block Diagram of AES–LDPC Cryptcoding
5. Security Analysis, Performance Evaluation, and Discussion
5.1. Key Strength Analysis of Proposed Key/Subkey Generation Technique
5.1.1. Frequency Test
5.1.2. Bit Independence Tests (BITs)
- (i)
- Completeness (dc): a function f is said to be complete if each output bit depends upon all input bits.
- (ii)
- Avalanche effect (da): a function f has the avalanche effect if a one bit change in input affects more than half of the output bits.
- (iii)
- Strict avalanche criteria (SAC-dsa): a function f satisfies the SAC if the complement of a single bit in input affects more than half of the output bits.
5.1.3. Bitwise Uncorrelation Tests (BUCT)
- A bitwise uncorrelation test finds out if all subkeys are bitwise uncorrelated with each other.
- A new sequence is generated by using Equation (15). Sequence generation is conducted by XORing all possible combinations of bits of subkeys Xi and Xj.
- (i)
- Frequency test: this test is the same as the one explained in Section 5.1.1. However, this test is carried out on the sequence generated by Equation (15).
- (ii)
- Poker test: this test finds out how many times the p-bit block appears in the sequence derived from Equation (18). The sequence is divided into N non-overlapping blocks, each of length P. bi is the ith bit of a P-bit sequence. Equation (16) is used to find a distribution of P-bit blocks.
5.2. Performance Parameters
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ramachandran, B.; Subramaniam, K. Secure and efficient data forwarding in untrusted cloud environment. Clust. Comput. 2019, 22, 3727–3735. [Google Scholar] [CrossRef]
- Wang, H.; Wu, S.; Chen, M.; Wang, W. Security protection between users and the mobile media cloud. IEEE Commun. Mag. 2014, 52, 73–79. [Google Scholar] [CrossRef]
- Kaur, J.; Sharma, S. HESSIS: Hybrid Encryption Scheme for Secure Image Sharing in a Cloud Environment. In Proceedings of the International Conference on Advanced Informatics for Computing Research, Shimla, India, 14–15 July 2018; Springer: Singapore, 2018; pp. 204–216. [Google Scholar]
- Pasupuleti, S.K.; Ramalingam, S.; Buyya, R. An efficient and secure privacy-preserving approach for outsourced data of resource constrained mobile devices in cloud computing. J. Netw. Comput. Appl. 2016, 64, 12–22. [Google Scholar] [CrossRef]
- Saha, R.; Geetha, G.; Kumar, G.; Kim, T.-H. RK-AES: An Improved Version of AES Using a New Key Generation Process with Random Keys. Secur. Commun. Netw. 2018, 2018, 9802475. [Google Scholar] [CrossRef]
- Zeghid, M.; Machhout, M.; Khriji, L.; Baganne, A.; Tourki, R. A modified AES based algorithm for image encryption. Int. J. Comput. Sci. Eng. 2007, 1, 70–75. [Google Scholar]
- Awan, I.A.; Shiraz, M.; Hashmi, M.U.; Shaheen, Q.; Akhtar, R.; Ditta, A. Secure framework enhancing AES algorithm in cloud computing. Secur. Commun. Netw. 2020, 2020, 8863345. [Google Scholar] [CrossRef]
- Chourasia, S.; Bharadwaj, H.C.; Das, Q.; Agarwal, K.; Lavanya, K. Vectorized neural key exchange using tree parity machine. Compusoft 2019, 8, 3140–3145. [Google Scholar]
- Wang, Z.-X.; Lou, Y.; Wang, W.-Q.; Zhang, M.; Li, X.-L. Research on the application of LDPC code in chaotic sequence image encryption. Clust. Comput. 2019, 22, 6359–6370. [Google Scholar] [CrossRef]
- Gupta, M.; Gupta, M.; Deshmukh, M. Single secret image sharing scheme using neural cryptography. Multimed. Tools Appl. 2020, 79, 12183–12204. [Google Scholar] [CrossRef]
- Li, N.; Lin, K.; Lin, W.; Deng, Z. A joint encryption and error correction method used in satellite communications. China Commun. 2014, 11, 70–79. [Google Scholar]
- Mursi, M.F.M.; Ahmed, H.E.H.; El-Samie, F.E.A.; El-Aziem, A.H.A. Combination of Hybrid Chaotic Encryption and LDPC for Secure Transmission of Images over Wireless Networks. Int. J. Image Graph. Signal Process. 2014, 6, 8–16. [Google Scholar] [CrossRef]
- Pisek, E.; Abu-Surra, S.; Taori, R.; Dunham, J.; Rajan, D. Enhanced cryptcoding: Joint security and advanced dual-step quasi-cyclic LDPC coding. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–7. [Google Scholar]
- Afzal, S.; Yousaf, M.; Afzal, H.; Alharbe, N.; Mufti, M.R. Cryptographic strength evaluation of key schedule algorithms. Secur. Commun. Netw. 2020, 2020, 3189601. [Google Scholar] [CrossRef]
- Shakir, H.R. An image encryption method based on selective AES coding of wavelet transform and chaotic pixel shuffling. Multimed. Tools Appl. 2019, 78, 26073–26087. [Google Scholar] [CrossRef]
- Liu, J.; Tong, X.; Liu, Y.; Zhang, M.; Ma, J. A joint encryption and error correction scheme based on chaos and LDPC. Nonlinear Dyn. 2018, 93, 1149–1163. [Google Scholar] [CrossRef]
- Arab, A.; Rostami, M.J.; Ghavami, B. An image encryption method based on chaos system and AES algorithm. J. Supercomput. 2019, 75, 6663–6682. [Google Scholar] [CrossRef]
- Rahman, Z.; Yi, X.; Billah, M.; Sumi, M.; Anwar, A. Enhancing AES Using Chaos and Logistic Map-Based Key Generation Technique for Securing IoT-Based Smart Home. Electronics 2022, 11, 1083. [Google Scholar] [CrossRef]
- Lakshmi, C.; Thenmozhi, K.; Rayappan, J.B.B.; Rajagopalan, S.; Amirtharajan, R.; Chidambaram, N. Neural-assisted image-dependent encryption scheme for medical image cloud storage. Neural Comput. Appl. 2021, 33, 6671–6684. [Google Scholar] [CrossRef]
- Kakkad, V.; Patel, M.; Shah, M. Biometric authentication and image encryption for image security in cloud framework. Multiscale Multidiscip. Model. Exp. Des. 2019, 2, 233–248. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Q.; Ren, K.; Cao, N.; Lou, W. Toward Secure and Dependable Storage Services in Cloud Computing. IEEE Trans. Serv. Comput. 2011, 5, 220–232. [Google Scholar] [CrossRef]
- Sood, S.K. A combined approach to ensure data security in cloud computing. J. Netw. Comput. Appl. 2012, 35, 1831–1838. [Google Scholar] [CrossRef]
- Elhoseny, M.; Ramírez-González, G.; Abu-Elnasr, O.M.; Shawkat, S.A.; Arunkumar, N.; Farouk, A. Secure medical data transmission model for IoT-based healthcare systems. IEEE Access 2018, 6, 20596–20608. [Google Scholar] [CrossRef]
- Raja, S.P. Joint medical image compression–encryption in the cloud using multiscale transform-based image compression encoding techniques. Sādhanā 2019, 44, 28. [Google Scholar] [CrossRef]
- Mondal, B.; Mandal, T. A light weight secure image encryption scheme based on chaos & DNA computing. J. King Saud Univ. Comput. Inf. Sci. 2017, 29, 499–504. [Google Scholar]








| Paper | Correlation Coefficient | Histogram Analysis | Entropy | NPCR | UACI | BER | PSNR | MSE | SSIM | Key Strength Analysis |
|---|---|---|---|---|---|---|---|---|---|---|
| [1] | Communication cost, encryption, and decryption time analysis | |||||||||
| [10] | ✓ | ✓ | ✓ | |||||||
| [6] | ✓ | ✓ | ✓ | |||||||
| [17] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| [19] | ✓ | ✓ | ✓ | |||||||
| [20] | Analysis to check Accuracy, cost and devices required | |||||||||
| [5] | Related key attack analysis, Fault injection analysis, Differential and Linear cryptanalysis | |||||||||
| [18] | Cryptanalysis, Calculation of key generation time analysis | |||||||||
| [15] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| [12] | ✓ | ✓ | ✓ | |||||||
| [16] | ✓ | ✓ | ||||||||
| [11] | ✓ | ✓ | ||||||||
| [13] | ✓ | |||||||||
| [14] | ✓ | |||||||||
| Proposed Approach (SARNC) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Modulation | BPSK |
| Coding | LDPC |
| Code rate | 1/2 |
| Frame size | 64,800 |
| No. of iterations | 10 |
| Channel | AWGN |
| Ciphering | AES-128 with LDPC coding |
| Completeness dc | Avalanche da | Strict Avalanche dsa | |
|---|---|---|---|
| Proposed SARNC technique | 1 | 1 | 0.904879 |
| Original AES-128 | 0.7 | 0.7 | 0.605883 |
| Frequency Test in (%) | Poker Test in (%) | |
|---|---|---|
| Proposed SARNC technique | 98 | 94.5 |
| Original AES-128 | 97 | 93.6 |
| Original AES-128 | Ref. [21] | Ref. [24] | Ref. [25] | Proposed SARNC Technique | |
|---|---|---|---|---|---|
| PSNR | 36.1236 | - | 54.26 | - | 48.1648 |
| MSE | 16 | - | 0.24 | - | 1 |
| SSIM | 0.7495 | - | 0.99 | - | 0.99996 |
| Correlation coefficient | −0.0121 | −0.0036 | - | 0.001178542895092 | −0.0074 |
| NPCR (%) | 99.4141 | 99.60 | - | 99.7570 | 99.5117 |
| UACI (%) | 33.2802 | 33.41 | - | 39.12 | 33.2837 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kulkarni, P.; Khanai, R.; Torse, D.; Iyer, N.; Bindagi, G. Neural Crypto-Coding Based Approach to Enhance the Security of Images over the Untrusted Cloud Environment. Cryptography 2023, 7, 23. https://doi.org/10.3390/cryptography7020023
Kulkarni P, Khanai R, Torse D, Iyer N, Bindagi G. Neural Crypto-Coding Based Approach to Enhance the Security of Images over the Untrusted Cloud Environment. Cryptography. 2023; 7(2):23. https://doi.org/10.3390/cryptography7020023
Chicago/Turabian StyleKulkarni, Pallavi, Rajashri Khanai, Dattaprasad Torse, Nalini Iyer, and Gururaj Bindagi. 2023. "Neural Crypto-Coding Based Approach to Enhance the Security of Images over the Untrusted Cloud Environment" Cryptography 7, no. 2: 23. https://doi.org/10.3390/cryptography7020023
APA StyleKulkarni, P., Khanai, R., Torse, D., Iyer, N., & Bindagi, G. (2023). Neural Crypto-Coding Based Approach to Enhance the Security of Images over the Untrusted Cloud Environment. Cryptography, 7(2), 23. https://doi.org/10.3390/cryptography7020023






