The Relationship between Environmental Factors and Catch Abundance of Hairtail in the East China Sea Using Empirical Dynamic Modeling
Abstract
:1. Introduction
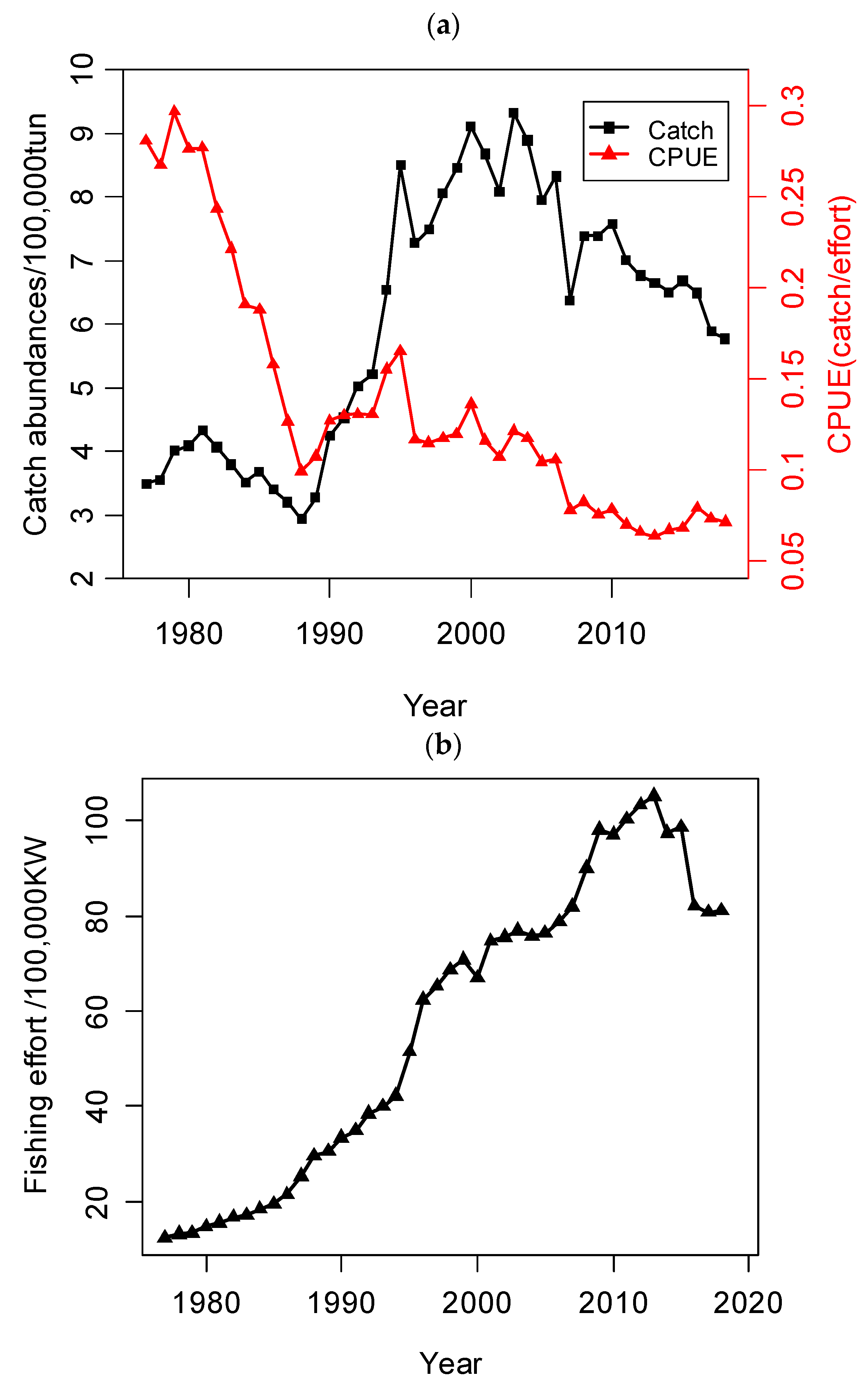
2. Materials: Study Area and Dataset
3. Method
3.1. Attractor Reconstruction
3.2. Prediction
3.3. Causality Test and Analysis
3.4. Multivariate Analysis
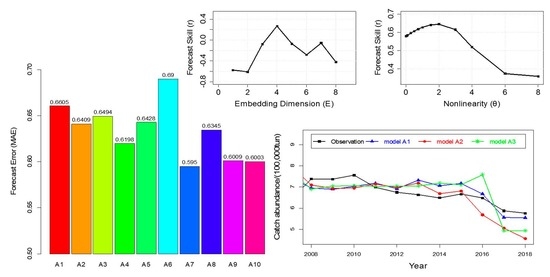
4. Results
4.1. Nonlinearity Analysis and Causality Analysis
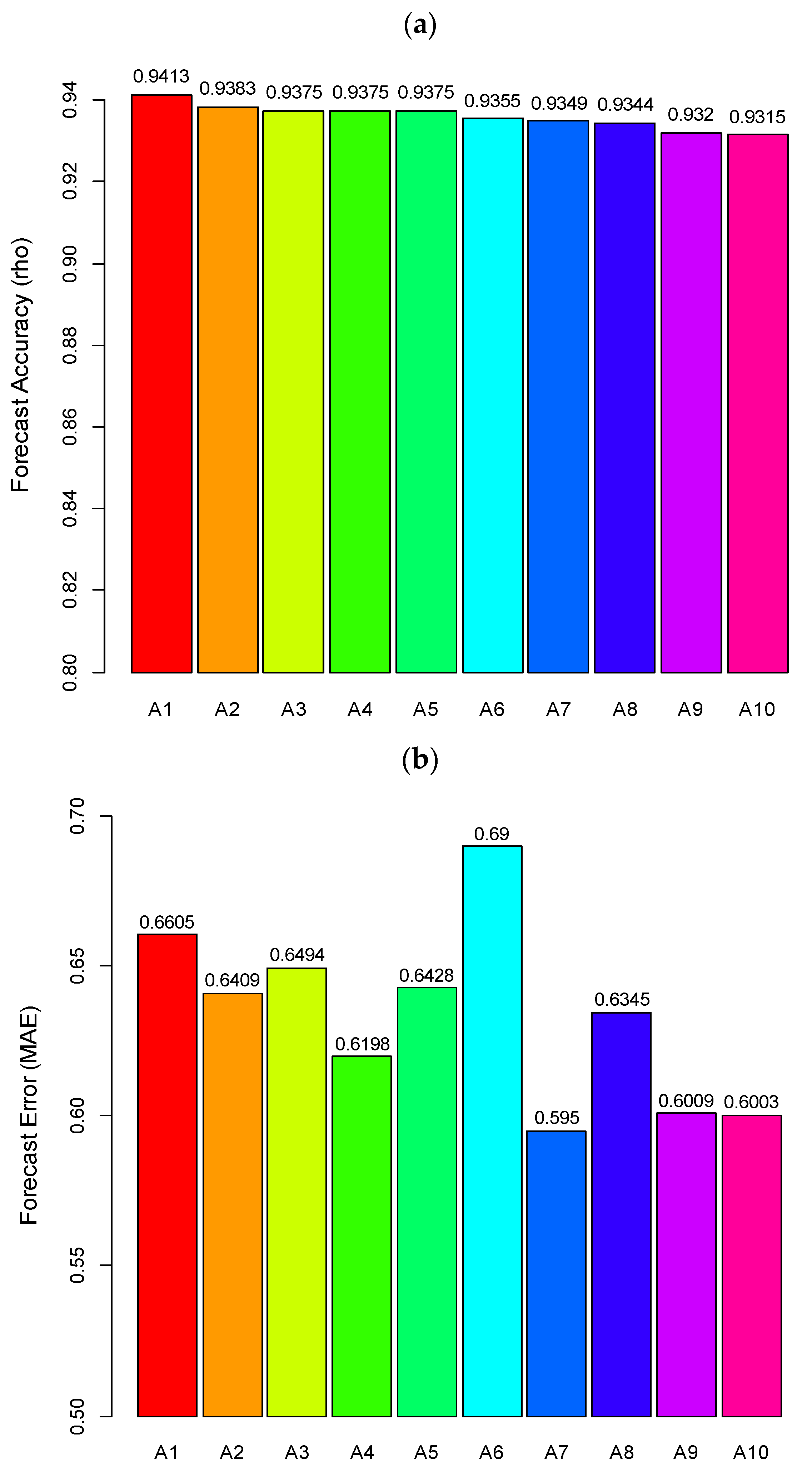
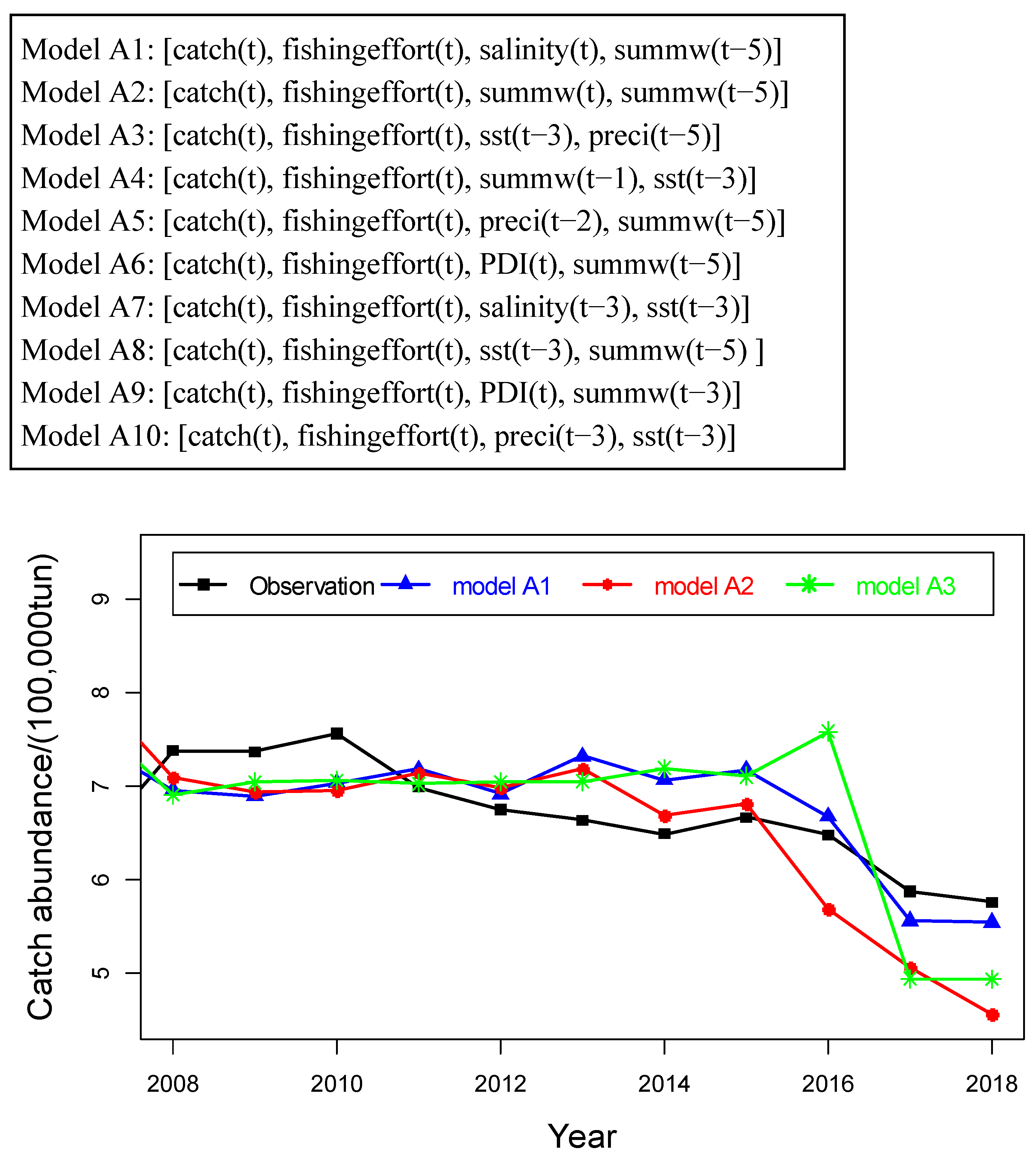
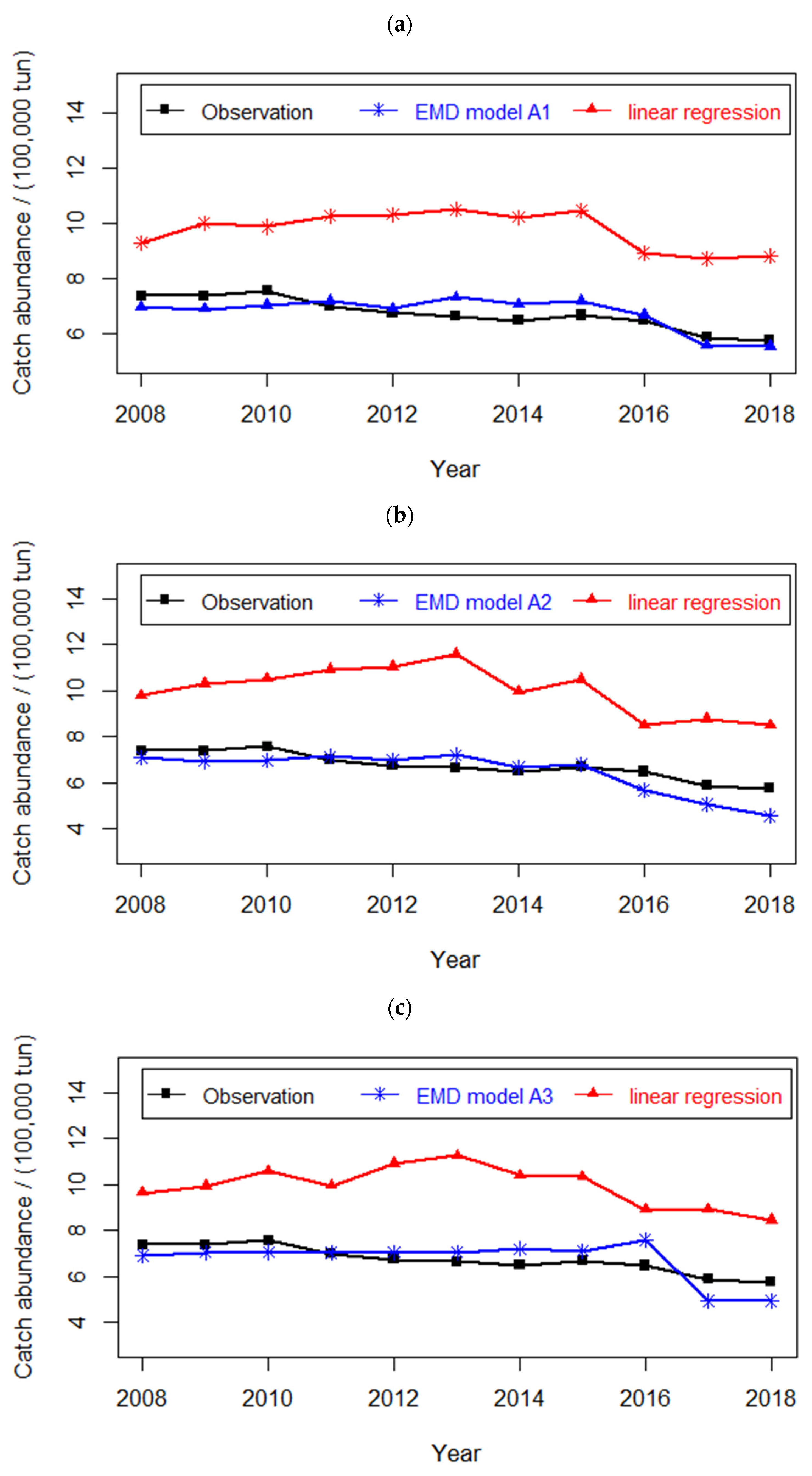
4.2. Prediction of Hairtail Abundances: Model Generation and Validation
4.3. Comparison of Catch Forecast Models
5. Discussion
5.1. Environmental Factors
5.2. EDM for Nonlinear Analysis
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sun, P.; Chen, Q.; Fu, C.; Zhu, W.; Li, J.; Zhang, C.; Yu, H.; Sun, R.; Tian, Y. Daily growth of young-of-the-year largehead hairtail (Trichiurus japonicas) in relation to environmental variable in the East China Sea. J. Mar. Syst. 2020, 201, 103243. [Google Scholar] [CrossRef]
- Qiu, Y.; Lin, Z.; Wang, Y. Responses of fish production to fishing and climate variability in the northern South China Sea. Prog. Oceanogr. 2010, 85, 197–212. [Google Scholar] [CrossRef]
- Wang, Y.; Jia, X.; Lin, Z.; Sun, D. Responses of Trichiurus japonicas catches to fishing and climate variability in the East China Sea. J. Fish. China 2011, 35, 1881–1889. (In Chinese) [Google Scholar]
- Jahncke, J.; Saenz, B.L.; Abraham, C.L.; Rintoul, C.; Bradley, R.W.; Sydeman, W.J. Ecosystem responses to short-term climate variability in the Gulf of the Farallones, California. Prog. Oceanogr. 2008, 77, 182–193. [Google Scholar] [CrossRef]
- Zainuddin, M.; Kiyofuji, H.; Saitoh, K.; Saitoh, S.I. Using multi-sensor satellite remote sensing and catch data to detect ocean hot spots for albacore (Thunnus alalunga) in the northwestern North Pacific. Deep Sea Res. II 2006, 53, 419–431. [Google Scholar] [CrossRef]
- Dutta, S.; Chanda, A.; Akhand1, A.; Hazra1, S. Correlation of Phytoplankton Biomass (Chlorophyll-a) and Nutrients with the Catch Per Unit Effort in the PFZ Forecast Areas of Northern Bay of Bengal during Simultaneous Validation of Winter Fishing Season. Turk. J. Fish. Aquat. Sc. 2006, 16, 767–777. [Google Scholar]
- Tian, Y.; Kidokoro, H.; Watanabe, T.; Iguchi, N. The late 1980s regime shift in the ecosystem of Tsushima warm current in the Japan/East Sea: Evidence from historical data and possible mechanisms. Prog. Oceanogr. 2008, 7, 127–1445. [Google Scholar] [CrossRef]
- Yu, H.; Yu, H.; Ito, S.-I.; Tian, Y.; Wang, H.; Liu, Y.; Xing, Q.; Bakun, A.; Kelly, R. Potential environmental drivers of Japanese anchovy (Engraulis japonicus) recruitment in the Yellow Sea. J. Mar. Syst. 2020, 212, 103431. [Google Scholar] [CrossRef]
- Chifamba, P.C. The relationship of temperature and hydrological factors to catch per unit effort, condition and size of the freshwater sardine, Limnothrissa miodon (Boulenger), in Lake Kariba. Fish. Res. 2000, 45, 271–281. [Google Scholar] [CrossRef]
- Ling, J.; Yan, L.; Lin, L.; Li, J.; Cheng, J. Reasonable utilization of hairtail Trichiurus japonicas resource in the East China Sea based on its fecundity. J. Fish. China 2005, 12, 726–730. (In Chinese) [Google Scholar]
- Xu, Z.; Chen, J. Migratory routes of Trichiurus lepturus in the East China Sea, Yellow Sea and Bohai Sea. J. Fish. China 2015, 39, 824–835. (In Chinese) [Google Scholar]
- Liu, Z.-F.; Xu, H.-X.; Zhou, Y.-D. An ameliorative study on the forecast of recruitment stock and catch in winter seasons of hairtail, Trichiurus haumela in the East China Sea. J. Zhejiang Ocean Univ. (In Chinese). 2004, 23, 14–18. [Google Scholar]
- Ye, H.; Beamish, R.J.; Glaser, S.M.; Grant, S.C.H.; Hsieh, C.-H.; Richards, L.J.; Schnute, J.T.; Sugihara, G. Equation-free mechanistic ecosystem forecasting using empirical dynamic modeling. Proc. Natl. Acad. Sci. USA 2015, 112, E1569–E1576. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mcgowan, J.; Deyle, E.; Ye, H.; Carter, M.; Peretti, C. Predicting coastal algal blooms in southern California. Ecology 2018, 98, 1419–1433. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, M.; Yoshimura, C.; Allam, A.; Kimura, F.; Honma, T. Causality analysis and prediction of 2-methylisoborneol production in a reservoir using empirical dynamic modeling. Water Res. 2019, 163, 114864. [Google Scholar] [CrossRef]
- Sarah, G.M.; Hao, Y.; George, S. A nonlinear, low data requirement model for producing spatially explicit fishery forecasts. Fish Oceanogr. 2014, 23, 45–53. [Google Scholar]
- Bureau of Fisheries of the Ministry of Agriculture. China Fishery Statistical Yearbook 1978–2019; China Agricultural Press: Beijing, China, 2019. [Google Scholar]
- Maunder, M.N.; Sibert, J.R.; Fonteneau, A.; Hampton, J.; Kleiber, P.; Harley, S.J. Interpreting catch per unit effort data to assess the status of individual stocks and communities. ICES J. Mar. Sci. 2006, 63, 1373–1385. [Google Scholar] [CrossRef]
- Poulsen, R.T.; Holm, P. What Can Fisheries Historians Learn from Marine Science? The Concept of Catch per Unit Effort (CPUE). Int. J. Marit. Hist. 2007, 19, 89–112. [Google Scholar] [CrossRef]
- Maunder, M.N.; Punt, A.E. Standardizing catch and effort data: A review of recent approaches. Fish. Res. 2004, 70, 141–159. [Google Scholar] [CrossRef]
- Maunder, M.N.; Thorson, J.T.; Xu, H.; Oliveros-Ramos, R.; Hoyle, S.D.; Tremblay-Boyer, L.; Lee, H.H.; Kai, M.; Chang, S.K.; Kitakado, T.; et al. The need for spatio-temporal modeling to determine catch-per-unit effort based indices of abundance and associated composition data for inclusion in stock assessment models. Fish. Res. 2020, 229, 105594. [Google Scholar] [CrossRef]
- Harley, S.J.; Myers, R.A.; Dunn, A. A meta-analysis of the relationship between catch-per-unit-effort and abundance. Can. J. Fish. Aquat. Sci. 2001, 58, 1705–1772. [Google Scholar] [CrossRef]
- Thorson, J.T.; Fonner, R.; Haltuch, M.A.; Ono, K.; Winker, H. Accounting for spatiotemporal variation and fisher targeting when estimating abundance from multispecies fishery data. Can. J. Fish. Aquat. Sci. 2017, 74, 1794–1807. [Google Scholar] [CrossRef] [Green Version]
- Korman, J.; Yard, M.D. Effects of environmental covariates and density on the catchability of fish populations and interpretation of catch per unit effort trends. Fish. Res. 2017, 189, 18–34. [Google Scholar] [CrossRef] [Green Version]
- Kai, M.; Thorson, J.T.; Piner, K.R.; Maunder, M.N. Spatio-temporal variation in size-structured populations using fishery data: An application to shortfin mako (Isurus oxyrinchus) in the Pacific Ocean. Can. J. Fish. Aquat. Sci. 2017, 74, 1765–1780. [Google Scholar] [CrossRef] [Green Version]
- Kai, M. Spatio-temporal changes in catch rates of pelagic sharks caught by Japanese research and training vessels in the western and central North Pacific. Fish. Res. 2019, 216, 177–195. [Google Scholar] [CrossRef]
- Nielsen, J.R.; Kristensen, K.; Lewy, P.; Bastardie, F. A statistical model for estimation of fish density including correlation in size, space, time and between species from research survey data. PLoS ONE 2014, 9, e99151. [Google Scholar]
- Punt, A.E.; Walker, T.I.; Taylor, B.L.; Pribac, F. Standardization of catch and effort data in a spatially-structured shark fishery. Fish. Res. 2000, 45, 129–145. [Google Scholar] [CrossRef]
- Emanuel, K. Increasing destructiveness of tropical cyclones over the past 30 years. Nature 2005, 436, 686–688. [Google Scholar] [CrossRef]
- Liu, H.; Fogarty, M.J.; Glaser, S.M.; Altman, I.; Hsieh, C.-H.; Kaufman, L.; Rosenberg, A.A.; Sugihara, G. Nonlinear dynamic features and co-predictability of the Georges Bank fish community. Mar. Ecol. Prog. Ser. 2012, 464, 195–207. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, C.H.; Glaser, S.M.; Lucas, A.J.; Sugihara, G. Distinguishing random environmental fluctuations from ecological catastrophes for the North Pacific Ocean. Nature 2005, 435, 336–340. [Google Scholar] [CrossRef]
- Glaser, S.M.; Fogarty, M.J.; Liu, H.; Altman, I.; Hsieh, C.-H.; Kaufman, L.; MacCall, A.D.; Rosenberg, A.A.; Ye, H.; Sugihara, G. Complex dynamics may limit prediction in marine fisheries. Fish Fish. 2014, 15, 616–633. [Google Scholar] [CrossRef]
- Horan, R.D.; Fenichel, E.P.; Drury, K.L.S.; Lodge, D. Managing ecological thresholds incoupled environmental-human systems. Proc. Natl. Acad. Sci. USA 2011, 108, 7333–7338. [Google Scholar] [CrossRef] [Green Version]
- Deyle, E.R.; Sugihara, G. Generalized theorems for nonlinear state space reconstruction. PLoS ONE 2011, 6, e18295. [Google Scholar] [CrossRef] [PubMed]
- Sugihara, G.; May, R.; Ye, H.; Hsieh, C.-H.; Deyle, E.; Fogarty, M.; Much, S. Detecting causality in complex ecosystems. Science 2012, 338, 496–500. [Google Scholar] [CrossRef] [PubMed]
- Takens, F. Detecting strange attractors in turbulence. In Symposium on Dynamical Systems and Turbulence; Lecture Notes in Mathematics; Rand, D.A., Young, L.S., Eds.; Springer: Berlin/Heidelberg, Germany, 1981; Volume 898, pp. 366–381. [Google Scholar]
- Sugihara, G.; May, R.M. Nonlinear forecasting as a way of distinguishing chaos from measurement error in time series. Nature 1990, 344, 734–741. [Google Scholar] [CrossRef] [PubMed]
- Van Nes, E.H.; Scheffer, M.; Brovkin, V.; Lenton, T.M.; Ye, H.; Deyle, E.; Sugihara, G. Causal feedbacks in climate change. Nat. Clim. Chang. 2015, 5, 445–448. [Google Scholar] [CrossRef]
- Li, Y.H. Material exchange between the East China Sea and the Kuroshio Current. Terr. Atmos. Ocean. Sci. 1994, 5, 625–631. [Google Scholar] [CrossRef]
- Shi, Y.-L.; Yang, W.; Ren, M.-E. Hydrological characteristics of the Changjiang and its relation to sediment transport to the sea. Cont. Shelf Res. 1985, 4, 5–15. [Google Scholar]
- Morgan, M.J.; ORiordan, R.M.; Culloty, S.C. Climate change impacts on potential recruitment in an ecosystem engineer. Ecol. Evol. 2013, 3, 581–594. [Google Scholar] [CrossRef]
- Zheng, G.M.; Tang, D.L. Offshore and nearshore chlorophyll increases induced by typhoon winds and subsequent terrestrial rainwater runoff. Mar. Ecol. Prog. Ser. 2007, 333, 61–74. [Google Scholar] [CrossRef] [Green Version]
- Glaser, S.M.; Ye, H.; Maunder, M.; MacCall, A.; Fogarty, M.J.; Sugihara, G. Detecting and forecasting complex nonlinear dynamics in spatially-structured catch-per-unit effort time series for North Pacific albacore (Thunnus alalunga). Can. J. Fish. Aquat. Sci. 2011, 68, 400–412. [Google Scholar] [CrossRef]
- Munch, S.B.; Giron-Nava, A.; Sugihara, G. Nonlinear dynamics and noise in fisheries recruitment: A global meta-analysis. Fish Fish. 2018, 19, 964–973. [Google Scholar] [CrossRef]


| Nonlinear Causal Effects of Fishing Effort & Environmental Drivers | |||
|---|---|---|---|
| Candidate Variable (Xi) | Prediction Time (Year) | Cross-Map Skill (Catch→Xi) | Linear Cross-Correlation (Catch and Xi) |
| Fishing effort | 0 | 0.818 * | 0.772 |
| SST | 0 | 0.347 * | 0.076 |
| Precipitation | −2 | 0.269 * | −0.121 |
| Ocean_salinity | −2 | 0.231 * | 0.102 |
| Summer_wind_speed | −1 | 0.308 * | 0.122 |
| Winter_wind_speed | 0 | 0.306 * | 0.237 * |
| PDI | −4 | 0.304 * | 0.302 * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Wang, P.; Zhang, H. The Relationship between Environmental Factors and Catch Abundance of Hairtail in the East China Sea Using Empirical Dynamic Modeling. Fishes 2021, 6, 80. https://doi.org/10.3390/fishes6040080
Hu J, Wang P, Zhang H. The Relationship between Environmental Factors and Catch Abundance of Hairtail in the East China Sea Using Empirical Dynamic Modeling. Fishes. 2021; 6(4):80. https://doi.org/10.3390/fishes6040080
Chicago/Turabian StyleHu, Jinfei, Ping Wang, and Hailong Zhang. 2021. "The Relationship between Environmental Factors and Catch Abundance of Hairtail in the East China Sea Using Empirical Dynamic Modeling" Fishes 6, no. 4: 80. https://doi.org/10.3390/fishes6040080
APA StyleHu, J., Wang, P., & Zhang, H. (2021). The Relationship between Environmental Factors and Catch Abundance of Hairtail in the East China Sea Using Empirical Dynamic Modeling. Fishes, 6(4), 80. https://doi.org/10.3390/fishes6040080