Estimating the Purse Seine Net Geometry during a Hauling Operation Using a Data Assimilation Method
Abstract
1. Introduction
2. Materials and Methods
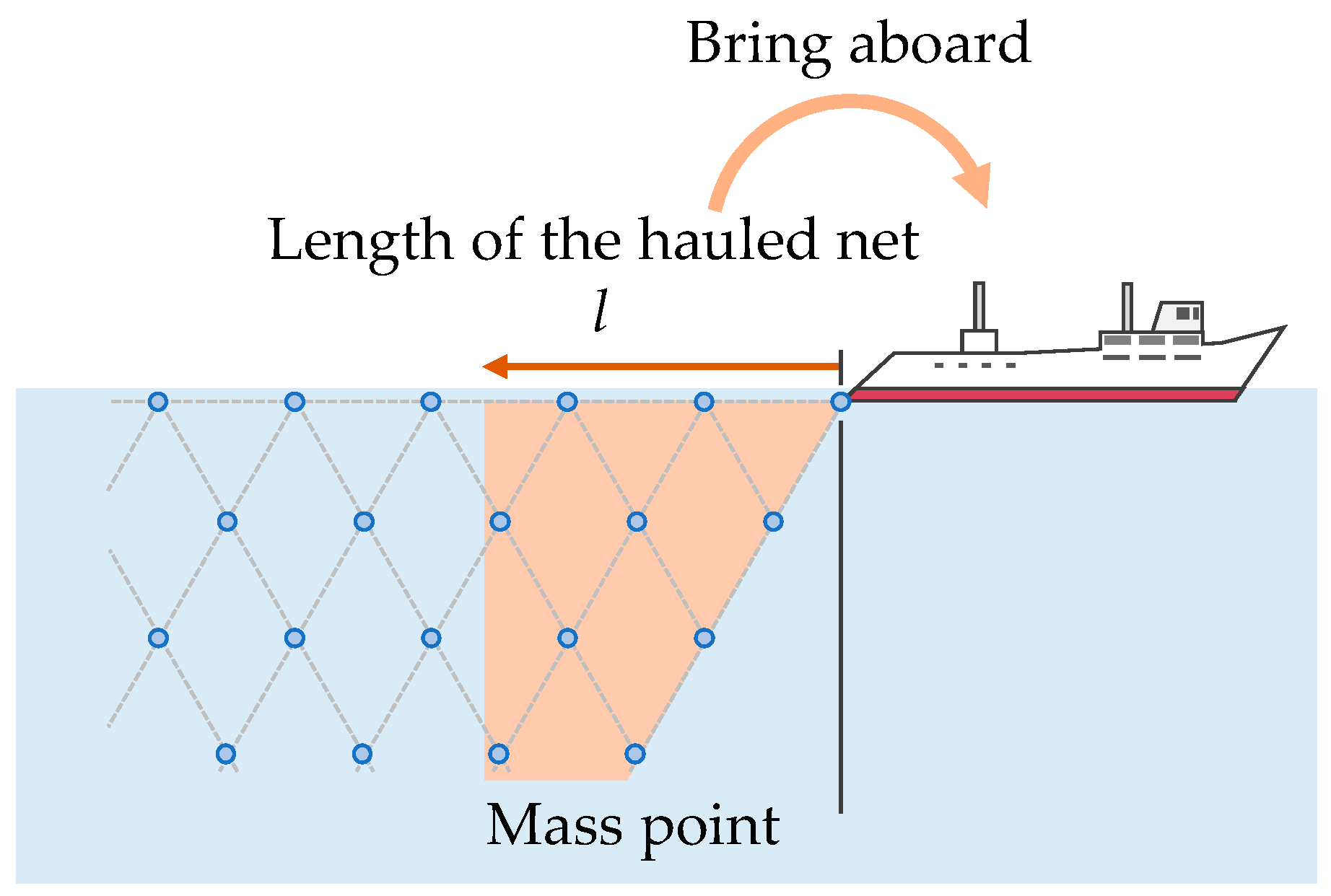
2.1. Numerical Model for Estimating the Deformation of a Purse Seine Net
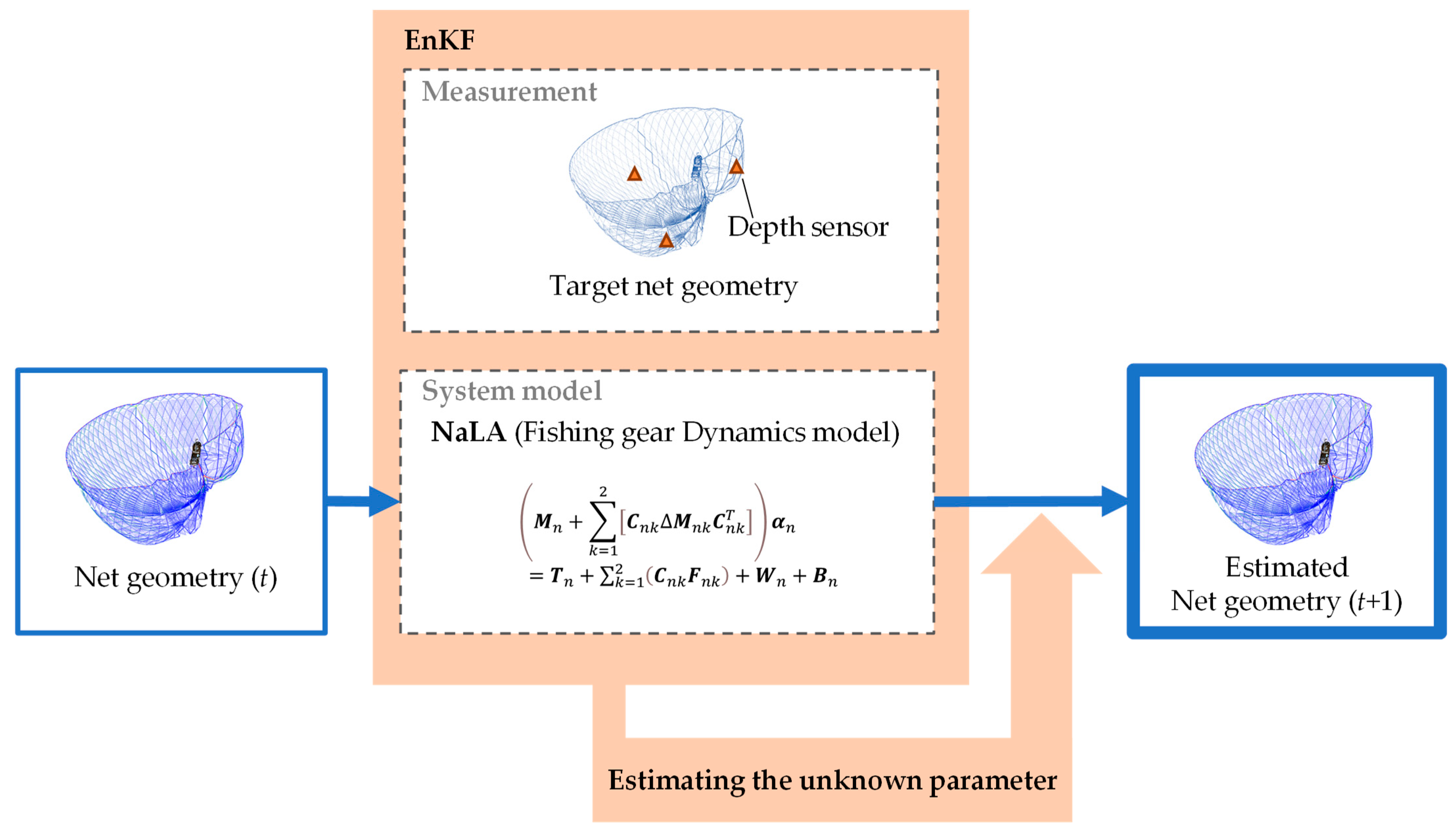
2.2. Integrating the Ensemble Kalman Filter into the NaLA System
2.3. Operation Data
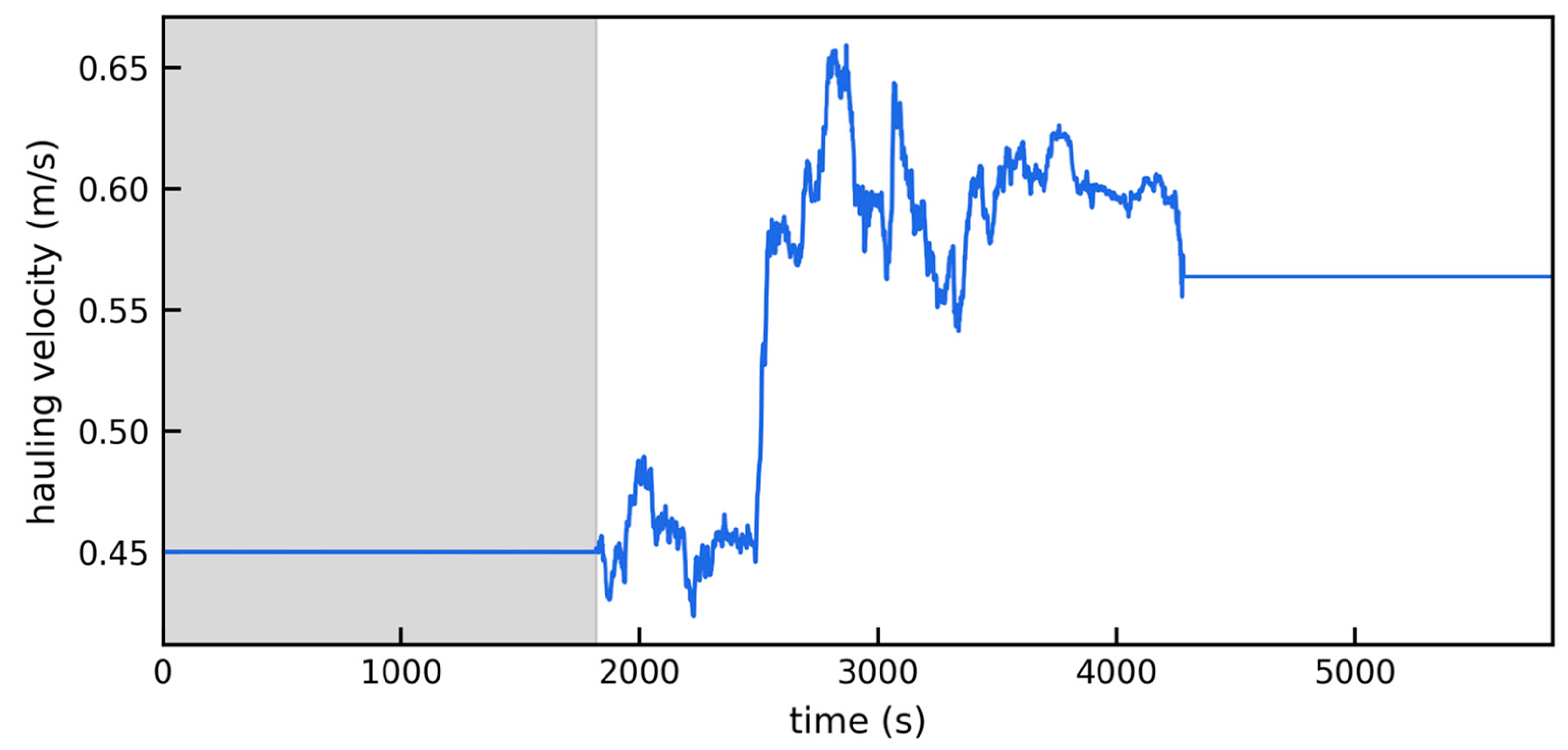
2.4. Estimation of Hauling Velocity
3. Results
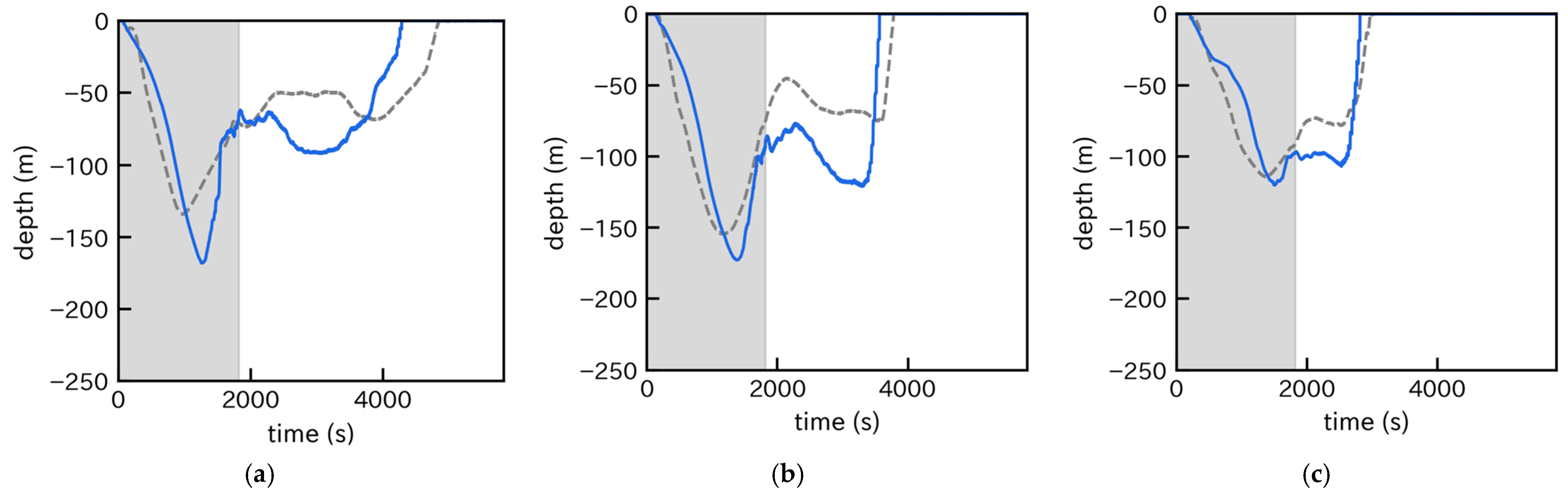
3.1. Estimated Hauling Velocity and Length of Hauling Net
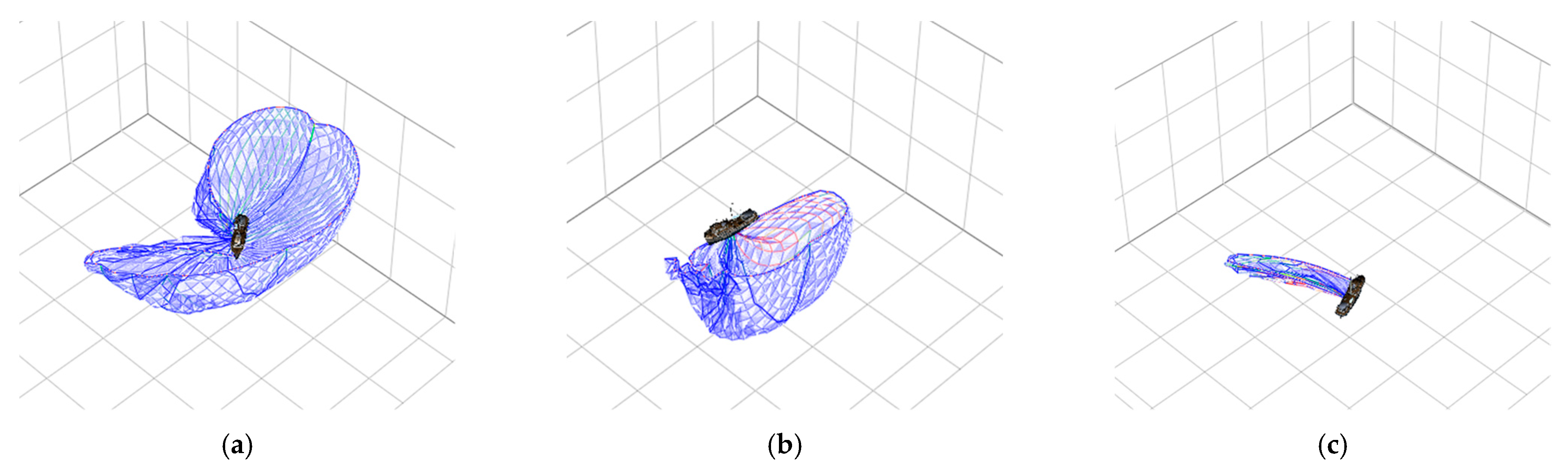
3.2. Results of the Dynamic Simulation Using the Estimated Net-Hauling Velocity
4. Discussion
4.1. Estimation and Application of Hauling-Net Dynamics
4.2. Unknown Parameter Estimation and Control of Net Fishing Gear Dynamics
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Watson, R.A.; Tidd, A. Mapping nearly a century and a half of global marine fishing: 1869–2015. Mar. Policy 2018, 93, 171–177. [Google Scholar] [CrossRef]
- Cashion, T.; Al-Abdulrazzak, D.; Belhabib, D.; Derrick, B.; Divovich, E.; Moutopoulos, D.K.; Noël, S.-L.; Palomares, M.L.D.; Teh, L.C.L.; Zeller, D.; et al. Reconstructing global marine fishing gear use: Catches and landed values by gear type and sector. Fish. Res. 2018, 206, 57–64. [Google Scholar] [CrossRef]
- O’Neill, F. Axisymmetric trawl cod-ends made from netting of a generalized mesh shape. IMA J. Appl. Math. 1999, 62, 245–262. [Google Scholar] [CrossRef]
- Lee, C.-W.; Lee, J.-H.; Cha, B.-J.; Kim, H.-Y.; Lee, J.-H. Physical Modeling for Underwater Flexible Systems Dynamic Simulation. Ocean Eng. 2005, 32, 331–347. [Google Scholar] [CrossRef]
- Lader, P.F.; Fredheim, A. Dynamic properties of a flexible net sheet in waves and current—A numerical approach. Aqua. Eng. 2006, 35, 228–238. [Google Scholar] [CrossRef]
- Balash, C.; Colbourne, B.; Bose, N.; Raman-Nair, W. Aquaculture net drag force and added mass. Aqua. Eng. 2009, 41, 14–21. [Google Scholar] [CrossRef]
- Bi, C.-W.; Zhao, Y.-P.; Dong, G.-H.; Wu, Z.-M.; Zhang, Y.; Xu, T.-J. Drag on and flow through the hydroid-fouled nets in currents. Ocean Eng. 2018, 161, 195–204. [Google Scholar] [CrossRef]
- Martin, T.; Kamath, A.; Bihs, H. A Lagrangian approach for the coupled simulation of fixed net structures in a Eulerian fluid model. J. Fluids Struct. 2020, 94, 102962. [Google Scholar] [CrossRef]
- Takagi, T.; Suzuki, K.; Hiraishi, T. Development of the numerical simulation method of dynamic fishing net shape. Nippon Suisan Gakkaishi 2002, 68, 320–326. [Google Scholar] [CrossRef][Green Version]
- Takagi, T.; Shimizu, T.; Suzuki, K.; Hiraishi, T.; Yamamoto, K. Validity and layout of “Nala”: A net configuration and loading analysis system. Fish. Res. 2004, 66, 235–243. [Google Scholar] [CrossRef]
- Shimizu, T.; Takagi, T.; Korte, H.; Hiraishi, T.; Yamamoto, K. Application of Nala, a fishing net configuration and loading analysis system, to drift gill nets. Fish. Res. 2005, 76, 67–80. [Google Scholar] [CrossRef]
- Takagi, T.; Shimizu, T.; Korte, H. Evaluating the impact of gillnet ghost fishing using a computational analysis of the geometry of fishing gear. ICES J. Mar. Sci. 2007, 64, 1517–1524. [Google Scholar] [CrossRef]
- Shimizu, T.; Takagi, T.; Korte, H.; Hiraishi, T.; Yamamoto, K. Application of Nala, a fishing net configuration and loading analysis system, to bottom gill nets. Fish. Sci. 2007, 73, 489–499. [Google Scholar] [CrossRef]
- Takagi, T.; Miyata, S.; Fusejima, I.; Oshima, T.; Uehara, T.; Suzuki, K.; Nomura, Y.; Kanechiku, M.; Torisawa, S. Effect of mesh size on sinking characteristics of purse seine net: A parametric study by numerical simulation. Fish. Eng. 2014, 51, 11–19. [Google Scholar]
- Suzuki, K.; Takagi, T.; Shimizu, T.; Hiraishi, T.; Yamamoto, K.; Nashimoto, K. Validity and visualization of a numerical model used to determine dynamic configurations of fishing nets. Fish. Sci. 2003, 69, 695–705. [Google Scholar] [CrossRef]
- Shimizu, T.; Takagi, T.; Suzuki, K.; Hiraishi, T.; Yamamoto, K. Refined calculation model for Nala, a fishing net shape simulator, applicable to gill nets. Fish. Sci. 2004, 70, 401–411. [Google Scholar] [CrossRef]
- Suuronen, P.; Chopin, F.; Glass, C.; Løkkeborg, S.; Matsushita, Y.; Queirolo, D.; Rihan, D. Low impact and fuel efficient fishing—Looking beyond the horizon. Fish. Res. 2012, 119–120, 135–146. [Google Scholar] [CrossRef]
- Gomi, S.; Takagi, T.; Suzuki, K.; Shiraki, R.; Ogino, I.; Asaumi, S. Controlling a fishing net geometry underwater using a data assimilation method. Appl. Ocean Res. 2021, 106, 102467. [Google Scholar] [CrossRef]
- Lee, C.-W.; Lee, J.; Park, S. Prediction of shooting trajectory of tuna purse seine fishing. Fish. Res. 2018, 208, 189–201. [Google Scholar] [CrossRef]
- Tang, H.; Xu, L.; Hu, F.; Kumazawa, T.; Hirayama, M.; Zhou, C.; Wang, X.; Liu, W. Effect of mesh size modifications on the sinking performance, geometry and forces acting on model purse seine nets. Fish. Res. 2019, 211, 158–168. [Google Scholar] [CrossRef]
- Kim, Y.-H.; Park, M.-C. The simulation of the geometry of a tuna purse seine under current and drift of purse seiner. Ocean Eng. 2009, 36, 1080–1088. [Google Scholar] [CrossRef]
- Zhou, C.; Xu, L.; Tang, H.; Hu, F.; He, P.; Kumazawa, T.; Wang, X.; Wan, R.; Dong, S. Identifying the design alternatives and flow interference of tuna purse seine by the numerical modelling approach. J. Marine Sci. Eng. 2019, 7, 405. [Google Scholar] [CrossRef]
- Evensen, G. Sequential Data Assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. C Oceans 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Evensen, G. The ensemble Kalman filter: Theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Evensen, G. The ensemble Kalman filter for combined state and parameter estimation. IEEE Control Syst. 2009, 29, 83–104. [Google Scholar] [CrossRef]
- Riziotis, V.A.; Katsaounis, G.M.; Papadakis, G.; Voutsinas, S.G.; Bergeles, G.; Tzabiras, G.D. Numerical and experimental analysis of the hydroelastic behavior of purse seine nets. Ocean Eng. 2013, 58, 88–105. [Google Scholar] [CrossRef]
- Tenningen, M.; Macaulay, G.J.; Rieucau, G.; Peña, H.; Korneliussen, R.J. Behaviours of Atlantic herring and mackerel in a purse-seine net, observed using multibeam sonar. ICES J. Mar. Sci. 2016, 74, 359–368. [Google Scholar] [CrossRef]
- Tenningen, M.; Pobitzer, A.; Handegard, N.O.; de Jong, K. Estimating purse seine volume during capture: Implications for fish densities and survival of released unwanted catches. ICES J. Mar. Sci. 2019, 76, 2481–2488. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomi, S.; Takagi, T.; Suzuki, K.; Oshima, T.; Wada, S.; Shiraki, R.; Nishiyama, Y.; Ogino, I. Estimating the Purse Seine Net Geometry during a Hauling Operation Using a Data Assimilation Method. Fishes 2024, 9, 392. https://doi.org/10.3390/fishes9100392
Gomi S, Takagi T, Suzuki K, Oshima T, Wada S, Shiraki R, Nishiyama Y, Ogino I. Estimating the Purse Seine Net Geometry during a Hauling Operation Using a Data Assimilation Method. Fishes. 2024; 9(10):392. https://doi.org/10.3390/fishes9100392
Chicago/Turabian StyleGomi, Shintaro, Tsutomu Takagi, Katsuya Suzuki, Tatsuki Oshima, Shoko Wada, Rika Shiraki, Yoshihiro Nishiyama, and Ichiya Ogino. 2024. "Estimating the Purse Seine Net Geometry during a Hauling Operation Using a Data Assimilation Method" Fishes 9, no. 10: 392. https://doi.org/10.3390/fishes9100392
APA StyleGomi, S., Takagi, T., Suzuki, K., Oshima, T., Wada, S., Shiraki, R., Nishiyama, Y., & Ogino, I. (2024). Estimating the Purse Seine Net Geometry during a Hauling Operation Using a Data Assimilation Method. Fishes, 9(10), 392. https://doi.org/10.3390/fishes9100392






