Effect of t2g-Correlations and Doping in CrSBr Ferromagnetic Semiconductor
Abstract
:1. Introduction
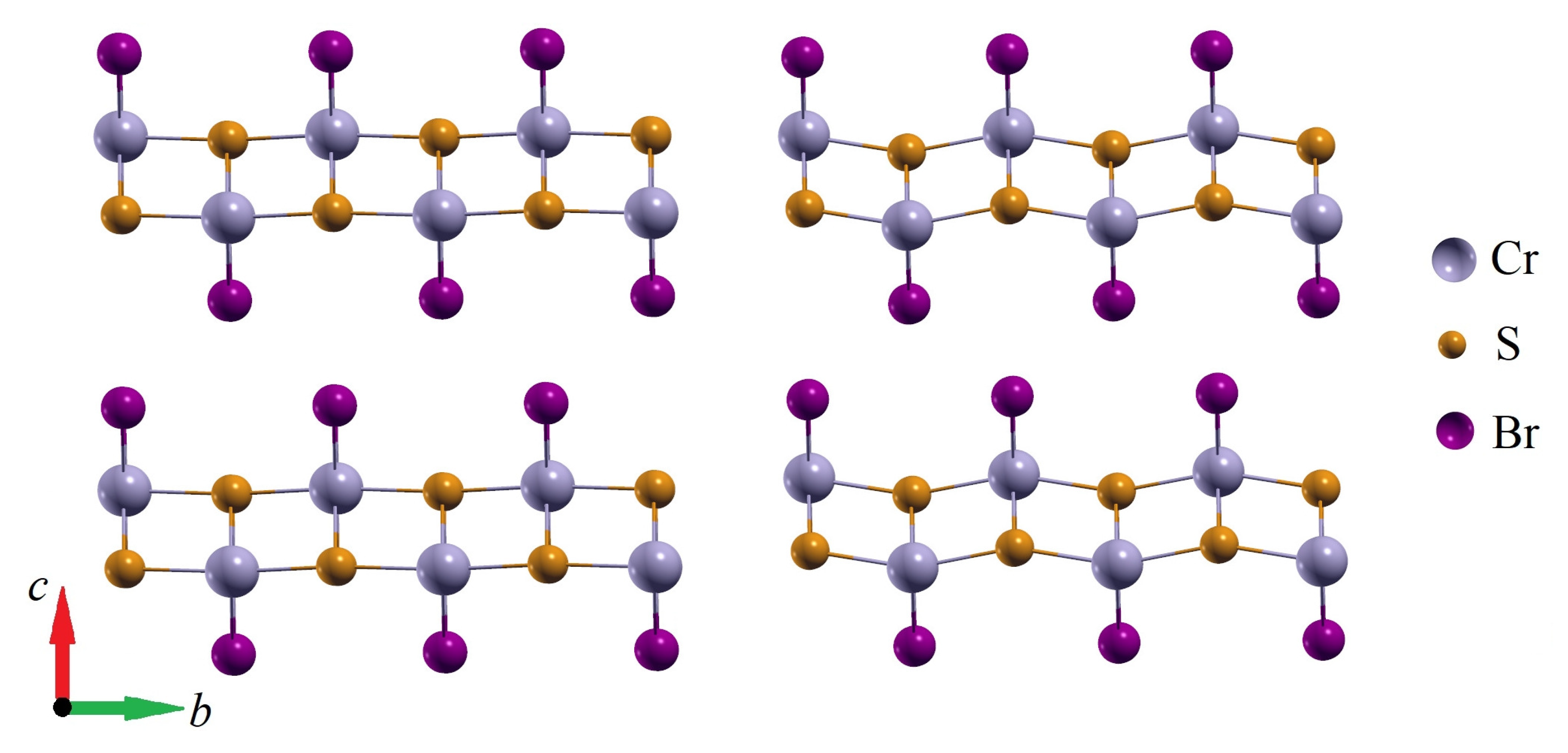
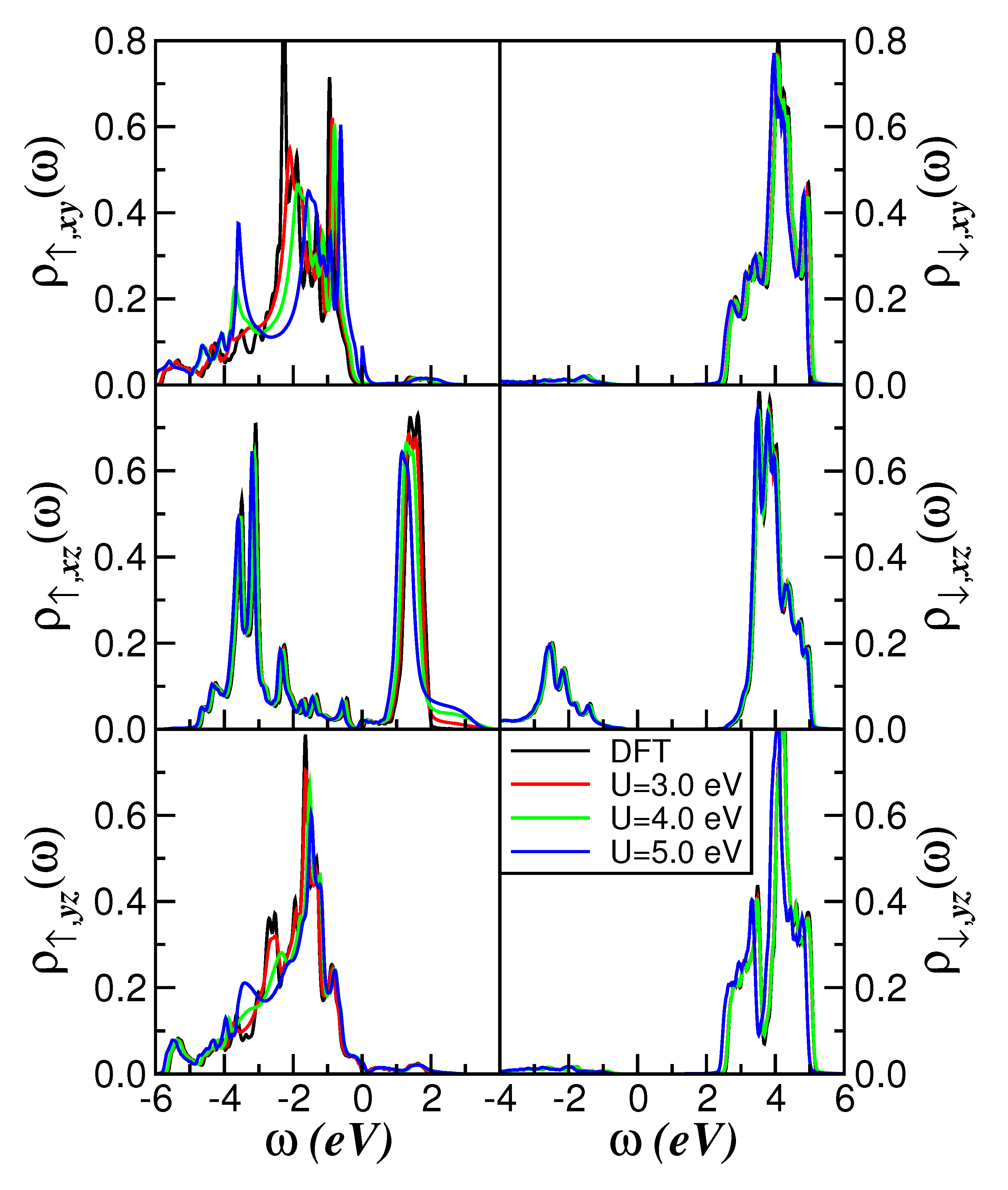
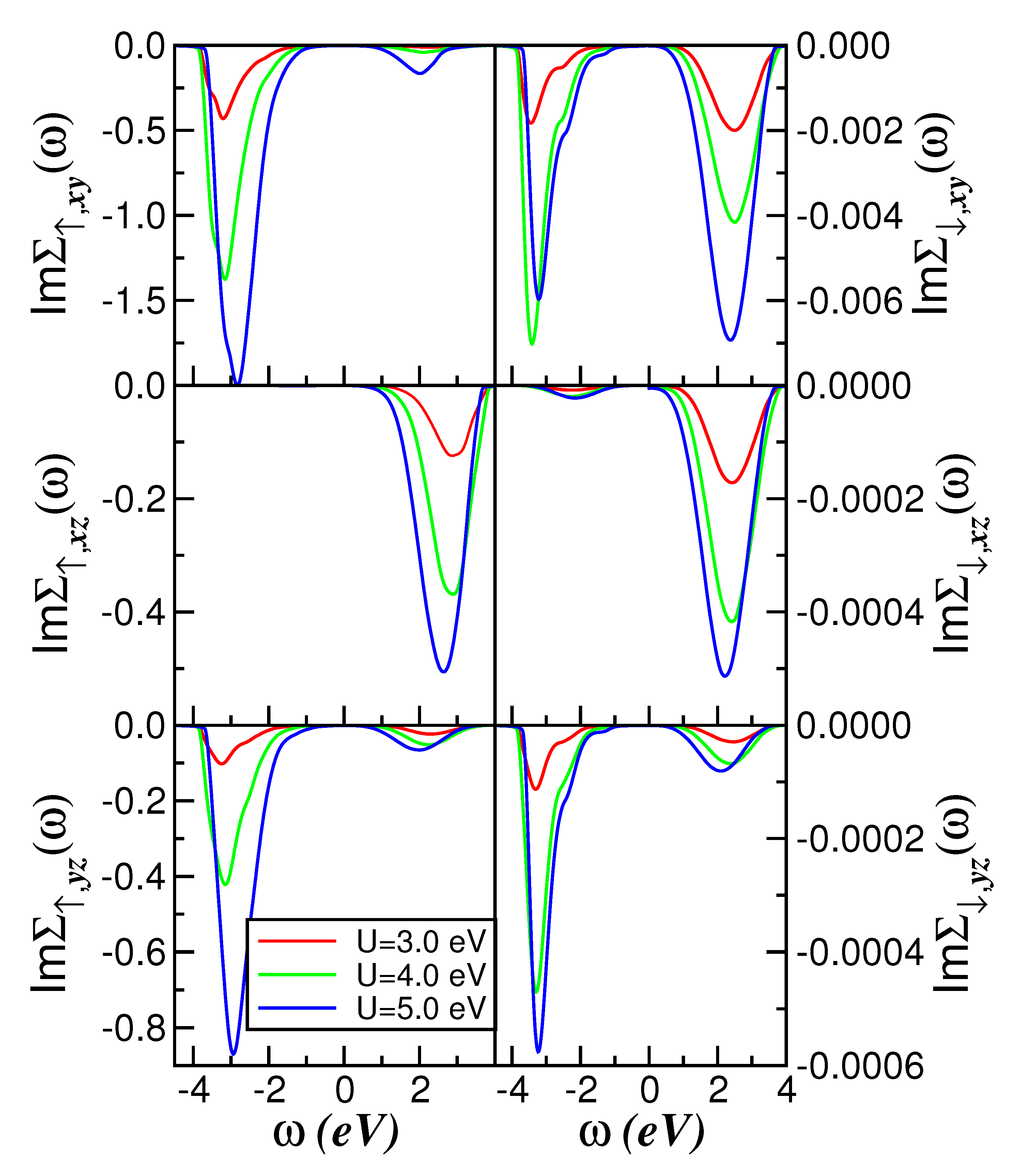
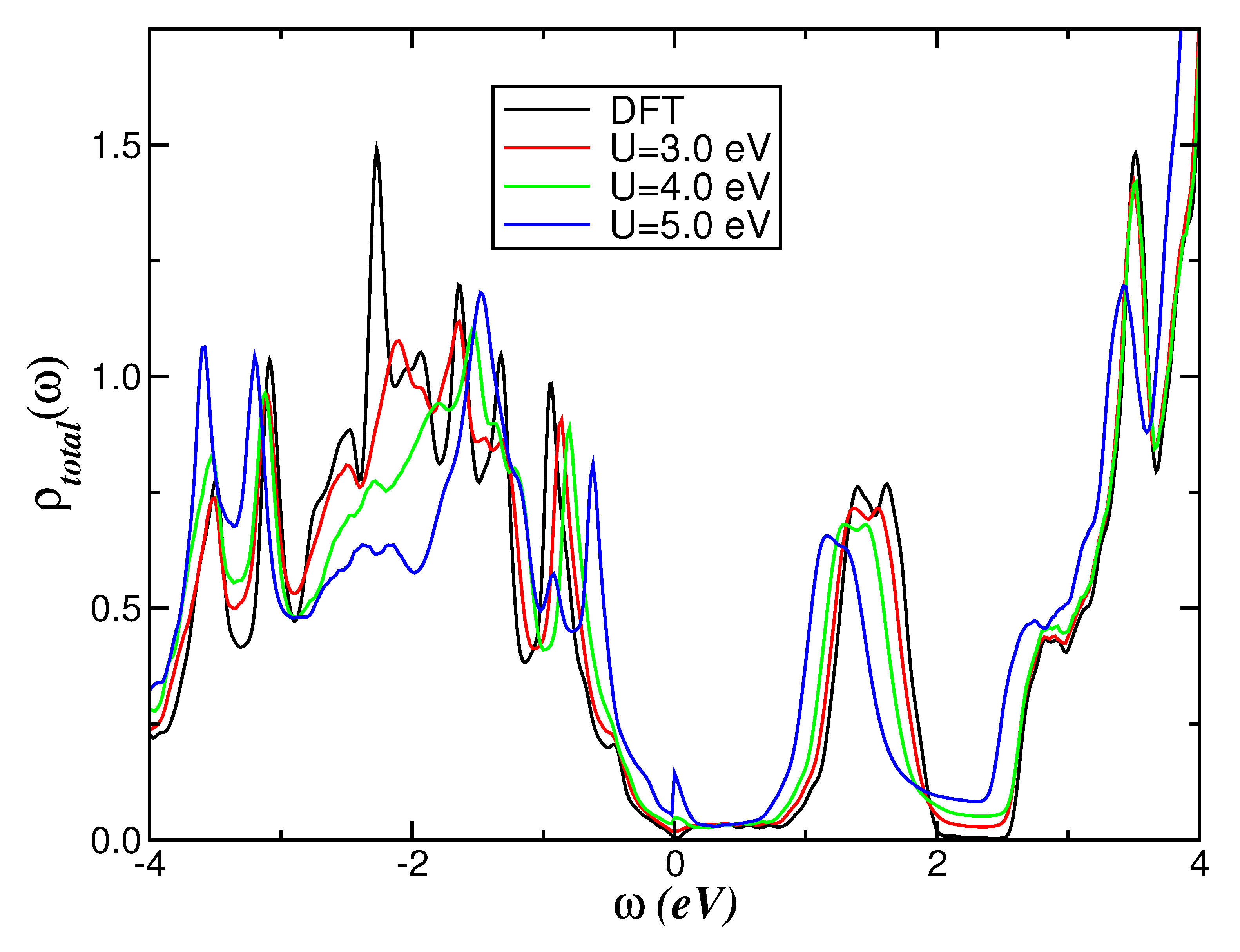
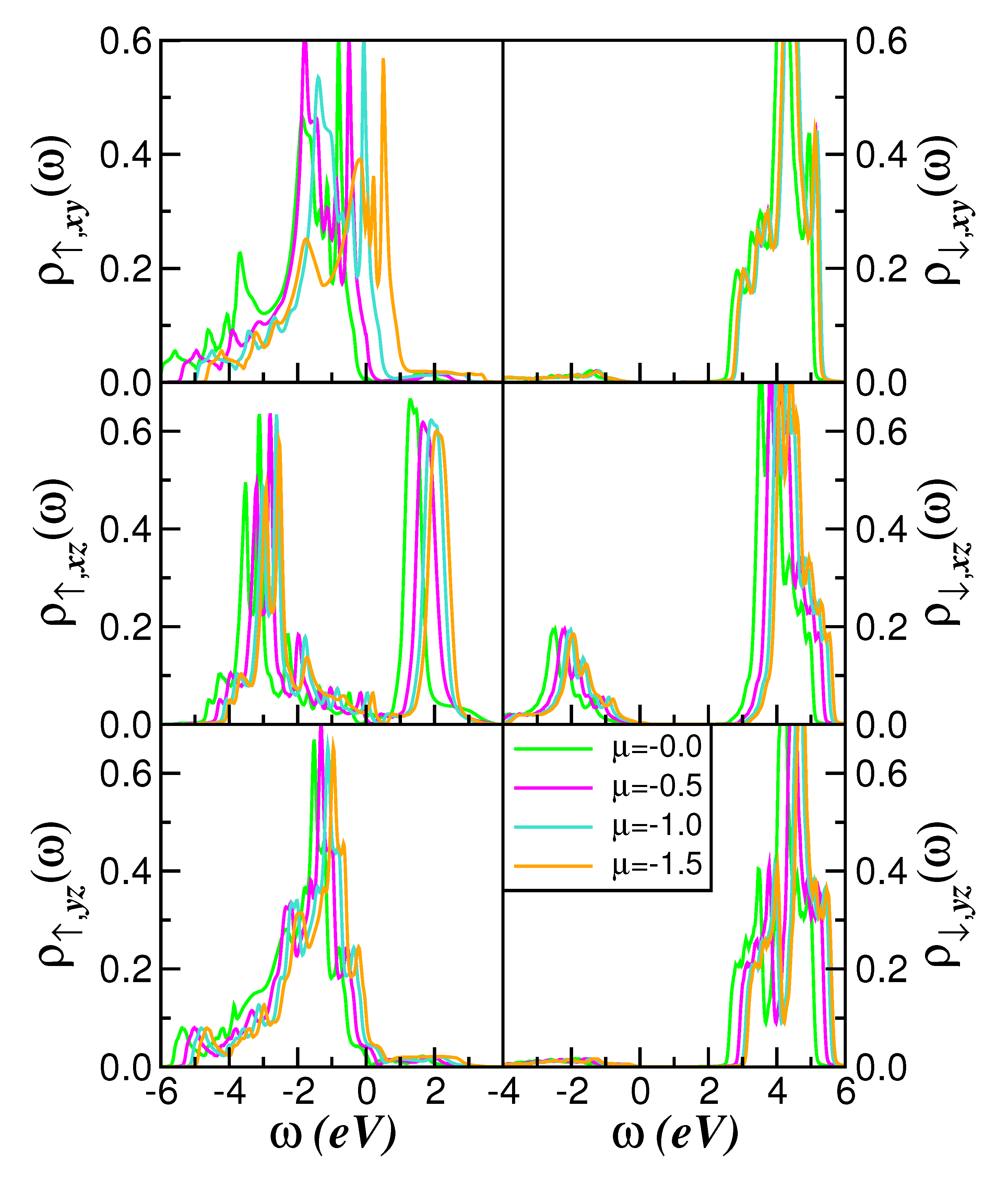
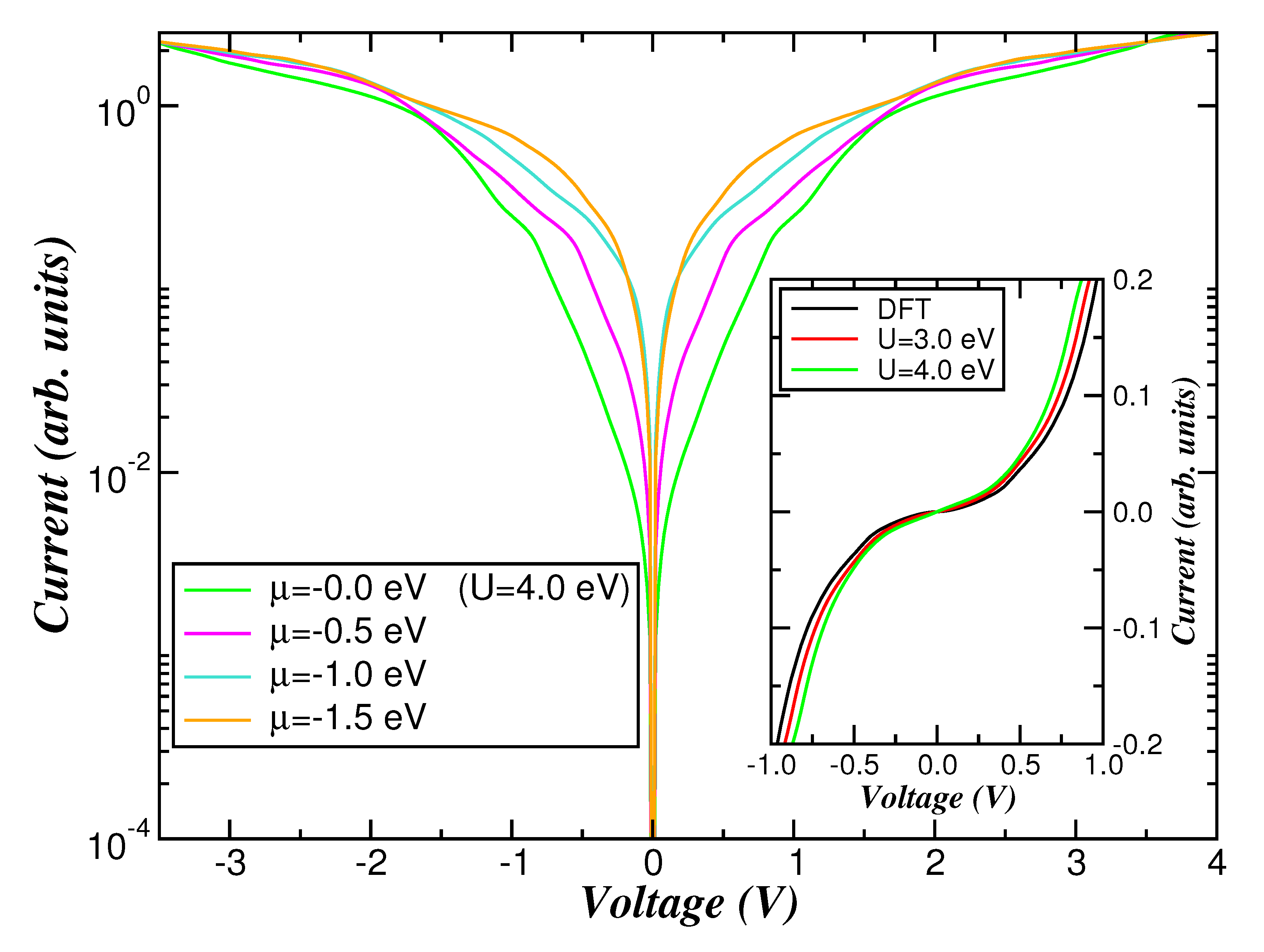
2. Results and Discussion
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A. A Electric field effect in atomically thin carbon films. Science 2004, 306, 666. [Google Scholar] [CrossRef] [PubMed]
- Long, F.; Mosina, K.; Hübner, R.; Sofer, Z.; Klein, J.; Prucnal, S.; Helm, M.; Dirnberger, F.; Zhou, S. Intrinsic magnetic properties of the layered antiferromagnet CrSBr. Appl. Phys. Lett. 2023, 123, 222401. [Google Scholar] [CrossRef]
- Huang, B.; Clark, G.; Navarro-Moratalla, E.; Klein, D.R.; Cheng, R.; Seyler, K.L.; Zhong, D.; Schmidgall, E.; McGuire, M.A.; Cobden, D.H.; et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 2017, 546, 265. [Google Scholar] [CrossRef] [PubMed]
- Gong, G.; Li, L.; Li, Z.; Ji, H.; Stern, A.; Xia, Y.; Cao, T.; Bao, W.; Wang, C.; Wang, Y.; et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 2017, 546, 265. [Google Scholar] [CrossRef]
- Craco, L.; Carara, S.S.; Shao, Y.-C.; Chuang, Y.-D.; Freelon, B. Mott localization in the van der Waals crystal CrI3: A GGA + DMFT study. Phys. Rev. B 2020, 102, 195130. [Google Scholar] [CrossRef]
- Craco, L.; Carara, S.S.; Shao, Y.-C.; Chuang, Y.-D.; Freelon, B. Electronic structure of rhombohedral CrX3 (X = Br, Cl, I) van der Waals crystals. Phys. Rev. B 2021, 103, 235119. [Google Scholar] [CrossRef]
- Wang, Q.H.; Bedoya-Pinto, A.; Blei, M.; Dismukes, A.H.; Hamo, A.; Jenkins, S.; Koperski, M.; Liu, Y.; Sun, Q.C.; Telford, E.J.; et al. The magnetic genome of two-dimensional van der Waals materials. ACS Nano 2020, 16, 6960. [Google Scholar] [CrossRef]
- Wolf, S.A.; Awschalom, D.D.; Buhrman, R.A.; Daughton, J.M.; Molnar, S.V.; Roukes, M.L.; Chtchelkanova, Y.A.; Treger, D.M. Spintronics: A spin-based electronics vision for the future. Science 2021, 294, 1488. [Google Scholar] [CrossRef]
- Awschalom, D.D.; Flatté, M.E. Challenges for semiconductor spintronics. Nat. Phys. 2007, 3, 153. [Google Scholar] [CrossRef]
- Li, H.; Ruan, S.; Zeng, Y.J. Intrinsic van der Waals magnetic materials from bulk to the 2D limit: New frontiers of spintronics. Adv. Mater. 2019, 31, 1900065. [Google Scholar] [CrossRef]
- Jin, C.; Lin, F.; Suenaga, K.; Iijima, S. Fabrication of a freestanding boron nitride single layer and its defect assignments. Phys. Rev. Lett. 2009, 102, 195505. [Google Scholar] [CrossRef] [PubMed]
- Splendiani, A.; Sun, L.; Zhang, Y.; Li, T.; Kim, J.; Chim, C.Y. Emerging photoluminescence in monolayer MoS2. Nano Lett. 2010, 10, 1271–1275. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Galli, G. Electronic properties of MoS2 nanoparticles. J. Phys. Chem. C 2007, 111, 16192. [Google Scholar] [CrossRef]
- Upreti, D.; Basnet, R.; Sharma, M.M.; Chhetri, S.K.; Acharya, G.; Nabi, M.R.U.; Sakon, J.; Da, B.; Mortazavin, M.; Hu, J. Tuning magnetism in Ising-type van der Waals magnet FePS3 by lithium intercalation. J. Phys. Condens. Matter 2025, 37, 135805. [Google Scholar] [CrossRef]
- Basnet, R.; Upreti, D.; Patel, T.; Karki Chhetri, S.; Acharya, G.; Nabi, M.R.U.; Sharma, M.M.; Sakon, J.; Mortazavi, M.; Hu, J. Field-induced spin polarization in the lightly Cr-substituted layered antiferromagnet NiPS3. Phys. Rev. B 2024, 109, 184405. [Google Scholar] [CrossRef]
- Dinesh Upreti, D.; Basnet, R.; Sharma, M.M.; Chhetri, S.K.; Acharya, G.; Nabi, M.R.U.; Sakon, J.; Benamara, M.; Mortazavi, M.; Jin, H. Medium-entropy engineering of magnetism in layered antiferromagnet CuxNi2(1−x)CrxP2S6. Adv. Func. Mater. 2024, 35, 2418722. [Google Scholar] [CrossRef]
- Wang, F.; Mathur, N.; Janes, A.N.; Sheng, H.; He, P.; Zheng, X.; Yu, P.; DeRuiter, A.J.; Schmidt, J.R.; He, J.; et al. Defect-mediated ferromagnetism in correlated two-dimensional transition metal phosphorus trisulfides. Sci. Adv. 2021, 7, eabj4086. [Google Scholar] [CrossRef]
- Odile, J.P.; Steger, J.J.; Wold, A. Preparation and properties of the solid solution series zinc iron phosphorus trisulfide (Zn1−xFexPS3). Inorg. Chem. 1975, 14, 2400. [Google Scholar] [CrossRef]
- Han, H.; Lin, H.; Gan, W.; Liu, Y.; Xiao, R.; Zhang, L.; Li, Y.; Zhang, C.; Li, H. Emergent mixed antiferromagnetic state in MnPS3(1−x)Se3x. Appl. Phys. Lett. 2023, 122, 033101. [Google Scholar] [CrossRef]
- Mi, M.; Zheng, X.; Wang, S.; Zhou, Y.; Yu, L.; Xiao, H.; Song, H.; Shen, B.; Li, F.; Bai, L.; et al. Variation between antiferromagnetism and ferrimagnetism in NiPS3 by electron doping. Adv. Funct. Mater. 2022, 32, 2112750. [Google Scholar] [CrossRef]
- Göser, O.; Paul, W.; Kahle, H.G. Magnetic properties of CrSBr. J. Magn. Magn. Mater. 1990, 92, 129. [Google Scholar] [CrossRef]
- Song, C.; Bai, H.; Zhou, Z.; Han, L.; Reichlova, H.; Dil, J.H.; Liu, J.; Chen, X.; Pan, F. Altermagnets as a new class of functional materials. Nat. Rev. Mater. 2025. in print. [Google Scholar] [CrossRef]
- Pei, F.; Yu, J.; Zhou, J.; Wang, S.; Liu, D.; Yuan, Y.; Xi, L.; Jin, F.; Kan, X.; Wang, C.; et al. Surface-sensitive detection of magnetic phase transition in van Der Waals magnet CrSBr. Adv. Funct. Mater. 2024, 34, 2309335. [Google Scholar] [CrossRef]
- Scheie, A.; Ziebel, M.; Chica, D.G.; Bae, Y.J.; Wang, X.; Kolesnikov, A.I.; Zhu, X.; Roy, X. Spin Waves and Magnetic Exchange Hamiltonian in CrSBr. Adv. Sci. 2022, 9, 2202467. [Google Scholar] [CrossRef]
- Telford, E.J.; Dismukes, A.H.; Lee, K.; Cheng, M.; Wieteska, A.; Bartholomew, A.K.; Chen, Y.-S.; Xu, X.; Pasupathy, A.N.; Zhu, X.; et al. Layered antiferromagnetism induces large negative magnetoresistance in the van der Waals Semiconductor CrSBr. Adv. Mater. 2020, 32, 2003240. [Google Scholar] [CrossRef]
- Lee, K.; Dismukes, A.H.; Telford, E.J.; Wiscons, R.A.; Wang, J.; Xu, X.; Nuckolls, C.; Dean, C.R.; Roy, X.; Zhu, X. Magnetic order and symmetry in the 2D semiconductor CrSBr. Nano Lett. 2021, 21, 3511. [Google Scholar] [CrossRef]
- Liu, W.; Guo, X.; Schwartz, J.; Xie, H.; Dhale, N.U.; Sung, S.H.; Kondusamy, A.L.N.; Wang, X.; Zhao, H.; Berman, D.; et al. A three-stage magnetic phase transition revealed in ultrahigh-quality van der Waals bulk magnet CrSBr. ACS Nano 2022, 6, 15917. [Google Scholar] [CrossRef]
- Rizzo, D.J.; McLeod, A.S.; Carnahan, C.; Telford, E.J.; Dismukes, A.H.; Wiscons, R.A.; Dong, Y.; Nuckolls, C.; Dean, C.R.; Pasupathy, A.N.; et al. Visualizing atomically layered magnetism in CrSBr. Adv. Mater. 2022, 34, 2201000. [Google Scholar] [CrossRef]
- Telford, E.J.; Dismukes, A.H.; Dudley, R.L.; Wiscons, R.A.; Lee, K.; Chica, D.G.; Ziebel, M.E.; Han, M.-G.; Yu, J.; Shabani, S.; et al. Coupling between magnetic order and charge transport in a two-dimensional magnetic semiconductor. Nat. Mater. 2022, 21, 754. [Google Scholar] [CrossRef]
- Klein, J.; Song, Z.; Pingault, B.; Dirnberger, F.; Chi, H.; Curtis, J.B.; Dana, R.; Bushati, R.; Quan, J.; Dekanovsky, L.; et al. Sensing the local magnetic environment through optically active defects in a layered magnetic semiconductor. ACS Nano 2023, 17, 288. [Google Scholar] [CrossRef]
- Wu, F.; Gutierrez-Lezama, I.; Lopez-Paz, S.A.; Gibertini, M.; Watanabe, K.; Taniguchi, T.; von Rohr, F.O.; Ubrig, N.; Morpurgo, A.F. Quasi-1D electronic transport in a 2D magnetic semiconductor. Adv. Mater. 2022, 34, 2109759. [Google Scholar] [CrossRef] [PubMed]
- Lopez-Paz, S.A.; Guguchia, Z.; Pomjakushin, V.Y.; Witteveen, C.; Cervellino, A.; Luetkens, H.; Casati, N.; Morpurgo, A.F.; von Rohr, F.O. Dynamic magnetic crossover at the origin of the hidden-order in van der Waals antiferromagnet CrSBr. Nat. Commun. 2022, 13, 4745. [Google Scholar] [CrossRef] [PubMed]
- Boix-Constant, C.; Manas-Valero, S.; Ruiz, A.M.; Rybakov, A.; Konieczny, K.A.; Pillet, S.; Baldovi, J.J.; Coronado, E. Probing the spin dimensionality in single-layer CrSBr van der Waals heterostructures by magneto-transport measurements. Adv. Mater. 2022, 34, 2204940. [Google Scholar] [CrossRef] [PubMed]
- Beck, J. Über chalkogenidhalogenide des Chroms synthese, kristallstruktur und magnetismus von chromsulfidbromid, CrSBr. Z. Anorg. Allg. Chem. 1990, 585, 157. [Google Scholar] [CrossRef]
- Jo, J.; Mañas-Valero, S.; Coronado, E.; Casanova, F.; Gobbi, M.; Hueso, L.E. Nonvolatile electric control of antiferromagnet CrSBr. Nano Lett. 2024, 24, 4471. [Google Scholar] [CrossRef]
- Ziebel, M.E.; Feuer, M.L.; Cox, J.; Zhu, X.; Dean, C.R.; Roy, X. CrSBr: An air-stable, two-dimensional magnetic semiconductor. Nano Lett. 2024, 24, 4319. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, C.; Gao, Y.; Chen, Z.; Gu, P.; Te, Y. Probing spin textures in atomically thin CrSBr through tunneling magnetoresistance. arXiv 2024, arXiv:2407.13230. [Google Scholar]
- Yang, B.; Bhujel, B.; Chica, D.G.; Telford, E.J.; Roy, X.; Ibrahim, F.; Chshiev, M.; Cosset-Chéneau, M.; van Wees, B.J. Electrostatically controlled spin polarization in graphene-CrSBr magnetic proximity heterostructures. Nat. Commun. 2024, 15, 4459. [Google Scholar] [CrossRef]
- Li, Z.; Liu, R.; Chu, Y.; Feng, S.; Lan, W.; Duan, H.; Liu, C.; Yan, W. Dual-terminal artificial synapse in two-dimensional CrSBr memristor for neuromorphic computing. J. Mater. Sci. Mater Electron 2024, 35, 1091. [Google Scholar] [CrossRef]
- Kotliar, G.; Savrasov, S.Y.; Haule, K.; Oudovenko, V.S.; Parcollet, O.; Marianetti, C.A. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 2006, 78, 865. [Google Scholar] [CrossRef]
- Wilson, N.P.; Lee, K.; Cenker, J.; Xie, K.; Dismukes, A.H.; Telford, E.J.; Fonseca, J.; Sivakumar, S.; Dean, C.; Cao, T.; et al. Interlayer electronic coupling on demand in a 2D magnetic semiconductor. Nat. Mater. 2021, 20, 1657. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Luo, N.; Zeng, J.; Tang, L.-M.; Chen, K.-Q. Magnetic anisotropy and electric field induced magnetic phase transition in the van der Waals antiferromagnet CrSBr. Phys. Rev. B 2023, 108, 054401. [Google Scholar] [CrossRef]
- Guo, H.-T.; Guo, S.-D.; Ang, Y.S. Electric-field induced half-metal in monolayer CrSBr. arXiv 2023, arXiv:2308.03430. [Google Scholar]
- Bo, X.; Li, F.; Xu, X.; Wan, X.; Pu, Y. Calculated magnetic exchange interactions in the van der Waals layered magnet CrSBr. New J. Phys. 2023, 25, 013026. [Google Scholar] [CrossRef]
- Yang, K.; Wang, G.; Liu, L.; Lu, D.; Wu, H. Triaxial magnetic anisotropy in the two-dimensional ferromagnetic semiconductor CrSBr. Phys. Rev. B 2021, 104, 144416. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Junquera, J.; Paz, Ó.; Sánchez-Portal, D.; Artacho, E. Numerical atomic orbitals for linear-scaling calculations. Phys. Rev. B 2001, 64, 235111. [Google Scholar] [CrossRef]
- Moreno, J.; Soler, J.M. Optimal meshes for integrals in real- and reciprocal-space unit cells. Phys. Rev. B 1992, 45, 13891. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, D.J. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Craco, L.; Leoni, S.; Laad, M.S.; Rosner, H. Orbital-selective charge dynamics in YTiO3 across the magnetic transition: Combined local-density approximation and dynamical mean-field theory. Phys. Rev. B 2007, 76, 115128. [Google Scholar] [CrossRef]
- Craco, L.; Carara, S.S.; Leoni, S. Electronic structure of BiFeO3 in the presence of strong electronic correlations. Phys. Rev. B 2019, 99, 045112. [Google Scholar] [CrossRef]
- Craco, L.; Laad, M.S.; Müller-Hartmann, E. Orbital Kondo effect in CrO2: A combined local-spin-density-approximation dynamical-mean-field-theory study. Phys. Rev. Lett. 2003, 90, 237203. [Google Scholar] [CrossRef]
- Muneta, I.; Ohya, S.; Terada, H.; Tanaka, M. Sudden restoration of the band ordering associated with the ferromagnetic phase transition in a semiconductor. Nature Commun. 2016, 7, 12013. [Google Scholar] [CrossRef]
- Craco, L. Quantum orbital entanglement: A view from the extended periodic Anderson model. Phys. Rev. B 2008, 77, 125122. [Google Scholar] [CrossRef]
- Craco, L.; Carara, S.S.; de Arruda, A.S.; de Arruda, P.H.Z.; Leoni, S. Tunable analog and nearly digital responses in hole-doped LiNbO2 memristors. Solid State Commun. 2025, 401, 115911. [Google Scholar] [CrossRef]
- Craco, L.; Leoni, S. Theory of two-fluid metallicity in superconducting FeSe at high pressure. Phys. Rev. B 2019, 100, 121101. [Google Scholar] [CrossRef]
- Craco, L.; Leoni, S. Mott and pseudogap localization in pressurized NbO2. Phys. Rev. B 2020, 102, 045142. [Google Scholar] [CrossRef]
- Hybertsen, M.S.; Louie, S.G. Electron correlation in semiconductors and insulators: Band gaps and quasiparticle energies. Phys. Rev. B 1986, 34, 5390. [Google Scholar] [CrossRef] [PubMed]
- Chemla, D.S.; Shah, J. Many-body and correlation effects in semiconductors. Nature 2001, 411, 549. [Google Scholar] [CrossRef] [PubMed]
- Tuan, D.V.; Dery, H. Excitons and trions in monolayer semiconductors with correlated electrons. Phys. Rev. B 2023, 108, 085303. [Google Scholar] [CrossRef]
- Koga, A.; Kawakami, N.; Peters, R.; Pruschke, T. Quantum phase transitions in the extended periodic Anderson model. Phys. Rev. B 2008, 77, 045120. [Google Scholar] [CrossRef]
- Martin, R.; Allen, J. Theory of mixed valence: Metals or small gap insulators. J. Appl. Phys. 1979, 50, 7561. [Google Scholar] [CrossRef]
- Dzero, M.; Sun, K.; Galitski, V.; Coleman, P. Topological Kondo Insulators. Phys. Rev. Lett. 2010, 104, 106408. [Google Scholar] [CrossRef]
- Feuer, M.L.; Thinel, M.; Huang, X.; Cui, Z.-H.; Shao, Y.; Kundu, A.K.; Chica, D.G.; Han, M.-G.; Pokratath, R.; Telford, E.J.; et al. Doping-induced charge density wave and ferromagnetism in the van der Waals semiconductor CrSBr. Adv. Mater. 2025, 2418066. [Google Scholar] [CrossRef]
- Mosina, K.; Wu, B.; Antonatos, N.; Luxa, J.; Mazánek, V.; Söll, A.; Sedmidubsky, D.; Klein, J.; Ross, F.M.; Sofer, Z. Electrochemical intercalation and exfoliation of CrSBr into ferromagnetic fibers and nanoribbons. Small Methods 2024, 8, 2300609. [Google Scholar] [CrossRef]
- Craco, L. Two-band electronic reconstruction induced via correlation and CDW order effects. Condens. Matter 2024, 9, 42. [Google Scholar] [CrossRef]
- Rossnagel, K. On the origin of charge-density waves in select layered transition-metal dichalcogenides. J. Phys. Condens. Matter 2011, 23, 213001. [Google Scholar] [CrossRef]
- Torres, T.; Kuc, A.; Maschio, L.; Pham, T.; Reidy, K.; Dekanovsky, L.; Sofer, Z.; Ross, F.M.; Klein, J. Probing defects and spin-phonon coupling in CrSBr via resonant Raman scattering. Adv. Funct. Materails 2023, 3, 2211366. [Google Scholar] [CrossRef]
- Souza, I.J.; de Arruda, P.H.Z.; Godoy, M.; Craco, L.; de Arruda, A.S. Random crystal-field effects in a mixed spin-1 and spin-3/2 ferrimagnetic Ising system. Physica A 2016, 44, 589. [Google Scholar] [CrossRef]
- Meir, Y.; Wingreen, N.S. Landauer formula for the current through an interacting electron region. Phys. Rev. Lett. 1992, 68, 2512. [Google Scholar] [CrossRef] [PubMed]
- Craco, L.; Kang, K. Perturbation treatment for transport through a quantum dot. Phys. Rev. B 1999, 59, 12244. [Google Scholar] [CrossRef]
- Cuniberti, G.; Craco, L.; Porath, D.; Dekker, C. Backbone-induced semiconducting behavior in short DNA wires. Phys. Rev. B 2002, 65, 241314(R). [Google Scholar] [CrossRef]
- Bao, X.-X.; Wang, X.-F. Effects of long-range dispersive interaction on the electron transport in short single strands of guanine bases. Int. J. Quantum Chem. 2023, 1, e27251. [Google Scholar] [CrossRef]
- Craco, L.; Chagas, E.F.; Carara, S.S.; Freelon, B. Atomristor Mott theory of Sn adatom adlayer on a Si surface. Condens. Matter 2024, 9, 32. [Google Scholar] [CrossRef]
- Waser, R.; Aono, M. Nanoionics-based resistive switching memories. Nat. Mater. 2007, 6, 833. [Google Scholar] [CrossRef]
- Wang, R.; Yang, J.-Q.; Mao, J.-Y.; Wang, Z.-P.; Wu, S.; Zhou, M.; Chen, T.; Zhou, Y.; Han, S.-T. Recent advances of volatile memristors: Devices, mechanisms, and applications. Adv. Intell. Syst. 2020, 2, 202000055. [Google Scholar] [CrossRef]
- Sangwan, V.K.; Hersam, M.C. Neuromorphic nanoelectronic materials. Nat. Nanotechnol. 2020, 15, 517. [Google Scholar] [CrossRef]
- Song, M.-K.; Kang, J.-H.; Zhang, X.; Ji, W.; Ascoli, A.; Messaris, I.; Demirkol, A.S.; Dong, B.; Aggarwal, S.; Wan, W.; et al. Recent advances and future prospects for memristive materials, devices, and systems. ACS Nano 2023, 17, 11994. [Google Scholar] [CrossRef] [PubMed]
- Ran, Y.; Pei, Y.; Zhou, Z.; Wang, H.; Sun, Y.; Wang, Z.; Hao, M.; Zhao, J.; Chen, J.; Yan, X. A review of Mott insulator in memristors: The materials, characteristics, applications for future computing systems and neuromorphic computing. Nano Res. 2023, 16, 1165. [Google Scholar] [CrossRef]
- Chen, A.; Fu, Y.; Yang, G.; Liu, N.; Zhao, X.; Zhang, Z.; Tao, L.; Wan, H.; Rao, Y.; Duan, J.; et al. The Co-improvement of selectivity and uniformity on NbOx-based selector by Al-doping. IEEE Electron Device Lett. 2022, 43, 870. [Google Scholar] [CrossRef]
- Mehonic, A.; Ielmini, D.; Roy, K.; Mutlu, O.; Kvatinsky, S.; Serrano-Gotarredona, T.; Linares-Barranco, B.; Spiga, S.; Savel’ev, S.; Balanov, A.G.; et al. Roadmap to neuromorphic computing with emerging technologies. APL Mater. 2024, 12, 109201. [Google Scholar] [CrossRef]
- Liu, L.; Wang, D.; Wang, D.; Sun, Y.; Lin, H.; Gong, X.; Zhang, Y.; Tang, R.; Mai, Z.; Hou, Z.; et al. Domain wall magnetic tunnel junction-based artificial synapses and neurons for all-spin neuromorphic hardware. Nat. Commun. 2024, 15, 4534. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Craco, L.; Carara, S.S. Effect of t2g-Correlations and Doping in CrSBr Ferromagnetic Semiconductor. Condens. Matter 2025, 10, 27. https://doi.org/10.3390/condmat10020027
Craco L, Carara SS. Effect of t2g-Correlations and Doping in CrSBr Ferromagnetic Semiconductor. Condensed Matter. 2025; 10(2):27. https://doi.org/10.3390/condmat10020027
Chicago/Turabian StyleCraco, Luis, and Sabrina Silva Carara. 2025. "Effect of t2g-Correlations and Doping in CrSBr Ferromagnetic Semiconductor" Condensed Matter 10, no. 2: 27. https://doi.org/10.3390/condmat10020027
APA StyleCraco, L., & Carara, S. S. (2025). Effect of t2g-Correlations and Doping in CrSBr Ferromagnetic Semiconductor. Condensed Matter, 10(2), 27. https://doi.org/10.3390/condmat10020027






