Ab Initio Study of the Electronic, Vibrational, and Mechanical Properties of the Magnesium Diboride Monolayer
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jones, M.E.; Marsh, R.E. The preparation and structure of magnesium boride, MgB2. J. Am. Chem. Soc. 1953, 76, 5. [Google Scholar] [CrossRef]
- Nagamatsu, J.; Nakagawa, N.; Muranaka, T.; Zenitani, Y.; Akimitsu, J. Superconductivity at 39 K in magnesium diboride. Nature 2001, 410, 63. [Google Scholar] [CrossRef] [PubMed]
- Bud’ko, S.L.; Lapertot, G.; Petrovic, C.; Cunningham, C.E.; Anderson, N.; Canfield, P.C. Boron Isotope Effect in Superconducting MgB2. Phys. Rev. Lett. 2001, 86, 1877. [Google Scholar] [CrossRef] [PubMed]
- Pickett, W. Superconductivity: 2D Physics, Unknown Mechanisms, Current Puzzles. Emerg. Phenom. Correl. Matter Lect. Notes Autumn School Corr. Electron. 2013, 2013, 45. [Google Scholar]
- Choi, H.J.; Roundy, D.; Sun, H.; Cohen, M.L.; Steven Louie, G. The origin of the anomalous superconducting properties of MgB2. Nature 2002, 418, 758. [Google Scholar] [CrossRef]
- Kortus, J.; Mazin, I.I.; Belaachenko, K.D.; Antropov, V.P.; Boyer, L.L. Superconductivity of Metallic Boron in MgB2. Phys. Rev. Lett. 2001, 86, 4656. [Google Scholar] [CrossRef]
- An, J.M.; Pickett, W.E. Superconductivity of MgB2: Covalent Bonds Driven Metallic. Phys. Rev. Lett. 2001, 86, 4366. [Google Scholar] [CrossRef] [PubMed]
- Liu, A.Y.; Mazin, I.I.; Kortus, J. Beyond Eliashberg Superconductivity in MgB2: Anharmonicity, Two-Phonon Scattering, and Multiple Gaps. Phys. Rev. Lett. 2001, 87, 087005. [Google Scholar] [CrossRef] [PubMed]
- Kong, Y.; Dolgov, O.V.; Jepsen, O.; Andersen, O.K. Electron-phonon interaction in the normal and superconducting states of MgB2. Phys. Rev. B 2001, 64, 020501. [Google Scholar] [CrossRef]
- Bohnen, K.-P.; Heid, R.; Renker, B. Phonon Dispersion and Electron-Phonon Coupling in MgB2 and AlB2. Phys. Rev. Lett. 2001, 86, 5771. [Google Scholar] [CrossRef] [PubMed]
- Kunc, K.; Loa, I.; Syassen, K.; Kremer, R.K.; Ahn, K. MgB2 under pressure: phonon calculations, Raman spectroscopy, and optical reflectance. J. Phys. Condens. Matter 2001, 13, 9945. [Google Scholar] [CrossRef]
- Choi, H.J.; Roundy, D.; Sun, H.; Cohen, M.L.; Louie, S.G. First-principles calculation of the superconducting transition in MgB2 within the anisotropic Eliashberg formalism. Phys. Rev. B 2002, 66, 020513. [Google Scholar] [CrossRef]
- Canfield, P.C.; Crabtree, G.W. Magnesium Diboride: Better Late than Never. Phys. Today 2003, 56, 34. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Katsnelson, M.I.; Novoselov, K.S.; Geim, A.K. Chiral tunnelling and the Klein paradox in graphene. Nat. Phys. 2006, 2, 620–625. [Google Scholar] [CrossRef]
- Katsnelson, M.I. Zitterbewegung, chirality, and minimal conductivity in graphene. Eur. Phys. J. B 2006, 51, 157–160. [Google Scholar] [CrossRef]
- Rusin, T.M.; Zawadzki, W. Zitterbewegung of electrons in graphene in a magnetic field. Phys. Rev. B 2008, 78, 125419. [Google Scholar] [CrossRef]
- Pisana, S.; Lazzeri, M.; Casiraghi, C.; Novoselov, K.S.; Geim, A.K.; Ferrari, A.C.; Mauri, F. Breakdown of the adiabatic Born-Oppenheimer approximation in graphene. Nat. Mater. 2007, 6, 198–201. [Google Scholar] [CrossRef] [PubMed]
- Piscanec, S.; Lazzeri, M.; Mauri, F.; Ferrari, A.C.; Robertson, J. Kohn Anomalies and Electron-Phonon Interactions in Graphite. Phys. Rev. Lett. 2004, 93, 85503. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Jiang, Z.; Zhang, Y.; Morozov, S.V.; Stormer, H.L.; Zeitler, U.; Maan, J.C.; Boebinger, G.S.; Kim, P.; Geim, A.K. Room-temperature quantum Hall effect in graphene. Science 2007, 315, 1379. [Google Scholar] [CrossRef]
- Zhou, S.Y.; Gweon, G.-H.; Fedorov, A.V.; First, P.N.; de Heer, W.A.; Lee, D.-H.; Guinea, F.; Castro Neto, A.H.; Lanzara, A.; et al. Substrate-induced bandgap opening in epitaxial graphene. Nat. Mater. 2007, 6, 770–775. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, Y.; Stormer, H.L.; Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 2005, 438, 201–204. [Google Scholar] [CrossRef]
- Bekaert, J.; Aperis, A.; Partoens, B.; Oppeneer, P.M.; Milošević, M.V. Evolution of multigap superconductivity in the atomically thin limit: Strain-enhanced three-gap superconductivity in monolayer MgB2. Phys. Rev. B 2017, 96, 094510. [Google Scholar]
- Morshedloo, T.; Roknabadi, M.R.; Behdani, M. First-principles study of the superconductivity in MgB2 bulk and in its bilayer thin film based on electron–phonon coupling. Physica C 2015, 509. [Google Scholar] [CrossRef]
- Calandra, M.; Profeta, G.; Mauri, F. Superconductivity in metal-coated graphene. Phys. Status Solidi (b) 2012, 249, 2544. [Google Scholar] [CrossRef]
- Ludbrook, B.M.; Levy, G.; Nigge, P.; Zonno, M.; Schneider, M.; Dvorak, D.J.; Veenstra, C.N.; Zhdanovich, S.; Wong, D.; Dosanjh, P.; et al. Evidence for superconductivity in Li-decorated monolayer graphene. Proc. Natl. Acad. Sci. USA 2015, 112, 11795. [Google Scholar] [CrossRef] [PubMed]
- Profeta, G.; Calandra, M.; Mauri, F. Phonon-mediated superconductivity in graphene by lithium deposition. Nat. Phys. 2012, 8, 131–134. [Google Scholar] [CrossRef]
- Pešić, J.; Gajić, R.; Hingerl, K.; Belić, M. Strain-enhanced superconductivity in Li-doped graphene. Europhys. Lett. 2014, 108, 67005. [Google Scholar] [CrossRef]
- Szczesniak, D.; Durajski, A.P.; Szczesniak, R. Influence of lithium doping on the thermodynamic properties of graphene based superconductors. J. Phys-Condens. Mat. 2014, 26, 255701. [Google Scholar] [CrossRef]
- Durajski, A.; Skoczylas, K.; Szczesniak, R. Superconductivity in bilayer graphene intercalated with alkali and alkaline earth metals. Phys. Chem. Chem. Phys. 2019, 21, 5925. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.-J.; Margine, E.R. First-principles calculations of the superconducting properties in Li-decorated monolayer graphene within the anisotropic Migdal-Eliashberg formalism. Phys. Rev. B 2016, 94, 064509. [Google Scholar] [CrossRef]
- Margine, E.R.; Lambert, H.; Giustino, F. Electron-phonon interaction and pairing mechanism in superconducting Ca-intercalated bilayer graphene. Sci. Rep. 2016, 6, 21414. [Google Scholar] [CrossRef]
- Mazin, I.I.; Antropov, V.P. Electronic structure, electron–phonon coupling, and multiband effects in MgB2. Phys. C Supercond. 2003, 385, 49–65. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno, N.M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Quantum espresso: A modular and open-source software project for quantum simulations of materials. J. Phys. Condensed Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Lu, N.; Guo, H.; Zhuo, Z.; Wang, L.; Wu, X.; Zeng, X.C. Twisted MX2/MoS2 heterobilayers: effect of van der Waals interaction on the electronic structure. Nanoscale 2017, 9, 19131–19138. [Google Scholar] [CrossRef] [PubMed]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter. 2002, 14, 2745. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef]
- Golesorkhtabar, R.; Pavone, P.; Spitaler, J.; Puschnig, P.; Draxl, C. ElaStic: A tool for calculating second-order elastic constants from first principles. Comput. Phys. Commun. 2013, 184, 1861–1873. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511. [Google Scholar] [CrossRef]
- Lindemann, F.A. The calculation of molecular vibration frequencies. Phys. Z. 1910, 11, 609. [Google Scholar]
- Andrew, R.C.; Mapasha, R.E.; Ukpong, A.M.; Chetty, N. Mechanical properties of graphene and boronitrene. Phys. Rev. B 2012, 85, 125428. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, Y.; Penev, E.S.; Yakobson, B.I. Elasticity, Flexibility, and Ideal Strength of Borophenes. Adv. Func. Mater. 2017, 27, 1605059. [Google Scholar] [CrossRef]
- Zhong, H.; Huang, K.; Yu, G.; Yuan, S. Electronic and mechanical properties of few-layer borophene. Phys. Rev. B 2018, 98, 054104. [Google Scholar] [CrossRef]
- Mannix, A.J.; Zhou, X.F.; Kiraly, B.; Wood, J.D.; Alducin, D.; Myers, B.D.; Liu, X.; Fisher, B.L.; Santiago, U.; Guest, J.R.; et al. Synthesis of borophenes: Anisotropic, two-dimensional boron polymorphs. Science 2015, 350, 1513–1516. [Google Scholar] [CrossRef]
- Wang, H.; Li, Q.; Gao, Y.; Miao, F.; Zhou, X.-F.; Wan, X.G. Strain effects on borophene: Ideal strength, negative Possion’s ratio and phonon instability. New J. Phys. 2016, 18, 073016. [Google Scholar] [CrossRef]
- De la Pena-Seaman, O.; de Cross, R.; Heid, R.; Bohnen, K.-P. Effects of Al and C doping on the electronic structure and phonon renormalization in MgB2. Phys. Rev. B 2009, 79, 134523. [Google Scholar] [CrossRef]
- Ponce, S.; Margine, E.R.; Verdi, C.; Giustino, F. EPW: Electron-phonon coupling, transport and superconducting properties using maximally localized Wannier functions. Comp. Phys. Commun. 2016, 209, 116–133. [Google Scholar] [CrossRef]
- Margine, E.R.; Giustino, F. Anisotropic Migdal-Eliashberg theory using Wannier functions. Phys. Rev. B 2013, 87, 024505. [Google Scholar] [CrossRef]
- Damljanovic, V.; Gajic, R. Existence of Dirac cones in the Brillouin zone of diperiodic atomic crystals according to group theory. J. Phys. Condens. Matter 2016, 28, 085502. [Google Scholar] [CrossRef]
- Damljanovic, V.; Gajic, R. Addendum to ‘Existence of Dirac cones in the Brillouin zone of diperiodic atomic crystals according to group theory’. J. Phys. Condens. Matter 2016, 28, 439401. [Google Scholar] [CrossRef]
- Poulet, H.; Mathieu, J.P. Vibration Spectra and Symmetry of Crystals; Gordon and Breach: New York, NY, USA, 1976. [Google Scholar]
- Szalowski, K. Critical temperature of MgB2 ultrathin superconducting films: BCS model calculations in the tight-binding approximation. Phys. Rev. B 2006, 74, 094501. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Wang, D.; Zhang, Y.; Liu, Z.-H.; Feng, Q.-R.; Gan, Z.-Z. Suppression of superconductivity in epitaxial MgB2 ultrathin films. J. Appl. Phys. 2013, 114, 023903. [Google Scholar] [CrossRef]
- Ao, B.; Zhang, Z.; Tang, T.; Zhao, Y. Potential enhancement of superconductivity in MgB2 nanosheets: First-principles calculations. Chem. Phys. Lett. 2014, 591, 185–188. [Google Scholar] [CrossRef]
- Romero-Bermudez, A.; Garcıa-Garcıa, A.M. Shape resonances and shell effects in thin-film multiband superconductors. Phys. Rev. B 2014, 89, 024510. [Google Scholar] [CrossRef]
- Romero-Bermudez, A.; Garcıa-Garcıa, A.M. Size effects in superconducting thin films coupled to a substrate. Phys. Rev. B 2014, 89, 064508. [Google Scholar] [CrossRef]
- Acharya, N.; Wolak, M.A.; Cunnane, D.P.; Karasik, B.S.; Xi, X.X. MgB2 ultrathin films fabricated by hybrid physical chemical vapor deposition and ion milling. APL Mater. 2016, 4, 086114. [Google Scholar] [CrossRef]
- Valentinis, D.; van der Marel, D.; Berthod, C. Rise and fall of shape resonances in thin films of BCS superconductors. Phys. Rev. B 2016, 94, 054516. [Google Scholar] [CrossRef]
- Narlikar, A.V. Small Superconductors: Introduction. In The Oxford Handbook of Small Superconductors, 1st ed.; Narlikar, A.V., Ed.; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Gariglio, S.; Scheurer, M.; Schmalian, J.; Monteiro, A.M.R.V.L.; Goswami, S.; Caviglia, A. Surface and Interface Superconductivity. In The Oxford Handbook of Small Superconductors, 1st ed.; Narlikar, A.V., Ed.; Oxford University Press: Oxford, UK, 2017. [Google Scholar]




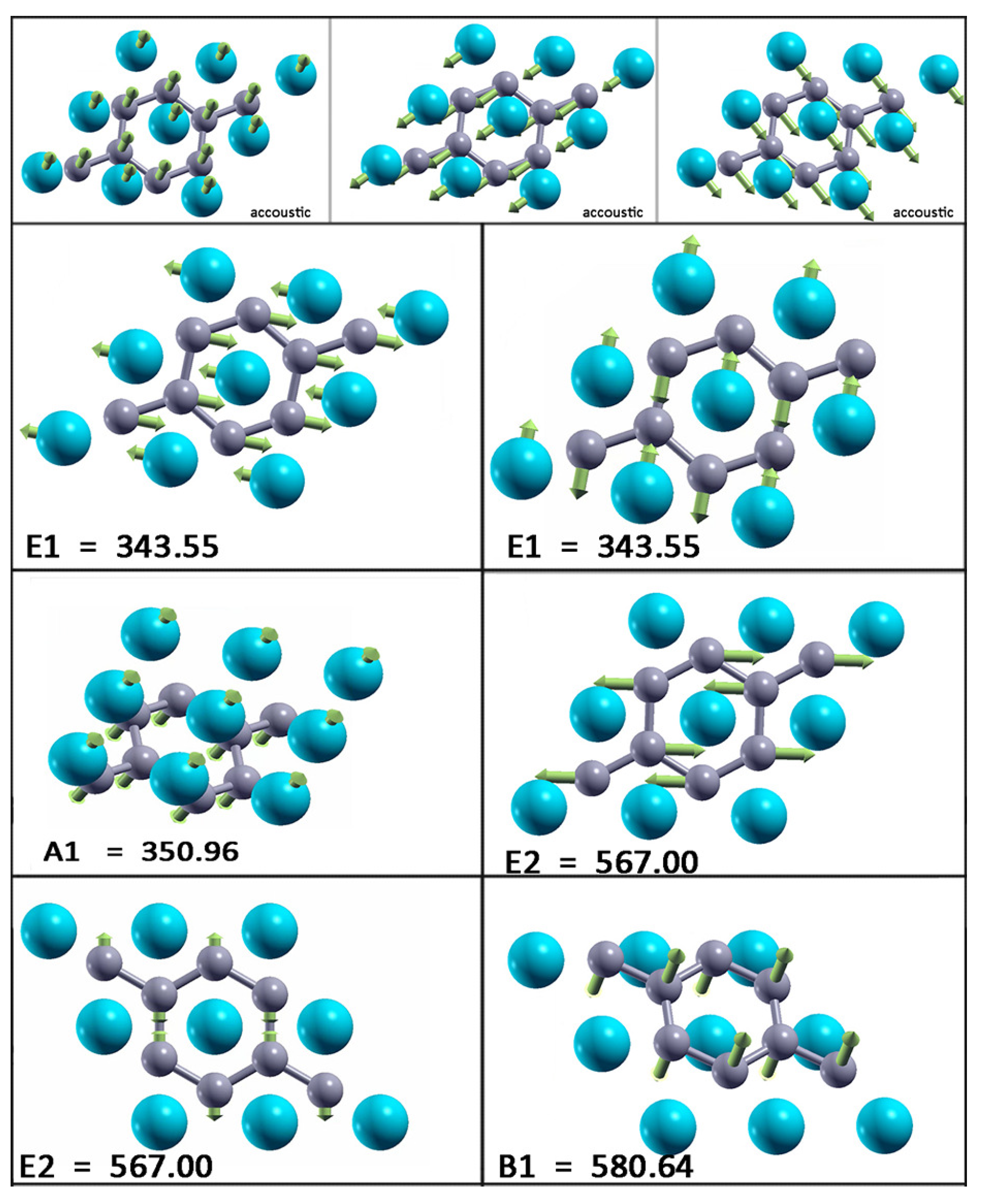
| Y | G | |||||
|---|---|---|---|---|---|---|
| 63.4 | 33.3 | 30.18 | 63.29 | 33.3 |
| Raman Tensors | |
|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pešić, J.; Popov, I.; Šolajić, A.; Damljanović, V.; Hingerl, K.; Belić, M.; Gajić, R. Ab Initio Study of the Electronic, Vibrational, and Mechanical Properties of the Magnesium Diboride Monolayer. Condens. Matter 2019, 4, 37. https://doi.org/10.3390/condmat4020037
Pešić J, Popov I, Šolajić A, Damljanović V, Hingerl K, Belić M, Gajić R. Ab Initio Study of the Electronic, Vibrational, and Mechanical Properties of the Magnesium Diboride Monolayer. Condensed Matter. 2019; 4(2):37. https://doi.org/10.3390/condmat4020037
Chicago/Turabian StylePešić, Jelena, Igor Popov, Andrijana Šolajić, Vladimir Damljanović, Kurt Hingerl, Milivoj Belić, and Radoš Gajić. 2019. "Ab Initio Study of the Electronic, Vibrational, and Mechanical Properties of the Magnesium Diboride Monolayer" Condensed Matter 4, no. 2: 37. https://doi.org/10.3390/condmat4020037
APA StylePešić, J., Popov, I., Šolajić, A., Damljanović, V., Hingerl, K., Belić, M., & Gajić, R. (2019). Ab Initio Study of the Electronic, Vibrational, and Mechanical Properties of the Magnesium Diboride Monolayer. Condensed Matter, 4(2), 37. https://doi.org/10.3390/condmat4020037





