Mechanism of High-Temperature Superconductivity in Correlated-Electron Systems
Abstract
:1. Introduction
2. Part I. Superconductivity in Many-Electron Systems
2.1. Possibility of High- Superconductivity
2.2. Electron Correlation and Superconductivity
- The Cooper pair has d-wave symmetry.
- The superconducting phase exists near the antiferromagnetic phase and parent materials are a Mott insulator.
- The CuO plane is commonly contained and the on-site Coulomb repulsive interaction works between d electrons.
- The size of Cooper pair is very small being of order of 2 Å.
- The CuO plane is high anisotropic and there is a weak Josephson coupling between two layers.
2.3. Superconductivity in Strongly Correlated Electron Systems
3. Part II. Mechanism of Superconductivity in Cuprates
3.1. Model for High- Cuprates
3.2. Optimization Variational Monte Carlo Method
3.2.1. Off-Diagonal Wave Function
3.2.2. Antiferromagnetic Wave Function
3.2.3. Superconducting Wave Function
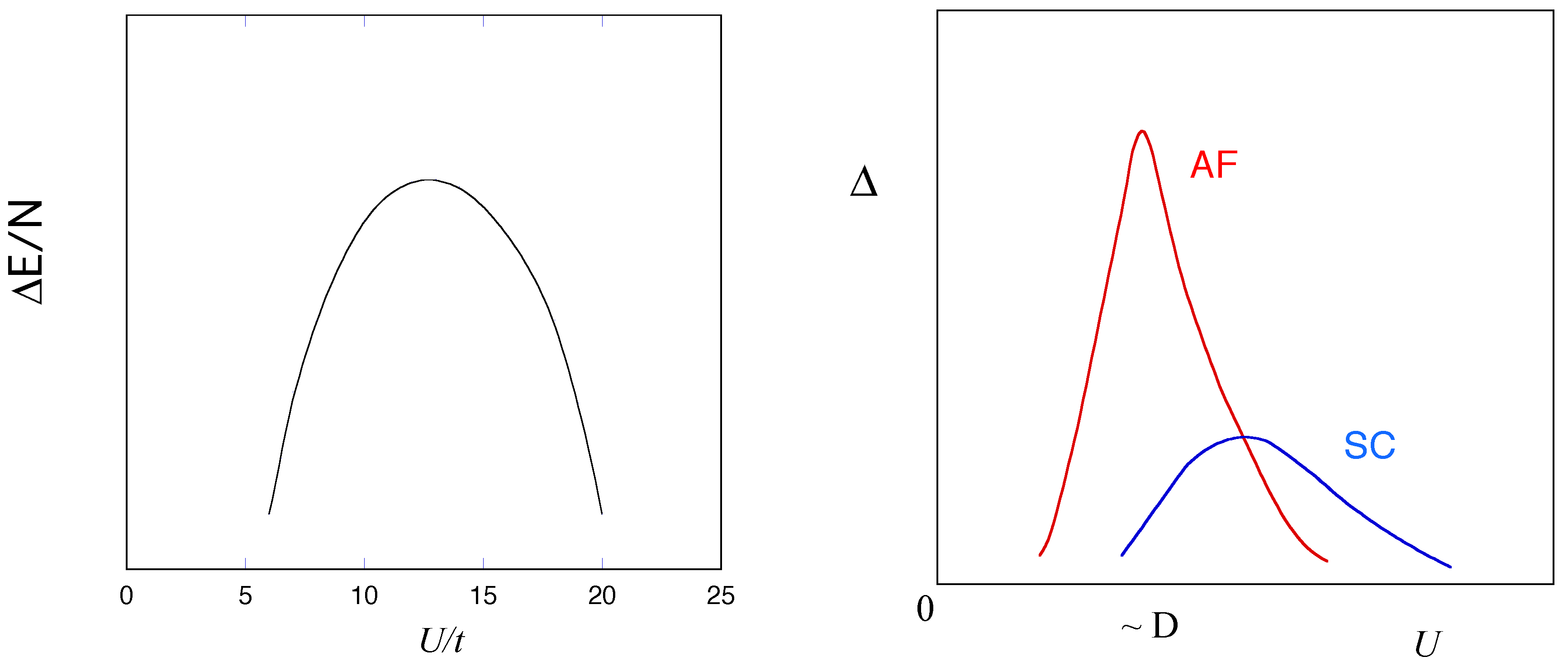
3.3. Correlated Superconductivity
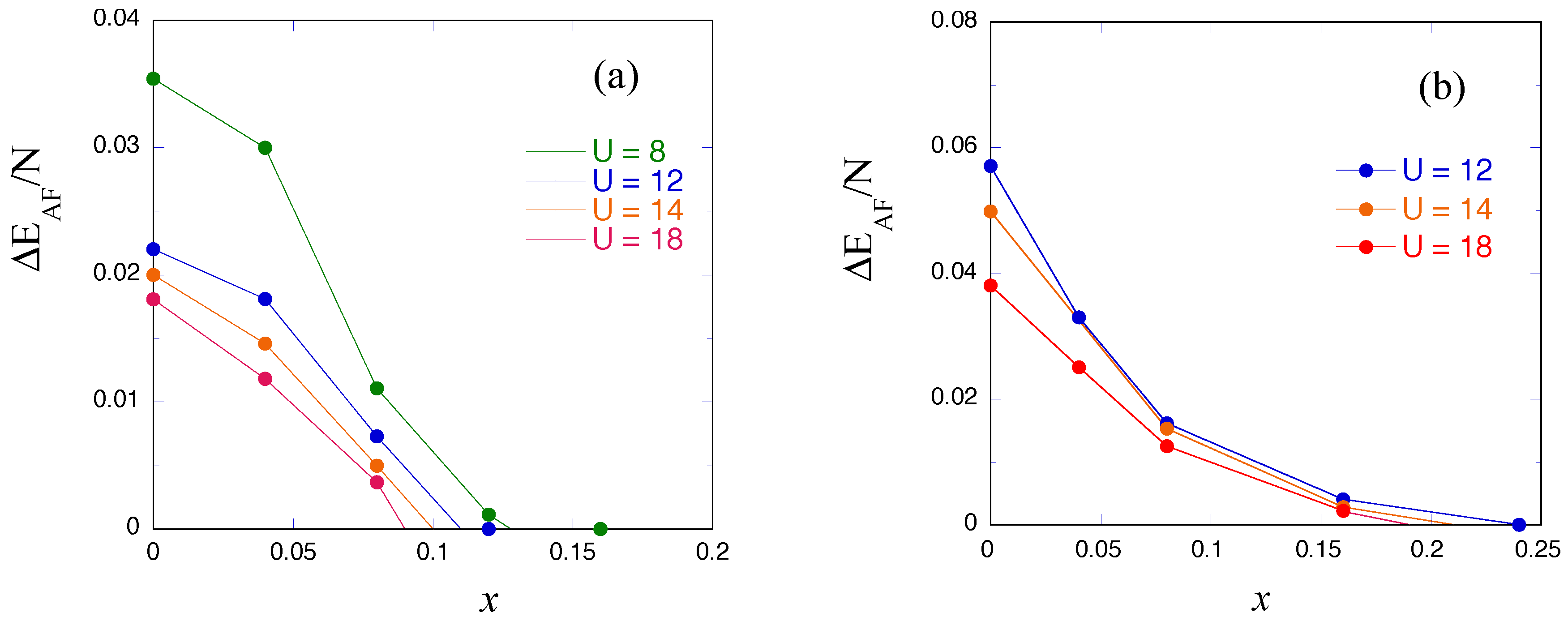
3.4. Stability of Antiferromagnetic State
3.4.1. Hubbard Model
3.4.2. Three-Band d-p Model
3.5. Phase Diagram for the Hubbard Model
4. Summary
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| OVMC | optimization variational Monte Carlo method |
| AF | antiferromagnetic |
| SC | superconductivity or superconducting |
| 2D | two-dimensional |
| AFI | antiferromagnetic insulator |
| PI | paramagnetic insulator |
References
- Bednorz, J.B.; Müller, K.A. Possible high Tc superconductivity in the Ba-La-Cu-O system. Z. Phys. B Condens. Matter 1986, B64, 189–193. [Google Scholar] [CrossRef]
- Keimer, B.; Kivelson, S.A.; Norman, M.R.; Uchida, S.; Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 2015, 518, 179. [Google Scholar] [CrossRef] [PubMed]
- Rybicki, D.; Jurkutat, M.; Reichart, S.; Kapusta, C.; Haase, J. Perspective on the phase diagram of cuprate high-temperature superconductors. Nat. Commun. 2016, 7, 11413. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cooper, L.N. Bound Electron Paira in a Degenerate Fermi Gas. Phys. Rev. 1956, 104, 1189. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Microscopic Theory of Superconductivity. Phys. Rev. 1957, 106, 162. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175. [Google Scholar] [CrossRef]
- Emery, V.J. Theory of high-Tc superconductivity in oxides. Phys. Rev. Lett. 1987, 58, 2794. [Google Scholar] [CrossRef] [PubMed]
- Hirsch, J.E.; Loh, E.Y.; Scalapino, D.J.; Tang, S. Pairing interaction in CuO clusters. Phys. Rev. B 1989, 39, 243. [Google Scholar] [CrossRef]
- Scalettar, R.T.; Scalapino, D.J.; Sugar, R.L.; White, S.R. Antiferromagnetic, charge-transfer, and pairing correlations in the three-band Hubbard model. Phys. Rev. B 1991, 44, 770. [Google Scholar] [CrossRef]
- Unger, P.; Fulde, P. Spectral function of holes in the Emergy model. Phys. Rev. B 1993, 48, 16607. [Google Scholar] [CrossRef]
- Oguri, A.; Asahatam, T.; Maekawa, S. Gutzwiller wave function in the three-band Hubbard model: A variational Monte Carlo study. Phys. Rev. B 1994, 49, 6880. [Google Scholar] [CrossRef] [PubMed]
- Koikegami, S.; Yamada, K. Antiferromagnetic and superconducting correlations on the d-p model. J. Phys. Soc. Jpn. 2000, 69, 768. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Koike, S.; Yamaji, K. Ground state of the three-band Hubbard model. Phys. Rev. B 2001, 64, 184509. [Google Scholar] [CrossRef] [Green Version]
- Koikegami, S.; Yanagisawa, T. Superconducting gap of the two-dimensional d-p model with small Ud. J. Phys. Soc. Jpn. 2001, 70, 3499–3502. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Koike, S.; Yamaji, K. Lattice distortions, incommensurability, and stripes in the electronic model for high-Tc cuprates. Phys. Rev. B 2003, 67, 132408. [Google Scholar] [CrossRef]
- Koikegami, S.; Yanagisawa, T. Superconductivity in Sr2RuO4 mediated by Coulomb scattering. Phys. Rev. B 2003, 67, 134517. [Google Scholar] [CrossRef]
- Koikegami, S.; Yanagisawa, T. Superconductivity in multilayer perovskite. J. Phys. Soc. Jpn. 2006, 75, 034715. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Miyazaki, M.; Yamaji, K. Incommensurate antiferromagnetism coexisting with superconductivity in two-dimensional d-p model. J. Phys. Soc. Jpn. 2009, 78, 031706. [Google Scholar] [CrossRef]
- Weber, C.; Lauchi, A.; Mila, F.; Giamarchi, T. Orbital currents in extended Hubbard model of High-Tc cuprate superconductors. Phys. Rev. Lett. 2009, 102, 017005. [Google Scholar] [CrossRef]
- Lau, B.; Berciu, M.; Sawatzky, G.A. High spin polaron in lightly doped CuO2 planes. Phys. Rev. Lett. 2011, 106, 036401. [Google Scholar] [CrossRef]
- Weber, C.; Giamarchi, T.; Varma, C.M. Phase diagram of a three-orbital model for high-Tc cuprate superconductors. Phys. Rev. Lett. 2014, 112, 117001. [Google Scholar] [CrossRef] [PubMed]
- Avella, A.; Mancini, F.; Paolo, F.; Plekhanov, E. Emery vs. Hubbard model for cuprate superconductors: A composite operator method study. Eur. Phys. J. 2013, B86, 265. [Google Scholar] [CrossRef]
- Ebrahimnejad, H.; Sawatzky, G.A.; Berciu, M. Differences between the insulating limit quasiparticles of one-band and three-band cuprate models. J. Phys. Condens. Matter 2016, 28, 105603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tamura, S.; Yokoyama, H. Variational study of magnetic ordered state in d-p model. Phys. Procedia 2016, 81, 5–8. [Google Scholar] [CrossRef]
- Hubbard, J. Electron correlations in narrow energy bands. Proc. R. Soc. Lond. 1963, 276, 238–257. [Google Scholar]
- Hubbard, J. Electron correlations in narrow energy bands III. Proc. R. Soc. Lond. 1964, 281, 401–419. [Google Scholar]
- Gutzwiller, M.C. Effect of correlation on the ferromagnetism of transition metals. Phys. Rev. Lett. 1963, 10, 159. [Google Scholar] [CrossRef]
- Ceperley, D.; Chester, G.V.; Kalos, K.H. Monte Carlo simulation of a many-fermion study. Phys. Rev. B 1977, 16, 3081. [Google Scholar] [CrossRef]
- Gros, C.; Joynt, R.; Rice, T.M. Antiferromagnetic correlations in almost-localized Fermi liquids. Phys. Rev. B 1987, 36, 381. [Google Scholar] [CrossRef]
- Yokoyama, H.; Shiba, H. Variational Monte Carlo studies of Hubbard model I. J. Phys. Soc. Jpn. 1987, 56, 1490–1506. [Google Scholar] [CrossRef]
- Giamarchi, T.; Lhuillier, C. Phase diagrams of the two-dimensional Hubbard and t-J models by a variational Monte Carlo study. Phys. Rev. B 1991, 43, 12943. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Carlson, J.; Gubernatis, J.E. Constrained path Monte Carlo method for fermion ground states. Phys. Rev. B 1997, 55, 7464. [Google Scholar] [CrossRef]
- Zhang, S.; Carlson, J.; Gubernatis, J.E. Pairing correlation in the two-dimensional Hubbard model. Phys. Rev. Lett. 1997, 78, 4486. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Shimoi, Y. Exact results in strongly correlated electrons. Int. J. Mod. Phys. 1996, B10, 3383–3450. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Shimoi, Y. Ground state of the Kondo-Hubbard model at half-filling. Phys. Rev. Lett. 1995, 74, 4939. [Google Scholar] [CrossRef] [PubMed]
- Nakanishi, T.; Yamaji, K.; Yanagisawa, T. Variational Monte Carlo indications of d-wave superconductivity in the two-dimensional Hubbard model. J. Phys. Soc. Jpn. 1997, 66, 294–297. [Google Scholar] [CrossRef]
- Yamaji, K.; Yanagisawa, T.; Nakanishi, T.; Koike, S. Variational Monte Carlo study on the superconductivity in the two-dimensional Hubbard model. Physica C 1998, 304, 225–238. [Google Scholar] [CrossRef] [Green Version]
- Yamaji, K.; Yanagisawa, T.; Koike, S. Bulk limit of superconducting condensation energy in 2D Hubbard model. Physica B 2000, 284–288, 415–416. [Google Scholar] [CrossRef]
- Yamaji, K.; Yanagisawa, T.; Miyazaki, M.; Kadono, R. Superconducting condensation energy of the two-dimensional Hubbard model in the large-negative-t’ region. J. Phys. Soc. Jpn. 2011, 80, 083702. [Google Scholar] [CrossRef]
- Hardy, T.M.; Hague, P.; Samson, J.H.; Alexandrov, A.S. Superconductivity in a Hubbard-Fröhlich model in cuprates. Phys. Rev. B 2009, 79, 212501. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Miyazaki, M.; Yamaji, K. Correlated-electron systems and high-temperature superconductivity. J. Mod. Phys. 2013, 4, 33. [Google Scholar] [CrossRef]
- Bulut, N. dx2−y2 superconductivity and the Hubbard model. Adv. Phys. 2002, 51, 1587–1667. [Google Scholar] [CrossRef]
- Yokoyama, H.; Tanaka, Y.; Ogata, M.; Tsuchiura, H. Crossover of superconducting properties and kinetic-energy gain in two-dimensional Hubbard model. J. Phys. Soc. Jpn. 2004, 73, 1119–1122. [Google Scholar] [CrossRef]
- Yokoyama, H.; Ogata, M.; Tanaka, Y. Mott transitions and d-wave superconductivity in half-filled-band Hubbard model on square lattice with geometric frustration. J. Phys. Soc. Jpn. 2006, 75, 114706. [Google Scholar] [CrossRef]
- Aimi, T.; Imada, M. Does simple two-dimensional Hubbard model account for high-Tc superconductivity in copper oxides? J. Phys. Soc. Jpn. 2007, 76, 113708. [Google Scholar] [CrossRef]
- Miyazaki, M.; Yanagisawa, T.; Yamaji, K. Diagonal stripe states in the light-doping region in the two-dimensional Hubbard model. J. Phys. Soc. Jpn. 2004, 73, 1643–1646. [Google Scholar] [CrossRef]
- Yanagisawa, T. Phase diagram of the t-U2 Hamiltonian of the weak coupling Hubbard model. New J. Phys. 2008, 10, 023014. [Google Scholar] [CrossRef]
- Yanagisawa, T. Enhanced pair correlation functions in the two-dimensional Hubbard model. New J. Phys. 2013, 15, 033012. [Google Scholar] [CrossRef] [Green Version]
- Yokoyama, H.; Ogata, M.; Tanaka, Y.; Kobayashi, K.; Tsuchiura, H. Crossover between BCS superconductor and doped Mott insulator of d-wave pairing state in two-dimensional Hubbard model. J. Phys. Soc. Jpn. 2013, 82, 014707. [Google Scholar] [CrossRef]
- Yanagisawa, T. Crossover from wealy to strongly correlated regions in the two-dimensional Hubbard model—Off-diagonal Monte Carlo studies of Hubbard model II—. J. Phys. Soc. Jpn. 2016, 85, 114707. [Google Scholar] [CrossRef]
- Noack, R.M.; White, S.R.; Scalapino, D.J. The doped two-chain Hubbard model. EPL 1995, 30, 163. [Google Scholar] [CrossRef]
- Noack, R.M.; Bulut, N.; Scalapino, D.J.; Zacher, M.J. Enhanced dx2−y2 pairing correlations in the two-leg Hubbard ladder. Phys. Rev. B 1997, 56, 7162. [Google Scholar] [CrossRef]
- Yamaji, K.; Shimoi, Y.; Yanagisawa, T. Superconductivity indications of the two-chain Hubbard model due to the two-band effect. Physica C 1994, 235, 2221. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Shimoi, Y.; Yamaji, K. Superconducting phase of a two-chain Hubbard model. Phys. Rev. B 1995, 52, R3860. [Google Scholar] [CrossRef] [PubMed]
- Nakano, T.; Kuroki, K.; Onari, S. Superconductivity due to spin fluctuations originating from multiple Fermi surfaces in the double chain superconductor Pr2Ba4Cu7O15−δ. Phys. Rev. B 2007, 76, 014515. [Google Scholar] [CrossRef]
- Koike, S.; Yamaji, K.; Yanagisawa, T. Effect of the medium-range transfer energies to the superconductivity in the two-chain Hubbard model. J. Phys. Soc. Jpn. 1999, 68, 1657–1663. [Google Scholar] [CrossRef]
- Mott, N.F. Metal-Insulator Transitions; Taylor and Francis Ltd.: London, UK, 1974. [Google Scholar]
- Moriya, T. Spin Fluctuations in Itinerant Electron Magnetism; Springer: Berlin, Germany, 1985. [Google Scholar]
- Yosida, K. Theory of Magnetism; Springer: Berlin, Germany, 1996. [Google Scholar]
- Tranquada, J.M.; Axe, J.D.; Ichikawa, N.; Nakamura, Y.; Uchida, S.; Nachumi, B. Neutron-scattering study of stripe-phase order of holes and spins in La1.48Nd0.4Sr0.12CuO4. Phys. Rev. B 1996, 54, 7489. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, T.; Goto, T.; Shinoda, T.; Fukase, T.; Kimura, H.; Yamada, K.; Ohashi, M.; Yamaguchi, Y. Observation of modulated magnetic long-range order in La1.88Sr0.12CuO4. Phys. Rev. B 1998, 57, R3229. [Google Scholar] [CrossRef]
- Yamada, K.; Lee, C.H.; Kurahashi, K.; Wada, J.; Wakimoto, S.; Ueki, S.; Kimura, H.; Endoh, Y.; Hosoya, S.; Shirane, G.; et al. Doping dependence of the spatially modulated dynamical spin correlations and the superconducting-transition temperature in La2−xSrxCuO4. Phys. Rev. B 1998, 57, 6165. [Google Scholar] [CrossRef]
- Arai, M.; Nishijima, T.; Endoh, Y.; Egami, T.; Tajima, S.; Tomimoto, K.; Shiohara, Y.; Takahashi, M.; Garrett, A.; Bennington, S.M. Incommensurate spin dynamics of underdoped superconductor YBa2Cu3Y6.7. Phys. Rev. Lett. 1999, 83, 608. [Google Scholar] [CrossRef]
- Mook, H.A.; Pengcheng, D.; Dogan, F.; Hunt, R.D. One-dimensional nature of the magnetic fluctuations in YBa2Cu3O6.6. Nature 2000, 404, 729. [Google Scholar] [CrossRef] [PubMed]
- Wakimoto, S.; Birgeneau, R.J.; Kastner, M.A.; Lee, Y.S.; Erwin, R.; Gehring, P.M.; Lee, S.H.; Fujita, M.; Yamada, K.; Endoh, Y.; et al. Direct observation of a one-dimensional static spin modulation in insulating La1.95Sr0.05CuO4. Phys. Rev. B 2000, 61, 3699. [Google Scholar] [CrossRef]
- Bianconi, A.; Saini, N.L.; Lanzara, A.; Missori, M.; Rossetti, T.; Oyanagi, H.; Yamaguchi, H.; Oka, K.; Ito, T. Determination of the local lattice distortions in the CuO2 plane of La1.85Sr0.15CuO4. Phys. Rev. Lett. 1996, 76, 3412. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, A. Quantum materials: Shape resonances in superstripes. Nat. Phys. 2013, 9, 536. [Google Scholar] [CrossRef]
- Hoffman, J.E.; McElroy, K.; Lee, D.-H.; Lang, K.M.; Eisaki, H.; Uchida, S.; Davis, J.C. Imaging quasiparticle interference in Bi2Sr2CaCu2O8+δ. Science 2002, 295, 466. [Google Scholar] [CrossRef] [PubMed]
- Wise, W.D.; Boyer, M.C.; Chatterjee, K.; Kondo, T.; Takeuchi, T.; Ikuta, J.; Wang, Y.; Hudson, E.W. Charge-density-wave origin of cuprate checkerboard visualized by scanning tunnelling microscopy. Nat. Phys. 2008, 4, 696. [Google Scholar] [CrossRef]
- Hanaguri, T.; Lupien, C.; Kohsaka, Y.; Lee, D.-H.; Azuma, M.; Takano, M.; Takagi, H.; Davis, J. A checkerboard electronic crystal state in lightly hole-doped Ca2−xNaxCuO2Cl2. Nature 2004, 430, 1001. [Google Scholar] [CrossRef]
- Miyazaki, M.; Yanagisawa, T.; Yamaji, K. Checkerboard states in the two-dimensional Hubbard model with the Bi2212-type band. J. Phys. Soc. Jpn. 2009, 78, 043706. [Google Scholar] [CrossRef]
- Anderson, P.W. The resonating valence bond states in La2CuO4. Science 1987, 253, 1196. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Koike, S.; Yamaji, K. Off-diagonal wave function Monte Carlo Studies of Hubbard model I. J. Phys. Soc. Jpn. 1998, 67, 3867–3874. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Miyazaki, M. Mott transition in cuprate high-temperature superconductors. EPL 2014, 107, 27004. [Google Scholar] [CrossRef] [Green Version]
- Yanagisawa, T. Antiferromagnetism, superconductivity and phase diagram in the two-dimensional Hubbard model—Off-diagonal wave function Monte Carlo studies of Hubbard model III—. J. Phys. Soc. Jpn. 2019, 88, 054702. [Google Scholar] [CrossRef]
- Eliashberg, G.M. Interactions between electrons and lattice vibrations in a superconductor. Sov. Phys. JETP 1960, 11, 696–702. [Google Scholar]
- Carbotte, J.P. Properties of boson-exchange superconductors. Rev. Mod. Phys. 1990, 62, 1027. [Google Scholar] [CrossRef]
- McMillan, W.L. Transition temperature of strong-coupled superconductors. Phys. Rev. 1968, 167, 331. [Google Scholar] [CrossRef]
- Allen, P.B.; Dynea, R.C. Transition temperature of strong-coupled superconductors reanalyzed. Phys. Rev. B 1968, 12, 905. [Google Scholar] [CrossRef]
- Ashcroft, N.W. Metallic hydrogen: A high-temperature superconductor? Phys. Rev. Lett. 1968, 21, 1748. [Google Scholar] [CrossRef]
- Drozdov, A.P.; Eremets, M.I.; Troyan, I.A.; Ksenofontov, V.; Shylin, S.I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 2015, 525, 73. [Google Scholar] [CrossRef] [PubMed]
- Peng, F.; Sun, Y.; Pickard, C.J.; Needs, R.J.; Wu, Q.; Ma, Y. Hydrogen clathrate structures in rare earth hydrides at high pressures: Possible route to room-temperature superconductivity. Phys. Rev. Lett. 2017, 119, 107001. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Naumov, I.I.; Hoffmann, R.; Schcroft, N.W.; Hemley, R.J. Potential high-Tc superconducting lanthanum and yttrium hydrides at high pressure. Proc. Natl. Acad. Sci. USA 2017, 114, 6990–6995. [Google Scholar] [CrossRef] [PubMed]
- Innocenti, D.; Poccia, N.; Ricci, A.; Valletta, A.; Caprara, S.; Perali, A.; Bianconi, A. Resonant and crossover phenomena in a multiband superconductor: Tuning the chemical potential near a band edge. Phys. Rev. B 2010, 82, 184528. [Google Scholar] [CrossRef]
- Mazziotti, M.V.; Valletta, A.; Campi, G.; Innocenti, D.; Perali, A.; Bianconi, A. Possible Fano resonance for high-Tc multi-gap superconductivity in p-Terphenyl doped at the Lifshitz transition. EPL 2017, 118, 37003. [Google Scholar] [CrossRef]
- Moskalenko, V.A. Fiz. Metal Metallored. 1959, 8, 2518.
- Suhl, H.; Mattias, B.T.; Walker, L.R. Bardeen-Cooper-Schrieffer theory of superconductivity in the case of overlapping bands. Phys. Rev. Lett. 1959, 3, 552. [Google Scholar] [CrossRef]
- Peretti, J. Superconductivity of transition elements. Phys. Lett. 1962, 2, 275. [Google Scholar] [CrossRef]
- Kondo, J. Superconductivity in transition metals. Prog. Theor. Phys. 1963, 29, 1–9. [Google Scholar] [CrossRef]
- Stanev, V.; Tesanovic, Z. Three-band superconductivity and the order parameter that breaks time-reversal symmetry. Phys. Rev. B 2010, 81, 134522. [Google Scholar] [CrossRef]
- Tanaka, Y.; Yanagisawa, T. Chiral ground state in three-band superconductors. J. Phys. Soc. Jpn. 2010, 79, 114706. [Google Scholar] [CrossRef]
- Tanaka, Y.; Yanagisawa, T. Chiral state in three-gap superconductors. Solid State Commun. 2010, 150, 1980–1982. [Google Scholar] [CrossRef]
- Dias, R.G.; Marques, A.M. Frustrated multiband superconductivity. Superconduct. Sci. Technol. 2011, 24, 085009. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Tanaka, Y.; Hase, I.; Yamaji, K. Vortices and chirality in multi-band superconductors. J. Phys. Soc. Jpn. 2012, 81, 024712. [Google Scholar] [CrossRef]
- Hu, X.; Wang, Z. Stability and Josephson effect of time-reversal-symmetry-broken multicomponent superconductivity induced by frustrated intercomponent coupling. Phys. Rev. B 2012, 85, 064516. [Google Scholar] [CrossRef]
- Stanev, V. Model of collective modes in three-band superconductors with repulsive interband interactions. Phys. Rev. B 2012, 85, 174520. [Google Scholar] [CrossRef]
- Platt, C.; Thomale, R.; Homerkamp, C.; Zhang, S.C.; Hanke, W. Mechanism for a pairing with time-reversal symmetry breaking in iron-based superconductors. Phys. Rev. B 2012, 85, 180502. [Google Scholar] [CrossRef]
- Maiti, S.; Chubukov, A.V. s + is state with broken time-reversal symmetry in Fe-based superconductors. Phys. Rev. B 2013, 87, 144511. [Google Scholar] [CrossRef]
- Wilson, B.J.; Das, M.P. Time-reversal-symmetry-broken state in the BCS formalism for a multi-band superconductor. J. Phys. Condens. Matter 2013, 25, 425702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ganesh, R.; Baskaran, G.; van den Brink, J.; Efremov, D.V. Theoretical prediction of a time-reversal broken chiral superconducting phase driven by electronic correlations in a single TiSe2 layer. Phys. Rev. Lett. 2014, 113, 177001. [Google Scholar] [CrossRef]
- Yerin, Y.S.; Omelyanchouk, A.N.; Il’ichev, E. Dc SQUID based on a three-band superocnductor with broken time-reversal symmetry. Superconduct. Sci. Technol. 2015, 28, 095006. [Google Scholar] [CrossRef]
- Hillier, A.D.; Quintanilla, J.; Cywinskii, R. Evidence for time-reversal symmetry breaking in the noncentrosymmetric superconductor LaNiC2. Phys. Rev. Lett. 2009, 102, 117007. [Google Scholar] [CrossRef]
- Hase, I.; Yanagisawa, T. Electronic structure of RNiC2 (R = La, Y, and Th). J. Phys. Soc. Jpn. 2009, 78, 084724. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Hase, I. Massless modes and abelian gauge fields in multi-band superconductors. J. Phys. Soc. Jpn. 2013, 82, 124704. [Google Scholar] [CrossRef]
- Lin, S.Z.; Hu, X. Phase solitons in multi-band superconductors with and without time-reversal symmetry. New J. Phys. 2012, 14, 063021. [Google Scholar] [CrossRef]
- Kobayashi, K.; Machida, M.; Ota, Y.; Nori, F. Massless collective excitations in frustrated multiband superconductors. Phys. Rev. B 2013, 88, 224516. [Google Scholar] [CrossRef]
- Koyama, T. Collective modes in multiband superconductors: Rigorous study based on the Ward-Takahashi relations. J. Phys. Soc. Jpn. 2014, 83, 074715. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Tanaka, Y. Fluctuation-induced Nambu-Goldstone bosons in a Higs-Josephson model. New J. Phys. 2014, 16, 123014. [Google Scholar] [CrossRef]
- Tanakai, Y.; Hase, I.; Yanagisawa, T.; Kato, G.; Nishio, T.; Arisawa, S. Current-induced massless mode of the interband phase difference in two-band superconductors. Physica C 2015, 516, 10. [Google Scholar] [CrossRef]
- Valletta, A.; Bianconi, A.; Perali, A.; Saini, N.L. Electronic and superconducting properties of a superlattice of quantum stripes at the atomic limit. Z. Physik B Condens. Matter 1997, 104, 707. [Google Scholar] [CrossRef]
- Choi, H.Y.; Yun, J.H.; Bang, Y.; Lee, H.C. Model for the inverse isotope effect of FeAs-based superconductors in the π-phase-shifted pairing state. Phys. Rev. B 2009, 80, 052505. [Google Scholar] [CrossRef]
- Shirage, P.M.; Kihou, K.; Miyazawa, K.; Lee, C.-H.; Kito, H.; Eisaki, H.; Yanagisawa, T.; Tanaka, Y.; Iyo, A. Inverse iron isotope effect on the transition temperature of the (Ba,K)Fe2As2 superconductor. Phys. Rev. Lett. 2009, 103, 257003. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Odagiri, K.; Hase, I.; Yamaji, K.; Shirage, P.M.; Tanaka, Y.; Iyo, A.; Eisaki, H. Isotope effect in multi-band and multi-channel attractive systems and inverse isotope effect in iron-based superconductors. J. Phys. Soc. Jpn. 2009, 78, 094718. [Google Scholar] [CrossRef]
- Perali, A.; Innocenti, D.; Valletta, A.; Bianconi, A. Anomalous isotope effect near a 2.5 Lifshitz transition in a multi-band multi-condensates superconductor made of a superlattice of stripes. Superconduct. Sci. Technol. 2012, 25, 124002. [Google Scholar] [CrossRef]
- Izyumov, Y.A.; Laptev, V.M. Vortex structure in superconductors with a many-component order parameter. Phase Transit. 1990, 20, 95. [Google Scholar] [CrossRef]
- Volovik, G.E. The Universe in a Helium Droplet; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Kuplevakhsky, S.V.; Omelyanchouk, A.N.; Yerin, Y.S. Soliton states in mesoscopic two-band superconducting cylinders. J. Low Temp. Phys. 2011, 37, 667. [Google Scholar] [CrossRef]
- Tanaka, Y.; Yamamori, H.; Yanagisawa, T.; Nishio, T.; Arisawa, S. Experimental formation of a fractional vortex in a superconducting bi-layer. Physica C 2018, 548, 44. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Hase, I.; Tanaka, Y. Massless and quantized modes of kinks in the phase space of superconducting gaps. Phys. Lett. A 2018, 382, 3483. [Google Scholar] [CrossRef]
- Littlewood, P.B.; Varma, C.M. Amplitude collective modes in superconductors and their coupling to charge-density wave. Phys. Rev. B 1982, 26, 4883. [Google Scholar] [CrossRef]
- Cea, T.; Benfatto, L. Nature and Raman signature of the Higgs amplitude modes in the coexisting superconducting and charge-density-wave mode. Phys. Rev. B 2014, 90, 224515. [Google Scholar] [CrossRef]
- Pekker, D.; Varma, C.M. Amplitude/Higgs modes in condensed matter physics. Annu. Rev. Condens. Matter Phys. 2015, 6, 269–297. [Google Scholar] [CrossRef]
- Cea, T.; Castellani, C.; Seibold, G.; Benfatto, L. Nonrelativistic dynamics of the amplitude (Higgs) mode in superconductors. Phys. Rev. Lett. 2015, 115, 157002. [Google Scholar] [CrossRef]
- Koyama, T. Perturbative approach to the collective modes in the TRSB phase of multiband superconductors. J. Phys. Soc. Jpn. 2016, 85, 064715. [Google Scholar] [CrossRef]
- Yanagisawa, T. Fluctuation modes in multi-gap superconductors. In Vortices and Nanostructured Superconductors; Crisan, A., Ed.; Springer: Berlin, Germany, 2017. [Google Scholar]
- Yanagisawa, T. Nambu-Goldstone bosons characterized by the order parameters in spontaneous symmetry breaking. J. Phys. Soc. Jpn. 2017, 86, 104711. [Google Scholar] [CrossRef]
- Aitchison, I.J.R.; Ao, P.; Thouless, D.; Zhu, X.M. Effective Lagrangian for BCS superconductors at T = 0. Phys. Rev. B 1995, 51, 6531. [Google Scholar] [CrossRef] [PubMed]
- Murotani, Y.; Tsuji, N.; Aoki, H. Theory of light-induced resonances with collective Higgs and Leggett modes in multiband superconductors. Phys. Rev. B 2017, 95, 104503. [Google Scholar] [CrossRef] [Green Version]
- Yanagisawa, T. Theory of Green’s functions of Nambu-Goldstone and Higgs modes in superconductors. J. Superconduct. Novel Magn. 2019. [Google Scholar] [CrossRef]
- Perali, A.; Bianconi, A.; Lanzara, A.; Saini, N.L. The gap amplification at a shape resonance in a superlattice of quantum stripes: A mechanism for high Tc. Solid State Commun. 1996, 100, 181–186. [Google Scholar] [CrossRef]
- Bianconi, A.; Valletta, A.; Perali, A.; Saini, N.L. Superconductivity of s striped phase at the atomic limit. Physica C 1998, 296, 269–280. [Google Scholar] [CrossRef]
- Kusmartsev, F.V.; Di Castro, D.; Bianconi, G.; Bianconi, A. Transformation of strings into an inhomogeneous phase of stripes and itinerant carriers. Phys. Lett. A 2000, 275, 118. [Google Scholar] [CrossRef]
- Müller, K.A.; Zhao, G.M.; Conder, K.; Keller, H. The ratio of small polarons to free carriers in derived from susceptibility measurements. J. Phys. Condens. Matter 1998, 10, L291. [Google Scholar] [CrossRef]
- Bianconi, A. On the Fermi liquid coupled with a generalized Wigner polaronic CDW giving high Tc superconductivity. Solid State Commun. 1994, 91, 1–5. [Google Scholar] [CrossRef]
- Harris, A.B.; Lange, R.V. Single-particle excitations in narrow energy bands. Phys. Rev. 1967, 157, 295. [Google Scholar] [CrossRef]
- Chao, K.A.; Spalek, J.; Oleś, A.M. Kinetic exchange interaction in a narrow s-band. J. Phys. C 1977, 10, L271. [Google Scholar] [CrossRef]
- Chao, K.A.; Spalek, J.; Oleś, A.M. Canonical perturbation expansion of the Hubbard model. Phys. Rev. B 1978, 18, 3453. [Google Scholar] [CrossRef]
- Micnas, R.; Ranninger, J.; Robaszkiewicz, S. Superconductivity in narrow-band systems with local nonretarded attractive interactions. Rev. Mod. Phys. 1990, 62, 113. [Google Scholar] [CrossRef]
- Robaszkiewicz, S.; Pawlowski, G. Effects of finite pair binding energy in a model for a superconductor with local electron pairing. Physica C 1993, 210, 61–79. [Google Scholar] [CrossRef]
- Arrigoni, E.; Strinati, G.C. Doping-induced incommensurate antiferromagnetism in a Mott-Hubbard insulator. Phys. Rev. B 1991, 44, 7455. [Google Scholar] [CrossRef] [PubMed]
- Kapcia, K.; Robaszkiewicz, S.; Micnas, R. Phase separation in a lattice model of a superconductor with pair hopping. J. Phys. Condens. Matter 2012, 24, 215601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feiner, L.F.; Jefferson, J.H.; Raimondi, R. Effective single-band models for high-Tc cuprates I Coulomb interactions. Phys. Rev. B 1996, 53, 8751. [Google Scholar] [CrossRef]
- Kuroki, K.; Onari, S.; Arita, R.; Usui, H.; Tanaka, Y.; Kontani, H.; Aoki, H. Unconventional Pairing Originating from the Disconnected Fermi Surfaces of Superconducting LaFeAsO1−xFx. Phys. Rev. Lett. 2008, 101, 087004. [Google Scholar] [CrossRef]
- Grewe, N.; Steglich, F. Heavy fermions. Handb. Phys. Chem. Of Rare Earths 1991, 14, 343. [Google Scholar]
- Hewson, A.C. The Kondo Problem to Heavy Fermions; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Onuki, Y. Physics of Heavy Fermions: Heavy Fermions and Strongly Correlated Electron Systems; World Scientific Pub Co Inc.: Singapore, 2018. [Google Scholar]
- Ishiguro, T.; Yamaji, K.; Saito, G. Organic Superconductors; Springer: Berlin, Germany, 2012. [Google Scholar]
- Akashi, R.; Kawamura, M.; Tsuneyuki, S.; Nomura, Y.; Arita, R. First-principles study of the pressure and crystal-structure dependences of the superconducting transition temperature in compressed sulfur hydrides. Phys. Rev. B 2015, 91, 224513. [Google Scholar] [CrossRef] [Green Version]
- Steglich, R.; Asrts, J.; Bredl, C.D.; Lieke, W.; Meschede, D.; Franz, W.; Schäfer, H. Superconductivity in the presence of strong Pauli paramagnetism: CeCu2Si2. Phys. Rev. Lett. 1979, 43, 1892. [Google Scholar] [CrossRef]
- Kittaka, S.; Aoki, Y.; Shimura, Y.; Sakakibara, T.; Seiro, S.; Geibel, C.; Steglich, F.; Ikeda, H.; Machida, K. Multiband superconductivity with unexpected deficiency of nodal quasiparticles in CeCu2Si2. Phys. Rev. Lett. 2014, 112, 0607002. [Google Scholar] [CrossRef] [PubMed]
- Stewart, G.R.; Fisk, Z.; Smith, J.L.; Willis, J.O.; Wire, M.S. New heavy-fermion system NpBe13 with a comparison to UBe13 and PuBe13. Phys. Rev. Lett. 1984, 52, 679. [Google Scholar] [CrossRef]
- Ott, H.R.; Rudingier, H.; Delsing, P.; Fisk, Z. Magnetic ground state of a heavy-electron system: U2Zn17. Phys. Rev. Lett. 1984, 52, 1551. [Google Scholar] [CrossRef]
- Palstra, T.T.; Menovsky, A.A.; van den Berg, J. Superconducting and magnetic transitions in the heavy-fermion system URu12. Phys. Rev. Lett. 1985, 55, 2727. [Google Scholar] [CrossRef] [PubMed]
- Amitsuka, H.; Sato, M.; Metoki, N.; Yokoyama, M.; Kuwahara, K.; Sakakibara, T.; Morimoto, H.; Kawarazaki, S.; Miyako, Y.; Mydosh, J.A. Effect of pressure on tiny antiferromagnetic moment in the heavy-electron compound URu2Si2. Phys. Rev. Lett. 1999, 83, 5114. [Google Scholar] [CrossRef]
- Ohkuni, H.; Inada, Y.; Tokiwa, Y.; Sakurai, K.; Settai, R.; Honma, T.; Haga, Y.; Yamamoto, E.; Onuki, Y.; Yamagami, H.; et al. Fermi surface properties and de Haas-van Alphen oscillation in both the normal and superconducting mixed states of URu2Si2. Philos. Mag. 1999, B79, 1045. [Google Scholar]
- Hedo, M.; Inada, Y.; Yamamoto, E.; Haga, Y.; Onuki, Y.; Aoki, Y.; Matsuda, D.; Sato, H.; Takahashi, S. Superconducting properties of CeRu2. J. Phys. Soc. Jpn. 1998, 67, 272–279. [Google Scholar] [CrossRef]
- Geibel, G.; Schank, C.; Thies, S.; Kitazawa, H.; Bredl, C.D.; Bohm, A.; Rau, M.; Grauel, A.; Caspary, R.; Helfrich, R.; et al. Heavy-fermion superconductivity at T=2K in the antiferromagnet UPd2Al3. Z. Phys. B 1991, 84, 1–2. [Google Scholar] [CrossRef]
- Kyogaku, M.; Kitaoka, Y.; Asayama, K.; Geibel, C.; Schank, C.; Steglich, F. NMR and NQR studies of magnetism and superconductivity in the antiferromagnetic heavy fermion superconductors UM2Al3 (M = Ni and Pd). J. Phys. Soc. Jpn. 1993, 62, 4016–4030. [Google Scholar] [CrossRef]
- Inada, Y.; Yamagami, H.; Haga, Y.; Sakurai, K.; Tokiwa, Y.; Honma, T.; Yamamoto, E.; Onuki, Y.; Yanagisawa, T. Fermi surface and de Haas-van Alphen oscillation in both the normal and superconducting mixed states of UPd2Al3. J. Phys. Soc. Jpn. 1999, 68, 3643–3654. [Google Scholar] [CrossRef]
- Ishida, K.; Mukuda, H.; Kitaoka, Y.; Asayama, K.; Mao, Z.Q.; Mori, Y.; Maeno, Y. Spin-triplet superconductivity in UNi2Al3 revealed by the 27Al knight shift measurement. Phys. Rev. Lett. 2002, 89, 037002. [Google Scholar] [CrossRef] [PubMed]
- Petrovic, C.; Pagliuso, P.G.; Hundley, M.F.; Movshovich, R.; Sarrao, J.L.; Thompson, J.D.; Fisk, Z.; Monthoux, P. heavy-fermion superconductivity in CeCoIn5 at 2.3 K. J. Phys. Condens. Matter 2001, 13, L337. [Google Scholar] [CrossRef]
- Izawa, K.; Yamaguchi, H.; Matsuda, Y.; Shishido, H.; Settai, R.; Onuki, Y. Angular position of nodes in the superconducting gap of quasi-2D heavy-fermion superconductor CeCoIn5. Phys. Rev. Lett. 2001, 87, 057002. [Google Scholar] [CrossRef] [PubMed]
- Hegger, H.; Petrovic, C.; Moshopoulou, E.G.; Hundley, M.F.; Sarrao, J.L.; Fisk, Z.; Thompson, J.D. Pressure-induced superconductivity in quasi-2D CeRhIn5. Phys. Rev. Lett. 2000, 84, 4986. [Google Scholar] [CrossRef] [PubMed]
- Movshovich, R.; Graf, T.; Mandrus, D.; Thompson, J.D.; Smith, J.L.; Fisk, Z. Superconductivity in heavy-fermion CeRh2Si2. Phys. Rev. B 1996, 53, 8241. [Google Scholar] [CrossRef] [PubMed]
- Saxena, S.S.; Agarwal, P.; Ahilan, K.; Grosche, F.M.; Haselwimmer, R.K.W.; Steiner, M.J.; Pugh, E.; Walker, I.R.; Julian, S.R.; Monthoux, P.; et al. Superconductivity on the border of itinerant-electron ferromagnetism in UGe2. Nature 2000, 406, 587. [Google Scholar] [CrossRef] [PubMed]
- Aoki, D.; Huxley, A.; Ressouche, E.; Braithwaite, D.; Flouquet, J.; Brison, J.-P.; Lhotel, E.; Paulsen, C. Coexistence of superconductivity and ferromagnetism in URhGe. Nature 2001, 413, 613. [Google Scholar] [CrossRef] [PubMed]
- Maeno, Y.; Hashimoto, H.; Yoshida, K.; Nishizaki, S.; Fujita, T.; Bednorz, J.G.; Lichtenberg, F. Superconductivity in a layered perovskite without copper. Nature 1994, 372, 532. [Google Scholar] [CrossRef]
- Bauer, E.D.; Frederick, N.A.; Ho, P.-C.; Zapf, V.S.; Maple, M.B. Superconductivity and heavy fermion behavior in PrOs4Sb12. Phys. Rev. B 2002, 65, R100506. [Google Scholar] [CrossRef]
- Takada, K.; Sakurai, H.; Takayama-Muromachi, E.; Izumi, F.; Dilanian, F.A.; Sakai, T. Superconductivity in two-dimensional CoO2 layers. Nature 2003, 422, 53. [Google Scholar] [CrossRef] [PubMed]
- Chaillout, C.; Remeika, J.P.; Santoro, A.; Mareizo, M. The determination of the Bi valence state in BaBiO3 by neutron powder diffraction data. Solid State Commun. 1985, 56, 829–831. [Google Scholar] [CrossRef]
- Nagamatsu, J.; Nakagawa, N.; Muranaka, T.; Zenitani, Y.; Akimitsu, J. Superconductivity at 39 K in magnesium diboride. Nature 2001, 410, 63. [Google Scholar] [CrossRef] [PubMed]
- Kamihara, Y.; Watanabe, T.; Hirano, M.; Hosono, H. Iron-based layered superconductor La(O1−xFx)FeAs (x = 0.05 − 0.12) with Tc = 26 K. J. Am. Chem. Soc. 2000, 130, 3296. [Google Scholar] [CrossRef] [PubMed]
- Kito, H.; Eisaki, H.; Iyo, A. Superconductivity at 54 K in F-free NdFeAsO1−y. J. Phys. Soc. Jpn. 2008, 77, 063707. [Google Scholar] [CrossRef]
- Drozdov, A.P.; Minkov, V.S.; Besedin, S.P.; Kong, P.P.; Kuzovnikov, M.A.; Knyazev, D.A.; Eremets, M.I. Superconductivity at 250 K in lanthanum hydride at high pressures. Nature 2019, 569, 528. [Google Scholar] [CrossRef] [PubMed]
- Somayazulu, M.; Ahart, M.; Mishra, A.K.; Geballe, Z.M.; Baldini, M.; Meng, Y.; Struzhkin, V.V.; Hemley, R.J. Evidence for superconductivity above 260 K in lanthanum superhydride at megabar pressures. Phys. Rev. Lett. 2019, 122, 027001. [Google Scholar] [CrossRef] [PubMed]
- Bickers, N.E.; Scalapino, D.J.; White, S.R. Convserving Approximations for Strongly Correlated Electron Systems: Bethe-Salpeter Equation and Dynamics for the Two-Dimensional Hubbard Model. Phys. Rev. Lett. 1989, 62, 961. [Google Scholar] [CrossRef]
- Pao, C.-H.; Bickers, N.E. Anisotropic superconductivity in the 2D Hubbard model: Gap function and interaction weight. Phys. Rev. B 1994, 49, 1586. [Google Scholar] [CrossRef]
- Monthoux, P.; Scalapino, D.J. Self-consistent pairing in a two-dimensional Hubbard model. Phys. Rev. Lett. 1994, 72, 1874. [Google Scholar] [CrossRef]
- Loram, J.W.; Mirza, K.A.; Cooper, J.R.; Liang, W.Y. Electronic specific heat of YBa2Cu3O6+x from 1.8 to 300 K. Phys. Rev. Lett. 1993, 71, 1740. [Google Scholar] [CrossRef]
- Hao, Z.; Clem, J.R.; McElfresh, M.W.; Civale, L.; Malozemoff, A.P.; Holtzberg, F. Model for the reversible magnetization of high-κ type-II superconductors: Application to high-Tc superconductors. Phys. Rev. B 1991, 43, 2844. [Google Scholar] [CrossRef] [PubMed]
- Weber, C.; Haule, K.; Kotliar, G. Critical weights and waterfalls in doped charge-transfer insulators. Phys. Rev. B 2008, 78, 134519. [Google Scholar] [CrossRef]
- Hybertsen, M.S.; Schlüter, M.; Christensen, N.E. Calculation of Coulomb-interaction parameter for La2CuO4 using a constrained-density-functional approach. Phys. Rev. B 1989, 39, 9028. [Google Scholar] [CrossRef] [PubMed]
- Eskes, H.; Sawatzky, G.A.; Feiner, L.F. Effective transfer for singlets formed by hole doping in the high-Tc superconductors. Physica C 1989, 160, 424–430. [Google Scholar] [CrossRef]
- McMahan, A.K.; Annett, J.F.; Martin, R.M. Cuprate parameters from numerical Wannier functions. Phys. Rev. B 1990, 42, 6268. [Google Scholar] [CrossRef]
- Eskes, H.; Sawatzky, G. Single-, triple-, or multiplel-band Hubbard models. Phys. Rev. B 1991, 43, 119. [Google Scholar] [CrossRef]
- Otsuka, H. Variational Monte Carlo studies of the Hubbard model in one- and two-dimensions. J. Phys. Soc. Jpn. 1992, 61, 1645–1656. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Koike, S.; Yamaji, K. d-wave state with multiplicative correlation factors for the Hubbard model. J. Phys. Soc. Jpn. 1999, 68, 3608–3614. [Google Scholar] [CrossRef]
- Eichenberger, D.; Baeriswyl, D. Superconductivity and antiferromagnetism in the-dimensional Hubbard model: A variational study. Phys. Rev. B 2007, 76, 180504. [Google Scholar] [CrossRef]
- Baeriswyl, D.; Eichenberger, D.; Menteshashvii, M. Variational ground states of the two-dimensional Hubbard model. New J. Phys. 2009, 11, 075010. [Google Scholar] [CrossRef]
- Baeriswyl, D. Superconductivity in the repulsive Hubbard model. J. Superconduct. Novel Magn. 2011, 24, 1157–1159. [Google Scholar] [CrossRef]
- Yanagisawa, T. Quantum Monte Carlo diagonalization for many-fermion systems. Phys. Rev. B 2007, 75, 224503. [Google Scholar] [CrossRef] [Green Version]
- Misawa, T.; Imada, M. Origin of high-Tc superconductivity in doped Hubbard models and their extensions: Roles of uniform charge fluctuations. Phys. Rev. B 2014, 90, 115137. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Miyazaki, M.; Yamaji, K. Crossover induced electron pairing and superconductivity by kinetic renormalization in correlated electron systems. Condens. Matter 2018, 3, 26. [Google Scholar] [CrossRef]
- Kondo, J. The Physics of Dilute Magnetic Alloys; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Yanagisawa, T. Kondo effect in the presence of spin-orbit coupling. J. Phys. Soc. Jpn. 2012, 81, 094713. [Google Scholar] [CrossRef]
- Yanagisawa, T. Kondo effect in Dirac systems. J. Phys. Soc. Jpn. 2015, 84, 074705. [Google Scholar] [CrossRef]
- Ellis, R.K.; Stirling, W.J.; Webber, B.R. QCD and Collider Physics; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Nozieres, P.; Schmitt-Rink, S. Bose condensation in an attractive fermi gas: From weak to strong coupling superconductivity. J. Low Temp. Phys. 1985, 59, 195–211. [Google Scholar] [CrossRef]
- Rajaraman, R. Solitons and Instantons; North-Holland: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Solyom, J. The Fermi gas model of one-dimensional conductors. Adv. Phys. 1979, 28, 201–303. [Google Scholar] [CrossRef] [Green Version]
- Yanagisawa, T. Chiral sine-Gordon model. EPL 2016, 113, 41001. [Google Scholar] [CrossRef] [Green Version]
- Yanagisawa, T. Renormalization group analysis of the hyperbolic sine-Gordon model. Prog. Theor. Exp. Phys. 2019, 2019, 023A01. [Google Scholar] [CrossRef]
- Gross, D.; Neveu, A. Dynamical Symmetry breaking in asymptotically free field theories. Phys. Rev. D 1974, 10, 3235. [Google Scholar] [CrossRef]






| t or | |||||
|---|---|---|---|---|---|
| Cuprate superconductors | 5000 K | 5 | 1000 | 100 K | eV [142] |
| Iron pnictides | 1000 K | 500 | 50 K | eV [143] | |
| Heavy fermion materials | 10,000 K | 100∼1000 | 10∼100 | 1∼10 K | [144,145,146] |
| Organic superconductors | 200∼500 K | 2∼5 | 100 | 10 K | [147] |
| Hydrides | 1000 K | 1000 | 100 K | [148] |
| Materials | Pair Symmetry | Crystal Structure | ||
|---|---|---|---|---|
| CeCuSi | 0.6 K | s or d | bc tetragonal | [149,150] |
| UPt | 0.52 K | p or f | Hexagonal | [151] |
| UBe | 0.86 K | p | Cubic | [152] |
| URuSi | 1.2 K | bc tetragonal | [153,154,155] | |
| CeRu | 6.2 K | s | Laves Cubic | [156] |
| UPdAl | 2 K | d | Hexagonal | [157,158,159] |
| UNiAl | 1 K | p? | Hexagonal | [158,160] |
| CeCoIn | 2.3 K | d | HoCoGa type | [161,162] |
| CeRhIn | 2.1 K | d | HoCoGa type | [163] |
| (16.3 kbar) | bc tetragonal | |||
| CeRhSi | 0.35 K | bc tetragonal | [164] | |
| (9 kbar) | ||||
| UGe | 0.8 K | p? | Orthorhombic | [165] |
| (13.5 kbar) | ||||
| URhGe | 0.25 K | p? | Orthorhombic | [166] |
| SrRuO | 1.4 K | p or f | Perovskite | [167] |
| PrOsSb | 1.85 K | line nodes? | Skutterudite | [168] |
| NaCoO·HO | 5 K | p? | Triangular lattice | [169] |
| BaKBiO | 30 K | s | Perovskite | [170] |
| MgB | 39 K | s | Hexagonal | [171] |
| LaSrCuO | 36 K | d | Perovskite | |
| YBaCuO | 90 K | d | Perovskite | |
| TlBaCaCuO | 125 K | d | Perovskite | |
| HgBaCaCuO | 135 K | d | Perovskite | |
| LaOFFeAs | 26 K | ZrCuSiAs type | [172] | |
| NdFeAsO | 54 K | ZrCuSiAs type | [173] | |
| HS | 203 K | s | (under pressure) | [81] |
| LaH | 260 K | s | (under pressure) | [82,83,174,175] |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yanagisawa, T. Mechanism of High-Temperature Superconductivity in Correlated-Electron Systems. Condens. Matter 2019, 4, 57. https://doi.org/10.3390/condmat4020057
Yanagisawa T. Mechanism of High-Temperature Superconductivity in Correlated-Electron Systems. Condensed Matter. 2019; 4(2):57. https://doi.org/10.3390/condmat4020057
Chicago/Turabian StyleYanagisawa, Takashi. 2019. "Mechanism of High-Temperature Superconductivity in Correlated-Electron Systems" Condensed Matter 4, no. 2: 57. https://doi.org/10.3390/condmat4020057
APA StyleYanagisawa, T. (2019). Mechanism of High-Temperature Superconductivity in Correlated-Electron Systems. Condensed Matter, 4(2), 57. https://doi.org/10.3390/condmat4020057




