Suppression of the s-Wave Order Parameter Near the Surface of the Infinite-Layer Electron-Doped Cuprate Superconductor Sr0.9La0.1CuO2
Abstract
:Preface
1. Introduction
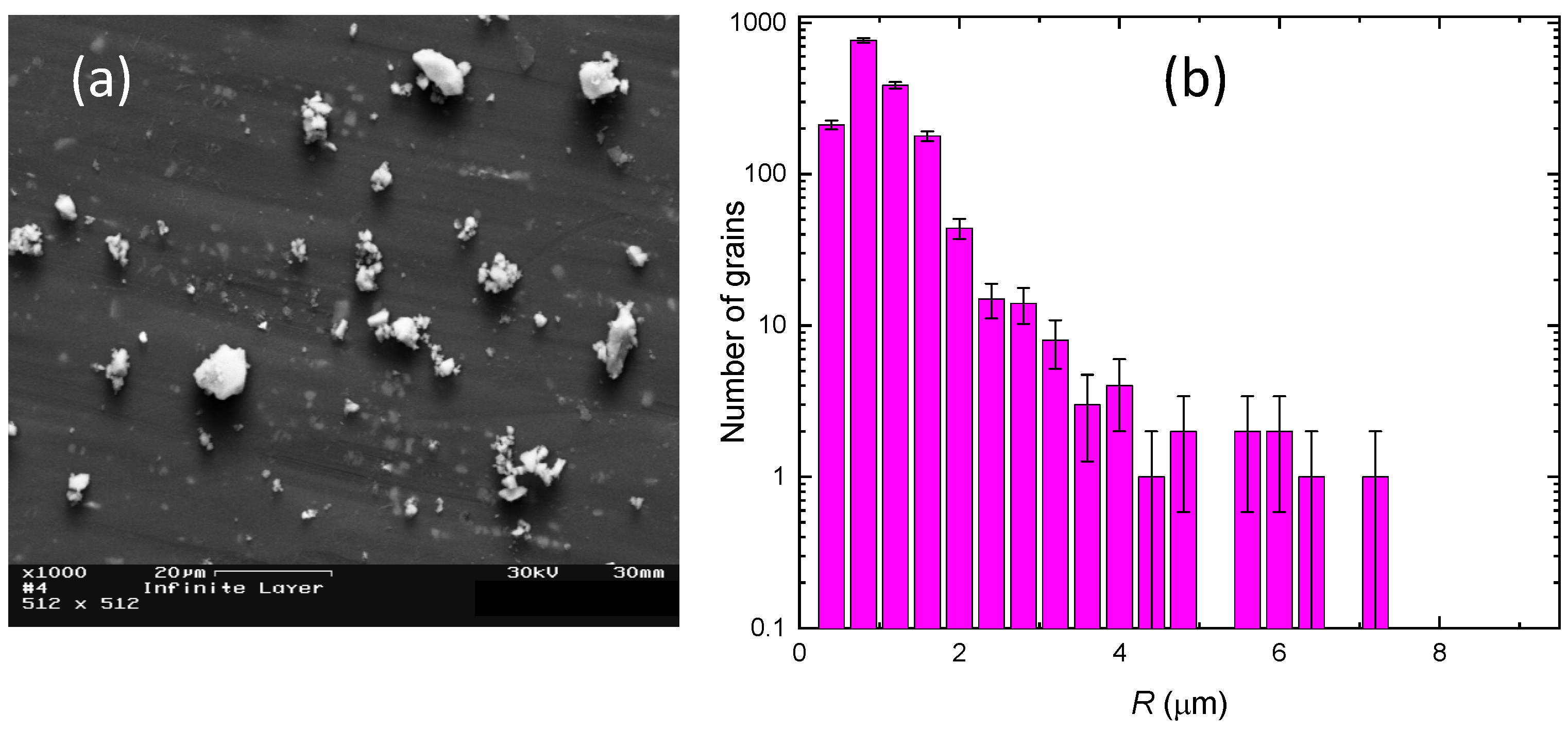
2. Experimental Details
3. Results and Discussion
- (i)
- When a small magnetic field is applied along the c-axis, the screening currents flow in the -plane, decaying at a distance from the grain surface, so that .
- (ii)
- With the magnetic field applied perpendicular to the c-axis, the screening currents flow within the -plane and along the c-axis, thus implying that both components ( and ) enter the measured AC magnetization. For (which is generally the case for highly anisotropic HTSs), the effective penetration depth is mainly determined by the out-of-plane component, and for grains of arbitrary size, the relation holds [37].
- (i)
- The absolute value of the s-wave gap is larger than the maximum value of the anisotropic d-wave gap (Table 1 and Panels (a) and (b) of Figure 3) with and , respectively ( K). This implies that in electron-doped SrLaCuO, the s-wave component of the order parameter is the dominant one. This agrees with the results of small-angle neutron scattering experiments revealing that at fields higher than 1.5 T, the superfluid density of SrLaCuO is determined entirely by the s-wave component of the order parameter [44].
- (ii)
- (iii)
- The temperature dependence of the anisotropic d-wave contribution to the superfluid density (solid red line in Figure 3c) is very close to the quadratic () dependence (dash-dotted line in Figure 3c), which is often observed in various electron-doped HTSs (see [30] and the references therein). Generally, the behavior is attributed to a “dirty” d-wave scenario and is explained by impurity scattering of the carriers. However, it is difficult to explain how an order parameter that changes sign persists in the dirty limit, since any scattering centers would act as pair breakers [46]. Therefore, we believe that the anisotropic d-wave approach is more appropriate for electron-doped HTSs.
- (iv)
- For , the s-wave contribution to the superfluid density is almost negligible (), whereas for , it is substantial () (see Table 1). Bearing in mind that our experiments were performed in the Meissner state, the different behavior of and can be explained within the scenario proposed by Müller [21,22]. Since is rather small (see Table 1), one can assume that its temperature dependence is mainly determined by surface properties and therefore follows the one expected for a d-wave superconductor. In contrast, is almost a factor 10 larger than , and thus, contains contributions from both the surface and the bulk (mixed -wave order parameter).
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References and Note
- Shen, Z.-X.; Dessau, D.S.; Wells, B.O.; King, D.M.; Spicer, W.E.; Arko, A.J.; Marshall, D.; Lombardo, L.W.; Kapitulnik, A.; Dickinson, P.; et al. Anomalously large gap anisotropy in the a−b plane of Bi2Sr2CaCu2O8+δ. Phys. Rev. Lett. 1993, 70, 1553–1556. [Google Scholar] [CrossRef] [PubMed]
- Ding, H.; Norman, M.R.; Campuzano, J.C.; Randeria, M.; Bellman, A.F.; Yokoya, T.; Takahashi, T.; Mochiku, T.; Kadowaki, K. Angle-resolved photoemission spectroscopy study of the superconducting gap anisotropy in Bi2Sr2CaCu2O8+x. Phys. Rev. B 1996, 54, R9678–R9681. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Matsui, H.; Terashima, K.; Sato, T.; Takahashi, T.; Fujita, M.; Yamada, K. Direct observation of a nonmonotonic dx2−y2-wave superconducting gap in the electron-doped high-Tc superconductor Pr0.89LaCe0.11CuO4. Phys. Rev. Lett. 2005, 95. [Google Scholar] [CrossRef] [Green Version]
- Harter, J.W.; Maritato, L.; Shai, D.E.; Monkman, E.J.; Nie, Y.; Schlom, D.G.; Shen, K.M. Nodeless superconducting phase arising from a strong (π,π) antiferromagnetic phase in the infinite-layer electron-doped Sr1−xLaxCuO2 compound. Phys. Rev. Lett. 2012, 109, 267001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsuei, C.C.; Kirtley, J.R.; Chi, C.C.; Yu-Jahnes, L.S.; Gupta, A.; Shaw, T.; Sun, J.Z.; Ketchen, M.B. Pairing symmetry and flux quantization in a tricrystal superconducting ring of YBa2Cu3O7−δ. Phys. Rev. Lett. 1994, 73, 593–596. [Google Scholar] [CrossRef] [PubMed]
- Tsuei, C.C.; Kirtley, J.R. Phase-sensitive evidence for d-wave pairing symmetry in electron-doped cuprate superconductors. Phys. Rev. Lett. 2000, 85, 182–185. [Google Scholar] [CrossRef] [Green Version]
- Tsuei, C.C.; Kirtley, J.R. Pairing symmetry in cuprate superconductors. Rev. Mod. Phys. 2000, 72, 969–1016. [Google Scholar] [CrossRef]
- Tomaschko, J.; Scharinger, S.; Leca, V.; Nagel, J.; Kemmler, M.; Selistrovski, T.; Koelle, D.; Kleiner, D. Phase-sensitive evidence for dx2−y2-pairing symmetry in the parent-structure high-Tc cuprate superconductor Sr1−xLaxCuO2. Phys. Rev. B 2012, 86, 094509. [Google Scholar] [CrossRef] [Green Version]
- Martindale, J.A.; Hammel, P.C.; Hults, W.L.; Smith, J.L. Temperature dependence of the anisotropy of the planar oxygen nuclear spin-lattice relaxation rate in YBa2Cu3Oy. Phys. Rev. B 1998, 57, 11769–11774. [Google Scholar] [CrossRef]
- Masui, T.; Limonov, M.; Uchiyama, H.; Lee, S.; Tajima, S.; Yamanaka, A. Raman study of carrier-overdoping effects on the gap in high-Tc superconducting cuprates. Phys. Rev. B 2003, 68, 060506(R). [Google Scholar] [CrossRef] [Green Version]
- Friedl, B.; Thomsen, C.; Cardona, M. Determination of the superconducting gap in RBa2Cu3O7−δ. Phys. Rev. Lett. 1990, 65, 915–918. [Google Scholar] [CrossRef] [PubMed]
- Furrer, A. Admixture of an s-wave component to the d-wave gap symmetry in high-temperature superconductors. In High-Tc Superconductors and Related Transition Metal Compounds; Bussmann-Holder, A., Keller, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 135–141. [Google Scholar]
- Rubio Temprano, D.; Mesot, J.; Janssen, S.; Conder, K.; Furrer, A.; Mutka, H.; Müller, K.A. Large isotope effect on the pseudogap in the high-temperature superconductor HoBa2Cu4O8. Phys. Rev. Lett. 2000, 84, 1990. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rubio Temprano, D.; Conder, K.; Furrer, A.; Mutka, H.; Trounov, V.; Müller, K.A. Oxygen and copper isotope effects on the pseudogap in the high-temperature superconductor La1.81Ho0.04Sr0.15CuO4 studied by neutron crystal-field spectroscopy. Phys. Rev. B 2002, 66, 184506. [Google Scholar] [CrossRef] [Green Version]
- Khasanov, R.; Shengelaya, A.; Maisuradze, A.; La Mattina, F.; Bussmann-Holder, A.; Keller, H.; Müller, K.A. Experimental evidence for two gaps in the high-temperature La1.83Sr0.17CuO4 superconductor. Phys. Rev. Lett. 2007, 98, 057007. [Google Scholar] [CrossRef] [Green Version]
- Khasanov, R.; Shengelaya, A.; Bussmann-Holder, A.; Karpinski, J.; Keller, H.; Müller, K.A. s-wave symmetry along the c-axis and s + d in-plane superconductivity in bulk YBa2Cu4O8. J. Supercond. Nov. Magn. 2008, 21, 81–85. [Google Scholar] [CrossRef] [Green Version]
- Khasanov, R.; Strässle, S.; Di Castro, D.; Masui, T.; Miyasaka, S.; Tajima, S.; Bussmann-Holder, A.; Keller, H. Multiple gap symmetries for the order parameter of cuprate superconductors from penetration depth measurements. Phys. Rev. Lett. 2007, 99, 237601. [Google Scholar] [CrossRef]
- Müller, K.A. Possible coexistence of s-and d-wave condensates in copper oxide superconductors. Nature (London) 1995, 377, 133–135. [Google Scholar] [CrossRef]
- Müller, K.A. Two gap behavior observed in YBCO (100) a-axis, (110) c-axis tunnel junctions. J. Phys. Soc. Jpn. 1996, 65, 3090–3091. [Google Scholar] [CrossRef]
- Müller, K.A.; Keller, H. ”s“ and ”d“ wave symmetry components in high-temperature cuprate superconductors. InHigh-Tc Superconductivity 1996: Ten Years after Discovery; Kaldis, E., Liarokapis, E., Müller, K.A., Eds.; Springer: Dordrecht, The Netherland, 1997; pp. 7–29. [Google Scholar]
- Müller, K.A. On the macroscopic s- and d-wave symmetry in cuprate superconductors. Philos. Mag. Lett. 2002, 82, 279–288. [Google Scholar] [CrossRef]
- Müller, K.A. Estimation of the surface-d to bulk-s crossover in the macroscopic superconducting wavefunction in cuprates. J. Supercond. Nov. Magn. 2004, 17, 3–6. [Google Scholar] [CrossRef] [Green Version]
- Müller, K.A. The unique properties of superconductivity in cuprates. J. Supercond. Nov. Magn. 2014, 27, 2163–2179. [Google Scholar] [CrossRef]
- Müller, K.A. The polaronic basis for high-temperature superconductivity. J. Supercond. Nov. Magn. 2017, 30, 3007–3018. [Google Scholar] [CrossRef]
- Iachello, F. A model of cuprate superconductors based on the analogy with atomic nuclei. Philos. Mag. Lett. 2002, 82, 289–295. [Google Scholar] [CrossRef]
- Iachello, F. Symmetry of high-Tc superconductors. In Symmetry and Heterogeneity in High Temperature Superconductors; Bianconi, A., Ed.; NATO science Series II: Mathematics, Physics and Chemistry; Springer: Dordrecht, The Netherlands, 2006; Volume 214, pp. 165–180. [Google Scholar]
- Khasanov, R.; Eshchenko, D.G.; Di Castro, D.; Shengelaya, A.; La Mattina, F.; Maisuradze, A.; Baines, C.; Luetkens, H.; Karpinski, J.; Kazakov, S.M.; et al. Magnetic penetration depth in RbOs2O6 studied by muon spin rotation. Phys. Rev. B 2005, 72, 104504. [Google Scholar] [CrossRef] [Green Version]
- Khasanov, R.; Klamut, P.W.; Shengelaya, A.; Bukowski, Z.; Savić, I.M.; Baines, C.; Keller, H. Muon-spin rotation measurements of the penetration depth of the Mo3Sb7 superconductor. Phys. Rev. B 2008, 78, 014502. [Google Scholar] [CrossRef] [Green Version]
- Khasanov, R.; Zhou, H.; Amato, A.; Guguchia, Z.; Morenzoni, E.; Dong, X.; Zhang, G.; Zhao, Z. Proximity-induced superconductivity within the insulating (Li0.84Fe0.16)OH layers in (Li0.84Fe0.16)OHFe0.98Se. Phys. Rev. B 2016, 93, 224512. [Google Scholar] [CrossRef] [Green Version]
- Prozorov, R.; Giannetta, R.W. Magnetic penetration depth in unconventional superconductors. Supercond. Sci. Technol. 2006, 19, R41–R67. [Google Scholar] [CrossRef] [Green Version]
- Sonier, J.E.; Brewer, J.H.; Kiefl, R.F. μSR studies of the vortex state in type-II superconductors. Rev. Mod. Phys. 2000, 72, 769–811. [Google Scholar] [CrossRef]
- Khasanov, R.; Kondo, T.; Strässle, S.; Heron, D.O.G.; Kaminski, A.; Keller, H.; Lee, S.L.; Takeuchi, T. Evidence for a competition between the superconducting state and the pseudogap state of (BiPb)2(SrLa)2CuO6+δ from muon spin rotation experiments. Phys. Rev. Lett. 2008, 101, 227002. [Google Scholar] [CrossRef] [Green Version]
- Khasanov, R.; Kondo, T.; Bendele, M.; Hamaya, Y.; Kaminski, A.; Lee, S.L.; Ray, S.J.; Takeuchi, T. Suppression of the antinodal coherence of superconducting (Bi,Pb)2(Sr,La)2CuO6+δ as revealed by muon spin rotation and angle-resolved photoemission. Phys. Rev. B 2010, 82, 020511(R). [Google Scholar] [CrossRef] [Green Version]
- Khasanov, R.; Shengelaya, A.; Maisuradze, A.; Di Castro, D.; Savić, I.M.; Weyeneth, S.; Park, I.M.; Jang, I.M.; Lee, S.-I.; Keller, H. Nodeless superconductivity in the infinite-layer electron-doped cuprate superconductor Sr0.9La0.1CuO2. Phys. Rev. B 2008, 77, 184512. [Google Scholar] [CrossRef] [Green Version]
- Jung, S.I.; Kim, J.Y.; Kim, M.S.; Park, M.S.; Kim, H.J.; Yao, Y.; Lee, S.Y.; Lee, S.-I. Synthesis and pinning properties of the infinite-layer superconductor Sr0.9La0.1CuO2. Physica C 2002, 366, 299–305. [Google Scholar] [CrossRef] [Green Version]
- Shoenberg, D. Properties of superconducting colloids and emulsions. Proc. R. Soc. A 1940, 175, 49–70. [Google Scholar]
- Porch, A.; Cooper, J.R.; Zheng, D.N.; Waldram, J.R.; Campbell, A.M.; Freeman, P.A. Temperature dependent magnetic penetration depth of Co and Zn doped YBa2Cu3O7 obtained from the AC susceptibility of magnetically aligned powders. Phycica C 1993, 214, 350–358. [Google Scholar] [CrossRef]
- Kim, M.S.; Lemberger, T.R.; Jung, C.U.; Choi, J.H.; Kim, J.Y.; Kim, H.J.; Lee, S.-I. Anisotropy and reversible magnetization of the infinite-layer superconductor Sr0.9La0.1CuO2. Phys. Rev. B 2002, 66, 214509. [Google Scholar] [CrossRef]
- and can be equally well analyzed within the framework of s+s-wave and s+ anisotropic s-wave models
- Carrington, A.; Manzano, F. Magnetic penetration depth of MgB2. Physica C 2003, 385, 205–214. [Google Scholar] [CrossRef]
- Khasanov, R.; Gupta, R.; Das, D.; Leithe-Jasper, A.; Svanidze, E. Single-gap versus two-gap scenario: Specific heat and thermodynamic critical field of the noncentrosimmetric superconductor BeAu. Phys. Rev. B 2020, 102, 014514. [Google Scholar] [CrossRef]
- Eremin, I.; Tsoncheva, E.; Chubukov, A.V. Signature of the nonmonotonic d-wave gap in electron-doped cuprates. Phys. Rev. B 2008, 77, 024508. [Google Scholar] [CrossRef] [Green Version]
- Blumberg, G.; Koitzsch, A.; Gozar, A.; Dennis, B.S.; Kendziora, C.A.; Fournier, P.; Greene, R.L. Nonmonotonic dx2−y2 superconducting order parameter in Nd2−xCexCuO4. Phys. Rev. Lett. 2002, 88, 107002. [Google Scholar] [CrossRef] [Green Version]
- White, J.S.; Forgan, E.M.; Laver, M.; Häfliger, P.S.; Khasanov, R.; Cubitt, R.; Dewhurst, C.D.; Park, M.S.; Jang, D.J.; Lee, S.-I. Finite gap behaviour in the superconductivity of the ’infinite layer’ n-doped high-Tc superconductor Sr0.9La0.1CuO2. J. Phys. Condens. Matter. 2008, 20, 104237. [Google Scholar] [CrossRef]
- Kohen, A.; Leibovitch, G.; Deutscher, G. Andreev reflections on Y1−xCaxBa2Cu3O7−δ: Evidence for an unusual proximity effect. Phys. Rev. Lett. 2003, 90, 207005. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Millis, A.J.; Sachdev, S.; Varma, C.M. Inelastic scattering and pair breaking in anisotropic and isotropic superconductors. Phys. Rev. B 1988, 37, 4975–4986. [Google Scholar] [CrossRef] [PubMed]
- Pümpin, B.; Keller, H.; Kündig, W.; Odermatt, W.; Savić, I.M.; Schneider, J.W.; Simmler, H.; Zimmermann, P.; Kaldis, E.; Rusiecki, S.; et al. Muon-spin-rotation measurements of the London penetration depths in YBa2Cu3O6.97. Phys. Rev. B 1990, 42, 8019–8029. [Google Scholar] [CrossRef] [PubMed]



| Method | Quantity | a | ||||
|---|---|---|---|---|---|---|
| (meV) | (meV) | (nm) | ||||
| ACsusc. | 10.9(1) | 7.03(6) | 0.90(2) | 0.04(2) | 157(15) | |
| 0.54(2) | 1140(100) | |||||
| TF-SR [34] | 10.9 | 7.03 | 0.90 | 0.72(4) | 93(2) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khasanov, R.; Shengelaya, A.; Brütsch, R.; Keller, H. Suppression of the s-Wave Order Parameter Near the Surface of the Infinite-Layer Electron-Doped Cuprate Superconductor Sr0.9La0.1CuO2. Condens. Matter 2020, 5, 50. https://doi.org/10.3390/condmat5030050
Khasanov R, Shengelaya A, Brütsch R, Keller H. Suppression of the s-Wave Order Parameter Near the Surface of the Infinite-Layer Electron-Doped Cuprate Superconductor Sr0.9La0.1CuO2. Condensed Matter. 2020; 5(3):50. https://doi.org/10.3390/condmat5030050
Chicago/Turabian StyleKhasanov, Rustem, Alexander Shengelaya, Roland Brütsch, and Hugo Keller. 2020. "Suppression of the s-Wave Order Parameter Near the Surface of the Infinite-Layer Electron-Doped Cuprate Superconductor Sr0.9La0.1CuO2" Condensed Matter 5, no. 3: 50. https://doi.org/10.3390/condmat5030050
APA StyleKhasanov, R., Shengelaya, A., Brütsch, R., & Keller, H. (2020). Suppression of the s-Wave Order Parameter Near the Surface of the Infinite-Layer Electron-Doped Cuprate Superconductor Sr0.9La0.1CuO2. Condensed Matter, 5(3), 50. https://doi.org/10.3390/condmat5030050






