Next Article in Journal
Using In-Situ Laboratory and Synchrotron-Based X-ray Diffraction for Lithium-Ion Batteries Characterization: A Review on Recent Developments
Previous Article in Journal
The Pseudopotential Approach within Density-Functional Theory: The Case of Atomic Metallic Hydrogen
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Condensed Matter
Volume 5
Issue 4
10.3390/condmat5040073
condensedmatter-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

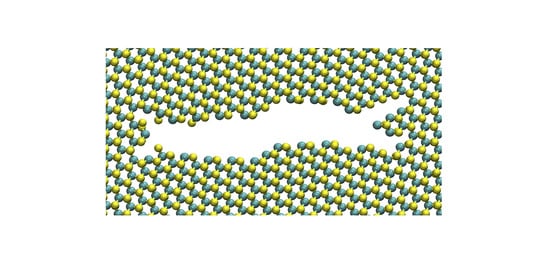
On the Elastic Properties and Fracture Patterns of MoX2 (X = S, Se, Te) Membranes: A Reactive Molecular Dynamics Study

by
Marcelo Lopes Pereira Júnior
1,
Cícera Maria Viana de Araújo
1,
José Moreira De Sousa
2,
Rafael Timóteo de Sousa Júnior
3,
Luiz Fernando Roncaratti Júnior
1,
William Ferreira Giozza
3 and
Luiz Antonio Ribeiro Júnior
1,*
1
Institute of Physics, University of Brasília, Brasília 70910-900, Brazil
2
Federal Institute of Education, Science and Technology of Piauí, São Raimundo Nonato, Piauí 64770-000, Brazil
3
Department of Electrical Engineering, University of Brasília, Brasília 70919-970, Brazil
*
Author to whom correspondence should be addressed.
Condens. Matter 2020, 5(4), 73; https://doi.org/10.3390/condmat5040073
Submission received: 19 October 2020 / Revised: 9 November 2020 / Accepted: 10 November 2020 / Published: 13 November 2020
(This article belongs to the Section Physics of Materials)
Browse Figures
Versions Notes

Abstract

:
We carried out fully-atomistic reactive molecular dynamics simulations to study the elastic properties and fracture patterns of transition metal dichalcogenide (TMD) MoX 2 (X = S, Se, Te) membranes, in their 2H and 1T phases, within the framework of the Stillinger–Weber potential. Results showed that the fracture mechanism of these membranes occurs through a fast crack propagation followed by their abrupt rupture into moieties. As a general trend, the translated arrangement of the chalcogen atoms in the 1T phase contributes to diminishing their structural stability when contrasted with the 2H one. Among the TMDs studied here, 2H-MoSe 2 has a higher tensile strength (25.98 GPa).

Graphical Abstract

1. Introduction

Transition metal dichalcogenide (TMD) monolayers are atomically thin semiconductors that belong to the family of 2 D nanosheets [1,2]. They present an MX 2 arrangement, where M is a transition metal, and X is a chalcogen. The combination of chalcogen (e.g., S, Se, or Te) and transition metal atoms (typically Mo, W, Nb, Re, Ni, or V) yields more than 40 different materials [3,4]. Each monolayer has a thickness of 6–7 Å and is hexagonally-packed by transition metal atoms sandwiched between two layers of chalcogen atoms [3]. TMDs are graphene cognate and possible to be synthesized by applying the same chemical methods usually employed in producing the latter [5,6]. These materials have received much attention in the fields of biomedicine [7,8], optoelectronics [9,10], and energy conversion and storage [11,12]. Particularly, MoS 2 and MoTe 2 monolayers—direct bandgap semiconductors with bandgaps about 1.9 eV [13] and 1.0 eV [14], respectively—have emerged as promising candidates in replacing gapless graphene to develop novel applications in which semiconducting materials are desired [15]. MoSe 2 , in turn, is an indirect bandgap semiconductor (with a bandgap about 1.58 eV [16]) that has also been widely employed in developing new applications in flat electronics [17,18]. To further explore the potential of these TMDs species in boosting new advances in the research fields mentioned above, their mechanical properties should be deeply understood.
TMD nanostructures have three different structural arrangements, named 2H, 1T, and 1T’ [19]. 2H and 1T refer to the hexagonal and trigonal structures, respectively. The 1T’ phase is a distorted form of 1T. The octahedral phase 1T can be spontaneously converted into its distorted octahedral phase 1T’. The 1T and 1T’ phases have metallic and semiconducting characteristics, respectively [19,20]. Significant theoretical and experimental efforts have been employed in understanding the mechanical properties of layered MoS 2 [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35], MoSe 2 [36,37,38,39], and MoTe 2 [14,40,41,42,43,44,45] on both 2H and 1T forms. In these investigations, they experimentally studied a few layers (5–25) of these TMDs species, and Young’s modulus obtained ws approximately 330 GPa [22], 117 GPa [39], and 110 GPa [43] for MoS 2 , MoSe 2 , and MoTe 2 , respectively. By using density functional theory and reactive molecular dynamic simulations, theoretical studies have predicted Young’s modulus values for single-layer MoS 2 , MoSe 2 , and MoTe 2 ranging in the intervals 170–250 GPa [21,25,34], 165–185 GPa [39,46], and 60–115 GPa [42,44,45], respectively. These works promoted substantial advances in understanding the mechanical properties of TMDs. However, an overall description of their elastic properties and fracture dynamics is still missing.
Herein, we carried out extensive fully-atomistic reactive molecular dynamics simulations to study the elastic properties and fracture dynamics of MoX 2 (X = S, Se, Te) membranes in their 2H and 1T phases. The elastic properties were obtained from the stress–strain relationship. Only recently, 1T phases of these materials were experimentally realized [19]. In this sense, a detailed description of the mechanical properties of these nanostructures considering both 2H and 1T phases is highly attractive.

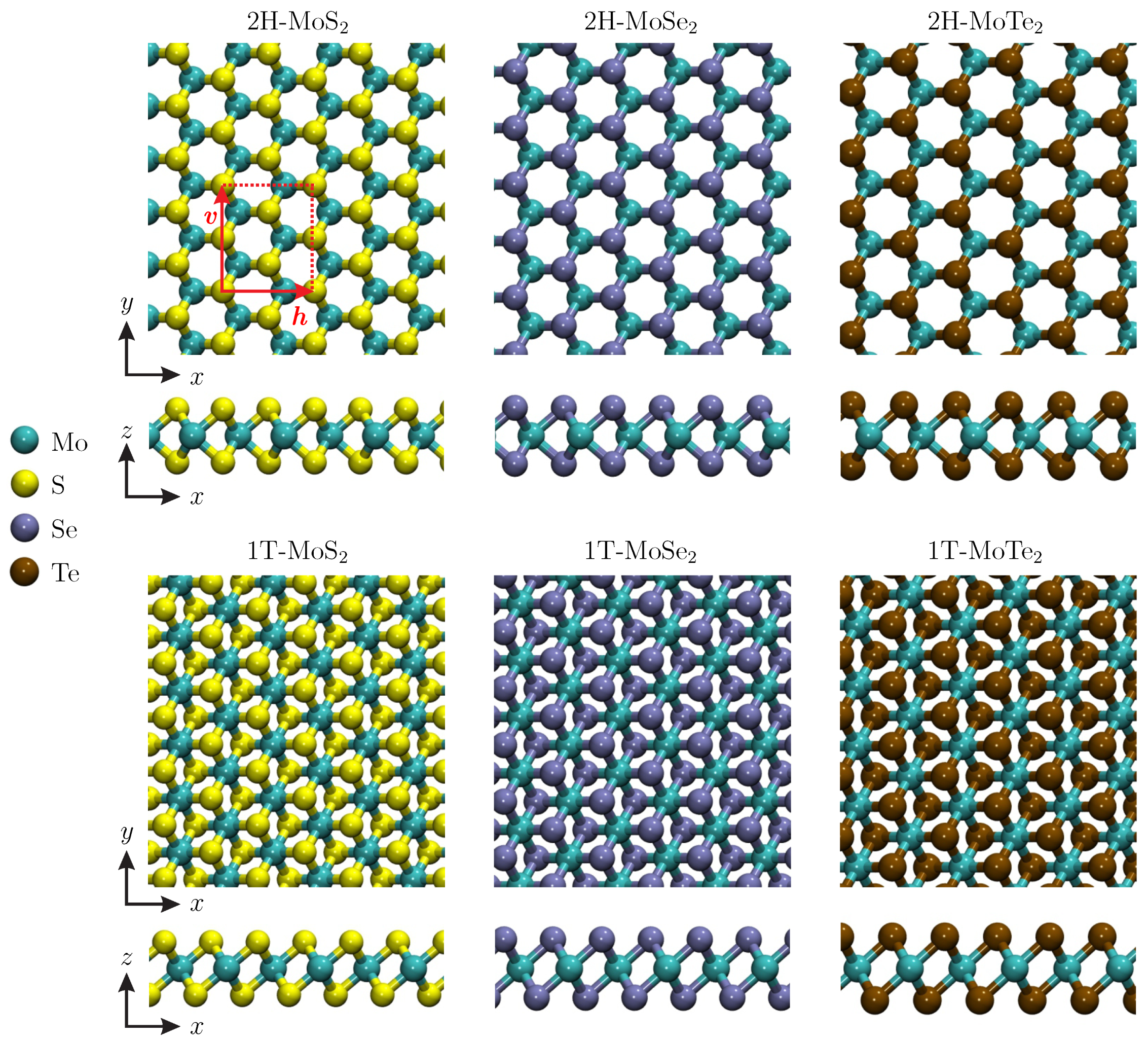
2. Details of Modeling

We performed fully-atomistic molecular dynamics (MD) simulations using the Stillinger–Weber (SW) [26,27] potential as implemented by LAMMPS [47]. Differently from regular MD simulations, in the reactive MD ones, the breaking and formation of bonds are described. Figure 1 illustrates the model TMD’s monolayers studied here in their 2H and 1T phases. The left, middle, and bottom panels illustrate the MoS 2 , MoSe 2 , and MoTe 2 monolayers, respectively, in the H (top panels) and T phases (bottom panels). Their atomistic structure contains 3456, 3348, and 2688 atoms, respectively, and they were built intended in yielding 2D membranes with dimensions of about 100 × 100 Å 2 , with periodic boundary conditions. It is worthwhile to stress that the simulation results are not sensitive to the selected computational cell size (as can occur when studying 2D materials using density functional theory calculations [48,49]), which has been checked using a system with larger dimensions. In this sense, the periodic boundary condition was applied to remove the lateral boundary effect and simulate the intrinsic properties of the MoX 2 membranes.
The equations of motion were solved using the velocity-Verlet integrator with a time-step of 0.1 fs. The tensile stress was considered in the system by applying a uniaxial strain along the periodic h and v directions, using an engineering strain rate of 10 − 6 fs − 1 . The TMD membranes were stressed up to their complete rupture. To eliminate any residual stress within the membranes, they were equilibrated within an NPT ensemble at constant temperatures (1K and 300K) and null pressures using the Nosé–Hoover thermostat during 200 ps. By adopting this simulation protocol, Young’s modulus ( Y M ), fracture strain (FS), and ultimate strength (US) are the elastic properties derived from the stress–strain curves. The fracture dynamics, in turn, are studied through MD snapshots and the von Mises stress (VM) per-atom values, calculated at every 100 fs [50]. The VM values provide useful local structural information on the fracture mechanism, once they can determine the region from which the structure has started to yield the fractured lattice. The MD snapshots and trajectories were obtained by using free visualization and analysis software VMD [51].
To better analyze the outcomes from the stretching dynamics, we calculated the von Mises stress (VM) per-atom values [52]. The VM values provide useful local structural information on the fracture mechanism, once they can determine the region from which the structure has started to yield the fractured lattice. In this way, the VM equation can be written as
σ v k = ( σ x x k − σ y y k ) 2 + ( σ y y k − σ z z k ) 2 + ( σ x x k − σ z z k ) 2 + 6 ( ( σ x y k ) 2 + ( σ y z k ) 2 + ( σ z x k ) 2 ) 2 ,
where σ x x k , σ y y k , and σ z z k are the components of the normal stress and σ x y k , σ y z k , and σ z x k are the components of the shear stress. The MD snapshots and trajectories were obtained by using free visualization and analysis software VMD [51].
In Equation (1), the elements of the per-atom stress tensor (computed by LAMMPS) are used. The tensor for each atom is symmetric with 6 components: x x , y y , z z , x y , x z , and y z . The computed quantity is in units of pressure*volume. It would need to be divided by a per-atom volume to have units of stress (pressure), but an individual atom’s volume is not well defined or easy to compute in a deformed solid or a liquid. Therefore, if the diagonal components of the per-atom stress tensor are summed for all atoms in the system and the sum is divided by D × V , where D is the dimension and V the volume of the system, respectively, the result should be − P , where P is the total pressure of the system [53,54,55,56].

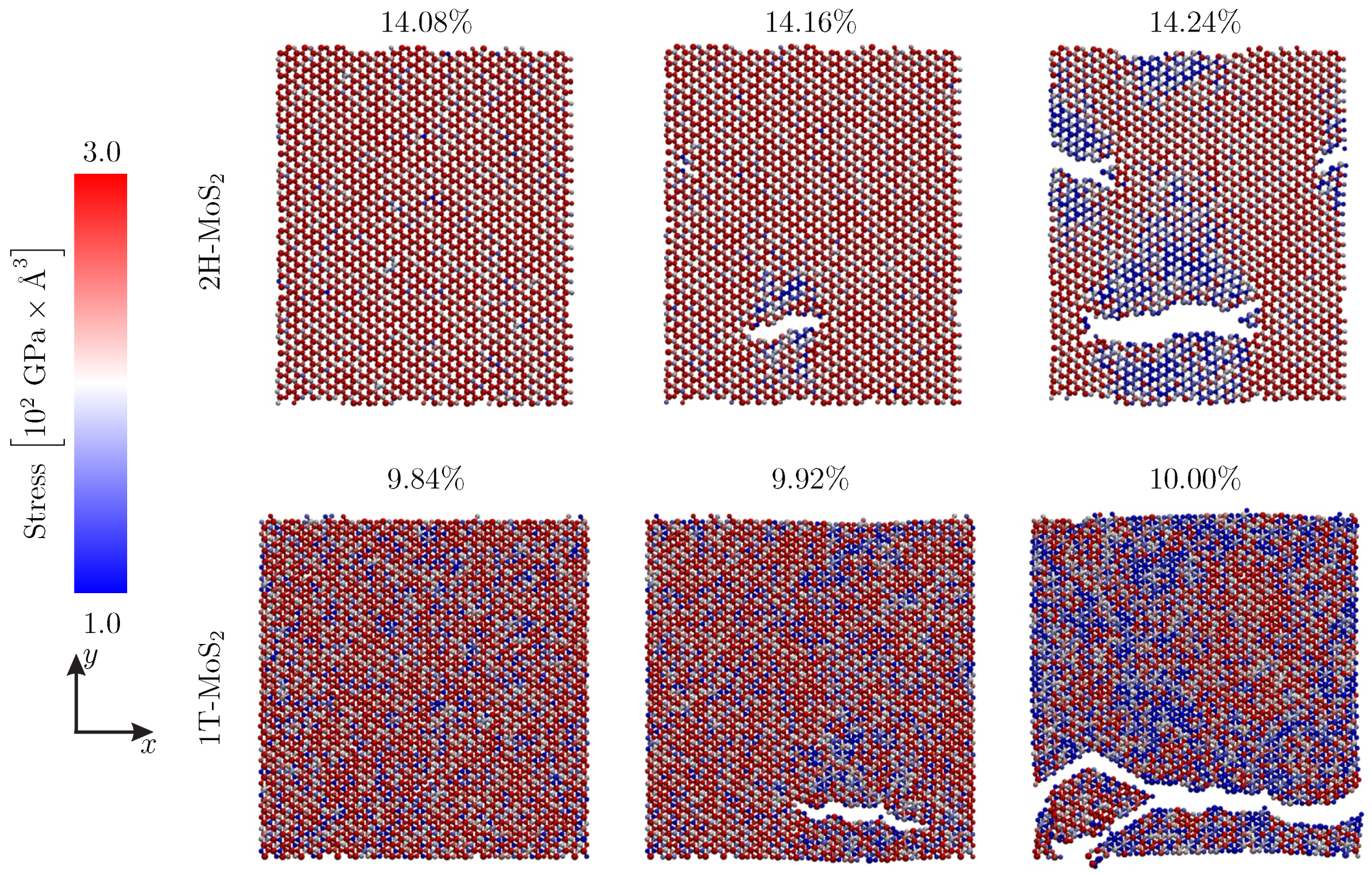
3. Results

We begin our discussions by showing representative MD snapshots of the fracture dynamics for the 2H-MoS 2 (top sequence of panels) and 1T-MoS 2 (bottom sequence of panels) monolayers at 300K and considering a uniaxial strain applied along the h-direction, as shown in Figure 2. In the 2H-MoS 2 case, one can note an abrupt rupture followed by a fast propagation of the fracture along the v − direction is accomplished at 11.60% of strain. The membrane is considered fractured at 11.68% of strain, once the atoms in the edges of the two fractures moieties are not interacting. A different fracture trend is realized for a 1T-MoS 2 membrane. The very first striking outcome obtained here, when contrasting the fracture dynamics of 2H-MoS 2 and 1T-MoS 2 , is the considerably higher degree of fragility of the latter case. In Figure 2, one can observe that the critical strain for the beginning of the fracture in the 1T-MoS 2 (5.44%) is almost two times smaller than the one for 2H-MoS 2 . Another clear trend showed in this figure is that the fracture dynamics of 1T-MoS 2 leads to a brittle lattice structure. This rupture trend is different from the one obtained for the 2H-MoS 2 case, in which two well concise MoS 2 fragments were produced as a final stage of the fracture process. This brittle signature for the 1T-MoS 2 case is obtained for 5.60% of strain. These results suggest that the translated arrangement of the chalcogen atoms in the 1T phase is crucial in diminishing the structural stability of TMDs.
An interesting result arises when a uniaxial strain is applied along the v-direction, as depicted in Figure 3. This figure shows the cases related to Figure 2. When the tensile stretching is applied in the v-direction, the critical strain to realize the beginning of the fracture of 2H-MoS 2 and 1T-MoS 2 membranes is considerably higher than the ones presented in Figure 2. The difference between the fracture strains for these species is smaller when the stretching is applied along the v-direction. As illustrated in Figure 3, the fracture (critical) strains for the beginning of the rupture are 14.08% and 9.84% for the 2H-MoS 2 and 1T-MoS 2 membranes, respectively. After that critical value, the crack propagation takes place for 14.16% and 9.92% for the 2H-MoS 2 and 1T-MoS 2 cases, respectively. Interestingly, the brittle trend for the 1T-MoS 2 fracture, obtained for the v-direction stretching, does not occur when it comes to the v-direction stretching. After 14.24% and 10.0%, a fast crack propagation occurs for the 2H-MoS 2 and 1T-MoS 2 monolayers, respectively.
Figure 4 illustrates the representative MD snapshots for the 2H/1T-MoSe 2 and 2H/1T-MoTe 2 membranes. For the sake of convenience, we presented just the snapshots that show the crack propagation and the fractured form of these TMD species. The top and bottom panels depict the results when the uniaxial strain is applied along the h and v directions, respectively. In the top panels, one can note that the critical strain for the membrane rupture is 17.60%, 7.52%, 18.56%, and, 8.24% for the 2H-MoSe 2 , 1T-MoSe 2 , 2H-MoTe 2 , and 1T-MoTe 2 , respectively. In the bottom panels, we can observe that the critical strain for the membrane rupture is 19.84%, 8.56%, 20.48%, and, 9.44% for the 2H-MoSe 2 , 1T-MoSe 2 , 2H-MoTe 2 , and 1T-MoTe 2 , respectively. A comparison of the tensile strength among the TMDs studied here is presented below with Table 1. As for the MoS 2 cases, in the MoSe 2 and MoTe 2 cases, the fracture propagation undergoes in the direction opposite to the stretching. It is worthwhile to stress that both MoSe 2 and MoTe 2 present a fracture mechanism defined by a fast crack propagation followed by an abrupt rupture of the membranes into parts with a good degree of integrity (i.e., no brittle structures were observed). Theses results suggest that MoSe 2 and MoTe 2 monolayers may present greater structural stability than the MoS 2 ones.
Finally, we present the elastic properties obtained from the simulations discussed above. These properties are Young’s modulus ( Y M , in units of GPa), fracture strain (FS (%)), and the maximum stress US (which is called ultimate tensile strength US (GPa)). They were estimated considering stretching regimes before mechanical failure (fracture) of the TMD membranes. These stretching regimes can be inferred from Figure 5, which illustrates the calculated stress–strain curves for all TMD membranes when subjected to 10K and 300K, considering a uniaxial strain applied in both h and v directions. Recently, the impact of temperature on the elastic properties of 2H-MoS 2 was studied by using the SW potential as implemented in LAMMPS [57]. The highest temperature simulated was 600K. It was concluded that Young’s modulus decreased with increasing temperature. In addition, the 2H-MoS 2 has smaller fracture strain at a higher temperature. These behaviors were related to stronger thermal vibrations at higher temperatures, which resulted in longer extensions of atomic bonds. Figure 5a–f are describing the stress–strain relationship for the 2H/1T-MoS 2 , 2H/1T-MoSe 2 , and 2H/1T-MoTe 2 membranes, respectively. Table 1 presents a summary of the mechanical properties of the TMD monolayers studied in this work. In our simulation protocol, these monolayers were stretched at a constant rate until their total rupture. The stress–strain curves show the two following common regions: a non-linear elastic region that is observed up to the ultimate strength value and a region of null stress (after a critical fracture strain) in which the TMD membranes ultimately break. In Figure 5, one can see that the US values are slightly higher for the cases in which the tensile stretching was applied in the v-direction. This trend occurs since the bond angle variations in h − and v − direction are different, and they govern the fracture strain. The fracture strains range from 5.44% (1T-MoS 2 at 300K) up to 29.86% (2H-MoTe 2 at 10K). As expected, increasing the temperature to 300K, there is a decrease in the critical tensile strain (fracture strain) values for all TMD membranes (see Table 1). The highest Young’s modulus was obtained for 2H-MoSe 2 monolayer at 10K (154.65 GPa). The TMD of the higher tensile strength (highest ultimate stress value) is the 2H-MoSe 2 membrane at 10K (25.98 GPa). As discussed above, generally, the translated arrangement of the chalcogen atoms in the 1T phase can contribute to diminishing their structural stability when compared with TMD membranes in the 2H phase. Importantly, Table 1 summarizes the elastic properties ( Y M , FS, and US) that were obtained by fitting the stress–strain curves for the TMD monolayers investigated here. It is worthwhile to stress that the fracture is a random process. The scatter for the elastic property values obtained using different MD trajectories is useful to estimate the precision of our calculations. In this way, we performed ten additional simulations for the 2H-MoS 2 case by changing the initial seed for the random number generation. In these simulations, the strain was applied in the h-direction at 300 K. We obtained the following values for the elastic properties: Y M = 135 ± 13 GPa, FS = 12 ± 2 % , and the US = 14 ± 3 GPa.

4. Discussion

In summary, we carried out fully-atomistic reactive molecular dynamics simulations to perform a comparative study on the elastic properties and fracture patterns of MoX 2 (X = S, Se, Te) membranes, in the 2H and 1T phases, within the framework of the Stillinger–Weber potential. The results showed that the fracture mechanism of a 2H-MoS 2 monolayer occurs through an abrupt rupture followed by fast crack propagation. A different fracture trend is realized for a 1T-MoS 2 membrane. The fracture dynamics of this material leads to a brittle structure. Both MoSe 2 and MoTe 2 presented a fracture mechanism defined by a fast crack propagation followed by an abrupt rupture of the membranes into parts with a good degree of integrity (i.e., no brittle structures were observed). These results suggest that these monolayers may present greater structural stability than the MoS 2 ones. The highest Young’s modulus was obtained for 2H-MoSe 2 monolayer at 10K (154.65 GPa). The TMD of higher tensile strength is the 2H-MoSe 2 membrane at 300 K (21.88 GPa). Generally, the critical strain to realize the TMD membranes fracture is considerably higher when the strain was applied along the v-direction. It was also obtained here as a general trend that the translated arrangement of the chalcogen atoms in the 1T phase can contribute to diminishing their structural stability when compared with TMD membranes in the 2H phase. As a consequence, among the 2H and 1T phases, the 1T presented lower tensile strength. For instance, Young’s modulus value for single-layer graphene is about 2.4 ± 0.4 TPa [58], which is almost ten times higher than the ones obtained here for the MoX 2 membranes. As it is well known, the lack of a bandgap in pristine graphene hampers its application in semiconducting devices. Since MoS 2 has a semiconducting bandgap (about 1.8 eV [22]) and possesses comparable tensile strength, it can be an alternative to substitute/complement graphene in semiconducting applications, mostly when it comes to the field of flat nano-electronics.

Author Contributions

M.L.P.J., J.M.D.S., C.M.V.d.A.: methodology, formal analysis, data Curation, and writing—original draft preparation. L.F.R.J., L.A.R.J., and R.T.d.S.J., and W.F.G.: conceptualization, supervision, funding acquisition, and writing—reviewing and editing. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by CAPES grant numbers 88882.383674/2019-01 and 88887.144009/2017-00, CNPq grant numbers 465741/2014-2, 312180/2019-5, and, 302236/2018-0, FAP-DF grant numbers 0193.001366/2016, 00193.0000248/2019-32, and 0193.001365/2016, DPI/DIRPE/UnB (Edital DPI/DPG 03/2020) grant number 23106.057541/2020-89, and IFD/UnB (Edital 01/2020) grant number 23106.090790/2020-86.

Acknowledgments

The authors gratefully acknowledge the financial support from Brazilian research agencies CNPq, FAPESP, and FAP-DF. M.L.P.J. gratefully acknowledges the financial support from CAPES grant 88882.383674/2019-01. R.T.S.J. gratefully acknowledges, respectively, the financial support from CNPq grants 465741/2014-2 and 312180/2019-5, CAPES grant 88887.144009/2017-00, and FAP-DF grants 0193.001366/2016 and 0193.001365/2016. L.A.R.J acknowledges the financial support from a Brazilian Research Council FAP-DF and CNPq grants 00193.0000248/2019-32 and 302236/2018-0, respectively. L.A.R.J. and M.L.P.J. acknowledge CENAPAD-SP for providing the computational facilities. L.A.R.J. gratefully acknowledges the financial support from DPI/DIRPE/UnB (Edital DPI/DPG 03/2020) grant 23106.057541/2020-89 and from IFD/UnB (Edital 01/2020) grant 23106.090790/2020-86.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Manzeli, S.; Ovchinnikov, D.; Pasquier, D.; Yazyev, O.V.; Kis, A. 2D transition metal dichalcogenides. Nat. Rev. Mater. 2017, 2, 17033. [Google Scholar] [CrossRef]
  2. Chhowalla, M.; Shin, H.S.; Eda, G.; Li, L.J.; Loh, K.P.; Zhang, H. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 2013, 5, 263–275. [Google Scholar] [CrossRef]
  3. Tan, C.; Zhang, H. Two-dimensional transition metal dichalcogenide nanosheet-based composites. Chem. Soc. Rev. 2015, 44, 2713–2731. [Google Scholar] [CrossRef]
  4. Chhowalla, M.; Liu, Z.; Zhang, H. Two-dimensional transition metal dichalcogenide (TMD) nanosheets. Chem. Soc. Rev. 2015, 44, 2584–2586. [Google Scholar] [CrossRef]
  5. Xu, M.; Liang, T.; Shi, M.; Chen, H. Graphene-like two-dimensional materials. Chem. Rev. 2013, 113, 3766–3798. [Google Scholar] [CrossRef] [PubMed]
  6. Butler, S.Z.; Hollen, S.M.; Cao, L.; Cui, Y.; Gupta, J.A.; Gutiérrez, H.R.; Heinz, T.F.; Hong, S.S.; Huang, J.; Ismach, A.F.; et al. Progress, challenges, and opportunities in two-dimensional materials beyond graphene. ACS Nano 2013, 7, 2898–2926. [Google Scholar] [CrossRef] [PubMed]
  7. Qian, X.; Shen, S.; Liu, T.; Cheng, L.; Liu, Z. Two-dimensional TiS 2 nanosheets for in vivo photoacoustic imaging and photothermal cancer therapy. Nanoscale 2015, 7, 6380–6387. [Google Scholar] [CrossRef] [PubMed]
  8. Chen, Y.; Tan, C.; Zhang, H.; Wang, L. Two-dimensional graphene analogues for biomedical applications. Chem. Soc. Rev. 2015, 44, 2681–2701. [Google Scholar] [CrossRef]
  9. Wang, Q.H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J.N.; Strano, M.S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 2012, 7, 699–712. [Google Scholar] [CrossRef]
  10. Wilson, J.A.; Yoffe, A. The transition metal dichalcogenides discussion and interpretation of the observed optical, electrical and structural properties. Adv. Phys. 1969, 18, 193–335. [Google Scholar] [CrossRef]
  11. Eda, G.; Yamaguchi, H.; Voiry, D.; Fujita, T.; Chen, M.; Chhowalla, M. Photoluminescence from chemically exfoliated MoS2. Nano Lett. 2011, 11, 5111–5116. [Google Scholar] [CrossRef] [PubMed]
  12. Yun, Q.; Lu, Q.; Zhang, X.; Tan, C.; Zhang, H. Three-dimensional architectures constructed from transition-metal dichalcogenide nanomaterials for electrochemical energy storage and conversion. Angew. Chem. Int. Ed. 2018, 57, 626–646. [Google Scholar] [CrossRef]
  13. Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically thin MoS2: A new direct-gap semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  14. Ruppert, C.; Aslan, O.B.; Heinz, T.F. Optical properties and band gap of single-and few-layer MoTe2 crystals. Nano Lett. 2014, 14, 6231–6236. [Google Scholar] [CrossRef] [PubMed]
  15. Jariwala, D.; Sangwan, V.K.; Lauhon, L.J.; Marks, T.J.; Hersam, M.C. Emerging device applications for semiconducting two-dimensional transition metal dichalcogenides. ACS Nano 2014, 8, 1102–1120. [Google Scholar] [CrossRef] [Green Version]
  16. Zhang, Y.; Chang, T.R.; Zhou, B.; Cui, Y.T.; Yan, H.; Liu, Z.; Schmitt, F.; Lee, J.; Moore, R.; Chen, Y.; et al. Direct observation of the transition from indirect to direct bandgap in atomically thin epitaxial MoSe2. Nat. Nanotechnol. 2014, 9, 111. [Google Scholar] [CrossRef]
  17. Eftekhari, A. Molybdenum diselenide (MoSe2) for energy storage, catalysis, and optoelectronics. Appl. Mater. Today 2017, 8, 1–17. [Google Scholar] [CrossRef]
  18. Eda, G.; Maier, S.A. Two-dimensional crystals: Managing light for optoelectronics. ACS Nano 2013, 7, 5660–5665. [Google Scholar] [CrossRef]
  19. Zhang, X.; Lai, Z.; Ma, Q.; Zhang, H. Novel structured transition metal dichalcogenide nanosheets. Chem. Soc. Rev. 2018, 47, 3301–3338. [Google Scholar] [CrossRef]
  20. Yu, Y.; Nam, G.H.; He, Q.; Wu, X.J.; Zhang, K.; Yang, Z.; Chen, J.; Ma, Q.; Zhao, M.; Liu, Z.; et al. High phase-purity 1T’-MoS2-and 1T’-MoSe2-layered crystals. Nat. Chem. 2018, 10, 638–643. [Google Scholar] [CrossRef]
  21. Ostadhossein, A.; Rahnamoun, A.; Wang, Y.; Zhao, P.; Zhang, S.; Crespi, V.H.; Van Duin, A.C. ReaxFF reactive force-field study of molybdenum disulfide (MoS2). J. Phys. Chem. Lett. 2017, 8, 631–640. [Google Scholar] [CrossRef] [PubMed]
  22. Castellanos-Gomez, A.; Poot, M.; Steele, G.A.; Van Der Zant, H.S.; Agraït, N.; Rubio-Bollinger, G. Elastic properties of freely suspended MoS2 nanosheets. Adv. Mater. 2012, 24, 772–775. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  23. Castellanos-Gomez, A.; van Leeuwen, R.; Buscema, M.; van der Zant, H.S.; Steele, G.A.; Venstra, W.J. Single-layer MoS2 mechanical resonators. Adv. Mater. 2013, 25, 6719–6723. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  24. Castellanos-Gomez, A.; Roldán, R.; Cappelluti, E.; Buscema, M.; Guinea, F.; van der Zant, H.S.; Steele, G.A. Local strain engineering in atomically thin MoS2. Nano Lett. 2013, 13, 5361–5366. [Google Scholar] [CrossRef] [Green Version]
  25. Cooper, R.C.; Lee, C.; Marianetti, C.A.; Wei, X.; Hone, J.; Kysar, J.W. Nonlinear elastic behavior of two-dimensional molybdenum disulfide. Phys. Rev. B 2013, 87, 035423. [Google Scholar] [CrossRef] [Green Version]
  26. Jiang, J.W.; Park, H.S. Mechanical properties of MoS2/graphene heterostructures. Appl. Phys. Lett. 2014, 105, 033108. [Google Scholar] [CrossRef] [Green Version]
  27. Jiang, J.W.; Park, H.S.; Rabczuk, T. Molecular dynamics simulations of single-layer molybdenum disulphide (MoS2): Stillinger-Weber parametrization, mechanical properties, and thermal conductivity. J. Appl. Phys. 2013, 114, 064307. [Google Scholar] [CrossRef] [Green Version]
  28. Kang, J.; Sahin, H.; Peeters, F.M. Mechanical properties of monolayer sulphides: A comparative study between MoS2, HfS 2 and TiS 3. Phys. Chem. Chem. Phys. 2015, 17, 27742–27749. [Google Scholar] [CrossRef]
  29. Khan, M.B.; Jan, R.; Habib, A.; Khan, A.N. Evaluating mechanical properties of few layers MoS2 nanosheets-polymer composites. Adv. Mater. Sci. Eng. 2017, 2017, 3176808. [Google Scholar] [CrossRef] [Green Version]
  30. Liang, T.; Phillpot, S.R.; Sinnott, S.B. Parametrization of a reactive many-body potential for Mo–S systems. Phys. Rev. B 2009, 79, 245110. [Google Scholar] [CrossRef]
  31. Liu, K.; Yan, Q.; Chen, M.; Fan, W.; Sun, Y.; Suh, J.; Fu, D.; Lee, S.; Zhou, J.; Tongay, S.; et al. Elastic properties of chemical-vapor-deposited monolayer MoS2, WS2, and their bilayer heterostructures. Nano Lett. 2014, 14, 5097–5103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  32. Manzeli, S.; Allain, A.; Ghadimi, A.; Kis, A. Piezoresistivity and strain-induced band gap tuning in atomically thin MoS2. Nano Lett. 2015, 15, 5330–5335. [Google Scholar] [CrossRef] [Green Version]
  33. Yazyev, O.V.; Kis, A. MoS2 and semiconductors in the flatland. Mater. Today 2015, 18, 20–30. [Google Scholar] [CrossRef]
  34. Mortazavi, B.; Ostadhossein, A.; Rabczuk, T.; Van Duin, A.C. Mechanical response of all-MoS2 single-layer heterostructures: A ReaxFF investigation. Phys. Chem. Chem. Phys. 2016, 18, 23695–23701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  35. Miró, P.; Ghorbani-Asl, M.; Heine, T. Two dimensional materials beyond MoS2: Noble-transition-metal dichalcogenides. Angew. Chem. Int. Ed. 2014, 53, 3015–3018. [Google Scholar] [CrossRef] [PubMed]
  36. Frisenda, R.; Drüppel, M.; Schmidt, R.; de Vasconcellos, S.M.; de Lara, D.P.; Bratschitsch, R.; Rohlfing, M.; Castellanos-Gomez, A. Biaxial strain tuning of the optical properties of single-layer transition metal dichalcogenides. NPJ 2D Mater. Appl. 2017, 1, 1–7. [Google Scholar] [CrossRef]
  37. Jaques, Y.M.; Manimunda, P.; Nakanishi, Y.; Susarla, S.; Woellner, C.F.; Bhowmick, S.; Asif, S.A.S.; Galvão, D.S.; Tiwary, C.S.; Ajayan, P.M.; et al. Differences in the Mechanical Properties of Monolayer and Multilayer WSe2/MoSe2. MRS Adv. 2018, 3, 373–378. [Google Scholar] [CrossRef] [Green Version]
  38. Jiang, M.; Zhang, J.; Wu, M.; Jian, W.; Xue, H.; Ng, T.W.; Lee, C.S.; Xu, J. Synthesis of 1T-MoSe2 ultrathin nanosheets with an expanded interlayer spacing of 1.17 nm for efficient hydrogen evolution reaction. J. Mater. Chem. A 2016, 4, 14949–14953. [Google Scholar] [CrossRef]
  39. Iguiñiz, N.; Frisenda, R.; Bratschitsch, R.; Castellanos-Gomez, A. Revisiting the buckling metrology method to determine the Young’s modulus of 2D materials. Adv. Mater. 2019, 31, 1807150. [Google Scholar] [CrossRef] [Green Version]
  40. Johari, P.; Shenoy, V.B. Tuning the electronic properties of semiconducting transition metal dichalcogenides by applying mechanical strains. ACS Nano 2012, 6, 5449–5456. [Google Scholar] [CrossRef]
  41. Kumar, A.; Ahluwalia, P. Mechanical strain dependent electronic and dielectric properties of two-dimensional honeycomb structures of MoX2 (X = S, Se, Te). Phys. B Condens. Matter 2013, 419, 66–75. [Google Scholar] [CrossRef]
  42. Mortazavi, B.; Berdiyorov, G.R.; Makaremi, M.; Rabczuk, T. Mechanical responses of two-dimensional MoTe2; pristine 2H, 1T and 1T’ and 1T’/2H heterostructure. Extrem. Mech. Lett. 2018, 20, 65–72. [Google Scholar] [CrossRef] [Green Version]
  43. May, P.; Khan, U.; Coleman, J.N. Reinforcement of metal with liquid-exfoliated inorganic nano-platelets. Appl. Phys. Lett. 2013, 103, 163106. [Google Scholar] [CrossRef] [Green Version]
  44. Rano, B.R.; Syed, I.M.; Naqib, S. Ab initio approach to the elastic, electronic, and optical properties of MoTe2 topological Weyl semimetal. J. Alloys Compd. 2020, 829, 154522. [Google Scholar] [CrossRef] [Green Version]
  45. Sun, Y.; Pan, J.; Zhang, Z.; Zhang, K.; Liang, J.; Wang, W.; Yuan, Z.; Hao, Y.; Wang, B.; Wang, J.; et al. Elastic properties and fracture behaviors of biaxially deformed, polymorphic MoTe2. Nano Lett. 2019, 19, 761–769. [Google Scholar] [CrossRef] [PubMed]
  46. Deng, S.; Li, L.; Li, M. Stability of direct band gap under mechanical strains for monolayer MoS2, MoSe2, WS2 and WSe2. Phys. E Low Dimens. Syst. Nanostruct. 2018, 101, 44–49. [Google Scholar] [CrossRef] [Green Version]
  47. Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
  48. Freitas, R.R.; de Brito Mota, F.; Rivelino, R.; De Castilho, C.; Kakanakova-Georgieva, A.; Gueorguiev, G.K. Tuning band inversion symmetry of buckled III-Bi sheets by halogenation. Nanotechnology 2016, 27, 055704. [Google Scholar] [CrossRef]
  49. Dos Santos, R.; Rivelino, R.; de Brito Mota, F.; Gueorguiev, G.; Kakanakova-Georgieva, A. Dopant species with Al–Si and N–Si bonding in the MOCVD of AlN implementing trimethylaluminum, ammonia and silane. J. Phys. D Appl. Phys. 2015, 48, 295104. [Google Scholar] [CrossRef]
  50. Pereira, M.L.; Ribeiro, L.A. Thermomechanical insight into the stability of nanoporous graphene membranes. FlatChem 2020, 24, 100196. [Google Scholar] [CrossRef]
  51. Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
  52. Mises, R.V. Mechanik der festen Körper in plastisch-deformablen Zustand. Math. Phys. Klasse 1913, 4, 582–592. [Google Scholar]
  53. Heyes, D.M. Pressure tensor of partial-charge and point-dipole lattices with bulk and surface geometries. Phys. Rev. B 1994, 49, 755. [Google Scholar] [CrossRef] [PubMed]
  54. Sirk, T.W.; Moore, S.; Brown, E.F. Characteristics of thermal conductivity in classical water models. J. Chem. Phys. 2013, 138, 064505. [Google Scholar] [CrossRef] [PubMed]
  55. Thompson, A.P.; Plimpton, S.J.; Mattson, W. General formulation of pressure and stress tensor for arbitrary many-body interaction potentials under periodic boundary conditions. J. Chem. Phys. 2009, 131, 154107. [Google Scholar] [CrossRef] [Green Version]
  56. Surblys, D.; Matsubara, H.; Kikugawa, G.; Ohara, T. Application of atomic stress to compute heat flux via molecular dynamics for systems with many-body interactions. Phys. Rev. E 2019, 99, 051301. [Google Scholar] [CrossRef] [Green Version]
  57. Ghobadi, N. A comparative study of the mechanical properties of multilayer MoS2 and graphene/MoS2 heterostructure: Effects of temperature, number of layers and stacking order. Curr. Appl. Phys. 2017, 17, 1483–1493. [Google Scholar] [CrossRef]
  58. Lee, J.U.; Yoon, D.; Cheong, H. Estimation of Young’s modulus of graphene by Raman spectroscopy. Nano Lett. 2012, 12, 4444–4448. [Google Scholar] [CrossRef] [Green Version]
Condensedmatter 05 00073 g001 550
Figure 1. Schematic representation of the model transition metal dichalcogenide (TMD) monolayers in their 2H and 1T phases. The v and h red arrows highlighted in the 2H-MoS 2 panel denote the structure directions.
Figure 1. Schematic representation of the model transition metal dichalcogenide (TMD) monolayers in their 2H and 1T phases. The v and h red arrows highlighted in the 2H-MoS 2 panel denote the structure directions.
Condensedmatter 05 00073 g001
Condensedmatter 05 00073 g002 550
Figure 2. Representative molecular dynamics (MD) snapshots of the fracture dynamics for the 2H-MoS 2 (top sequence of panels) and 1T-MoS 2 (bottom sequence of panels) monolayers at 300K and considering a uniaxial strain applied along the h-direction.
Figure 2. Representative molecular dynamics (MD) snapshots of the fracture dynamics for the 2H-MoS 2 (top sequence of panels) and 1T-MoS 2 (bottom sequence of panels) monolayers at 300K and considering a uniaxial strain applied along the h-direction.
Condensedmatter 05 00073 g002
Condensedmatter 05 00073 g003 550
Figure 3. Representative MD snapshots of the fracture dynamics for the 1T-MoS 2 (top sequence of panels) and 1T-MoS 2 (bottom sequence of panels) monolayers at 300K and considering a uniaxial strain applied along the v-direction.
Figure 3. Representative MD snapshots of the fracture dynamics for the 1T-MoS 2 (top sequence of panels) and 1T-MoS 2 (bottom sequence of panels) monolayers at 300K and considering a uniaxial strain applied along the v-direction.
Condensedmatter 05 00073 g003
Condensedmatter 05 00073 g004 550
Figure 4. Representative MD snapshots of the fracture dynamics for the 2H/1T-MoSe 2 and 2H/1T-MoTe 2 monolayers at 300K. The top and bottom sequence of panels refer to the simulations considering a uniaxial strain applied along the h and v directions, respectively.
Figure 4. Representative MD snapshots of the fracture dynamics for the 2H/1T-MoSe 2 and 2H/1T-MoTe 2 monolayers at 300K. The top and bottom sequence of panels refer to the simulations considering a uniaxial strain applied along the h and v directions, respectively.
Condensedmatter 05 00073 g004
Condensedmatter 05 00073 g005 550
Figure 5. Calculated stress–strain curves for all TMD membranes studied here when subjected to 10K and 300K, considering a uniaxial strain applied in both h and v directions. (a,d), (b,e), and (c,f) are describing the stress–strain relationship for the 2H/1T-MoS 2 , 2H/1T-MoSe 2 , and 2H/1T-MoTe 2 membranes, respectively.
Figure 5. Calculated stress–strain curves for all TMD membranes studied here when subjected to 10K and 300K, considering a uniaxial strain applied in both h and v directions. (a,d), (b,e), and (c,f) are describing the stress–strain relationship for the 2H/1T-MoS 2 , 2H/1T-MoSe 2 , and 2H/1T-MoTe 2 membranes, respectively.
Condensedmatter 05 00073 g005
Table
Table 1. Elastic properties ( Y M , in units of GPa), fracture strain (FS (%)), and the maximum stress US (which is called ultimate tensile strength US (GPa)) that were obtained by fitting the stress–strain curves for the TMD monolayers investigated here.
Table 1. Elastic properties ( Y M , in units of GPa), fracture strain (FS (%)), and the maximum stress US (which is called ultimate tensile strength US (GPa)) that were obtained by fitting the stress–strain curves for the TMD monolayers investigated here.
Temperature [K]2H-MoS 2
Strain-hStrain-v
Y M [GPa]FS [%]US [GPa] Y M [GPa]FS [%]US [GPa]
10 K14519191392217
300 K13512141301414
Temperature [K]2H-MoSe 2
Strain-hStrain-v
Y M [GPa]FS [%]US [GPa] Y M [GPa]FS [%]US [GPa]
10 K16023261552725
300 K15417221492021
Temperature [K]2H-MoTe 2
Strain-hStrain-v
Y M [GPa]FS [%]US [GPa] Y M [GPa]FS [%]US [GPa]
10 K12525231223021
300 K12118191182018
Temperature [K]1T-MoS 2
Strain-hStrain-v
Y M [GPa]FS [%]US [GPa] Y M [GPa]FS [%]US [GPa]
10 K12413121201411
300 K1335711088
Temperature [K]1T-MoSe 2
Strain-hStrain-v
Y M [GPa]FS [%]US [GPa] Y M [GPa]FS [%]US [GPa]
10 K12712111241512
300 K1147811288
Temperature [K]1T-MoTe 2
Strain-hStrain-v
Y M [GPa]FS [%]US [GPa] Y M [GPa]FS [%]US [GPa]
10 K11813111141611
300 K1078810398
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Pereira Júnior, M.L.; Viana de Araújo, C.M.; De Sousa, J.M.; de Sousa Júnior, R.T.; Roncaratti Júnior, L.F.; Ferreira Giozza, W.; Ribeiro Júnior, L.A. On the Elastic Properties and Fracture Patterns of MoX2 (X = S, Se, Te) Membranes: A Reactive Molecular Dynamics Study. Condens. Matter 2020, 5, 73. https://doi.org/10.3390/condmat5040073

AMA Style

Pereira Júnior ML, Viana de Araújo CM, De Sousa JM, de Sousa Júnior RT, Roncaratti Júnior LF, Ferreira Giozza W, Ribeiro Júnior LA. On the Elastic Properties and Fracture Patterns of MoX2 (X = S, Se, Te) Membranes: A Reactive Molecular Dynamics Study. Condensed Matter. 2020; 5(4):73. https://doi.org/10.3390/condmat5040073

Chicago/Turabian Style

Pereira Júnior, Marcelo Lopes, Cícera Maria Viana de Araújo, José Moreira De Sousa, Rafael Timóteo de Sousa Júnior, Luiz Fernando Roncaratti Júnior, William Ferreira Giozza, and Luiz Antonio Ribeiro Júnior. 2020. "On the Elastic Properties and Fracture Patterns of MoX2 (X = S, Se, Te) Membranes: A Reactive Molecular Dynamics Study" Condensed Matter 5, no. 4: 73. https://doi.org/10.3390/condmat5040073

APA Style

Pereira Júnior, M. L., Viana de Araújo, C. M., De Sousa, J. M., de Sousa Júnior, R. T., Roncaratti Júnior, L. F., Ferreira Giozza, W., & Ribeiro Júnior, L. A. (2020). On the Elastic Properties and Fracture Patterns of MoX2 (X = S, Se, Te) Membranes: A Reactive Molecular Dynamics Study. Condensed Matter, 5(4), 73. https://doi.org/10.3390/condmat5040073

Article Metrics

Back to TopTop