Study of Multi-Pixel Scintillator Detector Configurations for Measuring Polarized Gamma Radiation
Abstract
:1. Introduction
2. Materials and Methods
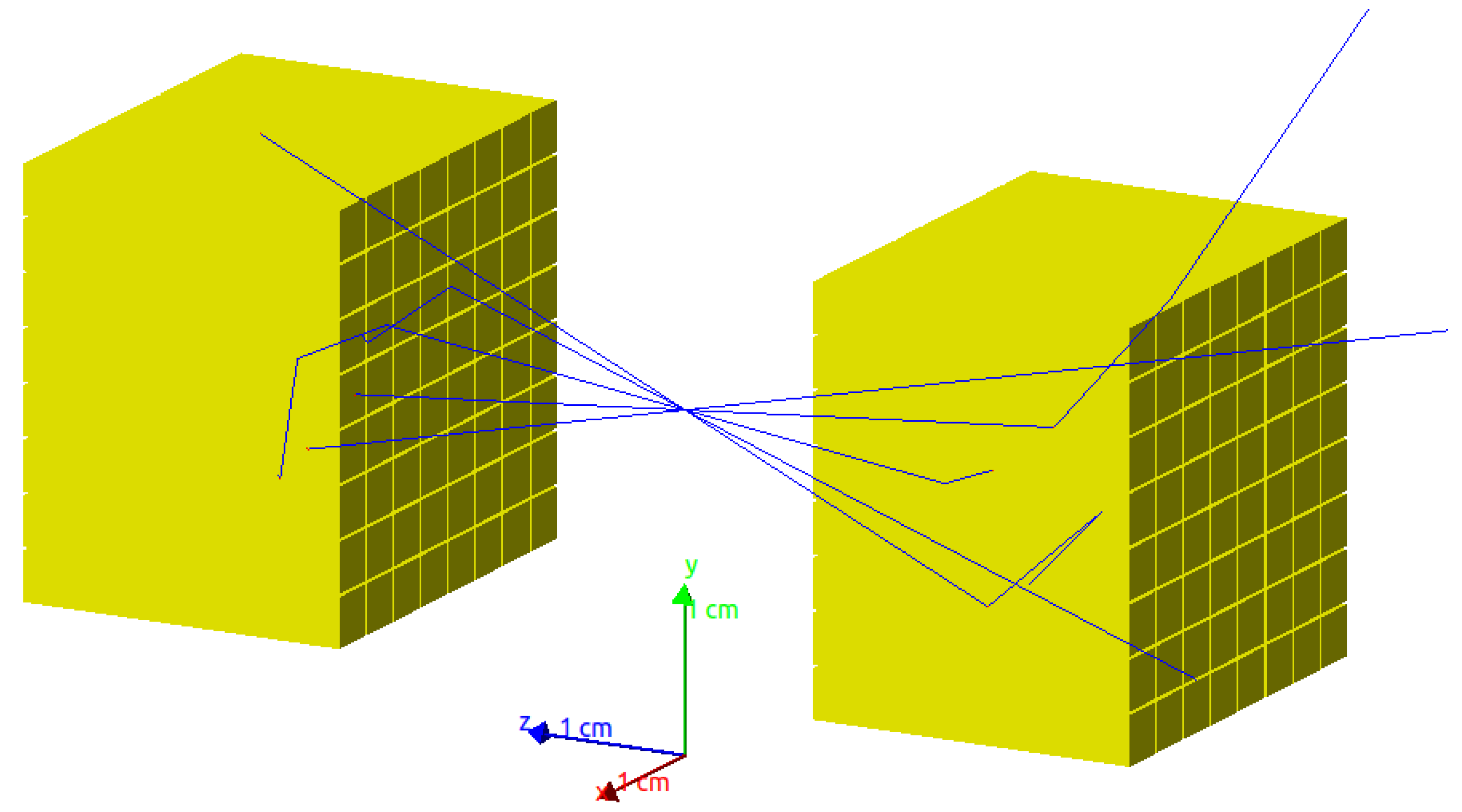
2.1. Monte Carlo Simulations
2.2. Reconstruction of Compton Events
2.3. Extraction of the Modulation Factors
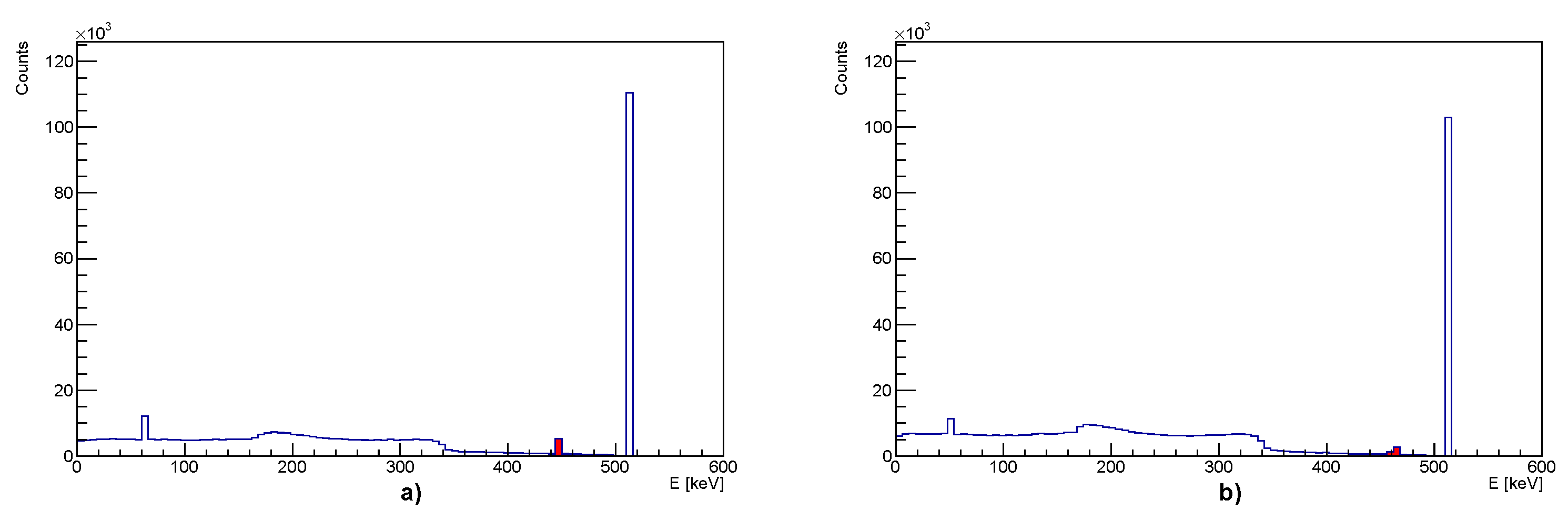
3. Results
3.1. GAGG Configuration
3.2. LYSO Configuration
3.3. Influence of the Escape X-ray on Detector Performance
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kuncic, Z.; McNamara, A.; Wu, K.; Boardman, D. Polarization enhanced X-ray imaging for biomedicine. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2011, 648, 208–210. [Google Scholar] [CrossRef]
- McNamara, A.; Toghyani, M.; Gillam, J.; Wu, K.; Kuncic, Z. Towards optimal imaging with PET: An in silico feasibility study. Phys. Med. Biol. 2014, 59, 7587–7600. [Google Scholar] [CrossRef] [PubMed]
- Toghyani, M.; Gillam, J.; McNamara, A.; Kuncic, Z. Polarisation-based coincidence event discrimination: An in silico study towards a feasible scheme for Compton-PET. Phys. Med. Biol. 2016, 61, 5803–5817. [Google Scholar] [CrossRef] [PubMed]
- Watts, D.P.; Bordes, J.; Brown, J.R.; Cherlin, A.; Newton, R.; Allison, J.; Bashkanov, M.; Efthimiou, N.; Zachariou, N.A. Photon quantum entanglement in the MeV regime and its application in PET imaging. Nat. Commun. 2021, 12, 2646. [Google Scholar] [CrossRef] [PubMed]
- Pryce, M.H.L.; Ward, J.C. Angular correlation effects with annihilation radiation. Nature 1947, 160, 435. [Google Scholar] [CrossRef]
- Makek, M.; Bosnar, D.; Pavelić, L.; Šenjug, P.; Žugec, P. Single-layer Compton detectors for measurement of polarization correlations of annihilation quanta. Nucl. Inst. Meth. Phys. Res. A 2019, 958, 162835. [Google Scholar] [CrossRef]
- Makek, M.; Bosnar, D.; Kožuljević, A.M.; Pavelić, L. Investigation of GaGG:Ce with TOFPET2 ASIC Readout for Applications in Gamma Imaging Systems. Crystals 2020, 10, 1073. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.A.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Behner, F.; et al. Geant4—A simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2003, 506, 250–303. [Google Scholar] [CrossRef] [Green Version]
- Epic-Crystal. Available online: https://www.epic-crystal.com/oxide-scintillators/lyso-ce-scintillator.html (accessed on 28 September 2021).
- Lythe, L.; Hilger Crystals Ltd., Margate, UK. Personal communication, 2019.
- Makek, M.; Bosnar, D.; Pavelić, L. Scintillator Pixel Detectors for Measurement of Compton Scattering. Condens. Matter 2019, 4, 24. [Google Scholar] [CrossRef] [Green Version]









| LYSO | GAGG | |
|---|---|---|
| Light yield (ph/MeV) | ∼29,000 | ∼55,000 |
| Decay time (ns) | 42 | 88 |
| Zeffective | 66 | 54.4 |
| Density (g/cm3) | 7.2 | 6.63 |
| d (mm) | |||
|---|---|---|---|
| 58.4% | 52.0% | 53.6% | |
| 61.4% | 55.5% | 54.7% | |
| 62.3% | 56.6% | 55.0% | |
| 65.1% | 60.5% | 56.5% | |
| 65.1% | 60.5% | 56.6% | |
| 65.7% | 62.1% | 56.6% |
| d (mm) | |||
|---|---|---|---|
| 54.5% | 47.4% | 50.2% | |
| 58.2% | 51.4% | 51.9% | |
| 58.9% | 52.1% | 52.1% | |
| 63.0% | 57.3% | 54.2% | |
| 65.2% | 60.4% | 55.6% | |
| 65.6% | 61.0% | 55.9% |
| (mm) | ||||
|---|---|---|---|---|
| 34.8°± 0.3° | 0.22 ± 0.03 | 37.1°± 0.2° | 0.13 ± 0.03 | |
| 19.1°± 0.3° | 0.26 ± 0.03 | 19.6°± 0.2° | 0.17 ± 0.03 | |
| 17.6°± 0.3° | 0.26 ± 0.03 | 18.0°± 0.2° | 0.17 ± 0.03 | |
| (mm) | ||||
|---|---|---|---|---|
| 33.4°± 0.4° | 0.19 ± 0.03 | 35.3°± 0.3° | 0.13 ± 0.03 | |
| 23.1°± 0.4° | 0.22 ± 0.03 | 24.2°± 0.3° | 0.15 ± 0.03 | |
| 13.8°± 0.3° | 0.21 ± 0.03 | 14.0°± 0.2° | 0.16 ± 0.03 | |
| Detector | LYSO | GAGG | |
|---|---|---|---|
| Neighbors | |||
| 1st adjacent | 3% | 2.2% | |
| 1st diagonal | 1% | 0.4% | |
| 2nd orthogonal | 0.1% | 0.01% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kožuljević, A.M.; Bosnar, D.; Kuncic, Z.; Makek, M.; Parashari, S.; Žugec, P. Study of Multi-Pixel Scintillator Detector Configurations for Measuring Polarized Gamma Radiation. Condens. Matter 2021, 6, 43. https://doi.org/10.3390/condmat6040043
Kožuljević AM, Bosnar D, Kuncic Z, Makek M, Parashari S, Žugec P. Study of Multi-Pixel Scintillator Detector Configurations for Measuring Polarized Gamma Radiation. Condensed Matter. 2021; 6(4):43. https://doi.org/10.3390/condmat6040043
Chicago/Turabian StyleKožuljević, Ana Marija, Damir Bosnar, Zdenka Kuncic, Mihael Makek, Siddharth Parashari, and Petar Žugec. 2021. "Study of Multi-Pixel Scintillator Detector Configurations for Measuring Polarized Gamma Radiation" Condensed Matter 6, no. 4: 43. https://doi.org/10.3390/condmat6040043
APA StyleKožuljević, A. M., Bosnar, D., Kuncic, Z., Makek, M., Parashari, S., & Žugec, P. (2021). Study of Multi-Pixel Scintillator Detector Configurations for Measuring Polarized Gamma Radiation. Condensed Matter, 6(4), 43. https://doi.org/10.3390/condmat6040043






