1. Introduction
Since their discovery, 35 years of exhaustive study of high-temperature superconducting cuprates has culminated in a consensus on the compositional and structural factors that maximize the transition temperature:
Cu-O diamonds often extended into prolate square pyramids with Cu-O distances that provide strong Cu-O electron–lattice coupling;
Arranged into fully ordered CuO
2 planes [
1,
2];
Stacked into layers no more than three or four planes high, typically connected by Ca2+ or Y3+ that give the optimum distance between these CuO2 planes, that are separated by other, epitaxially matched layers of certain compositions and structures;
Restriction of the carriers to within the CuO
2 layers by large distances between the stacks and to the apical O (O
ap) atoms that are the axial ligands to the Cu atoms on the outer planes of a stack [
3,
4];
Overlapping energies of the Cu 3
d and O 2
p states to increase their hybridization, which promotes O
2−→Cu
2/3+ charge transfer and the superexchange between the Cu atoms [
5,
6,
7];
Doping levels that give the optimum carrier concentration in the CuO
2 layers [
8];
The structural and chemical factors that maximize the hole concentration on the O atoms of the CuO
2 planes [
9,
10].
Number 6 is of particular interest because it is controlled via synthesis to span the range from the undoped parent materials to, and often through, the superconductivity that occurs over a relatively narrow range. The superconducting dome in the quantum phase diagram of cuprates (
Figure 1a), i.e., the plot of critical temperature (T
c) against the excess charge greater than two of the Cu in the CuO
2 planes (
p), has been an essential attribute of superconducting cuprates since shortly after their initial discovery. The dome, as presented by, e.g., Presland et al. in 1991 [
11], is appealing for several reasons. First, it appears applicable to all hole-doped cuprates, and is also often relevant to related compounds based on other transition metals. Second, it is highly correlated with the presumed common aspects of the crystal and electronic structures of the cuprates. Finally, it indicates that superconductivity is an emergent property originating in more fundamental characteristics in addition to the carrier concentration. These could be, e.g., electron–lattice coupling, Cu-O hybridization and Cu-Cu superexchange [
7] as the basis for the enhancement of the superconductivity with increased doping, with its loss resulting from the increasing disorder and loss of phase coherence from the same process [
12,
13,
14], whereby the adventitious O or a different atom in the lattice are defects.
On the underdoped side, the dome model is firmly established for its original purpose: showing the evolution of Tc as a function of the charge density in the superconducting CuO2 plane caused by oxygen addition or the substitution of aliovalent cations. Starting on the left, with the antiferromagnetic insulator in the homogeneous, undoped system, the introduction of holes initially turns on the superconductivity at p ~ 0.06–0.07. Additional doping increases Tc, concomitant with the formation of various competing charge (and pair) ordered states and the exotic metal state above Tc; followed by a brief reduced rate of increase or even local minimum in Tc in the structure with commensurate, static stripes at p = 0.125. The maximum Tc occurs at the optimum p value of ~0.15–0.16.
The commonality of these behaviors and their underlying structures has resulted in the assumption of a single structure: a function relationship applicable to all of the cuprates, whose slightly different properties would then be second-order variations on this unified theme [
9,
10]. This simplest interpretation of the phase diagram and other experimental data is not only logically based on shared behaviors, but also is appealing in its reduction of the high-temperature superconductivity (HTSC) problem to the properties of the universal components of the structure.
This assumption of the same pattern of behavior for all cuprates necessitates the extension of the universality of its ascending half on the underdoped to its descent on the overdoped side of the dome. Although largely true, reality is more complicated. For those compounds that have been made and measured, increased doping does suppress the superconductivity until Tc becomes 0 K at p ~ 0.26–0.27. However, not all compounds can be overdoped; in addition, some only tolerate cation substitution, which should not necessarily be taken as interchangeable with increasing the oxygen stoichiometry.
This assumed universal loss of superconductivity upon modestly increased doping constitutes what is arguably the most egregious error committed by the cuprate community. As shown in
Figure 1b, the reaction with O
2 gas up to a few hundred atm gave modestly increased O stoichiometries and extensions of the superconductivity in La
2CuO
4 (LCO) as well as the addition of oxygen into strained thin films electrochemically [
21] or with ozone [
22] raised T
c to ~50 K. However, starting in the early 1990s the use of potent solid oxidants such as chlorates in hydraulic presses at up to 5 GPa and >1000 °C, the High Pressure Oxygenation (HPO) method, resulted in superconducting compounds with O stoichiometries much higher than attainable with O
2 and T
cs > 50 K that did not decrease. Unfortunately, these reports have been ignored or misinterpreted by the larger community. The bias towards the dome has been so strong that one of the pioneering HPO chemists succumbed to using it to calculate the charges in the CuO
2 plane [
23] instead of the reverse. The rationale for this neglect was that the HPO treatment cannot give pure phases, and thus the superconductivity could be explained by remnant parent materials. Numerous examples demonstrate the fallacy of this assumption, e.g., the T
c = 84 K of HPO Cu
0.75Mo
0.25YSr
2Cu
2O
7.54 (YSCO-Mo) is one-third higher than the 63 K one of its optimally doped CuYSr
2Cu
2O
7±δ (YSCO) parent [
24,
25,
26].
Here, we describe the characteristics of a number of highly oxygenated superconducting cuprates, which unequivocally demonstrates that there is a large class of cuprates to which the dome model does not apply [
27,
28]. Up to their maximum attainable
p values, including the extreme case of
p = 1, these cuprates still retain, or even slightly improve, both their transition temperatures and superconducting volume. For example, the finding of a highly ordered CuYBa
2Cu
2O
7±δ (YBCO or sometimes 123) with δ approaching 1 (giving Cu a calculated valency near 3+) [
25] with T
c remaining above 90 K across the full range of O stoichiometry challenges much of our understanding of high-temperature superconductivity. This is further established by the unique behaviors of these materials that provide counterexamples to most of the listed criteria as well as others so taken for granted that there is no need to cite them:
These findings demonstrate that the insertion of extra O atoms by the HPO process gives different arrangements of the O sublattice compared to conventional methods. More importantly, the superconductivity in these compounds has unique characteristics that challenge our understanding of its occurrence in conventional cuprates, in particular the role of the lattice and the coupling of the structure beyond the CuO2 planes to the superconductivity. We anticipate that a new consideration of these results can provide new insights into the understanding of the superconductivity mechanism and its complexity.
2. Cuprate Structure
A starting point for evaluating the effects and consequences of over-oxygenating cuprates is the three families of materials delineated by their parent compounds and structural motifs: LCO, YBCO and (Cu1−xMx)2Sr2CaCu2O8 with M = Bi, Tl or Hg. A brief reminder of the structure and composition of the homologous series of superconducting cuprates is useful for the following discussion.
On the nanometer scale, the cuprates are intuitively multilayer heterostructures, conveniently described as constituting three different types of structural blocks named for their crystal structures: perovskite (P), rock salt (RS) and fluorite (F) blocks [
33]. By varying the layer thicknesses, these blocks combine to form two fundamental classes of homologous series. Class A consists of alternating P and RS blocks with the chemical formula
MmA2Q1−nCunOm+2+2n+d, which is rewritten by the homologous series systematic name notation as M-
m2(
n−1)
n. Class B includes inserted F layers in addition to the P and RS blocks and follows the formula
MmA2kRsCu1+kOm+4k+2s+d, i.e., M-
m(
2k)
s(
1+k). These designations of the structural features are illustrated in
Figure 2, derived from the in-depth description in [
33].
The focus of most research is the functional domains of the cuprates, especially the superconducting CuO
2-layers, also called the perovskite block. It consists of square-planar-coordinated Cu
2+ in an oxygen-deficient perovskite-type structure; the vacant oxygen position is systematically the O
ap. Although the Cu-O-Cu moiety is somewhat puckered, the Cu and O planes are completely flat. The “glue” holding multiple CuO
2 layers together consists of large anions Q, most commonly Ca
2+ or Y
3+. The number of CuO
2 layers in a stack,
n, can be varied widely without losing structural rigidity, although the maximum that retains the superconductivity is four. The upper limit is unknown: currently the highest number for the homologous series A are around
n = 8 [
39], but the phase purity in terms of maintaining a constant number of CuO
2 in every stack is already very challenging; plus, the phase is a combination of
n = 7 and
n = 8 structured layers [
36]. For the lowest limit,
n = 1 equals just one single CuO
2 plane, in which case Q is missing. Functionally, the CuO
2 layers host the itinerant carriers and are, therefore, the conducting domain of the material as well as the location of both its metallic behavior and its superconductivity. Accordingly, the conductivity of cuprates is highly anisotropic, being much greater within the
ab plane than along the
c axis. Insofar as the covalency and spatial overlap of the Cu-O bonds in the CuO
2 planes and the Cu-Cu superexchange results from both the overlap of the Cu 3
d and O 2
p states and the Cu-O bond length, disruptions in the regularity and flatness of the CuO
2 planes are known to reduce T
c. However, the main determining parameter for superconductivity is the charge and charge balance [
9,
10] in the planar CuO
2 layers. Upon overdoping, a corresponding fraction of the Cu
2+ is oxidized to Cu
3+.
The CuO
2 planes are bracketed by the dielectric AO layer that separates the CuO
2 planes and the “blocking blocks” or charge reservoirs. It is composed of the A atoms that are most commonly either Ba or Sr, but can also be a mixture, and the O
ap atoms. In La
2CuO
4+δ (LCO-O)-type compounds, where this layer doubles as the charge reservoir, its two layers exhibit the rock salt structure. In the other two types, the A-O
ap constitutes only a single layer that is ambidextrous: its interface with the P block matches its perovskite structure, and its interface with the RS block matches that one. In addition to the AO-bonding network in the
ab-oriented A plane, the
c-oriented bonding connection consists of the oxygen atoms of the AO structure doubling as the direct link between the O
ap of the bordering CuO
2 plane and the M of the charge reservoir layer. The O
ap atoms thus constitute the bridge along which the essential charge transfer from the reservoir to the conducting domain occurs. Otherwise, as its “dielectric” designation implies, it is considered inert with respect to superconductivity, with its function being to maintain the holes and resulting conductivity in the CuO
2 planes by impeding their back transfer to the reservoir. An intriguing, alternative idea supported by the finding of interfacial superconductivity in certain oxide heterostructures is that cuprate superconductivity also occurs at the interface between the CuO
2 planes and this dielectric layer [
33].
The fluorite layer appears in cuprates of Category B. In this category, the number of CuO
2 planes is fixed at two, and the fluorite block functions as a spacer between them. A wide range of thicknesses have been reported, up to s = 6 [
40]. Commonly, the base fluorite layer oxide is CeO
2 or YO
2, but significant substitution with other lanthanoids (up to 67%) is possible [
41,
42,
43,
44,
45]. Rare earth (RE) substitution shows a linear correlation between ionic radius and lattice parameter expansion but weak effects on the valence of Cu or on the Tc [
44]. Investigations into the B-series of cuprates have been useful in evaluating the Josephson coupling between the CuO
2 planes, which is sensitive to the interlayer distances and causes T
c to increase up to 3–4 layers [
46].
The so-called charge reservoir layer (MO)
m typically has a perovskite-type or rock salt structure. Its thickness varies as
m = 0–3; although higher members could be possible, we have found no examples. Among high-temperature superconducting cuprates, the rock salt structure predominates, e.g., cuprates where M = Hg, Bi, or Tl [
39,
47,
48,
49,
50]. When M is Cu in YBCO- and YSCO-type compounds, because of the preferred square-planar Cu geometry the block takes on an ordered, oxygen-deficient cupric perovskite-type structure, with the oxygen atoms along the
a axis and the vacancies between Cu atoms along the
b direction of the orthorhombic structure. The Cu, therefore, occurs as CuO
3vacancy
2-chains. The properties of these cuprates with this CuO
3 charge-reservoir, and in particular their response to HPO reaction conditions, are distinct, warranting the separation of these compounds into their own class. Adjustments in oxygen content are directly felt in the charge reservoir, as the added oxygen is incorporated here [
51]. In LCO-O and M-2212 compounds, the adventitious O atoms are located interstitially, causing atom displacements and lattice distortions in their vicinity. The charge balance of Cu is altered by substitutions to the M position [
32,
45,
51,
52,
53] or in the superconducting CuO
2-plane layer [
28,
32,
54,
55,
56]. Partial substitution with an element with fixed valence controls the doping and corresponding hole density on Cu. This alterative to O-doping is easily controlled and can be increased more effectively.
Our three selected families of materials (
Figure 3) represent the homologous series, A, in which the CuO
2 planes between dielectric layers are not separated. YBCO and (Cu
1−xM
x)
2Sr
2CaCu
2O
8 correspond to Cu-1212 and M-2212, respectively. The LCO-O compounds can be seen as a special ‘null’ case of the A series, denoted □-0201 (□ designates the absence of an M-species). It differs from the other A-series compounds in that it lacks both M and Q atoms, and the charge reservoir and dielectric domains are combined into one block of rock-salt-type La(Ba/Sr)O layer. Because the O
ap neighbor opposite to the Cu atom along the
c direction is the M type, the CuO
2 layers are displaced (1/2,1/2) relative to each other. Therefore, in the
c direction it is the alternating Cu atoms that are aligned. This displacement is characteristic, when the charge reservoir layer thickness
m is an even number,
m = 0 or
m = 2 and carries over to CuO
2 stacks as well as single planes (this also occurs for B series compounds of odd fluorite layer thicknesses). In the M-2212 compounds, it is, therefore, the stacks of CuO
2 planes that have the same (1/2,1/2) displacement while the CuO
2 planes within a stack are aligned.
The fundamental structural unit of the cuprate series is tetragonal or orthorhombic. Substitutions can cause mismatches between the sizes and geometries of the relatively rigid CuO
2 and more flexible charge reservoir domains, which are compensated by minor orthorhombic or more complicated distortions. Leaving out most of the tremendous body of work on various substitutions, a common one is the interchange of Sr
2+ and Ba
2+ in the dielectric layer. The higher T
c that often, but not always, occurs with Sr is understood as the decrease in Cu-O bond lengths (i.e., covalency) resulting from the smaller ion introducing chemical pressure, especially in the ab-plane [
54,
55,
57]. The effects on bonding and antibonding potential wells in the ab-plane could impact the oxygen absorption potential of the compound; our analysis indicates a higher aptitude for oxygen overdoping among the Sr samples. Other effects of the choice of A-site species are charge balance; e.g., substitution by europium [
58] adds charge flexibility to the layer by tolerating both oxidation states 2+ and 3+.
The superconductivity is much more sensitive to substitutions in the CuO
2 planes than in other sites [
59], with many substituting metals quenching it at only a few percent. In contrast, the Cu chains in the charge reservoir block remain stable with substitution and the materials remain superconducting; for example Cr, Ga, Ge, Fe and Mo have been incorporated, often at ratios around 10–20% [
23,
54,
56] and as high as 25% for Mo [
26,
28,
32,
44,
60]. The Mo solubility limit of 25% could be explained by a bond strain model: the differing bonding preferences of Mo and Cu drive nanoscale domain formation, which might be shifting into grain-level phase separation due to nanodomain percolation. In addition, substitutions can alter the O stoichiometry of the charge reservoir layer via the local stability of the substituting atom. For example, Mo prefers a higher coordination than Cu and readily allows its O
ap positions to be filled [
44].
3. The Phase Diagram of High-Pressure Oxygenized Compounds
In parallel with the quantum phase diagrams of conventional cuprates, the dependence of T
c on
p can also be shown for LCO-O- and YBCO-type for HPO compounds in a second one (
Figure 4), with single points for the former and multiple points for certain of the latter compounds. Instead of being suppressed by “overdoping”, superconductivity is maintained or even enhanced upon achieving remarkably high O stoichiometries and corresponding
p values; up to
p = 0.6 in Sr
2CuO
3 (T
c = 95 K) and
p = 1.0 in CuBa
2YCu
2O
8 (T
c = 91 K). These data were compiled from the literature (
Table 1), with the graph and table compiled from only a fraction of the reports. Doping was performed by both O addition and aliovalent cation substitution. The reliability of the O analysis methods that validate the O stoichiometry is discussed in the next section.
The
p values in the HPO phase diagram are derived from the reported O stoichiometries, for which the quality of the analyses is assessed in
Table 1. These values are then used to calculate the Cu valence assuming formal valences on the other atoms. The presence of the substitutional transition metals that can also assume multiple valences complicates this evaluation. The valence of the substitutional metal will be consistent with the high oxygen activity and potential of the oxidizer at the elevated temperature as well as pressure of the synthesis conditions; its stable geometry is compatible with the distorted octahedral or square planar one of the original chain Cu sites that it occupies, and its size is not overly different from that of the Cu. The valences meeting these criteria are readily assigned, after which the average planar Cu valence is obtained by using the original chain Cu charge of 2.7.
This has been checked by combined O K and Cu L XAS and Mo K XAFS for YSCO-Mo [
60]. The XAFS indicated the Mo to be Mo(VI). The XAS found that the planar Cu charge, ~2.5, was even higher than the direct calculation, which makes this a lower bound. The difference between the measured and calculated Cu charge would result from the unusual Mo geometry that shifts its XAFS energy higher than expected. These results, augmented by Ba
2CuO
3.2 and Sr
2CuO
3.3, give a quantum phase diagram without any vestige of a dome. In fact, T
c never decreases for any of the HPO cuprates up through the maximum attainable O stoichiometry and
p values, but continues to rise or sometimes plateau throughout. The parallel curves are notable, demonstrating that, although the precise locations of the excess O resulting from the HPO treatment are critical, the precise characteristics of the substitutional cation are much less so.
In addition, the transition temperatures are not low, being > 50 K for most compounds and up to 83 K for YSCO-Mo. Far from being lower, Tc for the measured phase of Sr2CuO3.3 is almost 2.5 times that of its parent material, exceeding both that of optimally doped YBCO and the boiling point of liquid nitrogen. The physics of the holes and their locations and interactions in the HPO cuprates clearly depart from that of the cation and O2-doped ones. Another possible significant anomaly is that, in some materials, the onset of the superconductivity may be on the underdoped side of the dome. If correct, this would be another unique aspect of the coupling between the superconductivity and the precise location of the excess O atoms. This interpretation is, however, less certain insofar as the results for YSCO-Mo show a higher value of the measured Cu charge with respect to the calculated one, suggesting that the special behavior of the HPO-added O atoms shifts the phase diagram to the right.
A related issue is the HPO treatment of SCO. In contrast to reports of a maximum transition temperature of 63 K for materials with δ up to 0.6 [
24,
25,
64], is one that reported δ of −0.16 with T
c of 63 K, which would corroborate superconductivity below the lower boundary of the dome. That the O stoichiometry was under 7 with the HPO treatment, determined by crystallographic analysis that located the O deficiency in the O
ap site [
26], implies that the problem could be aperiodic disorder in that site that increases the uncertainty of the O determination. This is the best explanation for the difference between the crystallographic structure of YSCO-Mo, which shows highly unusual geometries for the chain Cu atoms [
32], and the XAFS that is interpreted as demonstrating normal geometries with clustering of the Mo. This type of aperiodic disorder that is beyond crystallography disrupts the refinement in the locations in the unit cell where the disorder occurs. A final point concerning the high doping levels is that µSR spectroscopy of YSCO-Mo showed strong evidence for Fermi-liquid-type carriers in addition to the superconducting ones. This is another departure from BCS theory, in which all of the carriers at the Fermi level should be superconducting. Although cuprates exhibit multiple and variable superconducting gaps in momentum space, the coexistence of two types of carriers is much more difficult to explain. As discussed below, the coexistence of superconducting and normal carriers points to a scenario of electronic phase separation already proposed within a few years of their initial discovery for a variety of cuprate systems [
65].
4. High Pressure Oxygen Synthesis of Hyperstoichiometric Superconducting Cuprates
One often-overlooked influential factor for T
c, and especially for its experimental determination, is sample preparation. Especially, pressure is recognized to strongly influence bonding and crystal structure; many investigated phases are in fact metastable at ambient pressure. Crucial for our discussion, however, is how pressure affects the positions of the excess oxygen within superconducting cuprates and, specifically, whether this position depends on the synthetic approach. Bond compression is known to affect the shape of the potential well for apical oxygen [
66], which is known to influence T
c. It is, therefore, useful to discuss the synthesis routes for HPO cuprates.
The synthesis of highly oxygenated cuprates can, at most, include three different types of steps (
Figure 5):
Ambient-pressure (AP) synthesis;
Low-pressure oxygenation (LPO) steps;
High-pressure oxygenation (HPO) treatment.
The most used ambient pressure (AP) synthesis method is conventional solid-state synthesis, in which primary precursors, often primary metal oxides or carbonates, are ground together and then repeatedly heated (annealed) with intermediate grinding. At high temperatures (usually 700–1200 °C), a solid-state rearrangement of atoms is mediated by enhanced diffusion. Variants of the solid-state method are the nitrate route [
40,
51,
67] and sol-gel route [
30,
32,
68], in which the primary precursors are initially mixed by dissolution, followed by drying and annealing with intermediate grinding.
Low-pressure oxygenation (LPO) methods are taken to include the use of O
2 atmosphere under ambient pressure synthesis [
45,
58,
69,
70], but also pressurized treatments in gas phase, e.g., in an autoclave [
23,
47,
52,
54,
56] at pressures up to ca. 25 MPa. Liquid-phase oxidation by NaOBr-solution stirring has also been described [
68].
High-pressure oxygenation (HPO) is performed under extreme pressure of 1 GPa or higher, using a solid oxygen source. Described in
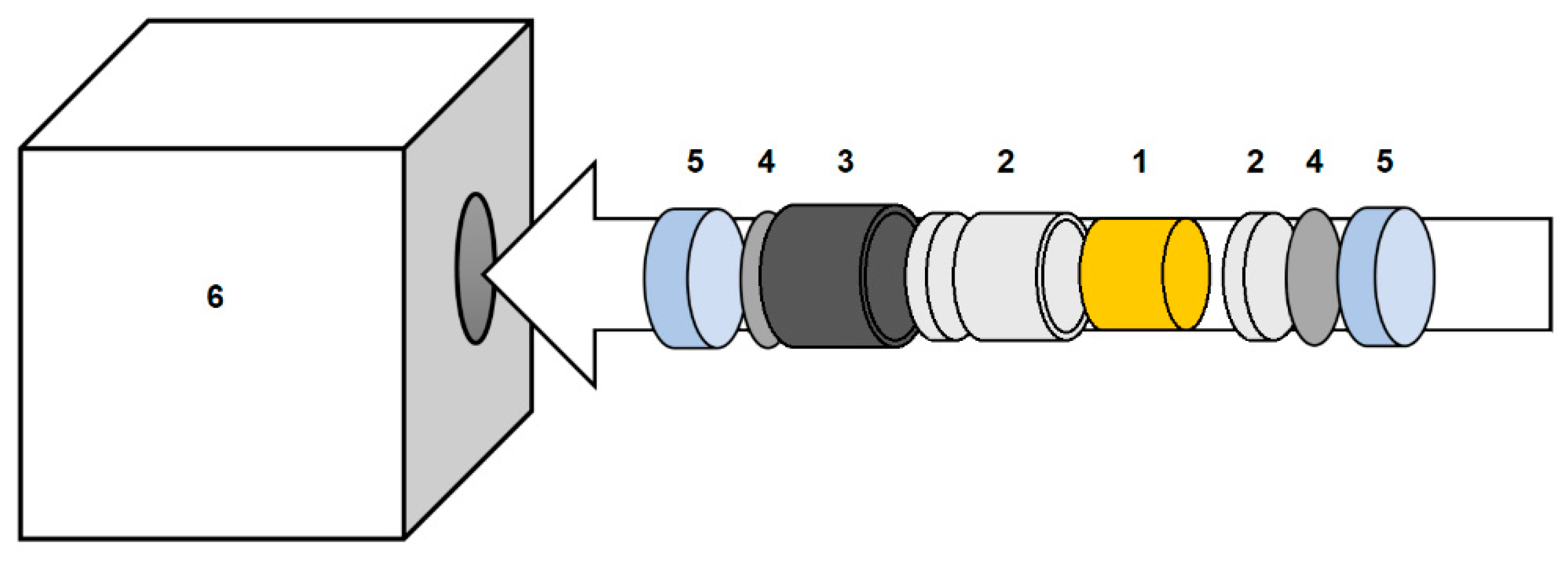
Figure 6, the sample size is limited to the size of the equipment in question; this is, generally, fractions of a gram. Pressure is amplified and conveyed to the sample via WC anvils of varying geometry. Most common is the cubic anvil assembly. Nesting an octahedral anvil assembly within the cubic assembly creates the Walker-type multi-anvil module, which is used for ultra-high-pressure experiments up to ca. 25 GPa.
The excess oxygen in HPO can be brought either internally or externally. Internal oxidation is achieved by carefully adjusting the overall stoichiometry of the precursor mix going into the HPO sample capsule, so that the stoichiometry precisely matches the composition of the wanted product, without leaving any residue. In rare cases, this can be achieved directly by balancing suitable primary precursors (often primitive metal oxides) or a mix of primary and secondary precursors [
31,
39,
71]. Common precursors used for internal oxygenation are BaO
2 and SrO
2. Alternatively, internal oxidation can be realized by LPO steps performed on intermediate precursors made by AP synthesis methods [
63,
69,
72]. In both cases, the final product is synthesized during the HPO step.
However, it is often impossible to find a suitable precursor mix for internal oxidation. External oxidizers are added to the HPO step as solids that release oxygen at high temperatures and leave behind a residue after the HPO treatment. The most common external oxidizers are Ag
2O
2 and KClO
3, and occasionally KClO
4 [
40,
50,
52], that result in Ag or KCl residues, respectively. KCl can be washed away, at the expense of risking sample degradation, while Ag residues are practically inseparable from the cuprate product. An external oxidizer can be used in HPO synthesis [
50,
58,
73,
74], but is more often employed in HPO treatment of pre-formed but oxygen-deficient products [
23,
55,
57,
58,
60,
61]. Intermediate APO steps are commonly used to minimize the amount of oxidizer needed at the HPO step, thus minimizing residue and maximizing the often very limited amount of the HPO sample [
30,
50,
56,
57,
61,
75]. In externally oxygenated treatment, the oxygen donor material can either be mixed in with the other material or separated from it by a thin gold foil or other barrier [
25,
54]. Using a barrier solves the issue of oxidizer residue contamination in the sample, but complicates stoichiometric control of the available oxygen within the very small sample capsule and can inhibit oxygen incorporation.
Within the Cu-1212 compounds, a preference for Ag2O2 is seen among compounds with Ba in the A position, while both oxidizers are equally used when Sr fills the A position. (Ba)Cu-1212 appears sensitive to the stronger oxidizing power of KClO3, which partially degrades the compound, possibly by the phase separation of BaO2. For the higher members of the series there appears to be no general rule regarding which oxidizer is more successful with what materials; systematic studies on this topic are lacking.
Heating is often needed in HP methods to facilitate reagent activation and diffusion. HPO treatments can be roughly categorized into two temperature groups: around 500 °C or around 1000 °C or more. The choice of temperature interval is connected to the overall synthesis route. Oxygenation of a pre-made product by an external oxidizer is often undertaken at medium-high temperatures around 500 °C, which are sufficient to degrade the solid oxidizer material. Temperatures of 500–700 °C are often combined with 2–5 GPa pressure and 30 min heating time; lower pressures are compensated by raising the temperature. When the final product is formed under pressure, extremely high temperatures of 1000–1600 °C are required to activate the precursors and facilitate diffusion of metallic species. Extremely high temperatures can also improve phase purity in cases where spurious oxides may form at lower temperatures, by matching the conventional AP-synthesis temperature of the wanted compound. It is worth pointing out that the HP-heating setup generally allows controlled cooling or quenching of the HPO samples.
As already pointed out, although some patterns are evident, the optimum or even feasible routes to desired products via HPO methods are determined by trial and error rather than prediction. The reduction of the oxygen content on heating indicates that many of these products are metastable. This result adds to the complexity. The temperatures and pressures are sufficiently high to enter regions of the phase diagram that could enable transitions into other phases that could enable or facilitate the incorporation of the excess oxygen.
5. Determination of Oxygen Content
Insofar as the entire concept of overdoped superconducting cuprates depends on the oxygen stoichiometry, its determination by various analytical means is crucial. A starting point for the YBCO-type compounds is their transformation from orthorhombic to tetragonal symmetry that is easily tracked in diffraction. Analogous changes in the space group correlated with the amount of oxidant used in the synthesis and the superconductivity are observed in other compounds as well [
76]. The choice of the synthesis route has a direct effect on sample characterization, especially determination of the oxygen content and the oxidation state of copper. The accuracy of initial reports for new compounds will have suffered from residual oxidant and decomposition products. Subsequent ones in which the synthesis has been optimized will be much more pure. Meanwhile, access to more precise analysis is often more restricted. A more detailed discussion on the accuracy of various oxygen content determination methods can be found in reference [
34]. We briefly present the main features and limitations of the most common techniques. For some materials, the oxygen analyses have been validated by various spectroscopies [
45,
58,
64,
67,
77], crystallographic refinement of partial occupations, or the thoroughness in terms of the number of syntheses with varying quantities of oxidants tracked by these methods [
23,
25].
Iodometric, coulometric and cerimetric titrations probe the O stoichiometry via the measured valence of dissolved metal species, but any oxidizing residues will interfere with the valence of the metal ions. Likewise, as thermogravimetric analysis (TGA) relies on measuring the mass of released oxygen upon heating, any oxygen-containing residue will interfere. Estimates can be made based on at what temperature mass loss has occurred, but some uncertainty will remain regardless. Both titrimetry and TGA are destructive methods that cannot discern sample inhomogeneities, impurities or crystallographic features. However, in the absence of residues of contaminant phases as determined by, e.g., diffraction, both TGA and titration methods can provide reliable descriptions of the overall oxygen content of the sample. Titrimetry can be extremely accurate with errors as small as ±0.01 (for the absolute value of δ), while a well-performed TGA can achieve ±0.02 accuracy. TGA and titration methods are also widely available, simple and inexpensive to perform.
Diffraction data are most commonly available as X-ray diffraction (XRD) measurements. Although high-quality XRD data can provide an excellent basis for structural refinements, the low-form factor of the O atom relative to the other metals impedes locating its positions and their occupancies, especially for disordered structures. Structural changes linked to oxygen content may be used to estimate the oxygen stoichiometry. Neutron diffraction (ND) is considerably more accurate for characterizing oxygen due to its relatively larger neutron cross section. Thus, the oxygen content can be calculated directly from reflection intensities correlating with oxygen-site occupancy. In the best case, the Rietveld-refined oxygen occupancy errors can be as small as ±0.03. In both diffraction methods, spurious phases will be visible as additional peaks; often, these can be identified to provide simultaneous information on phase composition of the sample. The availability of neutron diffraction facilities is a severely restricting factor for its wider use in sample characterization, as is the requirement for larger samples quantities. Both methods suffer from their insensitivity to amorphous phases, whose broad signals in the diffuse scattering may not be detected at the few percent level.
X-ray absorption near-edge structure (XANES) and extended X-ray absorption fine structure (EXAFS) are spectroscopic methods with high accuracy and selectivity. Based on the element-specific X-ray absorption find structure (XAFS) spectra that are determined by the local environment of the target atom, XANES probes the valence and local geometry of the target element while EXAFS identifies the numbers and types of neighbor atoms and their distances from the absorber to a radius of 3–8 Å. A principal advantage of XAFS over pair distribution function analysis is that its element specificity separates many of the atom pairs constituting the local structure from each other, enhancing the accuracy and sensitivity of the results. An additional step in cuprates is magnetic orientation of the sample powders. Since the X-ray beam is polarized, this orientation allows the structure to be probed relative to the magnetization direction. In cuprates, this is along the
c axis, separating the
ab- and
c-oriented structures. The accuracies of EXAFS for the metrical parameters of neighboring atom shells are ±1–4 in Z, ±15–30% in numbers of atoms in these shells, and ±0.01–0.03 Å in distance [
44,
45,
67]. I.e., these are comparable to differences between different chemical species. However, the precision of EXAFS in related measurements, where the chemical dependence of the phases and amplitudes that are identical is much greater, making it exquisitely sensitive to small changes in the structure with, e.g., temperature or the synthesis method. The precision also extends to the pair distributions and their underlying potentials. Further, with the ability to track the crystallographic origins of the signal, the influence of residual materials is drastically reduced. Finally, similar to inelastic neutron scattering, XAFS probes the dynamic structure. Complete structure determination, including static, amorphous and dynamic structure, therefore, requires the application of multiple methods.
Examples of using multiple methods for evaluation of the oxygen stoichiometry verify the accuracy of the results. The oxygen content and oxidation state of copper in (Cu,Mo)Sr
2(Ce,Y)Cu
2O
7+δ (Mo-1212) have been assessed by both iodometric titration and XANES in multiple studies, giving corroborating results [
58,
67]. Adding TGA to the analytical mix presented a discussion on whether the presence of Mo might influence the accuracy of calculating oxygen stoichiometry, purely based on XANES results for the valence of copper. The combined use of multiple methods allowed the oxygen content to be correlated with changes in the lattice parameters, providing a direct link between diffraction peak positions and oxygen stoichiometry. Dezaneti [
25] combined TGA and titrimetry with elemental composition analysis techniques (electron microprobe and Raman spectroscopy) for evaluation of the oxygen content in YBCO, thus providing a way to connect oxygen content with lattice parameter shifts. The application of multiple, complementary analysis methods can compensate for sample-caused inaccuracies and add reliability to the construction of ‘calibration scales’ with easier-to-access methods such as XRD. The possibility of estimating oxygen content based on phase-transition-related peak shifts is a valuable additional method for diffraction data, alongside Rietveld refinement, and has been widely used [
51,
57].
In summary, the critical issue of the determination of oxygen stoichiometry requires a degree of caution in both directions. Reports in which this parameter was calculated solely from the ratio of the elements in the original reaction mixture, under the presumptions of no decomposition and the incorporation of all of the oxygen, are likely to have exaggerated the oxygen content. However, using such initial, exploratory results as the rationale for discarding the substantial amount of very careful follow-up work is likewise an overreaction. The substantial quantity of accurate results is more than sufficient to validate superconductivity beyond the “dome” in the highly overdoped cuprates.
6. Unique Behaviors of HPO Compounds
The importance of the overdoped, superconducting HPO compounds is the insights into the still-unknown mechanism are derived from their differences with conventional materials. In fact, insofar the implication of their superconductivity over a much wider range is that the factor that suppresses it on the overdoped side of the dome is not present, the superconductivity may be more “pure” and easily studied in the HPO compounds.
Although the cited reports demonstrate that research on HPO cuprates was at the forefront in the period after the initial discovery of HTSC, within ten years it became a minor field followed by the neglect of the general community and subsequent disbelief. The initial reason is likely to have been the incompatibility of HPO methods with producing single crystals, physical vapor and pulsed laser deposition films, and the resulting absence of photoemission, scanning tunneling spectroscopy and other measurements requiring them. However, with the underdoped regime thoroughly explored, interest in the overdoped regime of conventionally prepared materials has recently been increasing. There are now some results that can be used as the starting point for addressing the mechanism by which overdoped HPO cuprates maintain their superconductivity, by comparing their properties with those of the conventional materials.
An immediate difficulty is the disorder that is inherent to all of the compounds but which takes on different modalities. Insofar as the carriers are induced by the non-stoichiometric addition of O or aliovalent substitution, or both, point defects including interstitial O [
47,
78] are unavoidable. Another more unavoidable and critical type of disorder is substitution of the ostensibly stoichiometric cations [
1,
47]. In addition to these single atom defects that can extend by clustering as heterostructures another source of internal stress, is epitaxial mismatch between the different layers, resulting in, e.g., the modulation of the structure in Bi-based cuprates. In general, these defects are found to suppress the superconductivity. However, the effects can be more complicated [
1,
2]. Sr-Ba and Ca-Y, as well as their mixtures, may not only help stabilize certain compounds because their different sizes can facilitate relaxation of the structures, but also since this process can minimize the substitutions or formations of other defects they can enhance and stabilize the superconductivity. Alternatively, a high degree of order of the defects by careful assembly of the structures via thin film methods also alleviates the loss of the superconductivity at high dopant levels [
14]. Its loss on the overdoped side of the dome may, therefore, not only be an electronic effect originating in scattering off of the defects and defect clusters that result in electronic phase separation [
13], but also be a chemical effect in which the distortion of the structure modifies the electronic states and occupancies. Given this behavior, it is not surprising that the three different classes differ in their properties both in their conventional forms and their HPO ones with extreme O stoichiometries.
LCO-O-type (□-0201) compounds differ from YBCO-type (Cu-1212) ones in that their neighboring CuO
2 planes are shifted by (1/2,1/2) in the
ab-plane, relative to each other. In Cu
2M
2CaCu
2O
8 (Cu-2212), this same shift is between neighboring CuO
2 plane blocks. The fusion of the charge reservoir and dielectric layers into a single La(Ba/Sr)O rock salt-type layer is consistent with the usual doping by cation substitution instead of excess O in LCO-O-type compounds. HTSC was originally discovered in LCO that was doped by substituting Ba for a fraction of the La, La
2-xBa
xCuO
4 [
79]. It was quickly learned that the smaller Sr
2+ ion was more effective than Ba
+2. Although, it also exhibits substantial disorder in its local environment that could propagate to the Cu sites [
80]. This process over a range of Ba/Sr stoichiometries gives the dome over the doping range, as previously described, with a maximum T
c up to 40 K in bulk samples and higher in strained of superoxygenated films (
Figure 1b). This original doping mode, with the O stoichiometry at or very close to 4.00, was subsequently augmented by the discovery that annealing with O
2 or electrochemical oxidation gave LCO-O with a higher maximum T
c of ~40–45 K for δ ~ 0.1. These materials also exhibit the onset of superconductivity at
p ~ 0.06, rising to a maximum at ~0.16, and then descending back towards 0 in the overdoped region—although sufficient O content to terminate the superconductivity has never been attained. I.e., the superconductivity in LCO-O also follows the dome over the available doping range. However, La
2CuO
4.13 produced with O
2 at pressures of 1–3 kbar of 600 °C gave a T
c to 30 K, which although lower than the optimum still places it outside of the standard dome [
16]. In addition, very recently thin films of La
2-xCa
xCuO
4 that are Ca-doped up to 0.5 (
p ~ 0.5) showed superconductivity with T
c of 15–20 K [
14]. This was attributed to “managing the disorder” of the substituting Ca atoms.
The uniformity of the effects of cation substitution in LCO thus contrasts with the extremely complicated behavior of the system doped with excess O, by either annealing with O
2 or electrochemically [
81] that which is also related to ordering. If the limited numbers of results from overdoped LCO-O samples are correct, the reduction in T
c indicative of the loss of superconductivity with overdoping is much slower than in the cation-doped materials. This might parallel the Ca substitution in thin films by being highly specific to the ordering that originates in nuances in the preparation. Accordingly, the behavior of LCO-O is quite complicated [
82] because of extensive cooperative effects among the holes [
83], the excess O that occupy interstitial positions between the two LaO layers and the lattice as a whole, including tilting of the CuO
6 oblate octahedra (
Figure 3). Thus, although the Cu-La chains remain parallel with the
c axis, the O
ap atoms can be displaced off those lines via the steric effects of the neighboring interstitial O atoms.
The sensitivity to the O stoichiometry results in the observation of a large number of, e.g., tetragonal, orthorhombic, monoclinic, etc., crystallographic phases [
84,
85], largely differing in the positions of these O atoms and coupled tilting or rotation of the CuO
6 units [
86,
87]. Microscopically, the low O mobility below 200 K freezes the O positions, most likely causing the spinodal decomposition [
88] of the excess O antiferromagnetic and metallic domains in regions with, respectively, lower and higher O stoichiometries. Modulation of the local O stoichiometry that also affects, e.g., the superconducting gap, is a common attribute of all of the cuprates, although the phase separation and signatures in the diffraction pattern are the greatest in the LCO-type compounds. The sizes of the local O stoichiometry domains span the range from a few unit cells up to around one micron [
89,
90]. This behavior would be the origin of the two types of Cu sites [
81] and the 10% differences in T
c resulting from the annealing history. The effects of the O positions and stoichiometry extend even further, with evidence for not only two coexisting superconducting phases [
83] but also a third, non-superconducting one at higher doping levels [
17] In addition, although the O positions are fixed, the structure of the La-O layer that includes both the apical and interstitial excess O atoms varies continuously down to ~100 K [
91].
Conventional superconductors often display multiple crystallographic phases in their normal states that are connected to the soft vibrational modes that also mediate their Cooper pairs. Perovskites and related compounds also possess soft modes involving cooperative rotations and distortions of the CuO
6 square pyramids, which have the same effects on their normal state structures. However, since the homogeneous charge distributions of metals are antithetical to ionic materials, the soft modes in cuprates are coupled to complex charge dynamics. The continued importance of these soft modes in the cuprates is nevertheless demonstrated by, e.g., the structural phase transition at 36 K in LCO [
92], the same temperature as the superconducting transition when doped and the suppression of structural transformations in the superconducting phase in both conventional superconductors and cuprates, resulting from their coupling to the Cooper pairs.
In contrast, HPO Ba
2CuO
3.2 and Sr
2CuO
3.3 display much higher T
cs than any of these conventionally prepared or PVD materials, up to, respectively, 73 K and 95 K. Furthermore, as noted, in Ba
2CuO
3.2 the square planar geometry of the Cu is inverted so that the Cu-O
ap distances are longer than the Cu-O
pl ones [
31]. This also causes an inversion of the 3
dx2−y2 and 3
dz2 energies and a substantial reduction in the two-dimensional character of the electronic states [
31]. The behavior of Sr
2CuO
3+δ in many ways recapitulates that of LCO-O. There are several closely related crystallographic phases that are slightly distorted variants of the base tetragonal structure that coexist unless the synthesis conditions are maintained very precisely [
93]. This behavior implies that the phase is dependent on the precise value of δ and other parameters of the preparation. These host different electronic phases. Beginning with a non-superconducting material, superconducting transitions occur at 48 K (37 K in a bulk crystal), 75 K, possibly 85–89 K and 95 K, with frequent indications of transitions at intermediate temperatures [
76].
The minor differences in structure and procedure imply that aperiodic and dynamic disorder, which do not give signatures in diffraction, are essential factors. As in LCO-O, the excess O atoms can order and the superconductivity is highly sensitive to the type of ordering. This has recently been confirmed by X-ray Absorption Fine Structure (XAFS) measurements that find both of these in radical departure, not only from the behavior of conventional cuprates but also from our conceptual basis of superconductivity. Opposite to all other cuprates, Sr
2CuO
3+δ orients in a magnetic field perpendicular to its
c axis. XAFS shows that this is because, despite the tetragonal symmetry of its Cu-Sr sublattice, its CuO
2 planes are actually CuO
~1.5 [
29,
30,
94] with the O sites filled along one axis and only half-filled on the one that aligns with the field (
Figure 7a). The O
ap sites are, therefore, only partly filled as well, resulting in a very high degree of local disorder in the O positions with a number of long, non-crystallographic Cu-O distances. The implication is that, rather than being a contradiction with the multiple phases, these multiple O sites and Cu-O distances provide the basis for the varying phases by displaying different types of nm-scale ordering. Most surprisingly, a major transformation in the dynamic structure of certain of these O sites accompanies the superconducting transition. This observation is in contradiction with our understanding of Bardeen–Cooper–Schrieffer (BCS) theory, in which the superconductivity occurs as a pairing of electrons of opposite momentum and spins across a fixed Fermi surface.
For YBCO (Cu-1212) and related compounds, the underdoped side has been thoroughly evaluated, defining the generic behavior of cuprates including the competition among the various charge ordered states. Extending this into the overdoped regime of YBCO has been more difficult because the synthetic methods that result in higher O stoichiometries in the other classes of materials are not successful, giving only a minor, incremental addition past optimum doping. Overdoping was, therefore, accomplished by cation substitution in CuBa
2Y
1−xCa
xCu
2O
7-δ [
95], showing that these materials adhere to the dome (
Figure 3b). It is in this cuprate family, however, that a large number of overdoped compounds have been made by substituting other metals for the chain Cu1 atoms in the charge reservoir layer [
27,
28].
A similar approach in Bi
2Sr
2CaCu
2O
8+δ, modifying the Bi:Sr ratio or adding small amounts of La
3+ to minimize Bi-Sr substitution and shift the intrinsic disorder from the Sr-O
ap plane to the Ca sites, raised T
c from the prevalent 89–91 K range in the literature to 96 K. The increase in T
c of TlBa
2Ca
2Cu
3O
9+δ from ~120 K to 133.5 K is also attributed to fine-tuning the synthesis to specifically minimize the disorder at the Ba site [
1]. As with the YBCO-type family, in addition to exhibiting the generic cuprate behavior on its underdoped side, this example of Bi
2Cu
2CaSr
2O
8+δ (Tl-1223) tracks the dome on its overdoped side as well.
The substitution mechanism in YBCO-type compounds is based principally on the substitution of the chain Cu atoms by other cations, mostly other transition metals. The model suggested by this pattern, now corroborated by XAFS, explains both the transformation from the orthorhombic to tetragonal structure and the difficulties with the crystallography. In contrast to the four nearest oxygen neighbors of Cu in its preferred square planar local geometry, the substituting cations support larger numbers. Greater numbers of O atoms in the Cu1 plane support the higher O stoichiometry. This will be especially true if, as found by XAFS, the substitutional ions cluster so that the chemical stress caused by larger or smaller numbers of neighboring O occurs only at the interfaces of these clusters with the Cu-based domains (
Figure 7b). Insofar as at
a- and
b-oriented cluster edges the direction of the continuous Cu-O chains can switch, the overall structure will be tetragonal. The numbers of atoms in the clusters are determined by the balance between this bond stress at the interface and the epitaxial stress from the larger or smaller size relative to the original size with the pure Cu-O chains. For the YSCO-Mo studied by XAFS, the difference between the Cu-O and Mo-O distances indicates Mo clusters just at or below the diffraction limit in size. This type of disorder, involving aperiodic atom displacements and vacancies not randomly distributed but in clusters too small to give diffraction peaks, would produce the substantial discrepancies between the normal atom positions consistent with XAFS and the highly displaced ones in the diffraction. An intriguing side note to this is the finding by XAFS that the local geometry of the Mo (VI) is not its preferred highly distorted octahedron with its terminal double bonds; instead, it is a regular octahedron with almost identical Mo-O bond lengths both within the chain Cu plane and to the O
ap atoms. The stability of the YBCO structure is apparently sufficient to influence the local structure and valence of the substitutional metals.
There are two unique aspects of Cu as the M species of the charge reservoir with its partially occupied perovskite structure instead of rock salt. The one that has already been discussed is the ability to increase the O stoichiometry up to δ = 1 [
25], by inserting it into the spaces between the Cu sites of the Cu-O chains [
28] (
Figure 7b). Although this does transform the structure from orthorhombic to tetragonal, as also occurs with the substitution of the Cu by other metals, it presumably also occurs with less stress than adding O interstitially. The second unusual behavior is that HPO treatment also gives compounds with Cu-O chains as the charge reservoir and three or four CuO
2 planes that are connected by Ca
2+ instead of Y
3+ [
70,
96,
97]. These are, therefore, both cation and O doped, with T
cs as high as ~120 K.
Insofar as the structures of these YBCO variants differ from the parent compound much less than that of Sr
2CuO
3.3, it is expected that the coupling of their dynamic structure to the superconductivity is also much less extreme. As in YBCO [
98,
99,
100], EXAFS measurements of YSCO-Mo also find a two-site Cu-O
ap distribution that is modified across the superconducting transition of the type that we have called an Internal Quantum Tunneling Polaron [
75]. It differs from that in the parent in several respects. The two Cu-O distances are with respect to the planar and not the chain Cu. Instead of partially collapsing at the superconducting transition, it undergoes a slight shift towards the Cu and a change in the relative occupations of the two O sites, so that its two-site distribution is non-degenerate. In addition, at a lower temperature this process repeats, dividing the Cu-O
ap phase diagram into four regions: the normal state above T
c, a fluctuation region within a few K of T
c and two regions in the superconducting state differentiated by their different Cu-distances and O occupancies. The remainder of the structure remains conserved, although a number of other pairs show unusual softening or hardening in the
c direction also at the superconducting transition.
Another unique behavior that is inconsistent with BCS theory is that this compound shows not only a superconducting phase but also a coexisting Fermi liquid [
32]. The single-phase characteristics of the sample, studied as indicated by neutron powder diffraction, rule out the possibility of the existence of a secondary phase responsible for superconductivity. A further argument against the possibility of extrinsic effects is the fairly large superconducting fraction ~30%, as measured by low-field magnetization and magnetic susceptibility. Thus, if the superconductivity was due to a secondary phase, this phase should occupy at least 30% of the sample and, therefore, easily be detected by diffraction. For completeness, one may consider the possibility that the hypothetical secondary phase forms a patchwork of small regions not detected by diffraction. However, since these regions would occupy at least 30% of the total sample volume, the YSCO-Mo phase would also form small regions not seen by diffraction. Finally, such a hypothetical secondary phase should have the same chemical composition as the main YSCO-Mo phase, otherwise phase decomposition would occur to generate other secondary phases that would be detected by diffraction. As a final argument against a scenario of secondary phases, the muon spin relaxation results for the very same YSCO-Mo samples indicate that the homogeneity of these samples is at least on length scales of ∼1 μm, corresponding to a few magnetic penetration depths, λ. Finally, in HPO YBCO the susceptibility data and inferred volume superconducting fractions are almost identical for δ = 0–1 [
25]. This corroborates the various findings in other materials, where the superconductivity is a bulk property of the majority phase.
All the above observations point at a scenario of bulk superconductivity with an electronic phase separation between superconducting and normal regions in a scale of ~100 nm, i.e., larger than the superconducting coherence length, ξ ~ 1–10 nm, but smaller than λ. This result implies that the pairing and condensation mechanisms are highly localized, acting on only a subset of the carriers at the Fermi level. Since it seems unlikely that the carriers are fluctuating between superconductivity and Fermi liquid within a single state—which should rapidly cause them to lose coherence—the alternative is that the two types of carriers each belong to a different electronic state. If so, these would most likely reside in separate components of the heterostructured material.