Laser-Induced Magnetization Dynamics in Si-Doped Yttrium-Iron Garnet Film
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dynamic Conditions:
2.2. Static Conditions
3. Results and Discussion
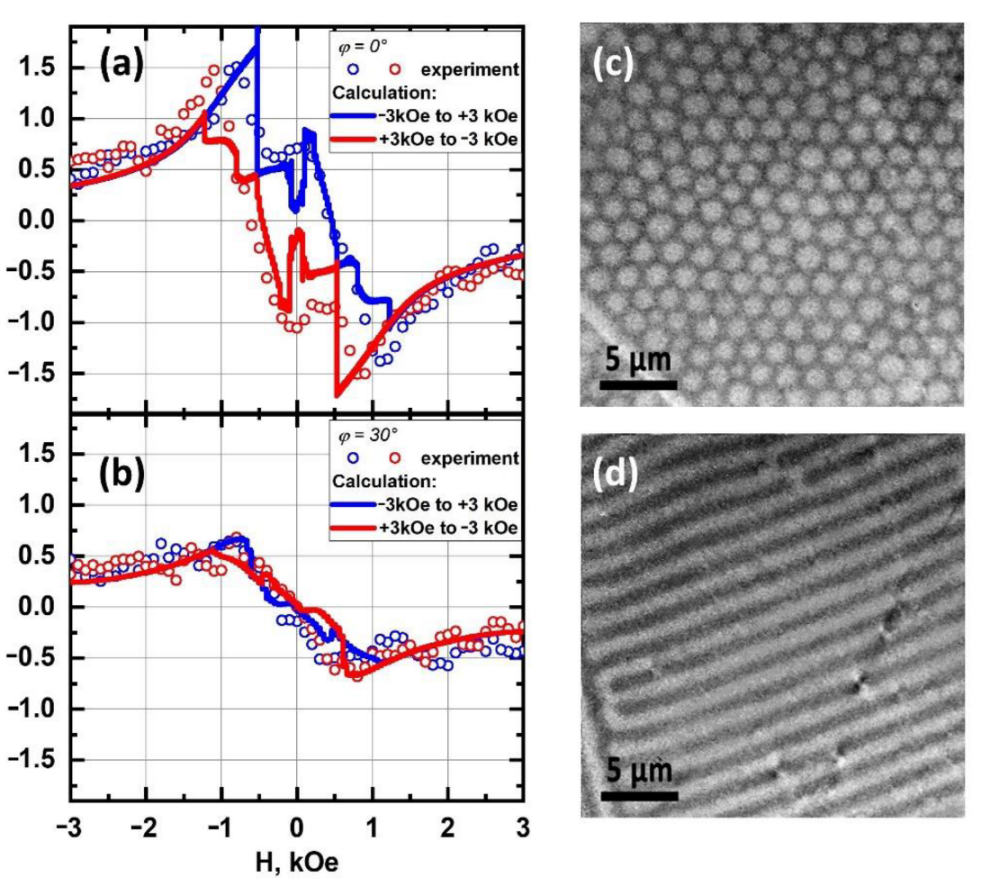
3.1. Static Conditions
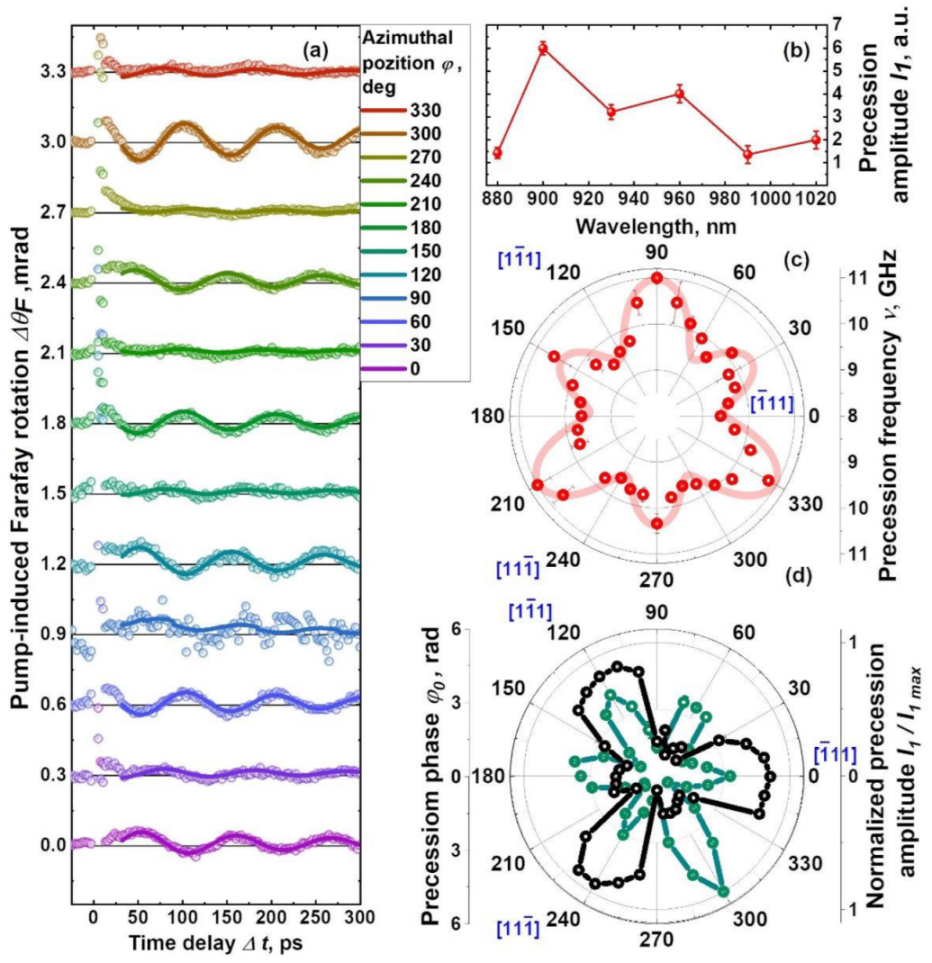
3.2. Dynamic Conditions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beaurepaire, E.; Merle, J.C.; Daunois, A.; Bigot, J.Y. Ultrafast spin dynamics in ferromagnetic nickel. Phys. Rev. Lett. 1996, 76, 4250. [Google Scholar] [CrossRef] [PubMed]
- Kimel, A.V.; Kalashnikova, A.M.; Pogrebna, A.; Zvezdin, A.K. Fundamentals and perspectives of ultrafast photoferroic recording. Phys. Rep. 2020, 852, 1–46. [Google Scholar] [CrossRef]
- Vedmedenko, E.Y.; Kawakami, R.K.; Sheka, D.D.; Gambardella, P.; Kirilyuk, A.; Hirohata, A.; Binek, C.; Chubykalo-Fesenko, O.; Sanvito, S.; Kirby, B.J.; et al. The 2020 magnetism roadmap. J. Phys. D. Appl. Phys. 2020, 53, 453001. [Google Scholar] [CrossRef]
- Kimel, A.V.; Li, M. Writing magnetic memory with ultrashort light pulses. Nat. Rev. Mater. 2019, 4, 189–200. [Google Scholar] [CrossRef]
- HAMR: The Next Leap Forward is Now. Available online: https://blog.seagate.com/craftsman-ship/hamr-next-leap-forward-now/ (accessed on 29 September 2022).
- Akagi, F.; Sakamoto, Y.; Matsushima, N. Effects of Static Magnetic Fields and Temperature Increase on 3D Magnetic Storage in Heated-Dot Magnetic Recording (Revised May 2021). In Proceedings of the 2021 IEEE International Magnetic Conference (INTERMAG), Lyon, France, 26–30 April 2021; pp. 1–5. [Google Scholar]
- Mohan, J.R.; Medwal, R.; Gupta, S.; Gogia, K.; Vas, J.V.; Gupta, R.; Deka, A.; Rawat, R.S.; Subramanian, A.; Fukuma, Y. Nonstoichiometric FePt Nanoclusters for Heated Dot Magnetic Recording Media. ACS Appl. Nano Mater. 2021, 4, 7079–7085. [Google Scholar] [CrossRef]
- Stanciu, C.D.; Hansteen, F.; Kimel, A.V.; Kirilyuk, A.; Tsukamoto, A.; Itoh, A.; Rasing, T. All-Optical Magnetic Recording with Circularly Polarized Light. Phys. Rev. Lett. 2007, 99, 047601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ovcharenko, S.V.; Yakushenkov, P.O.; Ilyin, N.A.; Brekhov, K.A.; Semenova, E.M.; Wu, A.; Mishina, E.D. Ultrafast Magnetization Reversal in DyFeCo Thin Film by Single Femtosecond Laser Pulse. Phys. Met. Metallogr. 2019, 120, 825–830. [Google Scholar] [CrossRef]
- Stupakiewicz, A.; Szerenos, K.; Afanasiev, D.; Kirilyuk, A.; Kimel, A.V. Ultrafast nonthermal photo-magnetic recording in a transparent medium. Nature 2017, 542, 71–74. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mangin, S.; Gottwald, M.; Lambert, C.-H.; Steil, D.; Uhlíř, V.; Pang, L.; Hehn, M.; Alebrand, S.; Cinchetti, M.; Malinowski, G.; et al. Engineered materials for all-optical helicity-dependent magnetic switching. Nat. Mater. 2014, 13, 286–292. [Google Scholar] [CrossRef]
- Zvezdin, A.K.; Kotov, V.A. Magneto-Optics of Thin Films; Nauka: Moscow, Ruassia, 1988. [Google Scholar]
- Hansteen, F.; Kimel, A.; Kirilyuk, A.; Rasing, T. Nonthermal ultrafast optical control of the magnetization in garnet films. Phys. Rev. B 2006, 73, 014421. [Google Scholar] [CrossRef]
- Davies, C.S.; Prabhakara, K.H.; Davydova, M.D.; Zvezdin, K.A.; Shapaeva, T.B.; Wang, S.; Zvezdin, A.K.; Kirilyuk, A.; Rasing, T.; Kimel, A.V. Anomalously Damped Heat-Assisted Route for Precessional Magnetization Reversal in an Iron Garnet. Phys. Rev. Lett. 2019, 122, 027202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stupakiewicz, A.; Davies, C.S.; Szerenos, K.; Afanasiev, D.; Rabinovich, K.S.; Boris, A.V.; Caviglia, A.; Kimel, A.V.; Kirilyuk, A. Ultrafast phononic switching of magnetization. Nat. Phys. 2021, 17, 489–492. [Google Scholar] [CrossRef]
- Stupakiewicz, A.; Szerenos, K.; Davydova, M.D.; Zvezdin, K.A.; Zvezdin, A.K.; Kirilyuk, A.; Kimel, A.V. Selection rules for all-optical magnetic recording in iron garnet. Nat. Commun. 2019, 10, 612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Szerenos, K.; Kimel, A.V.; Maziewski, A.; Kirilyuk, A.; Stupakiewicz, A. Fundamental Limits on the Repetition Rate of Photomagnetic Recording. Phys. Rev. Appl. 2019, 12, 044057. [Google Scholar] [CrossRef]
- Wood, D.L.; Remeika, J.P. Effect of Impurities on the Optical Properties of Yttrium Iron Garnet. J. Appl. Phys. 1967, 38, 1038–1045. [Google Scholar] [CrossRef]
- McGlashan-Powell, M.; Wolfe, R.; Dillon, J.F.; Fratello, V.J. Magneto-optic waveguide hysteresis loops of “planar” magnetic garnet films. J. Appl. Phys. 1989, 66, 3342–3347. [Google Scholar] [CrossRef]
- Donahue, M.J.; Porter, D.G. OOMMF User’s Guide, Version 1.0; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1999. [Google Scholar]
- Newnham, R. Magnetic garnets. Mater. Res. Bull. 1981, 16, 1473–1474. [Google Scholar] [CrossRef]
- Ovcharenko, S.V.; Gaponov, M.S.; Ilyin, N.A.; Logunov, M.V.; Wu, A.; Mishina, E.D. Laser-induced spin dynamics in the iron-yttrium garnet film doped with Si ions. Russ. Technol. J. 2020, 8, 58–66. [Google Scholar] [CrossRef]
- Dillon, J.F.; Gyorgy, E.M.; Remeika, J.P. Photoinduced Uniaxial Magnetic Anisotropy and Optical Dichroism in Silicon-Doped Yttrium Iron Garnet [YIG(Si)]. J. Appl. Phys. 1970, 41, 1211–1217. [Google Scholar] [CrossRef]
- Vashkovskii, A.V.; Lokk, É.G.; Shcheglov, V.I. Influence of induced uniaxial anisotropy on the domain structure and phase transitions of yttrium-iron garnet films. Phys. Solid State 1999, 41, 1868–1874. [Google Scholar] [CrossRef]
- Vonsovskii, S.V. Ferromagnetic Resonance; Elsevier, Pergamon Press: Oxford, UK, 1966; ISBN 9780080110271. Available online: https://www.elsevier.com/books/ferromagnetic-resonance/vonsovskii/978-0-08-011027-1 (accessed on 29 September 2022).
- Makino, H.; Hidaka, Y. Determination of magnetic anisotropy constants for bubble garnet epitaxial films using field orientation dependence in ferromagnetic resonances. Mater. Res. Bull. 1981, 16, 957–966. [Google Scholar] [CrossRef]
- Ma, T.P.; Zhang, S.F.; Yang, Y.; Chen, Z.H.; Zhao, H.B.; Wu, Y.Z. Distinguishing the laser-induced spin precession excitation mechanism in Fe/MgO(001) through field orientation dependent measurements. J. Appl. Phys. 2015, 117, 013903. [Google Scholar] [CrossRef]
- Khokhlov, N.E.; Gerevenkov, P.I.; Shelukhin, L.A.; Azovtsev, A.V.; Pertsev, N.A.; Wang, M.; Rushforth, A.W.; Scherbakov, A.V.; Kalashnikova, A.M. Optical Excitation of Propagating Magnetostatic Waves in an Epitaxial Galfenol Film by Ultrafast Magnetic Anisotropy Change. Phys. Rev. Appl. 2019, 12, 044044. [Google Scholar] [CrossRef] [Green Version]
- Mizukami, S.; Sajitha, E.P.; Watanabe, D.; Wu, F.; Miyazaki, T.; Naganuma, H.; Oogane, M.; Ando, Y. Gilbert damping in perpendicularly magnetized Pt/Co/Pt films investigated by all-optical pump-probe technique. Appl. Phys. Lett. 2010, 96, 152502. [Google Scholar] [CrossRef]
- Widom, A.; Vittoria, C.; Yoon, S.D. Gilbert ferromagnetic damping theory and the fluctuation-dissipation theorem. J. Appl. Phys. 2010, 108, 073924. [Google Scholar] [CrossRef]
- Ovcharenko, S.; Gaponov, M.; Klimov, A.; Tiercelin, N.; Pernod, P.; Mishina, E.; Sigov, A.; Preobrazhensky, V. Ultrafast manipulation of magnetic anisotropy in a uniaxial intermetallic heterostructure TbCo2 /FeCo. J. Phys. D Appl. Phys. 2022, 55, 175001. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaponov, M.; Ovcharenko, S.; Ilyin, N.; Mishina, E. Laser-Induced Magnetization Dynamics in Si-Doped Yttrium-Iron Garnet Film. Condens. Matter 2022, 7, 55. https://doi.org/10.3390/condmat7040055
Gaponov M, Ovcharenko S, Ilyin N, Mishina E. Laser-Induced Magnetization Dynamics in Si-Doped Yttrium-Iron Garnet Film. Condensed Matter. 2022; 7(4):55. https://doi.org/10.3390/condmat7040055
Chicago/Turabian StyleGaponov, Mikhail, Sergey Ovcharenko, Nikita Ilyin, and Elena Mishina. 2022. "Laser-Induced Magnetization Dynamics in Si-Doped Yttrium-Iron Garnet Film" Condensed Matter 7, no. 4: 55. https://doi.org/10.3390/condmat7040055
APA StyleGaponov, M., Ovcharenko, S., Ilyin, N., & Mishina, E. (2022). Laser-Induced Magnetization Dynamics in Si-Doped Yttrium-Iron Garnet Film. Condensed Matter, 7(4), 55. https://doi.org/10.3390/condmat7040055





