A Method for the Dynamics of Vortices in a Bose-Einstein Condensate: Analytical Equations of the Trajectories of Phase Singularities
Abstract
:1. Introduction
2. Model and System
3. Some Examples in the Homogenous System
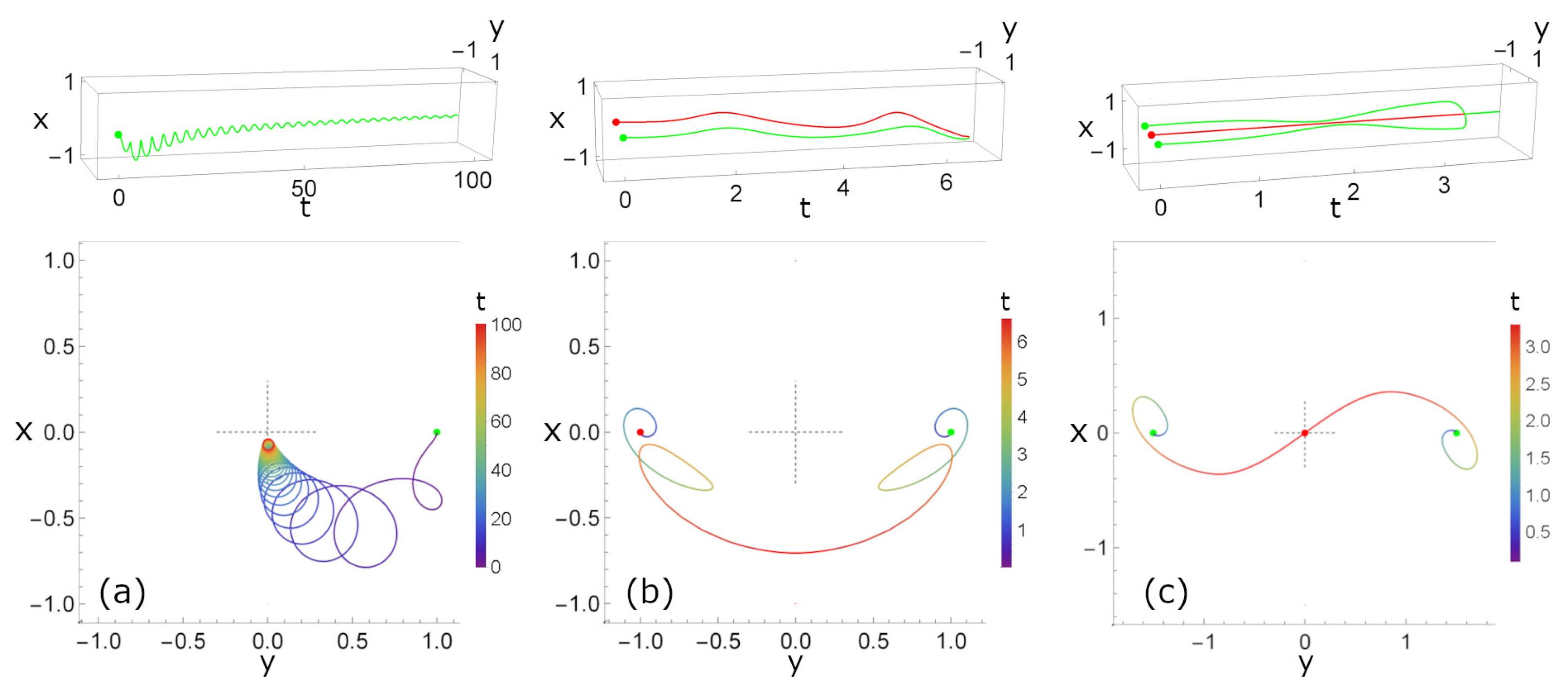
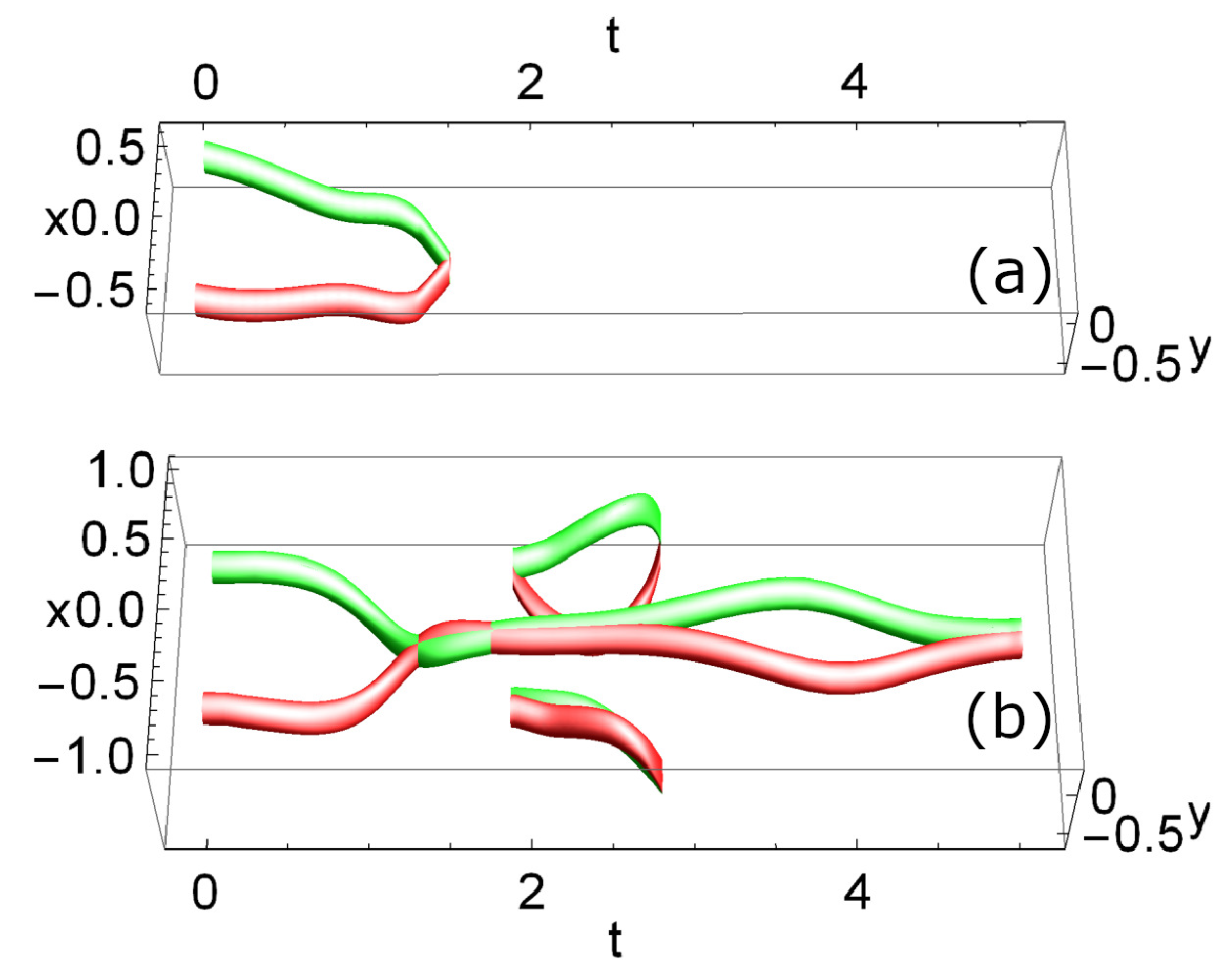
3.1. Two Initial Singularities, One Positive and One Negative
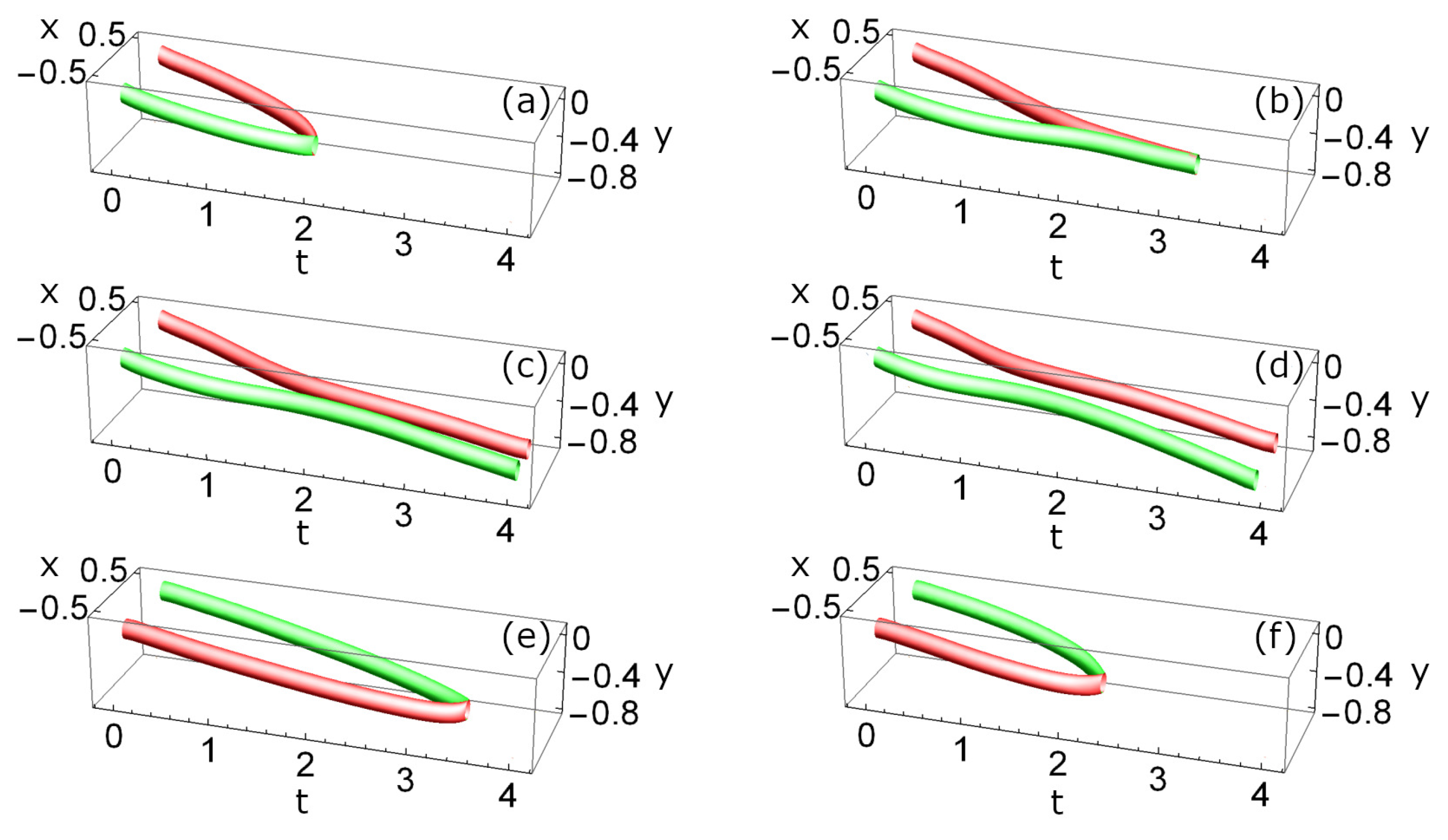
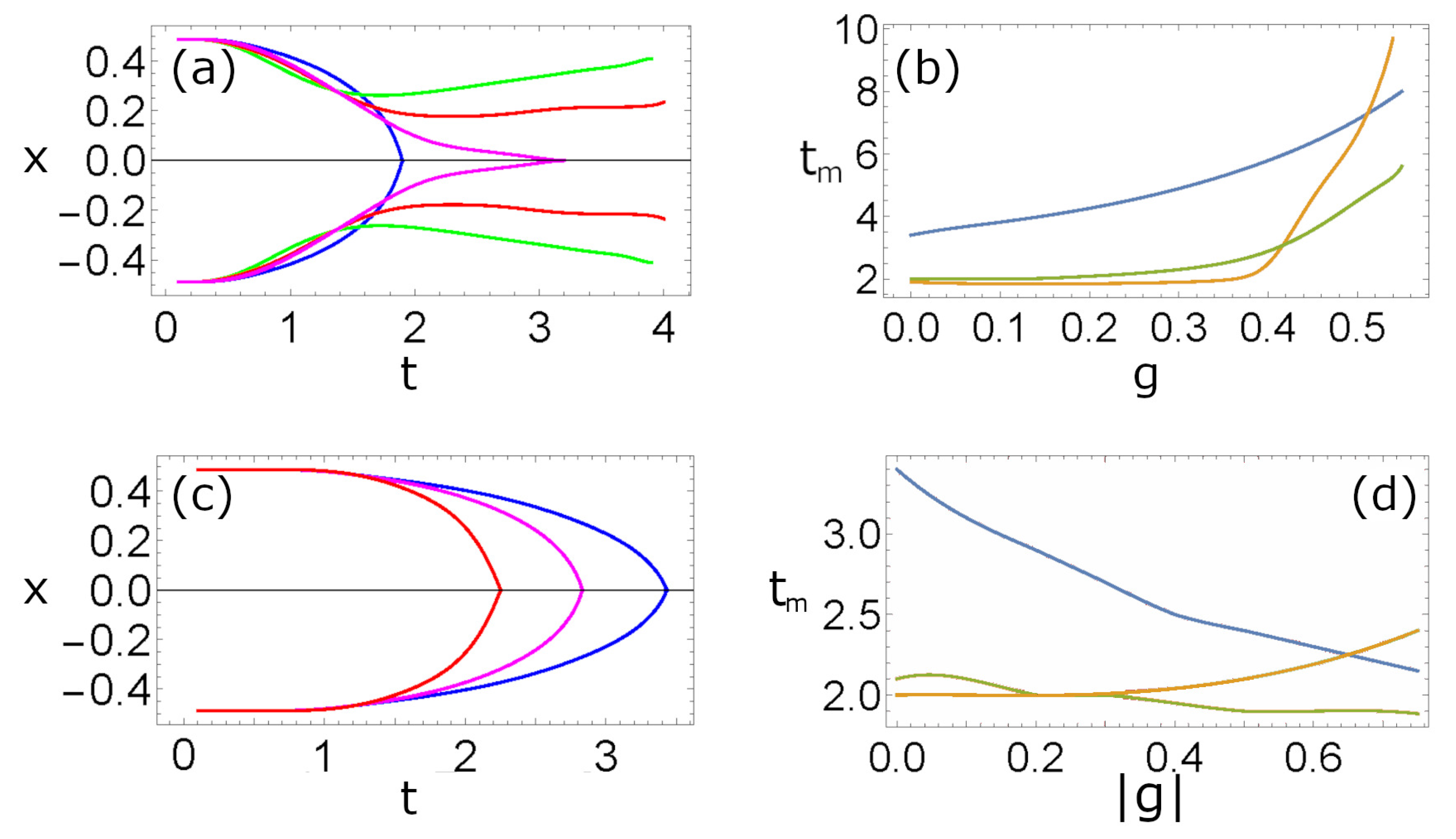
3.2. Two Positive Singularities and One Negative
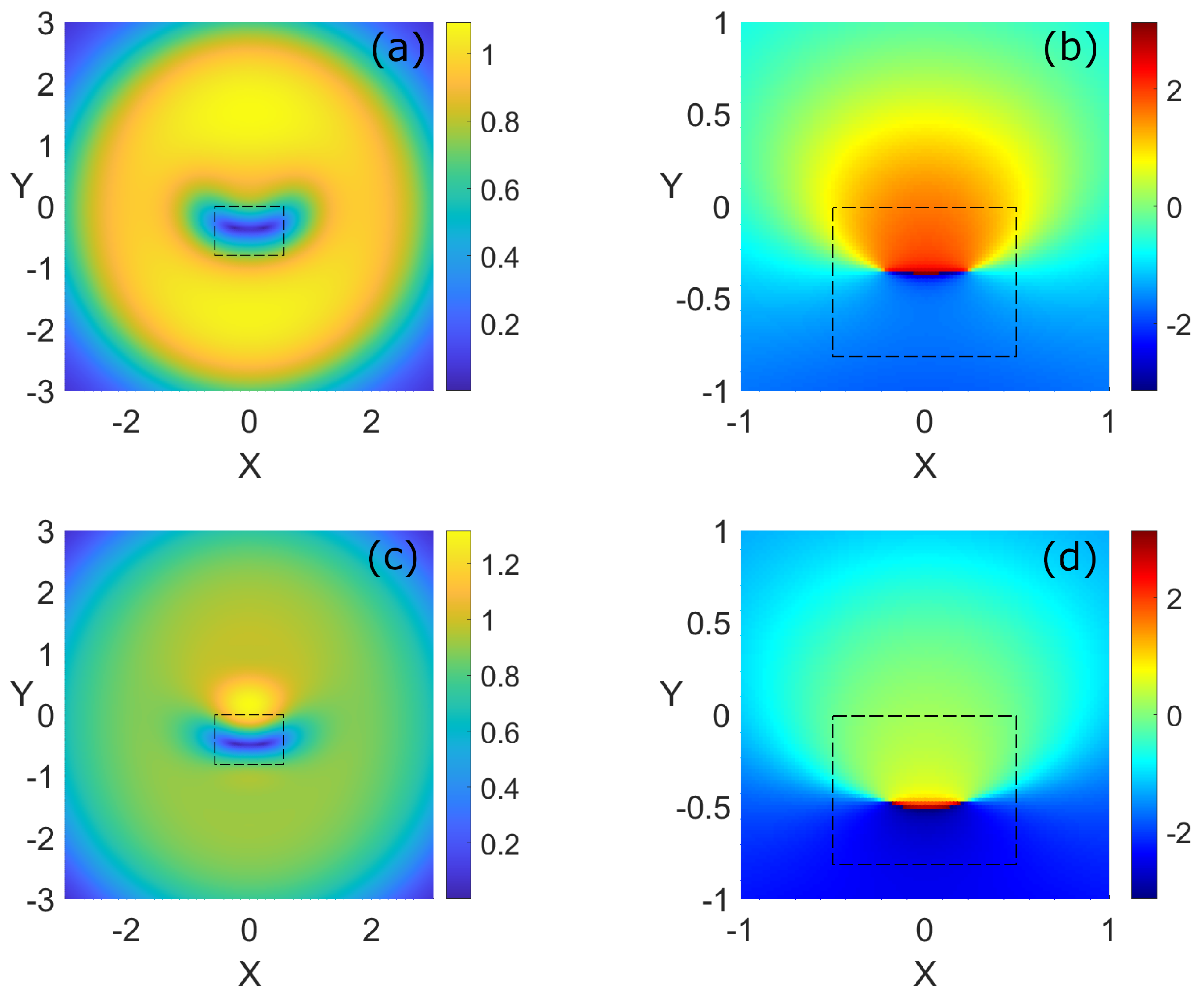
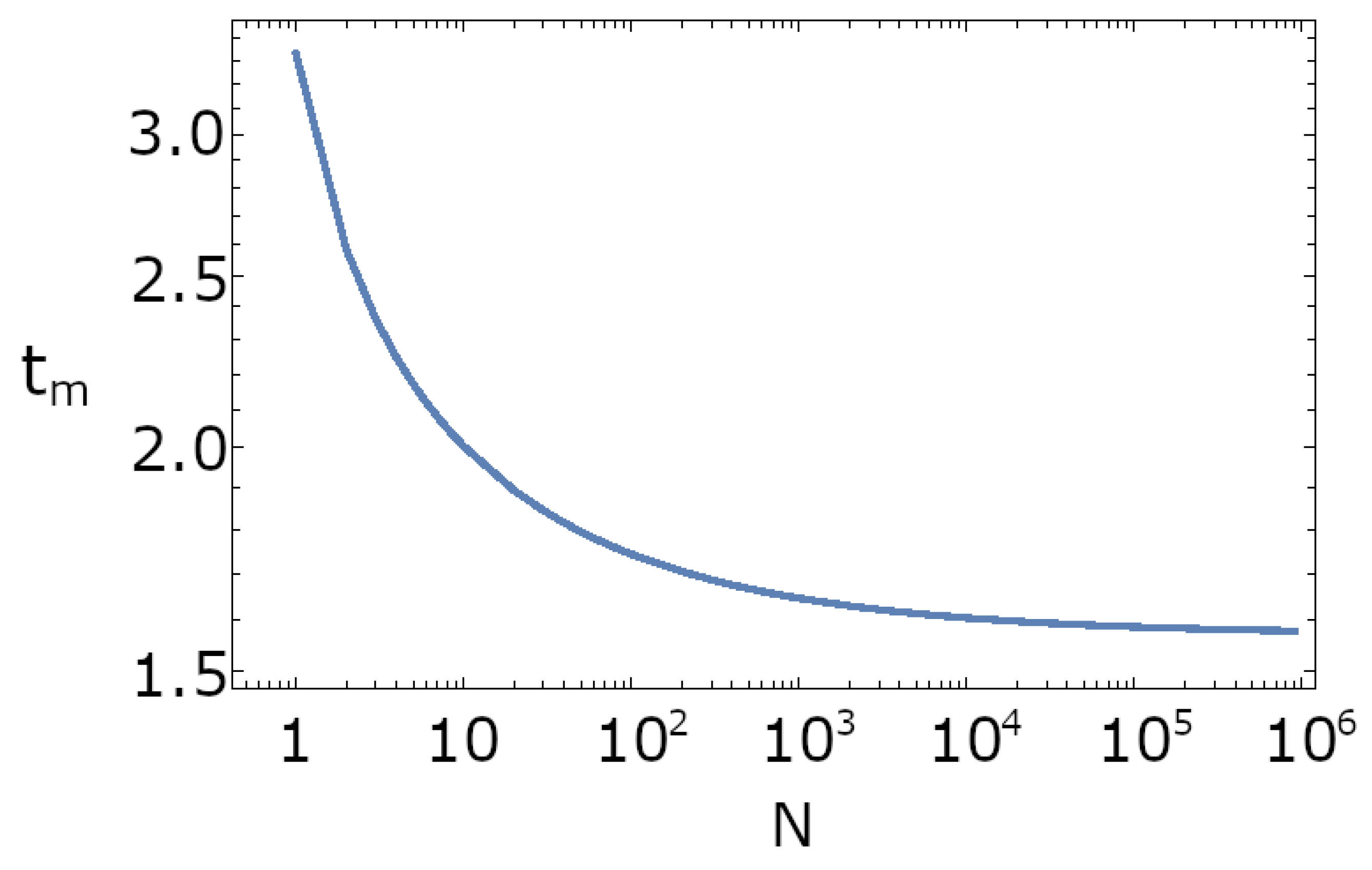
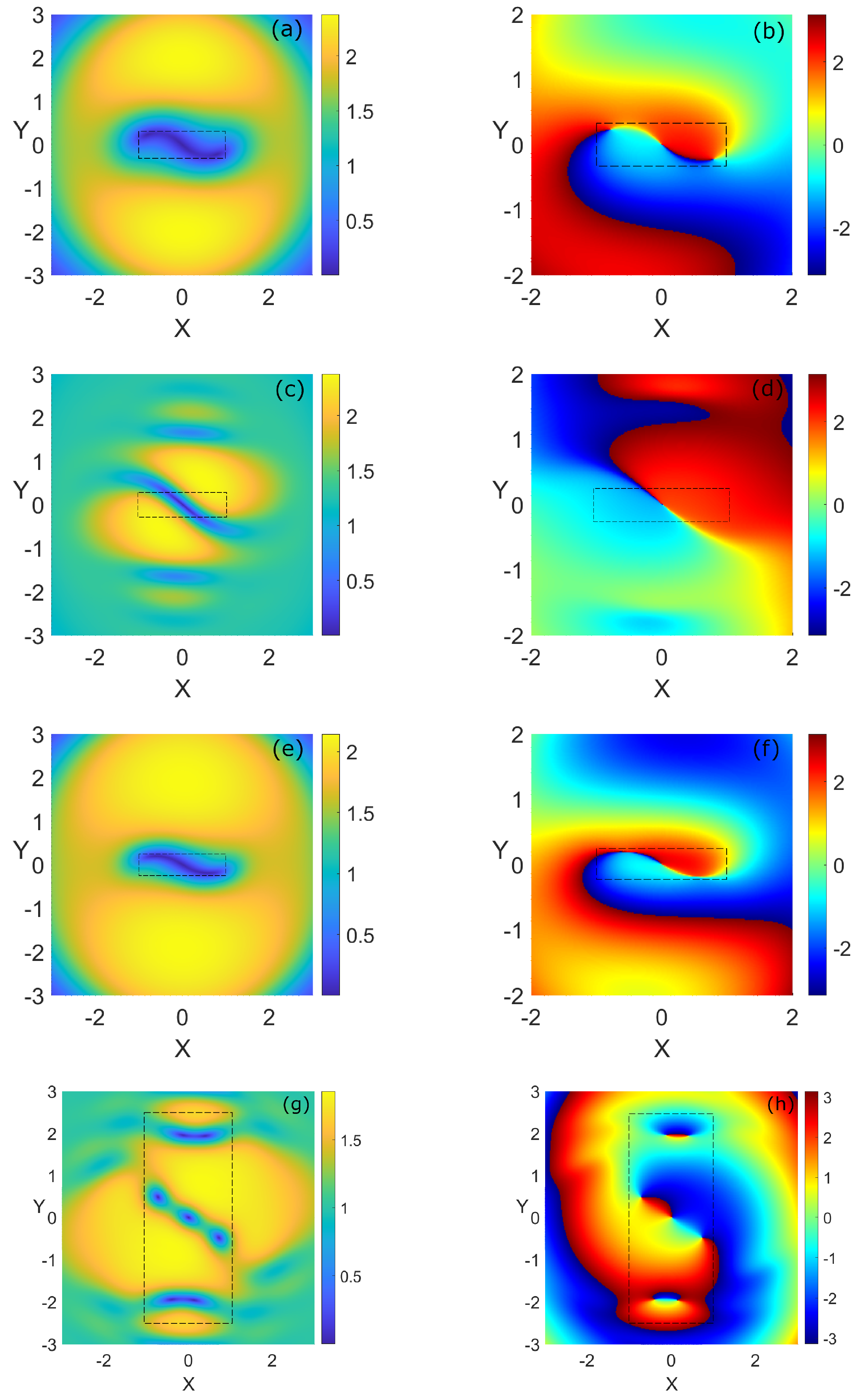
4. Some Examples in the Parabolically Trapped System
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Matthews, M.R.; Anderson, B.P.; Haljan, P.C.; Hall, D.S.; Wieman, C.E.; Cornell, E.A. Vortices in a bose-einstein condensate. Phys. Rev. Lett. 1999, 83, 2498–2501. [Google Scholar] [CrossRef] [Green Version]
- Abo-Shaeer, J.R.; Raman, C.; Vogels, J.M.; Ketterle, W. Observation of vortex lattices in bose-einstein condensates. Science 2001, 292, 476–479. [Google Scholar] [CrossRef] [Green Version]
- Madison, K.W.; Chevy, F.; Wohlleben, W.; Dalibard, J. Vortex formation in a stirred bose-einstein condensate. Phys. Rev. Lett. 2000, 84, 806. [Google Scholar] [CrossRef] [Green Version]
- Raman, C.; Abo-Shaeer, J.R.; Vogels, J.M.; Xu, K.; Ketterle, W. Vortex nucleation in a stirred bose-einstein condensate. Phys. Rev. Lett. 2001, 87, 210402. [Google Scholar] [CrossRef] [Green Version]
- Gauthier, G.; Reeves, M.T.; Yu, X.; Bradley, A.S.; Baker, M.A.; Bell, T.A.; Rubinsztein-Dunlop, H.; Davis, M.J.; Neely, T.W. Giant vortex clusters in a two-dimensional quantum fluid. Science 2019, 364, 1264–1267. [Google Scholar] [CrossRef] [Green Version]
- Leanhardt, A.E.; Görlitz, A.; Chikkatur, A.P.; Kielpinski, D.; Shin, Y.; Pritchard, D.E.; Ketterle, W. Imprinting vortices in a bose-einstein condensate using topological phases. Phys. Rev. Lett. 2002, 89, 190403. [Google Scholar] [CrossRef] [Green Version]
- Shin, Y.; Saba, M.; Vengalattore, M.; Pasquini, T.A.; Sanner, C.; Leanhardt, A.E.; Prentiss, M.; Pritchard, D.E.; Ketterle, W. Dynamical instability of a doubly quantized vortex in a bose-einstein condensate. Phys. Rev. Lett. 2004, 93, 160406. [Google Scholar] [CrossRef] [Green Version]
- Kwon, W.J.; Kim, J.H.; Seo, S.W.; Shin, Y. Observation of von kármán vortex street in an atomic superfluid gas. Phys. Rev. Lett. 2016, 117, 245301. [Google Scholar] [CrossRef] [Green Version]
- Scherer, D.R.; Weiler, C.N.; Neely, T.W.; Anderson, B.P. Vortex formation by merging of multiple trapped bose-einstein condensates. Phys. Rev. Lett. 2007, 98, 110402. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.-R.; Lin, K.-Y.; Chen, P.-K.; Chiu, N.-C.; Wang, J.-B.; Chen, C.-A.; Huang, P.; Yip, S.-K.; Kawaguchi, Y.; Lin, Y.-J. Spin–orbital-angular-momentum coupled bose-einstein condensates. Phys. Rev. Lett. 2018, 121, 113204. [Google Scholar] [CrossRef]
- Zhang, D.; Gao, T.; Zou, P.; Kong, L.; Li, R.; Shen, X.; Chen, X.-L.; Peng, S.-G.; Zhan, M.; Pu, H.; et al. Ground-state phase diagram of a spin-orbital-angular-momentum coupled bose-einstein condensate. Phys. Rev. Lett. 2019, 122, 110402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Donadello, S.; Serafini, S.; Tylutki, M.; Pitaevskii, L.P.; Dalfovo, F.; Lamporesi, G.; Ferrari, G. Observation of solitonic vortices in bose-einstein condensates. Phys. Rev. Lett. 2014, 113, 065302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weiler, C.N.; Neely, T.W.; Scherer, D.R.; Bradley, A.S.; Davis, M.J.; Anderson, B.P. Spontaneous vortices in the formation of bose–einstein condensates. Nature 2008, 455, 948–951. [Google Scholar] [CrossRef] [Green Version]
- Dum, R.; Cirac, J.I.; Lewenstein, M.; Zoller, P. Creation of dark solitons and vortices in bose-einstein condensates. Phys. Rev. Lett. 1998, 80, 2972–2975. [Google Scholar] [CrossRef] [Green Version]
- Castin, Y.; Dum, R. Bose-einstein condensates with vortices in rotating traps. Eur. Phys. J.-At. Mol. Opt. Plasma Phys. 1999, 7, 399–412. [Google Scholar] [CrossRef] [Green Version]
- García-Ripoll, J.J.; Molina-Terriza, G.; Pérez-García, V.M.; Torner, L. Structural instability of vortices in bose-einstein condensates. Phys. Rev. Lett. 2001, 87, 140403. [Google Scholar] [CrossRef] [Green Version]
- Ferrando, A.; Zacarés, M.; Garcia-March, M.-A. Vorticity cutoff in nonlinear photonic crystals. Phys. Rev. Lett. 2005, 95, 043901. [Google Scholar] [CrossRef] [Green Version]
- Ferrando, A.; Zacarés, M.; García-March, M.; Monsoriu, J.A.; de Córdoba, P.F. Vortex transmutation. Phys. Rev. Lett. 2005, 95, 123901. [Google Scholar] [CrossRef] [Green Version]
- Ferrando, A. Discrete-symmetry vortices as angular Bloch modes. Phys. Rev. 2005, 72, 036612. [Google Scholar] [CrossRef] [Green Version]
- VPérez-García, M.; García-March, M.A.; Ferrando, A. Symmetry-assisted vorticity control in bose-einstein condensates. Phys. Rev. 2007, 75, 033618. [Google Scholar] [CrossRef]
- Kanamoto, R.; Carr, L.D.; Ueda, M. Topological winding and unwinding in metastable bose-einstein condensates. Phys. Rev. Lett. 2008, 100, 060401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- García-March, M.; Ferrando, A.; Zacarés, M.; Vijande, J.; Carr, L.D. Angular pseudomomentum theory for the generalized nonlinear Schrödinger equation in discrete rotational symmetry media. Phys. D Nonlinear Phenom. 2009, 238, 1432. [Google Scholar] [CrossRef] [Green Version]
- García-March, M.A.; Dounas-Frazer, D.R.; Carr, L.D. Macroscopic superposition of ultracold atoms with orbital degrees of freedom. Phys. Rev. A 2011, 83, 043612. [Google Scholar] [CrossRef] [Green Version]
- Desyatnikov, A.S.; Buccoliero, D.; Dennis, M.R.; Kivshar, Y.S. Spontaneous knotting of self-trapped waves. Sci. Rep. 2012, 2, 771. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Proment, D.; Onorato, M.; Barenghi, C.F. Vortex knots in a bose-einstein condensate. Phys. Rev. E 2012, 85, 036306. [Google Scholar] [CrossRef] [Green Version]
- Ferrando, A.; García-March, M. Theory for the control of dark rays by means of discrete symmetry diffractive elements. J. Opt. 2013, 15, 044014. [Google Scholar] [CrossRef]
- White, A.C.; Anderson, B.P.; Bagnato, V.S. Vortices and turbulence in trapped atomic condensates. Proc. Natl. Acad. Sci. USA 2014, 111 (Suppl. S1), 4719–4726. [Google Scholar] [CrossRef] [Green Version]
- Taylor, A.J.; Dennis, M.R. Vortex knots in tangled quantum eigenfunctions. Nat. Commun. 2016, 7, 12346. [Google Scholar] [CrossRef] [Green Version]
- Ticknor, C.; Ruban, V.P.; Kevrekidis, P.G. Quasistable quantum vortex knots and links in anisotropic harmonically trapped bose-einstein condensates. Phys. Rev. A 2019, 99, 063604. [Google Scholar] [CrossRef] [Green Version]
- Kevrekidis, P.; Carretero-González, R.; Frantzeskakis, D.; Kevrekidis, I. Vortices in bose–einstein condensates: Some recent developments. Mod. Phys. Lett. B 2004, 18, 1481–1505. [Google Scholar] [CrossRef]
- Aftalion, A. Vortices in Bose-Einstein Condensates; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; Volume 67. [Google Scholar]
- Malomed, B.A. Vortex solitons: Old results and new perspectives. Phys. D Nonlinear Phenom. 2019, 399, 108–137. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Tahvildar-Zadeh, A.S. Formation of singularities in relativistic fluid dynamics and in spherically symmetric plasma dynamics. Contemp. Math 1999, 238, 151. [Google Scholar]
- Moffatt, H. Singularities in fluid mechanics. Phys. Rev. Fluids 2019, 4, 110502. [Google Scholar] [CrossRef] [Green Version]
- Coy, L.; Nash, E.R.; Newman, P.A. Meteorology of the polar vortex: Spring 1997. Geophys. Res. Lett. 1997, 24, 2693. [Google Scholar] [CrossRef]
- Desyatnikov, A.; Kivshar, Y.; Torner, L. Optical vortices and vortex solitons. Prog. Opt. 2005, 47, 291–391. [Google Scholar]
- Soskin, M.; Vasnetsov, M. Singular optics. Prog. Opt. 2001, 42, 219. [Google Scholar]
- Soskin, M.; Boriskina, S.V.; Chong, Y.; Dennis, M.R.; Desyatnikov, A. Singular optics and topological photonics. J. Opt. 2016, 19, 010401. [Google Scholar] [CrossRef]
- Dennis, M.; O’Holleran, K.; Padgett, M. Chapter 5 Singular Optics: Optical Vortices and Polarization Singularities; Elsevier: Amsterdam, The Netherlands, 2009; Volume 53. [Google Scholar]
- Ferrando, A. Discrete-gauss states and the generation of focusing dark beams. Phys. Rev. A 2014, 90, 023844. [Google Scholar] [CrossRef] [Green Version]
- Ferrando, A.; García-March, M. Analytical solution for multi-singular vortex Gaussian beams: The mathematical theory of scattering modes. J. Opt. 2016, 18, 064006. [Google Scholar] [CrossRef] [Green Version]
- Longhi, S. Modulational instability and space time dynamics in nonlinear parabolic-index optical fibers. Opt. Lett. 2003, 28, 2363–2365. [Google Scholar] [CrossRef]
- Richardson, K.; Kang, M.; Sisken, L.; Yadav, A.; Blanco, C.; Antia, M.; Novak, S.; Smith, C.; Buff, A.; Lepicard, A.; et al. Advances in infrared grin: A review of novel materials towards components and devices. Adv. Opt. Def. Appl. LWIR III 2018, 10627, 79–95. [Google Scholar]
- Jackson, B.; McCann, J.F.; Adams, C.S. Vortex line and ring dynamics in trapped bose-einstein condensates. Phys. Rev. A 1999, 61, 013604. [Google Scholar] [CrossRef] [Green Version]
- Lundh, E.; Ao, P. Hydrodynamic approach to vortex lifetimes in trapped bose condensates. Phys. Rev. A 2000, 61, 063612. [Google Scholar] [CrossRef] [Green Version]
- Svidzinsky, A.A.; Fetter, A.L. Stability of a vortex in a trapped bose-einstein condensate. Phys. Rev. Lett. 2000, 84, 5919–5923. [Google Scholar] [CrossRef]
- Svidzinsky, A.A.; Fetter, A.L. Dynamics of a vortex in a trapped bose-einstein condensate. Phys. Rev. A 2000, 62, 063617. [Google Scholar] [CrossRef] [Green Version]
- Fetter, A.L.; Kim, J.-K. Vortex precession in a rotating nonaxisymmetric trapped bose-einstein condensate. J. Low Temp. Phys. 2001, 125, 239–248. [Google Scholar] [CrossRef]
- McGee, S.A.; Holland, M.J. Rotational dynamics of vortices in confined bose-einstein condensates. Phys. Rev. A 2001, 63, 043608. [Google Scholar] [CrossRef] [Green Version]
- Anglin, J.R. Vortices near surfaces of bose-einstein condensates. Phys. Rev. A 2002, 65, 063611. [Google Scholar] [CrossRef] [Green Version]
- Sheehy, D.E.; Radzihovsky, L. Vortices in spatially inhomogeneous superfluids. Phys. Rev. A 2004, 70, 063620. [Google Scholar] [CrossRef] [Green Version]
- Khawaja, U.A. Vortex dynamics near the surface of a bose-einstein condensate. Phys. Rev. A 2005, 71, 063611. [Google Scholar] [CrossRef] [Green Version]
- Mason, P.; Berloff, N.G.; Fetter, A.L. Motion of a vortex line near the boundary of a semi-infinite uniform condensate. Phys. Rev. A 2006, 74, 043611. [Google Scholar] [CrossRef] [Green Version]
- Nilsen, H.M.; Baym, G.; Pethick, C.J. Velocity of vortices in inhomogeneous bose–einstein condensates. Proc. Natl. Acad. Sci. USA 2006, 103, 7978–7981. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jezek, D.M.; Cataldo, H.M. Vortex velocity field in inhomogeneous media: A numerical study in bose-einstein condensates. Phys. Rev. A 2008, 77, 043602. [Google Scholar] [CrossRef] [Green Version]
- Mason, P.; Berloff, N.G. Motion of quantum vortices on inhomogeneous backgrounds. Phys. Rev. A 2008, 77, 032107. [Google Scholar] [CrossRef]
- Koens, L.; Martin, A.M. Perturbative behavior of a vortex in a trapped bose-einstein condensate. Phys. Rev. A 2012, 86, 013605. [Google Scholar] [CrossRef] [Green Version]
- Dos Santos, F.E.A. Hydrodynamics of vortices in bose-einstein condensates: A defect-gauge field approach. Phys. Rev. A 2016, 94, 063633. [Google Scholar] [CrossRef] [Green Version]
- Biasi, A.; Bizoń, P.; Craps, B.; Evnin, O. Exact lowest-landau-level solutions for vortex precession in bose-einstein condensates. Phys. Rev. A 2017, 96, 053615. [Google Scholar] [CrossRef] [Green Version]
- Esposito, A.; Krichevsky, R.; Nicolis, A. Vortex precession in trapped superfluids from effective field theory. Phys. Rev. A 2017, 96, 033615. [Google Scholar] [CrossRef] [Green Version]
- Anderson, B.P.; Haljan, P.C.; Wieman, C.E.; Cornell, E.A. Vortex precession in bose-einstein condensates: Observations with filled and empty cores. Phys. Rev. Lett. 2000, 85, 2857–2860. [Google Scholar] [CrossRef] [Green Version]
- Bretin, V.; Rosenbusch, P.; Chevy, F.; Shlyapnikov, G.V.; Dalibard, J. Quadrupole oscillation of a single-vortex bose-einstein condensate: Evidence for kelvin modes. Phys. Rev. Lett. 2003, 90, 100403. [Google Scholar] [CrossRef] [Green Version]
- Hodby, E.; Hopkins, S.A.; Hechenblaikner, G.; Smith, N.L.; Foot, C.J. Experimental observation of a superfluid gyroscope in a dilute bose-einstein condensate. Phys. Rev. Lett. 2003, 91, 090403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Freilich, D.V.; Bianchi, D.M.; Kaufman, A.M.; Langin, T.K.; Hall, D.S. Real-time dynamics of single vortex lines and vortex dipoles in a bose-einstein condensate. Science 2010, 329, 1182–1185. [Google Scholar] [CrossRef] [PubMed]
- Serafini, S.; Barbiero, M.; Debortoli, M.; Donadello, S.; Larcher, F.; Dalfovo, F.; Lamporesi, G.; Ferrari, G. Dynamics and interaction of vortex lines in an elongated bose-einstein condensate. Phys. Rev. Lett. 2015, 115, 170402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mateo, A.M.; Delgado, V. Dynamical evolution of a doubly quantized vortex imprinted in a bose-einstein condensate. Phys. Rev. Lett. 2006, 97, 180409. [Google Scholar] [CrossRef] [PubMed]
- Foster, C.J.; Blakie, P.B.; Davis, M.J. Vortex pairing in two-dimensional bose gases. Phys. Rev. A 2010, 81, 023623. [Google Scholar] [CrossRef] [Green Version]
- Seman, J.A.; Henn, E.A.L.; Haque, M.; Shiozaki, R.F.; Ramos, E.R.F.; Caracanhas, M.; Castilho, P.; Branco, C.C.; Tavares, P.E.S.; Poveda-Cuevas, F.J.; et al. Three-vortex configurations in trapped bose-einstein condensates. Phys. Rev. A 2010, 82, 033616. [Google Scholar] [CrossRef] [Green Version]
- Middelkamp, S.; Torres, P.J.; Kevrekidis, P.G.; Frantzeskakis, D.J.; Carretero-González, R.; Schmelcher, P.; Freilich, D.V.; Hall, D.S. Guiding-center dynamics of vortex dipoles in bose-einstein condensates. Phys. Rev. A 2011, 84, 011605. [Google Scholar] [CrossRef] [Green Version]
- Navarro, R.; Carretero-González, R.; Torres, P.J.; Kevrekidis, P.G.; Frantzeskakis, D.J.; Ray, M.W.; Altuntaş, E.; Hall, D.S. Dynamics of a few corotating vortices in bose-einstein condensates. Phys. Rev. Lett. 2013, 110, 225301. [Google Scholar] [CrossRef] [Green Version]
- Groszek, A.J.; Paganin, D.M.; Helmerson, K.; Simula, T.P. Motion of vortices in inhomogeneous bose-einstein condensates. Phys. Rev. A 2018, 97, 023617. [Google Scholar] [CrossRef] [Green Version]
- Bradley, A.S.; Anderson, B.P. Energy spectra of vortex distributions in two-dimensional quantum turbulence. Phys. Rev. X 2012, 2, 041001. [Google Scholar] [CrossRef] [Green Version]
- Kwon, W.J.; Moon, G.; Choi, J.-Y.; Seo, S.W.; Shin, Y.-I. Relaxation of superfluid turbulence in highly oblate bose-einstein condensates. Phys. Rev. A 2014, 90, 063627. [Google Scholar] [CrossRef] [Green Version]
- Mateo, A.M.; Brand, J. Chladni solitons and the onset of the snaking instability for dark solitons in confined superfluids. Phys. Rev. Lett. 2014, 113, 255302. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Schloss, J.; Thomasen, A.; O’Riordan, L.J.; Busch, T.; White, A. Chaotic few-body vortex dynamics in rotating bose-einstein condensates. Phys. Rev. Fluids 2019, 4, 054701. [Google Scholar] [CrossRef] [Green Version]
- Neely, T.W.; Samson, E.C.; Bradley, A.S.; Davis, M.J.; Anderson, B.P. Observation of vortex dipoles in an oblate bose-einstein condensate. Phys. Rev. Lett. 2010, 104, 160401. [Google Scholar] [CrossRef] [PubMed]
- Neely, T.W.; Bradley, A.S.; Samson, E.C.; Rooney, S.J.; Wright, E.M.; Law, K.J.H.; Carretero-González, R.; Kevrekidis, P.G.; Davis, M.J.; Anderson, B.P. Characteristics of two-dimensional quantum turbulence in a compressible superfluid. Phys. Rev. Lett. 2013, 111, 235301. [Google Scholar] [CrossRef]
- Jones, C.A.; Roberts, P.H. Motions in a bose condensate. iv. axisymmetric solitary waves. J. Phys. A Math. Gen. 1982, 15, 2599. [Google Scholar] [CrossRef]
- Meyer, N.; Proud, H.; Perea-Ortiz, M.; O’Neale, C.; Baumert, M.; Holynski, M.; Kronjäger, J.; Barontini, G.; Bongs, K. Observation of two-dimensional localized jones-roberts solitons in bose-einstein condensates. Phys. Rev. Lett. 2017, 119, 150403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Commeford, K.A.; Garcia-March, M.A.; Ferrando, A.; Carr, L.D. Symmetry breaking and singularity structure in bose-einstein condensates. Phys. Rev. A 2012, 86, 023627. [Google Scholar] [CrossRef] [Green Version]
- García-March, M.-Á.; Ferrando, A.; Zacarés, M.; Sahu, S.; Ceballos-Herrera, D.E. Symmetry, winding number, and topological charge of vortex solitons in discrete-symmetry media. Phys. Rev. A 2009, 79, 053820. [Google Scholar] [CrossRef] [Green Version]
- Ferrando, A.; Khoroshun, G.M.; Riazantsev, A.O.; Bekshaev, A.; Popiołek-Masajada, A.; Szatkowski, M. Differential operator formalism for axial optical vortex beam and the double-phase-ramp converter. In Proceedings of the 2019 IEEE 8th International Conference on Advanced Optoelectronics and Lasers (CAOL), Sozopol, Bulgaria, 6–8 September 2019; pp. 522–525. [Google Scholar]
- Agrawal, G.P. Nonlinear Fiber Optics; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Popiołek-Masajada, A.; Fraczek, E.; Burnecka, E. Subpixel localization of optical vortices using artificial neural networks. Metrol. Meas. Syst. 2021, 28, 497–508. [Google Scholar]
- Metz, F.; Polo, J.; Weber, N.; Busch, T. Deep-learning-based quantum vortex detection in atomic bose–einstein condensates. Mach. Learn. Sci. Technol. 2021, 2, 035019. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De María-García, S.; Ferrando, A.; Conejero, J.A.; De Córdoba, P.F.; García-March, M.Á. A Method for the Dynamics of Vortices in a Bose-Einstein Condensate: Analytical Equations of the Trajectories of Phase Singularities. Condens. Matter 2023, 8, 12. https://doi.org/10.3390/condmat8010012
De María-García S, Ferrando A, Conejero JA, De Córdoba PF, García-March MÁ. A Method for the Dynamics of Vortices in a Bose-Einstein Condensate: Analytical Equations of the Trajectories of Phase Singularities. Condensed Matter. 2023; 8(1):12. https://doi.org/10.3390/condmat8010012
Chicago/Turabian StyleDe María-García, Sergi, Albert Ferrando, J. Alberto Conejero, Pedro Fernández De Córdoba, and Miguel Ángel García-March. 2023. "A Method for the Dynamics of Vortices in a Bose-Einstein Condensate: Analytical Equations of the Trajectories of Phase Singularities" Condensed Matter 8, no. 1: 12. https://doi.org/10.3390/condmat8010012
APA StyleDe María-García, S., Ferrando, A., Conejero, J. A., De Córdoba, P. F., & García-March, M. Á. (2023). A Method for the Dynamics of Vortices in a Bose-Einstein Condensate: Analytical Equations of the Trajectories of Phase Singularities. Condensed Matter, 8(1), 12. https://doi.org/10.3390/condmat8010012







