Angle-dependent Magnetoresistance of an Ordered Bose Glass of Vortices in YBa2Cu3O7-δ Thin Films with a Periodic Pinning Lattice
Abstract
1. Introduction
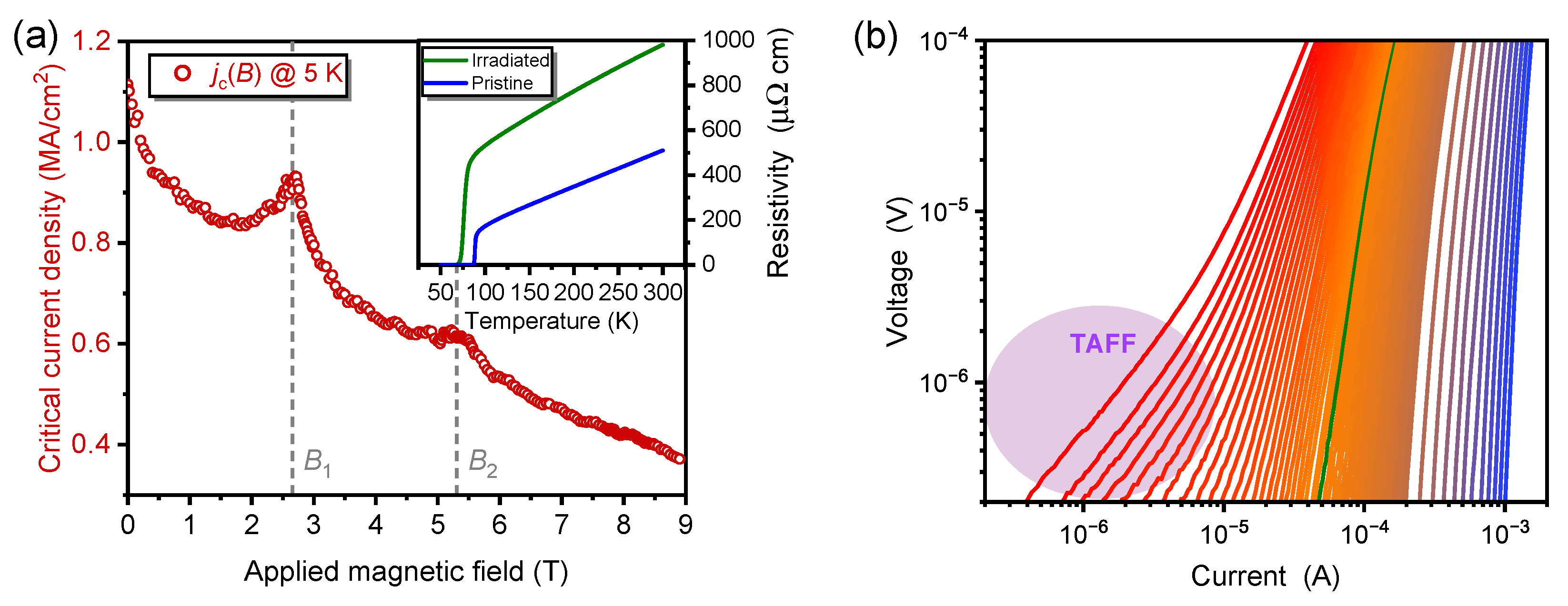
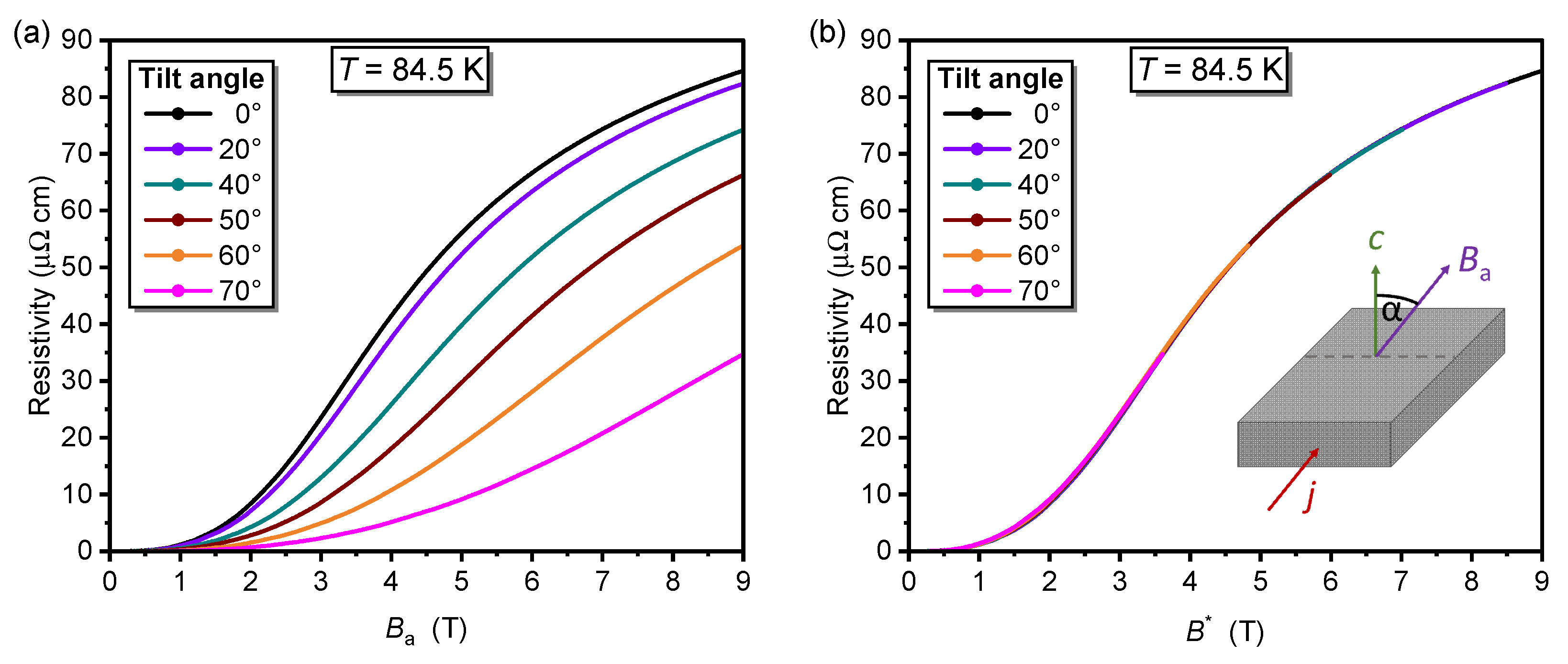
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blatter, G.; Feigel’man, M.V.; Geshkenbein, V.B.; Larkin, A.I.; Vinokur, V.M. Vortices in high-temperature superconductors. Rev. Mod. Phys. 1994, 66, 1125–1388. [Google Scholar] [CrossRef]
- Safar, H.; Gammel, P.L.; Huse, D.A.; Bishop, D.J.; Rice, J.P.; Ginsberg, D.M. Experimental Evidence for a First-Order Vortex-Lattice-Melting Transition in Untwinned, Single Crystal YBa2Cu3O7. Phys. Rev. Lett. 1992, 69, 824–827. [Google Scholar] [CrossRef] [PubMed]
- Fisher, M. Vortex Glass Superconductivity: A Possible New Phase in Bulk High-Tc Oxides. Phys. Rev. Lett. 1989, 62, 1415. [Google Scholar] [CrossRef]
- Fisher, D.S.; Fisher, M.P.A.; Huse, D.A. Thermal Fluctuations, Quenched Disorder, Phase Transitions, and Transport in Type-II Superconductors. Phys. Rev. 1991, 43, 130–159. [Google Scholar] [CrossRef] [PubMed]
- Krusin-Elbaum, L.; Civale, L.; Blatter, G.; Marwick, A.D.; Holtzberg, F.; Feild, C. Bose-glass melting in YBaCuO crystals with correlated disorder. Phys. Rev. Lett. 1994, 72, 1914–1917. [Google Scholar] [CrossRef]
- Nelson, D.R.; Vinokur, V.M. Boson Localization and Pinning by Correlated Disorder in High-Temperature Superconductors. Phys. Rev. Lett. 1992, 68, 2398–2401. [Google Scholar] [CrossRef]
- Nelson, D.R.; Vinokur, V.M. Boson Localization and Correlated Pinning of Superconducting Vortex Arrays. Phys. Rev. B 1993, 48, 13060–13097. [Google Scholar] [CrossRef] [PubMed]
- Wöltgens, P.J.M.; Dekker, C.; Swüste, J.; de Wijn, H.W. Superconducting Phase of YBa2Cu3O7-δ Films in High Magnetic Fields - Vortex Glass or Bose Glass. Phys. Rev. B 1993, 48, 16826–16829. [Google Scholar] [CrossRef] [PubMed]
- Safar, H.; Foltyn, S.R.; Jia, Q.X.; Maley, M.P. Bose glass vortex phase transition in twinned YBa2Cu3O7-δ superconductors. Philos. Mag. B 1996, 74, 647–654. [Google Scholar] [CrossRef]
- Grigera, S.A.; Morré, E.; Osquiguil, E.; Balseiro, C.; Nieva, G.; de la Cruz, F. Bose-Glass Phase in Twinned YBa2Cu3O7-δ. Phys. Rev. Lett. 1998, 81, 2348–2351. [Google Scholar] [CrossRef]
- Jiang, Z.; Dikin, D.A.; Chandrasekhar, V.; Metlushko, V.V.; Moshchalkov, V.V. Pinning phenomena in a superconducting film with a square lattice of artificial pinning centers. Appl. Phys. Lett. 2004, 84, 5371–5373. [Google Scholar] [CrossRef]
- Poccia, N.; Baturina, T.I.; Coneri, F.; Molenaar, C.G.; Wang, X.R.; Bianconi, G.; Brinkman, A.; Hilgenkamp, H.; Golubov, A.A.; Vinokur, V.M. Critical behavior at a dynamic vortex insulator-to-metal transition. Science 2015, 349, 1202–1205. [Google Scholar] [CrossRef]
- Backmeister, L.; Aichner, B.; Karrer, M.; Wurster, K.; Kleiner, R.; Goldobin, E.; Koelle, D.; Lang, W. Ordered Bose Glass of Vortices in Superconducting YBa2Cu3O7-δ Thin Films with a Periodic Pin Lattice Created by Focused Helium Ion Irradiation. Nanomaterials 2022, 12, 3491. [Google Scholar] [CrossRef] [PubMed]
- Hwa, T.; Nelson, D.R.; Vinokur, V.M. Flux-Line Pinning by Competing Disorders. Phys. Rev. B 1993, 48, 1167–1174. [Google Scholar] [CrossRef] [PubMed]
- Radzihovsky, L. Resurrection of the Melting Line in the Bose Glass Superconductor. Phys. Rev. Lett. 1995, 74, 4923–4926. [Google Scholar] [CrossRef]
- Trastoy, J.; Rouco, V.; Ulysse, C.; Bernard, R.; Palau, A.; Puig, T.; Faini, G.; Lesueur, J.; Briatico, J.; Villegas, J.E. Unusual magneto-transport of YBa2Cu3O7-δ films due to the interplay of anisotropy, random disorder and nanoscale periodic pinning. New J. Phys. 2013, 15, 103022. [Google Scholar] [CrossRef]
- Reichhardt, C.; van Otterlo, A.; Zimányi, G.T. Vortices Freeze like Window Glass: The Vortex Molasses Scenario. Phys. Rev. Lett. 2000, 84, 1994–1997. [Google Scholar] [CrossRef]
- Lang, W.; Richter, H.; Marksteiner, M.; Siraj, K.; Bodea, M.A.; Pedarnig, J.D.; Grigoropoulos, C.; Bäuerle, D.; Hasenfuss, C.; Palmetshofer, L.; et al. Masked ion beam irradiation of high-temperature superconductors: Patterning of nano-size regions with high point-defect density. Int. J. Nanotechnol. 2009, 6, 704–714. [Google Scholar] [CrossRef]
- Pedarnig, J.D.; Siraj, K.; Bodea, M.A.; Puica, I.; Lang, W.; Kolarova, R.; Bauer, P.; Haselgrübler, K.; Hasenfuss, C.; Beinik, I.; et al. Surface planarization and masked ion-beam structuring of YBa2Cu3O7 thin films. Thin Solid Film. 2010, 518, 7075–7080. [Google Scholar] [CrossRef]
- Swiecicki, I.; Ulysse, C.; Wolf, T.; Bernard, R.; Bergeal, N.; Briatico, J.; Faini, G.; Lesueur, J.; Villegas, J.E. Strong field-matching effects in superconducting YBa2Cu3O7-δ films with vortex energy landscapes engineered via masked ion irradiation. Phys. Rev. B 2012, 85, 224502. [Google Scholar] [CrossRef]
- Haag, L.T.; Zechner, G.; Lang, W.; Dosmailov, M.; Bodea, M.A.; Pedarnig, J.D. Strong vortex matching effects in YBCO films with periodic modulations of the superconducting order parameter fabricated by masked ion irradiation. Phys. C 2014, 503, 75–81. [Google Scholar] [CrossRef]
- Trastoy, J.; Malnou, M.; Ulysse, C.; Bernard, R.; Bergeal, N.; Faini, G.; Lesueur, J.; Briatico, J.; Villegas, J.E. Freezing and thawing of artificial ice by thermal switching of geometric frustration in magnetic flux lattices. Nat. Nanotechnol. 2014, 9, 710–715. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Liu, Y.; Wang, Y.; Feng, L.; He, Q.; Sun, J.; Tang, Y.; Wu, C.; Xiong, J.; Zhang, W.; et al. Intermediate bosonic metallic state in the superconductor-insulator transition. Science 2019, 366, 1505–1509. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Liu, H.; Liu, Y.; Wang, J.; Qiu, D.; Wang, S.; Wang, Y.; He, Q.; Li, X.; Li, P.; et al. Signatures of a strange metal in a bosonic system. Nature 2022, 601, 205–210. [Google Scholar] [CrossRef] [PubMed]
- Aichner, B.; Müller, B.; Karrer, M.; Misko, V.R.; Limberger, F.; Mletschnig, K.L.; Dosmailov, M.; Pedarnig, J.D.; Nori, F.; Kleiner, R.; et al. Ultradense Tailored Vortex Pinning Arrays in Superconducting YBa2Cu3O7-δ Thin Films Created by Focused He Ion Beam Irradiation for Fluxonics Applications. ACS Appl. Nano Mater. 2019, 2, 5108–5115. [Google Scholar] [CrossRef]
- Aichner, B.; Mletschnig, K.L.; Müller, B.; Karrer, M.; Dosmailov, M.; Pedarnig, J.D.; Kleiner, R.; Koelle, D.; Lang, W. Angular magnetic-field dependence of vortex matching in pinning lattices fabricated by focused or masked helium ion beam irradiation of superconducting YBa2Cu3O7-δ thin films. Low Temp. Phys. 2020, 46, 331–337. [Google Scholar] [CrossRef]
- Reichhardt, C.; Olson Reichhardt, C.J. Depinning and nonequilibrium dynamic phases of particle assemblies driven over random and ordered substrates: A review. Rep. Prog. Phys. 2017, 80, 026501. [Google Scholar] [CrossRef]
- Wang, X.Z.; Hellebrand, B.; Bäuerle, D.; Strecker, M.; Wortmann, G.; Lang, W. Oxygen ordering and superconductivity in GdBaSrCu3O7-x. Phys. C 1995, 242, 55–62. [Google Scholar] [CrossRef]
- Sefrioui, Z.; Arias, D.; González, E.M.; Léon, C.; Santamaria, J.; Vicent, J.L. Vortex liquid entanglement in irradiated YBa2Cu3O7-δ thin films. Phys. Rev. B 2001, 63, 064503. [Google Scholar] [CrossRef]
- Lang, W.; Pedarnig, J.D. Ion Irradiation of High-Temperature Superconductors and Its Application for Nanopatterning. In Nanoscience and Engineering in Superconductivity; Moshchalkov, V.V., Wördenweber, R., Lang, W., Eds.; Springer: Heidelberg, Germany, 2010; pp. 81–104. [Google Scholar] [CrossRef]
- Kes, P.H.; Aarts, J.; van den Berg, J.; van der Beek, J.C.; Mydosh, J.A. Thermally Assisted Flux Flow at Small Driving Forces. Supercond. Sci. Technol. 1989, 1, 242–248. [Google Scholar] [CrossRef]
- Lang, W.; Fussenegger, C.; Proyer, S.; Stangl, E.; Bäuerle, D. Observation of the vortex-glass transition in YBa2Cu3O7 by phase-resolved current-voltage measurements. Z. Phys. B 1996, 100, 13–18. [Google Scholar] [CrossRef]
- Koch, R.; Foglietti, V.; Gallagher, W.; Koren, G.; Gupta, A.; Fisher, M. Experimental Evidence for Vortex-Glass Superconductivity in Y-Ba-Cu-O. Phys. Rev. Lett. 1989, 63, 1511. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, R. High field vortex glass transition induced by line-like disorder. J. Phys. Soc. Jpn. 1999, 68, 728–731. [Google Scholar] [CrossRef]
- Blatter, G.; Geshkenbein, V.B.; Larkin, A.I. From Isotropic to Anisotropic Superconductors—A Scaling Approach. Phys. Rev. Lett. 1992, 68, 875–878. [Google Scholar] [CrossRef]
- Iye, Y.; Nakamura, S.; Tamegai, T.; Terashima, T.; Yamamoto, K.; Bando, Y. Angular dependent transport studies in the mixed state of YBa2Cu3O7-y and Bi2Sr2CaCu2O8+y. Phys. C 1990, 166, 62–70. [Google Scholar] [CrossRef]
- Metlushko, V.V.; DeLong, L.E.; Baert, M.; Rosseel, E.; Van Bael, M.J.; Temst, K.; Moshchalkov, V.V.; Bruynseraede, Y. Supermatching vortex phases in superconducting thin films with antidot lattices. Europhys. Lett. 1998, 41, 333–338. [Google Scholar] [CrossRef]
- Womack, F.N.; Adams, P.W.; Valles, J.M.; Catelani, G. Critical field behavior of a multiply connected superconductor in a tilted magnetic field. Phys. Rev. B 2019, 100, 174505. [Google Scholar] [CrossRef]
- Reichhardt, C.; Olson, C.J.; Nori, F. Nonequilibrium dynamic phases and plastic flow of driven vortex lattices in superconductors with periodic arrays of pinning sites. Phys. Rev. B 1998, 58, 6534. [Google Scholar] [CrossRef]
- Hardy, V.; Wahl, A.; Hébert, S.; Ruyter, A.; Provost, J.; Groult, D.; Simon, C. Accommodation of vortices to tilted line defects in high-Tc superconductors with various electronic anisotropies. Phys. Rev. B 1996, 54, 656–664. [Google Scholar] [CrossRef]
- Durrell, J.H.; Burnell, G.; Tsaneva, V.N.; Barber, Z.H.; Blamire, M.G.; Evetts, J.E. Critical currents in vicinal YBa2Cu3O7-δ films. Phys. Rev. B 2004, 70, 214508. [Google Scholar] [CrossRef]
- Feinberg, D.; Villard, C. Intrinsic Pinning and Lock-in Transition of Flux Lines in Layered Type-II Superconductors. Phys. Rev. Lett. 1990, 65, 919–922. [Google Scholar] [CrossRef]
- Bartolomé, E.; Vallés, F.; Palau, A.; Rouco, V.; Pompeo, N.; Balakirev, F.F.; Maiorov, B.; Civale, L.; Puig, T.; Obradors, X.; et al. Intrinsic anisotropy versus effective pinning anisotropy in YBa2Cu3O7 thin films and nanocomposites. Phys. Rev. B 2019, 100, 054502. [Google Scholar] [CrossRef]
- Gutiérrez, J.; Llordés, A.; Gázquez, J.; Gibert, M.; Romà, N.; Ricart, S.; Pomar, A.; Sandiumenge, F.; Mestres, N.; Puig, T.; et al. Strong isotropic flux pinning in solution-derived YBa2Cu3O7-x nanocomposite superconductor films. Nat. Mater. 2007, 6, 367–373. [Google Scholar] [CrossRef] [PubMed]
- Maccari, I.; Pokharel, B.K.; Terzic, J.; Dutta, S.; Jesudasan, J.; Raychaudhuri, P.; Lorenzana, J.; De Michele, C.; Castellani, C.; Benfatto, L.; et al. Transport signatures of fragile glass dynamics in the melting of the two-dimensional vortex lattice. Phys. Rev. B 2023, 107, 014509. [Google Scholar] [CrossRef]
- Tachiki, M.; Takahashi, S. Strong Vortex Pinning Intrinsic in High-Tc Oxide Superconductors. Solid State Commun. 1989, 70, 291–295. [Google Scholar] [CrossRef]
- Radzihovsky, L. Smectic vortex glass. Phys. Rev. B 2021, 104, 024510. [Google Scholar] [CrossRef]
- Gozar, A.; Litombe, N.E.; Hoffman, J.E.; Božović, I. Optical Nanoscopy of High Tc Cuprate Nanoconstriction Devices Patterned by Helium Ion Beams. Nano Lett. 2017, 17, 1582–1586. [Google Scholar] [CrossRef] [PubMed]
- Müller, B.; Karrer, M.; Limberger, F.; Becker, M.; Schröppel, B.; Burkhardt, C.J.; Kleiner, R.; Goldobin, E.; Koelle, D. Josephson Junctions and SQUIDs Created by Focused Helium-Ion-Beam Irradiation of YBa2Cu3O7. Phys. Rev. Appl. 2019, 11, 044082. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aichner, B.; Backmeister, L.; Karrer, M.; Wurster, K.; Kleiner, R.; Goldobin, E.; Koelle, D.; Lang, W. Angle-dependent Magnetoresistance of an Ordered Bose Glass of Vortices in YBa2Cu3O7-δ Thin Films with a Periodic Pinning Lattice. Condens. Matter 2023, 8, 32. https://doi.org/10.3390/condmat8020032
Aichner B, Backmeister L, Karrer M, Wurster K, Kleiner R, Goldobin E, Koelle D, Lang W. Angle-dependent Magnetoresistance of an Ordered Bose Glass of Vortices in YBa2Cu3O7-δ Thin Films with a Periodic Pinning Lattice. Condensed Matter. 2023; 8(2):32. https://doi.org/10.3390/condmat8020032
Chicago/Turabian StyleAichner, Bernd, Lucas Backmeister, Max Karrer, Katja Wurster, Reinhold Kleiner, Edward Goldobin, Dieter Koelle, and Wolfgang Lang. 2023. "Angle-dependent Magnetoresistance of an Ordered Bose Glass of Vortices in YBa2Cu3O7-δ Thin Films with a Periodic Pinning Lattice" Condensed Matter 8, no. 2: 32. https://doi.org/10.3390/condmat8020032
APA StyleAichner, B., Backmeister, L., Karrer, M., Wurster, K., Kleiner, R., Goldobin, E., Koelle, D., & Lang, W. (2023). Angle-dependent Magnetoresistance of an Ordered Bose Glass of Vortices in YBa2Cu3O7-δ Thin Films with a Periodic Pinning Lattice. Condensed Matter, 8(2), 32. https://doi.org/10.3390/condmat8020032








