Features of Light-Matter Coupling in Non-Ideal Lattice of Coupled Microcavities Containing Quantum Dots
Abstract
1. Introduction
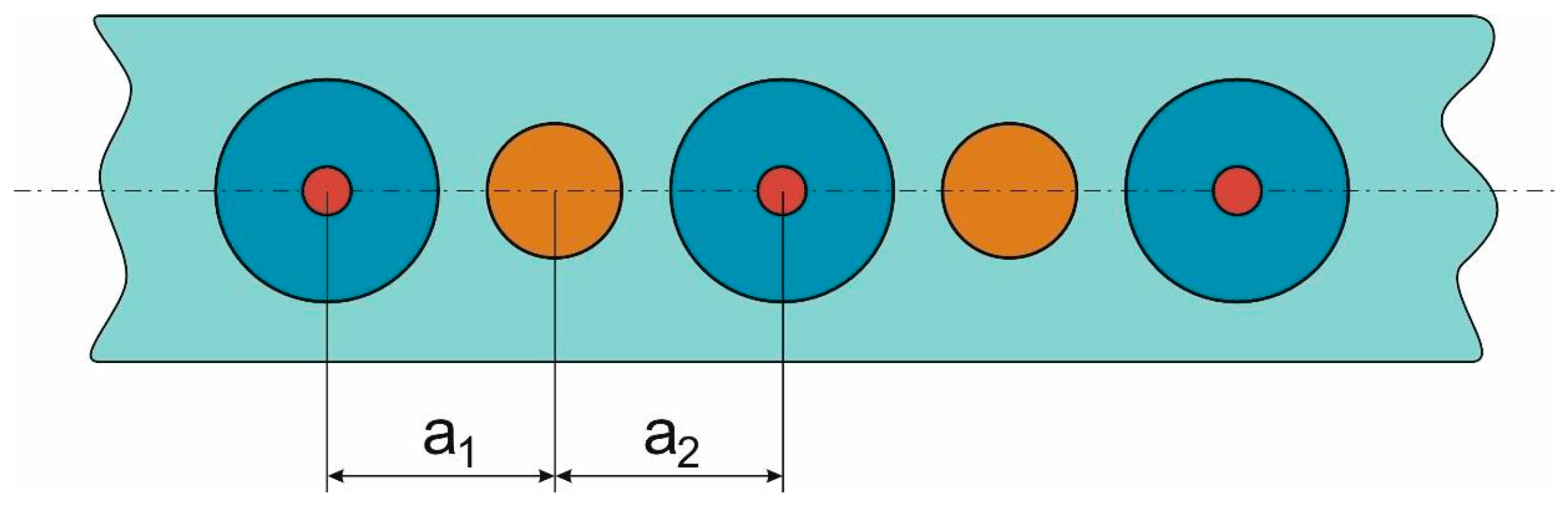
2. Theoretical Model
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Söllner, I.; Mahmoodian, S.; Hansen, S.L.; Midolo, L.; Javadi, A.; Kiršanskė, G.; Pregnolato, T.; El-Ella, H.; Lee, E.H.; Song, J.D.; et al. Deterministic photon–emitter coupling in chiral photonic circuits. Nat. Nanotechnol. 2015, 10, 775. [Google Scholar] [CrossRef] [PubMed]
- Lodahl, P. Quantum-dot based photonic quantum networks. Quantum Sci. Technol. 2018, 3, 013001. [Google Scholar] [CrossRef]
- Sedov, E.S.; Alodjants, A.P.; Arakelian, S.M.; Chuang, Y.-L.; Lin, Y.Y.; Yang, W.-X.; Lee, R.-K. Tunneling-assisted optical information storage with lattice polariton solitons in cavity-QED arrays. Phys. Rev. A 2014, 89, 033828. [Google Scholar] [CrossRef]
- Joannopoulos, J.D.; Johnso, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals. In Molding the Flow of Light, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Kaliteevskii, M.A. Coupled vertical microcavities. Tech. Phys. Lett. 1997, 23, 120–121. [Google Scholar] [CrossRef]
- Vahala, K.J. Optical microcavities. Nature 2003, 424, 839–846. [Google Scholar] [CrossRef] [PubMed]
- Tighineanu, P.; Sørensen, A.S.; Stobbe, S.; Lodahl, P. The Mesoscopic Nature of Quantum Dots in Photon Emission. In Quantum Dots for Quantum Information Technologies; Michler, P., Ed.; Nano-Optics and Nanophotonics; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Alodjants, A.P.; Barinov, I.O.; Arakelian, S.M. Strongly localized polaritons in an array of trapped two-level atoms interacting with a light field. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 095502. [Google Scholar] [CrossRef]
- Rumyantsev, V.V.; Fedorov, S.A.; Gumennyk, K.V.; Gurov, D.A.; Kavokin, A.V. Effects of elastic strain and structural defects on slow light modes in a one-dimensional array of microcavities. Superlattices Microstruct. 2018, 120, 642–649. [Google Scholar] [CrossRef]
- Rumyantsev, V.V.; Fedorov, S.A.; Gumennyk, K.V.; Sychanova, M.V.; Kavokin, A.V. Exciton-like electromagnetic excitations in non-ideal microcavity supercrystals. Nat. Sci. Rep. 2014, 4, 6945. [Google Scholar] [CrossRef] [PubMed]
- Rumyantsev, V.V.; Fedorov, S.A.; Gumennyk, K.V.; Sychanova, M.V.; Kavokin, A.V. Polaritons in a nonideal periodic array of microcavities. Superlattices Microstruct. 2016, 89, 409–418. [Google Scholar] [CrossRef]
- Dmitriev, S.V.; Baimova, Y.A. Effect of elastic deformation on phonon spectrum and characteristics of gap discrete breathers in crystal with NaCl-type structure. Tech. Phys. Lett. 2011, 37, 451–454. [Google Scholar] [CrossRef]
- Rumyantsev, V.V.; Fedorov, S.A.; Gumennyk, K.V.; Paladyan, Y.A. Electromagnetic excitations in a non-ideal two-sublattice microcavity chain. Phys. B Condens. Matter. 2019, 571, 296–300. [Google Scholar] [CrossRef]
- Agranovich, V.M. Theory of Excitons; Nauka: Moscow, Russia, 1968. [Google Scholar]
- Los’, V.F. Projection operator method in the theory of disordered systems. I. Spectra of quasiparticles. Theor. Math. Phys. 1987, 73, 85–102. [Google Scholar] [CrossRef]
- Ziman, J.M. Models of Disorder: The Theoretical Physics of Homogeneously Disordered Systems; Cambridge University Press: Cambridge, UK, 1979. [Google Scholar]
- Rumyantsev, V.V.; Fedorov, S.A. Novel Materials Based on Nonideal Supercrystal Formed by a Tunnel Connected Array of Microcavities Containing Ensembles of Quantum Dots. J. Mater. Polym. Sci. 2022, 2, 1–8. [Google Scholar]
- Rumyantsev, V.V.; Fedorov, S.A.; Gumennyk, K.V.; Rybalka, A.; Zavorotnev, Y.D. Polaritonic crystal formed of a tunnel-coupled microcavity array and an ensemble of quantum dots. J. Phys. Conf. Series 2021, 2052, 012036. [Google Scholar] [CrossRef]
- Yao, P.; Pathak, P.K.; Illes, E.; Hughes, S.; Münch, S.; Reitzenstein, S.; Franeck, P.; Löffler, A.; Heindel, T.; Höfling, S.; et al. Nonlinear photoluminescence spectra from a quantum-dot–cavity system: Interplay of pump-induced stimulated emission and anharmonic cavity QED. Phys. Rev. B 2010, 81, 033309. [Google Scholar] [CrossRef]
- Diguna, L.J.; Darma, Y.; Birowosuto, M.D. The coupling of single-photon exciton–biexciton quantum dot and cavity. J. Nonlinear Opt. Phys. Mater. 2017, 26, 1750029. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rumyantsev, V.V.; Fedorov, S.A.; Gumennyk, K.V.; Rybalka, A.Y. Features of Light-Matter Coupling in Non-Ideal Lattice of Coupled Microcavities Containing Quantum Dots. Condens. Matter 2023, 8, 41. https://doi.org/10.3390/condmat8020041
Rumyantsev VV, Fedorov SA, Gumennyk KV, Rybalka AY. Features of Light-Matter Coupling in Non-Ideal Lattice of Coupled Microcavities Containing Quantum Dots. Condensed Matter. 2023; 8(2):41. https://doi.org/10.3390/condmat8020041
Chicago/Turabian StyleRumyantsev, Vladimir V., Stanislav A. Fedorov, Konstantin V. Gumennyk, and Alexey Ye. Rybalka. 2023. "Features of Light-Matter Coupling in Non-Ideal Lattice of Coupled Microcavities Containing Quantum Dots" Condensed Matter 8, no. 2: 41. https://doi.org/10.3390/condmat8020041
APA StyleRumyantsev, V. V., Fedorov, S. A., Gumennyk, K. V., & Rybalka, A. Y. (2023). Features of Light-Matter Coupling in Non-Ideal Lattice of Coupled Microcavities Containing Quantum Dots. Condensed Matter, 8(2), 41. https://doi.org/10.3390/condmat8020041





