Influence of a Non-Resonant Intense Laser and Structural Defect on the Electronic and Optical Properties of a GaAs Quantum Ring under Inversely Quadratic Potential
Abstract
1. Introduction
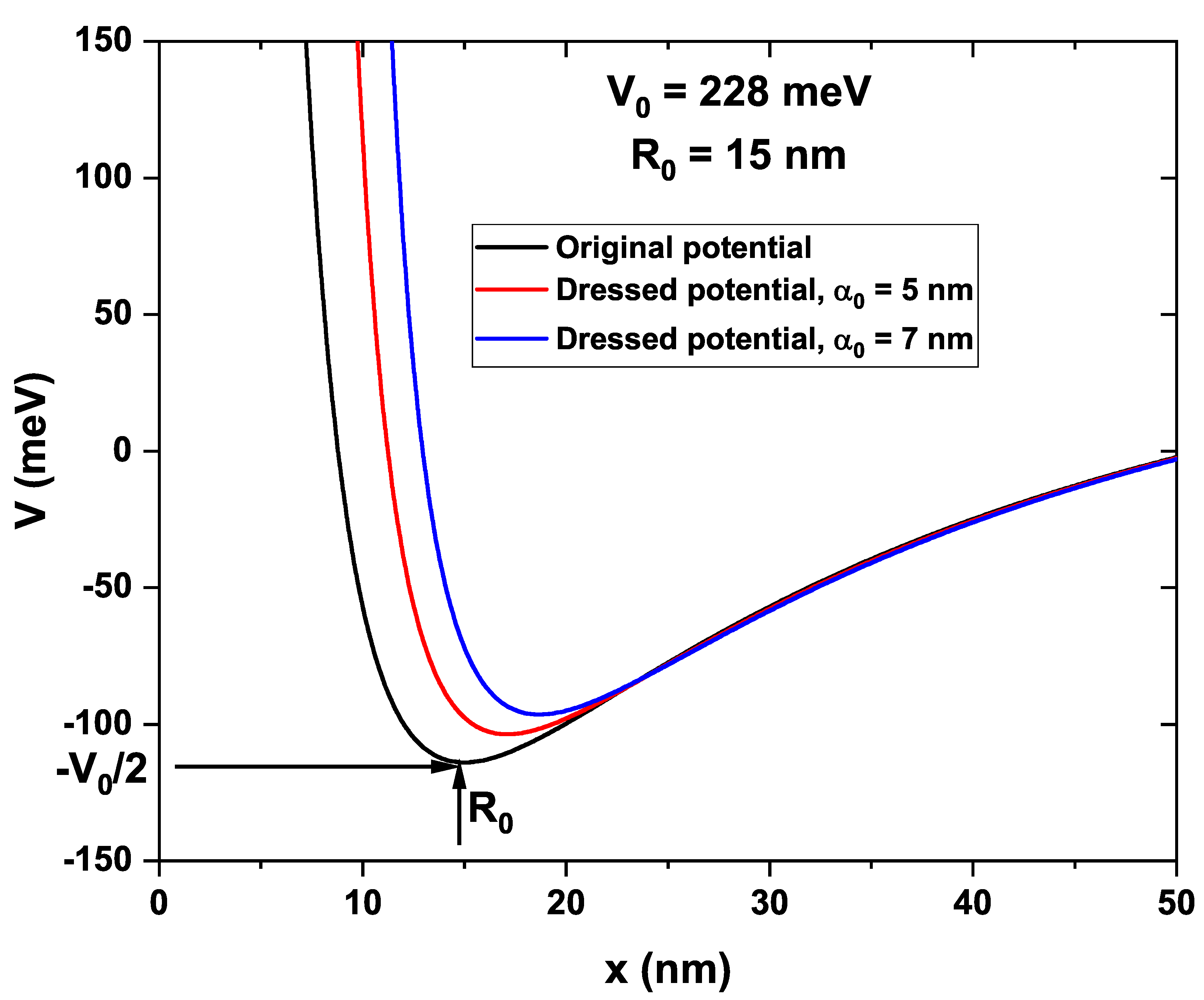
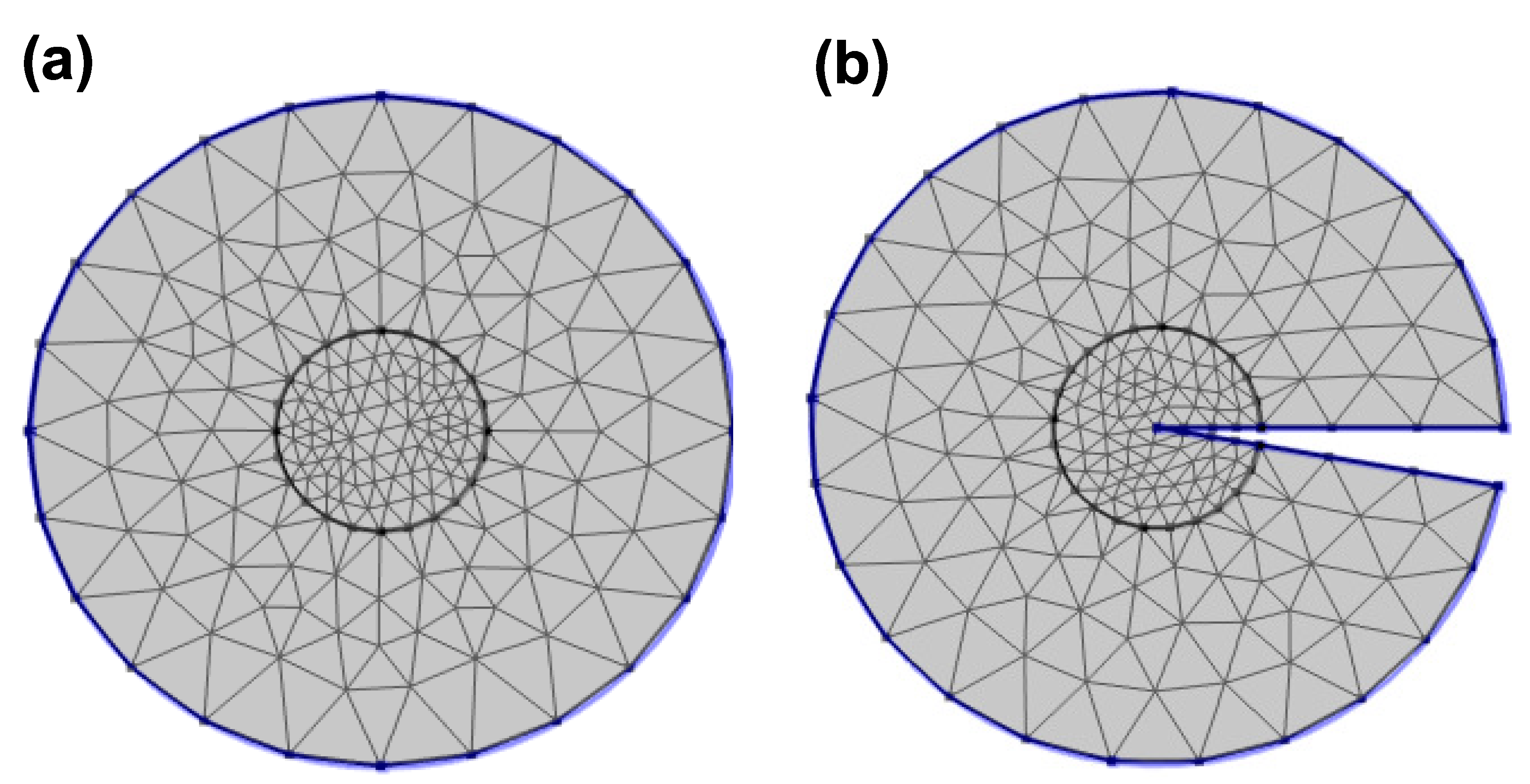
2. Theoretical Model
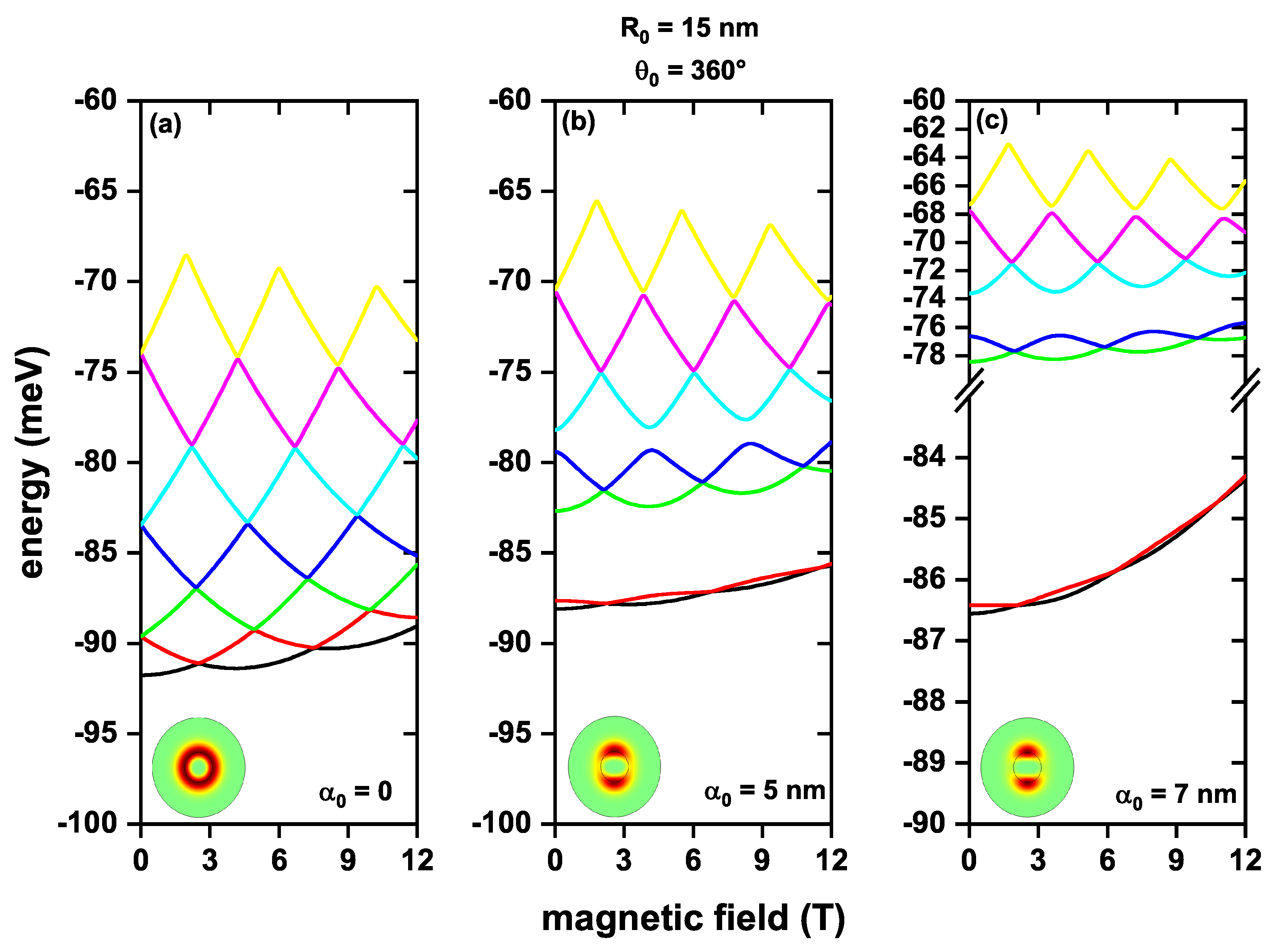
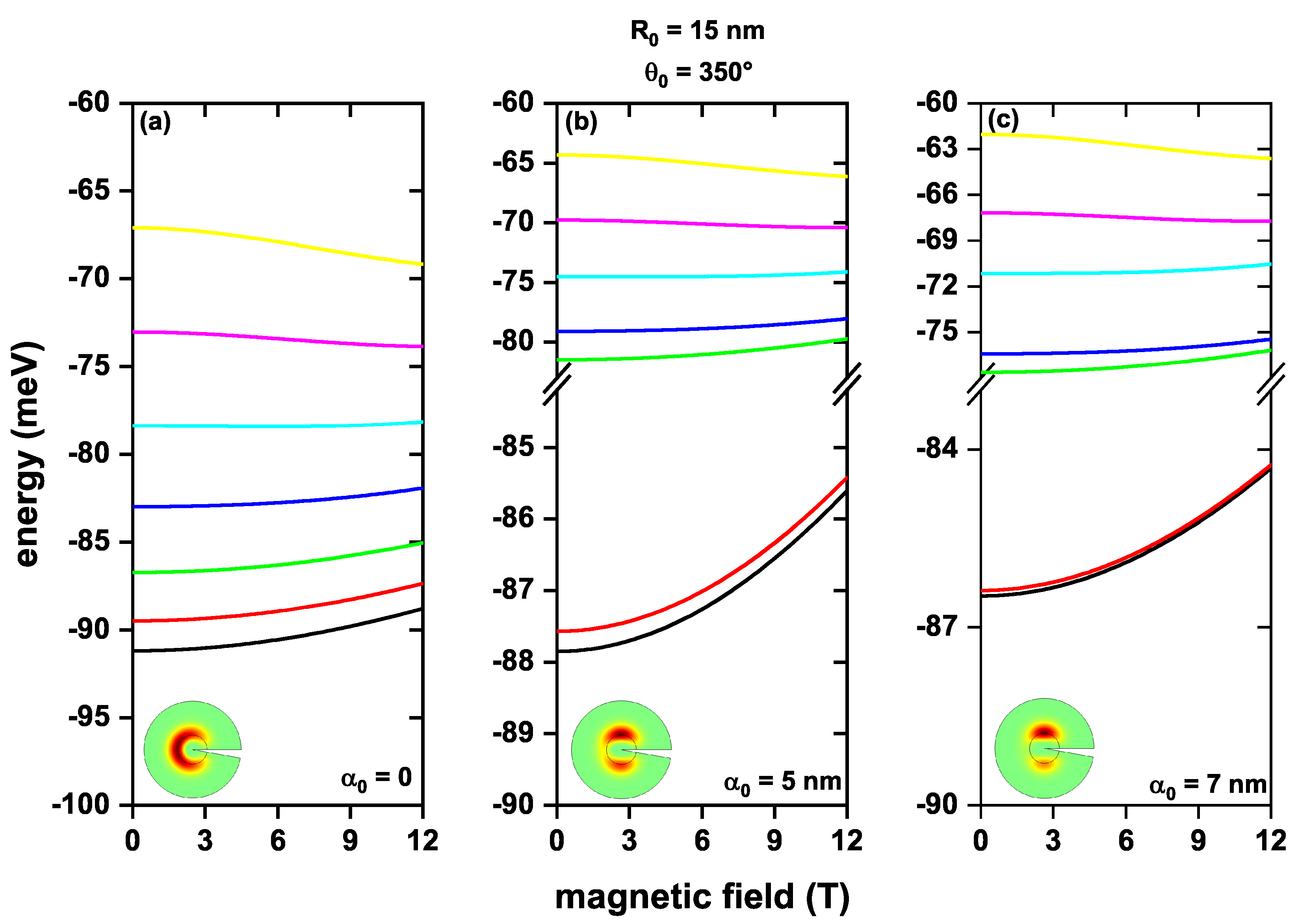
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baghramyan, H.M.; Barseghyan, M.G.; Duque, C.A.; Kirakosyan, A.A. Binding energy of hydrogenic donor impurity in GaAs/Ga1−xAlxAs concentric double quantum rings: Effects of geometry, hydrostatic pressure, temperature, and aluminum concentration. Phys. E Low-Dimens. Syst. Nanostruct. 2013, 48, 164–170. [Google Scholar] [CrossRef]
- Baghramyan, H.M.; Barseghyan, M.G.; Kirakosyan, A.A.; Laroze, D.; Duque, C.A. Donor-impurity related photoionization cross section in GaAs/Ga1−xAlxAs concentric double quantum rings: Effects of geometry and hydrostatic pressure. Phys. B Condens. Matter 2014, 449, 193–198. [Google Scholar] [CrossRef]
- Baghramyan, H.M.; Barseghyan, M.G.; Kirakosyan, A.A.; Restrepo, R.L.; Mora-Ramos, M.E.; Duque, C.A. Donor impurity-related linear and nonlinear optical absorption coefficients in GaAs/Ga1−xAlxAs concentric double quantum rings: Effects of geometry, hydrostatic pressure, and aluminum concentration. J. Lumin. 2014, 145, 676–683. [Google Scholar] [CrossRef]
- Ghanbari, A.; Khordad, R.; Taghizadeh, F.; Nasirizadeh, I.; Edet, C.O.; Ali, N. Impurity effect on thermal properties of tuned quantum dot/ring systems. Chem. Phys. Lett. 2022, 806, 140000. [Google Scholar] [CrossRef]
- Bejan, D.; Stan, C. Impurity and geometry effects on the optical rectification spectra of quasi-elliptical double quantum rings. Phys. E Low-Dimens. Syst. Nanostruct. 2023, 147, 115598. [Google Scholar] [CrossRef]
- Ghajarpour-Nobandegani, S.; Karim, M.J. Effects of hydrogenic impurity and external fields on the optical absorption in a ring-shaped elliptical quantum dot. Opt. Mater. 2018, 82, 75–80. [Google Scholar] [CrossRef]
- Duque, C.M.; Acosta, R.; Morales, A.L.; Mora-Ramos, M.E.; Restrepo, R.L.; Ojeda, J.H.; Kasapoglu, E.; Duque, C.A. Optical coefficients in a semiconductor quantum ring: Electric field and donor impurity effects. Opt. Mater. 2016, 60, 148–158. [Google Scholar] [CrossRef]
- Cai, C.; Ma, X.; Zhao, C.; Xiao, J. Impurity effect on the ground state binding energy of a fully coupled polaron in a double ring shaped quantum dot. Phys. B Condens. Matter 2022, 632, 413699. [Google Scholar] [CrossRef]
- Bejan, D.; Stan, C.; Niculescu, C. Optical properties of an elliptic quantum ring: Eccentricity and electric field effects. Opt. Mater. 2018, 78, 207–219. [Google Scholar] [CrossRef]
- Xie, W. Effect of an electric field on the nonlinear optical rectification of a quantum ring. Phys. B Condens. Matter 2014, 443, 60–62. [Google Scholar] [CrossRef]
- Restrepo, R.L.; Morales, A.L.; Martínez-Orozco, J.C.; Baghramyan, H.M.; Barseghyan, M.G.; Mora-Ramos, M.E.; Duque, C.A. Impurity-related nonlinear optical properties in delta-doped quantum rings: Electric field effects. Phys. B Condens. Matter 2014, 453, 140–145. [Google Scholar] [CrossRef]
- Manaselyan, A.K.; Barseghyan, M.G.; Kirakosyan, A.A.; Laroze, D.; Duque, C.A. Effects of applied lateral electric field and hydrostatic pressure on the intraband optical transitions in a GaAs/Ga1−xAlxAs quantum ring. Phys. E Low-Dimens. Syst. Nanostruct. 2014, 60, 95–99. [Google Scholar] [CrossRef]
- Toscano-Negrette, R.G.; León-González, J.C.; Vinazco, J.A.; Moreles, A.L.; Koc, F.; Kavruk, A.E.; Sahin, M.; Mora-Ramos, M.E.; Sierra-Oretega, J.; Martínez-Orozco, J.C.; et al. Optical properties in a ZnS/CdS/ZnS core/shell/shell spherical quantum dot: Electric and magnetic field and donor impurity effects. Nanomaterials 2023, 13, 550. [Google Scholar] [CrossRef]
- Nasri, D. Electronic and optical properties of eccentric quantum ring under parallel magnetic field. Phys. B Condens. Matter 2021, 615, 413077. [Google Scholar] [CrossRef]
- Duan, Y.; Li, X.; Chang, C.; Zhao, Z.; Zhang, L. Effects of hydrostatic pressure, temperature and Al-concentration on the second-harmonic generation of tuned quantum dot/ring under a perpendicular magnetic field. Phys. B Condens. Matter 2022, 631, 413644. [Google Scholar] [CrossRef]
- Xie, W. Optical properties of an exciton in a two-dimensional quantum ring with an applied magnetic field. Opt. Commun. 2013, 291, 386–389. [Google Scholar] [CrossRef]
- Liang, S.; Xie, W.; Shen, H. Optical properties in a two-dimensional quantum ring: Confinement potential and Aharonov–Bohm effect. Opt. Commun. 2011, 284, 5818–5828. [Google Scholar] [CrossRef]
- Elsaid, M.; Shaer, A.; Hjaz, E.; Yahya, M. Impurity effects on the magnetization and magnetic susceptibility of an electron confined in a quantum ring under the presence of an external magnetic field. Chin. J. Phys. 2020, 64, 9–17. [Google Scholar] [CrossRef]
- Voskoboynikov, O.; Lee, C.P. Magnetization and magnetic susceptibility of InAs nano-rings. Phys. E Low-Dimens. Syst. Nanostruct. 2004, 20, 278–281. [Google Scholar] [CrossRef]
- Sakiroglu, S.; Kilic, D.; Yesilgul, U.; Ungan, F.; Kasapoglu, E.; Sari, H.; Sokmen, I. Intense laser field effects on the third-harmonic generation in a quantum pseudodot system. Phys. B Condens. Matter 2017, 521, 215–220. [Google Scholar] [CrossRef]
- Sakiroglu, S.; Kilic, D.; Yesilgul, U.; Ungan, F.; Kasapoglu, E.; Sari, H.; Sokmen, I. Third-harmonic generation of a laser-driven quantum dot with impurity. Phys. B Condens. Matter 2018, 539, 101–105. [Google Scholar] [CrossRef]
- Ungan, F.; Martínez-Orozco, J.C.; Restrepo, R.L.; Mora-Ramos, M.E.; Kasapoglu, E.; Duque, C.A. Nonlinear optical rectification and second-harmonic generation in a semi-parabolic quantum well under intense laser field: Effects of electric and magnetic fields. Superlattices Microstruct. 2015, 81, 26–33. [Google Scholar] [CrossRef]
- Sakiroglu, S.; Ungan, F.; Yesilgul, U.; Mora-Ramos, M.E.; Duque, C.A.; Kasapoglu, E.; Sari, H.; Sökmen, I. Nonlinear optical rectification and the second and third harmonic generation in Pöschl–Teller quantum well under the intense laser field. Phys. Lett. A 2012, 376, 1875–1880. [Google Scholar] [CrossRef]
- Ungan, F.; Martínez-Orozco, J.C.; Restrepo, R.L.; Mora-Ramos, M.E. The nonlinear optical properties of GaAs-based quantum wells with Kratzer–Fues confining potential: Role of applied static fields and non-resonant laser radiation. Optik 2019, 185, 881–887. [Google Scholar] [CrossRef]
- Barseghyan, M.G. Intraband optical absorption in a single quantum ring: Hydrostatic pressure and intense laser field effects. Opt. Commun. 2016, 379, 41–44. [Google Scholar] [CrossRef]
- Restrepo, R.L.; González-Pereira, J.P.; Kasapoglu, E.; Morales, A.L.; Duque, C.A. Linear and nonlinear optical properties in the terahertz regime for multiple-step quantum wells under intense laser field: Electric and magnetic field effects. Opt. Mater. 2018, 86, 590–599. [Google Scholar] [CrossRef]
- Castaño-Yepes, J.D.; Amor-Quiroz, D.A.; Ramirez-Gutierrez, C.F.; Gómez, E. Impact of a topological defect and Rashba spin-orbit interaction on the thermo-magnetic and optical properties of a 2D semiconductor quantum dot with Gaussian confinement. Phys. E Low-Dimens. Syst. Nanostruct. 2019, 109, 59–66. [Google Scholar] [CrossRef]
- Mishra, T.; Sarkar, T.; Bandyopadhyay, J. Thermal properties of a particle confined to a parabolic quantum well in two-dimensional space with conical disclination. Phys. Rev. E 2014, 89, 012103. [Google Scholar] [CrossRef] [PubMed]
- Silva, W.C.F.; Bakke, K. Topological effects of a spiral dislocation on quantum rings. Ann. Phys. 2020, 241, 168277. [Google Scholar] [CrossRef]
- Fomin, V.M. Physics of Quantum Rings, 2nd ed.; Springer: Dresden, Germany, 2014. [Google Scholar]
- Barticevic, Z.; Pacheco, M.; Latgé, A. Quantum rings under magnetic fields: Electronic and optical properties. Phys. Rev. B 2000, 62, 6963. [Google Scholar] [CrossRef]
- Li, B.; Peeters, F. Tunable optical Aharonov-Bohm effect in a semiconductor quantum ring. Phys. Rev. B 2011, 83, 115448. [Google Scholar] [CrossRef]
- Duque, C.M.; Mora-Ramos, M.E.; Duque, C.A. Quantum disc plus inverse square potential. An analytical model for two-dimensional quantum rings: Study of nonlinear optical properties. Ann. Phys. 2012, 524, 327. [Google Scholar] [CrossRef]
- Duan, Y.; Li, X.; Chang, C.; Zhao, Z. The second and third-harmonic generation of spherical quantum dots under modified Kratzer plus screened Coulomb potential. Phys. B Phys. Condens. Matter 2022, 639, 413941. [Google Scholar] [CrossRef]
- Vinasco, J.A.; Radu, A.; Niculescu, E.; Mora-Ramos, M.E.; Feddi, E.; Tulupenko, V.; Restrepo, R.L.; Kasapoglu, E.; Morales, A.L.; Duque, C.A. Electronic states in GaAs-(Al,Ga)As eccentric quantum rings under nonresonant intense laser and magnetic fields. Sci. Rep. 2019, 5, 1427. [Google Scholar] [CrossRef] [PubMed]
- Kasapoglu, E.; Sari, H.; Sökmen, I.; Vinasco, J.A.; Laroze, D.; Duque, C.A. Effects of intense laser field and position dependent effective mass in Razavy quantum wells and quantum dots. Phys. E Low-Dimens. Syst. Nanostruct. 2021, 126, 114461. [Google Scholar] [CrossRef]
- COMSOL. Multiphysics v. 5.2a Semiconductor Module User’s Guide; COMSOL AB: Stockholm, Sweden, 2016. [Google Scholar]
- Ashrafi-Dalkhani, V.; Ghajarpour-Nobandegani, S.; Javad, M. Effects of spin-orbit interactions, external fields and eccentricity on the optical absorption of an elliptical quantum ring. Eur. Phys. J. 2019, 92, 2–6. [Google Scholar] [CrossRef]
- León-González, J.C.; Toscano-Negrette, R.G.; Morales, A.L.; Vinasco, J.A.; Yücel, M.B.; Sari, H.; Kasapoglu, E.; Sakiroglu, S.; Mora-Ramos, M.E.; Restrepo, R.L.; et al. Spin–Orbit and Zeeman Effects on the Electronic Properties of Single Quantum Rings: Applied Magnetic Field and Topological Defects. Nanomaterials 2023, 13, 1461. [Google Scholar] [CrossRef] [PubMed]
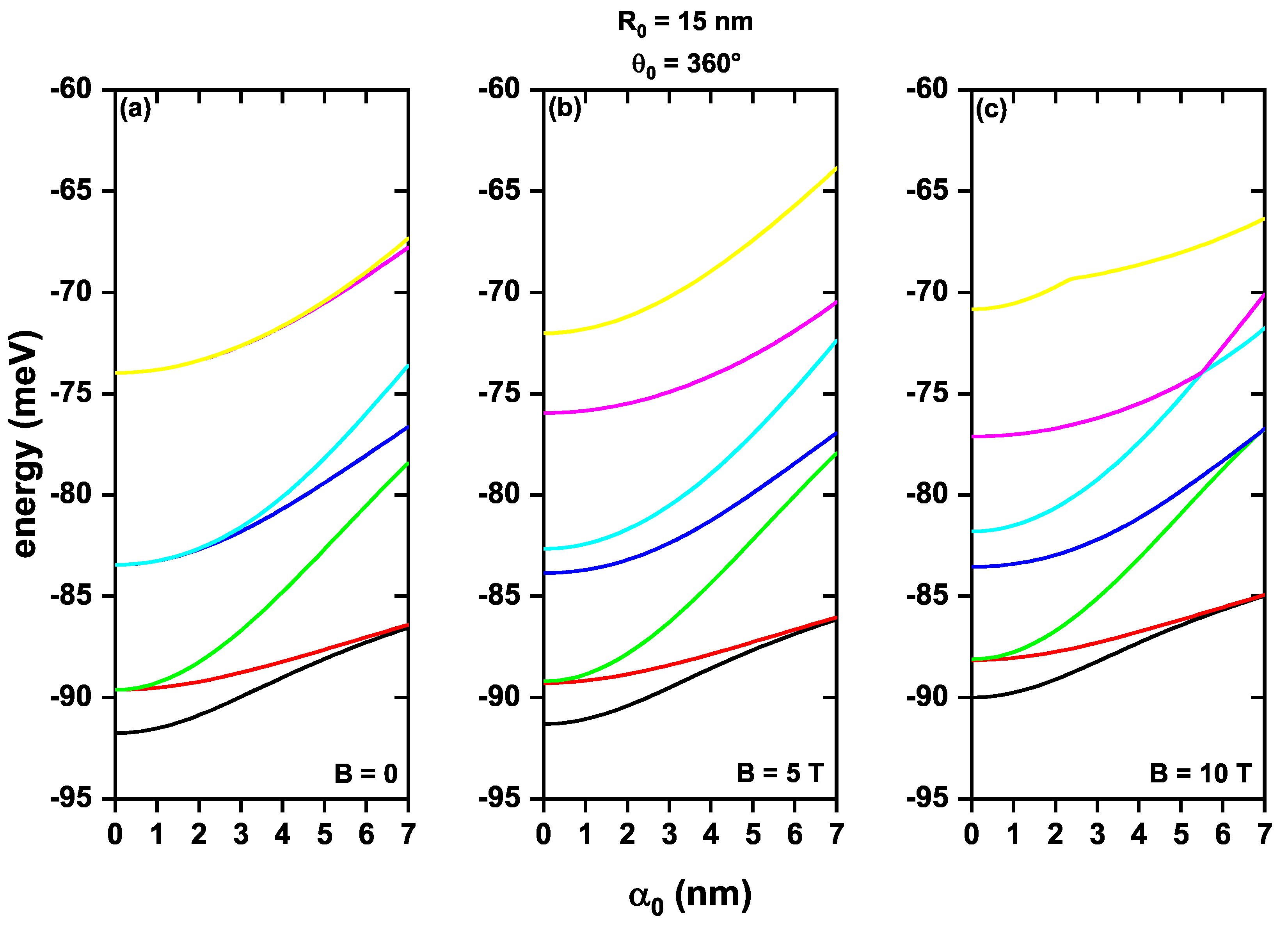
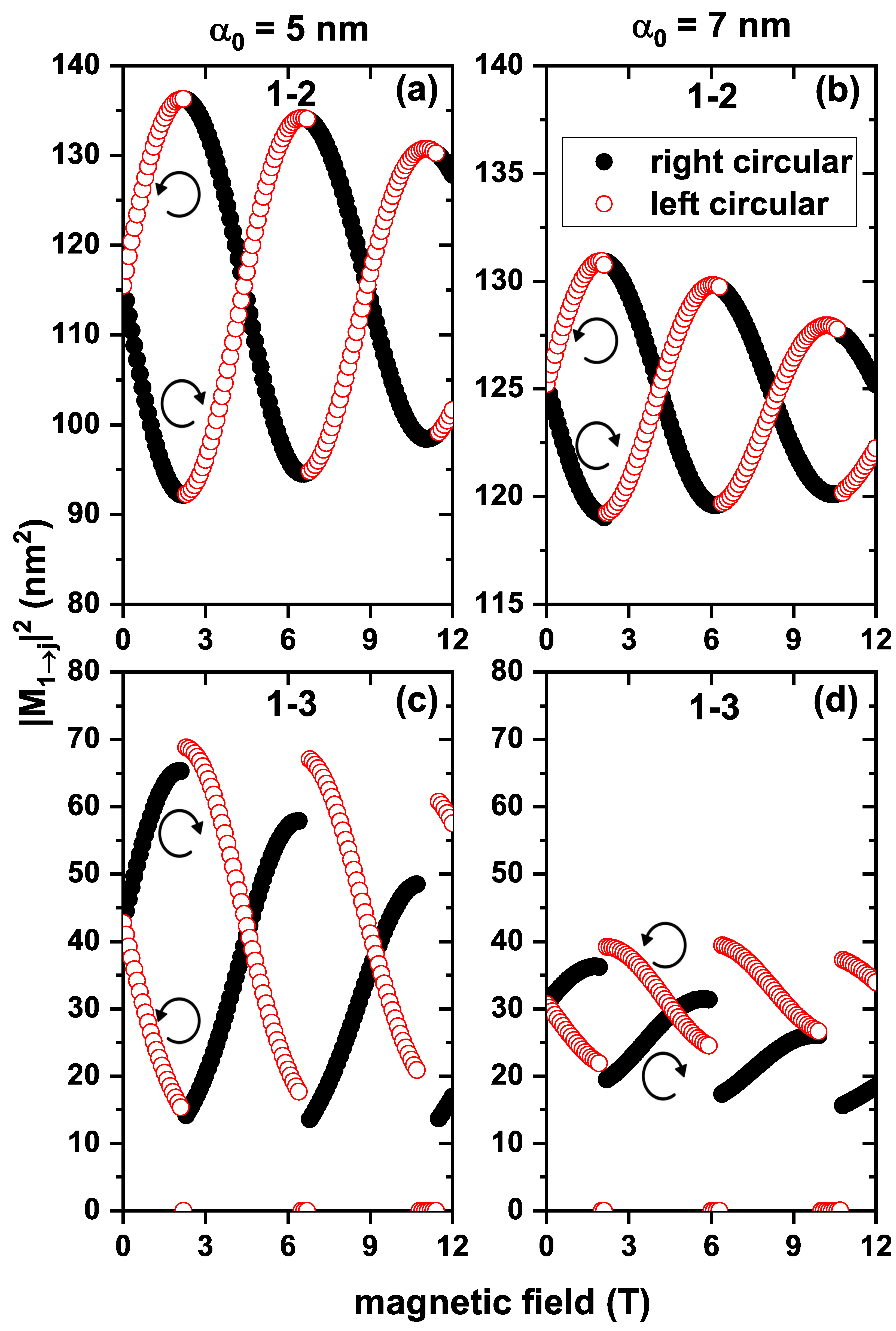
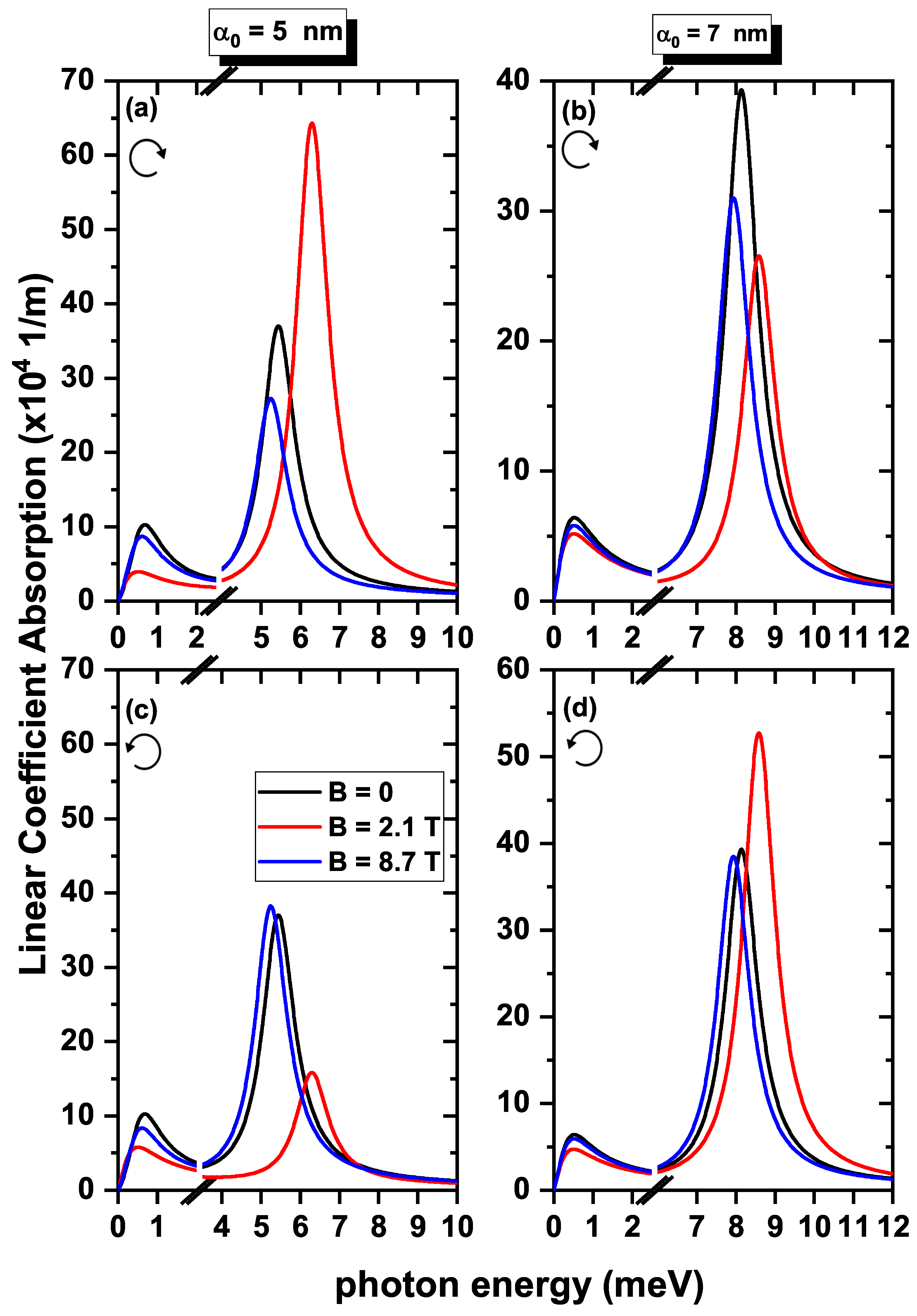
| θ0 = 360° | Right Circular Polarization | (nm) | Left Circular Polarization | ||||
|---|---|---|---|---|---|---|---|
| B (T) | B (T) | ||||||
| 0 | 2.1 | 8.7 | 0 | 2.1 | 8.7 | ||
| (nm2) | 115.51 | 92.28 | 117.71 | 5 | 115.51 | 136.29 | 112.98 |
| (nm2) | 42.79 | 65.36 | 32.37 | 42.79 | 15.36 | 45.96 | |
| (meV) | 0.46 | 0.05 | 0.34 | 0.46 | 0.05 | 0.34 | |
| (meV) | 5.42 | 6.28 | 5.22 | 5.42 | 6.28 | 5.22 | |
| (nm2) | 125.22 | 130.88 | 123.10 | 7 | 125.22 | 119.23 | 125.67 |
| (nm2) | 30.70 | 19.50 | 24.71 | 30.70 | 39.22 | 30.81 | |
| (meV) | 0.14 | 0.01 | 0.10 | 0.14 | 0.01 | 0.10 | |
| (meV) | 8.12 | 8.57 | 7.92 | 8.12 | 8.57 | 7.92 | |
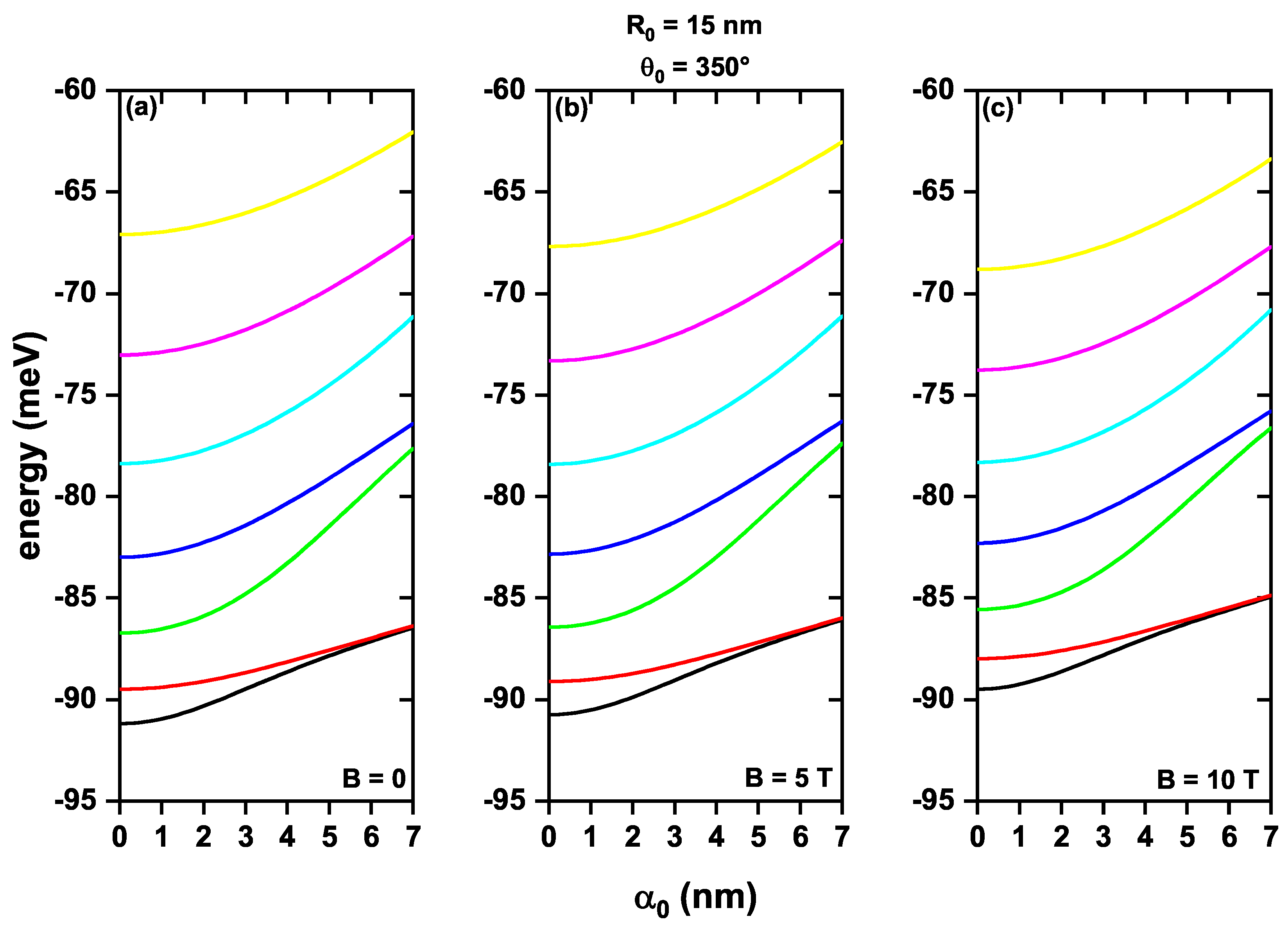
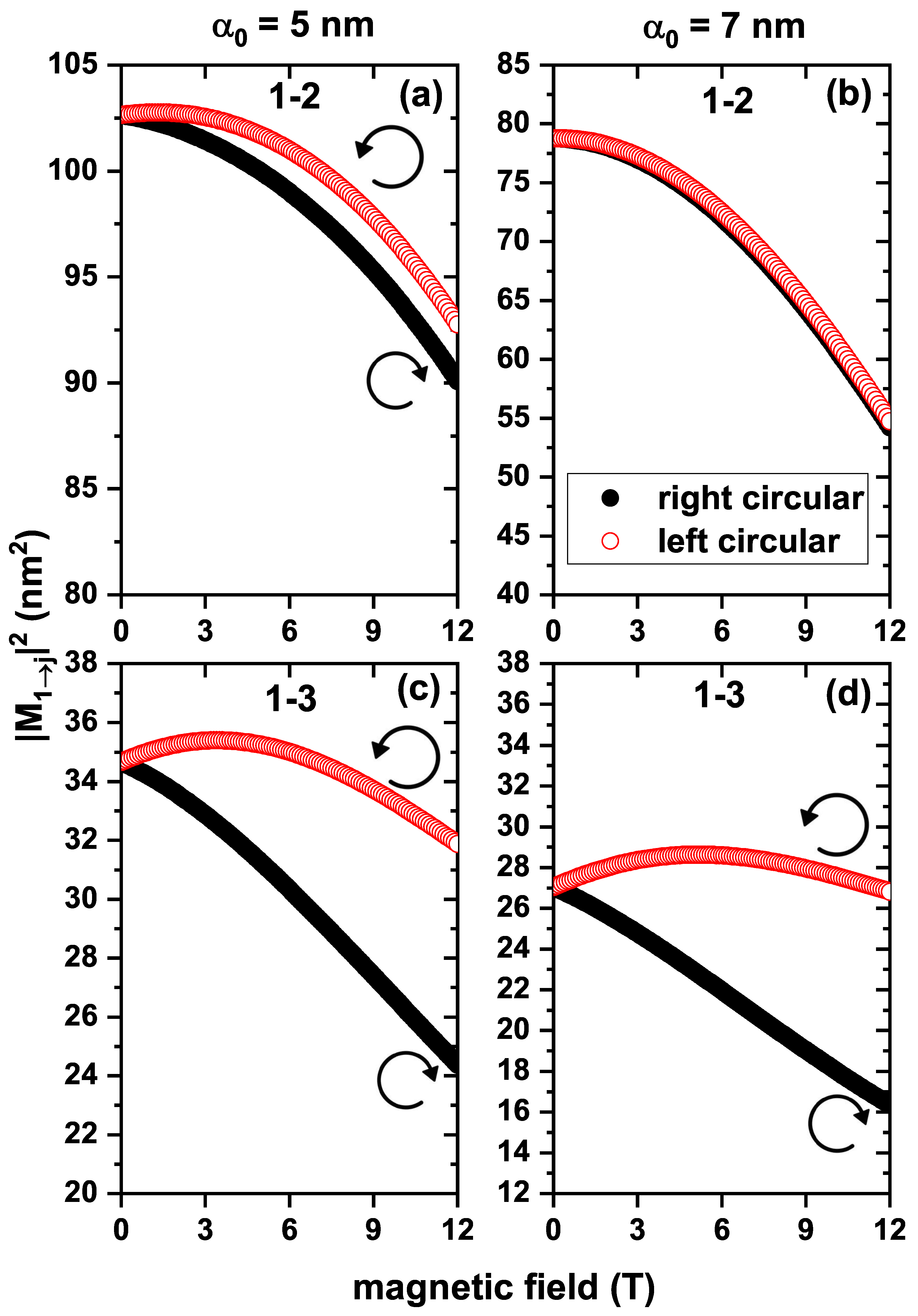
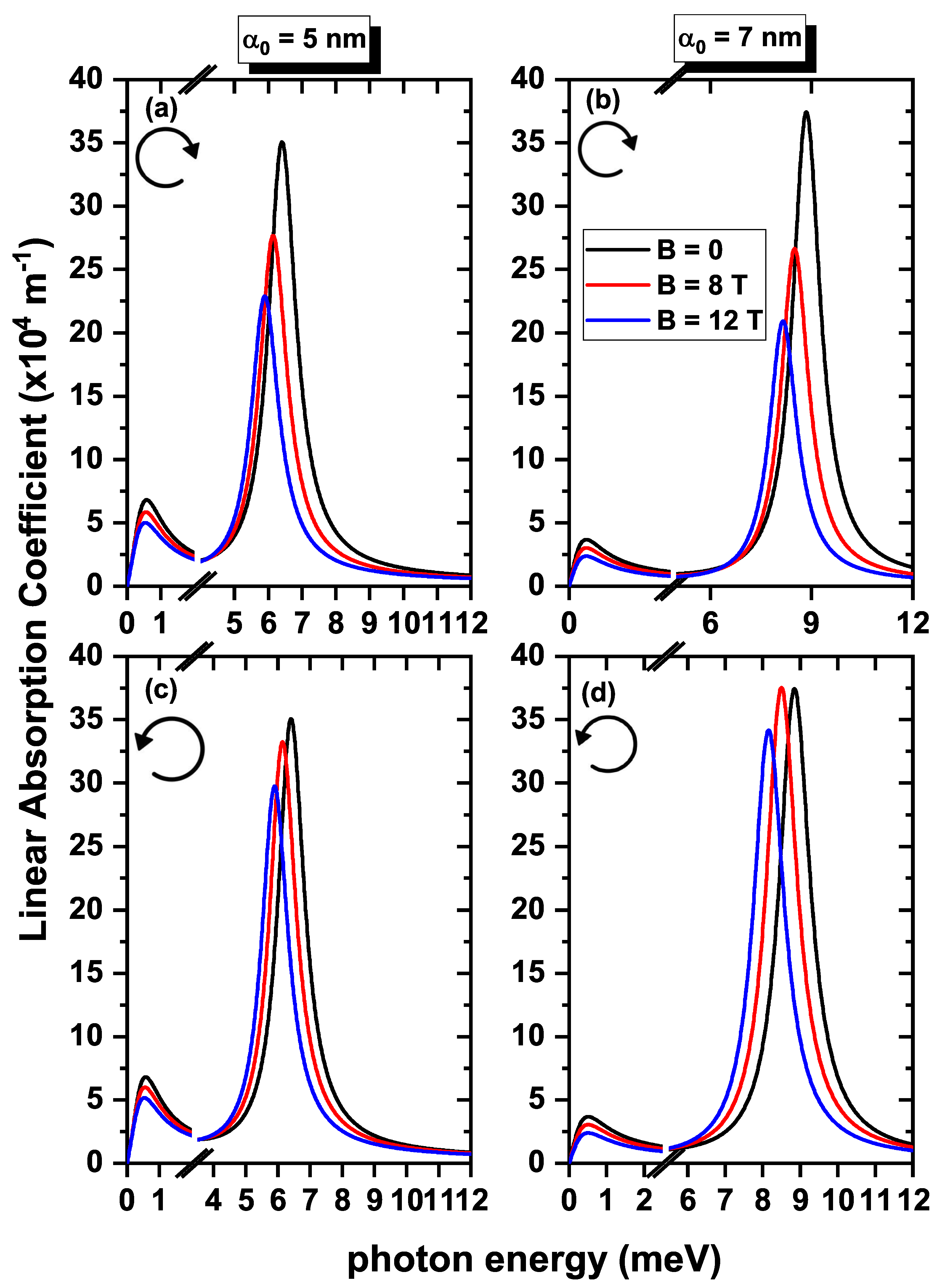
| θ0 = 350° | Right Circular Polarization | α0 (nm) | Left Circular Polarization | ||||
|---|---|---|---|---|---|---|---|
| B (T) | B (T) | ||||||
| 0 | 8 | 12 | 0 | 8 | 12 | ||
| (nm2) | 102.64 | 96.66 | 90.09 | 5 | 102.64 | 99.06 | 92.77 |
| (nm2) | 34.66 | 28.40 | 24.39 | 34.66 | 34.23 | 31.88 | |
| (meV) | 0.28 | 0.23 | 0.18 | 0.28 | 0.23 | 0.18 | |
| (meV) | 6.39 | 6.12 | 5.88 | 6.39 | 6.12 | 5.88 | |
| (nm2) | 78.78 | 67.12 | 54.23 | 7 | 78.78 | 67.67 | 54.75 |
| (nm2) | 27.05 | 19.99 | 16.35 | 27.05 | 28.25 | 26.82 | |
| (meV) | 0.09 | 0.07 | 0.06 | 0.09 | 0.07 | 0.06 | |
| (meV) | 8.83 | 8.49 | 8.14 | 8.83 | 8.49 | 8.14 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
León-González, J.C.; Toscano-Negrette, R.G.; Vinasco, J.A.; Morales, A.L.; Mora-Ramos, M.E.; Duque, C.A. Influence of a Non-Resonant Intense Laser and Structural Defect on the Electronic and Optical Properties of a GaAs Quantum Ring under Inversely Quadratic Potential. Condens. Matter 2023, 8, 52. https://doi.org/10.3390/condmat8020052
León-González JC, Toscano-Negrette RG, Vinasco JA, Morales AL, Mora-Ramos ME, Duque CA. Influence of a Non-Resonant Intense Laser and Structural Defect on the Electronic and Optical Properties of a GaAs Quantum Ring under Inversely Quadratic Potential. Condensed Matter. 2023; 8(2):52. https://doi.org/10.3390/condmat8020052
Chicago/Turabian StyleLeón-González, José C., Rafael G. Toscano-Negrette, Juan A. Vinasco, Alvaro L. Morales, Miguel E. Mora-Ramos, and Carlos A. Duque. 2023. "Influence of a Non-Resonant Intense Laser and Structural Defect on the Electronic and Optical Properties of a GaAs Quantum Ring under Inversely Quadratic Potential" Condensed Matter 8, no. 2: 52. https://doi.org/10.3390/condmat8020052
APA StyleLeón-González, J. C., Toscano-Negrette, R. G., Vinasco, J. A., Morales, A. L., Mora-Ramos, M. E., & Duque, C. A. (2023). Influence of a Non-Resonant Intense Laser and Structural Defect on the Electronic and Optical Properties of a GaAs Quantum Ring under Inversely Quadratic Potential. Condensed Matter, 8(2), 52. https://doi.org/10.3390/condmat8020052







