Structural, Electronic, and Optical Properties of Wurtzite VxAl1−xN Alloys: A First-Principles Study
Abstract
1. Introduction
2. Computational Methods
3. Results
3.1. Composition Dependence of Structural Properties
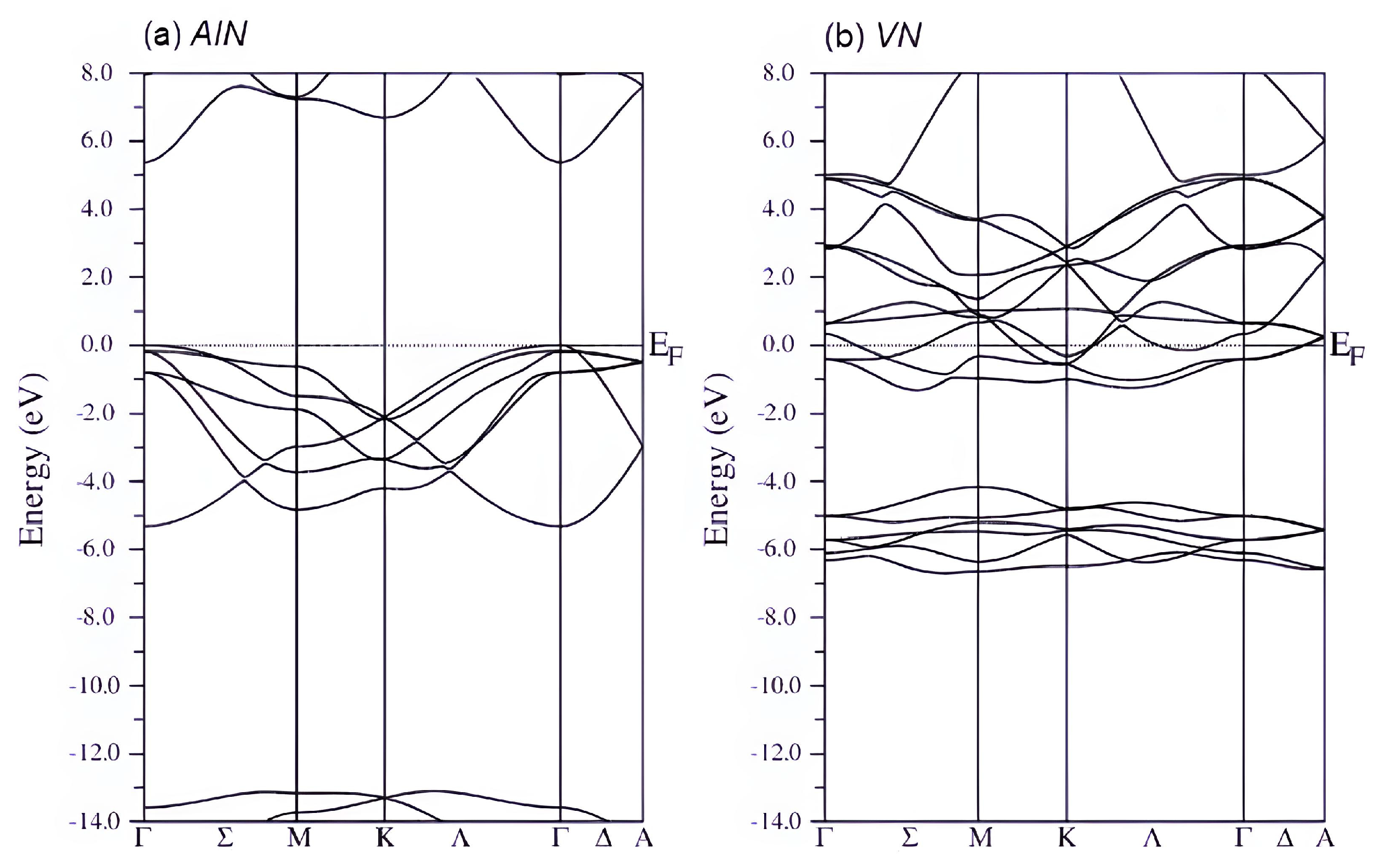
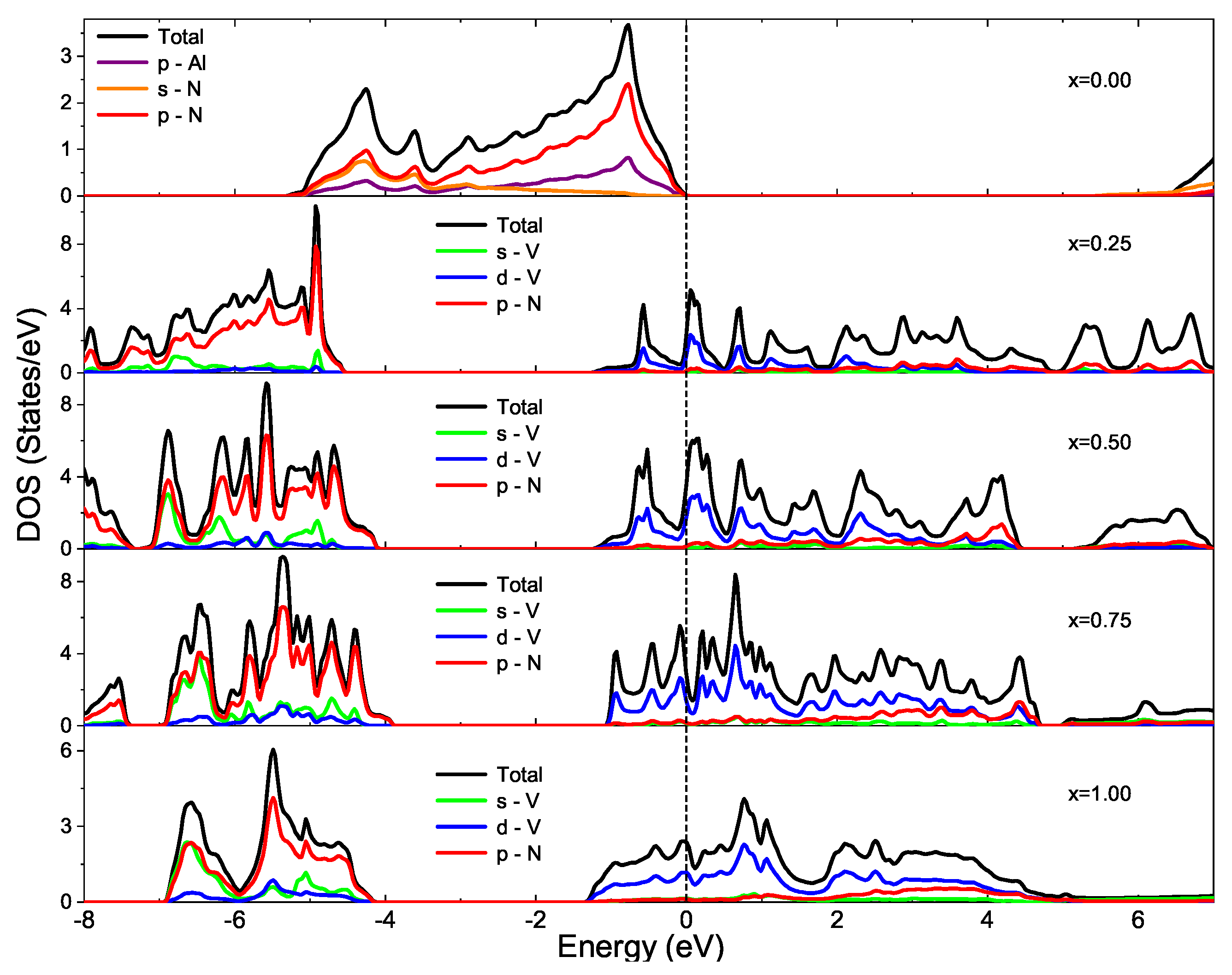
3.2. Electronic Structure
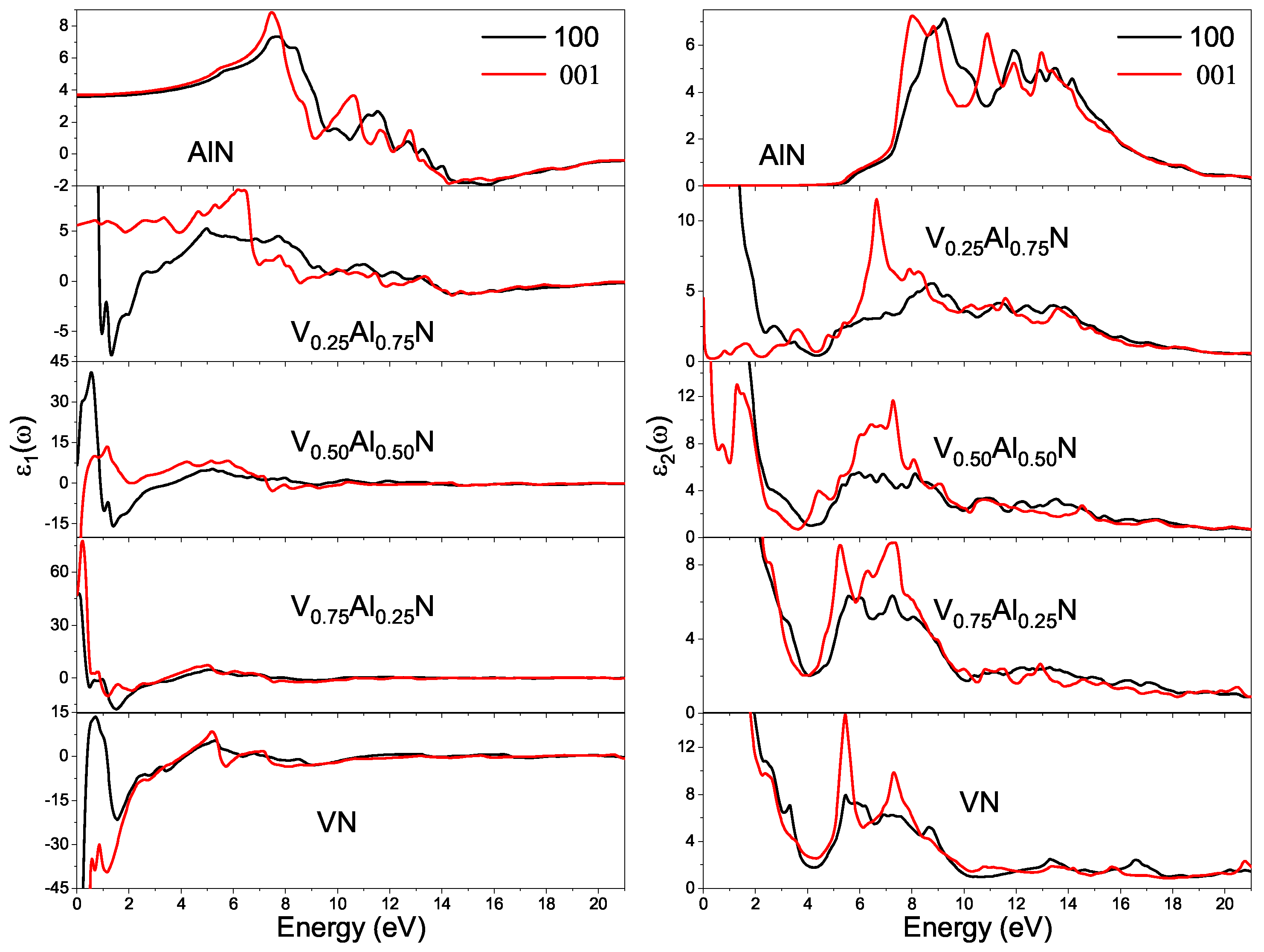
3.3. Optical Properties
3.3.1. Dielectric Function
3.3.2. Refractive Index and Extinction Coefficient
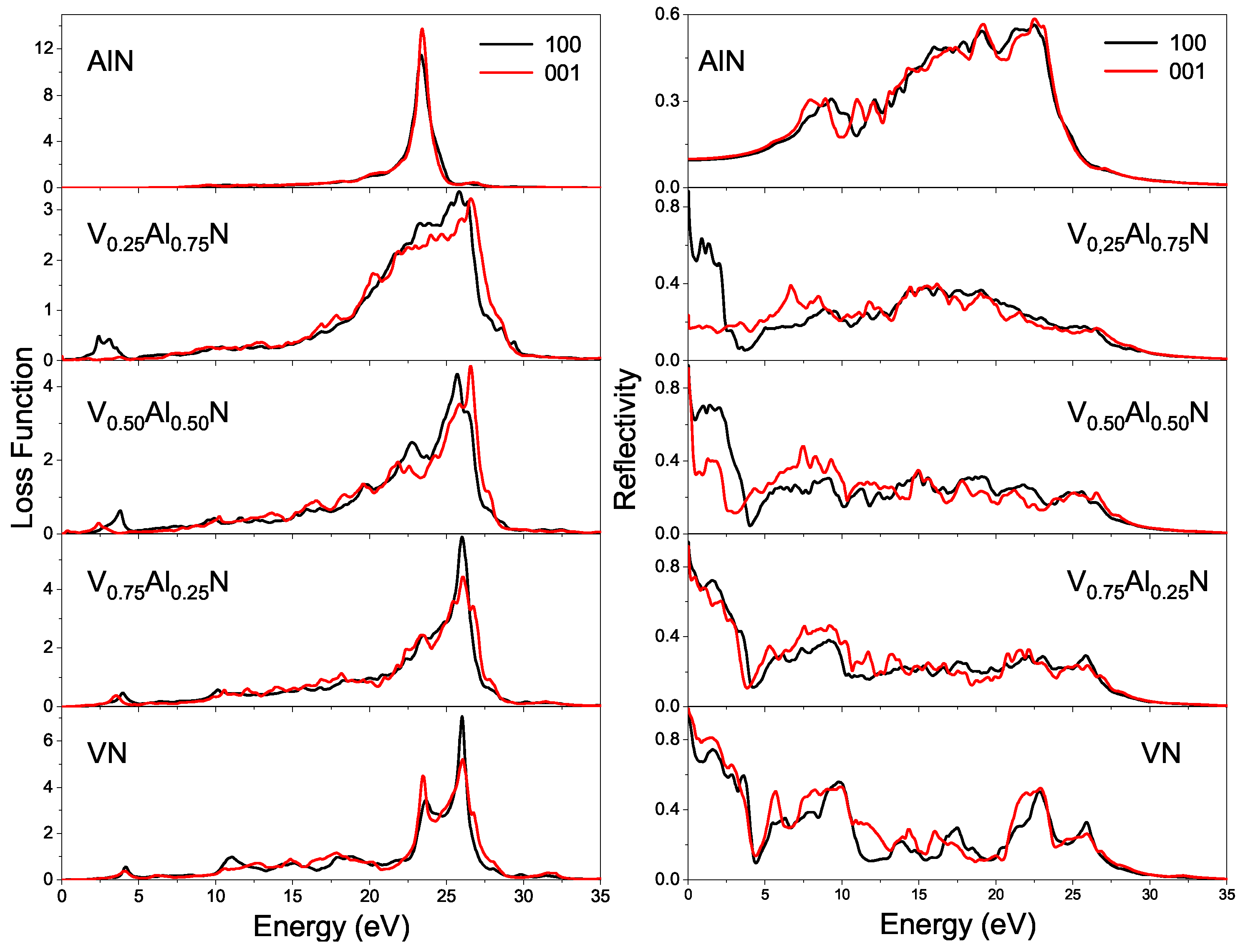
3.3.3. Energy Loss Function and Reflective Spectra
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ohno, H. Toward Functional Spintronics. Science 2001, 291, 840. [Google Scholar] [CrossRef] [PubMed]
- Miyashiro, F.; Iwase, N.; Tsuge, A.; Ueno, F.; Nakahashi, M.; Takahashi, T. High thermal conductivity aluminum nitride ceramic substrates and packages. IEEE Trans. Compon. Hybrids Manuf. Technol. 1990, 13, 313–319. [Google Scholar] [CrossRef]
- Fischer, A.J.; Allerman, A.A.; Crawford, M.H.; Bogart, K.H.A.; Lee, S.R.; Kaplar, R.J.; Chow, W.W.; Kurtz, S.R.; Fullmer, K.W.; Figiel, J.J. Room-temperature direct current operation of 290 nm light-emitting diodes with milliwatt power levels. Appl. Phys. Lett. 2004, 84, 3394–3396. [Google Scholar] [CrossRef]
- Rajan, S.; Waltereit, P.; Poblenz, C.; Heikman, S.J.; Green, D.S.; Speck, J.S.; Mishra, U.K. Power performance of AlGaN-GaN HEMTs grown on SiC by plasma-assisted MBE. IEEE Electron Device Lett. 2004, 25, 247–249. [Google Scholar] [CrossRef]
- Taniyasu, Y.; Kasu, M.; Makimoto, T. An aluminium nitride light-emitting diode with a wave length of 210 nanometers. Nature 2006, 441, 325–328. [Google Scholar] [CrossRef]
- Ozgit-Akgun, C.; Goldenberg, E.; Okyay, A.K.; Biyikli, N. Hollow cathode plasma-assisted atomic layer deposition of crystalline AlN, GaN and AlxGa1-xN thin films at low temperatures. J. Mater. Chem. C 2014, 2, 2123–2136. [Google Scholar] [CrossRef]
- Beiranvanda, R.; Valedbagi, S. Electronic and optical properties of advance semiconductor materials: BN, AlN and GaN nanosheets from first principles. Int. J. Light Electron Opt. 2016, 127, 1553–1560. [Google Scholar] [CrossRef]
- Adachi, S. Properties of Semiconductor Alloys: Group-IV, IIIV and IIVI Semiconductors; John Wiley and Sons Ltd.: West Sussex, UK, 2009. [Google Scholar]
- Doumi, B.; Mokaddem, A.; I-Boushaki, M.; Bensaid, D. First-principle investigation of magnetic and electronic properties of vanadium- and chromium-doped cubic aluminum phosphide. Mater. Sci. Semicond. Process. 2015, 32, 166–171. [Google Scholar] [CrossRef]
- Kervan, S.; Kervan, N. First-principles study on half-metallic ferromagnetism in the diluted magnetic semiconductor (DMS) Al1-xMnxP compounds. J. Magn. Magn. Mater. 2015, 382, 63–70. [Google Scholar] [CrossRef]
- Munekata, H.; Ohno, H.; von Molnar, S.; Segmuller, A.; Chang, L.L.; Esaki, L. Diluted magnetic III-V semiconductors. Phys. Rev. Lett. 1989, 63, 1849. [Google Scholar] [CrossRef]
- Dietl, T.; Ohno, H.; Matsukura, F.; Cibert, J.; Ferrand, D. Zener Model Description of Ferromagnetism in Zinc-Blende Magnetic Semiconductors. Science 2000, 287, 1019–1022. [Google Scholar] [CrossRef] [PubMed]
- Haury, A.; Wasiela, A.; Arnoult, A.; Cibert, J.; Tatarenko, S.; Dietl, T.; Merle, Y. Observation of a Ferromagnetic Transition Induced by Two-Dimensional Hole Gas in Modulation-Doped CdMnTe Quantum Wells. Phys. Rev. Lett. 1997, 79, 511. [Google Scholar] [CrossRef]
- Hansen, L.; Ferrand, D.; Richter, G.; Thierley, M.; Hock, V.; Schwarz, N.; Reuscher, G.; Schmidt, G.; Molenkamp, L.W.; Waag, A. Epitaxy and magnetotransport properties of the diluted magnetic semiconductor p-Be1-xMnxTe. Appl. Phys. Lett. 2001, 79, 3125–3127. [Google Scholar] [CrossRef]
- Fukushima, T.; Sato, K.; Katayama-Yoshida, H.; Dederichs, P.H. Spinodal Decomposition under Layer by Layer Growth Condition and High Curie Temperature Quasi-One-Dimensional Nano-Structure in Dilute Magnetic Semiconductors. Jpn. J. Appl. Phys. 2006, 45, L416. [Google Scholar] [CrossRef]
- Katayama-Yoshida, H.; Sato, K.; Fukushima, T.; Toyoda, M.; Kizaki, H.; Dinh, V.A.; Dederichs, P.H. Theory of ferromagnetic semiconductors. Phys. Status Solidi 2007, 204, 15. [Google Scholar] [CrossRef]
- Katayama-Yoshida, H.; Sato, K.; Fukushima, T.; Toyoda, M.; Kizaki, H.; Dinh, V.A.; Dederichs, P.H. Computational nano-materials design for high-ferromagnetism in wide-gap magnetic semiconductors. J. Magn. Magn. Mater. 2007, 310, 2070–2077. [Google Scholar] [CrossRef]
- Sato, K.; Fukushima, T.; Katayama-Yoshida, H. Super-Paramagnetic Blocking Phenomena and Room-Temperature Ferromagnetism in Wide Band-Gap Dilute Magnetic Semiconductor (Ga, Mn)N. Jpn. J. Appl. Phys. 2007, 46, L682. [Google Scholar] [CrossRef]
- Sato, K.; Schweika, W.; Dederichs, P.H.; Katayama-Yoshida, H. Low-temperature ferromagnetism in (Ga, Mn)N: Ab initio calculations. Phys. Rev. B 2004, 70, 201202. [Google Scholar] [CrossRef]
- Toyoda, M.; Akai, H.; Sato, K.; Katayama-Yoshida, H. Electronic structures of (Zn, TM)O (TM: V, Cr, Mn, Fe, Co, and Ni) in the self-interaction-corrected calculations. Phys. B Condens. Matter 2006, 376, 647–650. [Google Scholar] [CrossRef]
- Gopal, P.; Spaldin, N.A. Magnetic interactions in transition-metal-doped ZnO: An ab initio study. Phys. Rev. B Cover. Condens. Matter Mater. Phys. 2006, 74, 094418. [Google Scholar] [CrossRef]
- Cao, H.; Lu, P.; Cong, Z.; Yu, Z.; Cai, N.; Zhang, X.; Gao, T.; Wang, S. Magnetic properties in (Mn, Fe)-codoped ZnO nanowire. Thin Solid Film 2013, 548, 480–484. [Google Scholar] [CrossRef]
- Lee, H.J.; Jeong, S.Y.; Cho, C.R.; Park, C.H. Study of diluted magnetic semiconductor: Co-doped ZnO. Appl. Phys. Lett. 2002, 81, 4020–4022. [Google Scholar] [CrossRef]
- Huang, H.H.; Yang, C.A.; Lai, C.H.; Chin, T.S.; Huang, H.E.; Bor, H.Y.; Huang, R.T. Room-temperature fabricated ZnCoO diluted magnetic semiconductors. J. Appl. Phys. 2007, 101, 09H116. [Google Scholar] [CrossRef]
- Hori, H.; Sonada, S.; Sasaki, T.; Yamanoto, Y.; Shimizu, S.; Suga, K.; Kindo, K. High-TC ferromagnetism in diluted magnetic semiconducting GaN:Mn films. Phys. B Condens. Matter 2002, 324, 142–150. [Google Scholar] [CrossRef]
- Frazier, R.M.; Thaler, G.T.; Leifer, J.Y.; Hite, J.K.; Gila, B.P.; Abernathy, C.R.; Pearton, S.J. Role of growth conditions on magnetic properties of AlCrN grown by molecular beam epitaxy. Appl. Phys. Lett. 2005, 86, 052101. [Google Scholar] [CrossRef]
- Li, Y.F.; Zhou, Z.; Chen, Y.S.; Chen, Z.F. Do all wurtzite nanotubes prefer faceted ones? J. Chem. Phys. 2009, 130, 204706. [Google Scholar] [CrossRef]
- Ko, K.Y.; Barber, Z.H.; Blamire, M.G. Structural and magnetic properties of V-doped AlN thin films. J. Appl. Phys. 2006, 100, 083905. [Google Scholar] [CrossRef]
- Wu, Q.; Huang, Z.; Wu, R.; Chen, L. Cu-doped AlN: A dilute magnetic semiconductor free of magnetic cations from first principles study. J. Phys. Condens. Matter 2007, 19, 056209. [Google Scholar] [CrossRef]
- Shi, L.-J.; Zhu, L.-F.; Zhao, Y.-H.; Liu, B.-G. Nitrogen defects and ferromagnetism in Cr-doped dilute magnetic semiconductor AlN from first principles. Phys. Rev. B 2008, 78, 195206. [Google Scholar] [CrossRef]
- Yao, G.; Fan, G.; Xing, H.; Zheng, S.; Ma, J.; Zhang, Y.; He, L. Electronic structure and magnetism of V-doped AlN. J. Magn. Magn. Mater. 2013, 331, 117–121. [Google Scholar] [CrossRef]
- Heiba, Z.K.; Mohamed, M.B.; Ahmed, S.I. Optical and electronic correlation in Mg-doped nano cadmium sulfide. Opt. Quantum Electron. 2021, 53, 218. [Google Scholar] [CrossRef]
- Ściesiek, M.; Sawicki, K.; Pacuski, W.; Sobczak, K.; Kazimierczuk, T.; Golnik, A.; Suffczyński, J. Long-distance coupling and energy transfer between exciton states in magnetically controlled microcavities. Commun. Mater. 2020, 1, 78. [Google Scholar] [CrossRef]
- Brodbeck, S.; De Liberato, S.; Amthor, M.; Klaas, M.; Kamp, M.; Worschech, L.; Schneider, C.; Höfling, S. Experimental Verification of the Very Strong Coupling Regime in a GaAs Quantum Well Microcavity. Phys. Rev. Lett. 2017, 119, 027401. [Google Scholar] [CrossRef] [PubMed]
- Kavokin, A.; Malpuech, G.; Gil, B. Semiconductor microcavities: Towards polariton lasers. Internet J. Nitride Semicond. Res. 2003, 3, 1–25. [Google Scholar] [CrossRef]
- Thapa, R.; Saha, B.; Chattopadhyay, K.K. First principles analysis on V3+ doped aluminum nitride. Comput. Mater. Sci. 2010, 49, 363–367. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Madsen, G.K.H.; Kvasnicka, D.; Luitz, J. WIEN2k: An Augmented Plane Wave plus Local Orbital Program for Calculating Crystal Properties; Vienna University of Technology: Vienna, Austria, 2001. [Google Scholar]
- Perdew, J.P.; Burke, K.; Emzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Tran, F.; Blaha, P. Accurate Band Gaps of Semiconductors and Insulators with a Semilocal Exchange-Correlation Potential. Phys. Rev. Lett. 2009, 102, 226401. [Google Scholar] [CrossRef]
- Murnaghan, F.D. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244–247. [Google Scholar] [CrossRef]
- Yu, P.Y.; Cardona, M. Fundamental of Semiconductors: Physics and Materials Properties, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Alay-e-Abbas, S.M.; Nazir, S.; Noor, N.A.; Amin, N.; Shaukat, A. Thermodynamic stability and vacancy defect formation energies in SrHfO3. J. Phys. Chem. C 2014, 118, 19625–19634. [Google Scholar] [CrossRef]
- Alay-e-Abbas, S.M.; Shaukat, A. First principles study of structural, electronic and optical properties of polymorphic forms of Rb2Te. Solid State Sci. 2011, 13, 1052–1059. [Google Scholar] [CrossRef]
- Warner, J.M.; Bechstedt, F. Properties of strained wurtzite GaN and AlN: Ab initio studies. Phys. Rev. B 2002, 66, 115202. [Google Scholar]
- González, R.; López, W.; Rodríguez, J. AB initio studies of the structural and electronics properties of vanadium nitride. Rev. Cienc. e Ingeniería Neogranadina 2007, 17, 23–33. [Google Scholar] [CrossRef]
- Vegard, L. Die Konstitution der Mischkristalle und die Raumfüllung der Atome. Z. für Physik. 1921, 5, 17–26. [Google Scholar] [CrossRef]
- Caetano, C.; Marques, M.; Ferreira, L.G.; Teles, L.K. Anomalous lattice parameter of magnetic semiconductor alloys. Appl. Phys. Lett. 2009, 94, 241914. [Google Scholar] [CrossRef]
- González-García, A.; López-Pérez, W.; Barragán-Yani, D.; González-Hernández, R. A Comparative DFT and DFT+U Study on Magnetism in Nickel-Doped Wurtzite AlN. J. Supercond. Nov. Magn. 2015, 28, 3185–3192. [Google Scholar] [CrossRef]
- González-García, A.; López-Pérez, W.; González-Hernández, R. Theoretical study of magnetic ordering and electronic properties of AgxAl1-xN compounds. Solid State Commun. 2011, 151, 1794–1797. [Google Scholar] [CrossRef]
- González-Hernández, R.; López-Pérez, W.; Fajardo, F.; Rodríguez, J.A. Pressure effects on the electronic and magnetic properties of GaxV1-xN compounds: Ab-initio study. Mater. Sci. Eng. B 2009, 163, 190–193. [Google Scholar] [CrossRef]
- Dergal, M.; Faraoun, H.I.; Mahmoudi, A. First principles study on structural, electronic and optical properties of 3d transition metals-substituted CuGaSe2. Optik 2017, 135, 346–352. [Google Scholar] [CrossRef]
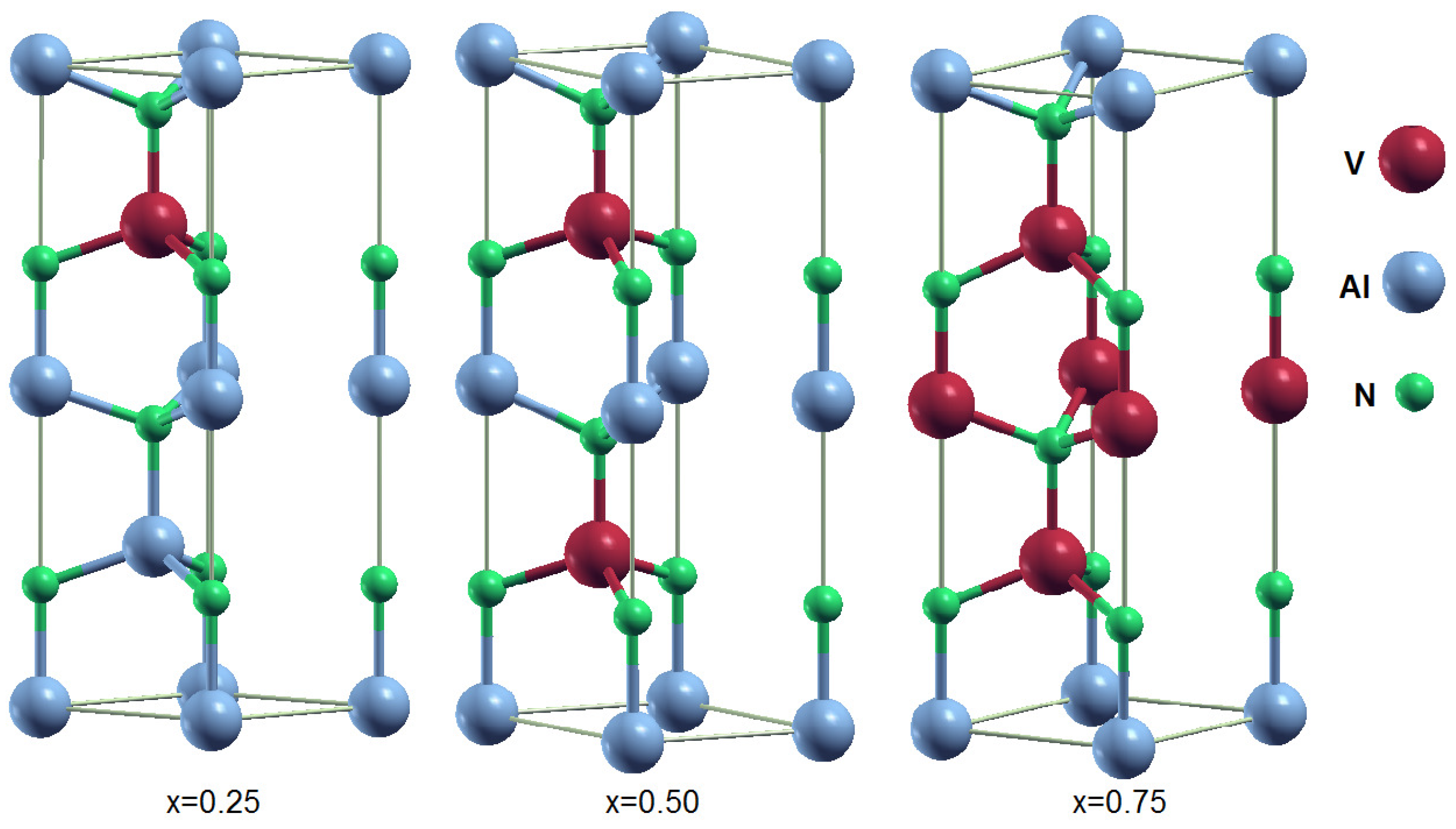
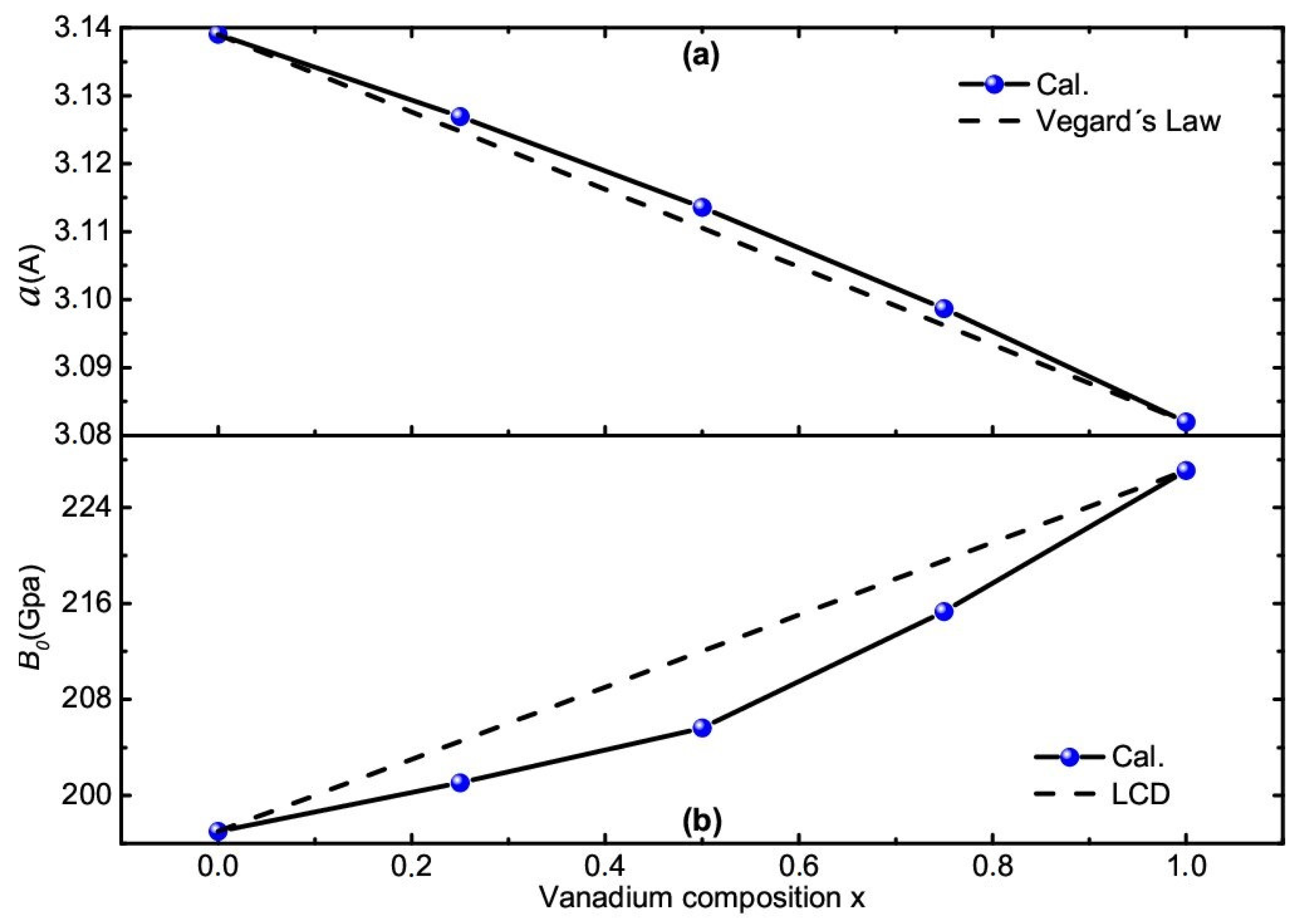

| x | a(Å) | c/a | (GPa) | () | (eV) |
|---|---|---|---|---|---|
| 0 | 3.139 | 1.602 | 196 | 21.436 | −14.839 |
| 0.25 | 3.126 | 1.66 | 202 | 21.939 | −15.403 |
| 0.50 | 3.110 | 1.71 | 201.6 | 22.232 | −16.051 |
| 0.75 | 3.105 | 1.70 | 219.3 | 22.071 | −17.101 |
| 1 | 3.094 | 1.64 | 227.08 | 21.898 | −18.167 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Escorcia-Salas, G.E.; Restrepo-Leal, D.; Martinez-Castro, O.; López-Pérez, W.; Sierra-Ortega, J. Structural, Electronic, and Optical Properties of Wurtzite VxAl1−xN Alloys: A First-Principles Study. Condens. Matter 2023, 8, 61. https://doi.org/10.3390/condmat8030061
Escorcia-Salas GE, Restrepo-Leal D, Martinez-Castro O, López-Pérez W, Sierra-Ortega J. Structural, Electronic, and Optical Properties of Wurtzite VxAl1−xN Alloys: A First-Principles Study. Condensed Matter. 2023; 8(3):61. https://doi.org/10.3390/condmat8030061
Chicago/Turabian StyleEscorcia-Salas, Gene Elizabeth, Diego Restrepo-Leal, Oscar Martinez-Castro, William López-Pérez, and José Sierra-Ortega. 2023. "Structural, Electronic, and Optical Properties of Wurtzite VxAl1−xN Alloys: A First-Principles Study" Condensed Matter 8, no. 3: 61. https://doi.org/10.3390/condmat8030061
APA StyleEscorcia-Salas, G. E., Restrepo-Leal, D., Martinez-Castro, O., López-Pérez, W., & Sierra-Ortega, J. (2023). Structural, Electronic, and Optical Properties of Wurtzite VxAl1−xN Alloys: A First-Principles Study. Condensed Matter, 8(3), 61. https://doi.org/10.3390/condmat8030061







