Effects of the Exciton Fine Structure Splitting on the Entanglement-Based Quantum Key Distribution

Abstract

The reliable transmission of secure keys is one of the essential tasks to be efficiently accomplished by quantum information processing, and the use of entangled particles is a very important tool toward that goal. However, efficient production of maximally entangled states is still a challenge for further progress in quantum computing and quantum communication. In the search for optimal sources of entanglement, quantum dots have emerged as promising candidates, but the presence of dephasing in the generated entangled states raises questions about their real usefulness in large-scale quantum networks. In this work, we evaluate the effects of the exciton fine structure splitting, present in most quantum dot samples, on the fidelity of the BBM92 protocol for quantum key distribution. We find that the protocol’s performance is heavily impacted by such splitting and establish an upper limit for the product between the energy splitting and the exciton lifetime to have a dependable distributed key.

1. Introduction

One of the first discoveries in quantum computing and quantum information involved the use of quantum mechanics to safely distribute secret keys in such a way that the encryption of a message is governed by the principles of quantum mechanics. This procedure is known as quantum key distribution (QKD) and is one of the cornerstones of quantum cryptography [1,2,3]. In this very active field of research, significant progress has been made recently, accounting for reliable key distribution across long distances [4,5] and for networking implementations of the key transmission [6,7].

In 1935, Einstein, Podolsky and Rosen introduced the attractive properties of non-separable two-particle states in what is nowadays known as the EPR paradox [8]. Later that year, Niels Bohr argued that, in an entangled state, one cannot speak of the individual properties of each particle, managing in this way to refute the argument raised by such paradox [9]. Further experiments demonstrated that the idea of entanglement, instead of weakening quantum mechanics as a consistent theory, is indeed a fact that richly expands its possibilities for applications in information processing [10,11].

In the last two decades, one of the most studied and developed techniques to produce entanglement is the so-called radiative cascade decay in quantum dots (QDs), which features noticeable advantages with respect to the spontaneous parametric down-conversion, which is the so-far most-used source of entangled photon pairs [12,13,14,15]. Based on tomographic analysis, the generation of polarization-entangled photon pairs (PEPPs) from the biexciton–exciton–vacuum cascade in QDs was reported for the first time in 2006 [16,17]. In those works, either magnetic fields or spectral filtering were necessary to achieve the necessary conditions to obtain the entanglement, because in most QD samples the fine structure splitting (FSS) between neutral exciton states drastically reduces the quality of the quantum correlation between the emitted photons.

More recently, C. Schimpf et. al. demonstrated the viability of using GaAs quantum dots as PEPP sources for QKD by means of the BBM92 protocol [18], achieving effective transmission of digital images [19,20,21]. The used QD was intentionally selected to have a very small FSS, involving a “cherry picking” process that raises questions about the real usefulness of this type of entanglement source.

In this work, we study the quantitative effect of the FSS on the reliability of the BBM92 protocol for transmitting secret keys when implemented with a QD as source of entangled photons.

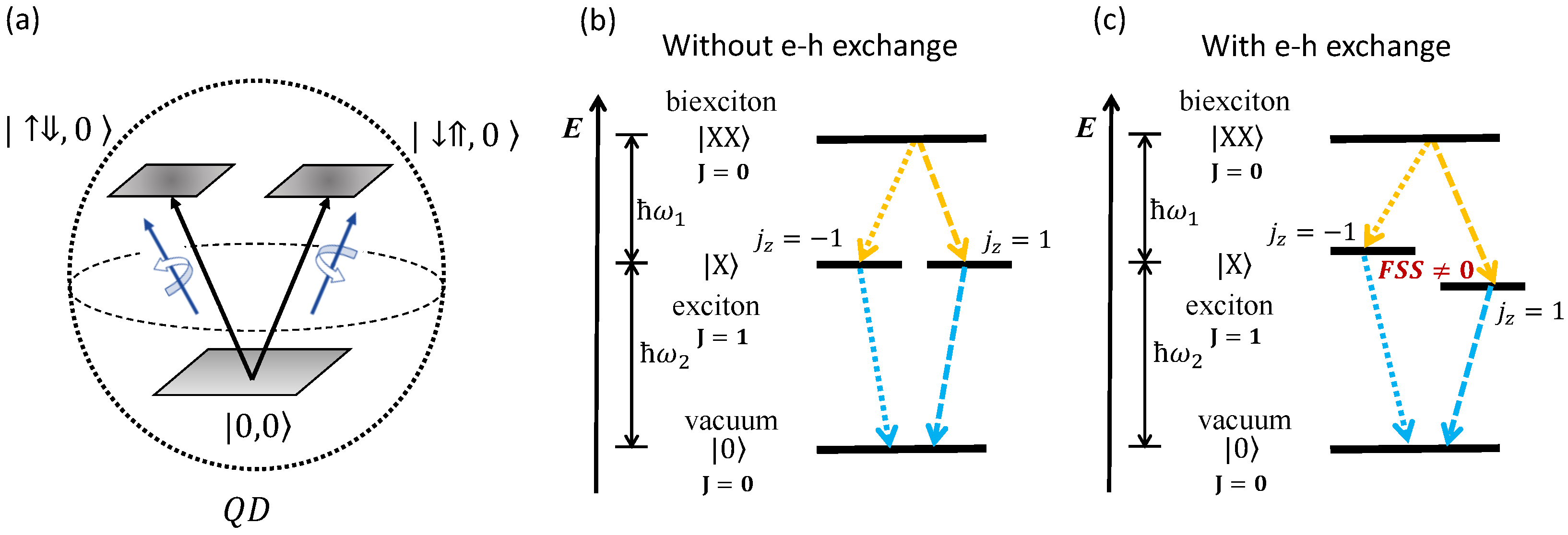
2. Fine Structure Splitting in Quantum Dots

In a typical III–V or II–VI semiconductor QD, the neutral exciton states with spin z-components $+1$ or $-1$ can be optically excited with either ${\sigma }^{+}$ or ${\sigma }^{-}$ circularly polarized light (see Figure 1a).

Those neutral exciton states are expected to be degenerate under the assumption that the relevant interactions between electron and hole (confinement potential and Coulomb interaction) are spin-independent, so that the z-component of the exciton angular momentum is conserved. Thus, there would be no energy difference between the states with exciton spin up or down, for a given coordinate system. This case is shown in Figure 1b.

Once the indistinguishability of quantum particles is considered, the exchange part of the electron–hole (e–h) Coulomb interaction, which is spin-dependent, plays an important role by breaking up the degeneracy and producing an energy splitting between the exciton states of different spins [22,23,24,25]. This is illustrated in Figure 1c.

This splitting between bright exciton states is a transversal issue to dots fabricated by different growth techniques and of various compositions [26,27,28,29,30]. In general, it is underlain by the long-range part of the e–h exchange and is related to the asymmetric shapes of the dots along their x-y cross-section.

To obtain a PEPP from a QD, the dot has to be initialized in the biexciton state, so that consecutive radiative decay from the biexciton to the exciton state, and then from the exciton to the ground state (exciton vacuum), yields strongly correlated photon pairs. If the $j_z=1$ and $j_z=-1$ exciton states are degenerated, two indistinguishable polarization decay paths are available and the two-photon state is maximally entangled [31,32,33]. In a basis of circularly polarized photons where $\left|\uparrow \right.〉$ and $\left|\downarrow \right.〉$ represent opposite polarizations, this state reads

$$\left|\Psi \right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left[\left|\uparrow \downarrow \right.〉-\left|\downarrow \uparrow \right.〉\right].$$

(1)

However, due to strong confinement and large electron hole overlap, the e–h exchange cannot be neglected and anisotropies in the QD shape lead to a measurable FSS in most QD samples. This represents an obstacle for production of PEPPs [34], since in that case the obtained two-photon state from the cascade radiative decay is

$$\left|\Psi \left(\theta \right)\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left[\left|\uparrow \downarrow \right.〉-e^{-i\theta \left(\tau \right)}\left|\downarrow \uparrow \right.〉\right],$$

(2)

where $\theta \left(\tau \right)=\frac{\mathcal{S}\tau }{\hslash }$, S is the FSS energy and $\tau$ is the lifetime of the neutral exciton state (elapsed time between the emission of the first and the second photon) [35].

Since the emission of the second photon will always require some finite time, if S becomes different from zero, the quantum correlations between the two photons in the bipartite state shall be impacted. This in turn, should affect the performance of any algorithm making use of such an entangled state.

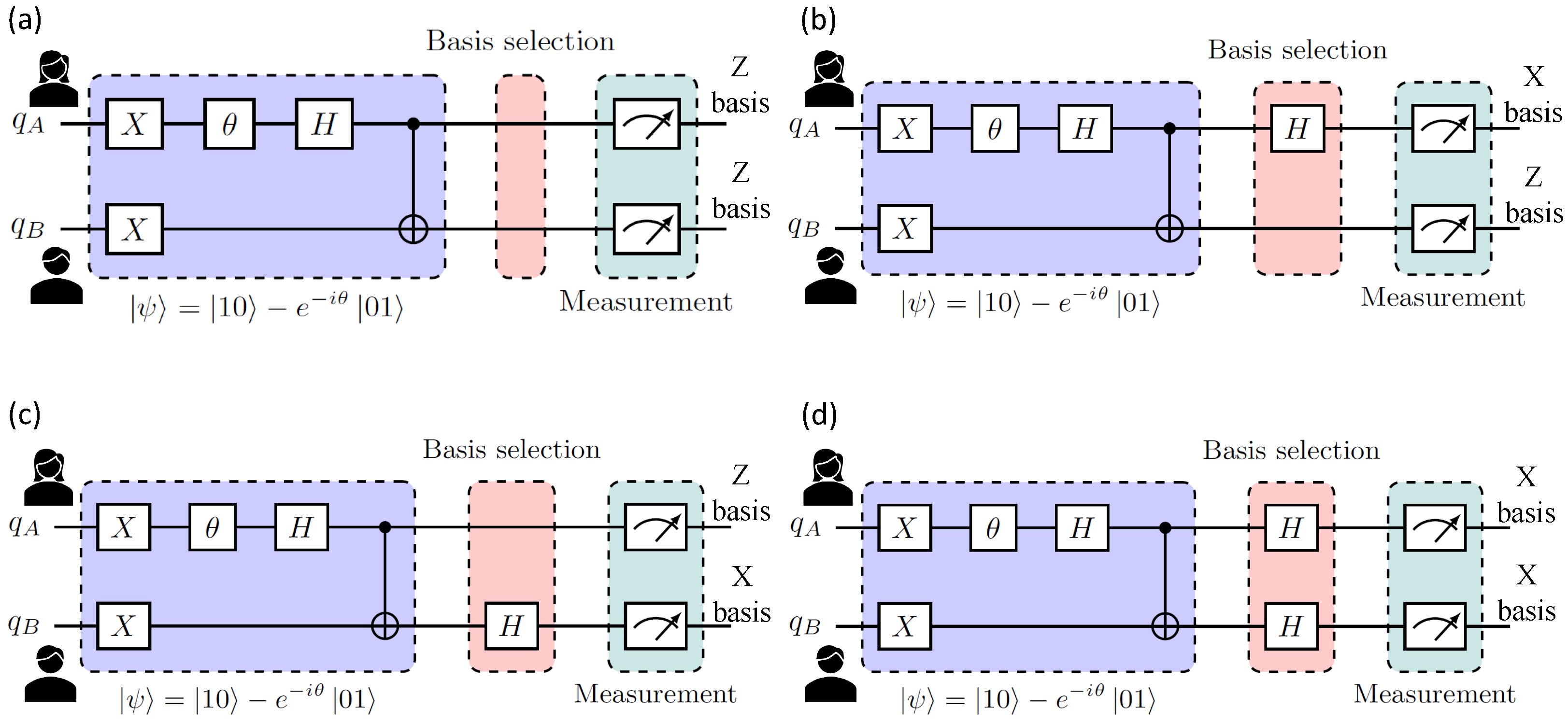
3. BBM92 Protocol for Quantum Key Distribution

The BBM92 is one of the most used protocols for QKD. It employs quantum entanglement for the secure transmission of data, without requiring Bell inequality measurements [18]. Its realization generally utilizes PEPPs.

Figure 2 shows a general scheme of the BBM92 protocol, where an ideal maximally entangled state is used to simultaneously transmit information to Alice and Bob in each event. Along a series of events, Alice and Bob randomly choose to carry out measurements on either the vertical–horizontal or the diagonal–antidiagonal basis. After comparison through a classical and non-necessarily secure channel as well as filtering, with certainty Alice and Bob end sharing a secret key perfectly anticorrelated (i.e., whenever Alice receives a “0”, Bob receives a “1” and vice-versa). The protocol guarantees that further screening can be performed to rule out eavesdropping, making the shared key completely safe.

Protocol Steps

The transmission of one bit of information in the BBM92 protocol is based on two main stages of information processing, where the first one is quantum and the second one is classical. The quantum communication part consists of the following: QI—Production of an entangled photon pair. QII—Distribution of the photon pair by means of waveguides, one to Alice and the other one to Bob. QIII—Alice and Bob separately and randomly chose a basis for measuring polarization of the corresponding photon. QIV—Each of them carry out the measurement in the chosen basis and registers it. As for the classical part, it consists of the following: CI—Alice and Bob share the information about the basis they used for the polarization measurement. CII—Alice and Bob compare such information and keep the bit only if the measurements were made in coincident basis; otherwise, the bit is discarded. CIII—If kept, Alice and Bob take the bit as part of the secret shared key, having into mind that the bits conserved by each of them are completely anticorrelated.

The protocol can be executed as many times as needed to transmit keys for as long as preferred.

4. Effects of the FSS in the QKD performance

The perfect anticorrelation between Alice’s and Bob’s data strings relies on the maximally entangled character of the bipartite state used for information transmission. Then, to address the effect that a reduction in the entanglement quality has on the reliability of the key distribution protocol, we need to evaluate the consequences of having S different from zero in Equation (2) [21].

To achieve that, it is necessary to consider the two-photon state generated by a radiative cascade decay in a QD in which the e–h exchange is not negligible (Equation (2)), written in a $\pi /2$ rotated basis ($\left|\to \right.〉$, $\left|\leftarrow \right.〉$), namely

$$\begin{array}{cc}\hfill \left|\Psi \left(\theta \right)\right.〉& ={\displaystyle \frac{1}{\sqrt{2}}}\left[{\displaystyle \frac{1}{2}}\left(\left|\to \right.〉+\left|\leftarrow \right.〉\right)\left(\left|\to \right.〉-\left|\leftarrow \right.〉\right)-{\displaystyle \frac{e^{-i\theta }}{2}}\left(\left|\to \right.〉-\left|\leftarrow \right.〉\right)\left(\left|\to \right.〉+\left|\leftarrow \right.〉\right)\right],\hfill \\ \hfill & ={\displaystyle \frac{1}{2\sqrt{2}}}[\left(1-e^{-i\theta }\right)\left|\to \to \right.〉-\left(1-e^{-i\theta }\right)\left|\leftarrow \leftarrow \right.〉+\left(1+e^{-i\theta }\right)\left|\leftarrow \to \right.〉\hfill \\ & -\left(1+e^{-i\theta }\right)\left|\to \leftarrow \right.〉].\hfill \end{array}$$

(3)

Thus, in the rotated basis, the probability of obtaining a given anticorrelated polarization measurement is

$$P_{\left|\leftarrow \to \right.〉}=P_{\left|\to \leftarrow \right.〉}={\left|{\displaystyle \frac{1+e^{-i\theta }}{2\sqrt{2}}}\right|}^2={\displaystyle \frac{1+cos\left(\theta \right)}{4}},$$

(4)

and the total probability of obtaining an anticorrelated measurement in any of the relevant basis is given by

$$\begin{array}{cc}\hfill P_{\mathrm{ant}}^T& =P_{\mathrm{Z}\mathrm{basis}}\left(P_{\left|\uparrow \downarrow \right.〉}+P_{\left|\downarrow \uparrow \right.〉}\right)+P_{\mathrm{X}\mathrm{basis}}\left(P_{\left|\to \leftarrow \right.〉}+P_{\left|\leftarrow \to \right.〉}\right),\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}\right)+{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{1+cos\left(\theta \right)}{4}}+{\displaystyle \frac{1+cos\left(\theta \right)}{4}}\right),\hfill \\ \hfill & ={\displaystyle \frac{3+cos\left(\theta \right)}{4}}.\hfill \end{array}$$

(5)

Since $\theta$ is a function of FFS, Equation (5) predicts the dependence of the probability of anticorrelation in a basis-coincident measurement, on the energy splitting of the QD the photon pair is emitted from. As expected, the anticorrelation is guaranteed ($P_{\mathrm{ant}}^T=1$) for the case $FSS=0$. As long as the product between the FSS and the delay time $\tau$ becomes significant, the correlation probability starts oscillating. As the probability $P_{\mathrm{ant}}^T$ departs from 1, the protocol becomes less reliable because there would be some uncertainty on each bit of the key shared between Alice and Bob. Such probability reaches a minimum of $\frac{1}{2}$ for the values $\theta =(2n+1)\pi$, with n integer. In those cases, the protocol becomes completely useless because that would correspond to the probability of having anticorrelated data just by randomly guessing the shared bit.

If we chose to focus on the part of the key in which the transmission fails, instead of on the part that is successfully distributed, the quantity to highlight would be the number of correlated bits normalized to the sifted data. This parameter would correspond to the commonly labeled qubit error rate (QBER). Such probability would be given by

$$QBER=1-P_{\mathrm{ant}}^T=\frac{1-cos\left(\theta \right)}{4}.$$

(6)

As expected, this error measurement behaves oppositely to the probability of desired anticorrelation, vanishing for $\theta =0$ and being maximum in $\theta =(2n+1)\pi$, with n integer.

Due to the fact that no eavesdropping is considered in the data transmission, the quantity $P_{\mathrm{ant}}^T$ is equivalent to the so-called secret key rate (SKR) for the protocol under the influence of $\theta$. Hence,

$$SKR+QBER=1,$$

(7)

holds in this case.

5. Quantum Computing Implementation

To verify the result presented in the previous section, we implement the BBM92 protocol using the quantum computing tool Qiskit [36,37], so that the theoretical prediction may be compared with the performance of the key distribution virtually executed by means of a quantum circuit.

To do that, on the one hand the polarization states are to be encoded in qubits, each of which is written in the computational basis $\left|0\right.〉$ and $\left|1\right.〉$. On the other hand, the generation of entangled states is performed by means of quantum gates (a Hadamard and a CNOT) applied on an initial two-qubit state of the form $|00\rangle$ [37]. To account for the physical reality of the QD source of PEPPs, a phase gate (rotation) is applied on one of the qubits, so that the corresponding part of the circuit yields a state as the one introduced in Equation (2). Thus, the effects of the exchange interaction between the electron and the hole confined in the zero-dimensional structure are included in the rotation angle $\theta$.

Afterwards, the section for random choice of basis for measurement by Alice and Bob was developed. In quantum circuits, the states are always measured in the base of the operator Z, the so-called computational basis. Then, to emulate measurements in other basis, it is necessary to correspondingly rotate the states to be measured. To do that, a pseudo-random number generator with options 0 or 1 was used. The four possible scenarios the program can go through are shown in Figure 3. The blue-shaded part in each circuit represents the QD-based entanglement generation.

The classical stage is carried out by standard “if” cycles, that compare and filter the strings of measurements from Alice and Bob, keeping only the data from coincident basis that constitutes the shared key using classical registers.

Since the optimal performance of the protocol is to yield perfectly anticorrelated data in the key strings, i.e., the number of anti-coincident bits (a “0” in Alice’s string corresponds to a “1” in Bob’s string and vice-versa) must be equal to the number of retained data after discarding the measurement from different basis. If the former is smaller than the latter, the QKD’s reliability is affected. Hence, we define the performance parameter (the SKR yielded by the quantum circuit)

$$P_P={\displaystyle \frac{\mathrm{Number}\mathrm{of}\mathrm{anti-coincident}\mathrm{bits}\mathrm{in}\mathrm{the}\mathrm{key}}{\mathrm{Number}\mathrm{of}\mathrm{sifted}\mathrm{bits}}}.$$

(8)

The smaller the $P_P$, the smaller the performance of the key distribution. The minimum possible value for this ratio is 0.5, that would correspond to the case in which the measurements are not correlated at all. This parameter, obtained from the execution of the quantum circuit, is to be compared with the theoretically found probability $P_{\mathrm{ant}}^T$ (Equation (5)).

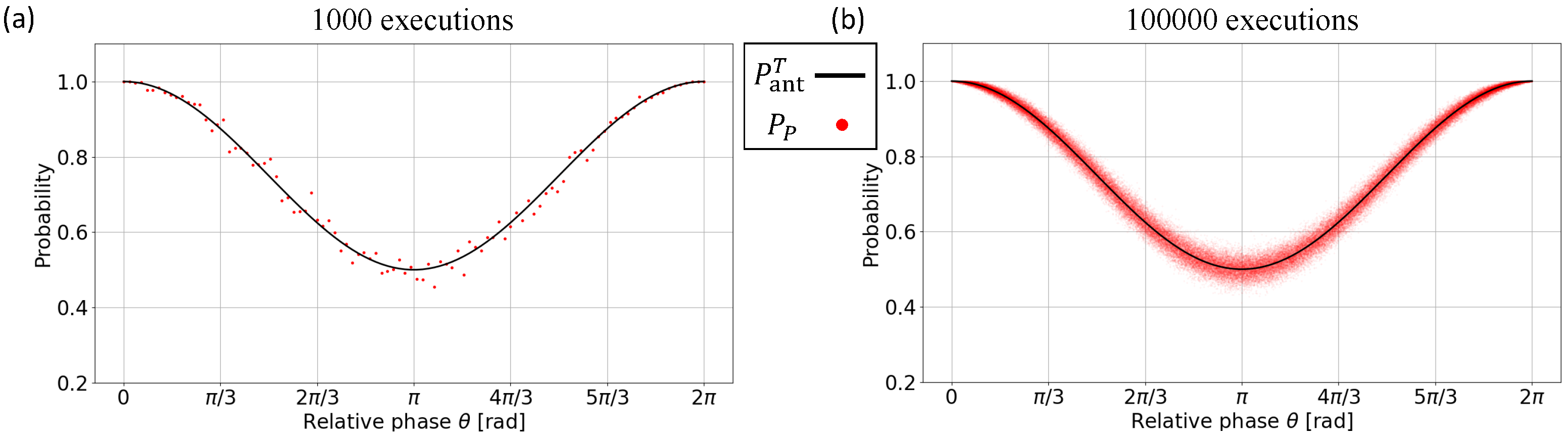
6. Results and Discussion

We execute the quantum computing implementation of the BBM92 protocol described in the previous section, in the IBM QASM simulator which supports jobs involving up to 32 qubits [36].

Figure 4 shows the comparison between the results for the virtual protocol execution and the theoretical prediction, for two different numbers of runs. The black line corresponds to the calculated probability $P_{\mathrm{ant}}^T$ while the red dots are the value of the parameter $P_P$ for each execution. In the first (second) case, the results from 1000 (100,000) runs are plotted. One thousand entangled states are used per run (number of measurements carried out by Alice and Bob for each $\theta$ value).

The match between the theoretically expected dependence on the angle and the computational results is evidenced. The fit for the $P_P$ values in the case of 1000 executions is 0.2513 $cos(1.0001\theta -0.0165)+0.7481$ with a correlation coefficient of 0.9884. In turn, the fit for the $P_P$ values in the case of 100,000 executions is 0.25 $cos(0.9998\theta +0.00052)+0.75$ with a correlation coefficient of 0.9999. As expected, the higher the number of executions, the better the agreement with the derived expression in Equation (5).

Now that the dependence of the QKD on the angle $\theta$ has been validated, we can quantitatively analyze the effect of the FSS on the fidelity of the key distributed by the BBM92 protocol.

According to these results and regarding the typical radiative lifetime of excitons in QDs which lies at the scale $\tau \sim 10$ ns, the protocol performance would be truly reliable for an extremely small FSS of $S\sim 0.02$ $\mathsf{\mu }$eV ($\theta <0.3\to P_{\mathrm{ant}}^T>0.99$).

As the FSS reaches the $\mathsf{\mu }$eV scale, the emission time should be at the hundreds of picoseconds. Hence, to be aware of this unavoidable trade-off between FSS and exciton lifetime becomes crucial for the plausibility of using QDs as sources of entangled photons for tasks requiring QKD.

Although the most common way of improving the quality of the entanglement obtained from radiative cascades in QDs is to diminish the FSS [32,33,34,38], it is worth noting that attempting to reduce the exciton lifetime may be an alternative to consider. That is, taking into account that the quantity to keep small is the phase $\theta$.

Particular schemes to tune the FSS to values with which the key distribution is trustworthy include fixing the axial asymmetry by mechanical strain or by application of time-independent electric or magnetic fields, and have proved to be effective [39]. However, due to the detailed characteristics of each individual QD, those methods solve the problem mostly on a dot-by-dot basis. Hence, fabrication of on-chip QD arrays for devices able of simultaneously generate multiple PEPPs remains an open problem, whose solution may also require to control the emission time rather than only the FSS [40,41].

Finally, it is worth noting that the inversion of Equation (5)

$$\begin{array}{cc}\hfill {\theta }_{-}\mathrm{mod}2\pi & =arccos(4P_P-3)\hfill \\ \hfill & \mathrm{or}\hfill \\ \hfill {\theta }_{+}\mathrm{mod}2\pi & =2\pi -{\theta }_{-},\hfill \end{array}$$

(9)

where ${\theta }_{\mp }\mathrm{mod}2\pi$ stands for the residual after dividing ${\theta }_{\mp }$ by $2\pi$, offers information about the phase $\theta$ from the parameter $P_P$. This opens new possibilities for gaining knowledge on quantum states of the form given in Equation (1). According to this result, after executing the protocol a high enough number of times, significant information about the phase of the superposition defining the state $\left|\Psi \right.〉$ can be obtained. Since that phase cannot be directly measured because any action on the state destroys it, and a succession of measurements of identical states on the same basis cannot establish more than the square of the superposition coefficients, currently the only way to assess that phase is quantum state tomography [42]. That procedure requires measurements respective to different bases to reconstruct the studied state. Although in Equation (9) there is ambiguity in having two possible values $\theta \mathrm{mod}2\pi$, this scheme only requires measurements along the computational basis and may then contribute to future studies on algorithms for more efficient quantum state reconstruction [43].

7. Conclusions

We studied the influence that the exchange interaction between electrons and holes, confined in quantum dots, has on the quantum distribution of information by means of the BBM92 protocol, when this is executed using entangled photon pairs emitted by such dots.

We showed that the product between the fine structure splitting, consequence of the exchange interaction, and the neutral exciton lifetime (normalized by ħ), is a critical quantity for the reliable transmission of a key. According to our finding, that product should be less than 0.3 radians, to have a protocol performance parameter above 99%.

Out theoretical prediction was validated by a quantum computing implementation whose multiple execution in an IBM quantum simulator exhibited clear agreement with the derived analytical expression.

These results provide valuable information toward the efficient use of quantum dot-based entanglement in quantum communication applications.