Towards the Construction of an Analog Solver for the Schrödinger and Ginzburg–Landau Equations Based on a Transmission Line
Abstract
:1. Introduction
1.1. Motivation behind the Development of Analog Computer Modeling Quantum Systems
1.2. Summary of the State of the Art in the RLC Circuit Design Simulating Quantum Mechanics
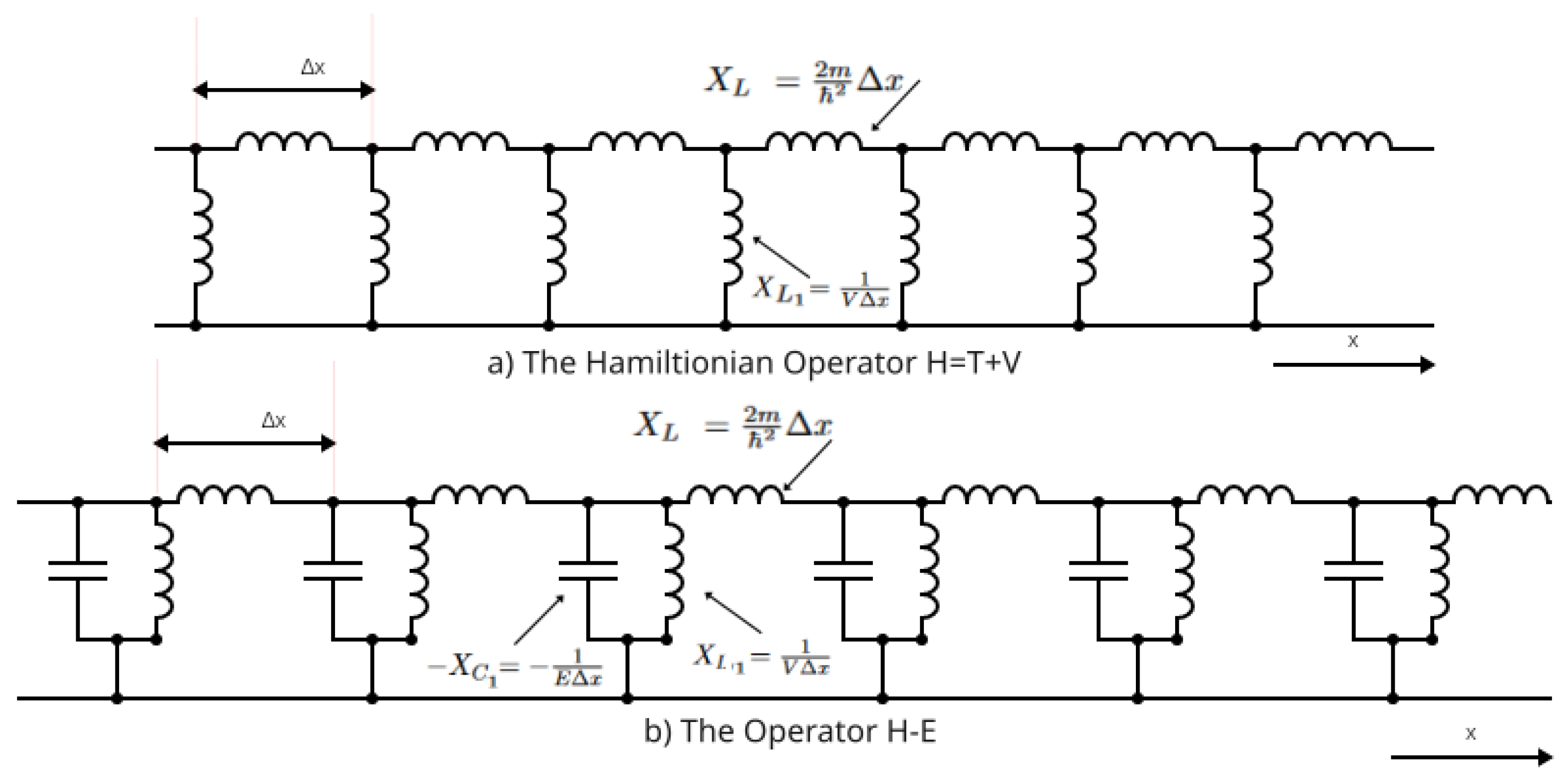
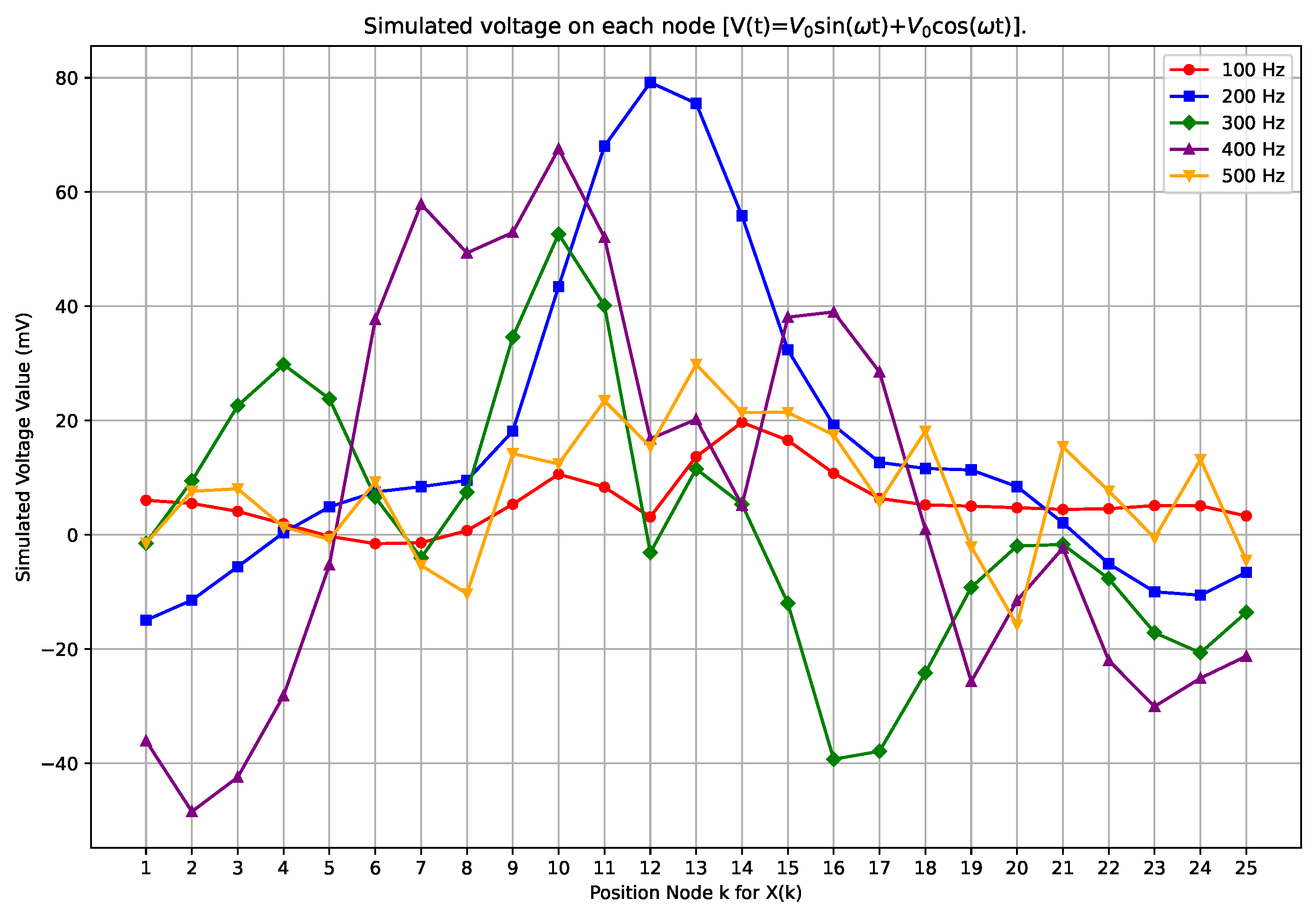
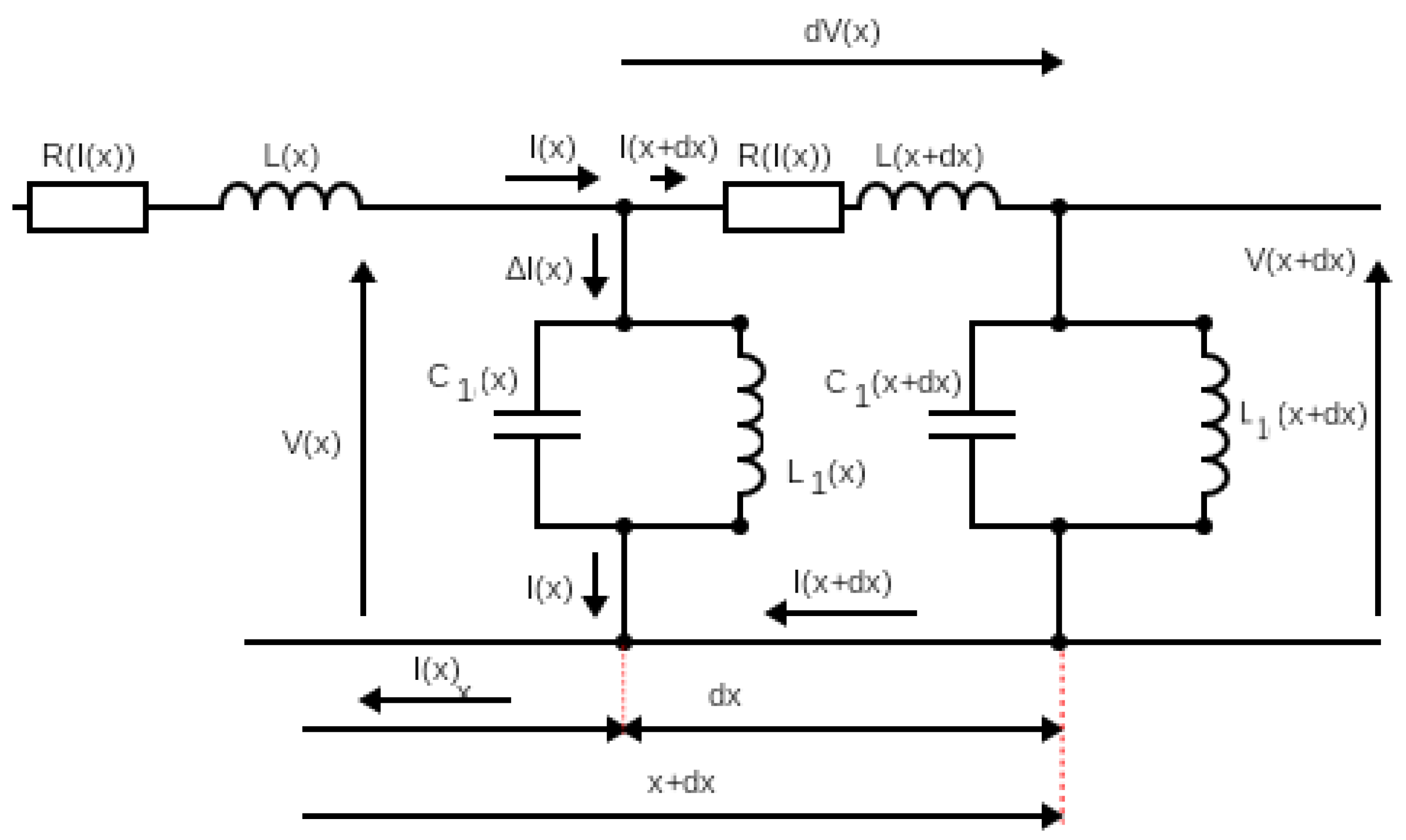
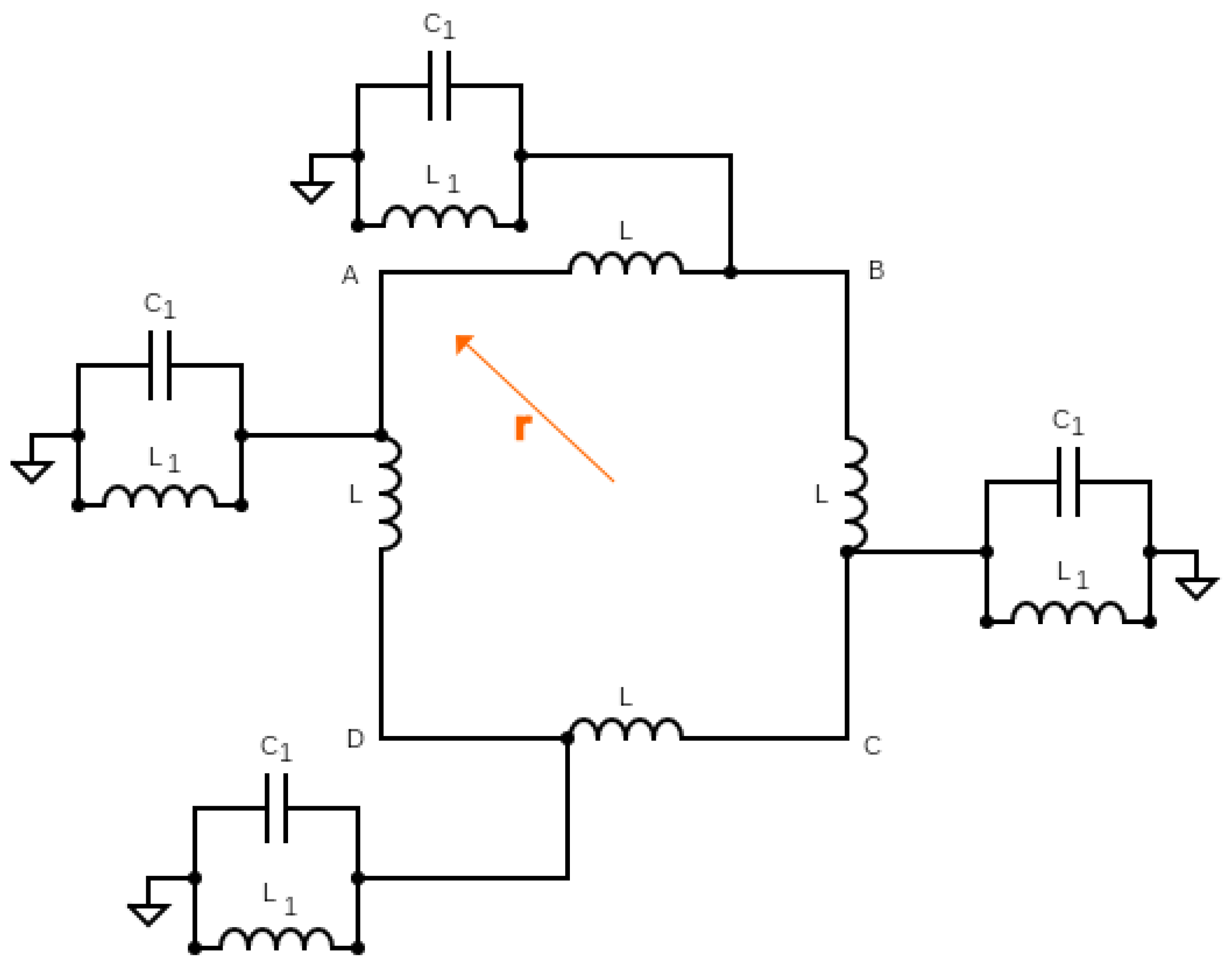
2. Kron’s Second Model of the Analog Hardware Solver for the Schrödinger Equation

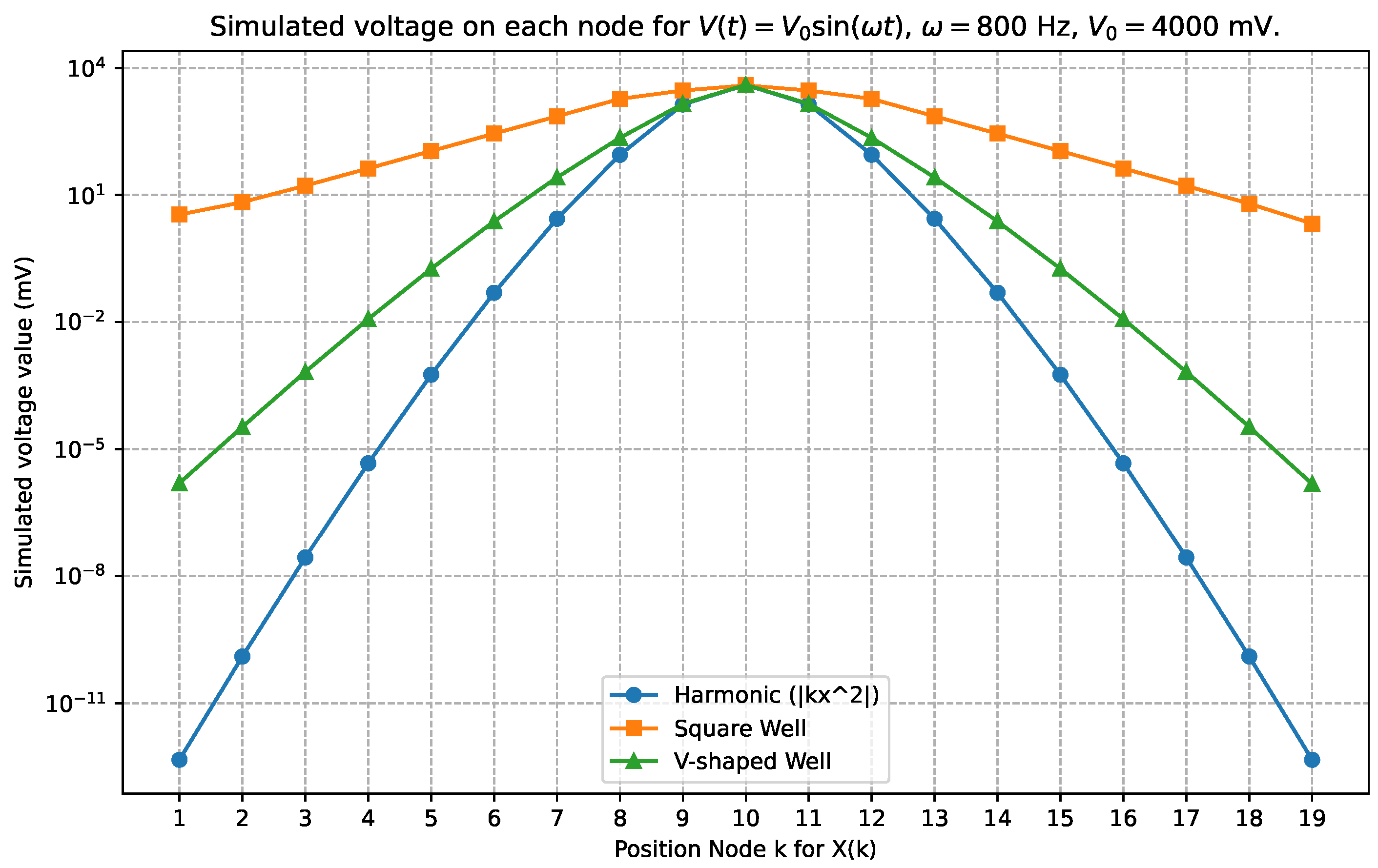
| Parameter | Value |
|---|---|
| Simulated Physical Time | 22 s, 24,120 s, 36,120 s |
| Time To Start Saving Data | 20 s, 24,000 s, 36,000 s, |
| Maximal Time Step | 0.00001 s, 0.00001 s, 0.00001 s, |
| x | 1, 1, 1 |
| Driving Signal Function | Sine, Sine, Sine, |
| Driving Signal Amplitude | 4 V, 4 V, 4 V |
| Driving Signal Frequency | 10 Hz, 2 Hz, 2 Hz |
| Position Index Of Node With Signal Generator | 13, 13, 13 |
| Capacitance (Same For All Nodes) | 1 F, 1 F, 1 F |
| Inductance For Sequential Coils | 1 mH, 1 H, 1 H |
| Inductances For Coils (1–9, 17–25): Square Pot | 1 mH |
| Inductances For Coils (10 To 16) With Square Pot | NaN; Coils Removed |
| Inductances For Coils (13) In V Or Harmonic | NaN; Coils Removed |
| Inductances For Coils (1, 25) In V Or Harmonic | 2 H, 0.00694 H |
| Inductances For Coils (2, 24) In V Or Harmonic | 4 H, 0.008264 H |
| Inductances For Coils (3, 23) In V Or Harmonic | 6 H, 0.01 H |
| Inductances For Coils (4, 22) In V Or Harmonic | 8 H, 0.012346 H |
| Inductances For Coils (5, 21) In V Or Harmonic | 10 H, 0.015625 H |
| Inductances For Coils (6, 20) In V Or Harmonic | 12 H, 0.0204082 H |
| Inductances For Coils (7, 19) In V Or Harmonic | 14 H, 0.0278 H |
| Inductances For Coils (8, 18) In V Or Harmonic | 16 H, 0.04 H |
| Inductances For Coils (9, 17) In V Or Harmonic | 18 H, 0.0625 H |
| Inductances For Coils (10, 16) In V Or Harmonic | 20 H, 0.111 H |
| Inductances For Coils (11, 15) In V Or Harmonic | 22 H, 0.25 H |
| Inductances For Coils (12–14) In V, Harmonic | 24 H, 1 H |
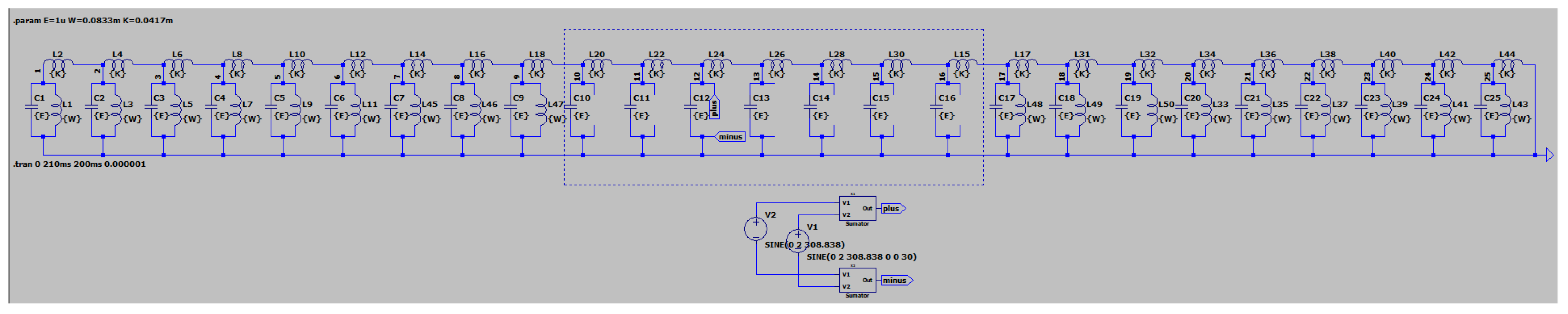
| Parameter of V-Shaped | Value | Renormalized Value 1/Renormalized Value 2 |
|---|---|---|
| Driving Signal Frequency | 2 Hz | 308.838 Hz/ 3098 Hz |
| Position Index Of Node With Signal Generator | 13 | 13 |
| Capacitance (All Nodes) | 1 F | 1 F |
| Inductance For Seq. Coils | 1 H | 0.0417 mH/0.417 H |
| Inductances For Coils (1, 25) | 2 H | 0.0833 mH/0.833 H |
| Inductances For Coils (2, 24) | 4 H | 0.167 mH/1.67 H |
| Inductances For Coils (3, 23) | 6 H | 0.25 mH/2.5 H |
| Inductances For Coils (4, 22) | 8 H | 0.34 mH/3.4 H |
| Inductances For Coils (5, 21) | 10 H | 0.417 mH /4.17 H |
| Inductances For Coils (6, 20) | 12 H | 0.5 mH/5 H |
| Inductances For Coils (7, 19) | 14 H | 0.583 mH/5.83 H |
| Inductances For Coils (8, 18) | 16 H | 0.67 mH/6.7 H |
| Inductances For Coils (9, 17) | 18 H | 0.75 mH/7.55 H |
| Inductances For Coils (10, 16) | 20 H | 0.833 mH/8.33 H |
| Inductances For Coils (11, 15) | 22 H | 0.91 mH/9.1 H |
| Inductances For Coils (12, 14) | 24 H | 1 mH/10 H |
| Inductances For Coil With Index 13 | NaN; Coil Removed | NaN; Coil Removed |
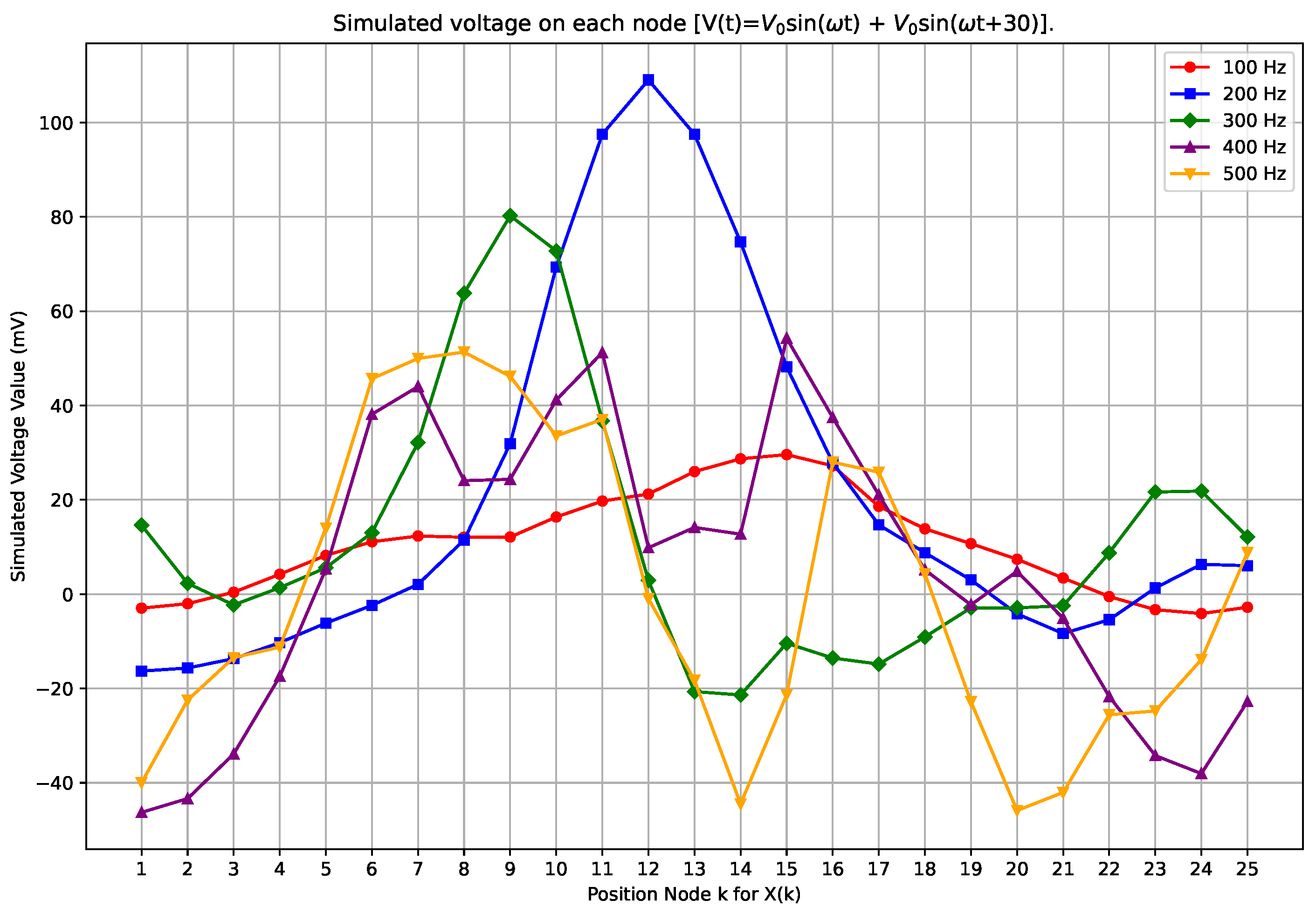
3. LTspice Simulation of Class of Kron’s Second Circuit


- The circuit typically needs a few cycles to stabilize.
- There is a visible spike in voltage at the point where the signal generator is located.
- Achieving measurement at the point where the current flowing through the signal generator equals exactly zero was effectively impossible, due to the limits of the simulation software.
- The circuit enables simulating any potential in spatial coordinates.
4. Derivation of Kron’s Model Expressed by a Long-Line Model and Its Generalization towards the Ginzburg–Landau Equation
4.1. Case of Modeling a Quantum Roton by the Classical Electrical Transmission Line
4.2. Case of Non-Linear Transmission Line Model Generalization of Kron’s Model
5. Linearized Ginzburg–Landau Equation Represented by RLC Transmission Line
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kankanamge, G.; Udayanga, N. Continuous-Time Algorithms and Analog Integrated Circuits for Solving Partial Differential Equations. Ph.D. Thesis, Florida International University, Miami, FL, USA, 2019. [Google Scholar]
- Dirac, P.A.M. Principles of Quantum Mechanics; Oxford University Press: Oxford, UK, 1958. [Google Scholar]
- Fitzpatrick, R. Quantum Mechanics; World Scientific Publishing: Singapore, 2015. [Google Scholar]
- Binney, J.; Skinner, D. The Physics of Quantum Mechanics; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Motta, M.; Rice, J.E. Emerging quantum computing algorithms for quantum chemistry. WIREs Comput. Mol. Sci. 2022, 12, e1580. [Google Scholar] [CrossRef]
- Streif, M.; Neukart, F.; Leib, M. Solving Quantum Chemistry Problems with a D-Wave Quantum Annealer. In Quantum Technology and Optimization Problems, QTOP; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2019; Volume 11413. [Google Scholar]
- Kron, G. Electric Circuit Models of the Schrödinger Equation; General Electric Company: Boston, MA, USA, 1944. [Google Scholar]
- Kouzaev, G.A. Circuit Approach for Simulation of EM-quantum Components. Applications of Advanced Electromagnetics. In Applications of Advanced Electromagnetics; Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2013; Volume 169. [Google Scholar]
- Kouzaev, G.A. Calculation of linear and nonlinear Schrödinger equations by the equivalent network approach and envelope technique. Mod. Phys. Lett. B 2010, 24, 1. [Google Scholar] [CrossRef]
- Edwards, M. Designing a Hybrid Digital/Analog Quantum Physics Emulator as Open Hardware. arXiv 2023, arXiv:2302.00821. [Google Scholar]
- Mourya, S.; Cour, B.R.L.; Sahoo, B.D. Emulation of Quantum Algorithms Using CMOS Analog Circuits. IEEE Trans. Quantum Eng. 2023, 4, 3102116. [Google Scholar] [CrossRef]
- Caruso, M. How classical circuits can simulate quantum aspects. arXiv 2022, arXiv:2209.10402. [Google Scholar]
- Blackwell, J.; Fewer, D.; Allen, L.; Cass, R. An Audio-Frequency Circuit Model of the One-Dimentional Schroedinger Equation and Its Sources of Error. Can. J. Phys. 2011, 33, 483–491. [Google Scholar] [CrossRef]
- Borgarino, M. Circuit-Based Compact Model of Electron Spin Qubit. Electronics 2022, 11, 526. [Google Scholar] [CrossRef]
- Rieger, C. Classical Simulability of Quantum Circuits; TU Munich, CERN: Munich, Germany, 2023. [Google Scholar]
- Nagai, N.; Takashi, Y. Circuit Theory Based on New Concepts and Its Application to Quantum Theory 8: Application of Circuit Theory to Schrödinger Equation. J. Signal Process. 2017, 21, 37–45. [Google Scholar] [CrossRef]
- Kengne, E.; Liu, W.; English, Q.L.Q.; Malomed, B.A. Ginzburg–Landau models of nonlinear electric transmission networks. Phys. Rep. 2022, 982, 1–124. [Google Scholar] [CrossRef]
- Lee, C.H.; Imhof, S.; Berger, C.; Bayer, F.; Brehm, J.; Molenkamp, L.W.; Kiessling, T.; Thomale, R. Topolectrical Circuits. Commun. Phys. 2018, 1, 39. [Google Scholar] [CrossRef]
- Pomorski, K.; Stojewski, B. Hybrid Schrödinger-Ginzburg–Landau (Sch-GL) approach to study of superconducting integrated structures. Mol. Cryst. Liq. Cryst. 2024, 768, 101–116. [Google Scholar] [CrossRef]
- Analog Devices: Analog Electronics Tutorials. Available online: https://www.analog.com/en/resources/simulation-models/spice-models.html (accessed on 1 January 2020).
- LTspice Community Documentation Supplement. Available online: https://ltwiki.org (accessed on 1 January 2020).
- Pluszyński, Ł. Analog Electric Computational Architectures and Simulation Techniques Modeling Quantum Processes and Quantum Devices. Master’s Thesis, Cracow Univesity of Technology, Kraków, Poland, 2023. [Google Scholar]
- Circuit Diagram: Circuit Diagram Free Circuit Design Application. Available online: https://www.circuit-diagram.org/ (accessed on 1 January 2020).
- Zubert, M.; Jankowski, M.; Kulesza, Z.; Napieralski, A. Modelling of Transmission Lines Inside Modern Integrated Semiconductor and Test Boards. IEEE Access 2021, 9, 87182–87195. [Google Scholar] [CrossRef]
- Stepien, L.; Pomorski, K. Bogomolny approach in description of superconducting structures. arXiv 2023, arXiv:2308.09172. [Google Scholar]
- Ezawa, M. Electric-circuit simulation of the Schrödinger equation and non-Hermitian quantum walks. Phys. Rev. B 2019, 100, 165419. [Google Scholar] [CrossRef]
- Irwin, D.; Hilton, G.C. Transition-edge sensors. In Cryogenic Particle Detection; Enss, C., Ed.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Pomorski, K.; Bednorz, A. Justification of the canonical quantization of the Josephson effect and its modifications due to high capacitance energy. J. Phys. A Math. Theor. 2016, 49, 125002. [Google Scholar] [CrossRef]
- Pomorski, K.; Giounanlis, P.; Blokhina, E.; Leipold, D.; Pęczkowski, P.; Staszewski, R.B. From two types of electrostatic position-dependent semiconductor qubits to quantum universal gates and hybrid semiconductor-superconducting quantum computer. In Superconductivity and Particle Accelerators; SPIE: Bellingham, WA, USA, 2019; Volume 11054. [Google Scholar]
- Stepien, L. Bogomolny equation for the BPS Skyrme model from strong necessary conditions. J. Phys. A Math. Theor. 2016, 49, 175202. [Google Scholar] [CrossRef]
- Malz, D.; Cirac, J. Few-Body Analog Quantum Simulation with Rydberg-Dressed Atoms in Optical Lattices. PRX Quantum 2023, 4, 020301. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pomorski, K.; Pluszyński, Ł.; Hałubek, E. Towards the Construction of an Analog Solver for the Schrödinger and Ginzburg–Landau Equations Based on a Transmission Line. Condens. Matter 2024, 9, 35. https://doi.org/10.3390/condmat9040035
Pomorski K, Pluszyński Ł, Hałubek E. Towards the Construction of an Analog Solver for the Schrödinger and Ginzburg–Landau Equations Based on a Transmission Line. Condensed Matter. 2024; 9(4):35. https://doi.org/10.3390/condmat9040035
Chicago/Turabian StylePomorski, Krzysztof, Łukasz Pluszyński, and Eryk Hałubek. 2024. "Towards the Construction of an Analog Solver for the Schrödinger and Ginzburg–Landau Equations Based on a Transmission Line" Condensed Matter 9, no. 4: 35. https://doi.org/10.3390/condmat9040035
APA StylePomorski, K., Pluszyński, Ł., & Hałubek, E. (2024). Towards the Construction of an Analog Solver for the Schrödinger and Ginzburg–Landau Equations Based on a Transmission Line. Condensed Matter, 9(4), 35. https://doi.org/10.3390/condmat9040035











