Luminescence Response and Quenching Models for Heavy Ions of 0.5 keV to 1 GeV/n in Liquid Argon and Xenon
Abstract
:1. Introduction
2. Materials and Methods
2.1. Track Structure
2.2. Biexcitonic Collision Kinetics
2.3. Recoil Ions for Dark Matter Searches
2.4. Heavy Recoil Ions in α-Decay
3. Results
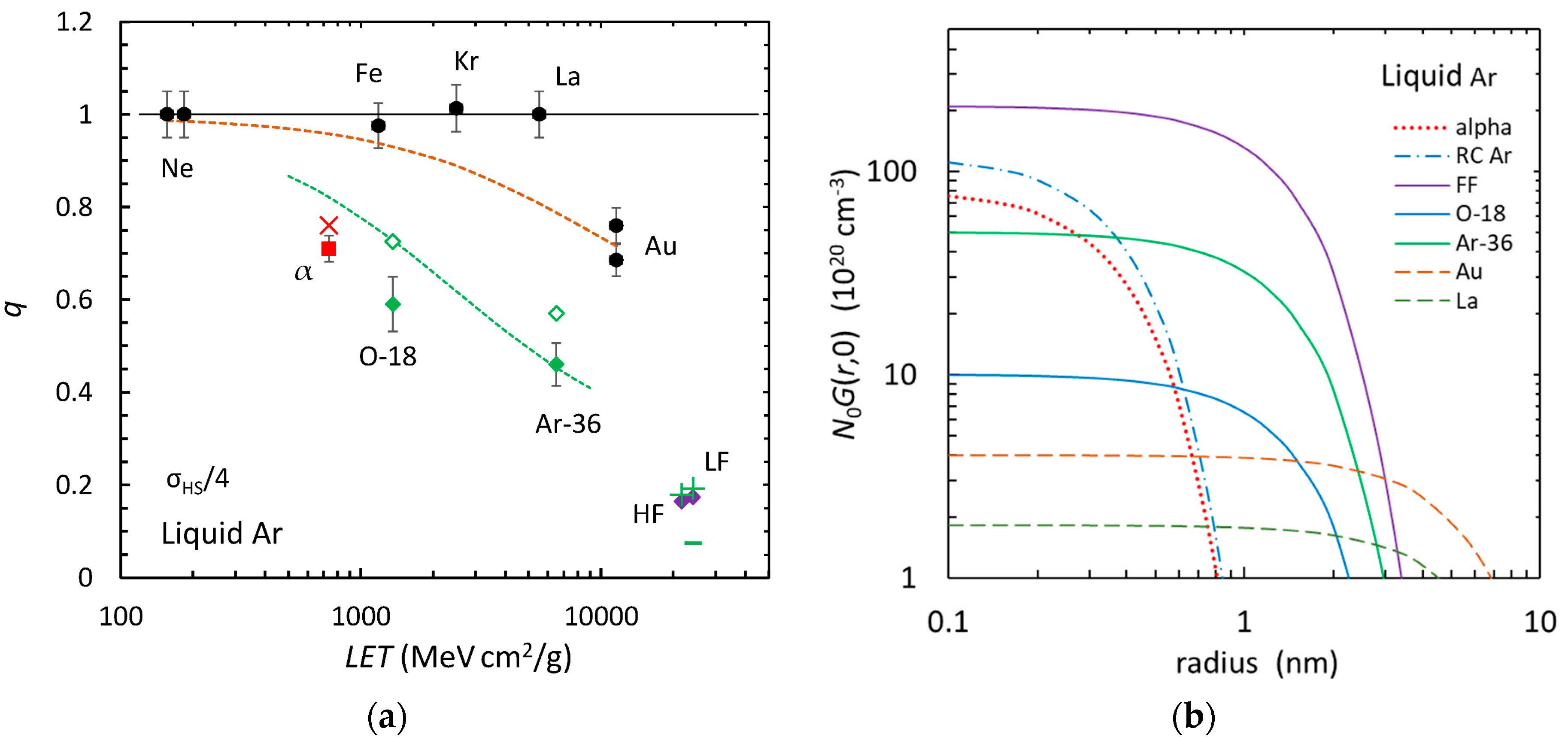
3.1. Fast Ions in Liquid Argon
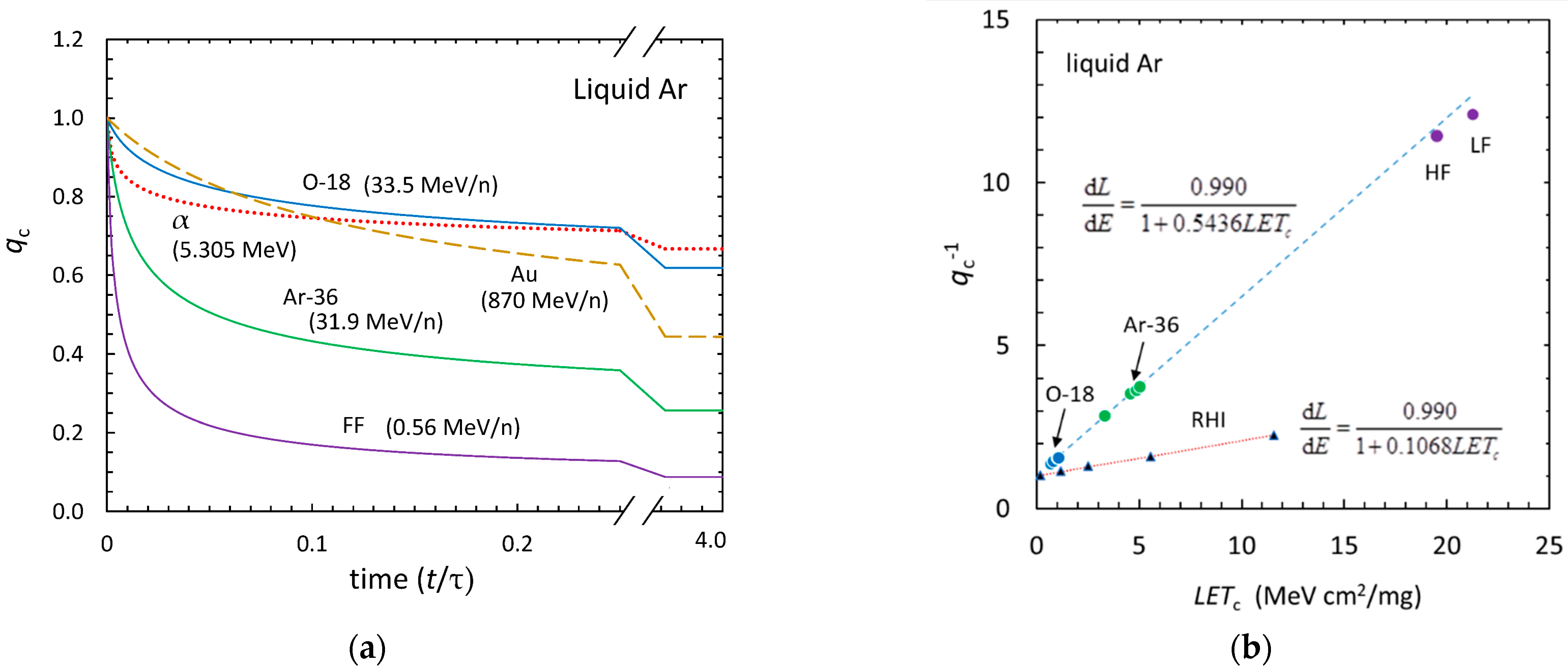
3.2. Heavy Recoils in α-Decay in Liquid Argon
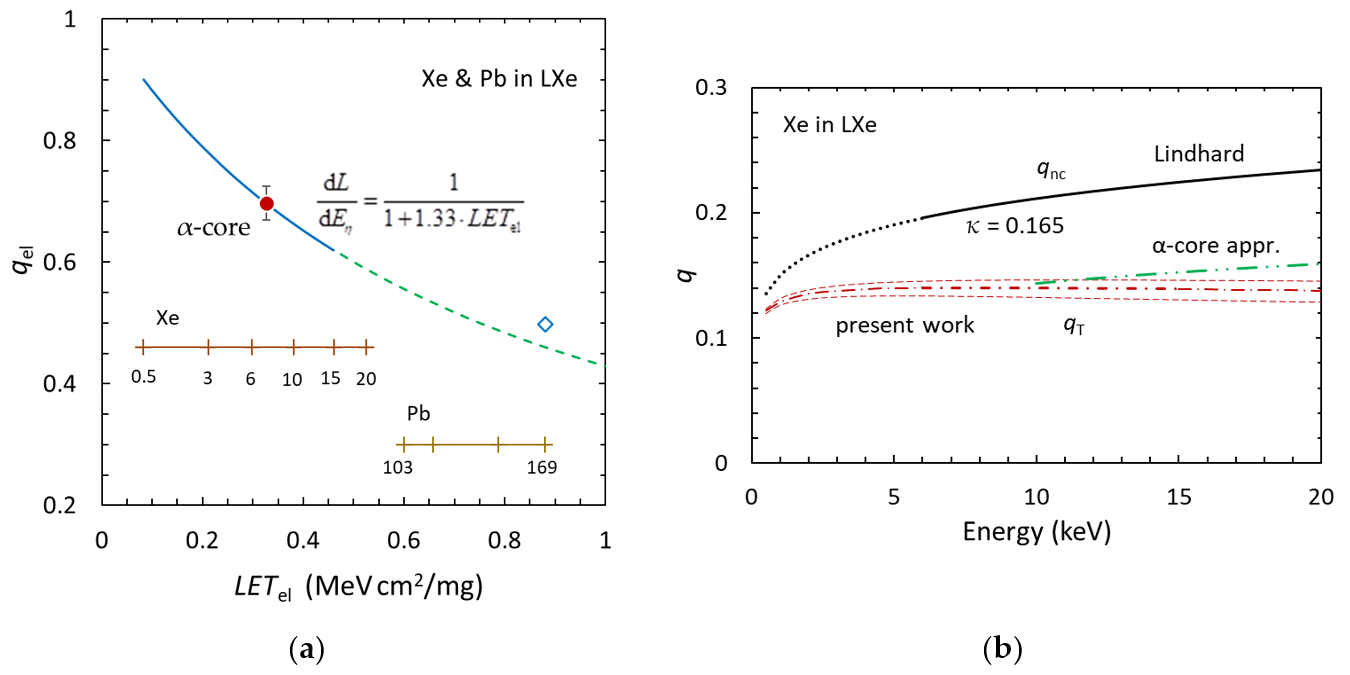
3.3. Xe Recoils and Heavy Recoils in α-Decay in Liquid Xenon
4. Discussion
4.1. Fast Ions in Liquid Argon
4.2. Recoil Ions in Dark Matter Searches
4.3. General Remarks on Dark Matter Searches
4.4. Birks’ Law and Second-Order Reaction Kinetics
- The radius of the initial ion track core should be regarded as constant since the reaction kinetics include the density n, not the specific number N.
- The boundary for kinetics, the track structure of heavy ions, has to be considered.
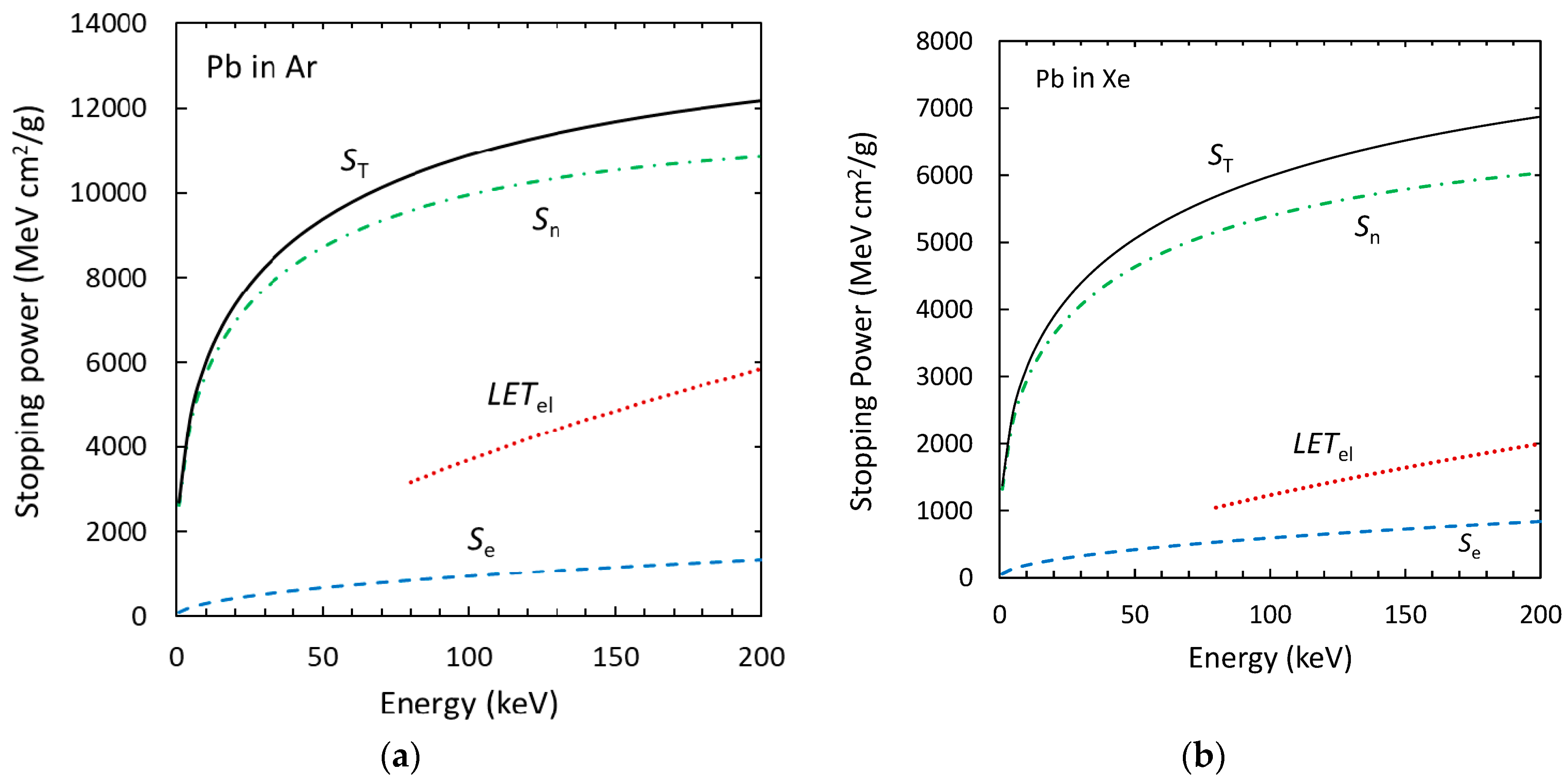
- LETel, not Se or ST, should be used in place of dE/dr in Birks’ law for slow recoils.
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CEνNS | coherent elastic neutrino-nucleus scattering |
| CSDA | continuous slowing down approximation |
| FFs | fission fragments |
| FWHM | full width at half maximum |
| HFs | heavy fragments |
| keVee | electron recoil equivalent energy in keV |
| LAr | liquid argon |
| LET | linear energy transfer (−dE/dx) |
| LETc | linear energy transfer in the track core |
| LETel | electronic linear energy transfer |
| LFs | light fragments |
| LXe | liquid xenon |
| NR | nuclear recoil |
| PET | positron emission tomography |
| PID | photoionization detector |
| PMT | photomultiplier tube |
| RC Ar | recoil argon |
| RHI | relativistic heavy ion |
| TPC | time projection chamber |
| VUV | vacuum ultraviolet |
| WIMPs | weakly interacting massive particles |
Appendix A
Birks’ Law and Reaction Kinetics

- Pseudo-first-order reaction
- 2.
- Second-order reaction under diffusion
References
- Aprile, E.; Doke, T. Liquid xenon detectors for particle physics and astrophysics. Rev. Mod. Phys. 2010, 82, 2053–2097. [Google Scholar] [CrossRef] [Green Version]
- Chepel, V.; Araujo, H. Liquid noble gas detectors for low energy particles. JINST 2013, 8, R04001, and references therein. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, S.; Hitachi, A. Application of rare gas liquids to radiation detectors. In Charged Particle and Photon Interactions with Matter: Recent Advances, Applications, and Interfaces; Hatano, Y., Katsumura, Y., Mozumder, A., Eds.; Taylor & Francis: Boca Raton, FL, USA, 2010; Chapter 31; pp. 879–922. [Google Scholar]
- Aprile, E.; Aalbers, J.; Agostini, F.; Alfonsi, M.; Amaro, F.D.; Anthony, M.; Antunes, B.; Arneodo, F.; Balata, M.; Barrow, P.; et al. (XENON collaboration). The XENON1T dark matter experiment. Eur. Phys. C 2017, 77, 881. [Google Scholar] [CrossRef]
- Barrow, P.; Baudis, L.; Cichon, D.; Danisch, M.; Franco, D.; Kaether, F.; Kish, A.; Lindner, M.; Undagoitia, T.M.; Mayani, D.; et al. Qualification test of the R11410-21 photomultiplier tubes for the XENON1T detector. J. Instrum. 2017, 12, P01024. [Google Scholar] [CrossRef] [Green Version]
- Akerib, D.S.; Alsum, S.; Araújo, H.M.; Bai, X.; Bailey, A.J.; Balajthy, J.; Beltrame, P.; Bernard, E.P.; Bernstein, A.; Biesiadzinski, T.P.; et al. (LUX collaboration). Low-energy (0.7–74 keV) nuclear recoil calibration of the LUX dark matter experiment using D-D neutron scattering kinematics. Phys. Rev. Lett. 2017, 118, 021303. [Google Scholar] [CrossRef]
- Tan, A.; Xiao, M.; Cui, X.; Chen, X.; Chen, Y.; Fang, D.; Fu, C.; Giboni, K.; Giuliani, F.; Gong, H.; et al. (PandaX-II collaboration). Dark matter results from first 98.7 days of data from the PandaX-II experiment. Phys. Rev. Lett. 2016, 117, 121303. [Google Scholar] [CrossRef]
- Agnes, P.; Albuquerque, I.F.; Alexander, T.; Alton, A.K.; Araujo, G.R.; Ave, M.; Back, H.O.; Baldin, B.; Batignani, G.; Biery, K.; et al. (DarkSide Collaboration). DarkSide-50 532-day dark matter search with low-radioactivity argon. Phys. Rev. D 2018, 98, 102006. [Google Scholar] [CrossRef] [Green Version]
- Lenardo, B.G.; Xu, J.; Pereverzev, S.; Akindele, O.A.; Naim, D.; Kingston, J.; Bernstein, A.; Kazkaz, K.; Tripathi, M.; Awe, C.; et al. Low-energy physics research of xenon detectors for nuclear-recoil-based dark matter and neutrino experiments. Phys. Rev. Lett. 2019, 123, 231106. [Google Scholar] [CrossRef]
- Akimov, D.; Albert, J.B.; An, P.; Awe, C.; Barbeau, P.S.; Becker, B.; Belov, V.; Brown, A.; Bolozdynya, A.; Cabrera-Palmer, B.; et al. (COHERNT collaboration). Observation of coherent elastic neutrino-nucleus scattering. Science 2017, 357, 1123–1126. [Google Scholar]
- Tayloe, R. (COHERENT collaboration). The CENNS-10 liquid argon detector to measure CEvNS at the spallation neutron source. arXiv 2018, arXiv:1801.00086. [Google Scholar]
- Doke, T.; Crawford, H.J.; Hitachi, A.; Kikuchi, J.; Lindstrom, P.J.; Masuda, K.; Shibamura, E.; Takahashi, T. LET dependence of scintillation yields in liquid argon. Nucl. Instrum. Methods Phys. Res. Sect. A 1988, 269, 291–296. [Google Scholar] [CrossRef]
- Hitachi, A.; LaVerne, J.A.; Kolata, J.; Doke, T. Energy resolution of allene doped liquid argon detectors for ions of energy 23–34 MeV/amu. Nucl. Instrum. Methods Phys. Res. Sect. A 1994, 340, 546–550. [Google Scholar] [CrossRef]
- LaVerne, J.A.; Hitachi, A.; Kolata, J.J.; Doke, T. Scintillation and ionization in allene-doped liquid argon irradiated with 18O and 36Ar ions of 30 MeV/u. Phys. Rev. B 1996, 54, 15724–15729. [Google Scholar] [CrossRef]
- Hitachi, A.; Doke, T.; Mozumder, A. Luminescence quenching in liquid argon under charged-particle impact: Relative scintillation yield at different linear energy transfers. Phys. Rev. B 1992, 46, 11463–11470. [Google Scholar] [CrossRef]
- Hitachi, A. Exciton kinetics in condensed rare gases. J. Chem. Phys. 1984, 80, 745. [Google Scholar] [CrossRef]
- Hitachi, A.; Takahashi, T.; Funayama, N.; Masuda, K.; Kikuchi, J.; Doke, T. Effect of ionization density on the time dependence of luminescence from liquid argon and xenon. Phys. Rev. B 1983, 27, 5279–5285. [Google Scholar] [CrossRef]
- Birks, J.B. Scintillations from organic crystals: Specific fluorescence and relative response to different radiations. Proc. Phys. Soc. 1951, 64, 874–877. [Google Scholar] [CrossRef]
- Birks, J.B. The Theory and Practice of Scintillation Counting; Pergamon: Oxford, UK, 1964. [Google Scholar]
- Chatterjee, A.; Shaefer, H.J. Microdosimetric structure of heavy ion tracks in tissue. Radiat. Environm. Biophys. 1976, 13, 215–227. [Google Scholar] [CrossRef]
- Mozumder, A. Fundamentals of Radiation Chemistry; Academic: San Diego, CA, USA, 1999. [Google Scholar]
- Lindhard, J.; Winther, A. Stopping power of electron gas and equipartition rule. Fys. Medd. Dan. Vid. Selsk. 1964, 34, 1–21. [Google Scholar]
- Lindhard, J.; Nielsen, V.; Sharff, M.; Thomsen, P.V. Integral equations governing radiation effects. Mat. Fys. Medd. Dan. Vid. Selsk. 1963, 33, 1–42. [Google Scholar]
- Biersack, J.P. Range of recoil atoms in isotropic stopping materials. Eur. Phys. J. A 1968, 211, 495–501. [Google Scholar] [CrossRef]
- Hitachi, A. Properties of liquid xenon scintillation for dark matter searches. Astropart. Phys. 2005, 24, 247–256. [Google Scholar] [CrossRef] [Green Version]
- Hitachi, A. Bragg-like curve for dark matter searches: Binary gases. Radiat. Phys. Chem. 2008, 77, 1311–1317. [Google Scholar] [CrossRef] [Green Version]
- Madsen, B.S. Ionization measurements on single recoil particles from Po, ThC, and ThC’. Mat. Fys. Medd. Dan. Vid. Selsk. 1945, 23, 1–16. [Google Scholar]
- Jesse, W.P.; Sadauskis, J. Recoil particles from Po210 and their ionization in argon and helium. Phys. Rev. 1956, 102, 389–390. [Google Scholar] [CrossRef]
- Cano, G.L. Total ionization and range of low-energy recoil particles in pure and binary gases. Phys. Rev. 1968, 169, 277–280. [Google Scholar] [CrossRef]
- Ling, R.C.; Knipp, J.K. Ionization by recoil particles from alpha-decay. Phys. Rev. 1950, 80, 106. [Google Scholar] [CrossRef]
- Watanabe, T.; Katsuura, K. Ionization of atoms by collision with excited atoms. II. A formula without the rotating-atom approximation. J. Chem. Phys. 1967, 47, 800. [Google Scholar] [CrossRef]
- Dexter, D.L. A Theory of sensitized luminescence in solids. J. Chem. Phys. 1953, 21, 836–850. [Google Scholar] [CrossRef]
- SRIM2013. Available online: http://www.srim.org/ (accessed on 6 October 2020).
- Hitachi, A.; Mozumder, A. Properties for liquid argon scintillation for dark matter searches. arXiv 2019, arXiv:1903.05815. [Google Scholar]
- Xu, J.; Stanford, C.; Westerdale, S.; Calaprice, F.; Wright, A.; Shi, Z. First measurement of surface nuclear recoil background for argon dark matter searches. Phys. Rev. D 2017, 96, 061101(R). [Google Scholar] [CrossRef] [Green Version]
- Cao, H.; Alexander, T.; Aprahamian, A.; Avetisyan, R.; Back, H.O.; Cocco, A.G.; DeJongh, F.; Fiorillo, G.; Galbiati, C.; Guardincerri, Y.; et al. (SCENE collaboration). Measurement of scintillation and ionization yield and scintillation pulse shape from nuclear recoils in liquid argon. Phys. Rev. D 2015, 91, 092007. [Google Scholar] [CrossRef] [Green Version]
- Galbiati, C. (WARP Collaboration). First Physics Results from WARP 2.3 Liter Prototype. Available online: http://cosmology.berkeley.edu/inpac/CDMSCE_Jun06/Talks/WARP%20SUSY06.pdf (accessed on 24 November 2020).
- Tanaka, M.; Doke, T.; Hitachi, A.; Kato, T.; Kikuchi, J.; Masuda, K.; Murakami, T.; Nishikido, F.; Okada, H.; Ozaki, K.; et al. LET dependence of scintillation yields in liquid xenon. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2001, 457, 454–463. [Google Scholar] [CrossRef]
- Dahl, C.E. The Physics of Background Discrimination in Liquid Xenon, and First Results from XENON10 in the Hunt for WIMP Dark Matter. Ph. D. Thesis, Princeton University, Princeton, NJ, USA, 2009. [Google Scholar]
- Murray, R.B.; Mayer, A. Scintillation response of activated ionic crystals to various charged particles. Phy. Rev. 1961, 122, 815–826. [Google Scholar] [CrossRef]
- Doke, T.; Shibamura, E.; Kubota, S. Maximum scintillation yield in NaI(Tl). J. Phys. Soc. Jpn. 1999, 68, 2433–2438. [Google Scholar] [CrossRef]
- Yunoki, A.; Doke, T.; Fukuda, N.; Kase, M.; Kato, T.; Kikuchi, J.; Masuda, K.; Niimura, M.; Okada, H.; Ozaki, K.; et al. An allene-doped liquid argon ionization chamber for Ar and Ca ions at around 100 MeV/n. Nucl. Instrum. Methods Phys. Res. Sect. A 1999, 432, 332–341. [Google Scholar] [CrossRef]
- Anderson, D.F. The effects of photosensitive dopants on electron mobility in liquid argon. Nucl. Instr. Meth. A 1992, 313, 151–154. [Google Scholar] [CrossRef]
- Hitachi, A.; Ichinose, H.; Doke, T.; Shibamura, E.; Kikuchi, J.; Masuda, K. Photoionization quantum yields of organic molecules in liquid argon and xenon. Phys. Rev. B 1997, 55, 5742–5748. [Google Scholar] [CrossRef]
- Mu, W.; Xiong, X.; Ji, X. Scintillation efficiency for low energy nuclear recoils in liquid xenon dark matter detectors. Astropart. Phys. 2015, 61, 56–61. [Google Scholar] [CrossRef] [Green Version]
- Barker, D.; Mei, D.-M. Germanium detector response to nuclear recoils in search for dark matter. Astrop. Phys. 2012, 38, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Lindhard, J.; Sharff, M.; Schiøtt, H.E. Range concepts and heavy ion ranges. Mat. Fys. Medd. Dan. Vid. Selsk. 1963, 33, 1–42. [Google Scholar]
- Fano, U.; Lichten, W. Interpretation of Ar+-Ar collisions at 50 KeV. Phys. Rev. Lett. 1965, 14, 627–629. [Google Scholar] [CrossRef]
- Garcia, J.D.; Fortner, R.J.; Kavanagh, T.M. Inner-shell vacancy production in ion-atom collisions. Rev. Mod. Phys. 1973, 45, 111–177. [Google Scholar] [CrossRef]
- Guillaudin, O.; Billard, J.; Bosson, G.; Bourrion, O.; Lamy, T.; Mayet, F.; Santos, D.; Sortais, P. Quenching factor measurement in low pressure gas detector for directional dark matter search. In Proceedings of the Sygnus 2011: Third International Conference on Directional Detection of Dark Matter, Aussois, France, 7–10 June 2011; Fayet, F., Santos, D., Eds.; 2012; 53, pp. 119–127. [Google Scholar] [CrossRef]
- Bolotnikov, A.; Ramsey, B. The spectroscopic properties of high-pressure xenon. Nucl. Instrum. Methods Phys. Res. Sect. A 1997, 396, 360–370. [Google Scholar] [CrossRef]
- Kusano, H.; Ishikawa, T.; Lopes, J.A.; Miyajima, M.; Shibamura, E.; Hasebe, N. Scintillation and ionization yields produced by α-particles in high density gaseous xenon. Nucl. Instrum. Methods Phys. Res. Sect. A 2012, 683, 40–45. [Google Scholar] [CrossRef]
- Lopes, M.I.; Chepel, V. Rare gas liquid detectors. In Electronic Excitations in Liquified Rare Gases; Schmidt, W.F., Illenberger, E., Eds.; American Scientific Publishers: Portland, OR, USA, 2005; Chapter 11; pp. 331–338. [Google Scholar]
- Hitachi, A.; LaVerne, J.A.; Doke, T. Effect of an electric field on luminescence quenching in liquid argon. Phys. Rev. B 1992, 46, 540–543. [Google Scholar] [CrossRef]
- Salamon, M.H.; Ahlen, S.P. NaI:Tl response to relativistic Ne, Ar, and Fe ions. Phys. Rev. B 1981, 24, 5026–5036. [Google Scholar] [CrossRef]
- Collar, J.I.; Kavner, A.R.L.; Lewis, C.M. Response of CsI(Na) to nuclear recoils; Impact on coherent elastic neutrino-nucleus scattering (CEνNS). Phys. Rev. D. 2019, 100, 033003. [Google Scholar] [CrossRef] [Green Version]

| Units | 18O | 36Ar | Mo (LF) | Ba (HF) | |
|---|---|---|---|---|---|
| Energy | MeV/n | 33.5 | 31.9 | 0.98 | 0.56 |
| Range | μm | 3200 | 1270 | 44 | 37 |
| LET | MeVcm2/mg | 1.35 | 6.47 | 24.1 | 21.7 |
| Tc/T | 0.75 | 0.75 | 0.88 | 0.90 | |
| a0 | nm | 1.53 | 1.49 | 1.52 1 | 1.46 1 |
| qc | 0.64 | 0.27 | 0.083 | 0.087 | |
| q | 0.73 | 0.46 | 0.19 | 0.18 | |
| q expt. | 0.59 2 | 0.46 2 | 0.17 3 | 0.16 3 |
| Source | 210Po | 212Bi | 214Po | 212Po | |
|---|---|---|---|---|---|
| Recoil Ion | Units | 206Pb | 208Tl | 210Pb | 208Pb |
| Energy | keV | 103 | 116 | 146 | 169 |
| R | μm | 0.09 | 0.10 | 0.12 | 0.13 |
| LETel | MeVcm2/mg | 1.85 | 2.03 | 2.41 | 2.68 |
| a0 | nm | 0.45 1 | 0.47 1 | 0.51 1 | 0.54 1 |
| qnc | 0.23 | 0.24 | 0.27 | 0.29 | |
| qel | 0.38 | 0.36 | 0.33 | 0.31 | |
| qT | 0.086 | 0.087 | 0.089 | 0.090 | |
| EL | keV | 8.9 | 10 | 13 | 15 |
| EL | keVee | 10 | 11 | 14 | 17 |
| EL expt. | keVee | ~5 2 | 7.4 ± 0.4 2 |
| Source | 210Po | 212Po | 241Am | |||
|---|---|---|---|---|---|---|
| Recoil Ion | Units | Xe | Xe | 206Pb | 208Pb | α-Core |
| Energy | keV | 6 | 20 | 103 | 169 | 5490 × 0.76 |
| R | μm | – | – | 0.08 | 0.12 | 43 |
| LETel | MeVcm2/mg | 0.30 | 0.53 | 0.60 | 0.88 | 0.33 |
| a0 | nm | 0.48 1 | 0.51 2 | 0.55 2 | 0.66 2 | 0.48 1 |
| qnc | 0.20 | 0.23 | 0.14 | 0.18 | 1 | |
| qel | 0.72 | 0.59 | 0.56 | 0.50 3 | 0.70 | |
| qT | 0.14 | 0.14 | 0.08 | 0.09 | – | |
| EL | keV | 0.8 | 2.8 | 8 | 15 | – |
| EL | keVee | 0.9 | 3 | 9 | 17 | – |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hitachi, A. Luminescence Response and Quenching Models for Heavy Ions of 0.5 keV to 1 GeV/n in Liquid Argon and Xenon. Instruments 2021, 5, 5. https://doi.org/10.3390/instruments5010005
Hitachi A. Luminescence Response and Quenching Models for Heavy Ions of 0.5 keV to 1 GeV/n in Liquid Argon and Xenon. Instruments. 2021; 5(1):5. https://doi.org/10.3390/instruments5010005
Chicago/Turabian StyleHitachi, Akira. 2021. "Luminescence Response and Quenching Models for Heavy Ions of 0.5 keV to 1 GeV/n in Liquid Argon and Xenon" Instruments 5, no. 1: 5. https://doi.org/10.3390/instruments5010005
APA StyleHitachi, A. (2021). Luminescence Response and Quenching Models for Heavy Ions of 0.5 keV to 1 GeV/n in Liquid Argon and Xenon. Instruments, 5(1), 5. https://doi.org/10.3390/instruments5010005




