A Rapid, Non-Destructive Method to Detect Counterfeit Integrated Circuits Using a Resonant Cavity System
Abstract
:1. Introduction
1.1. Background
- We propose a rapid, low-cost, non-contact, non-destructive approach to differentiate an IC by its part number and authenticity based on the scattering parameters (S-parameters) obtained when the IC is placed inside a resonant cavity.
- The S-parameters obtained create a unique signature based on the structural layout (package, pad, pin, wire bond, and die structure) and functionality of the silicon die.
- The method can be applied to any IC regardless of technology type (analog, digital, mixed-signal), package (dual in-line package (DIP), quad flat no-leads (QFN), etc.), size (small, medium, large), or state (obsolete, active, new) without the need of any modification pre- or post-fabrication.
- The method only requires unique structures to precisely hold and place specific package types inside the resonant cavity.
- The method does not require access to the pins of the ICs.
- The system uses the S-parameters as quantitative metrics, thus eliminating the need for subject matter experts to operate the system. Unlike traditional techniques, such as visual inspection and X-ray radiography, which typically rely on qualitative assessments by experts, the resonant cavity system provides faster and more objective results based on measurable differences in the signatures.
1.2. Counterfeit Detection Methods
1.2.1. Physical Inspections
1.2.2. Electrical Inspections
1.2.3. Side-Channel Analysis
1.2.4. Microwave Techniques
1.2.5. Chip and Package ID
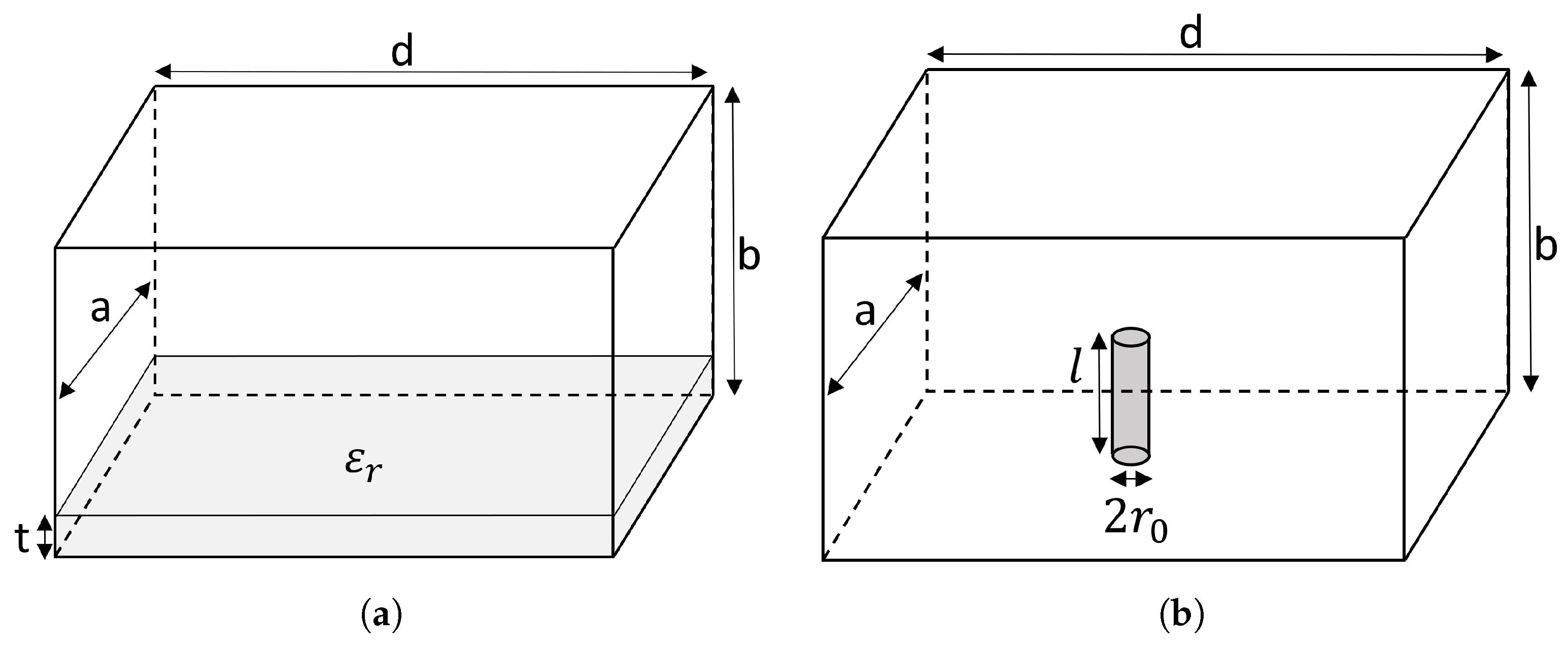
1.3. Resonant Cavity
1.3.1. Description and Applications
1.3.2. Resonant Frequencies
1.3.3. Perturbation Equations
1.4. Return Loss
1.5. IC EM Signature
1.6. Design
2. Materials and Methods
2.1. Setup and IC Placement
2.2. Measurement
2.3. Dataset
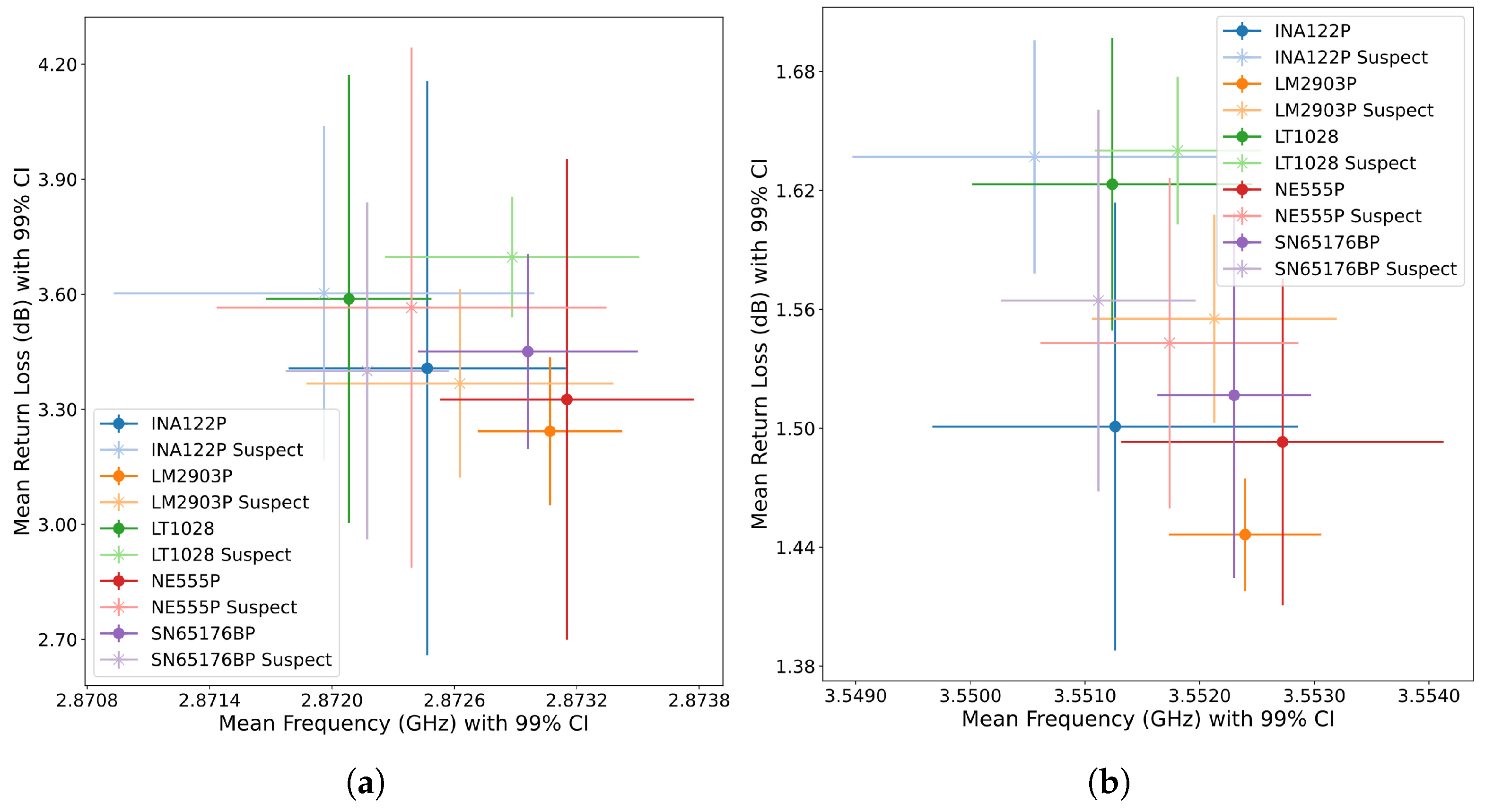
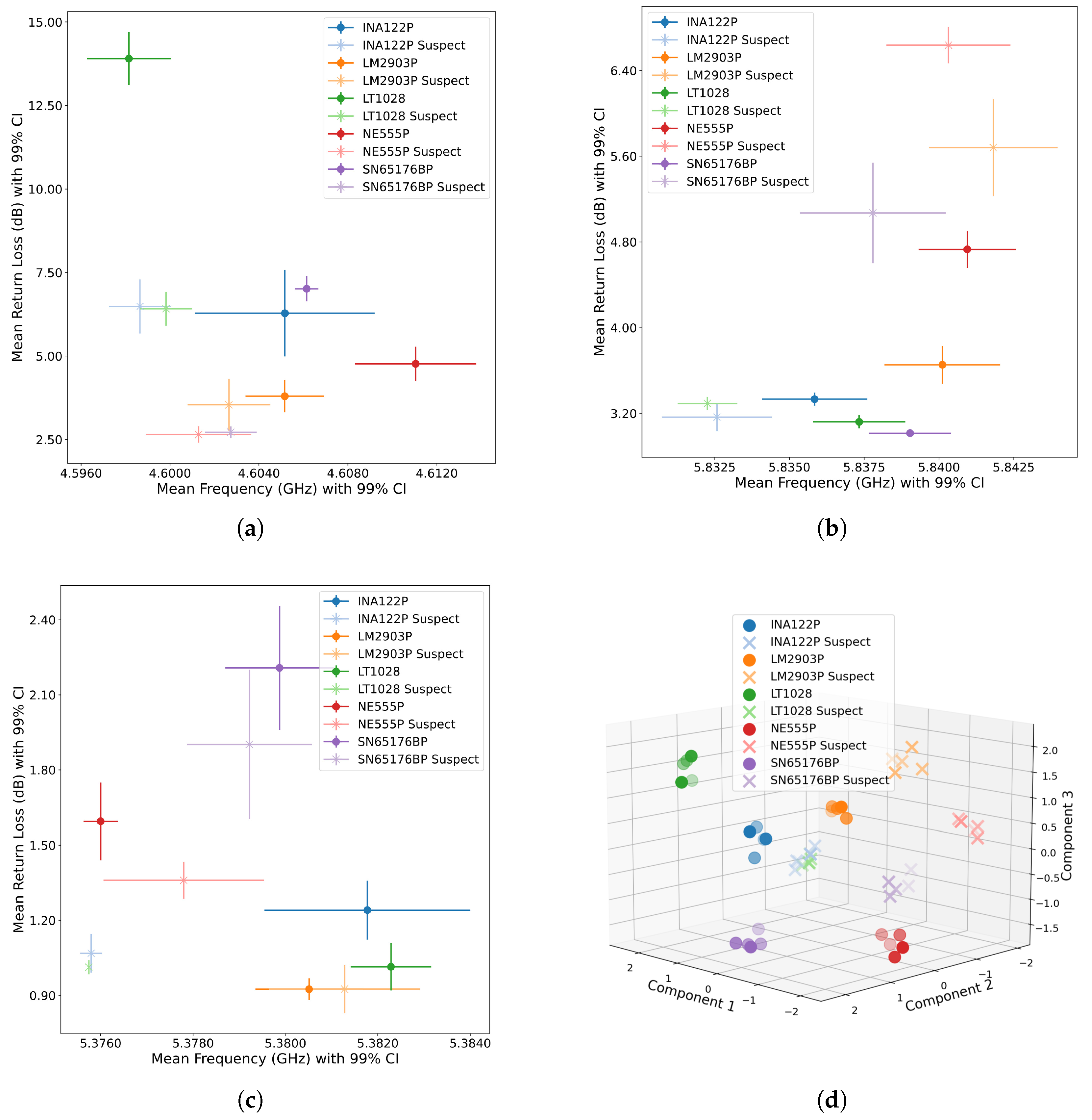
3. Results
- Calculate the sample mean ():
- Calculate the sample standard deviation (s):
- Determine the t-score for 99% confidence and degrees of freedom () from the t-distribution table.
- Calculate the margin of error ():
- Determine the confidence interval ():
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guin, U.; Dimase, D.; Tehranipoor, M. Counterfeit Integrated Circuits: Detection, Avoidance, and the Challenges Ahead. J. Electron. Test. 2014, 30, 9–23. [Google Scholar] [CrossRef]
- Nechiyil, A.; Lee, R.; Chapman, G. Detection of Anomalous Integrated Circuits Using a Cavity Resonator System with Machine Learning. In Proceedings of the 2021 IEEE Physical Assurance and Inspection of Electronics (PAINE), Washington, DC, USA, 30 November–2 December 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Nechiyil, A.; Lee, R.; Chapman, G.; McCue, J.J. Benchmarking ResCav—A Resonant Cavity System Used to Detect Counterfeit Microelectronics. In Proceedings of the 49th International Symposium for Testing and Failure Analysis, Phoenix, AZ, USA, 12–16 November 2023; pp. 131–135. [Google Scholar] [CrossRef]
- Nechiyil, A.; Xi, C.; Asadizanjani, N.; Lee, R.; Chapman, G. Evaluating a Multi-modal, Non-destructive Approach Combining a Resonant Cavity System and Infrared Spectroscopy to Detect Counterfeit and Anomalous Integrated Circuits. IEEE Trans. Components Packag. Manuf. Technol. 2024. [Google Scholar] [CrossRef]
- Mahmood, K.; Carmona, P.L.; Shahbazmohamadi, S.; Pla, F.; Javidi, B. Real-time automated counterfeit integrated circuit detection using x-ray microscopy. Appl. Opt. 2015, 54, D25–D32. [Google Scholar] [CrossRef]
- Ahmadi, B.; Heredia, R.; Shahbazmohamadi, S.; Shahbazi, Z. Non-destructive automatic die-level defect detection of counterfeit microelectronics using machine vision. Microelectron. Reliab. 2020, 114, 113893. [Google Scholar] [CrossRef]
- Dogan, H.; Alam, M.M.; Asadizanjani, N.; Shahbazmohamadi, S.; Forte, D.; Tehranipoor, M. Analyzing the Impact of X-ray Tomography on the Reliability of Integrated Circuits. In Proceedings of the 41st International Symposium for Testing and Failure Analysis, Portland, OR, USA, 1–5 November 2015; pp. 154–163. [Google Scholar] [CrossRef]
- Alam, M.; Shen, H.; Asadizanjani, N.; Tehranipoor, M.; Forte, D. Impact of X-Ray Tomography on the Reliability of Integrated Circuits. IEEE Trans. Device Mater. Reliab. 2017, 17, 59–68. [Google Scholar] [CrossRef]
- Barnaby, H.J. Total-Ionizing-Dose Effects in Modern CMOS Technologies. IEEE Trans. Nucl. Sci. 2006, 53, 3103–3121. [Google Scholar] [CrossRef]
- Ma, T.; Dressendorfer, P. Ionizing Radiation Effects in MOS Devices and Circuits; A Wiley-Interscience Publication, Wiley: Hoboken, NJ, USA, 1989. [Google Scholar]
- Parametric tests meet the challenge of high-density ICs: G. F. Nelson and W. F. Boggs. Electronics p. 108 (Dec. 1975). Microelectron. Reliab. 1976, 15, 177. [CrossRef]
- Soma, M. Fault coverage of DC parametric tests for embedded analog amplifiers. In Proceedings of the IEEE International Test Conference-(ITC), Baltimore, MD, USA, 17–21 October 1993; pp. 566–573. [Google Scholar] [CrossRef]
- Sharpe, T. Functional Electronic Clones—The Most Dangerous New Counterfeit Threat Facing the Entire Electronics Industry Today. In Proceedings of the 41st International Symposium for Testing and Failure Analysis, Portland, OR, USA, 1–5 November 2015; pp. 177–178. [Google Scholar] [CrossRef]
- Nguyen, L.; Cheng, C.L.; Werner, F.; Prvulovic, M.; Zajic, A. A Comparison of Backscattering, EM, and Power Side-Channels and Their Performance in Detecting Software and Hardware Intrusions. J. Hardw. Syst. Secur. 2020, 4, 150–165. [Google Scholar] [CrossRef]
- Nguyen, L.N.; Cheng, C.L.; Prvulovic, M.; Zajić, A. Creating a Backscattering Side Channel to Enable Detection of Dormant Hardware Trojans. IEEE Trans. Very Large Scale Integr. (Vlsi) Syst. 2019, 27, 1561–1574. [Google Scholar] [CrossRef]
- Agrawal, D.; Archambeault, B.; Rao, J.R.; Rohatgi, P. The EM Side—Channel(s). In Proceedings of the Cryptographic Hardware and Embedded Systems—CHES 2002, Redwood Shores, CA, USA, 13–15 August 2002; Kaliski, B.S., Koç, Ç.K., Paar, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 29–45. [Google Scholar]
- Kocher, P.; Jaffe, J.; Jun, B. Differential Power Analysis. In Proceedings of the Advances in Cryptology—CRYPTO’ 99, Santa Barbara, CA, USA, 15–19 August 1999; Wiener, M., Ed.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 388–397. [Google Scholar]
- Bergman, T.D.; Manager, C.P.; Liszewski, K.T. Battelle barricade: A nondestructive electronic component authentication and counterfeit detection technology. In Proceedings of the 2016 IEEE Symposium on Technologies for Homeland Security (HST), Waltham, MA, USA, 10–11 May 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Shinde, S.; Jothibasu, S.; Ghasr, M.T.; Zoughi, R. Wideband Microwave Reflectometry for Rapid Detection of Dissimilar and Aged ICs. IEEE Trans. Instrum. Meas. 2017, 66, 2156–2165. [Google Scholar] [CrossRef]
- Gassend, B.; Clarke, D.; Van Dijk, M.; Devadas, S. Silicon physical random functions. In Proceedings of the 9th ACM Conference on Computer and Communications Security, Association for Computing Machinery (ACM), Washington, DC, USA, 18–22 November 2002; pp. 148–160. [Google Scholar] [CrossRef]
- Gassend, B. Physical Random Functions. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2003. [Google Scholar]
- Lim, D.; Lee, J.W.; Gassend, B.; Suh, G.E.; van Dijk, M.; Devadas, S. Extracting secret keys from integrated circuits. IEEE Trans. Very Large Scale Integr. Syst. 2005, 13, 1200–1205. [Google Scholar] [CrossRef]
- Miller, M.; Meraglia, J.; Hayward, J. Traceability in the Age of Globalization: A Proposal for a Marking Protocol to Assure Authenticity of Electronic Parts; Technical Report; SAE Technical Paper: Warrendale, PA, USA, 2012. [Google Scholar] [CrossRef]
- Kuemin, C.; Nowack, L.; Bozano, L.; Spencer, N.D.; Wolf, H. Oriented Assembly of Gold Nanorods on the Single-Particle Level. Adv. Funct. Mater. 2012, 22, 702–708. [Google Scholar] [CrossRef]
- Das, J.; Scott, K.; Rajaram, S.; Burgett, D.; Bhanja, S. MRAM PUF: A Novel Geometry Based Magnetic PUF with Integrated CMOS. IEEE Trans. Nanotechnol. 2015, 14, 436–443. [Google Scholar] [CrossRef]
- Works, C.N.; Dakin, T.W.; Boggs, F.W. A resonant-cavity method for measuring dielectric properties at ultrahigh frequencies. Electr. Eng. 1944, 63, 1092–1098. [Google Scholar] [CrossRef]
- Melikyan, H.; Sargsyan, T.; Babajanyan, A.; Kim, S.; Kim, J.; Lee, K.; Friedman, B. Hard disk magnetic domain nano-spatial resolution imaging by using a near-field scanning microwave microscope with an AFM probe tip. J. Magn. Magn. Mater. 2009, 321, 2483–2487. [Google Scholar] [CrossRef]
- Bagdad, B.A.; Lozano, C.; Gamiz, F. Near-field scanning microwave microscope platform based on a coaxial cavity resonator for the characterization of semiconductor structures. Solid-State Electron. 2019, 159, 150–156. [Google Scholar] [CrossRef]
- Pozar, D. Microwave Engineering; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- SAE. Available online: https://www.sae.org/ (accessed on 1 March 2024).
- AS6171A. Available online: https://www.sae.org/standards/content/as6171a/ (accessed on 1 March 2024).
- AS6171/2A. Available online: https://www.sae.org/standards/content/as6171/2a/?src=as6171a (accessed on 1 March 2024).
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Shlens, J. A Tutorial on Principal Component Analysis. arXiv 2014, arXiv:1404.1100. [Google Scholar]


| Part Number | Manufacturer | Function |
|---|---|---|
| INA122P | Texas Instruments | Instrumentation amplifier |
| LM2903P | Texas Instruments | Comparator |
| LT1028CN8 | Linear Technology | Operational amplifier |
| NE555P | Texas Instruments | Precision timer |
| SN65176BP | Texas Instruments | Differential bus transceiver |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nechiyil, A.; Lee, R.; Chapman, G. A Rapid, Non-Destructive Method to Detect Counterfeit Integrated Circuits Using a Resonant Cavity System. Instruments 2024, 8, 37. https://doi.org/10.3390/instruments8030037
Nechiyil A, Lee R, Chapman G. A Rapid, Non-Destructive Method to Detect Counterfeit Integrated Circuits Using a Resonant Cavity System. Instruments. 2024; 8(3):37. https://doi.org/10.3390/instruments8030037
Chicago/Turabian StyleNechiyil, Aditya, Robert Lee, and Gregg Chapman. 2024. "A Rapid, Non-Destructive Method to Detect Counterfeit Integrated Circuits Using a Resonant Cavity System" Instruments 8, no. 3: 37. https://doi.org/10.3390/instruments8030037
APA StyleNechiyil, A., Lee, R., & Chapman, G. (2024). A Rapid, Non-Destructive Method to Detect Counterfeit Integrated Circuits Using a Resonant Cavity System. Instruments, 8(3), 37. https://doi.org/10.3390/instruments8030037






