Novel Heat Exchangers with Cross-Runners for Air and Water Cooling
Abstract
:1. Introduction
2. Tests of Heat-Transfer Performance
2.1. Experimental Setup for Air-Cooling Measurement
2.2. Experimental Setup for Water-Cooling Measurement
2.3. Data Reduction and Uncertainty Analysis
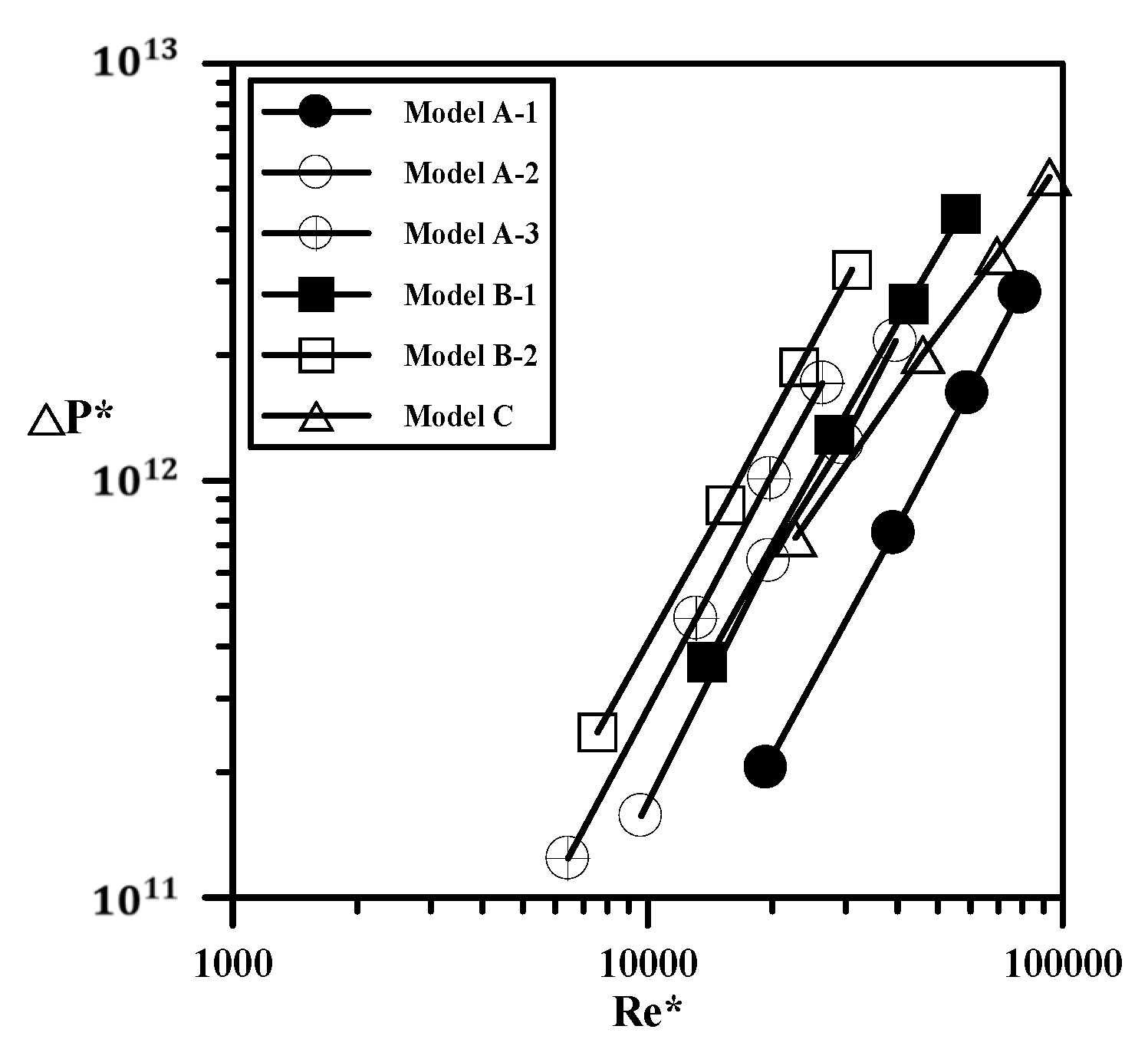
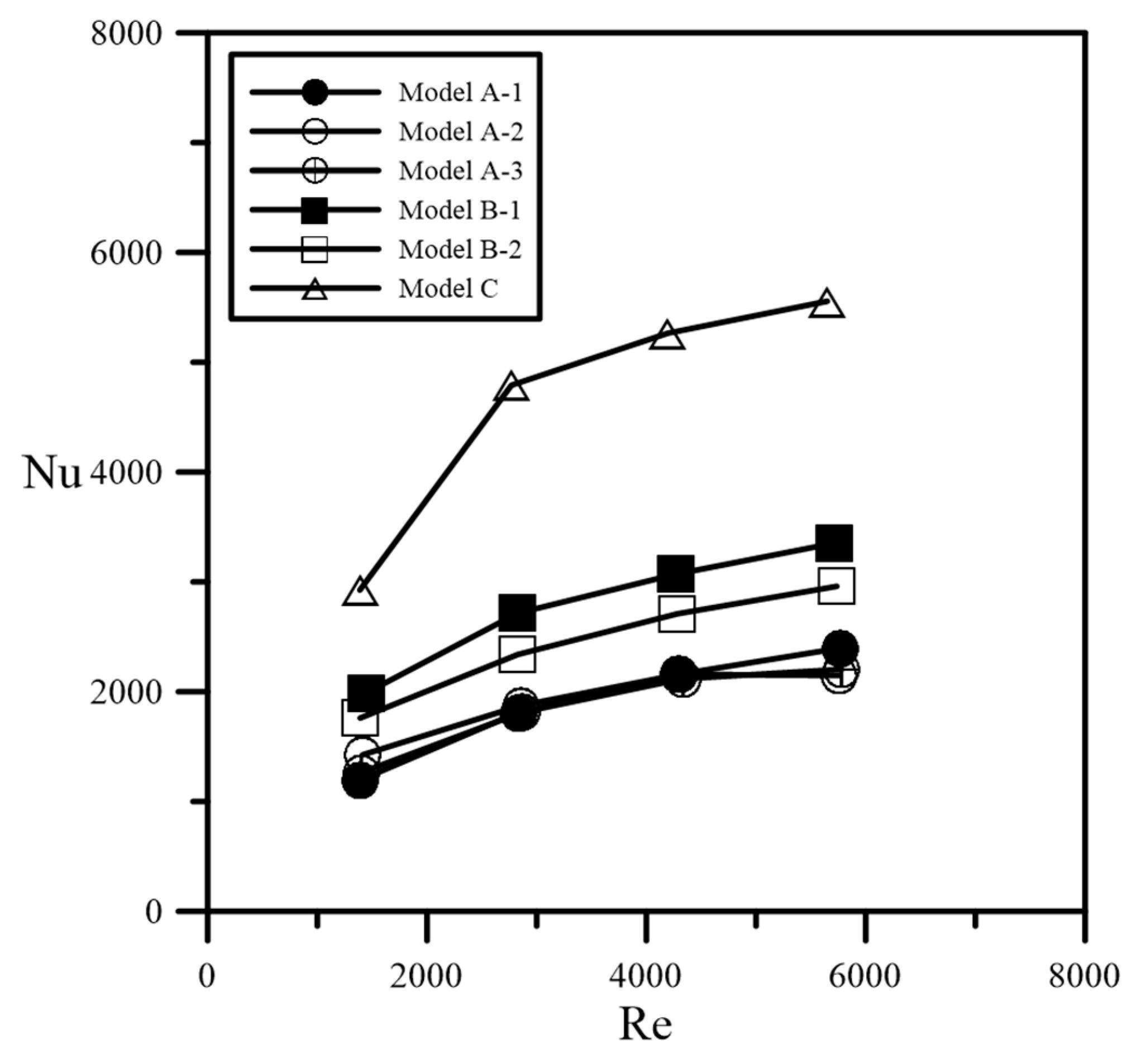
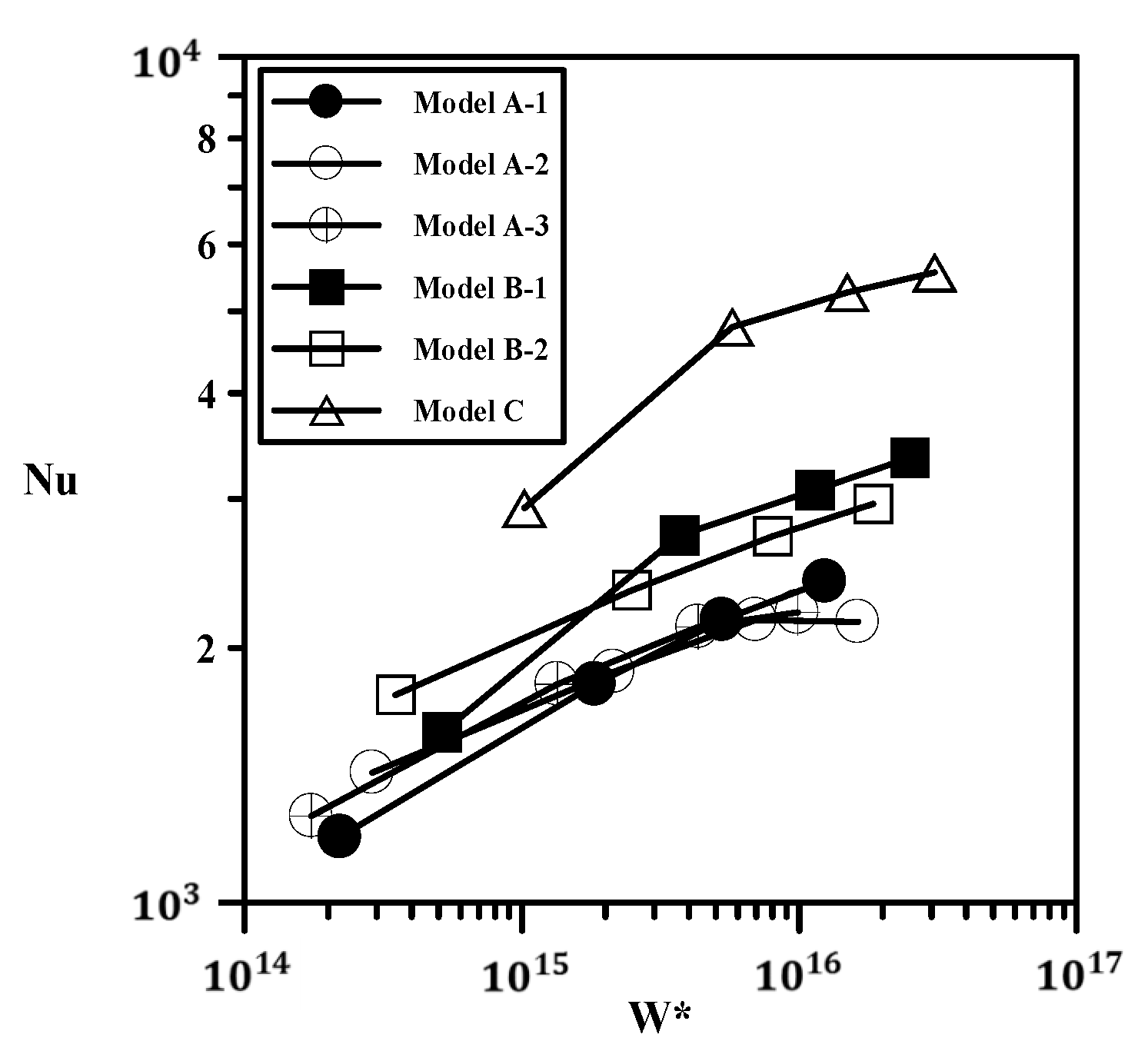
3. Results and Discussion
4. Conclusions
- (1)
- Increasing the heat-transfer area (AHT) and decreasing the porosity (ε) of the heat exchanger will obviously increase the flow resistance of the cross-runner heat exchanger.
- (2)
- The larger effective thermal conductivity (ke), larger heat-transfer area (AHT), and lower porosity (ε) are desired for the better conjugate heat transfer performance.
- (3)
- The experimental measurements using air-cooled heat transfer indicated that under the same pumping power, the heat transfer capacity of Model C was 2.27 and 1.67 times that of Models A and B, respectively. The semi-empirical correlations of the dimensionless pressure drop and Nusselt number in terms of the Reynolds number for different heat exchangers with various ke, AHT, and ε were proposed.
- (4)
- The feasibility of Model C as the heat exchanger for use in instantaneous water heating applications was confirmed by the water-cooling tests. The results showed the design has great commercial potential.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Vanfossen, G.J. Heat-transfer coefficients for staggered arrays of short pin fins. ASME J. Eng. Gas Turbines Power 1982, 104, 268–274. [Google Scholar] [CrossRef]
- Brigham, B.A.; Vanfossen, G.J. Length to diameter ratio and row number effects in short pin fin heat transfer. ASME J. Eng. Gas Turbines Power 1984, 106, 241–244. [Google Scholar] [CrossRef]
- Metzger, D.E.; Fan, C.S.; Haley, S.W. Effects of pin shape and array orientation on heat transfer and pressure loss in pin fin arrays. ASME J. Eng. Gas Turbines Power 1984, 106, 252–257. [Google Scholar] [CrossRef]
- Zukauskas, A.; Ulinskas, R. Efficiency parameters for heat transfer in tube banks. Heat Transf. Eng. 1985, 6, 19–25. [Google Scholar] [CrossRef]
- Armstrong, J.; Winstanley, D. A review of staggered array pin fin heat transfer for turbine cooling applications. ASME J. Turbomach. 1988, 110, 94–103. [Google Scholar] [CrossRef]
- Jubran, B.A.; Hamdan, M.A.; Abdualh, R.M. Enhanced heat transfer, missing pin, and optimization for cylindrical pin fin arrays. ASME J. Heat Transf. 1993, 115, 576–583. [Google Scholar] [CrossRef]
- Tahat, M.A.; Babus’Haq, R.F.; Probert, S.D. Forced steady-state convections from pin-fin arrays. Appl. Energy 1994, 48, 335–351. [Google Scholar] [CrossRef]
- Tahat, M.; Kodah, Z.H.; Jarrah, B.A.; Probert, S.D. Heat transfer from pin-fin arrays experiencing forced convection. Appl. Energy 2000, 67, 419–442. [Google Scholar] [CrossRef]
- Babus’Haq, R.F.; Akintunde, K.; Probert, S.D. Thermal performance of a pin-fin assembly. Int. J. Heat Fluid Flow 1995, 16, 50–55. [Google Scholar] [CrossRef]
- Sara, O.N.; Yapici, S.; Yilmaz, M.; Pekdemir, T. Second law analysis of rectangular channels with square pin-fins. Int. Commun. Heat Mass Transf. 2001, 28, 617–630. [Google Scholar] [CrossRef]
- Sara, O.N. Performance analysis of rectangular ducts with staggered square pin fins. Energy Convers. Manag. 2003, 44, 1787–1803. [Google Scholar] [CrossRef]
- Wang, Q.; Zeng, M.; Ma, T.; Du, X.; Yang, J. Recent development and application of several high-efficiency surface heat exchangers for energy conversion and utilization. Appl. Energy 2014, 15, 748–777. [Google Scholar] [CrossRef]
- Chen, L.; Feng, H.; Xie, Z.; Sun, F. Thermal efficiency maximization for H- and X-shaped heat exchangers based on constructal theory. Appl. Therm. Eng. 2015, 91, 456–462. [Google Scholar] [CrossRef]
- Li, W.; Yang, L.; Ren, J.; Jiang, H. Effect of thermal boundary conditions and thermal conductivity on conjugate heat transfer performance in pin fin arrays. Int. J. Heat Mass Transf. 2016, 95, 579–592. [Google Scholar] [CrossRef]
- Jadhav, R.S.; Balaji, C. Fluid flow and heat transfer characteristics of a vertical channel with detached pin-fin arrays arranged in staggered manner on two opposite endwalls. Int. J. Therm. Sci. 2016, 105, 57–74. [Google Scholar] [CrossRef]
- Schampheleire, S.D.; Jaeger, P.D.; Kerpel, K.D.; Ameel, B.; Huisseune, H.; Paepe, M.D. How to study thermal applications of open-cell metal foam: experiments and computational fluid dynamics. Materials 2016, 9, 94–120. [Google Scholar] [CrossRef] [Green Version]
- Chen, K.-C.; Wang, C.-C. Performance improvement of high power liquid-cooled heat sink via non-uniform metal foam arrangement. Appl. Therm. Eng. 2015, 87, 41–46. [Google Scholar] [CrossRef]
- Abadi, G.B.; Moon, C.; Kim, K.C. Experimental study on single-phase heat transfer and pressure drop of refrigerants in a plate heat exchanger with metal-foam-filled channels. Appl. Therm. Eng. 2016, 102, 423–431. [Google Scholar] [CrossRef]
- Feng, S.S.; Kuang, J.J.; Wen, T.; Lu, T.J.; Ichimiy, K. An experimental and numerical study of finned metal foam heat sinks under impinging air jet cooling. Int. J. Heat Mass Transf. 2014, 77, 1063–1074. [Google Scholar] [CrossRef]
- Shih, W.-H.; Liu, C.-C.; Hsieh, W.-H. Heat-transfer characteristics of aluminum-foam heat sinks with a solid aluminum core. Int. J. Heat Mass Transf. 2016, 97, 742–750. [Google Scholar] [CrossRef]
- Chen, H.-H. A Heat Exchanger of Sheet Configuration. Patent of ROC M428652, 1 May 2012. [Google Scholar]
- Moffat, R.J. Contributions to the theory of single-sample uncertainty analysis. ASME J. Fluids Eng. 1982, 104, 250–258. [Google Scholar] [CrossRef]
- Dittus, P.W.; Boelter, L.M.K. Heat Transfer in Automobile Radiators of the Tubular Type; University of California publications in engineering; University of California Press: Berkeley, CA, USA, 1930; Volume 2, pp. 443–461, reprinted in Int. Comm. Heat Mass Transf. 1985, 12, 3–22. [Google Scholar] [CrossRef]




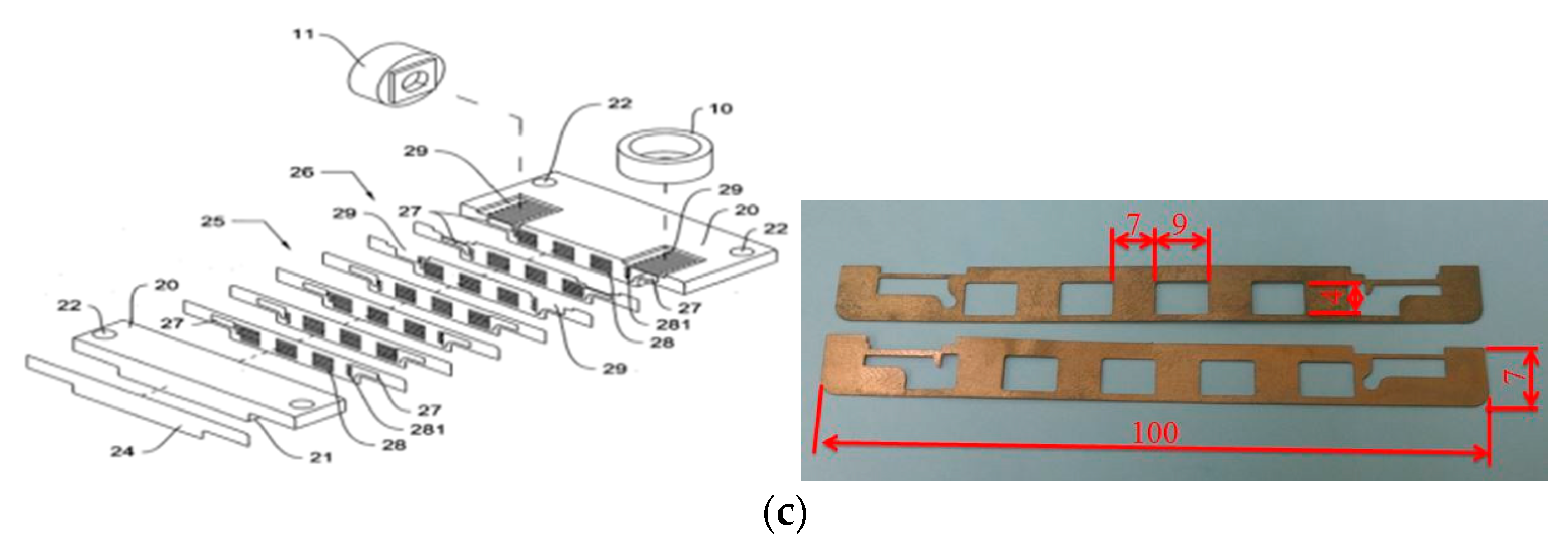








| Model Type | Material | ks* (≅ke) [W/m/K] | AHT [m2] × 106 | |
|---|---|---|---|---|
| Model A-1 | Al-alloy | 0.85 | 24.6 | 8706 |
| Model A-2 | Al-alloy | 0.85 | 24.6 | 11436 |
| Model A-3 | Al-alloy | 0.85 | 24.6 | 14166 |
| Model B-1 | Al-alloy | 0.59 | 67.2 | 17272 |
| Model B-2 | Al-alloy | 0.59 | 67.2 | 28235 |
| Model C | Copper | 0.31 | 257 | 19320 |
| Model Type | C2 | n2 |
|---|---|---|
| Model A-1 | 0.392 | 0.513 |
| Model A-2 | 2.518 | 0.330 |
| Model A-3 | 1.041 | 0.445 |
| Model B-1 | 0.208 | 0.549 |
| Model B-2 | 0.565 | 0.392 |
| Model C | 0.346 | 0.469 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeng, T.-M.; Tzeng, S.-C.; Tseng, C.-W.; Chang, C.-H.; Liu, Y.-C.; Peng, H.-Y.; Chen, H.-H. Novel Heat Exchangers with Cross-Runners for Air and Water Cooling. Inventions 2016, 1, 10. https://doi.org/10.3390/inventions1020010
Jeng T-M, Tzeng S-C, Tseng C-W, Chang C-H, Liu Y-C, Peng H-Y, Chen H-H. Novel Heat Exchangers with Cross-Runners for Air and Water Cooling. Inventions. 2016; 1(2):10. https://doi.org/10.3390/inventions1020010
Chicago/Turabian StyleJeng, Tzer-Ming, Sheng-Chung Tzeng, Ching-Wen Tseng, Chia-Hung Chang, Yi-Cheng Liu, Hsiao-Yun Peng, and Huang-Han Chen. 2016. "Novel Heat Exchangers with Cross-Runners for Air and Water Cooling" Inventions 1, no. 2: 10. https://doi.org/10.3390/inventions1020010
APA StyleJeng, T.-M., Tzeng, S.-C., Tseng, C.-W., Chang, C.-H., Liu, Y.-C., Peng, H.-Y., & Chen, H.-H. (2016). Novel Heat Exchangers with Cross-Runners for Air and Water Cooling. Inventions, 1(2), 10. https://doi.org/10.3390/inventions1020010





