Robust Control of Irrigation Systems Using Predictive Methods and Disturbance Rejection

Abstract

Ensuring that the world’s population meets its food needs, despite water restrictions, can be significantly improved by increasing irrigation efficiency and productivity. Achieving this goal necessitates technological advancements in control systems. Therefore, the implementation of effective control systems across the entire irrigation water distribution chain is crucial and requires technological modernization. This paper presents a control scheme that combines the benefits of model predictive control (MPC) and active disturbance rejection by using generalized proportional integral (GPI) observers. The proposed control scheme was applied to a three-canal irrigation system. The simulation results confirm that the proposed controller is robust to disturbances and ensures accurate tracking for all reference levels. The controller’s performance is highlighted by the improvement in response time and considerable reduction in overshoot compared with the optimized proportional integral (PI) controllers. Additionally, the use of GPI observers allows for the precise estimation of nonlinear disturbances and phase variables, enhancing the robustness of the system. The efficiency of the observer is due to its ability to adequately estimate global additive disturbances, including unknown parameters and external disturbances in the input–output dynamics.

1. Introduction

Irrigation consumes large amounts of water. It is estimated that irrigation represents 80% of the world’s total freshwater consumption, and that only 30% of this water is delivered to plants [1]. This low efficiency in water distribution can be attributed to several factors. Significant losses occur owing to evaporation, infiltration, and surface runoff during water transport through the canals. Additionally, improper maintenance of irrigation infrastructure, such as cracked or unlined canals, exacerbates seepage losses [2]. Inefficiencies are also linked to outdated or poorly managed water allocation practices that fail to match crop water needs with the delivery schedules. Furthermore, over irrigation, often caused by a lack of precise control systems, leads to water wastage and uneven distribution across fields. These factors collectively contribute to the substantial gap between the volume of water extracted and the amount effectively utilized by plants.

Current irrigation systems face several challenges, including water scarcity, inefficient water distribution, and the need for sustainable agricultural practices. These challenges are exacerbated by climate change and increasing global food demands. The necessity for improved control of irrigation systems is critical for enhancing water use efficiency and ensuring reliable water delivery to crops. Despite advancements in control technologies, there remain gaps in the literature regarding the integration of robust control strategies that can handle the nonlinearities and uncertainties inherent in irrigation systems [3,4,5].

Automatic control techniques are widely used in irrigation canals, most of which are based on local gate control using classical approaches such as PI controllers [6]. These decentralized approaches provide reasonable performances in many cases. However, because the coupling effect between different local controllers is not considered, there is often significant loss in the performance of the control system [7]. Studies such as [8,9,10,11,12,13] have used new techniques for the optimal tuning of the parameters of these controllers.

A global controller, or centralized control, is an excellent alternative for addressing the problem of dynamic coupling in multivariate systems. Model-based predictive control (MPC) approaches are a family of control algorithms whose common properties are state and output predictions using an internal model and performing optimization with current and forecasted future data [14,15]. These controllers have shown excellent results in open channels [16,17,18,19,20,21]. However, the inclusion of disturbance models is a typical prerequisite in any standard industrial MPC implementation because the sources of disturbances are known [16]. The difficulty in tuning these disturbance models lies in the unknown nature of the disturbances.

Some studies, such as [18], add a feedforward control component to a predictive control scheme for irrigation systems. This approach aims to counteract the effects of known disturbances by adjusting the control actions in advance, thereby enhancing system performance. However, the use of such a stage requires accurate measurement of the external disturbances, which can be quite challenging in real-world applications owing to the dynamic and unpredictable nature of environmental factors, such as weather conditions, soil moisture variability, and water flow inconsistencies.

Disturbance observers are often employed to adress this issue because they provide an effective estimate of disturbances without the need for direct measurement [22,23]. Disturbance observers monitor the system output and estimate the impact of disturbances based on deviations from the expected behavior. This estimation is then used to compensate for disturbances in real-time, thereby improving the control accuracy. Moreover, the use of disturbance observers has an added benefit: not only can they handle external disturbances, but they can also account for uncertainties in the plant model parameters or unmodeled dynamics. By treating these uncertainties as part of the disturbance, the control scheme can significantly improve the robustness and adaptability of the system to varying operating conditions, ensuring a more reliable and efficient irrigation process.

This paper proposes an active disturbance rejection approach combined with model-based predictive control to improve the performance of the irrigation channels. The proposed control scheme combines the benefits of MPC and active disturbance rejection using generalized proportional integral (GPI) observers and is applied to a three-canal irrigation system. The simulation results confirm that the proposed controller is robust to disturbances and ensures the accurate tracking of all reference levels. The controller’s performance is highlighted by the improvement in response time and considerable reduction in overshoot compared with traditional proportional integral (PI) controllers. Additionally, the use of GPI observers allows for the precise estimation of nonlinear disturbances and phase variables, enhancing the robustness of the system. The contributions of this study include the development of a robust control scheme, application to a practical system, and demonstration of improved performance metrics.

The document is organized as follows: Section 2 presents the Saint-Venant equations and dynamic model of the experimental channel. Section 3 discusses the design of the predictive controller and the disturbance observer for the experimental channel. Section 4 presents a comparison of the results of the proposed robust controller with those of a classical controller. Finally, Section 5 presents conclusions based on the experimental results.

2. Modeling of Hydraulic Channels

2.1. The Saint-Venant Equations

In addition to issues related to inefficient water management and unsatisfactory service to farmers, the hydraulic limitations of irrigation canals also significantly contribute to water loss and low efficiency. Factors such as canal design, wall roughness, inadequate slopes, and flow conditions directly impact infiltration and evaporation losses, as well as conduit discharge capacity [24]. These hydraulic characteristics, which are often interdependent with control and management strategies, must be considered when seeking solutions to improve the performance of irrigation systems. Therefore, the integration of models that include hydraulic aspects is essential to achieve more robust and effective control.

The one-dimensional equations governing unsteady open channel flow are widely known as the Saint-Venant equations. These equations were derived based on several key assumptions [24,25]:

• The flow is considered one-dimensional, implying that the velocity is uniform across any cross-section, and that the free-surface profile in the transverse direction is horizontal.
• The curvature of the streamlines was assumed to be minimal, and the vertical acceleration of the fluid was negligible. Consequently, the pressure distribution throughout the flow is hydrostatic.
• The flow resistance and turbulent losses are consistent with those of a steady uniform flow, regardless of depth variations, as long as the flow depth and velocity remain the same.
• The slope of the channel bed is small enough to allow the following approximations:

  $$cos\theta \approx 1,sin\theta \approx tan\theta .$$
• The density of the water is constant throughout the flow.

The Saint-Venant equations have traditionally been considered a complete tool for modeling irrigation system sections [24]. These processes are modeled by employing hyperbolic equations for the conservation of mass and momentum that represent the process of one-dimensional flow in a free sheet:

$${\displaystyle \frac{\partial A_w(x,t)}{\partial t}}+{\displaystyle \frac{\partial Q}{\partial x}}=q_l$$

(1)

$${\displaystyle \frac{\partial Q}{\partial t}}+{\displaystyle \frac{\partial (Q^2/A_w)}{\partial x}}+g{A}_w{\displaystyle \frac{\partial Z}{\partial x}}=-g{A}_w{S}_f+k{q}_{l}V(x,t)$$

(2)

where $A_w(x,t)$ is the wetted area $\left[{\mathrm{m}}^2\right]$; $S_f$ is the friction slope; $q_l\left(x\right)$ is the lateral discharge; $Q(x,t)$ is the discharge $[{\mathrm{m}}^3/\mathrm{s}]$ across section $A_w(x,t)$; $Z(x,t)$ is the water depth $\left[\mathrm{m}\right]$; $V(x,t)$ is the average velocity $[\mathrm{m}/\mathrm{s}]$; I is the bed slope; and g is the gravitational acceleration $[\mathrm{m}/{\mathrm{s}}^2]$ [26]. The initial and boundary conditions of the system are as follows.

$$Z(x,0)=Z_0\left(x\right),Q(x,0)=Q_0\left(x\right)$$

(3)

$$\begin{array}{c}\hfill Z(0,t)=Z_i\left(t\right),Q(0,t)=Q_i\left(t\right),\\ \hfill Z(X_f,t)=Z_f\left(t\right),Q(X_f,t)=Q_f\left(t\right)\end{array}$$

(4)

2.2. Simplified Linear Model for a Stretch of Channel

In some studies a method was proposed that linearizing the Saint-Venant equations around a state of equilibrium transforms them into the Laplace domain [1,27,28]. For a channel section in which there are no lateral retreats, the equations that relate the y levels at the origin and the end of the section with the q flows are

$$\left[\begin{array}{c}y(0,s)\\ y(1,s)\end{array}\right]=\left[\begin{array}{cc}{p}_{11}\left(s\right)& p_{12}\left(s\right)\\ p_{21}\left(s\right)& p_{22}\left(s\right)\end{array}\right]\left[\begin{array}{c}q(0,s)\\ q(1,s)\end{array}\right]$$

(5)

where the transfer functions in the Laplace domain $p_{ij}\left(s\right)$ are the integrator, delay, and zero (IDZ) models. The parameters that define the IDZ models are obtained analytically from the physical parameters of the section, such as the Manning coefficient, geometry, and slope, and they capture most of the flow dynamics [29].

The IDZ models corresponding to the end of tranche level $y(L,s)$ are

$$p_{21}\left(s\right)=\left({\displaystyle \frac{1}{A_{d}s}}+b_d\right)e^{-{\tau }_{d}s}$$

(6)

$$p_{22}\left(s\right)=\left({\displaystyle \frac{1}{A_{d}s}}+{\overline{b}}_d\right)$$

(7)

where $A_d$ is the equivalent area, $b_d$ and ${\overline{b}}_d$ are static gains, and ${\tau }_d$ is the delay. These values are functions of the physical parameters of the section; their exact expressions can be found in [29]. In distribution channels, it is recommended to use gate openings or closures as control variables rather than for manipulating flow rates. Therefore, Equation (5) must be transformed into another equivalent system of equations in which the inputs are the variations in the gates at the origin $c_1$ and the end of section $c_2$. The flow that circulates through a semi-submerged gate is defined as

$$Q=C_d{L}_{c}C\sqrt{2Y_1-Y_2}$$

(8)

$L_c$ is the gate width, C is the opening, $C_d$ is the discharge coefficient, $Y_1$ and $Y_2$ are the upstream and downstream levels of the gate, respectively, and g is the gravitational acceleration. Linearizing this expression to consider small deviations in the flow around an equilibrium point, the following expression is obtained,

$$q=K_1{Y}_1+K_2{Y}_2+K_{c}C$$

(9)

where $K_c=Q/L_c$, $K_1=Q/2(Y_1-Y_2)$ and $K_2=-K_1$. By substituting into Equation (5) the flow in Equation (9), we introduce the general expressions of the IDZ models and obtain the equation for the end-of-span level. In this context, the “end-of-span level” refers to the water level at the downstream boundary of a canal section or span, which is crucial for maintaining the desired hydraulic conditions and ensuring water delivery accuracy.

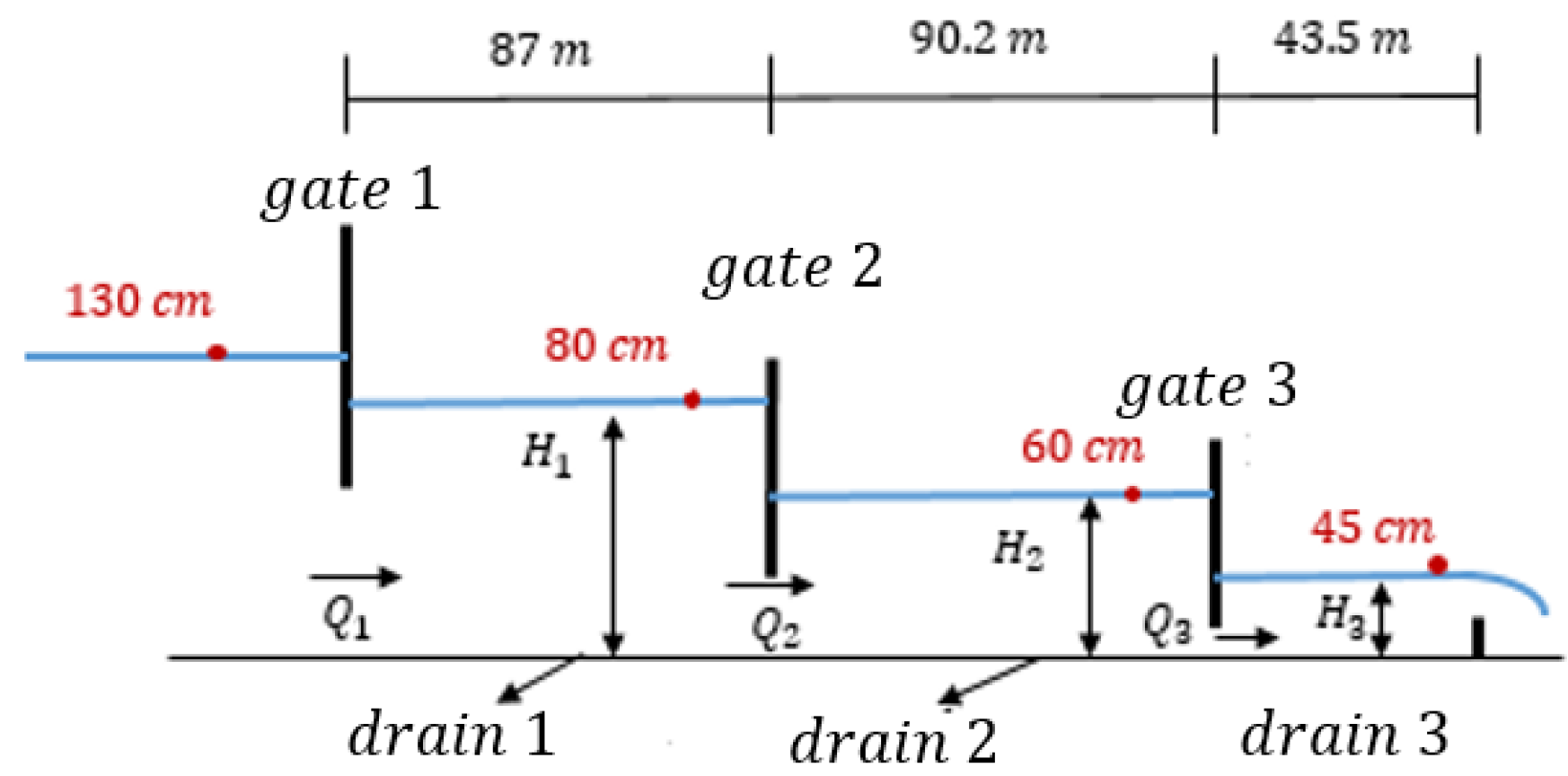
2.3. PAC-UPC Experimental Channel

The control algorithm testing laboratory of the Polytechnic University of Catalonia (PAC-UPC for its acronym in Spanish) is a laboratory-scale model of an irrigation canal, situated at the Polytechnic University of Catalonia. Specifically designed for conducting both fundamental and applied research in the domain of irrigation canal control, this channel integrates various subfields, such as instrumentation, modeling, and water measurement of irrigation canals.

Originally conceived to replicate the significant transport delays encountered in real irrigation control scenarios, the design features a long, zero-slope, rectangular cross-sectional canal. However, owing to spatial limitations within the laboratory, a serpentine configuration was adopted to maximize the length of the canal within the confined area.

This study utilizes the PAC-UPC channel, which measures 220 m in length and 0.44 m in width, maintains a zero slope, and exhibits a transport delay of 100 s, as illustrated in Figure 1. This delay represents the time taken for water to traverse from the start to the end of the canal. The PAC-UPC includes three motorized gates and several extraction points, and is arranged into three pools, each demarcated by one of the gates, with gravity intakes positioned at the downstream end of each pool [16].

The equations that relate the final levels of the section with their corresponding origin and end gates for the three study pools of the PAC-UPC are

$$\begin{array}{ccc}\hfill h_1\left(s\right)& =& G_{11}\left(s\right)u_1\left(s\right)+G_{12}\left(s\right)u_2\left(s\right)\hfill \\ \hfill h_2\left(s\right)& =& G_{22}\left(s\right)u_2\left(s\right)+G_{23}\left(s\right)u_3\left(s\right)\hfill \\ \hfill h_3\left(s\right)& =& G_{33}\left(s\right)u_3\left(s\right)\hfill \end{array}$$

(10)

By employing parametric identification with step-type inputs, like in ref. [28], the following dynamic model for the three pools of the UPC-PAC channel were obtained.

$$G_{11}\left(s\right)={\displaystyle \frac{0.5(s+0.007)}{s}}{e}^{-24s}{G}_{12}\left(s\right)={\displaystyle \frac{-0.5(s+0.011)}{s}}{e}^{-4s}$$

$$G_{22}\left(s\right)={\displaystyle \frac{0.6(s+0.02)}{s}}{e}^{-45s}{G}_{23}\left(s\right)={\displaystyle \frac{-0.4(s+0.004)}{s}}{e}^{-4s}$$

$$G_{33}\left(s\right)={\displaystyle \frac{0.45}{375s+1}}{e}^{-25s}$$

As observed, all models conform to the integrator-delay-zero (IDZ) type, with the exception of the $G_{33}\left(s\right)$ model, which is a first-order model featuring a time delay. This variation in modeling approaches stems from the presence of a spillway at the conclusion of the third segment of the canal, rather than a semi-submerged gate.

3. Robust Controller Design

The development of a model that integrates robust strategies for irrigation systems is a complex yet feasible task that uses advanced control and modeling approaches. Tools such as model-based predictive control (MPC) allow for the incorporation of uncertainties into a model through disturbance observers and active rejection techniques. Furthermore, the reliability of these models can be assessed both quantitatively and qualitatively. Quantitative methods include performance metrics, such as the mean squared error (MSE), settling time, and overshoot reduction. On the other hand, qualitative assessments can be conducted through comparative studies with traditional controllers, sensitivity analysis to critical parameter changes, and experimental validation under dynamic conditions.

This section presents a control approach that combines model-based predictive control and a disturbance observer for active rejection of disturbances in an experimental irrigation channel.

3.1. Predictive Control Overview

Model-based predictive control (MPC) is a sophisticated control technique that is widely recognized and adopted in various industrial and academic settings. The appeal of this method lies in its ability to handle multivariable systems with constraints, thereby providing a future-oriented control strategy that adjusts actions based on predicted outcomes.

MPC operates by forecasting future outputs over a prediction horizon N, with these outputs anticipated at each time step t using a process model. The predicted outputs $y(t+k\mid t)$ for $k=1\cdots N$ are dependent on the known values at time t and projected future control signals $u(t+k\mid t)$ for $k=1\cdots N-1$. These future control signals are computed and implemented in the system.

The calculation of the control sequence $u(t+k\mid t)$ for $k=1\cdots N-1$ involves an optimization process aimed at minimizing the deviation of the process from a predefined reference path $w(t+k)$. Optimization typically minimizes a quadratic cost function based on the discrepancy between the predicted output and the reference trajectory.

The immediate control signal executed during the process is $u(t\mid t)$. Signals from other times such as $y\left(t\right)$ are disregarded because by the next time step, $y(t+1)$, the outcome is already known, and thus, the control strategy updates using this new information. Accordingly, the control signal for the subsequent time step, $u(t+1\mid t+1)$, is calculated using freshly updated data.

To operationalize this strategy, MPC uses a foundational structure as depicted in Figure 2. This structure utilizes a predictive model to forecast the future behavior of the plant based on past and current values, along with optimal predictions derived from control actions. The optimizer, considering the defined cost function and any imposed constraints, computes these control actions.

One type of predictive control widely accepted in the industry and academia is generalized predictive control (GPC) [30]. The formulation of GPC using the transfer function structure is as follows:

$$A\left(z^{-1}\right)y\left(t\right)=B\left(z^{-1}\right)z^{-d}u(t-1)+C\left(z^{-1}\right){\displaystyle \frac{e\left(t\right)}{\Delta }}$$

(11)

Here, $\Delta =1-z^{-1}$, $e\left(t\right)$ is zero-mean white noise, A, B, and C are polynomials in the delay operator $z^{-1}$, and d is the dead time of the system and $u\left(t\right)$ and $y\left(t\right)$ are the input and output variables, respectively. Polynomial C can be used for the optimal rejection of disturbances, although its usefulness is greater in improving the robustness.

The GPC algorithm involves applying an optimization problem that minimizes the following cost function:

$$\begin{array}{c}\hfill J=\sum _{j=N_1}^{N_2}\delta \left(j\right){[\widehat{y}(t+j\mid t)-w(t+j)]}^2\\ \hfill +\sum _{j=1}^{N_u}\lambda \left(j\right){[\Delta u(t+j-1)]}^2\end{array}$$

(12)

where $\delta \left(j\right)$ and $\lambda \left(i\right)$ are weighting sequences that are generally constant. $\widehat{y}(t+j\mid t)$ is the optimal prediction of the output j steps forward, obtained with known data at time t. $N_1$, $N_2$, and $N_u$ are the minimum prediction horizon, maximum prediction horizon, and control horizon, respectively, and finally $w(t+j)$ is the future reference trajectory. The optimal prediction $\widehat{y}(t+j\mid t)$ is obtained by means of a recursive algorithm derived from the solution of a Diophantine equation [31]. The solution of this algorithm indicates that the future values of the output can be expressed as

$$\begin{array}{c}\hfill y(t+j)=F_{j}y\left(t\right)+E_{j}B\left(z^{-1}\right)\Delta u(t+j-d-1)\\ \hfill +E_{j}e(t+j)\end{array}$$

(13)

Polynomials $E_j$ and $F_j$ are derived from the Diophantine equation. The noise terms of Equation (13) will be investigated in the future. Therefore, the best prediction is given by

$$\begin{array}{c}\hfill \widehat{y}(t+j\mid t)=G_j\left(z^{-1}\right)\Delta u(t+j-d-1)\\ \hfill +F_j\left(z^{-1}\right)y\left(t\right)\end{array}$$

(14)

where $G_j\left(z^{-1}\right)=E_j\left(z^{-1}\right)B\left(z^{-1}\right)$.

The solution to the GPC problem involves obtaining the sequence of control signals $u\left(t\right)$, $u(t+1)$, ⋯, $u(t+N)$ that optimizes the cost function. Since the process has a dead time of d sampling periods, the system output will only be influenced by the control signal $u\left(t\right)$ after $d+1$ sampling periods. Therefore, the horizons of the GPC problem can be redefined as $N_1=d+1$, $N_2=d+N$, and $N_u=N$. Considering the following set of predictions of j steps, it is noted that

$$\begin{array}{ccc}\hfill \widehat{y}(t+d+1)& =& G_{d+1}\Delta u\left(t\right)+F_{d+1}y\left(t\right)\hfill \\ \hfill \widehat{y}(t+d+2)& =& G_{d+2}\Delta u(t+1)+F_{d+2}y\left(t\right)\hfill \\ & ⋮& \hfill \\ \hfill \widehat{y}(t+d+N)& =& G_{d+N}\Delta u(t+N-1)+F_{d+N}y\left(t\right)\hfill \end{array}$$

(15)

which can be written as

$$\mathbf{y}=\mathbf{G}\mathbf{u}+\mathbf{F}\left(z^{-1}\right)y\left(t\right)+{\mathbf{G}}^{\prime }\left(z^{-1}\right)\Delta u(t-1)$$

(16)

with

$$\mathbf{y}={[\widehat{y}(t+d+1\mid t)\cdots \widehat{y}(t+d+N\mid t)]}^T$$

(17)

$$\mathbf{u}={[\Delta u\left(t\right)\Delta u(t+1)\cdots \Delta u(t+N-1)]}^T$$

(18)

$$\mathbf{G}=\left[\begin{array}{cccc}{g}_0& 0& \cdots & 0\\ g_1& g_0& \cdots & 0\\ ⋮& ⋮& ⋮& ⋮\\ g_{N-1}& g_{N-2}& \cdots & g_0\end{array}\right]$$

(19)

$$\mathbf{G}\left(z^{-1}\right)=\left[\begin{array}{c}(G_{d+1}\left(z^{-1}\right)-g_0)z\\ (G_{d+2}\left(z^{-1}\right)-g_0-g_1\left(z^{-1}\right))z^2\\ ⋮\\ (G_{d+N}(z^{-1}-\cdots -g_{N-1}\left(z^{-(N-1)}\right)z^N)\end{array}\right]$$

(20)

$$\mathbf{F}\left(z^{-1}\right)=\left[\begin{array}{c}{F}_{d+1}\left(z^{-1}\right)\\ F_{d+2}\left(z^{-1}\right)\\ ⋮\\ F_{d+N}\left(z^{-1}\right)\end{array}\right]$$

(21)

The last two terms in the equation depend only on the past; therefore, these terms can be grouped in vector $\mathbf{f}$ of the free response. By rearranging the previous equation, the following expression is obtained,

$$\mathbf{y}=\mathbf{Gu}+\mathbf{f}$$

(22)

Under null initial conditions, the free response also becomes zero. By applying a unit step to the input of the system at time t, we have $\Delta u\left(t\right)=1, \Delta u(t+1)=0,\cdots ,\Delta u(t+N-1)=0$. The output sequence ${[\widehat{y}(t+1), \widehat{y}(t+2),\cdots ,\widehat{y}(t+N)]}^T$ is the same as the first column of the matrix $\mathbf{G}$.

Therefore, the first column of the matrix $\mathbf{G}$ can be calculated as the response of the system to the unit step in the manipulated variable. The free response can be calculated recursively as follows:

$${\mathbf{f}}_{j+1}=z(1-\tilde{A}\left(z^{-1}\right)){\mathbf{f}}_j+B\left(z^{-1}\right)\Delta u(t-d+j)$$

(23)

where ${\mathbf{f}}_0=y\left(t\right)$ and $\Delta u(t+j)=0$.

Finally, the cost function is expressed in a matrix scheme, as follows:

$$J={(\mathbf{Gu}+\mathbf{f}-\mathbf{w})}^T(\mathbf{Gu}+\mathbf{f}-\mathbf{w})+\lambda {\mathbf{u}}^{\mathbf{T}}\mathbf{u}$$

(24)

where $\mathbf{w}={\left[w(t+d+1)\cdots w(t+d+N)\right]}^T$.

3.2. Disturbance Observer

Consider the following n-dimensional dynamical system:

$$y^{\left(n\right)}=K(t,y)u+\psi \left(t\right)$$

(25)

where $K(t,y)$ is known, uniformly bounded, and far from zero, and the function $\psi \left(t\right)$ can be unknown and is uniformly bounded in an absolute manner, along with all of its time derivatives up to a finite order m. To follow a smooth known trajectory $y^{*}\left(t\right)$, $t\in [0,\infty )$ by means of a feedback control law u, the following observer-based linearizing controller is proposed,

$$u={\displaystyle \frac{1}{K(t,y)}}\left[y^{*}{\left(t\right)}^{\left(n\right)}-\sum _{i=0}^{n-1}{\mathit{k}}_{\mathit{i}}\left({\mathit{y}}_{\mathit{i}}-y^{*}{\left(t\right)}^{\left(i\right)}\right)-\widehat{\psi }\left(t\right)\right]$$

(26)

where $y_i$, $i=0,1,\dots ,n-1$, and $\widehat{\psi }=z_1$ are the variables generated by the following extended Luenberger observer, also known as the GPI observer:

$$\begin{array}{ccc}\hfill {\dot{y}}_0& =& y_1+{\lambda }_{m+n-1}(y-y_0)\hfill \\ \hfill {\dot{y}}_j& =& y_{j+1}+{\lambda }_{m+n-j-1}(y-y_0),\hfill \\ & & j=1,\dots ,n-2\hfill \\ \hfill {\dot{y}}_{n-1}& =& K(t,y)u+z_1+{\lambda }_m(y-y_0)\hfill \\ \hfill {\dot{z}}_i& =& z_{i+1}+{\lambda }_{m-1}(y-y_0),i=2,\dots ,m-1\hfill \\ \hfill {\dot{z}}_m& =& {\lambda }_0(y-y_0)\hfill \end{array}$$

(27)

The controller coefficients $k_j$ are selected in such a way that the following polynomial in the complex variable s is Hurwitz:

$$p_{cl}\left(s\right)=s^n+k_{n-1}{s}^{n-1}+\dots +k_{1}s+k_0=0$$

(28)

Similarly, the coefficients ${\lambda }_0,\dots ,{\lambda }_{m+n-1}$ of the observer are selected such that the following polynomial in the complex variable s is also Hurwitz.

$$p_{obs}\left(s\right)=s^n+{\lambda }_{n-1}{s}^{n-1}+\dots +{\lambda }_{1}s+{\lambda }_0=0$$

(29)

3.3. Integration of GPC and GPI Observer

The implementation of the generalized predictive control (GPC) integrated with the generalized proportional integral (GPI) observer follows the steps outlined below.

1.

Formulate the Transfer Function Model of the System:

• Develop the mathematical model of the irrigation canal system.
• Represent the system dynamics using transfer functions.

2.

Derive the Polynomials A, B, and C:

• Identify the system parameters and use them to derive the polynomials.
• Ensure that these polynomials accurately capture the system’s behavior.

3.

Set Up the Cost Function for the GPC Algorith:

• Define the prediction horizon N and control horizon.
• Construct the cost function, which is typically a quadratic function that balances tracking performance and control effort.

4.

Solve the Diophantine Equation to Obtain $E_j$ and $F_j$:

• Use the system model and cost function to derive the Diophantine equation.
• Solve for polynomials $E_j$ and $F_j$, which are used to predict future outputs.

5.

Implement the GPC Algorithm to Optimize the Control Signals:

• The derived polynomials and cost functions were used to compute the optimal control inputs at each time step.
• Ensure the control signals minimize the cost function while maintaining system stability and performance.

6.

Design the GPI Observer:

• Formulate the observer model to estimate the system states and disturbances.
• Tune the observer gains to ensure accurate and fast disturbance estimation.

7.

Use the Disturbance Estimates from the GPI Observer to Adjust the Control Inputs in the GPC Algorithm:

• Integrate the disturbance estimates into the GPC framework.
• The control inputs are adjusted dynamically based on the observer’s output to improve disturbance rejection.

3.4. Robust GPC with GPI Observer Design

This study aimed to regulate the water level at the downstream end of each canal pool by adjusting the discharge (both upstream and downstream) in response to both known and unknown disturbances. These disturbances include deviations such as the discharge extracted from the canal at the downstream end of the pools.

The parameters for the predictive controller were selected based on an analysis described in [16]. The weight parameter $\delta$ in Equation (13) was calculated as the reciprocals of the squares of the maximum permissible values:

$${\delta }_i={\displaystyle \frac{1}{MVP{e}^2}}$$

(30)

where MVPe is the expected maximum allowed value of the water level error signal and ${\delta }_i$ is the i-th element of the $\delta$ weight matrix. Similarly, the parameters for weight $\lambda$ of the cost function were established as the reciprocals of the squares of the maximum allowable deviations of the control variable. The formula used for the calculations is as follows:

$${\lambda }_i={\displaystyle \frac{1}{MVP{u}^2}}$$

(31)

The final tuned values of these parameters were ${\delta }_i=1111$ and ${\lambda }_i=4444$ for all the sections. When designing the disturbance observer, the planar outputs of the multivariate system described in Equation (10) were used to formulate the dynamic system shown in Equation (25). Utilizing these balanced outputs, a GPI observer was developed for each controlled variable, with its characteristic equation provided by

$$p_{obs}\left(s\right)=s^3+{\lambda }_2{s}^2+{\lambda }_{1}s+{\lambda }_0=0$$

(32)

For Section 1 and Section 2 of the canal the following characteristic polynomial was used for the observation error:

$$p_{obs}\left(s\right)={\left(s+0.8\right)}^3$$

(33)

where the gains of both observers were given by ${\lambda }_0=0.512$, ${\lambda }_1=1.92$ y ${\lambda }_2=2.4$.

Owing to its slow dynamics, in Section 3, the following characteristic polynomial for the observation error was determined.

$$p_{obs}\left(s\right)={\left(s+1\right)}^3$$

(34)

whereby the observer’s gains were given by ${\lambda }_0=1$, ${\lambda }_1=3$ and ${\lambda }_2=3$.

4. Numerical Validation Discussion

This section presents the simulation results of the GPC scheme with the proposed disturbance observer, applied to the linear model of the PAC-UPC experimental canal described in Section 2.3. The prediction horizons were set to 15 samples for segment 1 and 2 and 40 samples for segment 3. A sampling period of 10 s was used for the measurements and control, with gate adjustments performed at the same interval.

Figure 3, Figure 4 and Figure 5 present the simulation outcomes of the control tests conducted on the UPC-PAC channel. In these charts, the red line illustrates the performance of the tuned PI controller, whereas the blue line depicts the results of the proposed control scheme. The PI controllers were designed by optimizing the integral time squared error (ITSE) for each section, that is, by minimizing the following objective function:

$$J\left(t\right)={\int }_0^{\infty }te{\left(t\right)}^{2}dt$$

(35)

In Figure 3, a reference change is implemented for the level described in Section 1. It is observed that the GPC controller with disturbance rejection rapidly attains the set reference compared with the optimized PI controller. While the PI controller experiences an overshoot greater than 25% and takes approximately 12 min to adjust to the 10 cm reference change, the robust controller achieves the target in approximately 3 min. However, the cost of ensuring accurate tracking of the reference involves a slight fluctuation in the other two controlled variables: a maximum deviation of 2 cm for $y_2$ and approximately 4 mm for $y_3$.

In Figure 4, a reference change of 10 cm is displayed for the level in the second segment. Once again, the proposed controller demonstrates rapid reference tracking in comparison to the tuned PI controller. The MPC control with observer stabilizes within 5 min, while the PI controller requires approximately 13.5 min and exhibits significant overshoot. Analyzing the behavior of the level in span 1, the observer-based control swiftly rejects external disturbances, whereas the PI controller shows prolonged oscillations. For the variable $y_3$, a maximum fluctuation of 5 mm is observed, which is considered negligible.

In Figure 5, a reference change of 5 cm is shown for the level in the third segment. Furthemore, predictive control utilizing active disturbance rejection significantly outperforms the classic tuned controller. The PI controller requires 20.5 min to stabilize, whereas the robust control accomplishes this in only 7 min. Additionally, it should be noted that the levels in the other two sections are immediately regulated in response to disturbances arising from the reference change in Section 3.

The experimental test flume used in this study lacks a gradient and has a serpentine shape, which may influence the hydraulic conditions, including the flow patterns and hydraulic losses. These characteristics were considered in the design and analysis of the experiments. The absence of gradient simplifies the system dynamics, allowing a focus on the controller’s ability to handle disturbances and uncertainties, whereas the serpentine shape introduces realistic flow complexities that are common in irrigation systems with varying geometries. Although these features may not fully replicate all hydraulic conditions in real-world irrigation canals, they provide a controlled environment for evaluating the proposed control strategy under consistent and reproducible conditions.

5. Conclusions

This study introduces a novel control scheme that seamlessly merges the advantages of model predictive control with the precision of active disturbance rejection, utilizing GPI observers. This innovative control framework finds practical application in a three-canal irrigation system, serving as a testament to its real-world viability.

The simulation results, derived from a comprehensive analysis, unequivocally validate the robustness of the proposed controller when faced with disturbances, while also affirming its exceptional ability to accurately track the desired setpoints across various levels. This level of performance is underpinned by the efficacy of the observers, which plays a pivotal role in the control system. The key findings from this research indicate a significant improvement in response time and considerable reduction in overshoot compared with traditional PI controllers, highlighting the effectiveness of the proposed scheme.

Future work should focus on extending this control strategy to larger and more complex irrigation networks, incorporating real-time data analytics and machine learning techniques to enhance the adaptability and efficiency of the control system. Additionally, exploring the integration of IoT devices and sensors can provide more precise and timely data, further improving control accuracy and resource management.

The broader implications of this study in the field of irrigation and water resource management are substantial. Implementing such advanced control strategies can lead to more sustainable agricultural practices by optimizing water usage and reducing waste. This contributes not only to better crop yields but also to the conservation of vital water resources, which is crucial in the face of global climate change and increasing water scarcity.

By addressing both the technical and practical aspects of irrigation control, this research paves the way for future innovations in smart irrigation systems, ultimately contributing to the advancement of precision agriculture and efficient water management practices.