Modeling and Analysis of Contact Conditions during NC-Form Grinding of Cutting Edges

Abstract

Due to increasing demands on cutting tools, cutting edge preparation is of high priority because of its influence on the tool life. Current cutting edge preparation processes are mostly limited to generating simple roundings on the cutting edge. Multi-axis high precision form grinding processes offer great potential to generate defined cutting edge microgeometries. Knowledge about the relation between grinding strategy and material removal rate can achieve improved work results with regard to higher precision of shape and dimensional accuracy as well as enhanced cutting edge quality. Therefore, a kinematic-geometric model was developed in order to analyze the complex contact conditions during grinding cutting edge microgeometries by using a simulation approach based on the intersection of geometric bodies. The subsequent grinding tests largely validated the utilized simulation approach.

1. Introduction

Increasing demands on cutting tools with regard to quality and economy have led to constant progress in tool development and tool production. The cutting edge in particular is attracting much interest as it is an essential tool element for the cutting process. The properties of the cutting edge influence the process characteristics and the work results in machining with defined cutting edges [1,2]. The properties of the cutting edge can be divided into physical and chemical characteristics as well as into the geometry and surface topography of the cutting edge. The macro and micro geometrical design of the cutting edge affects the chip formation and the chip removal [3,4]. Investigations focusing on the effect of the cutting edge shape on tool wear in turning experiments showed that cutting edges rounded by brushing have a higher stability and therefore do not tend to have cutting edge breakouts [5]. Further studies about different methods for cutting edge preparation of micro mills made of tungsten carbide showed that magnetic abrasive finishing and drag finishing result in favorable wear behavior because of homogeneous cutting edge profiles [6]. The most common production processes for cutting edge preparation are magnetic abrasive finishing, abrasive blasting, laser machining, brushing, abrasive flow machining, vibratory finishing and drag finishing. These production processes usually generate simple cutting edge roundings. Until now, systematic studies on the influence of different defined cutting edge microgeometries were not possible, as all common cutting edge preparation processes are not able to produce complex and exact defined forms. Developing manufacturing processes to produce defined and complex cutting geometries in the industrial and scientific environment can increase the performance of cutting processes. Multi-axis high precision form grinding processes offer great potential to generate defined cutting edge microgeometries.

Due to its positive hardness and toughness characteristics, cemented carbide is often used as a material in cutting tools [7]. Most cemented carbides consist of a cobalt matrix and the hard material tungsten carbide. The cutting material is produced in a sinter process. The grain size of the sintered powder, as well as the mixing ratio, influences the properties of the material. Due to the high hardness of tungsten carbide of approximately Vicker Hardness 2000 HV0.05, economical machining of cemented carbide can be achieved by grinding processes only [8].

NC (Numerical Control)-form grinding processes with mounted points are used for manufacturing-free forms on difficult-to-machine materials. Examples of these are the machining of optical glasses and ceramic implants or prostheses for dental and medical applications. The main challenges in NC-form grinding are the positional accuracy and the stiffness of the machine axes due to the simultaneous axis movement. Furthermore, the complex tool paths mostly require NC-programming with CAD/CAM (Computer-aided Design/Computer-aided Manufacturing)technology. Tool paths are graphically planned on CAD models and converted into an appropriate NC-Code by post-processors.

Different form grinding strategies lead to different courses of chip cross-sectional areas and thus different material removal rates. As a result, different process forces occur that could lead to varying tool deflections and defects of the cutting edge. Knowledge about the relation between grinding strategy and material removal rate can lead to improved work results in the form of higher preciseness of shape and dimensional accuracy as well as enhanced cutting edge quality. CAD/CAM-programs do not provide a proper calculation of chip cross-sectional areas and thus material removal rates. Hence, it is necessary to develop suitable simulation models.

To enable a reproducible manufacturing of cutting edge geometries, different strategies for form grinding of cutting edge microgeometries, with regard to material removal rates by using permeation simulations, are examined. In grinding tests, the spindle power for the different grinding strategies is compared with the course of the graphs of the material removal rate. The aim of this analysis is to assess these different form grinding strategies with regard to material removal rates to increase the process performance and work results.

2. Test Conditions

The program to simulate the permeation of the tool and the workpiece was developed with the program software MATLAB, The MathWorks Inc., Natick, MA, USA. The form grinding processes of the cutting edge micro geometries were executed on a five-axis-machining center RXP600DSH of Röders GmbH, Soltau, Germany. Besides three linear axes (X, Y, Z), this machine is equipped with two rotatory axes (A, C). Furthermore, the integrated grinding spindle has a maximum power of 8.5 kW to enable a maximum rotation speed of 60,000 rpm. To dress the grinding tools, a dressing spindle with a sintered diamond form roller is integrated. To produce the required sharpness of the mounted points, a sharpening block is used and an automated sharpening process using the through-feed method was performed. Moreover, the grinding machine enables the determination of the geometry and the reference of the part with the help of a 3D-probe. The workpieces were cutting inserts made of cemented carbide of the type SNMA120408. As cooling lubricant, grinding oil of MKU-Chemie GmbH, Rödermark, Germany, with a viscosity of 7.6 mm²/s at 40 °C was used. Moreover, metal bonded diamond mounted points with a grain size of D20 were utilized. Only the use of diamond tools allows an economic grinding processing of cemented carbides. To reduce tool wear and thus dimensional deviations on the workpiece, metal bond tools were used. An important advantage of metal bonds is the shape stability of the tool profiles [9]. In order to gain process forces, conventional force measurement platforms cannot be satisfactorily used when grinding with 5-axis kinematics because of relocations of the self weight. Rotating multicomponent dynamometers could be suitable solutions but the non-contact signal transmission caused by the design principle can be used only at maximum spindle speeds of approximately 12,000 rpm. Therefore, the performance data of the grinding spindle was recorded and used to validate the simulation results. To verify the accuracy of this measurement method, the performance data was compared to force values recorded by a force measurement platform during a peripheral longitudinal grinding process, as shown in Figure 1.

It is shown that, with the used process parameters, both force progressions, from depths of cut of approximately 200 µm, show a good correlation. During manufacturing, cutting edge microgeometries with much smaller material removal rates than in Figure 1 will be realized. To create equally reliable statements between spindle power data and process forces, the material removal rate was increased by offsetting the target geometry in the workpiece, Figure 2.

Due to the relatively long tool paths of the mounted point with a constant depth of cut on the rake and flank face, these constant values of spindle power can be seen as the reference during grinding of the cutting edge. Therefore, it is possible to identify the actual machining of the cutting edge. The difference between the spindle power minimum and maximum is shown in the further graphs as a percentage increase of spindle performance in comparison to the minimum.

3. Kinematic-Geometric Model

3.1. Cutting Edge Microgeometries and Tool Types

In the investigations, two different cutting edge geometries were considered: an ideal radius and a waterfall radius. Both microgeometries can be characterized using the form-factor method. The form factor is the relationship between the cutting edge segment on the rake face S_γ and the cutting edge segment on the flank face S_α. The ideal radius has a form factor κ = 1. Therefore, the cutting edge segments on flank and rake faces, as well as the cutting edge radius, have the same value. The waterfall radius is characterized by a form factor greater than one, in this case κ = 1.5, Figure 3.

For both cutting edge microgeometries, different grinding strategies were examined, as shown in Figure 4. Grinding strategy I and II differ with regard to the active tool shape. In Strategy I, the sphere-shaped form of the cylinder ball end mounted point is used to cut orthogonally above the cutting edge, referred to as the course of the corner radius r_ε. Strategy II has the same tool kinematics but the cylindrical part of the mounted point is utilized for the cutting process. In Strategy III, the ball-shaped part of the mounted point is guided above the cutting edge at an angle of 45°, referred to as the course of the corner radius. For machining the waterfall geometries with a form factor κ = 1.5, the grinding strategies I and II match with the strategies of the ideal grinding radius.

3.2. Modelling of the Permeation

The aim of the developed process simulation is to identify the material removal rates of different grinding strategies and cutting edge microgeometries for one tool path movement. Thus, knowledge about forces involved and therefore about tool deflection can be generated to analyze different grinding strategies. The kinematic-geometrical model simulates the penetration of two geometrical bodies. 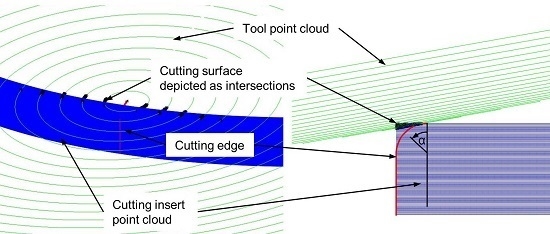The workpiece (cutting insert) is defined as a cylindrical surface and the mounted point is also defined as a cylindrical surface if the required tool type is cylindrical; if the required tool type is spherical, an appropriate partial surface is created, Figure 5. The geometric objects are described as point clouds. To reduce the computing time, the program minimizes the point clouds to the points of the contacting areas of both geometric objects.

The target geometry of the respective cutting edge microgeometry is precisely positioned as a numerical approximated curve in the workpiece point cloud. This curve is the reference for the radial position of the most external point of the tool point cloud. For each calculation step, the tool point cloud is placed at the following point of the cutting edge curve, from the flank face (angle position α = 0) to the rake face (angle position α = 90°). Therefore, the rotation of the approximated tool around the approximated cutting edge enables the determination of the exact section planes. In Figure 6, the green cycles represent the reduced tool point cloud and the blue area represents the reduced workpiece point cloud.

The red curve depicts the cutting curve of the cutting edge target geometry. The point distance of both point clouds is 0.1 µm to achieve high calculation accuracy. For each position of the tool point cloud, the intersection points are projected on a plane. Afterwards, the area within the external points can be determined which is equivalent to the section plane between the tool and workpiece, Figure 7.

Before running the simulation, the boundary conditions have to be defined. These include geometry data of the cutting edge microgeometry and the tool. Further simulation data is the feed speed and the resolution of geometric objects influencing the accuracy of the calculations.

4. Results

4.1. Simulation Results

The results of the simulation show the different material removal rate Q_w curve progressions for each grinding strategy, as shown in Figure 8. The lowest maximum material removal rate Q_w,max is achieved by grinding strategy II.

The maximum value is located at an angle position α of approximately 20°. Therefore, the maximum material removal rate Q_w,max of grinding strategy I was determined at the start angle position of the mounted point, referred to as the course of the rounded cutting edge radius r_β. It is the highest achieved value. Following the further angle positions, the curve is regressive and has low values from angle position α = 16°. The course of grinding strategy III is similar but has a higher peak than grinding strategy II. Therefore, it does not appear advantageous for process forces and consequently for tool deflections. Hence, further considerations relate to grinding strategies I and II. The courses of the different grinding strategies I and II for grinding waterfall radii with a form factor κ = 1.5 differ only slightly from the courses of the equivalent grinding strategies for the ideal radii, Figure 8. With an angle position of α = 70°, almost all the material is removed. This is caused by the larger curvature at the beginning of the cutting edge geometry and by the fact that the ratio of the tool radius to the cutting edge radius is approximately 100. This results in relatively flat tool geometry, as shown in Figure 6.

4.2. Experimental Results

To validate the kinematic-geometrical model, grinding tests were conducted. For this purpose, the spindle power of the different grinding strategies was recorded and compared with the courses of the material removal rates from the simulation calculations, as shown in Figure 9. Generally, for all test series, the courses of the spindle power are highly similar to the courses of the simulation calculations. However, small course deviations can be identified.

For both cutting edge geometries, slight deviations in the spindle power courses can be observed in comparison to the simulation results, Figure 9. The reason for this occurrence may be the inertia of the tool spindle’s continuous turn regulation in combination with the comparatively short process time of one tool path of approximately 8 s. Another important factor is the relatively small spindle load and therefore the less linear behavior between the material removal rate and process forces, as well as the correct determination of the relevant part of the spindle power course. Nevertheless, analysis of the spindle power data obtained in the grinding tests confirms the trend of the simulation results. The validation of the simulation model confirms the benefit of form grinding processes of cutting edge microgeometries for planning strategies. The kinematic-geometrical model enables the prediction of maximum material removal rates and subsequently indicates process forces and potential tool deflections. Furthermore, the influence of the grinding strategy on possible damages to the cutting edge can be analyzed.

5. Summary

Within the presented work, a kinematic-geometric model was developed in order to analyze the complex contact conditions during grinding cutting edge microgeometries. Therefore, a simulation approach based on the intersection of geometric bodies was used. The grinding tool and workpiece surface were defined as cylindrical point clouds and the cross section of the cutting edge microgeometry was determined by numerical approximation. By moving the tool point cloud stepwise along the coordinates of the cutting edge microgeometry for each position, the interface between the workpiece point cloud was calculated. Thus, the varying material removal rates could be determined and compared with the spindle power data. The relatively even curve progressions show the correlation between the material removal rate Q_w and the process forces. Therefore, the geometric-kinematic model can be used to analyze different form grinding strategies for manufacturing various cutting edge microgeometries with regard to process forces and consequently tool deflection. With the gathered information, the work results of form grinding cutting edge microgeometries, regarding the form accuracy and the chipping of the cutting edge, can be improved.