Molecular Thermodynamics Using Nuclear Magnetic Resonance (NMR) Spectroscopy
Abstract
:1. Introduction
2. Nuclear Magnetic Resonance (NMR) Spectroscopy
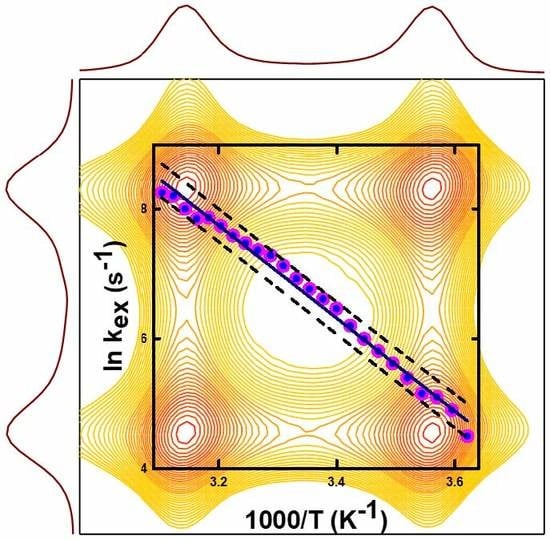
3. Chemical Exchange and Kinetics
4. Molecular Thermodynamics
5. Applications
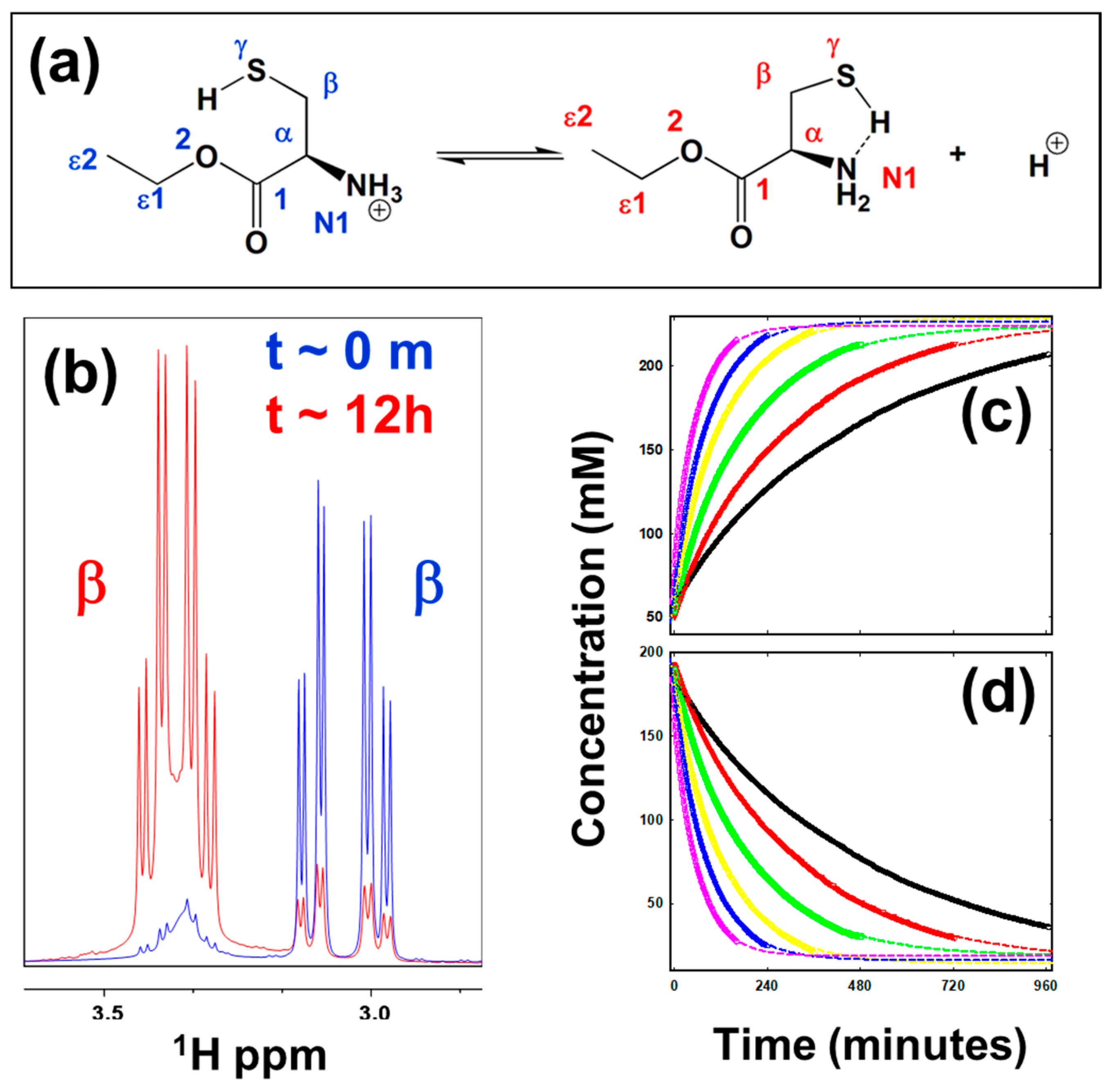
5.1. Thermodynamics of Parameters of the Oxidation Process in Model Cysteine Molecules
5.2. Intramolecular Conformational Exchange due to Partial Double Bond Rotation
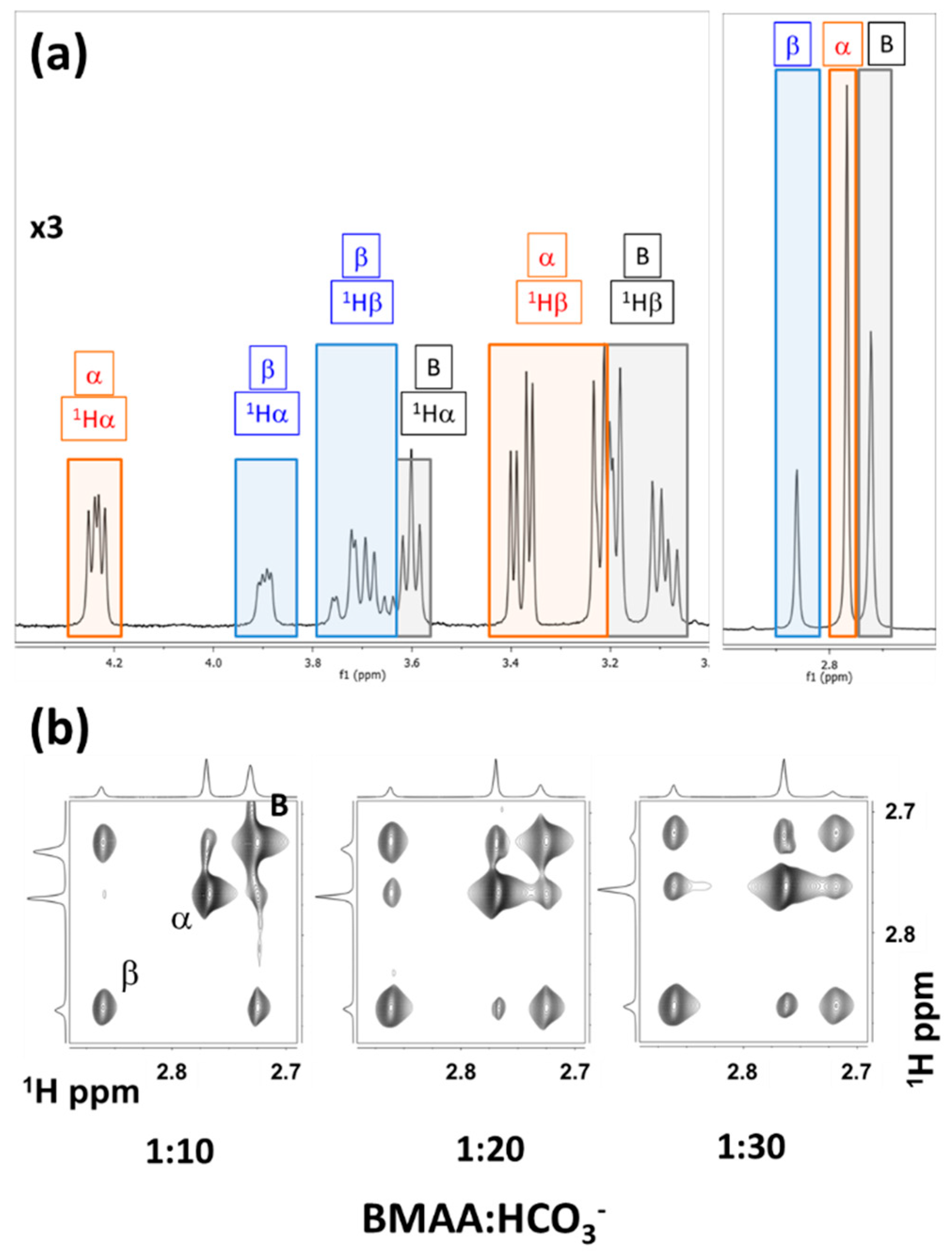
5.3. Intermolecular Exchange: BMAA and its Carbomates.
6. Summary
Funding
Acknowledgments
Conflicts of Interest
References
- Grant, D.M.; Harris, R.K. Encyclopedia of Nuclear Magnetic Resonance: Advances in NMR; Wiley: New York, NY, USA, 2002; Volume 1–10. [Google Scholar]
- Lindon, J.C.; Tranter, G.E.; Koppenaal, D. Encyclopedia of Spectroscopy and Spectrometry; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Ernst, R.R.; Anderson, W.A. Application of Fourier transform spectroscopy to magnetic resonance. Rev. Sci. Rev. Sci. Instrum. 1966, 37, 93–102. [Google Scholar] [CrossRef]
- Jeener, J.; Meier, B.H.; Bachmann, P.; Ernst, R.R. Investigation of exchange processes by 2-dimensional NMR-spectroscopy. J. Chem. Phys. 1979, 71, 4546–4553. [Google Scholar] [CrossRef]
- Bain, A.D. Chemical exchange in NMR. Prog. Nucl. Magn. Reson. Spectrosc. 2003, 43, 63–103. [Google Scholar] [CrossRef]
- Bain, A.D. Chemical exchange. In Annual Reports on NMR Spectroscopy; Webb, G.A., Ed.; Elsevier: Amsterdam, The Netherlands, 2008; Volume 63, pp. 23–48. [Google Scholar]
- Kaplan, J.I.; Fraenkel, G. NMR of chemically exchanging systems. In NMR of Chemically Exchanging Systems; Kaplan, J.I., Fraenkel, G., Eds.; Academic Press: Cambridge, MA, USA, 1980; pp. 1–165. [Google Scholar]
- Sandstrom, J. Dynamic NMR Spectroscopy/J. Sandstrom; Academic Press: London, UK; New York, NY, USA, 1982. [Google Scholar]
- Logan, S.R. The origin and status of the Arrhenius equation. J. Chem. Educ. 1982, 59, 279. [Google Scholar] [CrossRef]
- Eyring, H. The activated complex in chemical reactions. J. Chem. Phys. 1935, 3, 107–115. [Google Scholar] [CrossRef]
- Lente, G.; Fábián, I.; Poë, A.J. A common misconception about the Eyring equation. New J. Chem. 2005, 29, 759–760. [Google Scholar] [CrossRef]
- Akke, M. Conformational dynamics and thermodynamics of protein-ligand binding studied by NMR relaxation. Biochem. Soc. Trans. 2012, 40, 419–423. [Google Scholar] [CrossRef]
- Palmer, A.G. Chemical exchange effects in biological macromolecules. In Encyclopedia of Nuclear Magnetic Resonance, Advances in NMR; Wiley: Chichester, UK, 2002; Volume 9, pp. 344–353. [Google Scholar]
- Palmer, A.G., 3rd. Chemical exchange in biomacromolecules: Past, present, and future. J. Magn. Reson. 2014, 241, 3–17. [Google Scholar] [CrossRef] [Green Version]
- Wand, A.J.; Sharp, K.A. Measuring entropy in molecular recognition by proteins. Annu. Rev. Biophys. 2018, 47, 41–61. [Google Scholar] [CrossRef] [PubMed]
- Jocelyn, P.C. The Occurrence, Chemical Properties, Metabolism and Biological Function of Thiols and Disulphides; Academic Press: London, UK; New York, NY, USA, 1972. [Google Scholar]
- Kipton, S.H.; Bodwell, C. Oxidation of amino acids by dimethyl sulfoxide. J. Agric. Food Chem. 1973, 21, 235–237. [Google Scholar] [CrossRef]
- Snow, J.T.; Finley, J.W.; Friedman, M. Oxidation of sulfhydryl groups to disulfides by sulfoxides. Biochem. Biophys. Res. Commun. 1975, 64, 441–447. [Google Scholar] [CrossRef]
- Lowe, O.G. Oxidation of thiols and disulfides to sulfonic acids by dimethyl-sulfoxide. J. Org. Chem. 1976, 41, 2061–2064. [Google Scholar] [CrossRef]
- Balta, B.; Monard, G.; Ruiz-Lopez, M.F.; Antoine, M.; Gand, A.; Boschi-Muller, S.; Branlant, G. Theoretical study of the reduction mechanism of sulfoxides by thiols. J. Phys. Chem. A 2006, 110, 7628–7636. [Google Scholar] [CrossRef]
- Papanyan, Z.; Markarian, S. Detection of oxidation of l-cysteine by dimethyl sulfoxide in aqueous solutions by IR spectroscopy. J. Appl. Spectrosc. 2013, 80, 775–778. [Google Scholar] [CrossRef]
- Yiannios, C.N.; Karabinos, J.V. Oxidation of thiols by dimethyl sulfoxide. J. Org. Chem. 1963, 28, 3246–3248. [Google Scholar] [CrossRef]
- Wallace, T.J.; Mahon, J.J. Reactions of thiols with sulfoxides. 11. Kinetics and mechanistic implications. J. Am. Chem. Soc. 1964, 86, 4099–4103. [Google Scholar] [CrossRef]
- Dougherty, R.J.; Singh, J.; Krishnan, V.V. Kinetics and thermodynamics of oxidation mediated reaction in l-cysteine and its methyl and ethyl esters in dimethyl sulfoxide-d6 by NMR spectroscopy. J. Mol. Struct. 2017, 1131, 196–200. [Google Scholar] [CrossRef]
- Martin, O.A.; Villegas, M.E.; Vila, J.A.; Scheraga, H.A. Analysis of 13calpha and 13cbeta chemical shifts of cysteine and cystine residues in proteins: A quantum chemical approach. J. Biomol. NMR. 2010, 46, 217–225. [Google Scholar] [CrossRef]
- Drakenbe, T.; Forsen, S. Barrier to internal rotation in amides. 1. Formamide. J. Phys. Chem. 1970, 74, 1. [Google Scholar] [CrossRef]
- Forsen, S.; Hoffman, R.A. Study of moderately rapid chemical exchange reactions by means of nuclear magnetic double resonance. J. Chem. Phys. 1963, 39, 2892. [Google Scholar] [CrossRef]
- Gutowsky, H.S.; Vold, R.L.; Wells, E.J. Theory of chemical exchange effects in magnetic resonance. J. Chem. Phys. 1965, 43, 4107–4125. [Google Scholar] [CrossRef]
- Wiberg, K.B.; Rablen, P.R.; Rush, D.J.; Keith, T.A. Amides. 3. Experimental and theoretical studies of the effect of the medium on the rotational barriers for n,n-dimethylformamide and n,n-dimethylacetamide. J. Am. Chem. Soc. 1995, 117, 4261–4270. [Google Scholar] [CrossRef]
- Jensen, B.L.; Fort, R.C. Molecular mechanics and variable-temperature h-1 NMR studies on n,n-diethyl-m-toluamide—An undergraduate NMR and molecular modeling experiment. J. Chem. Educ. 2001, 78, 538–540. [Google Scholar] [CrossRef]
- Krishnan, V.V.; Thompson, W.B.; Goto, J.J.; Maitra, K.; Maitra, S. Modulations in restricted amide rotation by steric induced conformational trapping. Chem. Phys. Lett. 2012, 523, 124–127. [Google Scholar] [CrossRef] [Green Version]
- Ernst, R.R.; Bodenhausen, G.; Wokaun, A. Principles of Nuclear Magnetic Resonance in One and Two Dimensions; Clarendon Press: Oxford, UK, 1987. [Google Scholar]
- Meier, B.H.; Ernst, R.R. Elucidation of chemical exchange networks by two-dimensional NMR spectroscopy: The heptamethylbenzenonium ion. J. Am. Chem. Soc. 1979, 101, 6441–6442. [Google Scholar] [CrossRef]
- Dimitrov, V.S.; Vassilev, N.G. Dynamic NMR: A new procedure for the estimation of mixing times in the 2D EXSY experiments. A four-site exchange system studied by 1D and 2D EXSY spectroscopy. Magn. Reson. Chem. 1995, 33, 739–744. [Google Scholar] [CrossRef]
- Orrell, K.G.; Šik, V. Dynamic NMR spectroscopy in inorganic and organometallic chemistry. In Annual Reports on NMR Spectroscopy; Webb, G.A., Ed.; Academic Press: Cambridge, MA, USA, 1993; Volume 27, pp. 103–171. [Google Scholar]
- Perrin, C.L.; Dwyer, T.J. Application of 2-dimensional NMR to kinetics of chemical-exchange. Chem. Rev. 1990, 90, 935–967. [Google Scholar] [CrossRef]
- Fischer, G.; Kleinpeter, E. Application of 2D EXSY NMR spectroscopy to the study of the dynamic behaviour of aroylcyanoketene-s, s-dimethylacetals. Magn. Reson. Chem. 1991, 29, 204–206. [Google Scholar] [CrossRef]
- Krishnan, V.V.; Vazquez, S.; Maitra, K.; Maitra, S. Restricted amide rotation with steric hindrance induced multiple conformations. Chem. Phys. Lett. 2017, 689, 148–151. [Google Scholar] [CrossRef]
- Landy, S.B.; Rao, B.D.N. Dynamical NOE in multiple-spin systems undergoing chemical-exchange. J. Magn. Reson. 1989, 81, 371–377. [Google Scholar] [CrossRef]
- Vazquez, C.S. Substituent Effects on Double Bond Character: NMR Studies of Steric and Electronic Effects in DEET Analogs as a MODEL system; California State University Fresno, Fresno State Digital Repository: Fresno, CA, USA, 2014. [Google Scholar]
- Guerra, J. Amide Bond Modulation: Partial Amide Bond Rotation in Cyclic Amines of DEET Analogs Follow an Enthalpy-Entropy Compensation (EEC); California State University Fresno, Fresno State Digital Repository: Fresno, CA, USA, 2018. [Google Scholar]
- Devillers, J. 2d and 3d structure–activity modelling of mosquito repellents: A review. SAR QSAR Environ. Res. 2018, 29, 693–723. [Google Scholar] [CrossRef]
- Caller, T.A.; Field, N.C.; Chipman, J.W.; Shi, X.; Harris, B.T.; Stommel, E.W. Spatial clustering of amyotrophic lateral sclerosis and the potential role of BMAA. Amyotroph. Lateral Scler. Off. Publ. World Fed. Neurol. Res. Group Mot. Neuron Dis. 2012, 13, 25–32. [Google Scholar] [CrossRef]
- Chernoff, N.; Hill, D.J.; Diggs, D.L.; Faison, B.D.; Francis, B.M.; Lang, J.R.; Larue, M.M.; Le, T.T.; Loftin, K.A.; Lugo, J.N.; et al. A critical review of the postulated role of the non-essential amino acid, beta-n-methylamino-l-alanine, in neurodegenerative disease in humans. J. Toxicol. Environ. Health Part Bcritical Rev. 2017, 20, 1–47. [Google Scholar]
- Cox, P.A.; Kostrzewa, R.M.; Guillemin, G.J. Bmaa and neurodegenerative illness. Neurotox. Res. 2018, 33, 178–183. [Google Scholar] [CrossRef]
- Vega, A.; Bell, E.A.; Nunn, P.B. The preparation of l- and d-α-amino-β-methylaminopropionic acids and the identification of the compound isolated from cycas circinalis as the l-isomer. Phytochemistry 1968, 7, 1885–1887. [Google Scholar] [CrossRef]
- Nunn, P.B.; O’Brien, P. The interaction of beta-n-methylamino-l-alanine with bicarbonate: An 1H-NMR study. FEBS Lett. 1989, 251, 31–35. [Google Scholar] [CrossRef]
- Sundh, U.M.; Andersoon, C.; Rosén, J.; Fonnum, F.; Knudsen, I.; Sippola, S. Analysis, Occurrence, and Toxicity of ß-Methylaminoalanine (BMAA); Nordic Council of Ministers: Copenhagen, Denmark, 2007. [Google Scholar]
- Diaz-Parga, P.; Goto, J.J.; Krishnan, V.V. Chemistry and chemical equilibrium dynamics of BMAA and its carbamate adducts. Neurotox. Res. 2018, 33, 76–86. [Google Scholar] [CrossRef]
- Viso, A.; Fernandez de la Pradilla, R.; Garcia, A.; Flores, A. Alpha, beta-diamino acids: Biological significance and synthetic approaches. Chem. Rev. 2005, 105, 3167–3196. [Google Scholar] [CrossRef]
- Davis, A.J.; Hawkes, G.E.; Haycock, P.R.; O’Brien, P.; Kidd, B.L.; Mapp, P.I.; Naughton, D.; Grootveld, M. Generation of substance p carbamate in neutral aqueous solution. Relevance to inflammatory joint diseases. FEBS Lett. 1993, 329, 249–252. [Google Scholar] [CrossRef]
- Davis, A.J.; Obrien, P.; Nunn, P.B. Studies of the stability of some amino acid carbamates in neutral aqueous solution. Bioorgan. Chem. 1993, 21, 309–318. [Google Scholar] [CrossRef]
- Myers, T.G.; Nelson, S.D. Neuroactive carbamate adducts of beta-n-methylamino-l-alanine and ethylenediamine. Detection and quantitation under physiological conditions by 13c NMR. J. Biol. Chem. 1990, 265, 10193–10195. [Google Scholar]
- Zimmerman, D.; Goto, J.J.; Krishnan, V.V. Equilibrium dynamics of beta-n-methylamino-l-alanine (BMAA) and its carbamate adducts at physiological conditions. PLoS ONE 2016, 11, e0160491. [Google Scholar] [CrossRef]
- McConnell, H.M. Reaction rates by nuclear magnetic resonance. J. Chem. Phys. 1958, 28, 430–431. [Google Scholar] [CrossRef]
- Diaz-parga, P. Effects of Divalent Metals on the Dynamic Equilibria between BMAA and Its Carbamate Species; California State University, Fresno, College of Science and Mathematics, Henry Madden Library: Fresno, CA, USA, 2018. [Google Scholar]


© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krishnan, V.V. Molecular Thermodynamics Using Nuclear Magnetic Resonance (NMR) Spectroscopy. Inventions 2019, 4, 13. https://doi.org/10.3390/inventions4010013
Krishnan VV. Molecular Thermodynamics Using Nuclear Magnetic Resonance (NMR) Spectroscopy. Inventions. 2019; 4(1):13. https://doi.org/10.3390/inventions4010013
Chicago/Turabian StyleKrishnan, Viswanathan V. 2019. "Molecular Thermodynamics Using Nuclear Magnetic Resonance (NMR) Spectroscopy" Inventions 4, no. 1: 13. https://doi.org/10.3390/inventions4010013
APA StyleKrishnan, V. V. (2019). Molecular Thermodynamics Using Nuclear Magnetic Resonance (NMR) Spectroscopy. Inventions, 4(1), 13. https://doi.org/10.3390/inventions4010013