Peristaltic Propulsion of Jeffrey Nanofluid with Thermal Radiation and Chemical Reaction Effects
Abstract
:1. Introduction
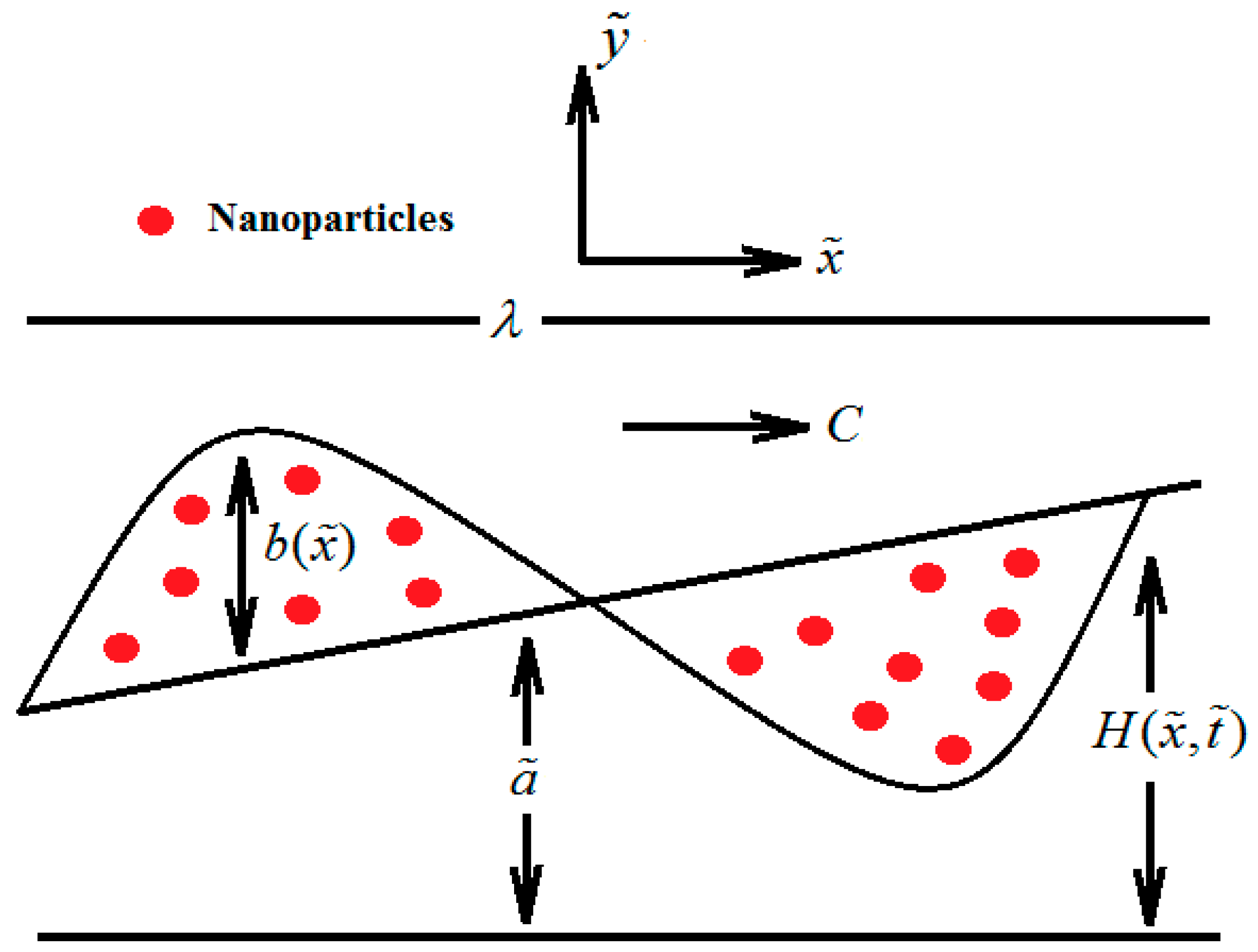
2. Mathematical Formulation
3. Solution of the Problem
4. Results and Discussion
5. Conclusions
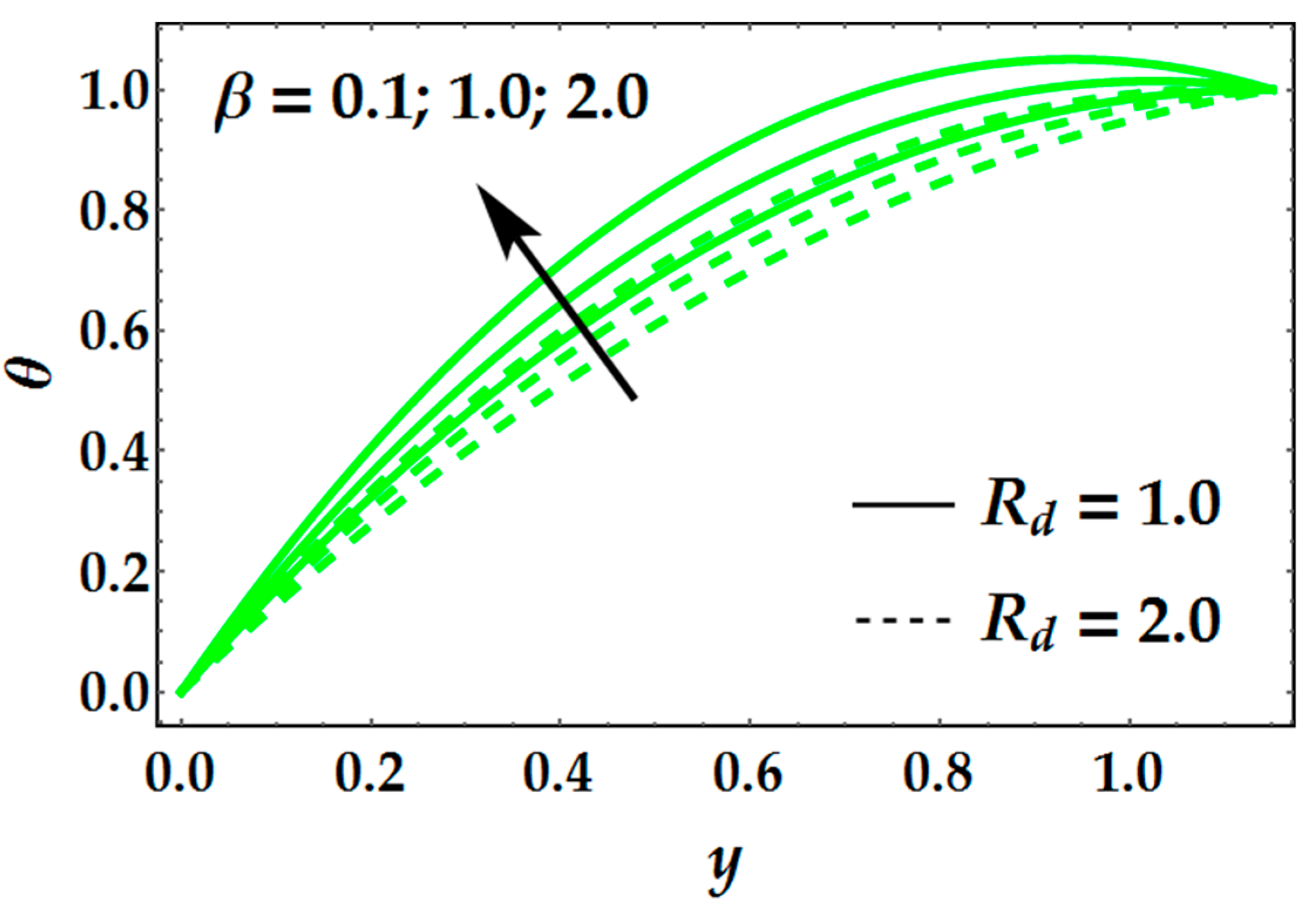
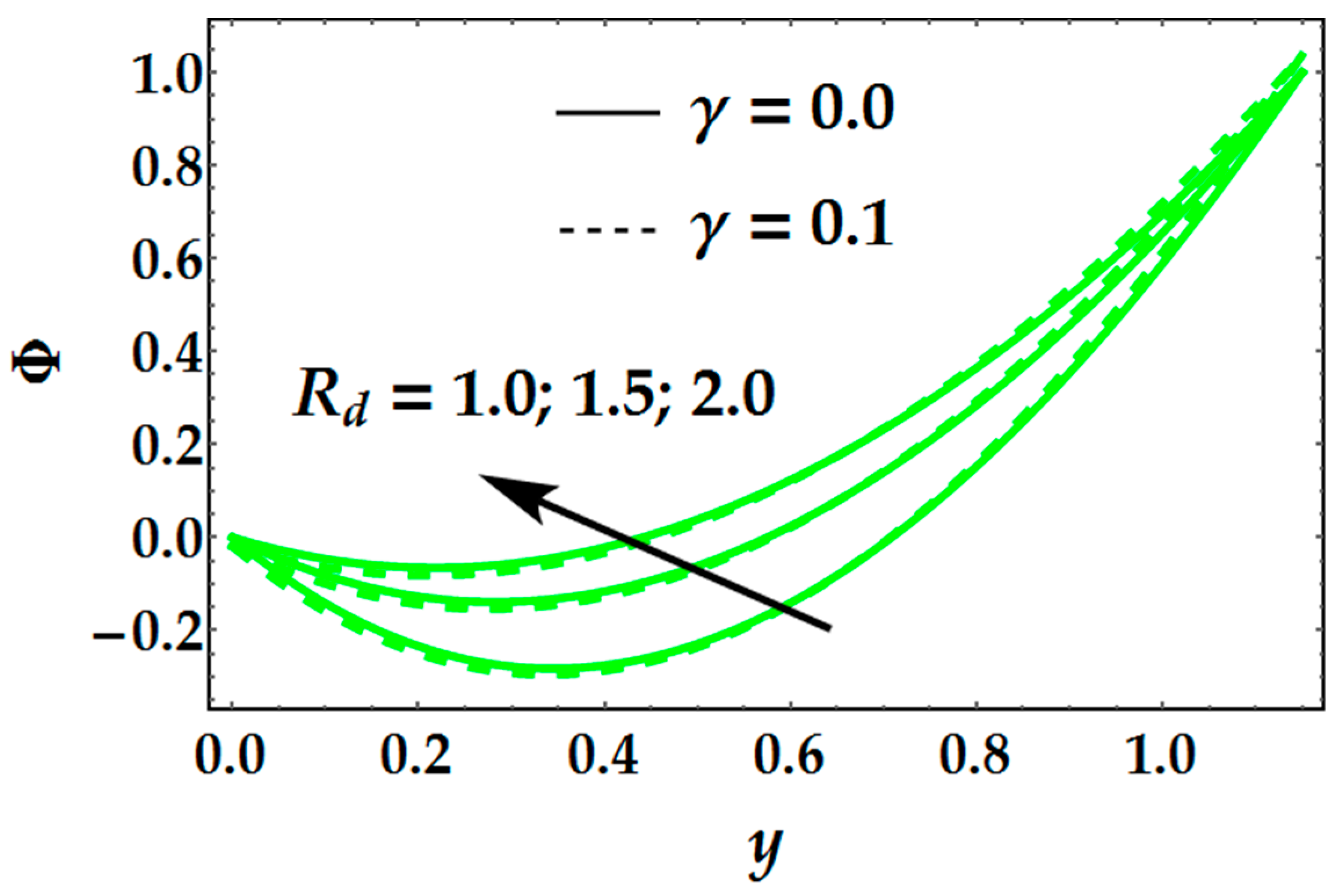
- Temperature profile increments with the augmentation in and β parameters.
- Radiation parameter provides a significant resistance in temperature profile.
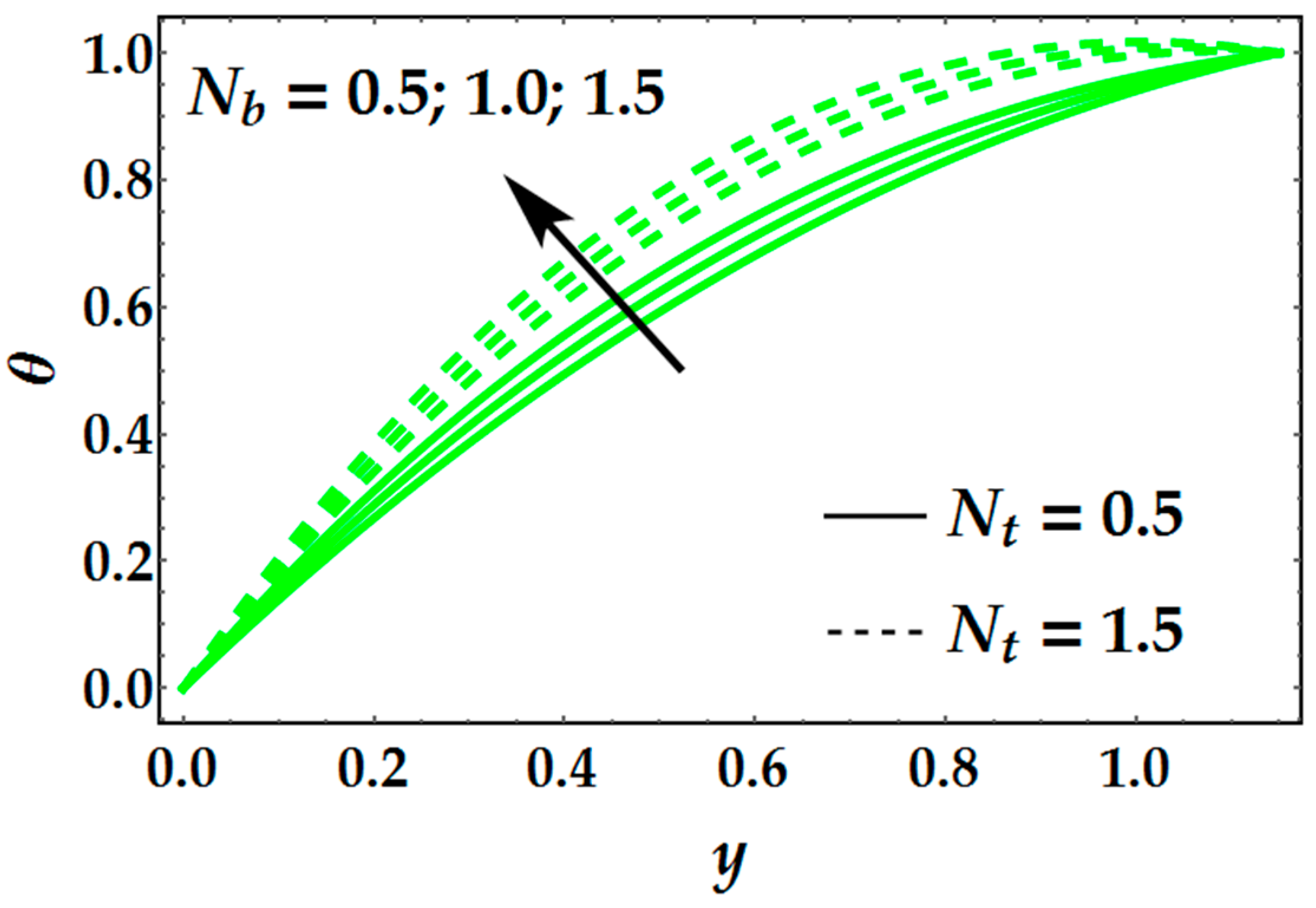
- Concentration profile increments, when Brownian movement parameter increments while its behavior is inverse for higher estimations of thermophoresis parameter .
- Chemical reaction parameter has an inverse behavior on concentration profile close to the wall.
- Radiation parameter also enhances significantly the concentration profile.
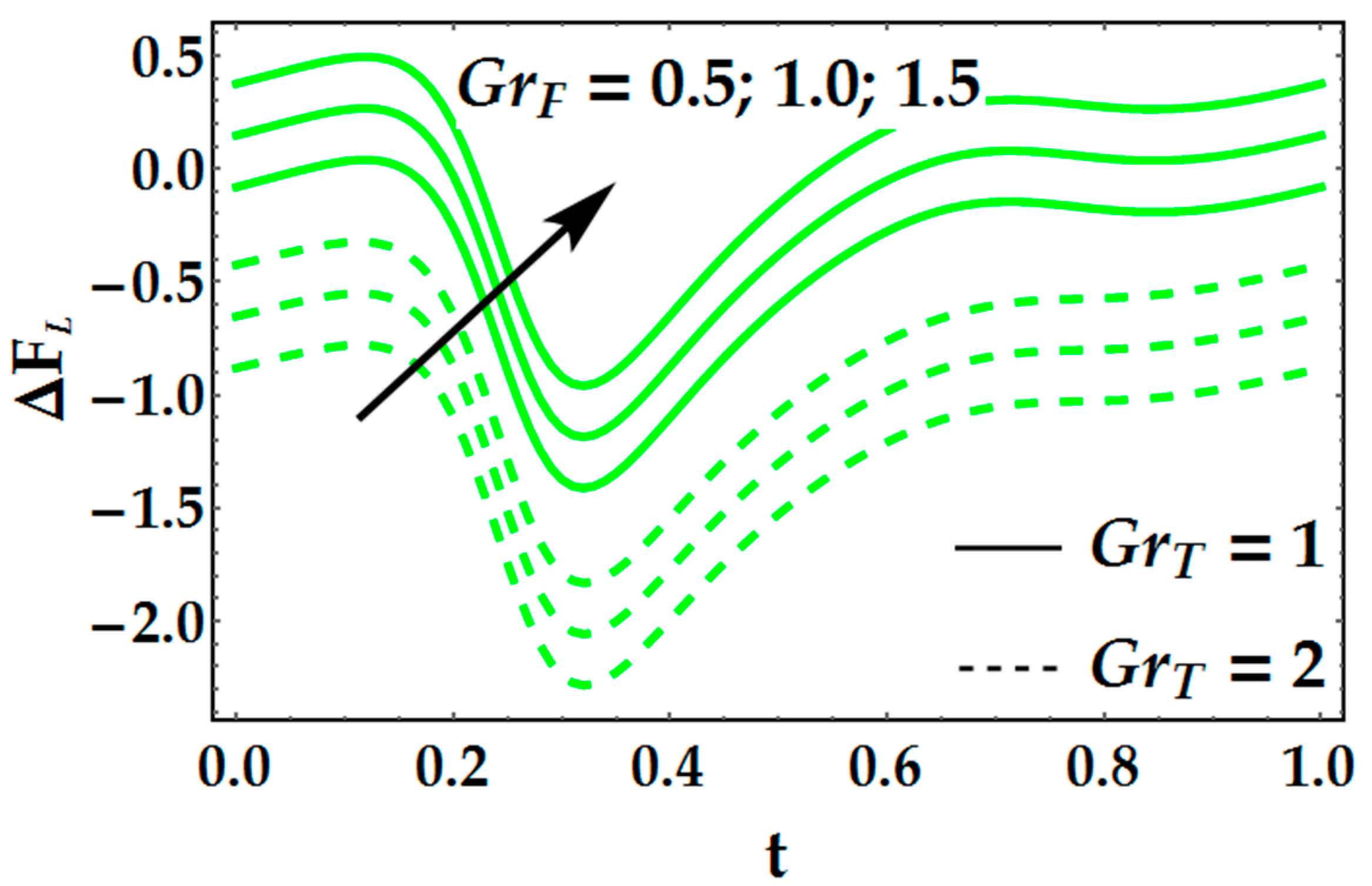
- Velocity profile shows converse behavior for higher values of thermal Grashof number and basic density Grashof number.
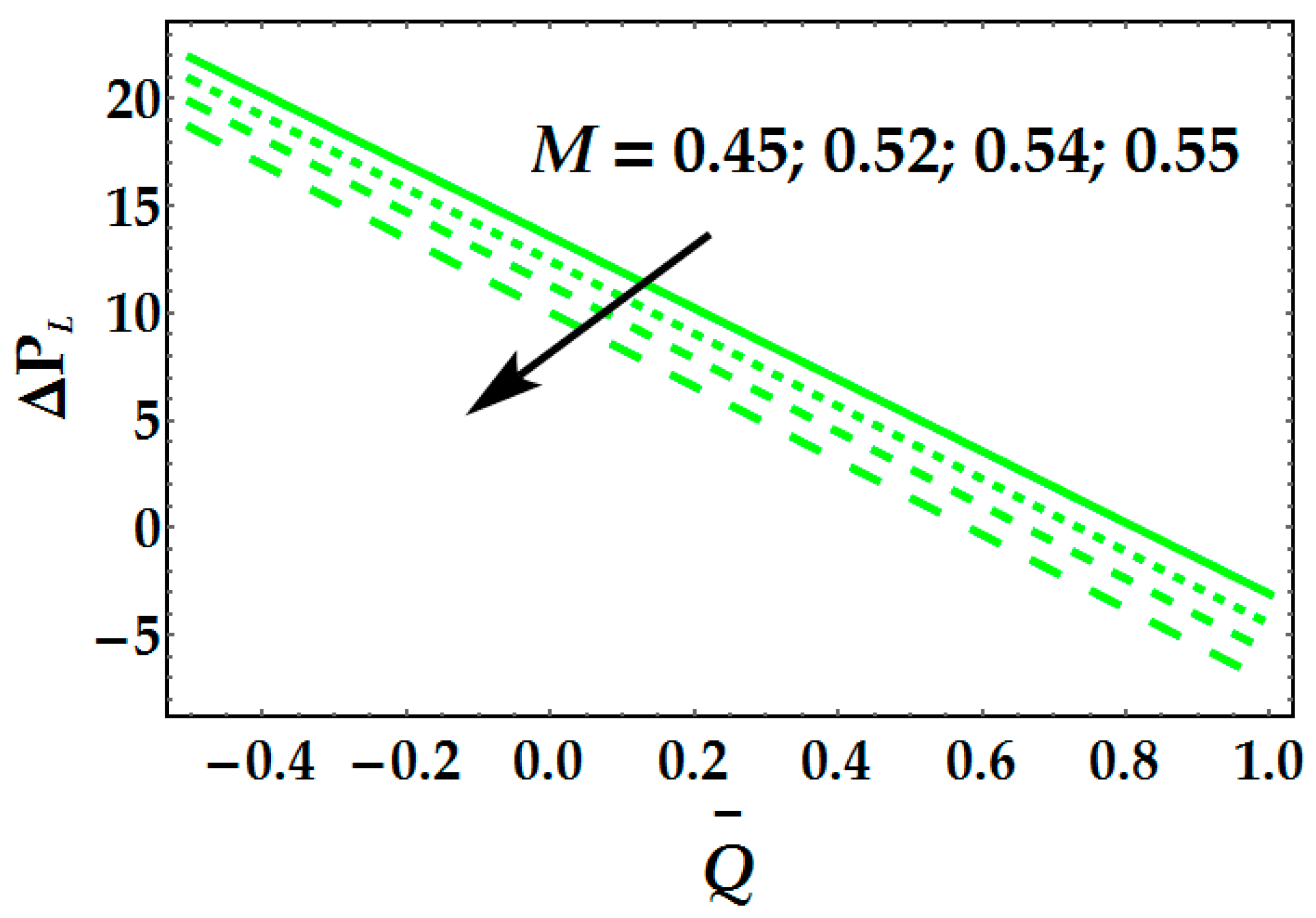
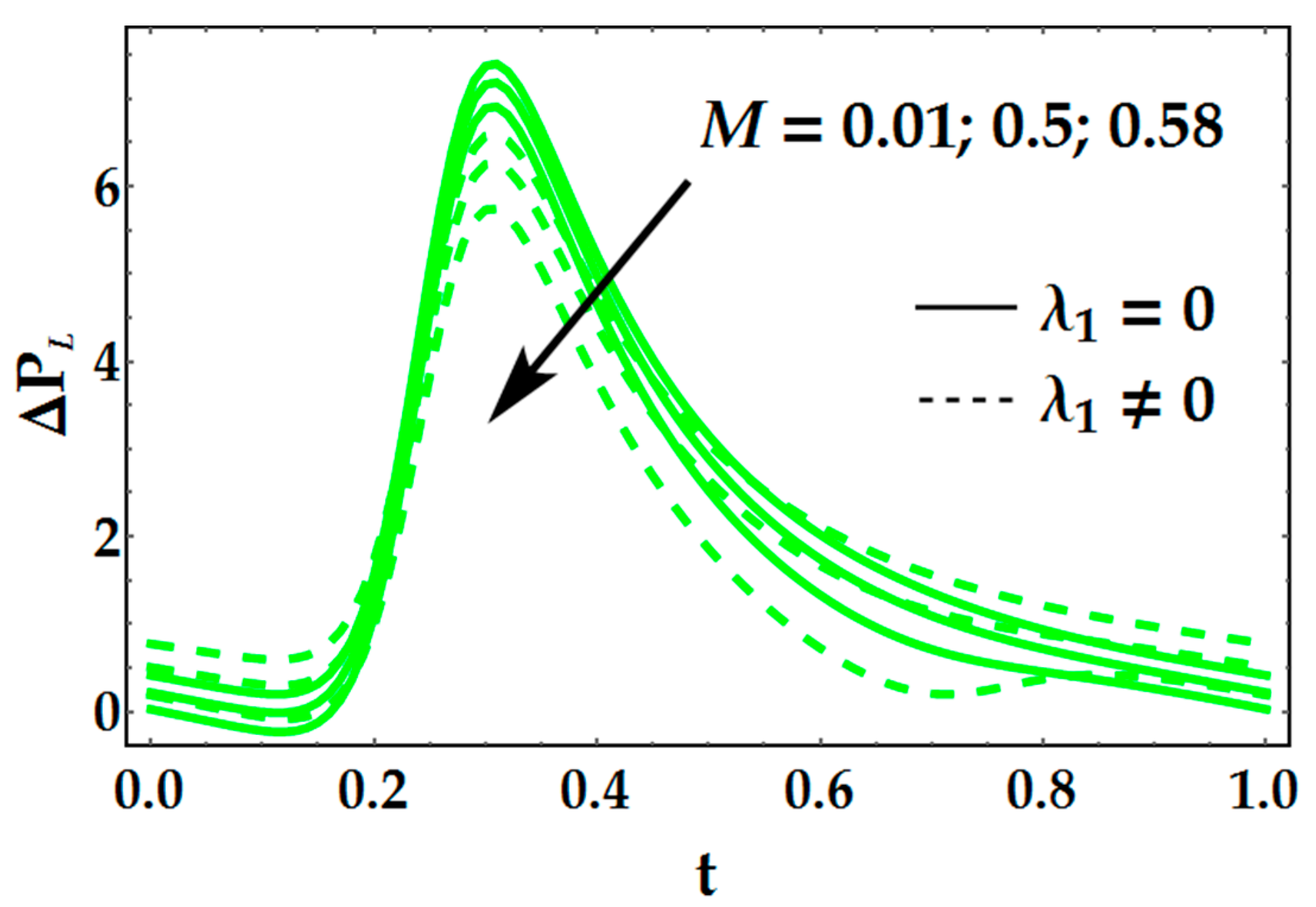
- Pumping rate increases for higher values of Hartmann number and thermal Grashof number.
- The present results reduce to Newtonian fluid model by taking in the modeled equations.
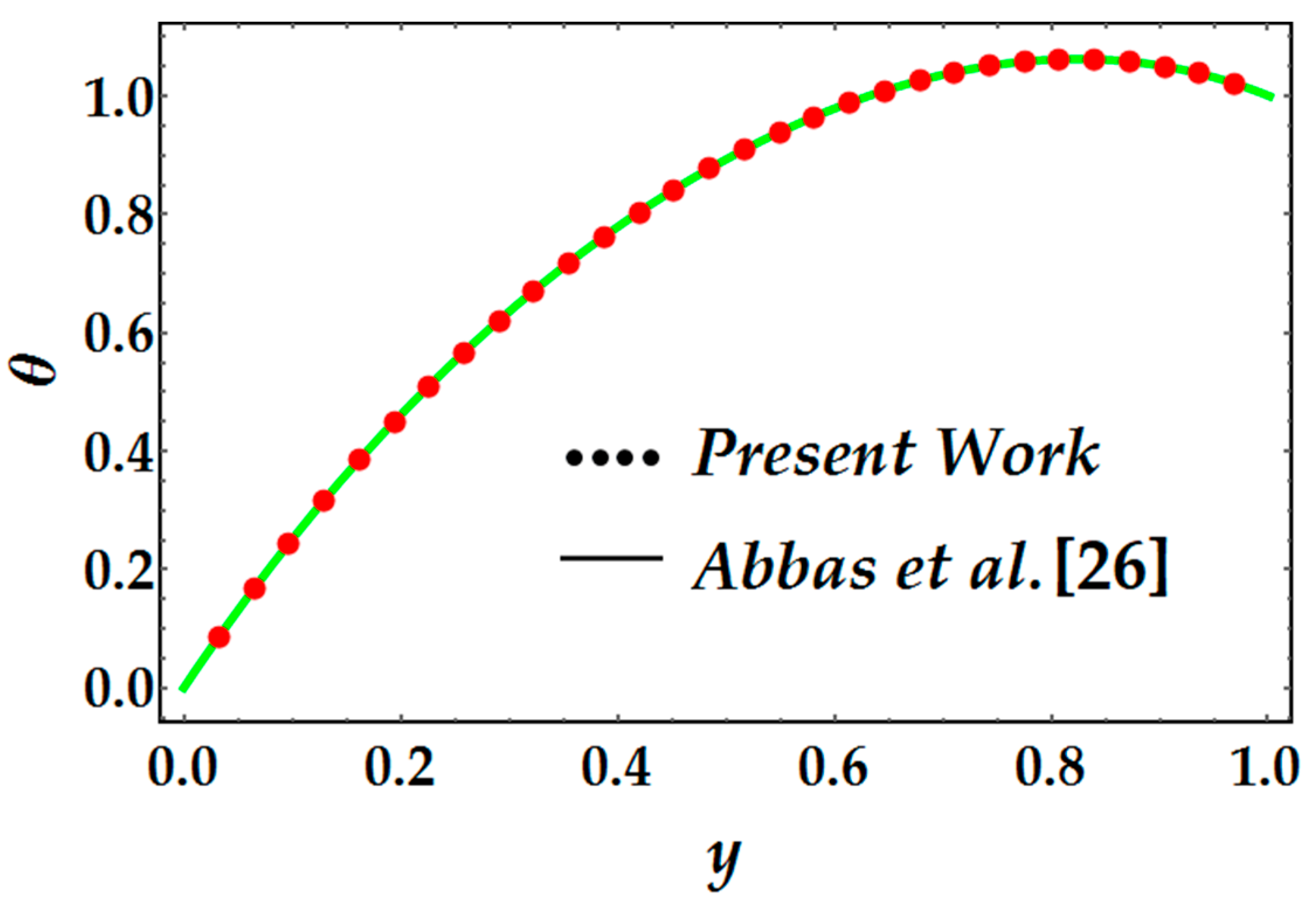
- The present results are also compared with previously published results [26] by taking to validate the current results and methodology.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| velocity components | |
| Cartesian coordinate | |
| pressure in fixed frame | |
| wave amplitude | |
| width of the channel | |
| wave velocity | |
| Prandtl number | |
| Reynolds number | |
| time | |
| basic density Grashof number | |
| thermal Grashof number | |
| Brownian motion parameter | |
| thermophoresis parameter | |
| constant | |
| magnetic field | |
| Weissenberg number | |
| volume flow rate | |
| temperature and concentration | |
| acceleration due to gravity | |
| Brownian diffusion coefficient | |
| thermophoretic diffusion coefficient | |
| mean absorption constant | |
| Hartman number | |
| stress tensor | |
| porosity parameter | |
| Greek Symbols | |
| chemical reaction parameter | |
| nanofluid thermal conductivity | |
| heat source/sink parameter | |
| viscosity of the fluid | |
| nano- particle volume fraction | |
| electrical conductivity | |
| wave number | |
| Stefan–Boltzmann constant | |
| effective heat capacity of nanoparticle | |
| nanofluid kinematic viscosity | |
| nanoparticle mass density | |
| fluid density | |
| fluid density at the reference temperature | |
| volumetric expansion coefficient | |
| heat capacity of fluid | |
| wavelength | |
| Amplitude ratio | |
References
- Sun, C.; Lee, J.S.H.; Zhang, M. Magnetic nanoparticles in MR imaging and drug delivery. Adv. Drug Deliv. Rev. 2018, 60, 1252–1265. [Google Scholar] [CrossRef] [PubMed]
- Berry, C.C. Progress in functionalization of magnetic nanoparticles for applications in biomedicine. J. Phys. D Appl. Phys. 2009, 42, 224003. [Google Scholar] [CrossRef]
- McBain, S.C.; Yiu, H.H.; Dobson, J. Magnetic nanoparticles for gene and drug delivery. Int. J. Nanomed. 2008, 3, 169. [Google Scholar]
- Cho, K.; Wang, X.U.; Nie, S.; Shin, D.M. Therapeutic nanoparticles for drug delivery in cancer. Clin. Cancer Res. 2008, 14, 1310–1316. [Google Scholar] [CrossRef] [PubMed]
- Veiseh, O.; Gunn, J.W.; Zhang, M. Design and fabrication of magnetic nanoparticles for targeted drug delivery and imaging. Adv. Drug Deliv. Rev. 2010, 62, 284–304. [Google Scholar] [CrossRef]
- Solanki, A.; Kin, J.D.; Lee, K.B. Nanotechnology for Regenerative Medicine: Nanomaterials for Stem Cell Imaging; Future Medicine: London, UK, 2008; Volume 3, pp. 567–578. [Google Scholar]
- Misra, J.C.; Sinha, A.; Shit, G.C. Theoretical analysis of blood flow through an arterial segment having multiple stenoses. J. Mech. Med. Biol. 2008, 8, 265–279. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S.; Hayat, T.; Hendi, A.A. Peristaltic flow of a nanofluid with slip effects. Meccanica 2012, 47, 1283–1294. [Google Scholar] [CrossRef]
- Tripathi, D.; Bég, O.A. A study on peristaltic flow of nanofluids: Application in drug delivery systems. Int. J. Heat Mass Transf. 2014, 70, 61–70. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Abelman, S. Two-phase simulation of nanofluid flow and heat transfer in an annulus in the presence of an axial magnetic field. IEEE Trans. Nanotechnol. 2015, 14, 561–569. [Google Scholar] [CrossRef]
- Akbar, N.S.; Raza, M.; Ellahi, R. Influence of induced magnetic field and heat flux with the suspension of carbon nanotubes for the peristaltic flow in a permeable channel. J. Magn. Magn. Mater. 2015, 381, 405–415. [Google Scholar] [CrossRef]
- Rashidi, M.; Bhatti, M.; Abbas, M.; Ali, M. Entropy generation on MHD blood flow of nanofluid due to peristaltic waves. Entropy 2016, 18, 117. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Zeeshan, A.; Ellahi, R. Simultaneous effects of coagulation and variable magnetic field on peristaltically induced motion of Jeffrey nanofluid containing gyrotactic microorganism. Microvasc. Res. 2017, 110, 32–42. [Google Scholar] [CrossRef] [PubMed]
- Iftikhar, N.; Rehman, A.; Sadaf, H.; Khan, M.N. Impact of wall properties on the peristaltic flow of Cu-water nano fluid in a non-uniform inclined tube. Int. J. Heat Mass Transf. 2018, 125, 772–779. [Google Scholar] [CrossRef]
- Abdelsalam, S.I.; Bhatti, M.M. The study of non-Newtonian nanofluid with hall and ion slip effects on peristaltically induced motion in a non-uniform channel. RSC Adv. 2018, 8, 7904–7915. [Google Scholar] [CrossRef]
- Mekheimer, K.S.; Hasona, W.M.; Abo-Elkhair, R.E.; Zaher, A.Z. Peristaltic blood flow with gold nanoparticles as a third grade nanofluid in catheter: Application of cancer therapy. Phys. Lett. A 2018, 382, 85–93. [Google Scholar] [CrossRef]
- Akram, S.; Zafar, M.; Nadeem, S. Peristaltic transport of a Jeffrey fluid with double-diffusive convection in nanofluids in the presence of inclined magnetic field. Int. J. Geometr. Methods Mod. Phys. 2018, 15, 1850181. [Google Scholar] [CrossRef]
- Prakash, J.; Siva, E.P.; Tripathi, D.; Kuharat, S.; Bég, O.A. Peristaltic pumping of magnetic nanofluids with thermal radiation and temperature-dependent viscosity effects: Modelling a solar magneto-biomimetic nanopump. Renew. Energy 2019, 133, 1308–1326. [Google Scholar] [CrossRef]
- Abdelsalam, S.I.; Bhatti, M.M. New Insight into AuNP Applications in Tumour Treatment and Cosmetics through Wavy Annuli at the Nanoscale. Sci. Rep. 2019, 9, 260. [Google Scholar] [CrossRef]
- Ray, A.K.; Vasu, B.; Bég, O.A.; Gorla, R.S.; Murthy, P.V. Homotopy Semi-Numerical Modeling of Non-Newtonian Nanofluid Transport External to Multiple Geometries Using a Revised Buongiorno Model. Inventions 2019, 4, 54. [Google Scholar] [CrossRef]
- Abbas, M.A.; Hussain, I. Statistical Analysis of the Mathematical Model of Entropy Generation of Magnetized Nanofluid. Inventions 2019, 4, 32. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.U.; Imran, M.; Bhatti, M.M. Thermally developed Falkner-Skan bioconvection flow of a magnetized nanofluid in the presence of motile gyrotactic microorganism: Buongiorno’s nanofluid model. Phys. Scr. 2019, 94, 115304. [Google Scholar] [CrossRef]
- Tlili, I.; Bhatti, M.M.; Hamad, S.M.; Barzinjy, A.A.; Sheikholeslami, M.; Shafee, A. Macroscopic modeling for convection of Hybrid nanofluid with magnetic effects. Phys. A Stat. Mech. Appl. 2019, 534, 122136. [Google Scholar] [CrossRef]
- Abdelsalam, S.; Bhatti, M.M.; Zeeshan, A.; Riaz, A.; Beg, O.A. Metachronal propulsion of a magnetized particle-fluid suspension in a ciliated channel with heat and mass transfer. Phys. Scr. 2019, 94, 115301. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.U.; Hassan, M.; Bhatti, M.M.; Imran, M. Analysis on the bioconvection flow of modified second-grade nanofluid containing gyrotactic microorganisms and nanoparticles. J. Mol. Liq. 2019, 291, 111231. [Google Scholar] [CrossRef]
- Abbas, M.A.; Bai, Y.Q.; Rashidi, M.M.; Bhatti, M.M. Application of drug delivery in magnetohydrodynamics peristaltic blood flow of nanofluid in a non-uniform channel. J. Mech. Med. Biol. 2016, 16, 1650052. [Google Scholar] [CrossRef]
- Wang, F.; Shuai, Y.; Wang, Z.; Leng, Y.; Tan, H. Thermal and chemical reaction performance analyses of steam methane reforming in porous media solar thermochemical reactor. Int. J. Hydrog. Energy 2014, 39, 718–730. [Google Scholar] [CrossRef]
- Akbarzadeh, P. The onset of MHD nanofluid convection between a porous layer in the presence of purely internal heat source and chemical reaction. J. Therm. Anal. Calorim. 2018, 131, 2657–2672. [Google Scholar] [CrossRef]
- Yadav, D. The onset of longitudinal convective rolls in a porous medium saturated by a nanofluid with non-uniform internal heating and chemical reaction. J. Therm. Anal. Calorim. 2019, 135, 1107–1117. [Google Scholar] [CrossRef]
- Chen, X.; Wang, F.; Han, Y.; Yu, R.; Cheng, Z. Thermochemical storage analysis of the dry reforming of methane in foam solar reactor. Energy Convers. Manag. 2018, 158, 489–498. [Google Scholar] [CrossRef]
- Chen, X.; Wang, F.; Yan, X.; Han, Y.; Cheng, Z.; Jie, Z. Thermochemical performance of solar driven CO2 reforming of methane in volumetric reactor with gradual foam structure. Energy 2018, 151, 545–555. [Google Scholar] [CrossRef]









| 0 | 0.6467 | 0.6458 | 0.6431 | 0.6456 |
| 0.115 | 0.6405 | 0.6397 | 0.6370 | 0.6395 |
| 0.230 | 0.6219 | 0.6212 | 0.6184 | 0.6211 |
| 0.345 | 0.5907 | 0.5903 | 0.5874 | 0.5903 |
| 0.460 | 0.5469 | 0.5467 | 0.5438 | 0.5468 |
| 0.575 | 0.4901 | 0.4903 | 0.4874 | 0.4904 |
| 0.690 | 0.4201 | 0.4206 | 0.4178 | 0.4207 |
| 0.805 | 0.3365 | 0.3372 | 0.3347 | 0.3373 |
| 0.920 | 0.2390 | 0.2397 | 0.2376 | 0.2398 |
| 1.035 | 0.1270 | 0.1275 | 0.1263 | 0.1275 |
| 1.115 | 0 | 0 | 0 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, M.A.; Bhatti, M.M.; Sheikholeslami, M. Peristaltic Propulsion of Jeffrey Nanofluid with Thermal Radiation and Chemical Reaction Effects. Inventions 2019, 4, 68. https://doi.org/10.3390/inventions4040068
Abbas MA, Bhatti MM, Sheikholeslami M. Peristaltic Propulsion of Jeffrey Nanofluid with Thermal Radiation and Chemical Reaction Effects. Inventions. 2019; 4(4):68. https://doi.org/10.3390/inventions4040068
Chicago/Turabian StyleAbbas, Munawwar Ali, Muhammad Mubashir Bhatti, and Mohsen Sheikholeslami. 2019. "Peristaltic Propulsion of Jeffrey Nanofluid with Thermal Radiation and Chemical Reaction Effects" Inventions 4, no. 4: 68. https://doi.org/10.3390/inventions4040068
APA StyleAbbas, M. A., Bhatti, M. M., & Sheikholeslami, M. (2019). Peristaltic Propulsion of Jeffrey Nanofluid with Thermal Radiation and Chemical Reaction Effects. Inventions, 4(4), 68. https://doi.org/10.3390/inventions4040068







