Wide-Speed Range Sensorless Control of an IPM Motor for Multi-Purpose Applications
Abstract
1. Introduction
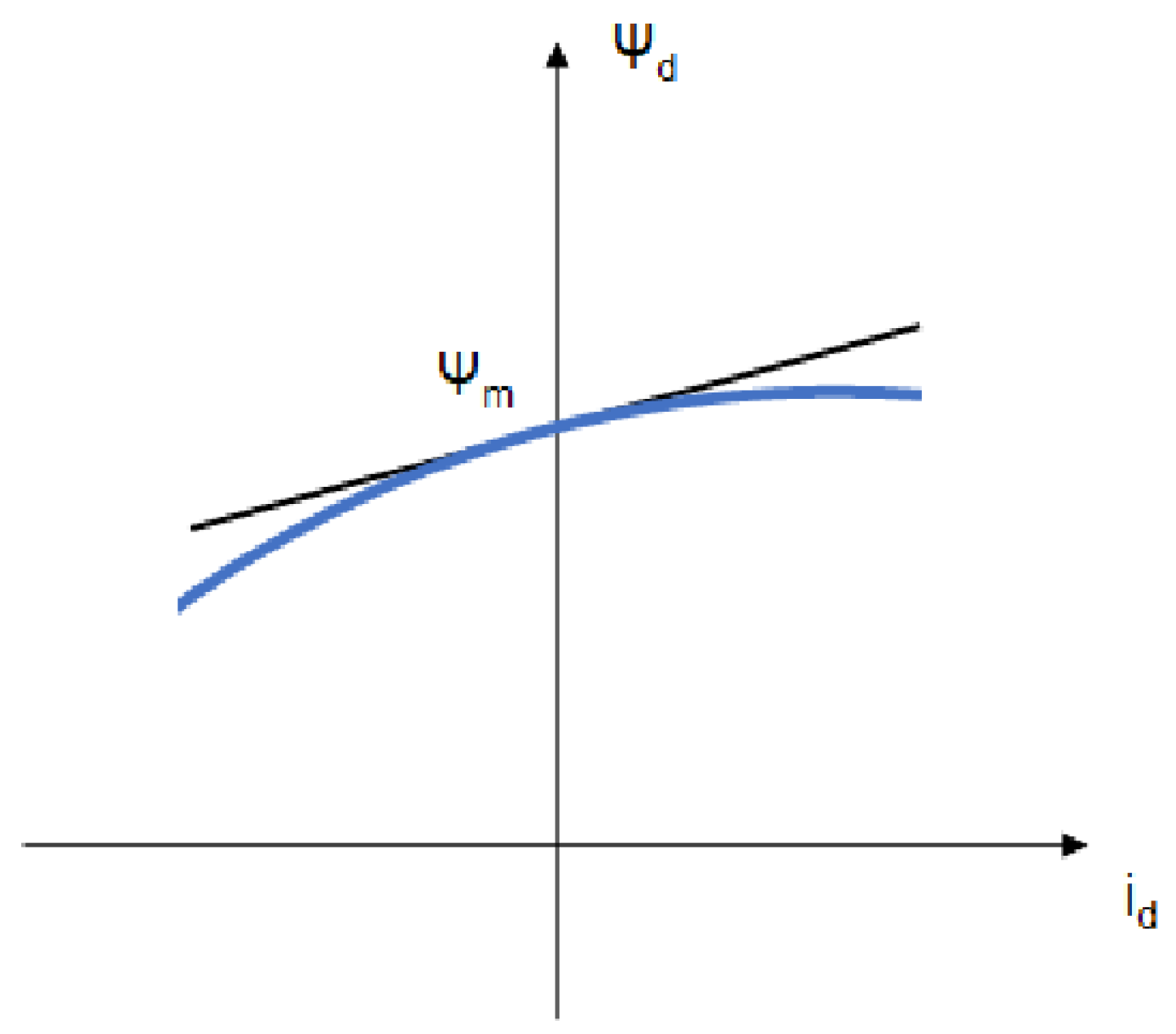
2. IPM Model
3. Sensorless Control
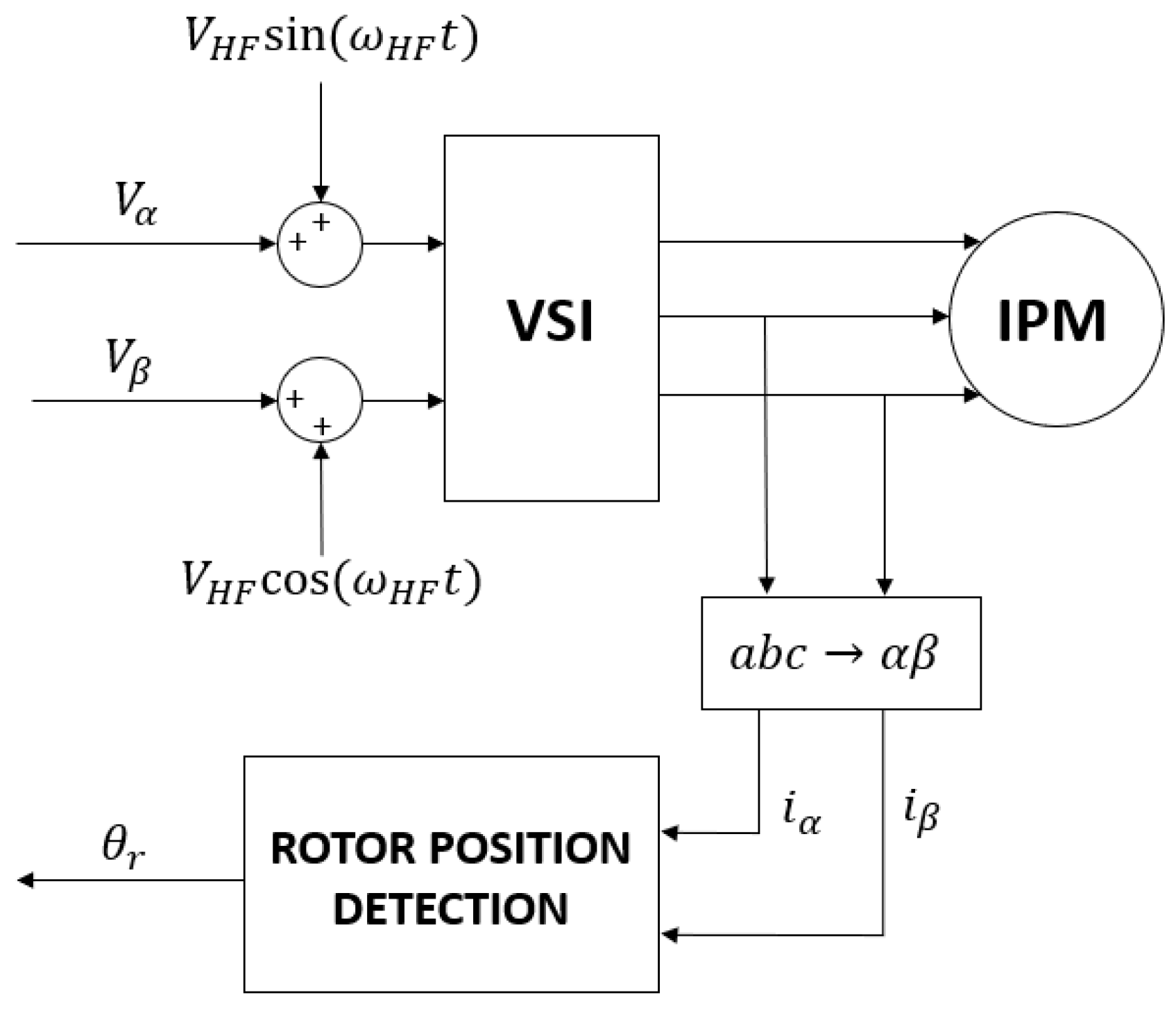
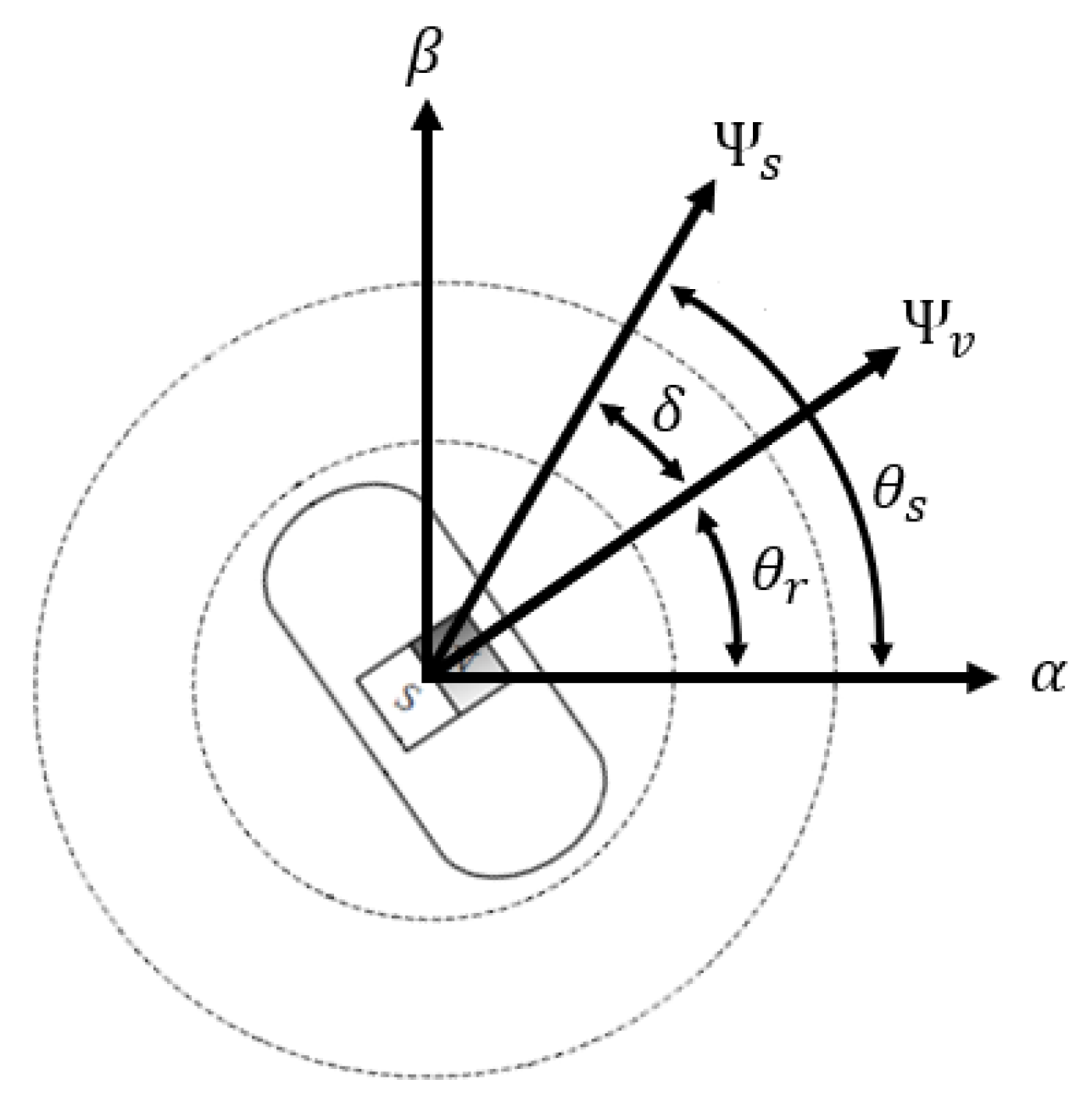
3.1. High Frequency Signal Injection
- The stator resistance is negligible compared to the stator inductance
- The back-EMF produced by the motor is negligible at standstill and very low speeds.
3.2. V-I Observer
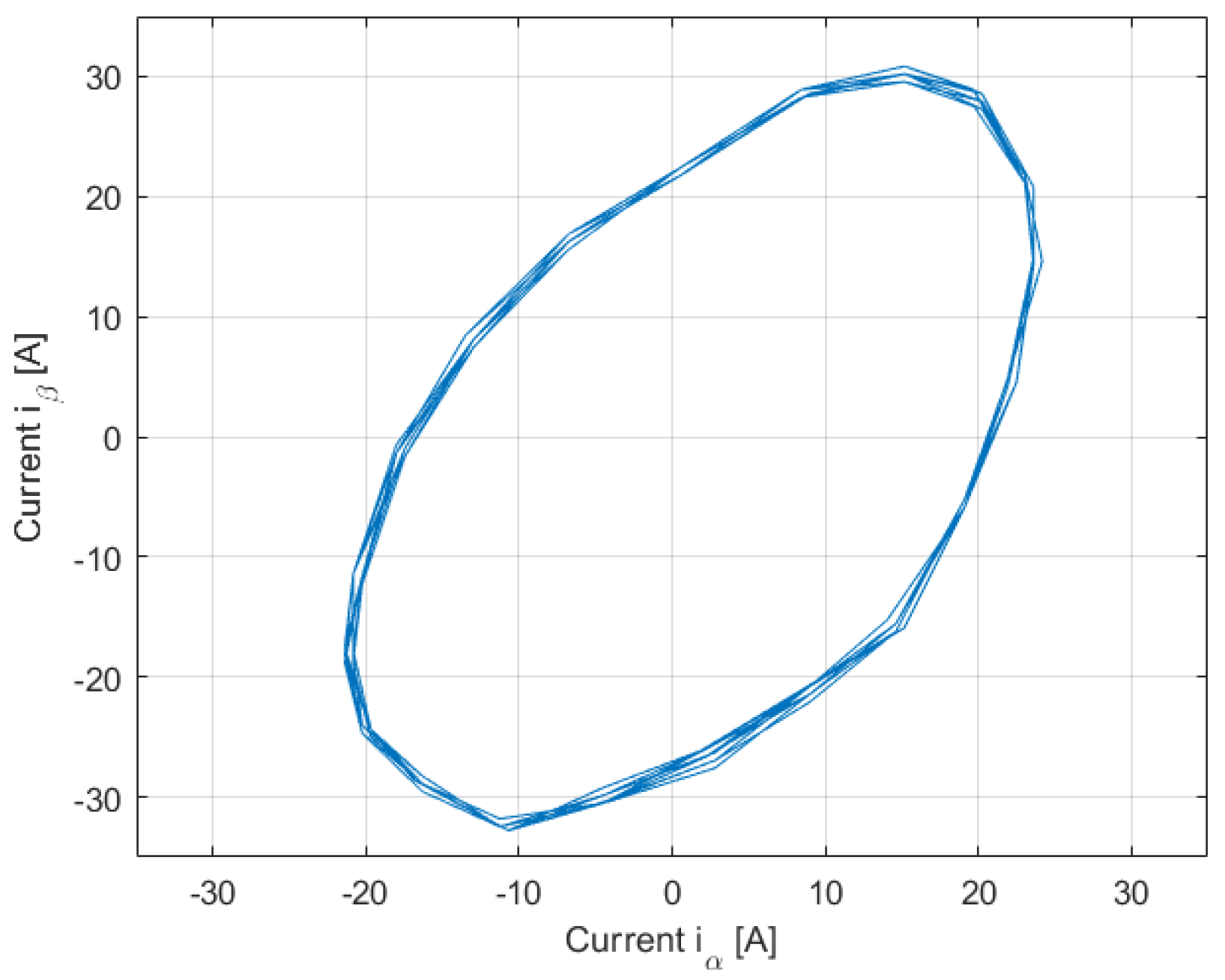
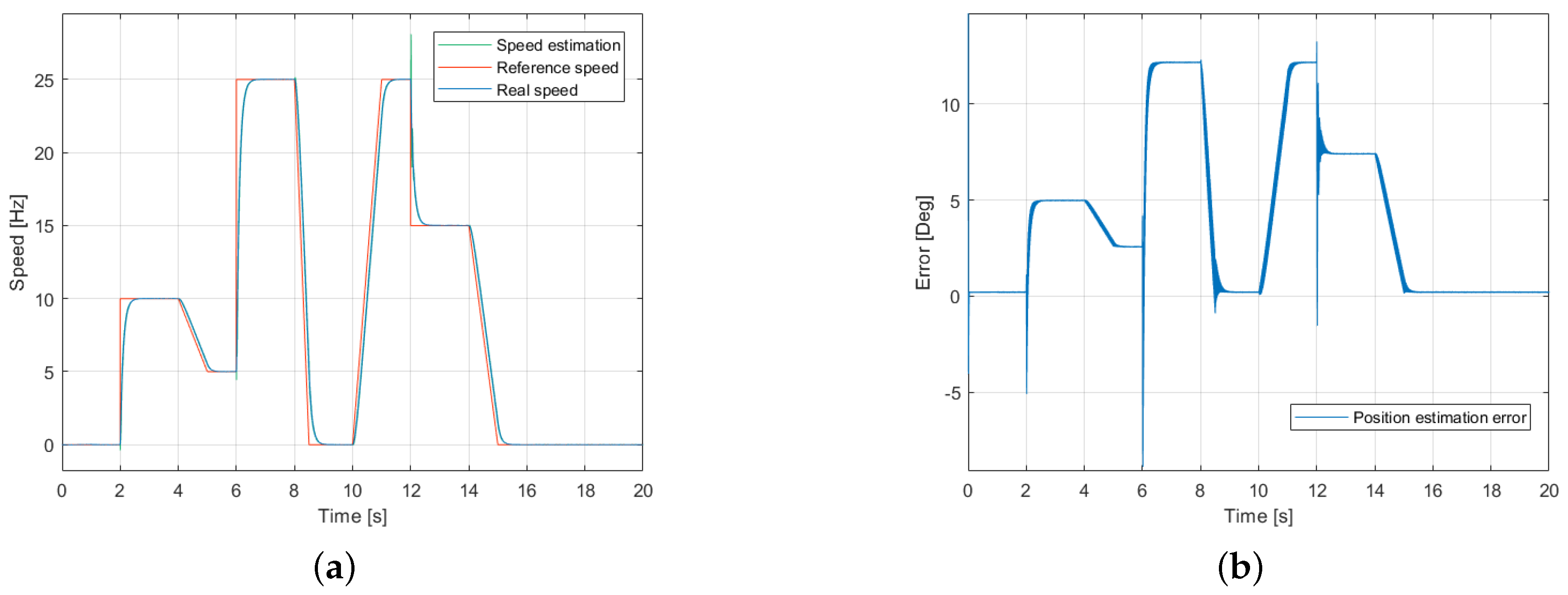
4. Simulation Results
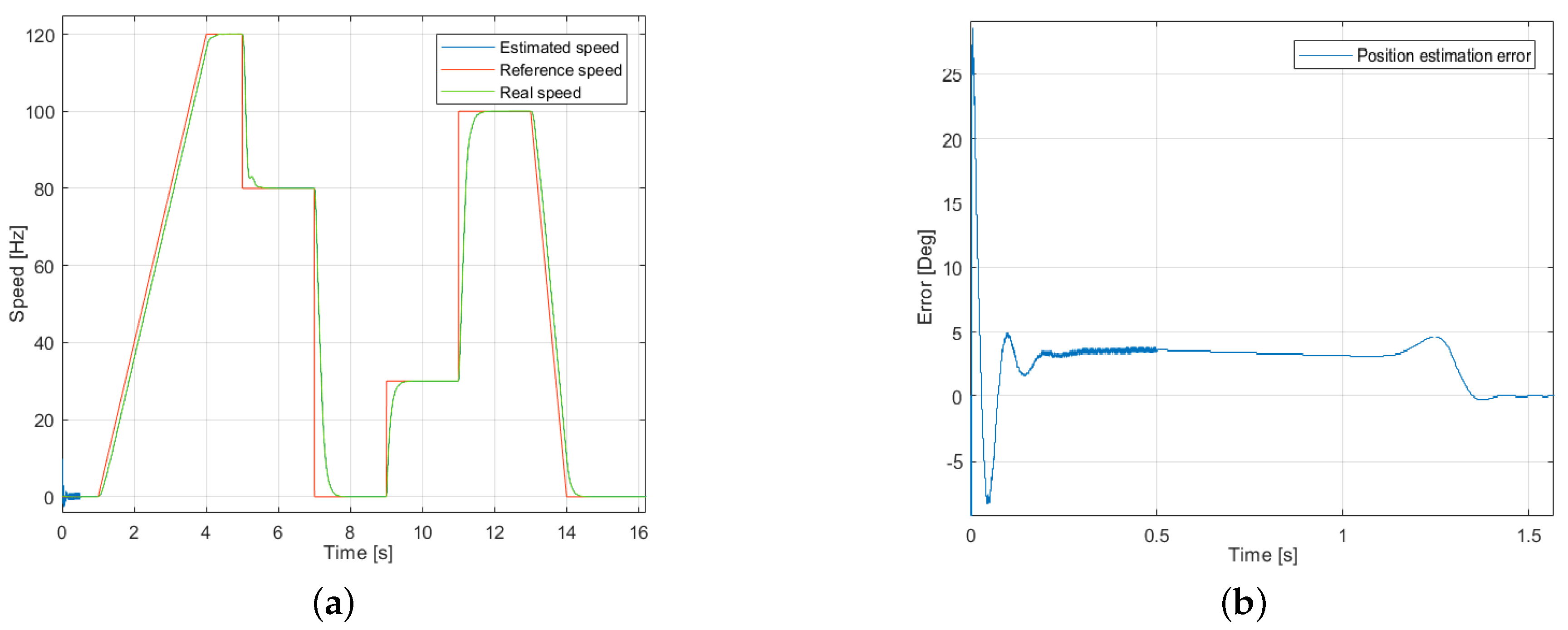
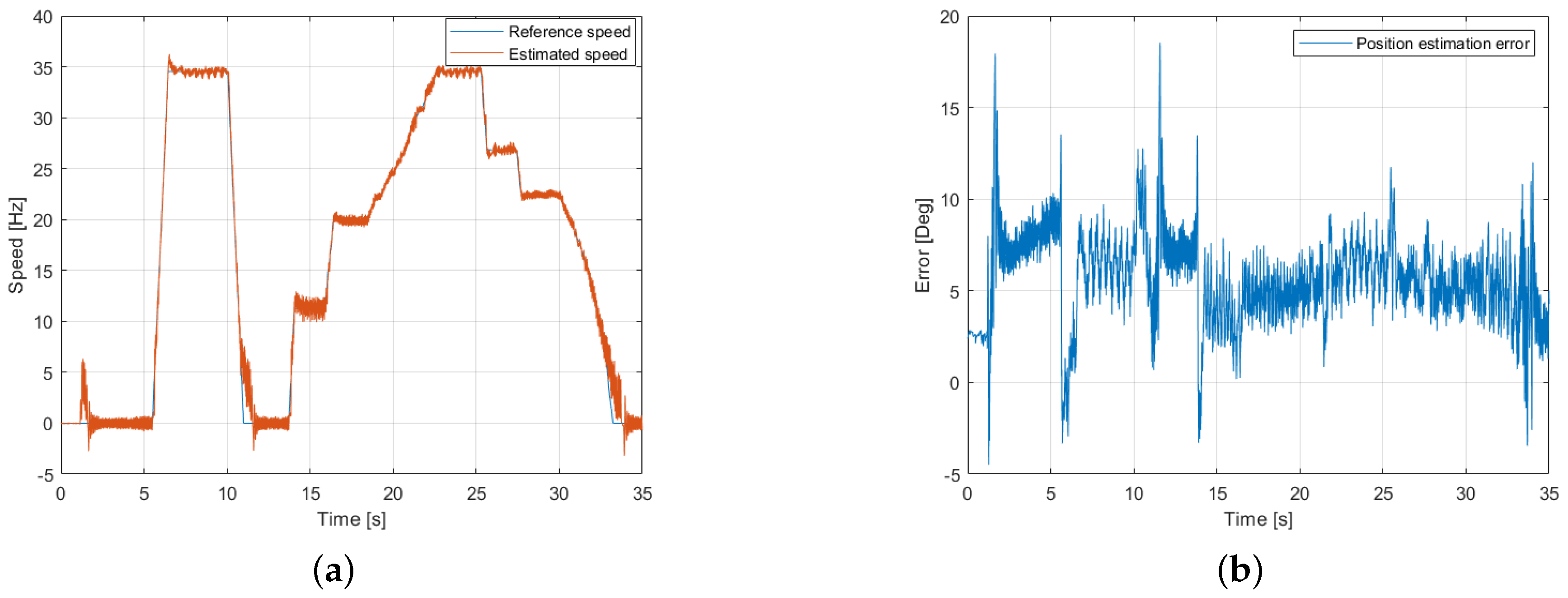
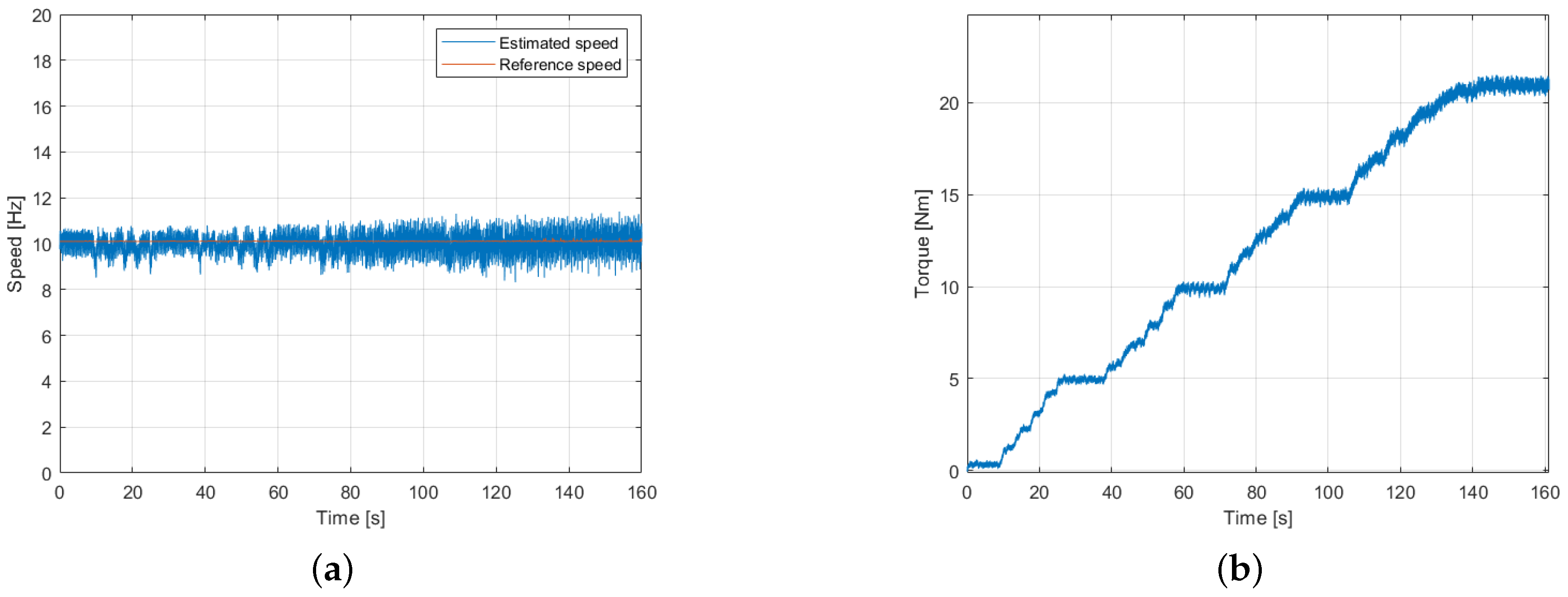
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tursini, M.; Petrella, R.; Parasiliti, F. Sensorless control of an IPM synchronous motor for city-scooter applications. In Proceedings of the 38th IAS Annual Meeting on Conference Record of the Industry Applications Conference, Salt Lake City, UT, USA, 12–16 October 2003; Volume 3, pp. 1472–1479. [Google Scholar]
- Vagati, A.; Pellegrino, G.; Guglielmi, P. Comparison between SPM and IPM motor drives for EV application. In Proceedings of the XIX International Conference on Electrical Machines-ICEM, Rome, Italy, 6–8 September 2010; Volume 3, pp. 1–6. [Google Scholar]
- Pellegrino, G.; Vagati, A.; Guglielmi, P.; Boazzo, B. Performance Comparison Between Surface-Mounted and Interior PM Motor Drives for Electric Vehicle Application. IEEE Trans. Ind. Electr. 2012, 59, 803–811. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Chan, C.C. Electrical machine topologies and technologies for electric, hybrid, and fuel cell vehicles. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Harbin, China, 3–5 September 2008; pp. 1–6. [Google Scholar]
- Awan, H.A.A.; Tuovinen, T.; Saarakkala, S.E.; Hinkkanen, M. Discrete-Time Observer Design for Sensorless Synchronous Motor Drives. IEEE Trans. Ind. Appl. 2016, 52, 3968–3979. [Google Scholar] [CrossRef]
- Foo, G.; Rahman, M.F. Sensorless Sliding-Mode MTPA Control of an IPM Synchronous Motor Drive Using a Sliding-Mode Observer and HF Signal Injection. IEEE Trans. Ind. Electron. 2010, 57, 1270–1278. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, S.S.; Kim, R.Y.; Hyun, D.S. A sensorless control using Extended Kalman Filter for an IPM synchronous motor based on an extended rotor flux. In Proceedings of the 38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 1631–1636. [Google Scholar]
- Foo, G.; Sayeef, S.; Rahman, M.F. An Extended Kalman filter for sensorless direct torque controlled IPM synchronous motor drive. In Proceedings of the IEEE International Conference on Power and Energy, Sydney, Australia, 14–17 December 2008; pp. 271–276. [Google Scholar]
- Xu, Z.; Rahman, M.F.; Wang, G.; Xu, D. Performance Evaluation of an Integrated Starter-Alternator with an IPM Synchronous Machine under Sensor-less Operation. J. Power Electron. 2012, 12, 49–57. [Google Scholar] [CrossRef][Green Version]
- Parasiliti, F.; Petrella, R.; Tursini, M. Speed sensorless control of an interior PM synchronous motor. In Proceedings of the Conference Record of the 2002 IEEE-Industry Applications Society Annual Meeting, Pittsburgh, PA, USA, 13–18 October 2002; Volume 1, pp. 657–664. [Google Scholar]
- Zhang, G.; Wang, G.; Xu, D. Saliency-based position sensorless control methods for PMSM drives—A review. Chin. J. Electr. Eng. 2017, 3, 14–23. [Google Scholar]
- Xie, G.; Lu, K.; Xu, D.; Dwivedi, S.K.; Rosholm, J.R. Improved INFORM method by minimizing the inverter nonlinear voltage error effects. In Proceedings of the IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Torino, Italy, 26–27 March 2015; pp. 188–194. [Google Scholar]
- Raca, D.; Garcia, P.; Reigosa, D.; Briz, F.; Lorenz, R.D. A comparative analysis of pulsating vs. rotating vector carrier signal injection-based sensorless control. In Proceedings of the Twenty-Third Annual IEEE Applied Power Electronics Conference and Exposition, Austin, TX, USA, 24–28 February 2008; pp. 879–885. [Google Scholar]
- Kim, H.; Lorenz, R.D. Carrier signal injection based sensorless control methods for IPM synchronous machine drives. In Proceedings of the 39th IAS Annual Meeting, Conference Record of the 2004 IEEE Industry Applications Conference, Seattle, WA, USA, 3–7 October 2004; Volume 2, pp. 977–984. [Google Scholar]
- Caruana, C.; Asher, G.M.; Sumner, M. Performance of HF signal injection techniques for zero-low-frequency vector control of induction Machines under sensorless conditions. IEEE Trans. Ind. Electron. 2006, 53, 225–238. [Google Scholar] [CrossRef]
- Ribeiro, A.S.; Degner, M.W.; Briz, F.; Lorenz, R. Comparison of carrier signal voltage and current injection for the estimation of flux angle or rotor position. In Proceedings of the Thirty-Third IAS Annual Meeting, Conference Record of 1998 IEEE Industry Applications Conference, St. Louis, MO, USA, 12–15 October 1998; Volume 1, pp. 452–459. [Google Scholar]
- Jeong, Y.; Lorenz, R.D.; Jahns, T.M.; Sul, S.-K. Initial rotor position estimation of an interior permanent-magnet synchronous machine using carrier-frequency injection methods. In Proceedings of the IEEE International Electric Machines and Drives Conference (IEMDC 2003), Madison, WI, USA, 1–4 June 2003; Volume 2, pp. 1218–1223. [Google Scholar]









| Symbol | Description | Value |
|---|---|---|
| Winding resistance | 8.7 [m] | |
| d-axis inductance | 100 [H] | |
| q-axis inductance | 130 [H] | |
| Magnetic flux linkage | 9.1 [V] @ 1000 rpm | |
| Rated voltage | ||
| Maximum phase current | 250 [A] | |
| Maximum speed | 6000 [rpm] | |
| Number of pole pairs | 4 | |
| Rated torque | 20 [Nm] | |
| Rated power | 7 [Kw] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bacci, M.L.; Mapelli, F.L.; Mossina, S.; Tarsitano, D.; Vignati, M. Wide-Speed Range Sensorless Control of an IPM Motor for Multi-Purpose Applications. Inventions 2020, 5, 24. https://doi.org/10.3390/inventions5030024
Bacci ML, Mapelli FL, Mossina S, Tarsitano D, Vignati M. Wide-Speed Range Sensorless Control of an IPM Motor for Multi-Purpose Applications. Inventions. 2020; 5(3):24. https://doi.org/10.3390/inventions5030024
Chicago/Turabian StyleBacci, Maria Laura, Ferdinando Luigi Mapelli, Stefano Mossina, Davide Tarsitano, and Michele Vignati. 2020. "Wide-Speed Range Sensorless Control of an IPM Motor for Multi-Purpose Applications" Inventions 5, no. 3: 24. https://doi.org/10.3390/inventions5030024
APA StyleBacci, M. L., Mapelli, F. L., Mossina, S., Tarsitano, D., & Vignati, M. (2020). Wide-Speed Range Sensorless Control of an IPM Motor for Multi-Purpose Applications. Inventions, 5(3), 24. https://doi.org/10.3390/inventions5030024







