Optimization of Power and Levelized Cost for Shrouded Small Wind Turbine
Abstract
:1. Introduction
2. Optimization
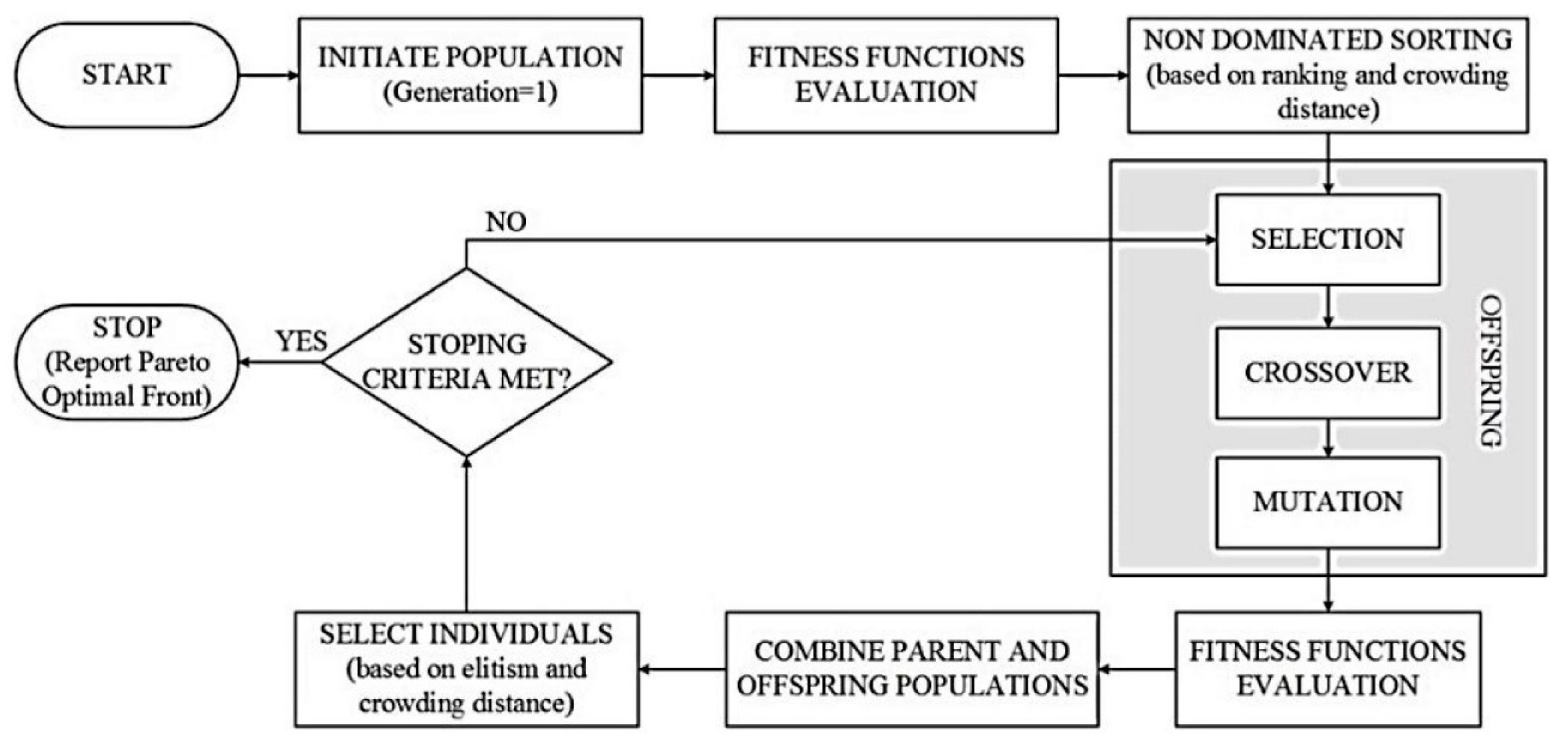
3. Non-Dominated Sorting Genetic Algorithm
4. The Study Areas
5. Small Wind Turbine Selection
6. Objective Functions
6.1. Minimize the Levelized Cost of Energy
6.2. Maximize Annual Energy Production (AEP)
7. Results and Discussion
8. Optimization Results
8.1. Results of the Study Model Wind Turbine without a Lens for the Kish and Firoozkooh Stations
8.2. Results of the Study Model Wind Lens Turbine for the Kish and Firoozkooh Stations
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Østergaard, P.A.; Duic, N.; Noorollahi, Y.; Kalogirou, S. Latest Progress in Sustainable Development Using Renewable Energy Technology. Renew. Energy 2020, 162, 1554–1562. [Google Scholar] [CrossRef]
- IEA. World Energy Outlook; International Energy Agency: Paris, France, 2015. [Google Scholar]
- Pishgar-Komleh, S.H.; Akram, A. Evaluation of wind energy potential for different turbine models based on the wind speed data of Zabol region, Iran. Sustain. Energy Technol. Assess. 2017, 22, 34–40. [Google Scholar] [CrossRef]
- Noorollahi, Y.; Yousefi, H.; Mohammadi, M. Multi-criteria decision support system for wind farm site selection using GIS. Sustain. Energy Technol. Assess. 2016, 13, 38–50. [Google Scholar] [CrossRef]
- Noorollahi, Y.; Jokar, M.A.; Kalhor, A. Using artificial neural networks for temporal and spatial wind speed forecasting in Iran. Energy Convers. Manag. 2016, 115, 17–25. [Google Scholar] [CrossRef]
- Noorollahi, Y.; Itoi, R.; Yousefi, H.; Mohammadi, M.; Farhadi, A. Modeling for diversifying electricity supply by maximizing renewable energy use in Ebino city southern Japan. Sustain. Cities Soc. 2017, 34, 371–384. [Google Scholar] [CrossRef]
- Lilley, G.M.; Rainbird, W.J.; Association, E.R. A Preliminary Report on the Design and Performance of Ducted Windmills; College of Aeronautics: New York, NY, USA, 1956. [Google Scholar]
- Oman Foreman, K.M.; Gilbert, B.L. A Progress Report on the Diffuser Augmented Wind Turbine. In Proceedings of the 3rd Biennial Wind energy Conversion Systems Conference, Washington, DC, USA, 1 May 1975; pp. 826–829. [Google Scholar]
- Igra, O. Cost-effectiveness of the vortex-augmented wind turbine. Energy 1979, 4, 119–130. [Google Scholar] [CrossRef]
- Kogan, A.; Seginer, A. Shrouded Aerogenerator Design Study II, Axisymmetrical Shroud Performance; Technion-Israel Institute of Technology, Department of Aeronautical Engineering: Tel-Aviv, Israel, 1963; p. 86. [Google Scholar]
- Gilbert, B.L.; Oman, R.A.; Foreman, K.M. Fluid dynamics of diffuser-augmented wind turbines. J. Energy 1978, 2, 368–374. [Google Scholar] [CrossRef]
- Gilbert, B.L.; Foreman, K.M. Experiments with a Diffuser-Augmented Model Wind Turbine. J. Energy Resour. Technol. 1983, 105, 46–53. [Google Scholar] [CrossRef]
- Igra, O. Research and development for shrouded wind turbines. Energy Convers. Manag. 1981, 21, 13–48. [Google Scholar] [CrossRef]
- Vasel-Be-Hagh, A. Wind farms with counter-rotating wind turbines. Sustain. Energy Technol. Assess. 2016. [Google Scholar] [CrossRef]
- Said, M.; EL-Shimy, M.; Abdelraheem, M.A. Improved framework for techno-economical optimization of wind energy production. Sustain. Energy Technol. Assess. 2017, 23, 57–72. [Google Scholar] [CrossRef]
- Waewsak, J.; Kongruang Chuleerat, G.Y. Assessment of wind power plants with limited wind resources in developing countries: Application to Ko Yai in southern Thailand. Sustain. Energy Technol. Assess. 2017, 19, 79–93. [Google Scholar] [CrossRef]
- Phillips, D.G.; Flay, R.G.J.; Nash, T.A. Aerodynamic analysis and monitoring of the Vortec 7 diffuser-augmented wind turbine. Trans. Inst. Prof. Eng. New Zealand. Electr. Mech. Chem. Eng. Sect. 1999, 26, 13–19. [Google Scholar]
- Abe, K.; Ohya, Y. An investigation of flow fields around flanged diffusers using CFD. J. Wind Eng. Ind. Aerodyn. 2004, 92, 315–330. [Google Scholar] [CrossRef]
- Ohya, Y.; Karasudani, T.; Sakurai, A.; Abe, K.; Inoue, M. Development of a shrouded wind turbine with a flanged diffuser. J. Wind Eng. Ind. Aerodyn. 2008, 96, 524–539. [Google Scholar] [CrossRef]
- Al-Sulaiman, F.A.; Yilbas, B.S. Thermoeconomic analysis of shrouded wind turbines. Energy Convers. Manag. 2015, 96, 599–604. [Google Scholar] [CrossRef]
- Nikolić, V.; Petković, D.; Shamshirband, S.; Ćojbašić, Ž. Adaptive neuro-fuzzy estimation of diffuser effects on wind turbine performance. Energy 2015, 89, 324–333. [Google Scholar] [CrossRef]
- Kosasih, B.; Tondelli, A. Experimental Study of Shrouded Micro-Wind Turbine. Procedia Eng. 2012, 49, 92–98. [Google Scholar] [CrossRef] [Green Version]
- Marmidis, G.; Lazarou, S.; Pyrgioti, E. Optimal placement of wind turbines in a wind park using Monte Carlo simulation. Renew. Energy 2008, 33, 1455–1460. [Google Scholar] [CrossRef]
- Emami, A.; Noghreh, P. New approach on optimization in placement of wind turbines within wind farm by genetic algorithms. Renew. Energy 2010, 35, 1559–1564. [Google Scholar] [CrossRef]
- Wang, X.; Wen Zhong, S.; Wei Jun, Z.; Jens Nørkær, S.; Chen, J. Shape optimization of wind turbine blades. Wind Energy 2009, 12, 781–803. [Google Scholar] [CrossRef]
- Kamjoo, A.; Maheri, A.; Dizqah, A.M.; Putrus, G.A. Multi-objective design under uncertainties of hybrid renewable energy system using NSGA-II and chance constrained programming. Int. J. Electr. Power Energy Syst. 2016, 74, 187–194. [Google Scholar] [CrossRef]
- Østergaard, P.A.; Duic, N.; Noorollahi, Y.; Mikulcic, H.; Kalogirou, S. Sustainable development using renewable energy technology. Renew. Energy 2020, 146, 2430–2437. [Google Scholar] [CrossRef]
- Ahmadi-Baloutaki, M.; Carriveau Rupp, T.D.S.-K. Performance of a vertical axis wind turbine in grid generated turbulence. Sustain. Energy Technol. Assess. 2015, 11, 178–185. [Google Scholar] [CrossRef]
- Allaei, D.; Andreopoulos, Y. INVELOX: Description of a new concept in wind power and its performance evaluation. Energy 2014, 69, 336–344. [Google Scholar] [CrossRef] [Green Version]
- Shirgholami, Z.; Namdar Zangeneh Soudabeh, B.M. Decision system to support the practitioners in the wind farm design: A case study for Iran mainland. Sustain. Energy Technol. Assess. 2016, 16, 1–10. [Google Scholar] [CrossRef]
- Elsevier Pareto Principle-an Overview ScienceDirect Topics. Available online: https://www.sciencedirect.com/topics/computer-science/pareto-principle (accessed on 24 November 2020).
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. Evol. Comput. IEEE Trans. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Coello, C.C.; Lamont, G.B.; van Veldhuizen, D.A. Evolutionary Algorithms for Solving Multi-Objective Problems; Springer: New York, NY, USA, 2007; ISBN 9780387367972. [Google Scholar]
- Deb, K.; Sinha, A. An efficient and accurate solution methodology for bilevel multi-objective programming problems using a hybrid evolutionary-local-search algorithm. Evol. Comput. 2010, 18, 403–449. [Google Scholar] [CrossRef]
- Lukic, N.L.; Bozin-Dakic, M.; Grahovac, J.A.; Dodic, J.M.; Jokic, A.I. Multi-objective optimization of microfiltration of baker’s yeast using genetic algorithm. Acta Period. Technol. 2017, 48, 211–220. [Google Scholar] [CrossRef] [Green Version]
- Wood, D. Small Wind Turbines: Analysis, Design, and Application; Springer: New York, NY, USA, 2011; ISBN 9781849961752. [Google Scholar]
- Ohya, Y.; Karasudani, T. A Shrouded Wind Turbine Generating High Output Power with Wind-lens Technology. Energies 2010, 3, 634. [Google Scholar] [CrossRef] [Green Version]
- Stankovic, S.; Campbell, N.; Harries, A. Urban Wind Energy; Earthscan: London, UK; ISBN 9781849770262.
- Gao, A. EQ Series Small Wind Turbine Generators Manual. Available online: http://www.callaglory.com/download.html (accessed on 20 June 2016).
- Minaeva, L.P.; Creative Commons Attribution-Share Alike 3.0 Unported, Department of Engineering Kyushu University, Kyushu, Japan. Personal communication, 2014.
- Cassedy, E.S. Prospects for Sustainable Energy: A Critical Assessment; Cambridge University Press: Cambridge, UK, 2000; ISBN 9780521631204. [Google Scholar]
- Tegen, S.; Lantz, E.; Hand, M.; Maples, B.; Smith, A.; Schwabe, P. 2011 Cost of Wind Energy Review; Prepared under Task No. WE11.1201; National Renewable Energy Laboratory: Golden, CO, USA, 2013; p. 50. [Google Scholar]
- Fingersh, L.; Laxson, A.H.M. Wind Turbine Design Cost and Scaling Model; Technical Report NREL/TP-500-40566; National Renewable Energy Laboratory: Golden, CO, USA.
- Hau, E. Wind Turbines: Fundamentals, Technologies, Application, Economics; Springer: New York, NY, USA, 2006; ISBN 9783540242406. [Google Scholar]
- Powell, W.R. An analytical expression for the average output power of a wind machine. Sol. Energy 1981, 26, 77–80. [Google Scholar] [CrossRef]
- Torres, J.L.; Prieto, E.; Garcia, A.; De Blas, M.; Ramirez, F.; De Francisco, A. Effects of the model selected for the power curve on the site effectiveness and the capacity factor of a pitch regulated wind turbine. Sol. Energy 2003, 74, 93–102. [Google Scholar] [CrossRef]




| Parameters | Values |
|---|---|
| Number of population | 5, 6, 7, 8 |
| Number of iterations | 100 |
| Percent of crossover | 0.9 |
| Percent of mutation | 0.1 |
| Parameters | Values |
|---|---|
| Vc | 2.73, 3.5 |
| Vr | 10 |
| Vf | 25 |
| m | 2 |
| αkish | 1.71 |
| αfiruzkuh | 1.7 |
| βkish | 4.94 |
| βfiruzkuh | 6.36 |
| ρ/ρ0 | 1 |
| Kish Island Station | Height (m) | 40 | 30 | 10 | |||
| Weibull function parameters | |||||||
| Fitting average annual speed (m/s) | 1.65 | 5.87 5.37 | 1.41 | 5.55 4.96 | 1.71 | 4.94 4.43 | |
| Firoozkooh Station | Height (m) | 40 | 20 | 10 | |||
| Weibull function parameters | |||||||
| Fitting average annual speed (m/s) | 1.81 5.22 | 6.65 | 1.78 4.71 | 6.6 | 1.7 | 6.36 4.98 | |
| Rated Power (kW) | 1 | 2 | 3 | 5 | 6 | 10 | 15 | 20 | 30 | 50 |
|---|---|---|---|---|---|---|---|---|---|---|
| Rated Rotation Speed (rpm) | 450 | 360 | 280 | 220 | 200 | 180 | 155 | 90 | 75 | 60 |
| Rotor Diameter (m) | 2.8 | 3.2 | 4.2 | 5.2 | 5.6 | 8 | 9.8 | 10 | 12 | 13.8 |
| Hub Height | 8 | 8 | 8 | 10 | 11 | 12 | 15 | 18 | 18 | 18 |
| Cut-in Speed (m/s) | 3.5 | 3.5 | 3.5 | 3.5 | 3.5 | 3.5 | 3.5 | 3.5 | 3.5 | 3.5 |
| Cut-out Speed (m/s) | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 |
| Rated Wind Speed (m/s) | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| Reason | Constraints |
|---|---|
| Typical range for the small wind turbine | 1 ≤≤ 50 |
| Calculation based on the relation | 6358 ≤≤ 25033 |
| Calculation based on the relation | 1202 ≤≤ 4153 |
| Calculation based on the relation | 2 ≤ ≤ 97 |
| Calculation based on the relation | 3 ≤ ≤ 157 |
| Area | AEP (kWh/year) | COE ($/KWh) | P (kW) |
|---|---|---|---|
| Kish Island | 79,692 | 0.319 | 50 |
| 47,815 | 0.497 | 30 | |
| 23,907 | 0.564 | 15 | |
| 15,938 | 0.773 | 10 | |
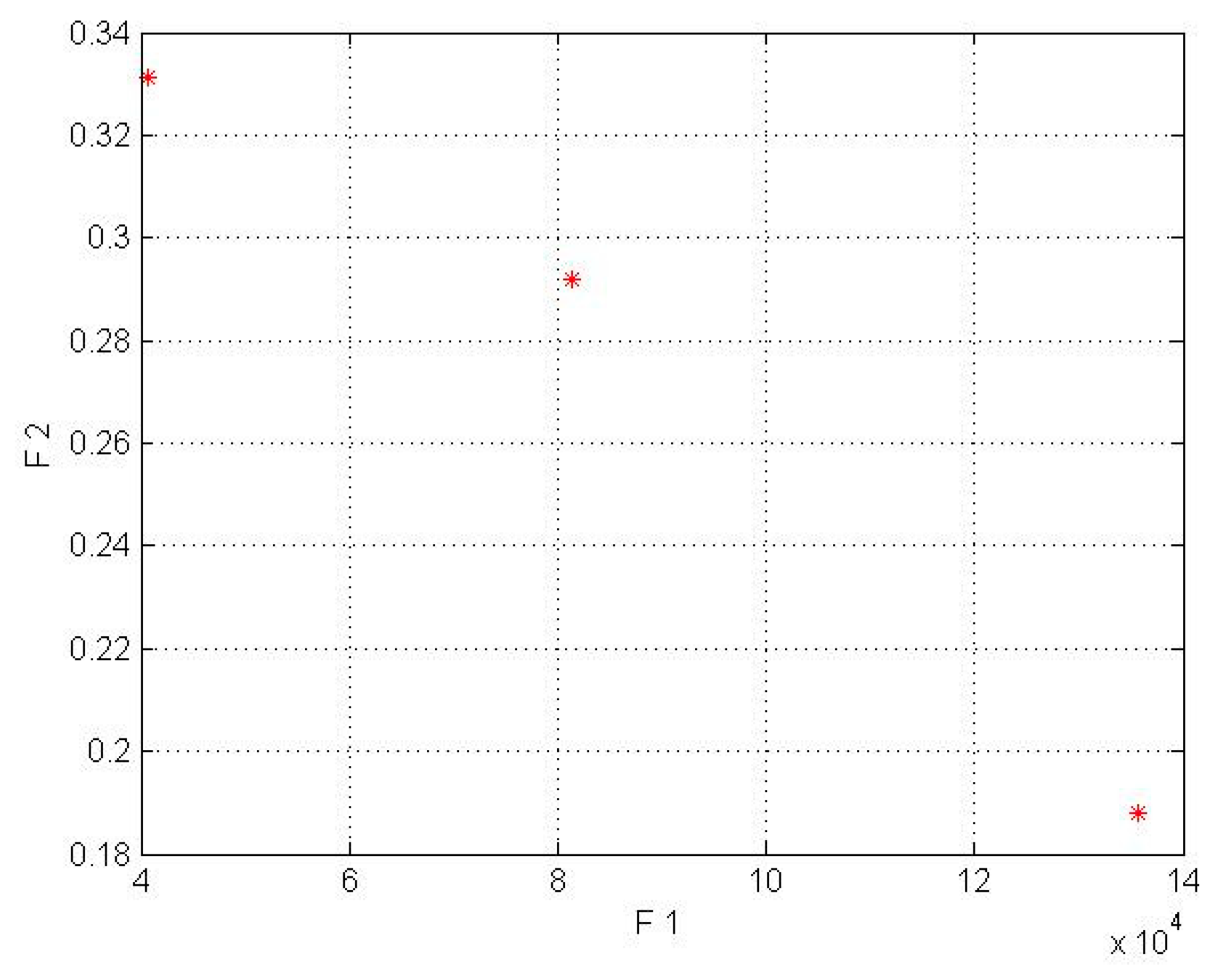
| Firoozkooh | 135,700 | 0.187 | 50 |
| 81,420 | 0.291 | 30 | |
| 40,710 | 0.331 | 15 |
| AEP (kWh/year) | COE ($/KWh) | P (kW) | |
|---|---|---|---|
| Kish Island | 146,564 | 0.179 | 50 |
| 87,939 | 0.277 | 30 | |
| 43,969 | 0.316 | 15 | |
| 29,313 | 0.431 | 10 | |
| 14,656 | 0.508 | 5 | |
| Firoozkooh | 237,140 | 0.111 | 50 |
| 142,284 | 0.171 | 30 | |
| 71,141 | 0.195 | 15 | |
| 28,456 | 0.268 | 6 | |
| 14,228 | 0.495 | 3 | |
| 9485 | 0.709 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khojasteh, H.; Noorollahi, Y.; Tahani, M.; Masdari, M. Optimization of Power and Levelized Cost for Shrouded Small Wind Turbine. Inventions 2020, 5, 59. https://doi.org/10.3390/inventions5040059
Khojasteh H, Noorollahi Y, Tahani M, Masdari M. Optimization of Power and Levelized Cost for Shrouded Small Wind Turbine. Inventions. 2020; 5(4):59. https://doi.org/10.3390/inventions5040059
Chicago/Turabian StyleKhojasteh, Hasanali, Younes Noorollahi, Mojtaba Tahani, and Mehran Masdari. 2020. "Optimization of Power and Levelized Cost for Shrouded Small Wind Turbine" Inventions 5, no. 4: 59. https://doi.org/10.3390/inventions5040059
APA StyleKhojasteh, H., Noorollahi, Y., Tahani, M., & Masdari, M. (2020). Optimization of Power and Levelized Cost for Shrouded Small Wind Turbine. Inventions, 5(4), 59. https://doi.org/10.3390/inventions5040059






