The Impact of Cattaneo–Christov Double Diffusion on Oldroyd-B Fluid Flow over a Stretching Sheet with Thermophoretic Particle Deposition and Relaxation Chemical Reaction
Abstract
:1. Introduction
2. Mathematical Formulation
Numerical Procedure
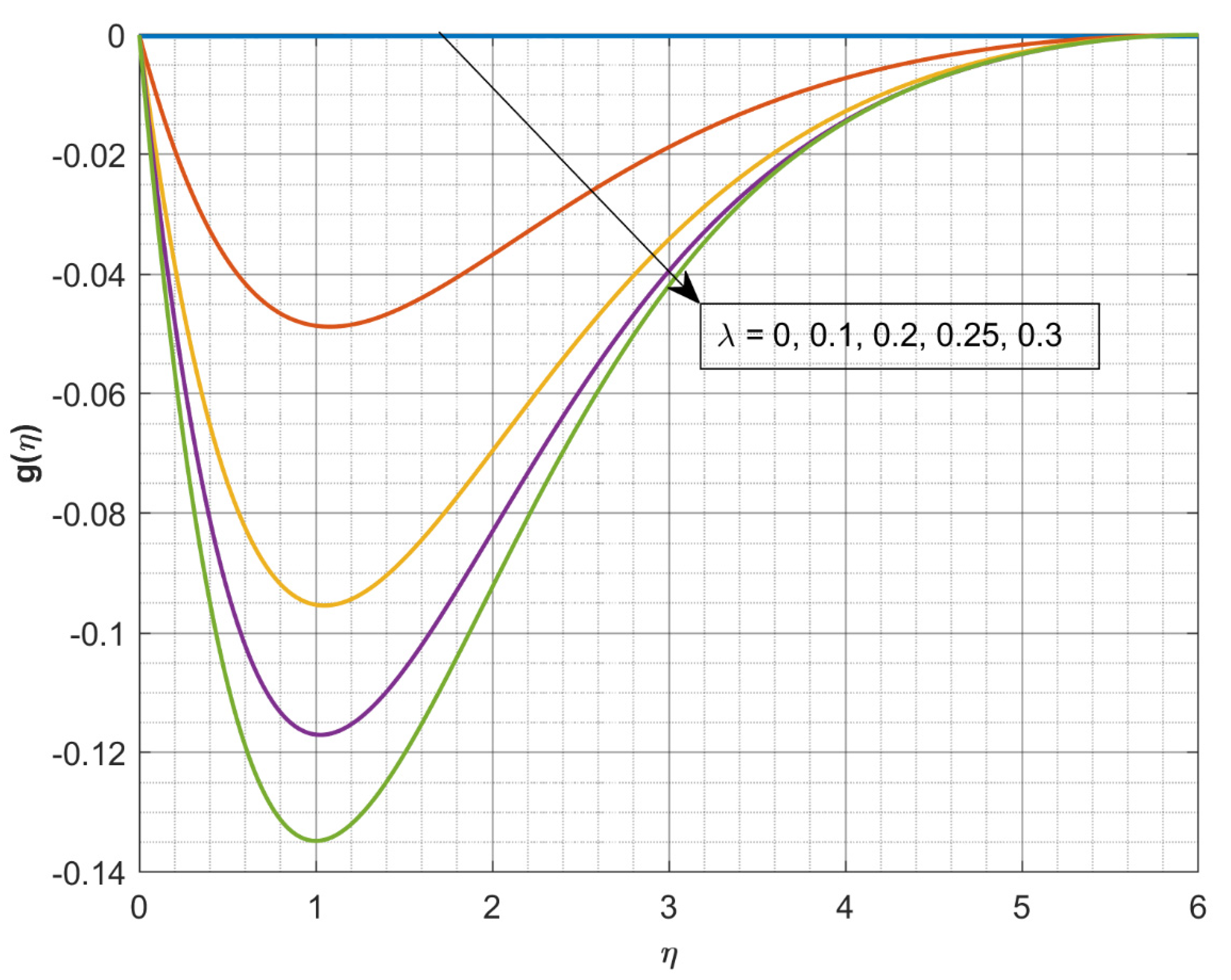
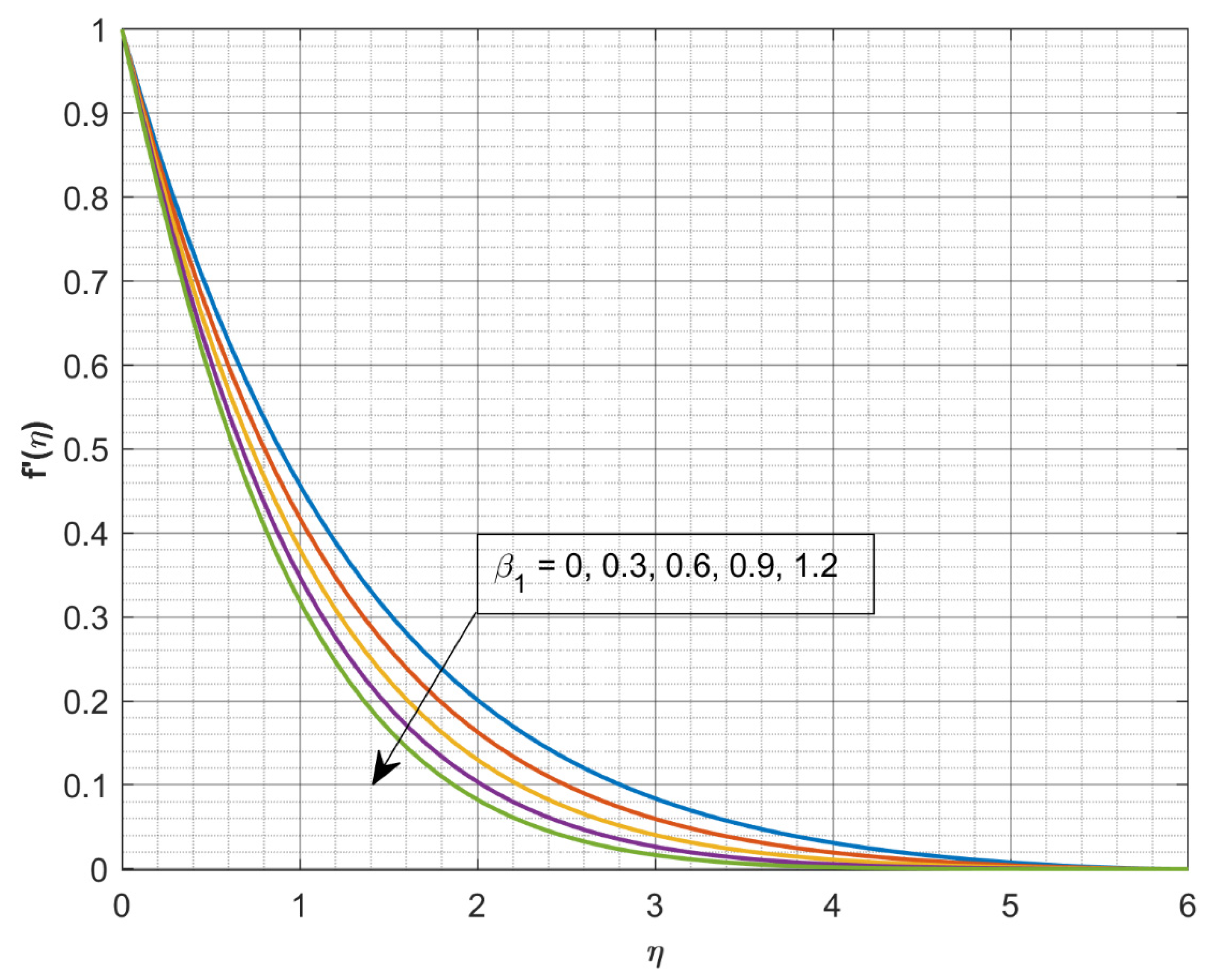
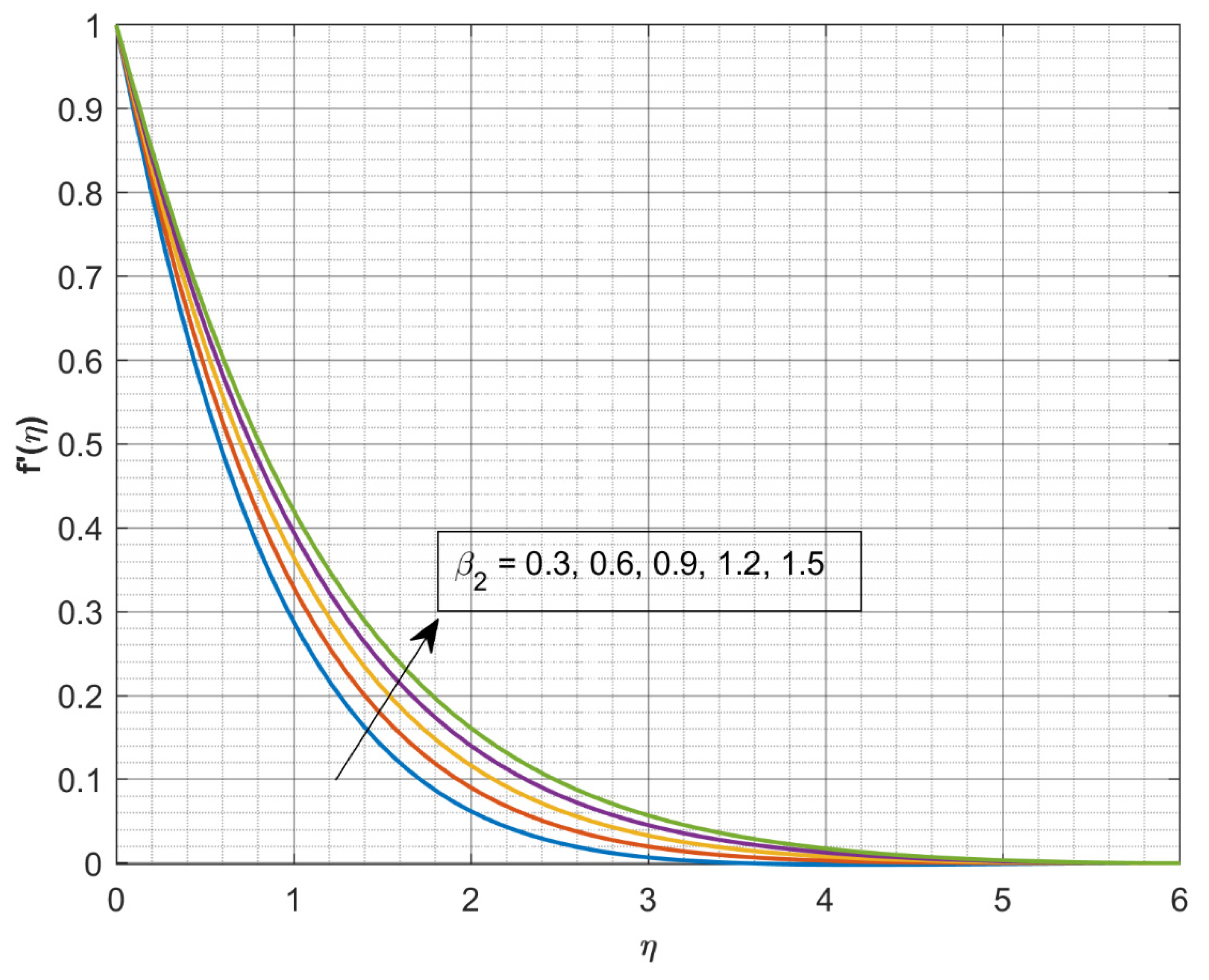
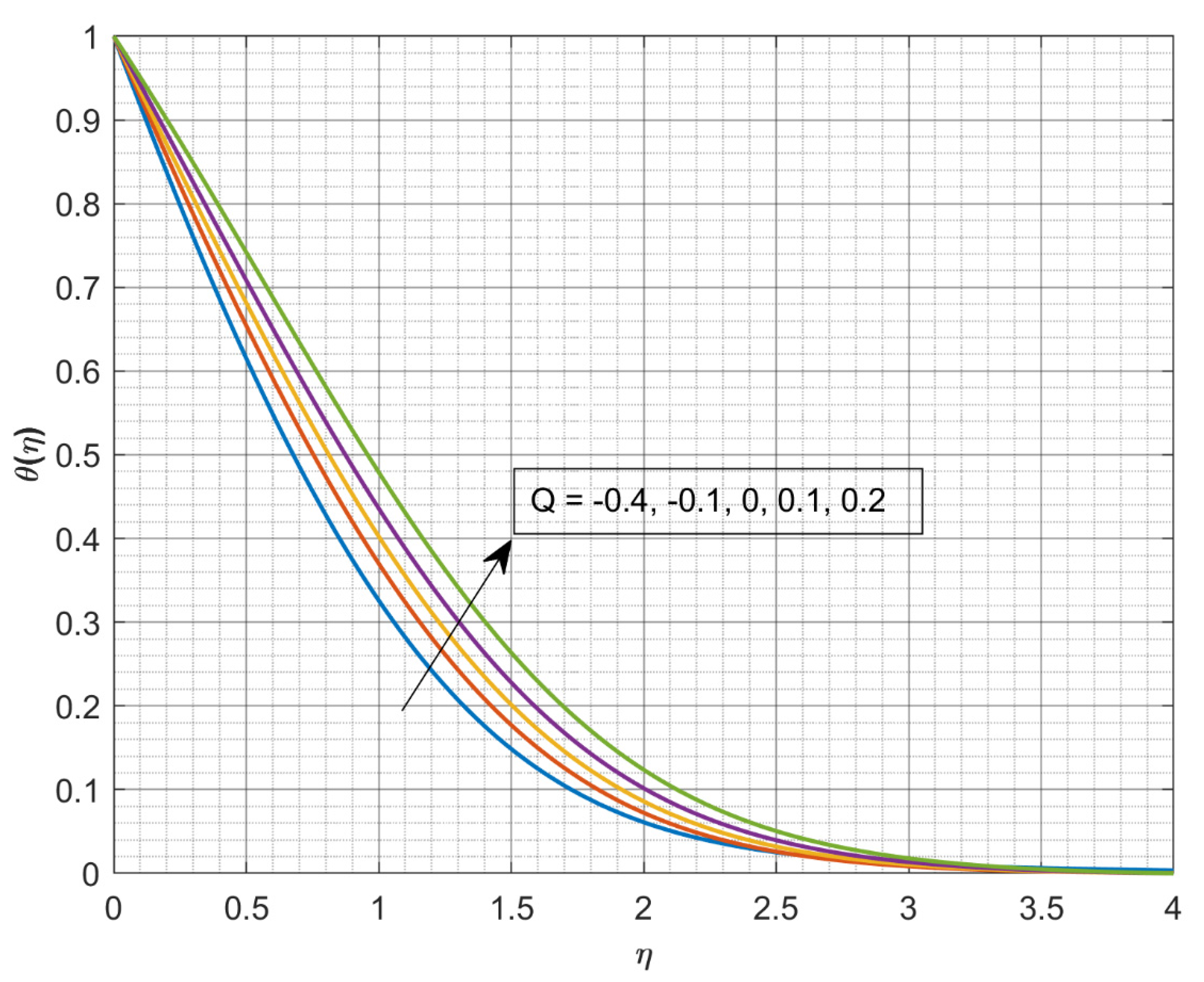
3. Results and Discussion
4. Conclusions
- ❖
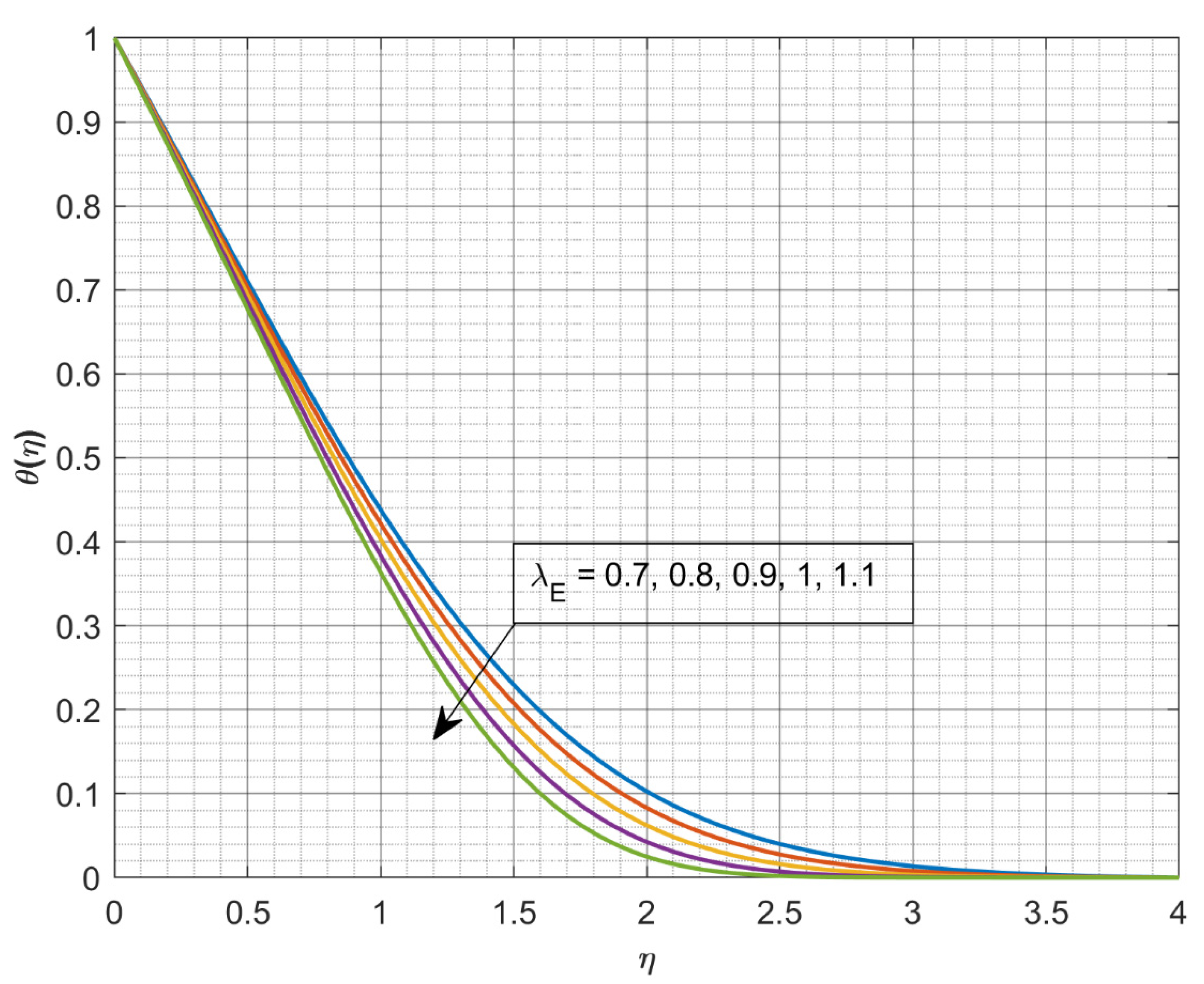
- The rise in values of declines and .
- ❖
- The increasing values of declines , but a converse trend is seen for enhanced values.
- ❖
- The rising values of improve .
- ❖
- The rising values of reduces .
- ❖
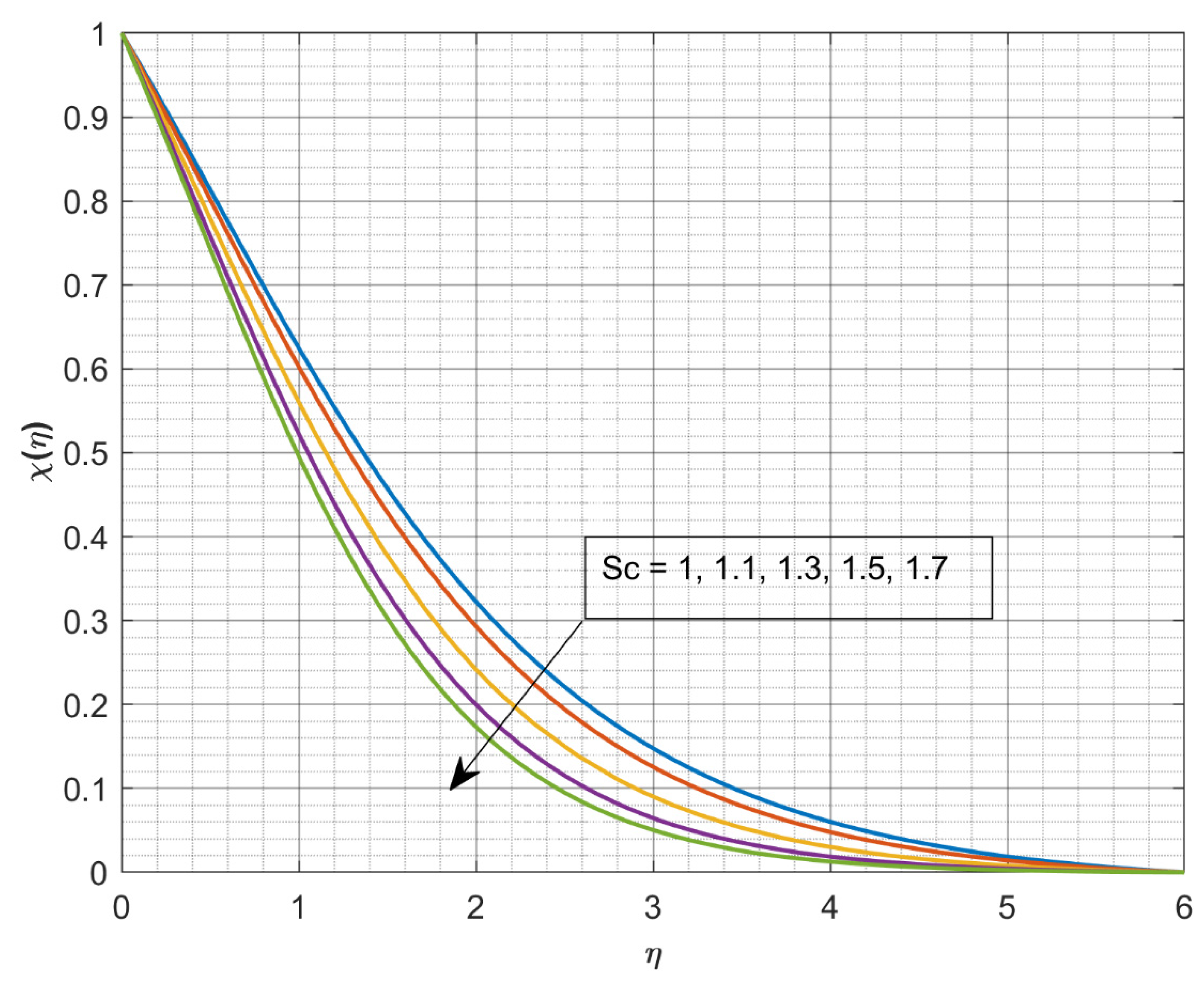
- The escalating values of and declines .
- ❖
- The increasing values of declines , but a reverse trend is seen for enhanced values.
- ❖
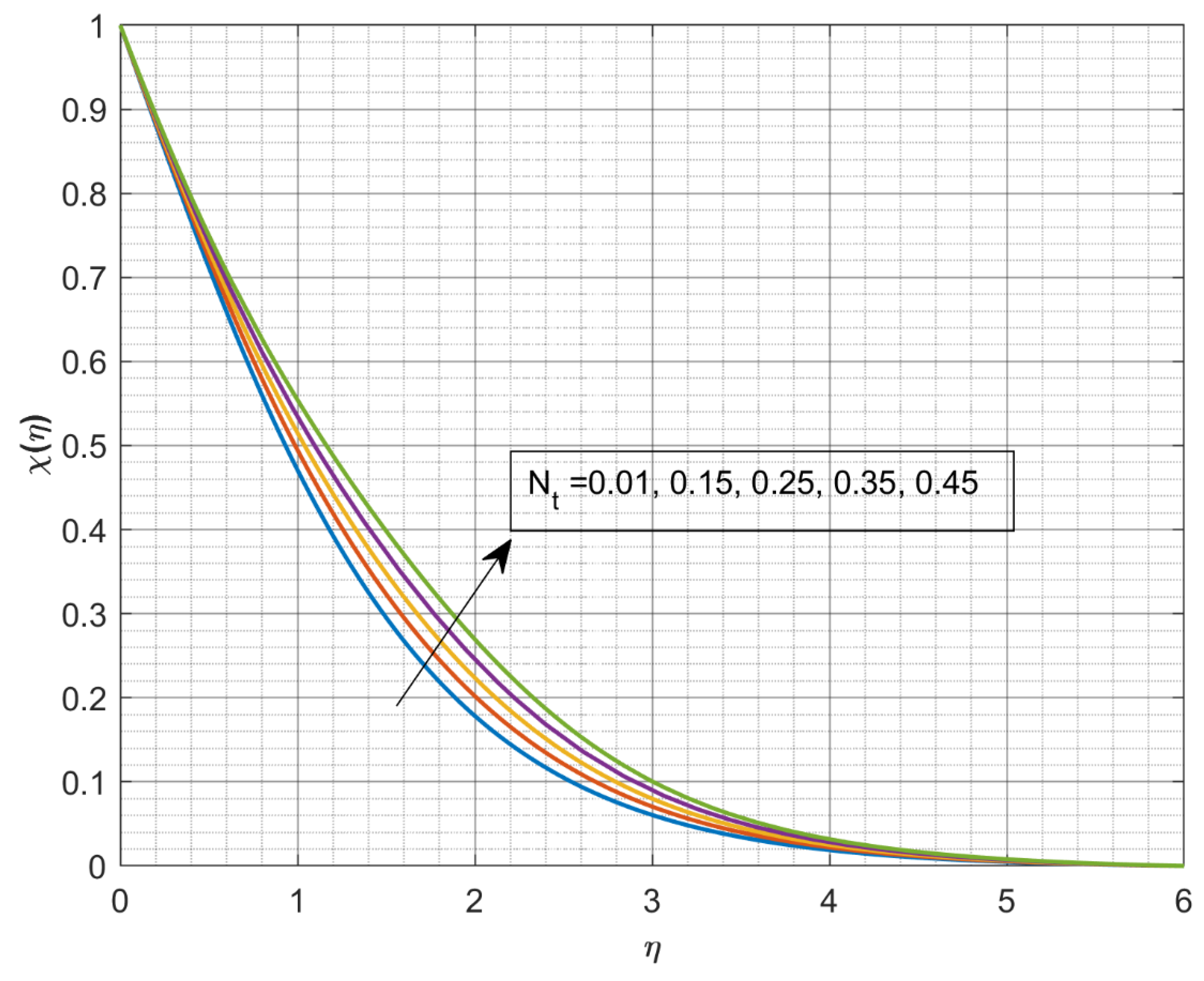
- The rise in values of and declines , but the opposite trend is detected for upward values of ,, and .
- ❖
- The growth in values of ,, and declines , but the conflicting trend is detected for upward values of .
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| velocity components | |
| directions | |
| density | |
| dynamic viscosity | |
| relaxation time | |
| ambient temperature | |
| relaxation time for mass flux | |
| reaction rate | |
| diffusion coefficient | |
| kinematic viscosity | |
| heat source/sink parameter | |
| wall concentration | |
| thermophoretic velocity | |
| similarity variable | |
| dimensionless concentration profile. | |
| rotation parameter | |
| relaxation time parameter of temperature | |
| Schmidt number | |
| thermophoretic parameter | |
| positive constant | |
| angular velocity | |
| retardation time | |
| specific heat | |
| thermal conductivity | |
| concentration | |
| Deborah number for retardation time | |
| heat source/sink coefficient | |
| temperature | |
| wall temperature | |
| thermophoretic coefficient | |
| reference temperature | |
| ambient concentration | |
| dimensionless velocity profiles | |
| dimensionless thermal profile | |
| relaxation time for heat flux | |
| Deborah number for relaxation time | |
| relaxation time parameter of concentration | |
| Prandtl number | |
| chemical reaction rate parameter |
References
- Irfan, M.; Khan, M.; Khan, W.; Alghamdi, M.; Ullah, M.Z. Influence of thermal-solutal stratifications and thermal aspects of non-linear radiation in stagnation point Oldroyd-B nanofluid flow. Int. Commun. Heat Mass Transf. 2020, 116, 104636. [Google Scholar] [CrossRef]
- Reddy, G.K.; Yarrakula, K.; Raju, C.S.K.; Rahbari, A. Mixed convection analysis of variable heat source/sink on MHD Maxwell, Jeffrey, and Oldroyd-B nanofluids over a cone with convective conditions using Buongiorno’s model. J. Therm. Anal. Calorim. 2018, 132, 1995–2002. [Google Scholar] [CrossRef]
- Almakki, M.; Nandy, S.K.; Mondal, S.; Sibanda, P.; Sibanda, D. A model for entropy generation in stagnation-point flow of non-Newtonian Jeffrey, Maxwell, and Oldroyd-B nanofluids. Heat Transf.-Asian Res. 2019, 48, 24–41. [Google Scholar] [CrossRef] [Green Version]
- Ramzan, M.; Howari, F.; Chung, J.D.; Kadry, S.; Chu, Y.-M. Irreversibility minimization analysis of ferromagnetic Oldroyd-B nanofluid flow under the influence of a magnetic dipole. Sci. Rep. 2021, 11, 1–19. [Google Scholar] [CrossRef]
- Sarada, K.; Gowda, R.; Sarris, I.; Kumar, R.; Prasannakumara, B. Effect of Magnetohydrodynamics on Heat Transfer Behaviour of a Non-Newtonian Fluid Flow over a Stretching Sheet under Local Thermal Non-Equilibrium Condition. Fluids 2021, 6, 264. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Shehzad, S.A.; Alsaedi, A. Chemical reaction and heat generation/absorption aspects in flow of Walters-B nanofluid with Cattaneo-Christov double-diffusion. Results Phys. 2017, 7, 4145–4152. [Google Scholar] [CrossRef]
- Gireesha, B.J.; Shankaralingappa, B.M.; Prasannakumar, B.C.; Nagaraja, B. MHD flow and melting heat transfer of dusty Casson fluid over a stretching sheet with Cattaneo–Christov heat flux model. Int. J. Ambient. Energy 2020, 1–9. [Google Scholar] [CrossRef]
- Sowmya, G.; Saleh, B.; Gowda, R.J.P.; Kumar, R.N.; Radhika, M. Analysis of radiative nonlinear heat transfer in a convective flow of dusty fluid by capitalizing a non-Fourier heat flux model. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2021, 09544089211041192. [Google Scholar] [CrossRef]
- Prasannakumara, B. Numerical simulation of heat transport in Maxwell nanofluid flow over a stretching sheet considering magnetic dipole effect. Partial. Differ. Equ. Appl. Math. 2021, 4, 100064. [Google Scholar] [CrossRef]
- Gowda, R.J.P.; Rauf, A.; Kumar, R.N.; Prasannakumara, B.C.; Shehzad, S.A. Slip flow of Casson–Maxwell nanofluid confined through stretchable disks. Indian J. Phys. 2021, 1–9. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Alsaedi, A.; Ahmad, B. Magnetohydrodynamic (MHD) nonlinear convective flow of Walters-B nanofluid over a nonlinear stretching sheet with variable thickness. Int. J. Heat Mass Transf. 2017, 110, 506–514. [Google Scholar] [CrossRef]
- Prasannakumara, B.C. Assessment of the local thermal non-equilibrium condition for nanofluid flow through porous media: A comparative analysis. Indian J. Phys. 2021, 1–9. [Google Scholar] [CrossRef]
- Christopher, A.J.; Magesh, N.; Gowda, R.J.P.; Kumar, R.N.; Kumar, R.S.V. Hybrid nanofluid flow over a stretched cylinder with the impact of homogeneous–heterogeneous reactions and Cattaneo–Christov heat flux: Series solution and numerical simulation. Heat Transf. 2021, 50, 3800–3821. [Google Scholar] [CrossRef]
- Gowda, R.J.P.; Jyothi, A.M.; Kumar, R.N.; Prasannakumara, B.C.; Sarris, I.E. Convective Flow of Second Grade Fluid Over a Curved Stretching Sheet with Dufour and Soret Effects. Int. J. Appl. Comput. Math. 2021, 7, 1–16. [Google Scholar] [CrossRef]
- Alhadhrami, A.; Vishalakshi, C.; Prasanna, B.; Sreenivasa, B.; Alzahrani, H.A.; Gowda, R.P.; Kumar, R.N. Numerical simulation of local thermal non-equilibrium effects on the flow and heat transfer of non-Newtonian Casson fluid in a porous media. Case Stud. Therm. Eng. 2021, 28, 101483. [Google Scholar] [CrossRef]
- Ali, B.; Hussain, S.; Shafique, M.; Habib, D.; Rasool, G. Analyzing the interaction of hybrid base liquid C2H6O2–H2O with hybrid nano-material Ag–MoS2 for unsteady rotational flow referred to an elongated surface using modified Buongiorno’s model: FEM simulation. Math. Comput. Simul. 2021, 190, 57–74. [Google Scholar] [CrossRef]
- Ali, B.; Naqvi, R.A.; Hussain, D.; Aldossary, O.M.; Hussain, S. Magnetic Rotating Flow of a Hybrid Nano-Materials Ag-MoS2 and Go-MoS2 in C2H6O2-H2O Hybrid Base Fluid over an Extending Surface Involving Activation Energy: FE Simulation. Mathematics 2020, 8, 1730. [Google Scholar] [CrossRef]
- Ali, B.; Shafiq, A.; Siddique, I.; Al-Mdallal, Q.; Jarad, F. Significance of suction/injection, gravity modulation, thermal radiation, and magnetohydrodynamic on dynamics of micropolar fluid subject to an inclined sheet via finite element approach. Case Stud. Therm. Eng. 2021, 28, 101537. [Google Scholar] [CrossRef]
- Ali, B.; Thumma, T.; Habib, D.; Salamat, N.; Riaz, S. Finite element analysis on transient MHD 3D rotating flow of Maxwell and tangent hyperbolic nanofluid past a bidirectional stretching sheet with Cattaneo Christov heat flux model. Therm. Sci. Eng. Prog. 2021, 101089. [Google Scholar] [CrossRef]
- Ali, B.; Siddique, I.; Ahmadian, A.; Senu, N.; Ali, L.; Haider, A. Significance of Lorentz and Coriolis forces on dynamics of water based silver tiny particles via finite element simulation. Ain Shams Eng. J. 2021. [Google Scholar] [CrossRef]
- Iasiello, M.; Vafai, K.; Andreozzi, A.; Bianco, N. Hypo- and hyperthermia effects on ldl deposition in a curved artery. Comput. Therm. Sci. Int. J. 2019, 11, 95–103. [Google Scholar] [CrossRef]
- Iasiello, M.; Vafai, K.; Andreozzi, A.; Bianco, N.; Tavakkoli, F. Effects of External and Internal Hyperthermia on LDL Transport and Accumulation Within an Arterial Wall in the Presence of a Stenosis. Ann. Biomed. Eng. 2015, 43, 1585–1599. [Google Scholar] [CrossRef]
- Iasiello, M.; Vafai, K.; Andreozzi, A.; Bianco, N. Low-density lipoprotein transport through an arterial wall under hyperthermia and hypertension conditions—An analytical solution. J. Biomech. 2016, 49, 193–204. [Google Scholar] [CrossRef]
- RamReddy, C.; Murthy, P.; Chamkha, A.J.; Rashad, A. Soret effect on mixed convection flow in a nanofluid under convective boundary condition. Int. J. Heat Mass Transf. 2013, 64, 384–392. [Google Scholar] [CrossRef]
- Ho, C.; Chen, D.-S.; Yan, W.-M.; Mahian, O. Buoyancy-driven flow of nanofluids in a cavity considering the Ludwig–Soret effect and sedimentation: Numerical study and experimental validation. Int. J. Heat Mass Transf. 2014, 77, 684–694. [Google Scholar] [CrossRef]
- Kim, J.; Kang, Y.T.; Choi, C.K. Soret and Dufour effects on convective instabilities in binary nanofluids for absorption application. Int. J. Refrig. 2007, 30, 323–328. [Google Scholar] [CrossRef]
- Manjunatha, P.; Gowda, R.P.; Kumar, R.N.; Suresha, S.; Sarwe, D.U. Numerical simulation of carbon nanotubes nanofluid flow over vertically moving disk with rotation. Partial. Differ. Equ. Appl. Math. 2021, 4, 100124. [Google Scholar] [CrossRef]
- Gkountas, A.A.; Benos, L.T.; Sofiadis, G.N.; Sarris, I.E. A printed-circuit heat exchanger consideration by exploiting an Al2O3-water nanofluid: Effect of the nanoparticles interfacial layer on heat transfer. Therm. Sci. Eng. Prog. 2021, 22, 100818. [Google Scholar] [CrossRef]
- Wang, F.; Asjad, M.I.; Zahid, M.; Iqbal, A.; Ahmad, H.; Alsulami, M. Unsteady thermal transport flow of Casson nanofluids with generalized Mittag–Leffler kernel of Prabhakar’s type. J. Mater. Res. Technol. 2021, 14, 1292–1300. [Google Scholar] [CrossRef]
- Kumar, R.N.; Mallikarjuna, H.B.; Tigalappa, N.; Gowda, R.J.P.; Sarwe, D.U. Carbon nanotubes suspended dusty nanofluid flow over stretching porous rotating disk with non-uniform heat source/sink. Int. J. Comput. Methods Eng. Sci. Mech. 2021, 1–10. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Mabood, F.; Rauf, A.; Tlili, I. Forced convective Maxwell fluid flow through rotating disk under the thermo-phoretic particles motion. Int. Commun. Heat Mass Transf. 2020, 116, 104693. [Google Scholar] [CrossRef]
- Kumar, R.N.; Jyothi, A.; Alhumade, H.; Gowda, R.P.; Alam, M.M.; Ahmad, I.; Gorji, M.; Prasannakumara, B. Impact of magnetic dipole on thermophoretic particle deposition in the flow of Maxwell fluid over a stretching sheet. J. Mol. Liq. 2021, 334, 116494. [Google Scholar] [CrossRef]
- Kumar, R.N.; Gowda, R.J.P.; Madhukesh, J.K.; Prasannakumara, B.C.; Ramesh, G.K. Impact of thermophoretic particle deposition on heat and mass transfer across the dynamics of Casson fluid flow over a moving thin needle. Phys. Scr. 2021, 96, 075210. [Google Scholar] [CrossRef]
- Chen, S.-B.; Shahmir, N.; Ramzan, M.; Sun, Y.-L.; Aly, A.A.; Malik, M. Thermophoretic particle deposition in the flow of dual stratified Casson fluid with magnetic dipole and generalized Fourier’s and Fick’s laws. Case Stud. Therm. Eng. 2021, 26, 101186. [Google Scholar] [CrossRef]
- Alhadhrami, A.; Alzahrani, H.A.; Kumar, R.N.; Gowda, R.P.; Sarada, K.; Prasanna, B.; Madhukesh, J.; Madhukeshwara, N. Impact of thermophoretic particle deposition on Glauert wall jet slip flow of nanofluid. Case Stud. Therm. Eng. 2021, 28, 101404. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, B.; Bai, Y.; Cao, Y.; Shen, Y. Unsteady Cattaneo-Christov double diffusion of Oldroyd-B fluid thin film with relaxation-retardation viscous dissipation and relaxation chemical reaction. Powder Technol. 2018, 338, 975–982. [Google Scholar] [CrossRef]
- Mburu, Z.M.; Nayak, M.K.; Mondal, S.; Sibanda, P. Impact of irreversibility ratio and entropy generation on three-dimensional Oldroyd-B fluid flow with relaxation–retardation viscous dissipation. Indian J. Phys. 2021, 1–17. [Google Scholar] [CrossRef]
- Khan, M.I.; Khan, S.A.; Hayat, T.; Qayyum, S.; Alsaedi, A. Entropy generation analysis in MHD flow of viscous fluid by a curved stretching surface with cubic autocatalysis chemical reaction. Eur. Phys. J. Plus 2020, 135, 249. [Google Scholar] [CrossRef]
- Gowda, R.P.; Kumar, R.N.; Jyothi, A.; Prasannakumara, B.; Sarris, I. Impact of Binary Chemical Reaction and Activation Energy on Heat and Mass Transfer of Marangoni Driven Boundary Layer Flow of a Non-Newtonian Nanofluid. Processes 2021, 9, 702. [Google Scholar] [CrossRef]
- Yusuf, T.; Mabood, F.; Prasannakumara, B.; Sarris, I. Magneto-Bioconvection Flow of Williamson Nanofluid over an Inclined Plate with Gyrotactic Microorganisms and Entropy Generation. Fluids 2021, 6, 109. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Alsaedi, A.; Hayat, T.; Alhuthali, M.S. Three-Dimensional Flow of an Oldroyd-B Fluid with Variable Thermal Conductivity and Heat Generation/Absorption. PLoS ONE 2013, 8, e78240. [Google Scholar] [CrossRef] [Green Version]
- Khan, W.; Irfan, M.; Khan, M. An improved heat conduction and mass diffusion models for rotating flow of an Oldroyd-B fluid. Results Phys. 2017, 7, 3583–3589. [Google Scholar] [CrossRef]
- Khan, M.I.; Rashid, S.; Hayat, T.; Ayub, M.; Alsaedi, A. Magnetic effects in rotating flow of an Oldroyd-B fluid with chemical reaction and convective surface. Indian J. Phys. 2019, 94, 1361–1367. [Google Scholar] [CrossRef]
- Shehzad, S.; Alsaedi, A.; Hayat, T.; Alhuthali, M. Thermophoresis particle deposition in mixed convection three-dimensional radiative flow of an Oldroyd-B fluid. J. Taiwan Inst. Chem. Eng. 2014, 45, 787–794. [Google Scholar] [CrossRef]
- Batchelor, G.; Shen, C. Thermophoretic deposition of particles in gas flowing over cold surfaces. J. Colloid Interface Sci. 1985, 107, 21–37. [Google Scholar] [CrossRef] [Green Version]
- Talbot, L.; Cheng, R.K.; Schefer, R.W.; Willis, D.R. Thermophoresis of particles in a heated boundary layer. J. Fluid Mech. 1980, 101, 737–758. [Google Scholar] [CrossRef] [Green Version]
- Abel, M.S.; Tawade, J.V.; Nandeppanavar, M.M. MHD flow and heat transfer for the upper-convected Maxwell fluid over a stretching sheet. Meccanica 2012, 47, 385–393. [Google Scholar] [CrossRef]
- Megahed, A.M. Variable fluid properties and variable heat flux effects on the flow and heat transfer in a non-Newtonian Maxwell fluid over an unsteady stretching sheet with slip velocity. Chin. Phys. B 2013, 22, 484–489. [Google Scholar] [CrossRef]
- Sadeghy, K.; Hajibeygi, H.; Taghavi, S.M. Stagnation-point flow of upper-convected Maxwell fluids. Int. J. Non-Linear Mech. 2006, 41, 1242–1247. [Google Scholar] [CrossRef]
- Mustafa, M.; Hayat, T.; Alsaedi, A. Rotating flow of Maxwell fluid with variable thermal conductivity: An application to non-Fourier heat flux theory. Int. J. Heat Mass Transf. 2017, 106, 142–148. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Wang, C.Y. Free Convection on a Vertical Stretching Surface. ZAMM 1989, 69, 418–420. [Google Scholar] [CrossRef]
- Gorla, R.S.R.; Sidawi, I. Free convection on a vertical stretching surface with suction and blowing. Flow Turbul. Combust. 1994, 52, 247–257. [Google Scholar] [CrossRef]



| 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.2 | |
|---|---|---|---|---|---|---|
| Abel et al. [47] | 0.999996 | 1.051948 | 1.101850 | 1.150163 | 1.196692 | 1.285257 |
| Megahed [48] | 0.999978 | 1.051945 | 1.101848 | 1.150160 | 1.196690 | 1.285253 |
| Sadeghy et al. [49] | 1.00000 | 1.05490 | 1.10084 | 1.15016 | 1.19872 | ---------- |
| Mustafa et al. [50] | 1.000000 | 1.051890 | 1.101903 | 1.150137 | 1.196711 | 1.285363 |
| Khan et al. [42] | 1.000000 | 1.051889 | 1.101903 | 1.150137 | 1.196711 | 1.285363 |
| Present results | 1.000000 | 1.051890 | 1.101903 | 1.150137 | 1.196711 | 1.285363 |
| 0.7 | 2.0 | 7.0 | |
|---|---|---|---|
| Khan and Pop [51] | 0.4539 | 0.9113 | 1.8954 |
| Wang [52] | 0.4539 | 0.9114 | 1.8954 |
| Gorla and Sidawi [53] | 0.4539 | 0.9114 | 1.8954 |
| Khan et al. [42] | 0.454374 | 0.911155 | 1.822020 |
| Present results | 0.454369 | 0.911148 | 1.822015 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shankaralingappa, B.M.; Prasannakumara, B.C.; Gireesha, B.J.; Sarris, I.E. The Impact of Cattaneo–Christov Double Diffusion on Oldroyd-B Fluid Flow over a Stretching Sheet with Thermophoretic Particle Deposition and Relaxation Chemical Reaction. Inventions 2021, 6, 95. https://doi.org/10.3390/inventions6040095
Shankaralingappa BM, Prasannakumara BC, Gireesha BJ, Sarris IE. The Impact of Cattaneo–Christov Double Diffusion on Oldroyd-B Fluid Flow over a Stretching Sheet with Thermophoretic Particle Deposition and Relaxation Chemical Reaction. Inventions. 2021; 6(4):95. https://doi.org/10.3390/inventions6040095
Chicago/Turabian StyleShankaralingappa, Bheemasandra M., Ballajja C. Prasannakumara, Bijjanal J. Gireesha, and Ioannis E. Sarris. 2021. "The Impact of Cattaneo–Christov Double Diffusion on Oldroyd-B Fluid Flow over a Stretching Sheet with Thermophoretic Particle Deposition and Relaxation Chemical Reaction" Inventions 6, no. 4: 95. https://doi.org/10.3390/inventions6040095
APA StyleShankaralingappa, B. M., Prasannakumara, B. C., Gireesha, B. J., & Sarris, I. E. (2021). The Impact of Cattaneo–Christov Double Diffusion on Oldroyd-B Fluid Flow over a Stretching Sheet with Thermophoretic Particle Deposition and Relaxation Chemical Reaction. Inventions, 6(4), 95. https://doi.org/10.3390/inventions6040095







