An Investigation on the Vortex Effect of a CALM Buoy under Water Waves Using Computational Fluid Dynamics (CFD)

Abstract

Floating offshore structures (FOS) must be designed to be stable, to float, and to be able to support other structures for which they were designed. These FOS are needed for different transfer operations in oil terminals. However, water waves affect the motion response of floating buoys. Under normal sea states, the free-floating buoy presents stable periodic responses. However, when moored, they are kept in position. Mooring configurations used to moor buoys in single point mooring (SPM) terminals could require systems such as Catenary Anchor Leg Moorings (CALM) and Single Anchor Leg Moorings (SALM). The CALM buoys are one of the most commonly-utilised type of offshore loading terminal. Due to the wider application of CALM buoy systems, it is necessary to investigate the fluid structure interaction (FSI) and vortex effect on the buoy. In this study, a numerical investigation is presented on a CALM buoy model conducted using Computational Fluid Dynamics (CFD) in ANSYS Fluent version R2 2020. Some hydrodynamic definitions and governing equations were presented to introduce the model. The results presented visualize and evaluate specific motion characteristics of the CALM buoy with emphasis on the vortex effect. The results of the CFD study present a better understanding of the hydrodynamic parameters, reaction characteristics and fluid-structure interaction under random waves.

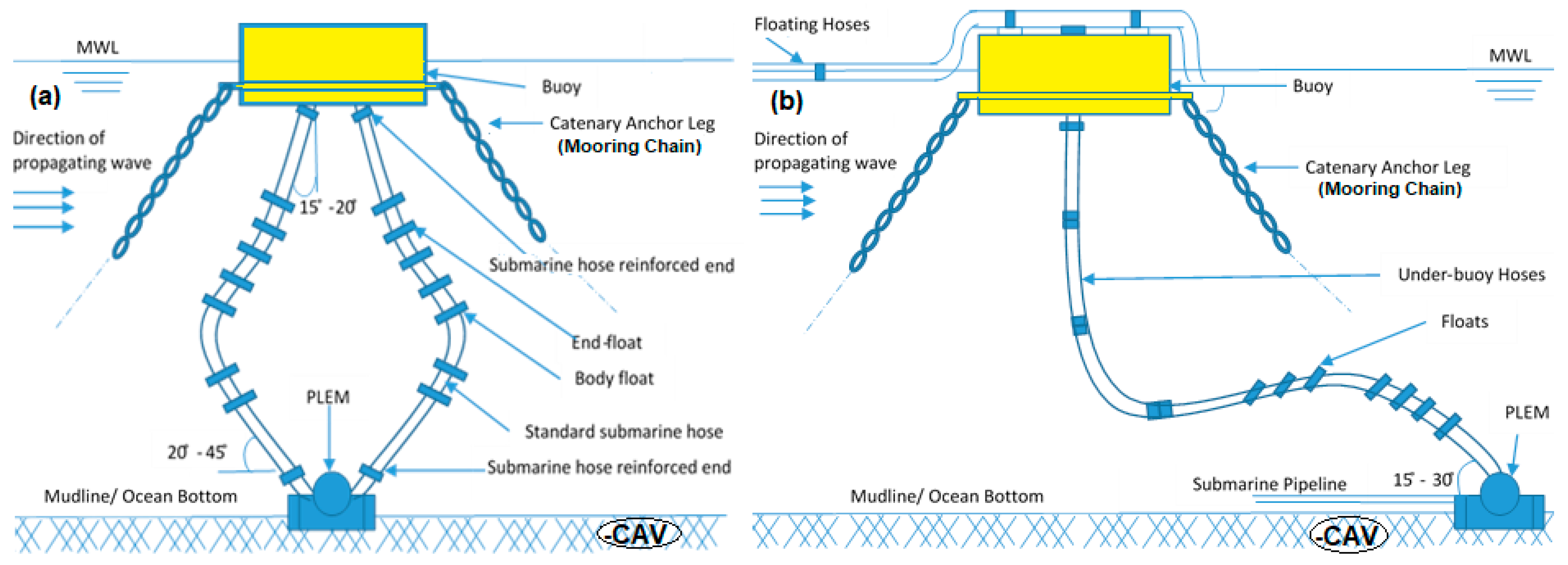
1. Introduction

In recent times, the most commonly-utilised type of offshore loading terminal is the Catenary Anchor-Leg Mooring (CALM). The CALM buoy is a floating buoy with catenary chain legs secured to anchors or piles that anchor it to the bottom, and the buoy also has attached marine hoses [1,2,3,4,5]. As a result of sheer limited inertia of the CALM buoys, mooring line reactions are extremely sensitive to waves, posing a significant wear risk to the mooring lines. Extreme waves can even cause mooring lines to break and affect the behaviour of marine hoses as reported in some CALM buoy system failures [6,7,8,9]. As a result, studying the motions of the CALM buoy in mild, squall and severe wave conditions is extremely important [10,11,12,13], as they also influence hose mechanics [14,15,16,17,18,19]. Over the years, there has been a number of motion response phenomena of floating CALM buoys, however, there are limited computational fluid dynamics (CFD) investigations presented. Different questions have been answered on marine riser mechanics [20,21,22], CALM buoy dynamics [23,24,25,26,27] and CALM buoy motion stability [28,29,30,31], but few works addressed other issues that encompass the motion response of CALM buoy in CFD, moored aspects of single point mooring (SPM) systems, flow vorticity, pressure distribution on CALM buoy, velocity impact on CALM buoy, and vortex-induced motion (VIM) on CALM buoys or similar floating offshore structures (FOS). The sketch the (un)loading operation on a CALM buoy with wave forces and boundary conditions and configured as (a) Chinese-lantern and (b) Lazy-S configurations in Figure 1. It shows the hose-string was attached at an end (named ‘End A’) under the buoy while the second end (named ‘End B’) connected unto the Pipeline End Manifold (PLEM).

In some recent studies [32,33,34,35], coupled simulations of a CALM buoy using a CFD-FEM model for wave-induced motion (WIM), whereby the mooring system’s FEM model is linked to the CALM buoy CFD model, and the Level-set method is utilised to simulate waves and free surface effects. The authors made use of MOORING3D in conjunction with a motion solver with 6 degrees of freedom (6DoFs). The CFD module calculated the hydrodynamic loading on the moored buoy, using the large eddy simulation (LES) applied on the turbulence model with the Finite-Analytic Navier-Stokes (FANS) code. They concluded that the WIM of the buoy is dominated by inertial and viscous effects of the hull, and that the results of coupled study on free-decay and wave-induced motions match well with model testing. In a similar study, Toxopeus et al. [36] conducted some CFD simulations under waves and calm water using a self-propelled free running 5415M ship model and presented some motion response distributions. Bandringa et al. [37] presented a CFD investigation which was validated using a linked CFD—dynamic mooring model for simulating the behaviour of a shallow water CALM buoy in extreme waves. In their study, a Navier-Stokes based finite-volume, VoF (volume of fluid) CFD solver was coupled with a dynamic mooring model to simulate an interactively moving CALM buoy in a horizontal mooring system. The CFD results were compared to model tests conducted during a ComFLOW-2 joint industry project (JIP) in MARIN’s shallow-water basin, and the authors concluded that the validation study focuses on accurately predicting the CALM buoy’s coupled responses in extreme, regular shallow-water waves. In addition, they opined that the CFD simulations in which the mooring system is represented by a linearly equivalent spring matrix, including cross terms, are offered as an alternative to simulations with a fully connected dynamic mooring setup. In another JIP called EXPRO-CFD EU FP5 project reported by Woodburn et al. [38,39], some predictions were conducting by utilizing results from a commercial CFD software with existing hydromechanics tools to forecast the response of floating structures in waves and currents, including viscous effects for the response of CALM buoys in waves. The dynamics of the floating structure, its moorings, and risers are modelled using the AQWA-NAUT platform, and CFD delivers the whole set of hydrodynamic forces and moments at each time step in the simulated motion. The CALM buoy has a 23 m diameter and a 2 m broad skirt attached 1m above the keel; the effects of flow separation off this skirt and the related viscous damping on the buoy’s motions were predicted to be considerable, especially around its natural period. Further experiments showed that the flaw in the potential flow technique appeared within the formulated extra viscous damping rather than the drag coefficient model values. Bunnik et al. [40] covered experimental work conducted to obtain insight into the tension variations in the mooring lines and export risers of a CALM buoy through a series of model studies. The tests were conducted on a model with on-linearities in the wave forces on the buoy, such as those caused by the presence of the skirt, were investigated via captive experiments in regular and irregular waves. The authors opined that to establish the dampening of the buoy’s oscillations and acquire the natural periods, decay tests were necessary as well as the mooring system’s dynamics, and the consequent dampening which has substantial impact on the buoy’s motions. Different CFD studies include validation studies on CALM buoys presented by various researchers [41,42,43], application using different CFD modelling methods for fluid studies [44,45,46] and coupled models [46,47,48]. Figure 2 shows a typical CALM buoy in the Baltic Sea offshore Lithuania installed by SOFEC [49].

In this study, a numerical investigation is presented on a CALM buoy model conducted using CFD in ANSYS Fluent version R2 2020. The aim of the research is to investigate the vortex effect of water waves on the CALM buoy. Section 1 presents some background on the research while Section 2 presents some governing equations and theoretical models. Section 3 presents the numerical model for the CFD study while Section 4 presents the results with some discussion. Section 5 presents the concluding remarks on the study.

2. Theoretical Model

The theories on the hydrodynamics and statics for CALM buoy with attached hoses is presented in this section.

2.1. Motion Forces, Drag and Damping Formulation

The formulation for the drag and damping of the buoy is based on some assumptions.

2.1.1. Buoy Model Assumptions

To achieve this, the following model assumptions are considered in this study:

• The body of the CALM buoy model is cylindrically shaped;
• The buoy has a circular skirt attached to it;
• The skirt is made from solid plates with thin thickness;
• The skirt is devoid of perforations, except where fairleads or mooring lines are attached;
• Viscous contributions of damping from skin friction can be neglected;
• It is assumed that the linear radiation-diffraction computations can be utilised to obtain the CALM buoy’s damping and added masses in the following: linear heave, linear surge, and linear pitch;
• It is assumed that the drag loads on the CALM buoy’s bilges are very small;
• It is assumed that the drag loads on the CALM buoy’s skirt can influence the quadratic pitch and heave damping contributions;
• The local fluid velocity around the skirt’s circumferential area utilised in computing these damping contributions. This is conducted by considering the CALM buoys’ velocity, but ignoring the flow’s disturbance due to the buoy’s presence and the wave orbital motions;
• It is assumed that the CALM buoy hull is positioned in X-Z axes, and subject to a flow direction;
• The buoy has 6 degrees of freedom (6DoFs) as illustrated in Figure 3. The buoy is considered typically as a single system, and as a floating buoy with a rigid body.

2.1.2. Added Mass & Damping Coefficients

The experimental investigation by Cozijn et al. [50,51] were conducted using forced oscillations for heave and pitch damping on CALM buoy. In that study, the loads in the 6-component force frame, as well as the motions of the CALM buoy model, were measured. The measured signals were subjected to a harmonic analysis, where the applied motion is used as the lead signal. The very first harmonic is the observed loads’ amplitudes and phase angles. The damping coefficient and the added mass coefficient were calculated using the CALM buoy’s motion. Figure 4 is the coordinate system of the CALM buoy hull.

Cozijn et al. [51] obtained the expressions for typical heave motion as given in Equations (1) and (2), where M denotes the dry mass of the CALM buoy model, C_zz denotes the heave hydrostatic restoring force coefficient, εF_z and F_z denote the measured heave force amplitude, and ω denotes the amplitude and frequency of the applied heave motion, and phase lag.

$$A_{zz}\left(\omega \right)=\frac{F_z.\cos \left(\epsilon F_z\right)-C_{zz}.z_a}{-\omega .z_a}-M$$

(1)

$$B_{zz}\left(\omega \right)=\frac{-F_z.\sin \left(\epsilon F_z\right)}{-\omega .z_a}$$

(2)

2.1.3. Load Computations on Buoy’s Skirt

The computation for the loads on the skirt are based on the CALM buoy’s geometry, as illustrated in Figure 5. It shows the diameter of the skirt, $D_S$, the diameter of the CALM buoy’s body, $D_B$, the tangential angle obtained from the skirt’s circumference, α.

Based on the assumption that the buoy is circular with a circular skirt section, the area of the skirt can be obtained using the following expression:

$$A_s=\frac{\pi }{4}.\left(D_S^2-D_B^2\right)$$

(3)

To obtain the radius of the buoy section, a representative skirt radius, $R_S$ is considered using Figure 5. This representatively provides an assumed definition to the position or locus where the application of the local drag loads is considered. Thus,

$$R_S=\frac{\left(D_S^{ }+D_B^{ }\right)}{4}$$

(4)

To obtain the width of the CALM buoy’skirt, the measurement is taken outer section of the skirt’s rim to the outer region of the buoy’s body, as expressed in Equation (5):

$$W_S=\frac{\left(D_S^{ }-D_B^{ }\right)}{2}$$

(5)

2.1.4. Viscous Damping Load Computations

A semi-empirical model including the drag term from Morison’s formulation is used to calculate the viscous contributions in the CALM buoy heave and pitch damping [51]. From the description provided on the CALM buoy, the skirt’s geometry and the load computation, it is possible to compute the load on a skirt segment. By bringing this force together using integration, the quadratic loads of heave and pitch damping are derived from the circumference of the skirt. The expression for the infinitesimally considered section of the skirt area where the local drag loads act, as provided in the literature [50,51], is:

$$dA=\frac{\left(D_S^{ 2 }-D_B^{ 2}\right)}{8}.d\alpha$$

(6)

It has been identified that the local velocity upon the skirt area, dA is a function of the velocities for the pitch (θ), roll (φ), and heave (z) motion, and which is computed using:

$$V\left(t,\alpha \right)=\dot{z}\left(t\right)+y\left(\alpha \right).\dot{\phi }\left(t\right)-x\left(\alpha \right).\dot{\theta }\left(t\right)$$

(7)

$$dF\left(t,\alpha \right)=-\frac{1}{2}.\rho .V\left(t,\alpha \right).\left|V\left(t,\alpha \right)\right|.C_D.dA$$

(8)

The value for $C_D$ is the only empirical parameter in Equation (8) for the model for which a suitable value should be chosen. Keulegan and Carpenter [52] discovered that when the flow is oscillatory, the $C_D$, the dimensionless drag coefficient, may be affected by the amplitude of the motion. Thus, the dimensionless KC number is frequently used to express the amplitude. In this study, it implies that the $C_D$’s value may be influenced by the motion amplitude of the skirt part in question, as model-tested in MARIN [50,51]. In summary, the drag loads on the CALM buoy skirt that have been examined are flow related. At a sharp edge, it is believed that separation and formation of eddies will occur. The $C_D$ value is independent of the Re value. The independence of the Re was also mentioned by Sarpkaya & O’Keefe [53] as a contribution in the instance of oscillating flow through sharp-edged plates.

2.1.5. Damping Computations on Buoy

The total frequency dependent damping is made up of a linear equivalent viscous term and a linear potential term when evaluating the CALM buoy damping in the frequency domain (FD). The quadratic drag loads on the skirt are represented by the viscous damping term [50,51]. As a corollary, it will be a dependent of the amplitude of the motion, as in Equation (9).

$$B_{ii}\left(\omega \right)=B_{ii,POT}\left(\omega \right)+B_{ii,VISC}\left(\omega \right)$$

(9)

For the heave damping, it is also assumed that the CALM buoy performs a harmonic motion, in the form given in Equation (10).

$$z\left(t\right)=z_a.\cos \omega t$$

(10)

For the pitch damping, the KC values considered in the literature [50,51], are given as:

$$KC=2\pi .\frac{z_a}{W_s}$$

(11)

$$KC=2\pi .\frac{R_s.{\theta }_a}{W_s}$$

(12)

2.1.6. Force Computations on Buoy

The forces that act on the buoy assume an irrotational motion and an ideal fluid and neglect the effect of viscosity; thus, they are calculated by the use of linear wave theory [54,55,56,57]. For small waves, the linearization of the dynamic free-surface boundary condition is assumed. For small buoys, an approximation can be carried out to determine the excitation force, while the diffracted wave is neglected [58]. However, for cylindrical shaped buoys, Froude-Krylov force can be calculated for its heave motion, as presented in Equation (13). In principle, Froude-Krylov force assumes an ideal flow, where the pressure field is undisturbed, by applying the linear airy wave theory.

$$f_{FK}^{heave}\left(\omega \right)=2\pi a\rho g\frac{J_1\left(ka\right)}{k}[(\frac{e^{-kd}}{1+e^{-2kh}})+(\frac{e^{kd}}{1+e^{2kh}})]$$

(13)

where a is the radius of the buoy, h is the water depth, d is the draft of the buoy, k is the wave number, $2\pi a$ is the circumference of the buoy, and J₁ is the first-order Bessel function.

The hydrostatic stiffness, F_h for a cylindrical buoy is given by Equation (14); where a is the radius of the buoy, g is the gravitational constant, and ${\epsilon }_b$ is a vector representing the translational degree of freedom of the buoy.

$$F_h=\rho g\pi a^2{\epsilon }_b$$

(14)

The heaving and swaying amplitude motions of the buoy is a factor of its slenderness ratio, as columnar buoys have lesser area around the water line than cylindrical buoys. This was given by the study by Jiang et al. [59] and Newman [60] on the heave inherent period of the buoy, given by Equation (15):

$$w_o=\surd (\frac{\rho g{A}_o}{M})$$

(15)

where w_o is the heave natural frequency of the buoy, ρ is seawater density, g is gravitational constant, M is the mass of the buoy and A_o is the waterline area of the buoy.

2.2. FSI Formulation & Governing Equations

The formulation for the fluid-structure interaction (FSI) and governing equations are presented in this section. The governing equations used in numerical modelling is based on applying Newton’s 2nd law of motion, Morison’s equation, hydrodynamic equations, Navier-Stokes equation and Continuity equation. Details on stability and motion equations exist in texts [61,62,63,64,65]. For irregular waves in the CFD model, the flow considered here is turbulent, thus we neglect the forces due to elasticity and the surface tension.

2.2.1. Newton’s 2nd Law of Motion

The Newton’s law of Equation is numerically presented in Equation (16), where the Newtonian Force, F is the external load of the system, Cv is the viscous damping, k is the spring constant, kx is the elastic force component and Ma is the inertia of the system. The Newtonian Force is given by the sum of the inertia force of the system, the viscous damping load and the elastic force components (also called the stiffness load of the system).

$$F=Ma+Cv+kx$$

(16)

2.2.2. Navier-Stokes Equations

The rule of Navier-Stokes Equations included here are for thermo-fluid incidents directed by these governing equations, based on the laws of conservation. The Navier-Stokes (N-S) equations is the broadly applied mathematical model to examine changes in those properties during dynamic interactions, thermal interactions, and fluidic motions. The Navier–Stokes equations assume that the fluid, at the scale of interest, is a continuum, in other words is not made up of discrete particles but rather a continuous substance. Hence, the Navier-Stokes equations consists of three (3) conservation laws: a time-dependent continuity equation for conservation of mass, three time-dependent conservation of momentum equations and a time-dependent conservation of energy equation.

For fluid that is considered incompressible and non-Newtonian, the Navier-Stokes Equations are applied [66,67]. The summation of the body force, pressure gradient and viscous force make up the fluid inertia. This is given in Equations (17)–(19), where P is the pressure, µ is the kinematic viscosity, F_x is the body force per unit mass in x-direction, F_y is the body force per unit mass in y-direction and F_z is the body force per unit mass in z-direction.

$$\left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}\right)=F_x-\frac{1}{\rho }\frac{\partial P}{\partial x}+\mu \left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}+\frac{{\partial }^{2}u}{\partial z^2}\right)$$

(17)

$$\left(\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}\right)=F_y-\frac{1}{\rho }\frac{\partial P}{\partial y}+\mu \left(\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}+\frac{{\partial }^{2}v}{\partial z^2}\right)$$

(18)

$$\left(\frac{\partial w}{\partial t}+u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z}\right)=F_z-\frac{1}{\rho }\frac{\partial P}{\partial z}+\mu \left(\frac{{\partial }^{2}w}{\partial x^2}+\frac{{\partial }^{2}w}{\partial y^2}+\frac{{\partial }^{2}w}{\partial z^2}\right)$$

(19)

Vortexes are basically formed as a result of instabilities generated from flow separations, as they travel through the hull. The flow is assumed to be incompressible; i.e., the energy of the vortexes are allowed to continuously increase or damp away, depending on the situation.

2.2.3. Continuity Equations

The Euler equation for incompressible flow is presented in Equation (20). In this paper, the CFD study was carried out for incompressible unsteady flow using continuity equations [67]. The dimensionless vector form of the continuity equations can be written as:

$$\frac{\partial \left\{u\right\}}{\partial t}+\left\{u\right\}.\nabla \left\{u\right\}+\left\{\nabla p\right\}-\frac{1}{R_e}{\nabla }^2\left\{u\right\}=0$$

(20)

The equations used in the formulation of finite volume method for incompressible and unsteady flow which is based on Navier Stokes and continuity equations, expresses nonlinear dimensionless parameters in Cartesian coordinate, as expressed in Equations (21) and (22).

$$\frac{\partial \Phi }{\partial t}+\Phi ·\nabla \Phi =\frac{1}{Re}{\nabla }^2\Phi -\nabla p$$

(21)

$$\nabla ·\Phi =0$$

(22)

where Φ is a non-dimensional velocity vector component, expressed in three directions; u, v and w. The Reynolds number ‘Re’ is expressed in terms of the flow incidence velocity U, the fluid viscosity v, and the cylinder diameter D, as given in Equation (23):

Re = UD/v

(23)

where the Reynold’s number Re is a measure of the flow velocity, the column diameter, and the kinematic viscosity of water.

However, mathematically, the expression for drag force is:

$$F_d=\frac{1}{2}\rho v^2{C}_{d}A$$

(24)

Therefore, the hydrodynamic drag in the X-direction is calculated as:

$$F_d=\frac{1}{2} \rho A{U}^2{C}_d$$

(25)

$$C_d= \frac{2F_d^i}{\rho A{U}^2}$$

(26)

However, considering the Keulegan Carpenter number, KC [51,52] which is given in Equation (26), as a function of the frequency of the oscillating wave f_w, vortex shedding and vortex induced motion (VIM) can be measured, thus the surface wave becomes an important parameter.

KC = U/f_wL

(27)

2.2.4. Morison’s Equations

Based on the forces on the risers, the Morison’s equation was used, as it considers the wave forces acting on a cylinder, due to the relative motion of body immersed in the fluid [68,69]. Thus, it yields the sum of the Froude-Kyrov force F_FK, the hydrodynamic force of the fluid, F_H, and the drag force, F_D. Morison’s equation is expressed in Equation (28):

$$F=\rho V\dot{u }+\rho C_{a}V\left(\dot{u}-\dot{v}\right)+\frac{1}{2}\rho C_{d}A\left(u-v\right)\left|u-v\right|$$

(28)

where V is the volume of the body, A is the area of the body, C_d is the drag coefficient, C_m is the inertial force coefficient. The equation can be simplified, as the fluid force is equal to the sum of the drag force and the force of inertia, thus Equation (29):

$$F=\Delta a_w+\rho C_a\Delta a_r+\frac{1}{2}+\rho C_{d}A{V}_r\left|V_r\right|$$

(29)

The global design conducted in this investigation was carried out under irregular wave, and the damping was calculated using the modified Morison Equation [46].

$$F=\rho V\dot{u }+\rho C_{a}DA\left(V_r\right)+\frac{1}{2}\rho C_{d}A\left(V_r\right)\left|V_r\right|$$

(30)

where V is the volume of the body, A is the area of the body, D is the diameter of the body, C_d is the drag coefficient, C_a is the added mass coefficient, C_m is the inertial force coefficient, and the V_r is the relative velocity of fluid particles.

3. Numerical Model

3.1. Model Description

The model is the numerical design of the CALM buoy, carried out in ANSYS Fluent. The effect of vortex flow around the buoy was also investigated using CFD in the present study. in the present study. Other comparatively-related researches on CALM buoys include experimental investigations that could be used to verify the flow behavior on buoys [26,27]. The present study was conducted using ANSYS Fluent R2 2020 [70,71,72,73,74], in 2D bounded walls, and in 3D. However, the results of the 2D study were only presented herein. The k-epsilon turbulence model was used to develop the 2D CFD model. In the model setup, the velocity specification method was based on magnitude normal to boundary. The reference frame was absolute and the Gauge Pressure of 0Pa was considered. The maximum iterations used per time step were 2000, with a time step size of 0.01 for 250 time-steps. In the turbulence model, the turbulence intensity was set at 5% and turbulent viscosity ratio was 10, given in

Table 1. Velocity parameters for inlet and Under-relaxation factor for the CFD model.

Parameters	Under-Relaxation Factor
Pressure	0.3
Density	1
Body Forces	1
Momentum	0.7
Turbulent Kinetic Energy	0.8
Turbulent Dissipation Rate	0.8
Turbulent Viscosity	1
Turbent Intensity	5%
Turbulent Viscosity Ratio	10

. The momentum input is taken in absolute reference frame. The turbulence model’s momentum was considered in the inlet zone using the magnitude velocity specification method which is applied normal to the boundary.

3.2. CFD Model

The CFD model is a pressure-based transient CFD model that uses k-epsilon (2 equations) standard turbulence model, with standard wall functions applied in near-wall treatment. The solver applies absolute approximations in the velocity formulation in 2D plane, for X and Y axes. The corresponding planar velocities are u and v, respectively. For the k-epsilon model, the model constants are given in

Table 2. Parameters for the constants used in k-epsilon Model.

Parameters	Constants
Cmu	0.09
CI-Epsilon	1.44
C2-Epsilon	1.92
TKE Prandtl Number	1
TDR Prandtl Number	1.3

.

3.3. Mesh Details

It was modelled in 2D as one body with surface area of 9721.5 m², 1 face, 5 edges and 4 vertices. The domain surface body has 82,846 Domain Nodes and 81,313 Elements, with mesh as shown in Figure 6. The statistics for the mesh details of the CALM buoy model conducted in ANSYS Fluent can be seen in

Table 3. Mesh statistics for the CFD model.

Parameters	Zone Type
81,313 mixed cells or elements	zone 2, binary
81,313 cell partition ids	zone 2, 2 partitions, binary
121,833 2D interior faces	zone 1, binary
560 2D wall faces	zone 5, binary
140 2D velocity-inlet faces	zone 6, binary
140 2D pressure-outlet faces	zone 7, binary
63 2D wall faces	zone 8, binary
41,423 nodes	binary
41,423 node flags	binary

. It summarises the amount of meshed sections applied on the 2D CFD model.

3.4. Solution Method

The solution method considered in the CFD modelling is pressure-velocity coupling. For the spatial discretization, the gradients were based on least square cell based gradient, second order pressure, second order upwind momentum, first order upwind turbulent kinetic energy, first order upwind turbulent dissipation rate and second order implicit turbulent dissipation rate. The result of the scaled residuals, with an absolute criterion of 0.01 is presented in Figure 7, for 34,000 iterations.

3.5. Boundary Conditions

The boundary conditions considered for this CFD model are presented in

Table 4. Boundary conditions for the k-epsilon CFD 2D model.

Parameters	Value	Unit
Inlet Velocity	1	m/s
Outlet Pressure	0	Pa
Wall	0	Pa

and

Table 5. Boundary physics showing boundaries and domain of the buoy in CFD.

Domain	Boundaries	Boundary Type
Surface Body	Boundary: Buoy	Type: Wall
	Boundary: Inlet	Type: Velocity-Inlet
	Boundary: Outlet	Type: Pressure-Outlet
	Boundary: Symmetry 1	Type: Symmetry
	Boundary: Symmetry 2	Type: Symmetry
	Boundary: Wall	Type: Wall

. For the buoy boundary, it was set as stationary wall with a “no slip” shear condition. For the other 2 outer adjacent boundary walls, the specified shear condition was applied, using standard roughness model, roughness height of 0m and roughness constant of 0.5 m. The buoy setup in ANSYS CFD showing the boundary conditions is presented in Figure 8.

3.6. Materials & Fluid Structure Interaction

The CFD study shows fluid structure interaction (FSI) using ANSYS Fluent R2 2020. The buoy model was developed using aluminum and steel materials. The density for sea water is 1003 kg/m³, the density for fresh water at normal temperature of 20 °C is 998.2 kg/m³, the density of aluminum is 2719 kg/m³, while the density of steel is 7800 kg/m³. Details of the fluid properties considered are given in

Table 6. Properties of fluid (sea water) used in the FSI model in ANSYS Fluent.

Parameters	Value	Unit
Area	1	m2
Density of Air	1.225	Kg/m3
Density of Water	998.2	Kg/m3
Depth	1	m
Length	1	m
Atm. air Pressure	0	Pa
Temperature	288.16	K
Velocity of Air	70	m/s
Viscosity of Air	1.7894 × 10−5	Kg/m.s
Viscosity of Water	0.001003	Kg/m.s

. The parameters for the 2D CFD buoy model in ANSYS Fluent are given in

Table 7. Parameters for 2D CFD buoy model in ANSYS Fluent.

Parameters	Value	Unit
Buoy Diameter (D1)	10	m
Horizontal Height of boundary near inlet to centre of buoy (H4)	60	m
Horizontal Height of boundary near outlet (H5)	80	m
Vertical height of boundary from top wall to centre of buoy (V2)	35	m
Vertical height of boundary from top wall to centre of buoy (V3)	35	m

and Figure 9.

4. Result and Discussion

The results and discussion of the CFD study are presented in this section.

4.1. Results of Flow Vorticity around Buoy

From the result obtained from the CFD study, it can be observed that the pressure and velocity have an effect on the profile of the flow around the CALM buoy. The resulting profile in Figure 10 and Figure 11 shows the velocity profiles for the flow around the CALM buoy. It can be observed that the flow from the inlet (LHS) moves towards the outlet (RHS) of the wall. The flow creates different flow patterns, depending on the force filed developed around the structure when the velocity is 0.45 m/s, 1.0 m/s and 10 m/s. This speed is chosen based on the environmental condition used in investigating the flow characteristics and motion behaviour. Another CFD model was carried out in ANSYS Fluent to investigate the sloshing effect of water waves on the CALM buoy. A total of 2 different velocities, of magnitudes 0.45 m/s and 1.5 m/s, were investigated for the CFD analysis of the CALM buoy, as they represent 2 different ocean conditions. This is confirmed in the streamline series for the velocity along directions in Figure 12 and Figure 13. In the velocity contours in Figure 10 and Figure 11, it can be observed that the higher the velocity, the higher the vorticity around the CALM buoy.

4.2. Results of Vortex Effect from the Flow Regimes

The investigation of the vortex effect on the buoy was conducted using different flow regimes as shown in Figure 11. It was studied using 3 different cases of velocities: 0.45 m/s for normal operation condition, 1.0m/s for extreme weather condition and 10m/s for survival weather condition. Due to the waves generated on the buoy, there was some ripple effect from viscous damping on the buoy. It was also noticed that there was a higher vortex flow on the buoy under a higher velocity profile, which is attributed to contributions from linear and quadratic damping from the buoy motion responses in the heave, roll and pitch motions. This can be seen in the streamline series in Figure 12 and Figure 13.

Based on the generated linear contributions partially resulting from radiated waves and the frictional viscous effect, it can be opined that the buoy has some eddies in the direction of the flow. On the other hand, the generated quadratic contributions partially resulting from the eddies separating the buoy’s vertices, and the sharp edges around the buoy’s skirt, it was found to develop much higher buildup of ripple-like vortices. Hence, these buildups result in some vortex effect on the buoy, however, further studies are recommended on postprocessing the vortex-induced motion (VIM) of the buoy.

4.3. Results of Pressure, Velocity and Wall Shear Profiles on the Buoy

The investigation of the pressure, velocity and wall shear profiles on the buoy were conducted using different flow regimes in Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19. In Figure 14 and Figure 15, the pressure profile can be seen to be higher with higher magnitude of velocity as seen for 0.45 m/s case is higher than the 1.5m/s case. Similarly in Figure 16 and Figure 17, the velocity profile can be seen to be higher with higher magnitude of velocity as seen for 0.45 m/s case is higher than the 1.50 m/s case. In Figure 18 and Figure 19, the wall shear can be seen to have highest distribution in a ripple for 0.45 m/s case which is higher than the 1.50 m/s case.

In this investigation, the highest velocity distribution for 0.45 m/s case is 1.963 m/s in Figure 14, while the highest velocity distribution for 1.50 m/s case is 2.611 m/s in Figure 15. Moreover, the highest-pressure distribution for 0.45 m/s case is 12.18 Pa in Figure 16, while the highest-pressure distribution for 1.50 m/s case is 5.766 Pa in Figure 17. Lastly, the highest wall shear distribution for 0.45 m/s case is 0.5809 Pa in Figure 18, while the highest wall shear distribution for 1.50 m/s case is 0.5963 Pa in Figure 19. In this investigation, the wall shear, pressure, and velocity profiles reflect some vorticity patterns in the axial direction which differed under different cases of velocity magnitudes.

4.4. Results of Turbulence Streamlines

The numerical calculation for the buoy profiles for different parameters to present individual turbulence streamlines are conducted in this sub-section. In Figure 20, the streamline series for the velocity cases is higher in 1.0 m/s compared to the 0.45 m/s across the x-axis and y-axis. Furthermore, in Figure 21, the streamline series for the pressure cases is higher in 1.0 m/s compared to the 0.45 m/s across the x-axis and y-axis. Similarly in Figure 22, the streamline series for the turbulence kinetic energy cases is higher in 1.0 m/s compared to the 0.45 m/s across the x-axis and y-axis. These results on turbulence kinetic energy show that the turbulence model has an influence on the buoy model in this CFD study. This implies that the parameters of the turbulence model can be used to improve the performance of the buoy model.

4.5. Results of Viscous Damping

The calculation for the viscous damping is a very important aspect of the modelling. In this present investigation, damping estimation was considered for the CALM buoy. In principle, there are quadratic and linear contributions on damping from the buoy motion responses in the heave, roll and pitch motions. The generation of the linear contributions partly result from radiated waves and the frictional viscous effect. Conversely, the generation of the quadratic contributions are partly resulting from the eddies that separate the buoy’s vertices, and the sharp edges around the buoy’s skirt. Using a semi-empirical model, using MARIN’s viscous study on CALM buoy [50,51], the values for the viscous damping coefficients are obtained. The viscous damping is proportional to a single drag coefficient, skirt plate geometry, wave frequency, velocity, and buoy amplitude. To compute this viscous damping semi-empirically, some model variations and parameters are considered, as given in

Table 8. Model parameters used in Empirical study for Viscous Damping.

Model	Metacentric Height (m)	Buoy Diameter (m)	Buoy Skirt Diameter (m)	Buoy Skirt Width (m)	Responses **
A1	0.25	10.00	13.90	0.1	LF + WF
A2	0.25	10.00	13.90	0.2	LF + WF
A3	0.25	10.00	13.90	0.3	LF + WF
B1	0.25	10.00	13.90	0.4	LF + WF
B2	0.25	10.00	13.90	0.5	LF + WF
B3	0.25	10.00	14.90	1.0	LF + WF
C1	0.25	10.00	15.90	1.5	LF + WF
C2	0.25	10.00	16.90	2.0	LF + WF
C3	0.25	10.00	17.90	2.5	LF + WF
D1	0.25	10.00	13.90	1.5	LF + WF
D2	0.50	10.00	13.90	1.5	LF + WF
D3	0.75	10.00	13.90	1.5	LF + WF

Note **: LF—Low Frequency heading, WF—Wave Frequency.

. The semi-empirical method for viscous damping is detailed in literature [6,51]. The results are compared with the prediction in the present study, as seen in Figure 23. However, detailed computations are not given in this paper.

In the study by Cozijn et al. [51], a comparison was performed between the damping values recorded in the forced oscillation experiments and the damping values computed using the pitch and heave damping model for the CALM buoy having a skirt. The drag coefficient C_D employed in the heave and pitch damping model was chosen to match the measured damping values as closely as possible. This strategy, however, can only be employed when model test data is available. In some circumstances, a different approach to determining a suitable value for the drag coefficient C_D is required. Empirically, the C_D values are examined in greater depth by using Equations (27) and (28) to compute for the C_D value for the CALM buoy’s skirt from each pitch and heave oscillation test result. The accompanying KC numbers, which are defined in the equations, can then be displayed as a function of the C_D values.

Some studies were conducted on perforated plates, free plates, and bounded plates [52,53,75,76,77]. Sarpkaya & O’Keefe [53] gave C_D values for a wall bounded plate in a 2D oscillating flow as a function of the KC number. Figure 23 depicts similar findings in a graph (black dots) from 2 publications [51,53]. The C_D values obtained from the heave and pitch forced oscillation tests for the CALM buoy skirt are presented in the same figure (coloured points) for comparison. The CALM buoy skirt C_D values are identical to the C_D values for a wall-bounded plate in a 2D oscillating flow, as shown in Figure 23. The CALM buoy skirt C_D values, on the other hand, appear to be slightly greater than the ones reported by Sarpkaya & O’Keefe [53]. This can be explained by the fact that, despite the same flow patterns, the flow around the buoy skirt is axi-symmetric 3D rather than 2D. It is also feasible that the drag loads on the CALM buoy bilge are not insignificant. In such instance, their contribution to total drag is included in the drag loads on the skirt in the study presented here, which could lead to an overestimation of the C_D values. Recent applications have been conducted by coupling CALM buoy models using related hydrodynamic formulations in literature [78,79,80,81].

5. Conclusions

In this research, the CALM buoy was numerically investigated under water waves using computational fluid dynamics (CFD) to investigate the vortex effect on the buoy. Some mathematical modelling and governing equations for the CALM buoy system were presented. By considering the complexity of a CALM buoy system, the boundary conditions were formed using some assumptions and some governing equations. Considerations were made using the damping to develop the equations by considering the buoy and its skirt. However, special attention is given to the CALM buoy and the skirt in the formulation. For the CFD study, the model was conducted using a 2D model. The results showed peculiar characteristics, which should be considered in the design due to the drag and damping implications on it. This research also presents findings from the vortex effect, velocity, pressure, wall shear and turbulence. This study is important to enable designers to design appropriately based on the CALM buoy system, buoy geometry and CFD data.

The model highlights include the following: firstly, a theoretical model is presented on motion characterization for CALM buoy model without attached hoses. Secondly, the CALM buoy model was conducted on the vortex effect in 2D CFD under different parameters. Thirdly, different novel techniques were applied in the numerical investigation to obtain the influence of the turbulence model on the CALM buoy. Fourthly, the study on the motion scenario from pressure, velocity, wall shear, and motion response study on waves upon the CALM buoy. Lastly, prediction of the turbulence and flow vorticity on the CALM buoy’s motion characteristics was presented from the study.

The study presented buoy motion profiles based on 2D CFD study and numerical and theoretical predictions. From an offshore mechanical point of view, the motion characterisation phenomenon has been confirmed to exist as a result of the response from the water waves and other global loads on the CALM buoy. The study shows more dimension on the CALM buoy in a water body and buoy motion. The study has presented a comprehensive formulation of the offshore structure as is necessary for understanding the stability and dynamics behaviour. The vortex flow effect on the free-floating buoy is investigated using CFD. Another validation is recommended on an engineering application by coupling using the Orcaflex FEM to prove it is a working application of the mathematical formulations presented herein. However, further studies are recommended on the CFD study on buoy motion with moorings based on the analytical approximations for the moving boundary of marine hoses, and investigation on hose-snaking behaviour.