Next Article in Journal
Review on Study Methods for Reciprocally Enwrapping Surfaces
Previous Article in Journal
The Mathematical Models of the Operation Process for Critical Production Facilities Using Advanced Technologies
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inventions
Volume 7
Issue 1
10.3390/inventions7010009
inventions-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Numerical Study on Plastic Strain Distributions and Mechanical Behaviour of a Tube under Bending

by
Chiemela Victor Amaechi
1,2,*,
Emmanuel Folarin Adefuye
1,3,
Abiodun Kolawole Oyetunji
4,5,
Idris Ahmed Ja’e
6,7,
Ibitoye Adelusi
1,
Agbomerie Charles Odijie
8 and
Facheng Wang
9
1
Department of Engineering, Lancaster University, Lancaster LA1 4YR, UK
2
Standard Organisation of Nigeria (SON), Abuja 900287, Nigeria
3
Department of Mechanical/Metalwork Technology, Federal College of Education (Technical), Lagos 100001, Nigeria
4
Lancaster Environment Centre (LEC), Lancaster University, Lancaster LA1 4YQ, UK
5
Department of Estate Management, University of Benin, Benin City 300287, Nigeria
6
Department of Civil Engineering, Universiti Teknologi PETRONAS, Seri Iskander 32610, Malaysia
7
Department of Civil Engineering, Ahmadu Bello University, Zaria 810107, Nigeria
8
Department of Engineering, MSCM Ltd., High Wycombe HP12 3TA, UK
9
Department of Civil Engineering, Tsinghua University, Beijing 100084, China
*
Author to whom correspondence should be addressed.
Inventions 2022, 7(1), 9; https://doi.org/10.3390/inventions7010009
Submission received: 9 September 2021 / Revised: 26 December 2021 / Accepted: 28 December 2021 / Published: 6 January 2022
(This article belongs to the Section Inventions and Innovation in Design, Modeling and Computing Methods)
Browse Figures
Versions Notes

Abstract

:
Tubular pipe structures have been used in various applications—domestic, aviation, marine, manufacturing and material testing. The applications of tubular pipes have been considered greatly in the installation of tubular pipes, marine risers and pipe bending. For the investigation of plastic strains and the mechanical behaviour of a tube under bending, considerations were made utilising an exponent model with assumptions on the plane strain. The bending moment, wall thickness effect, cross-sectional distribution, stresses during bending and neutral layer boundaries were all presented as necessary theoretical formulations on the physics of tubular pipe bending. This model was based on the analytical and numerical investigation. In principle, the application can be observed as the spooling of pipes, bending of pipes and reeling. Comparisons were made on two models developed on the finite element analysis in Simscale OpenFEA, namely the linear-elastic and the elasto-plastic models. This study presents visualization profiles using plastic strain to assess its effect on the tubular pipes. This can increase due to the limitation of plastic deformation on the composite materials selected.

1. Introduction

The exploration of fossil products has been the greatest application of pipelines [1,2,3,4] and other tubular structures like marine hoses [5,6,7,8,9]. It has been used in bending, relaxing, straightening, reeling and pipe-laying [10,11,12,13]. These include marine riser installation and pipeline installation; for example, using reel-lays has been described as one of the most cost-effective methods utilised in the industry [14,15,16,17]. The advances in pipeline technology including hoses and marine risers have led to new analytical formulations on the plastic deformation of pipes and tubes [18,19,20,21,22]. Over the years, there have been several tube-bending phenomena, which include bending moment, flattening, deviation from neutral axis and stress [23,24,25]. Different questions have been answered on tube bending over the years, although they did not address the phenomenon that encompasses tube bending and the bending of hose/pipe tubular structures applicable for composite riser pipes [26,27,28,29,30,31,32,33,34]. Different materials have been used ranging from composites to aluminum and steel [35,36,37,38,39,40].
Considering space conservation in pipeline technology, adequate length of the flexible pipelines led to advances in the technology of bending, spooling and reeling systems. Figure 1 shows an application of tubular pipe bending using two methods conducted in the Lancaster University Engineering Workshop. In principle, the application of tube bending requires a roller or moulder and the mandrel, while reeling requires a reeling drum and a material that goes around it. In this study, tubular pipes are considered, which involves tube bending with a roller and the moulder as the press tensioner. Tang [41] presented an analytical model on plastic deformation in tube bending, with some practical formulas that were applied unto the tube bending phenomena. These include the deviation in neutral axis (NA), tube flattening, bending moment, length of the bed during feed preparation, changes in wall thickness, shrinkage rate that occurs at the sections of the tube and the stresses occurring in the bend. However, the model presented by Tang [41] differed from the elastic and the elasto-plastic models by including the assumption of a higher bending radius ratio by Von Karman as early as 1911, and it could not obtain a strain that reaches 0.47. During the plastic flow, the dimensions of the elbow changes consistently based on the plastic deformation theory.
Lu et al. [24] presented an analytical and experimental investigation on plastic deformations cum predictions on the form-bending qualities of tubes based on numerical control, deduced from plane strain assumptions by using the deviation from the neutral layer. A typical example is seen in a reeled system as shown in Figure 2. It shows that reeled systems can also be bent after coating [42,43,44]. In another study, Lassen T. et al. [45] investigated marine-bonded tubular hoses, where the helix had experienced a common deformation behaviour reported to be either layer delamination or reinforcement helix rupture, thus helix fatigue tests have been carried out on helix sections. Wu et al. [46] experimented on the influence of the size of material grains, the bending velocities and the temperature gradients on the thickness of magnesium alloy AM30’s tubular wall draw-bent over a rotary draw. In another investigation, Liu et al. [47] conducted an experiment on the aluminium alloy 3A21 tubular pipe of a rectangular thin-walled cross-section and AM30 magnesium alloy tube to ascertain its cross-section distortion and the influence of production/bending die with vital factors affecting the distribution of wall thicknesses throughout the bending activity from numerical control bending.
The bending of tubular sections to get an elbow can be described as a metal-plastic flow process which was carried out using similar process bending parameters [49,50,51,52,53,54]. Guo et al. [55] conducted an investigation to examine the formability influence and increased axial tensions on equivalent curvature-diameter bending, excluding mandrels on 0Cr18Ni9 stainless steel tubes. A parametric investigation was carried out by experiment and numerical modelling on aluminium tubes under dynamic three-point bending by Bilston et al. [56]. Cheng et al. [57] conducted an investigation on a tubular with a rectangular thin-walled cross-section having a continuously different radius based on the ‘simple bending technique’ and the influence of the cross-section deformation behaviours. Guo et al. [58] examined the wall thickness distribution of Cu-Al bimetallic tubes based on the free-bending process. Wu et al. [59], presented one method for investigating the springback behavior of metallic spatial tubes (3D tubes). Jian et al. [60] presented an experimental and numerical buckling analysis on the toroidal shell segments under uniform external pressure. Li et al. [61] investigated on the multiple instability-constrained tubes bending limits by utilising 3D-FE models, analytical modelling and experimental validation by establishing a comprehensive map of the tube bending limits during rotary draw bending, which was obtained for some tube size ranges, processing parameters and material types. Over the years, these different researches have been conducted to understand the plastic deformation of tubular structures—tubular pipes, hoses and cylindrical tubes.
In this study, the numerical study on plastic strain distributions and mechanical behaviour of a tube under bending load is presented. It is aimed at an understanding on plastic strain distributions, stress/strain distributions and the mechanical behaviour of a tube during bending. In this paper, an introduction to tubular pipe bending is presented in Section 1. The local design of the tubular pipe in FEA is presented in Section 2, while Section 3 presents the materials and methodology applied in the numerical study in Simscale OpenFEA. The results of the reeling model are presented in Section 4, while the conclusion is presented in Section 5. Contour profiles for (a) epoxy composite, (b) carbon fibre composite and (c) Nylon PA66-GF glass fibre composite models were presented. The analysis of the stresses on the tubular pipe sections was conducted using local design pressure and not operation pressure, and as homogenized model. This study presents visualisations on the stress profiles to demonstrate the maximum stresses and suggest recommendations for the optimization from contact pressure.

2. Numerical Model

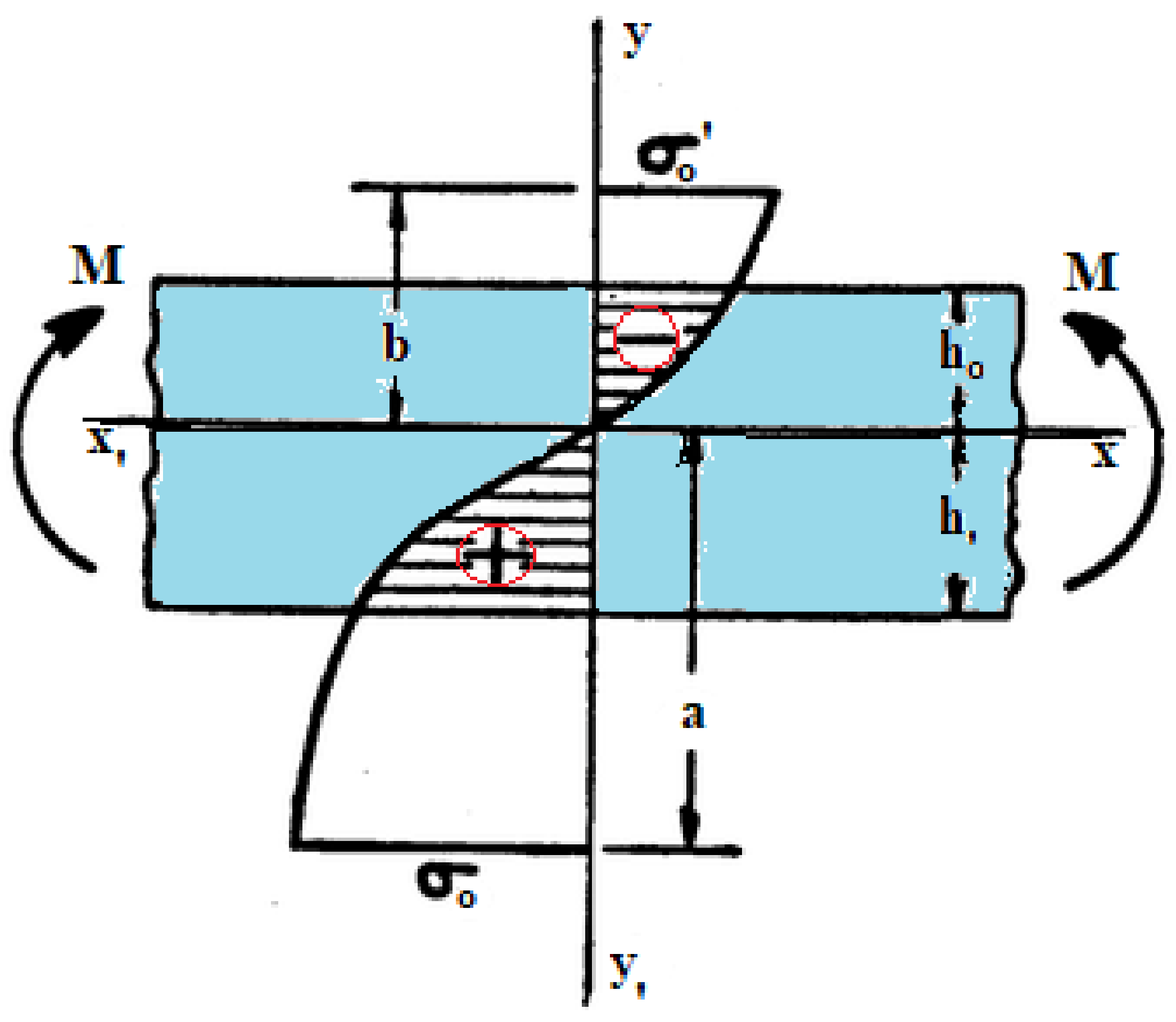
2.1. Tubular Bending

In theory, tubular pipes are subject to curvature and bending, among others. Early formulations on tube bending were based on Euler beam theory before Timoshenko beam theory. By description, plastic bending can be described as a nonlinear characteristic unique to ductile parts that frequently attain a far larger strength in ultimate bending over the elastic linearised bending model [62,63,64]. The strain profile is considered to be linearised around its neutral axis (NA) for both plastic and elastic bending calculations of a straight beam (plane sections remain plane), as in Figure 3.
This assumption results in a linear stress distribution in an elastic analysis, but in a plastic assessment, the resultant stress profile is nonlinearized as well as depending on the material of the beam. The maximal plastic bending strength can be thought of as an upper limit on a beam’s load-carrying capability because it represents the strength profile across that specific cross-sectional area but not the load-bearing capabilities of the beam. A beam might collapse before it reaches any point along its length due to global or localized instability. The deflections required to create the stresses suggested in a plastic analysis are usually excessive, to the point of being incompatible with the structure’s function. As a result, a second analysis may be necessary to guarantee that the design deflection limitations are not exceeded.
Furthermore, since working with materials in the plastic range can result in permanent deformation of the structure, further analytical work is recommended in another study. At the limit load, additional analyses may be necessary to verify that no irreversible deformations develop. Plastic bending’s massive deflections and stiffness variations, especially in statically indeterminate beams, can drastically alter the internal load distribution. Calculations should be based on the internal load distribution of the deformed shape and stiffness. Plastic bending occurs when an imposed moment causes the outermost fibres of a cross-sectional area to surpass the material’s yield point. Peak bending strains occur at the cross-outermost section’s fibres when only a moment is loaded. Through the sectional part, the cross-section would not yield linearly. The sign conventions for the cylindrical layer of tubular pipe showing force and deformations are depicted in Figure 4.

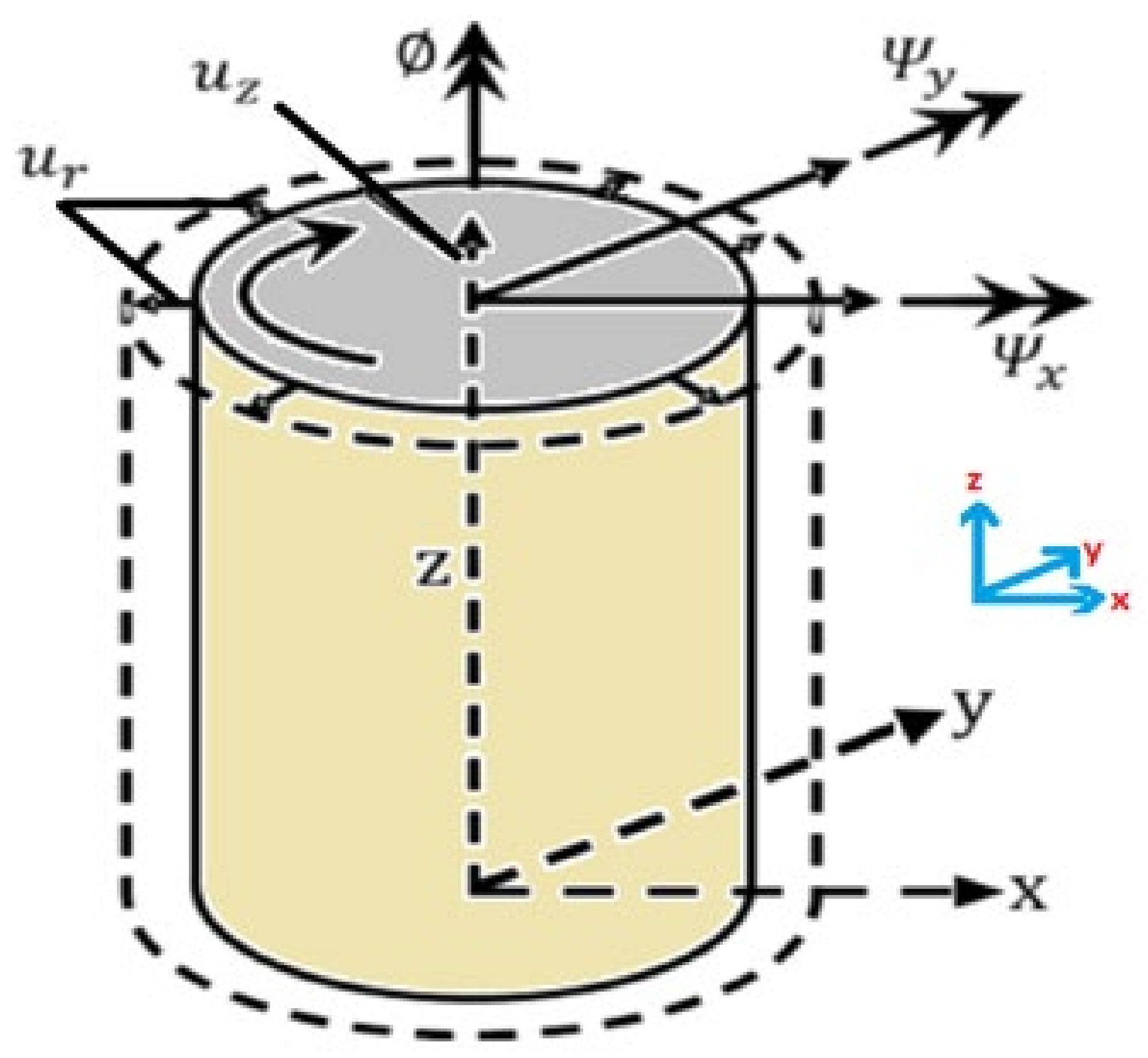
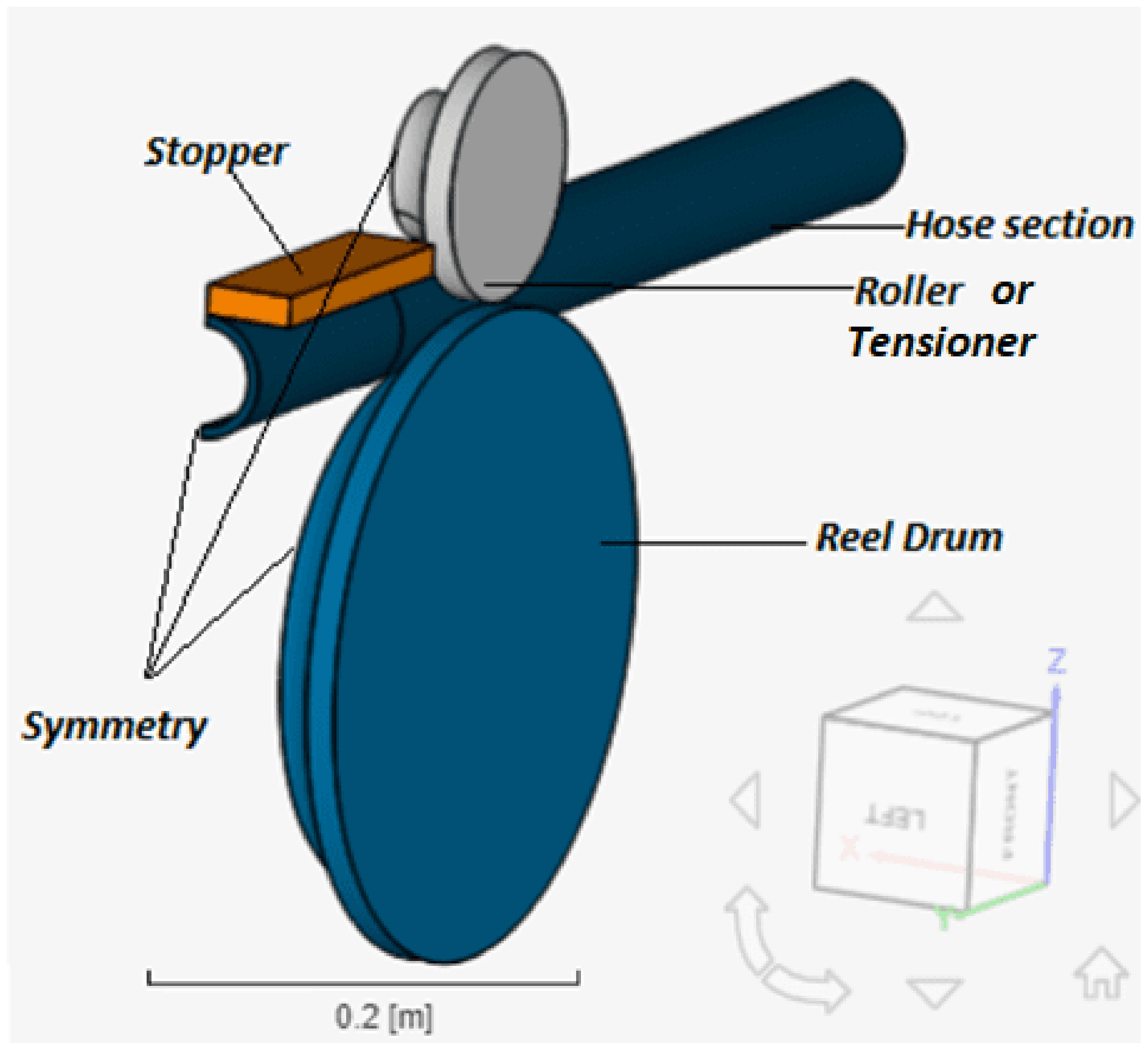
2.2. Model Description

The model is the local design of the tubular pipe, carried out in Simscale OpenFEA to ascertain the effective plastic strain. It was carried out to ascertain the different physics investigated on the loading conditions of the tubular pipe to present results from the both static and dynamic behaviour of the tubular pipe. The parameters for the tubular pipe model are presented in Table 1, and details are presented in Section 2.3 and Section 3. The tubular pipe geometry and the bending model is depicted in Figure 5. The friction coefficient was also considered in the contact between drum and hose.

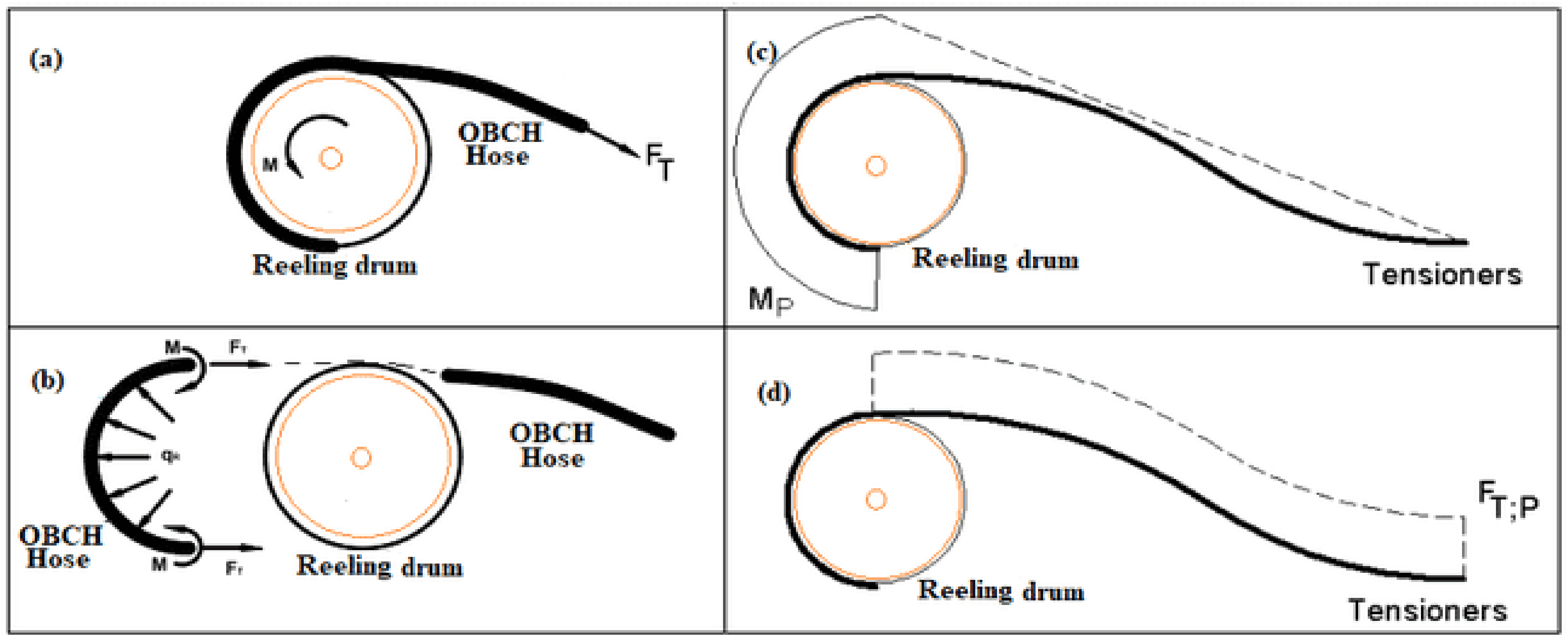
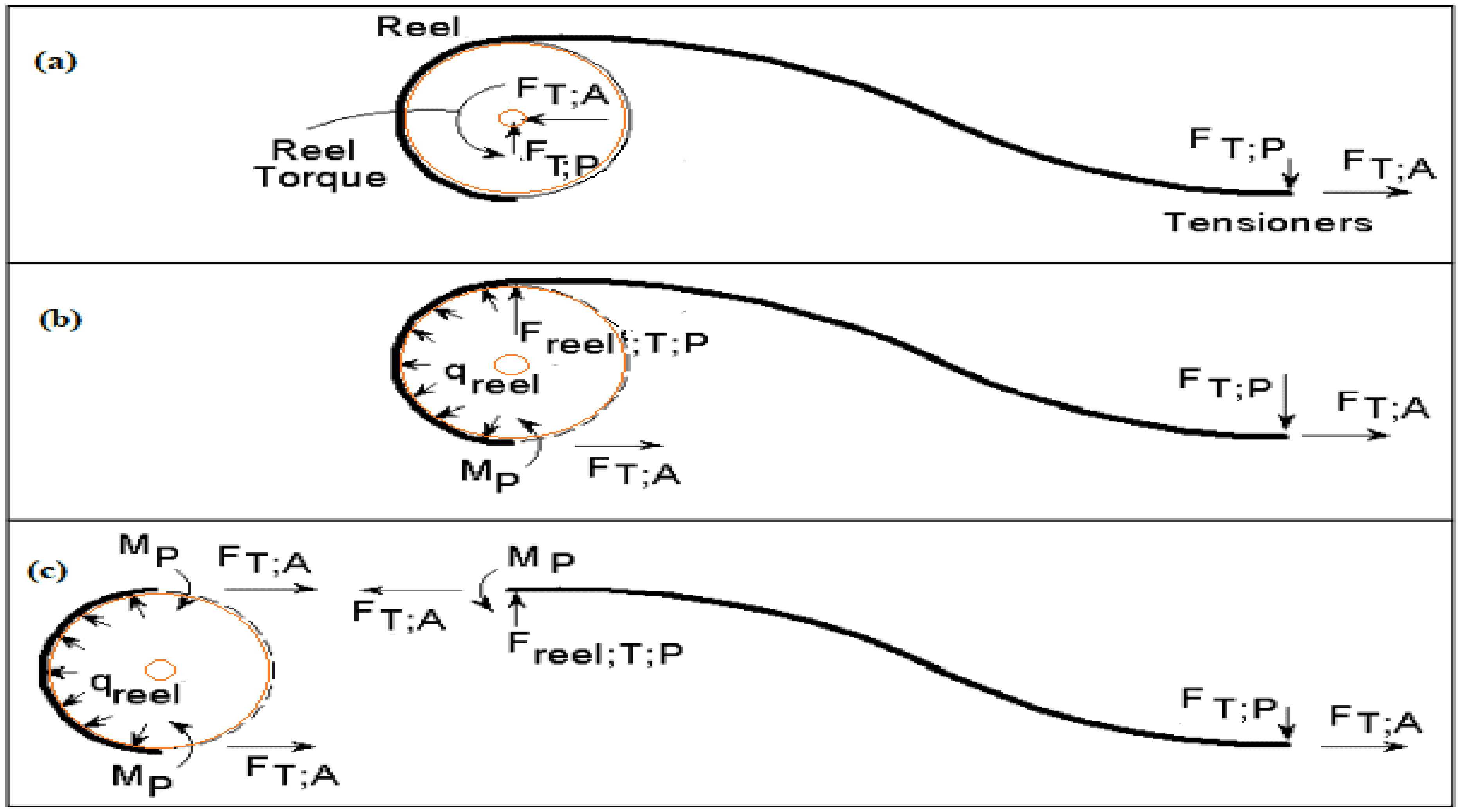
2.3. Bending and Reeling Model

The finite element model (FEM) was created and was used to simulate the pipe bending operation. A section of the long tubular pipe is considered a reeling hose and was developed as shown in Figure 5. The reeling hose is reeling on the reeling drum, and a roller was used to control the path. The spooling operation was considered, as it involves tensioning, as the hose is bent onto the reel drum plastically, which creates the highest curvature during the reeling process [65,66,67]. Hose-pipe mechanics of reeling hoses is illustrated in Figure 6. As seen on the illustration, the pulling force (FT) is applied at the end of the hoseline to keep it straight. During reeling, the hoseline is usually fully attached to the surface of the reeling drum, at which point the bending moment (M) reaches its peak, assuming the contacts between the hose and the reeling drum are maintained. Although the reaction force (qR) is applied to the hoseline, this can be spooled as required, as it may attain a buckling failure. These forces are as seen in Figure 6 and Figure 7.

2.4. Finite Element Model (FEM)

In this local design, the hose geometry was generated in a CAD using Solidworks 2020, as shown in Figure 8. It was then modelled in the Simscale OpenFEA platform, using Aster code. The results of the mechanical behaviour from the local design were analysed to achieve the best results on the model, by applying certain considerations. The hose model was simplified, and secondly was a homogenized aspect of the model. For the local design of the reeling hose in Simscale OpenFEA, the reeling drum and the hose were modelled using Aster code. The solver applied was a Multifrontal solver, which is quite easy to set up and works well for most nonlinear problems. The solver numerics considered the multifront by applying the MDA renumbering method, a precision singularity detection of eight and Newton type of nonlinear resolution. The convergence was relatively based on a tolerance of 1 × 10−4, a tangential prediction matrix and a tangential Jacobian matrix with a maximum number of 15 Newton iterations updated at every nth iteration of one. The simulation control was set to automatically define the time steps at a simulation interval of 1 s. The maximum length of time step was 0.05 s, while the minimum length of time steps was 1 × 105 s, for an additional 20 Newton iterations. To ensure that there is ease during the simulation, two fixed subdivisions and a maximum of three subdivision depths were applied with a fixed augmentation of 100 time-steps and an augmentation threshold of seven Newton iterations. The boundary conditions for the FEM are given in Section 3.4. Details of the FEM, element type, element size and number of elements are in Section 3.4 and Section 3.5.

2.5. Contact Details

In the numerical model, the friction coefficient considered in the contact between drum and hose is 1 × 1012 using a penalty method. The physical contacts were set with 10 maximum iterations and an iteration criterion of 0.05. For the contact between pipe, roller and drum, a penalty contact with a higher stiffness was used. The pipe was given an elastoplastic material by inputting the aluminum’s stress strain data. A stopper was utilised as a restraint, which was fixed in all directions while the roller was rotated by 130° clockwise under limitations.

3. Materials and Methodology

3.1. Material Properties

The material properties considered in this model is presented in Table 2. They were chosen based on their high potential for application within flexible bonded pipelines. These materials specifications are based on industry reeling applications, industry standards and technical reports as applied in literature [68,69,70,71]. These materials demonstrate high potential based upon their different properties, such as high strength, natural corrosion resistance, light weight and flexibility.

3.2. Elasto-Plasticity of Hose

The finite element model of the hose was designed with the consideration of elastoplasticity using the stress–strain relationship. The elastoplastic deformation of the hose during reeling is a function of the formulation of the homogenized hose material. This has been applied in similar hose models to improve the hose physics in the FEM [68,69,70,71]. Some of the materials used for the hose (carbon fiber composite and epoxy composite) show anisotropy in terms of their elastic properties. This can influence the results, as it has also been taken this into account, as presented in the stress–strain relationship in Section 4.5.

3.3. Design Load Conditions

The local design of this reeling hose model was considered design specified given the design standards for bonded pipes, in API 17K [72]. For a successful reeling operation, a boundary in terms of path with constraints are developed. The boundary conditions considered are in Section 3.4, and directions of forces are being applied to the system. In this present analysis, the fluid content is not considered. The analysis is based on the structural integrity and strain of the reeling hose. However, during operation of these flexible hoselines, the structure of the asset is subjected to both internal and external pressures.

3.4. Boundary Conditions

For the local design of the reeling hose, different boundary conditions were considered including fixed, symmetry and rotation boundary conditions. The boundary conditions considered in the model for the hose and two sections of the model were fixed boundary conditions upon the roller/tensioner and the stopper. Considering the reeling process, the rotation boundary condition on the roller was applied with the rotation angle given in Equation (1).
R = π 180 ×   130 ×   t   in   radians

3.5. Mesh Details

For the local design of the reeling hose in Simscale OpenFEA, the reeling drum and the hose were all meshed as shown in Figure 8. For the reeling hose model, the mesh model has 20.1 × 103 cells and 5.7 × 103 nodes, and second order elements were considered in the Simscale Open FEA based on Aster code [73]. The maximum precision of model and its entities considered was 1 × 10−8 m, and an absolute small feature tolerance of 1 × 10−5 m was applied in the numerics. Mesh refinements were made on the hoseline and the tensioner/roller. For the hose line, local element size refinements were applied with a minimum edge length of 0.002 m and maximum edge length of 5.6 × 10−3 m by using very coarse fineness to reduce computational cost in the nonlinear analysis. On the reel drum, local element size refinements were applied with a minimum edge length of 3.2 × 10−3 m and maximum edge length of 5.6 × 10−3 m by using very coarse fineness. Additionally, for the tensioner/roller, local element size refinements were applied with a minimum edge length of 2.4 × 10−3 m and maximum edge length of 5.6 × 10−3 m by using very coarse fineness. The metrics statistics for the mesh quality is presented in Table 3.

4. Results and Discussion

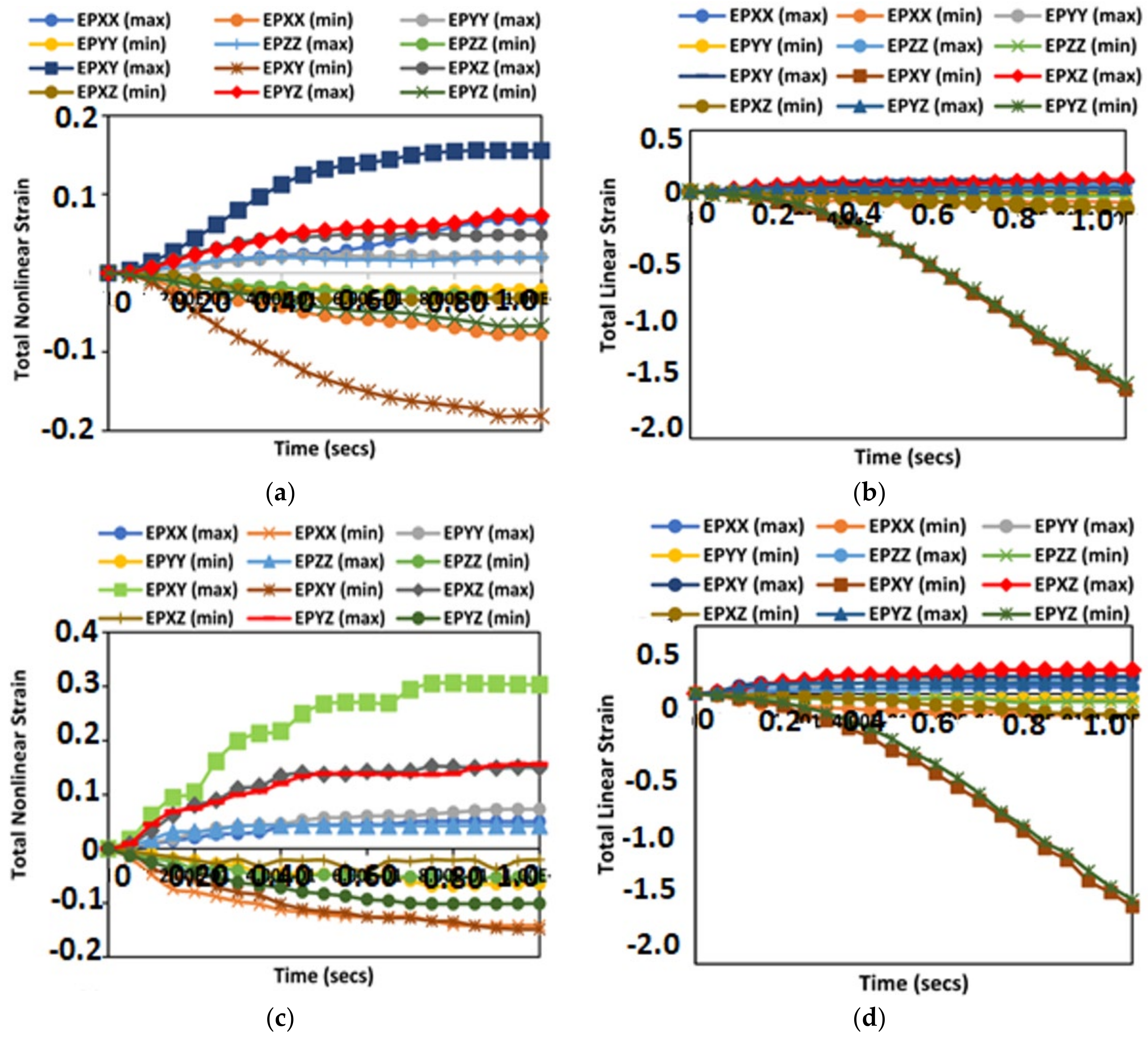
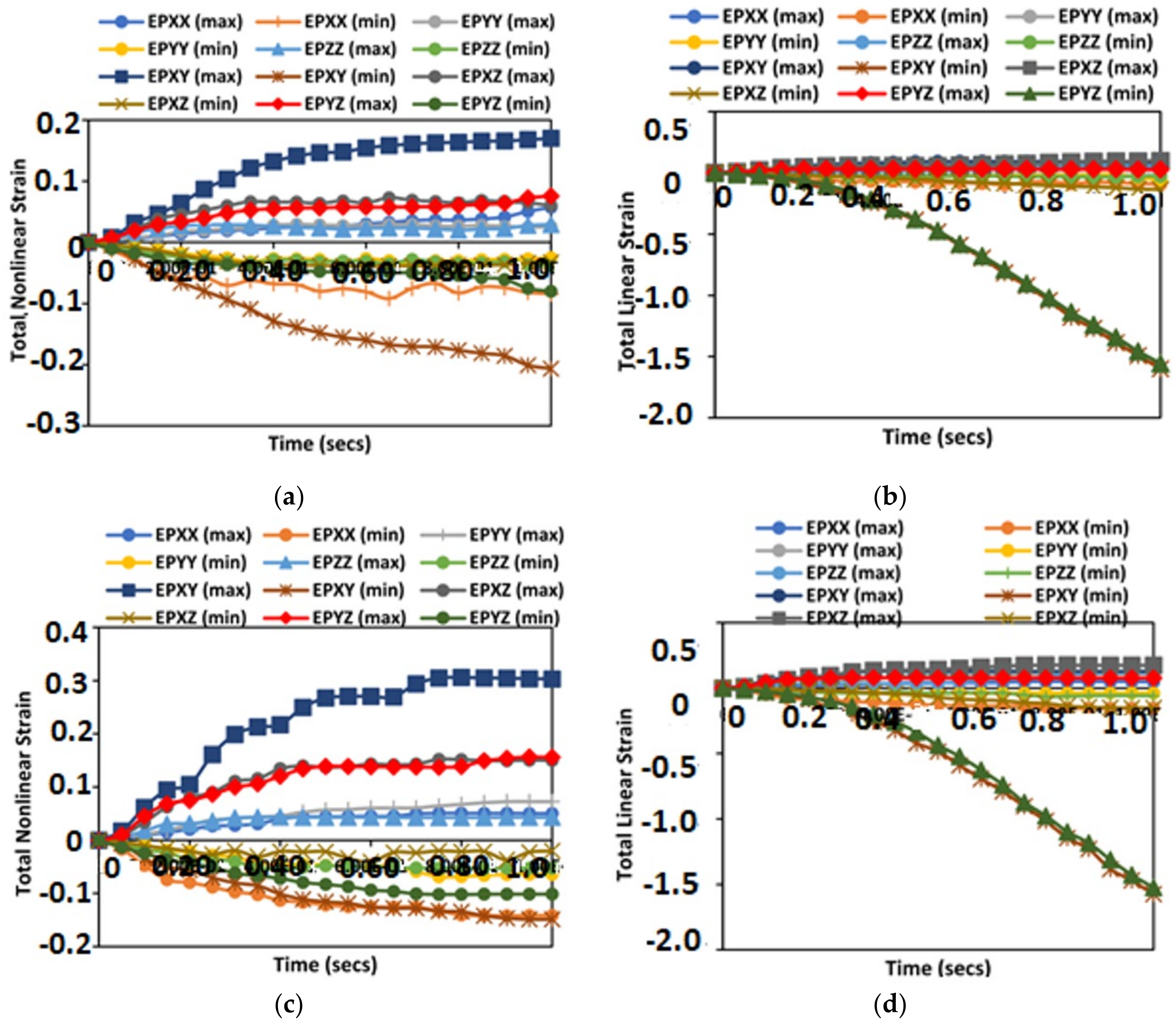
4.1. Results on Total Strain and Effective Plastic Strain (EPS)

For the reeling model, the results of the total strain presented in Figure 9, Figure 10 and Figure 11 are obtained on the reeling hose using three composite models: epoxy composite, carbon fibre composite and Nylon PA66-GF composite. It should be noted that the total strain is not the same as the effective plastic strain (EPS), as the latter is obtained from the former.
Herein, two models were used: The elastoplastic model and the elastic linearity model. Assessing strains on each model using the EPS, it is evident that the elastoplastic model had higher strains than the linear elastic model. Additionally, the maximum strain direction observed was the strain along EPXY at 0.173. Along the hoop direction, the material will become more hardened, especially in a homogenised model, than along the longitudinal direction of the material. Thus, this must be considered when investigating the hose behaviour during reeling if the layers are aligned along the axis of the reeling motion. Twisting and torsion were not included in this study, but were in a separate study to obtain the ultimate limit strain and the yield point of the hose model from the reeling. As seen in Figure 9, Figure 10 and Figure 11, the strains have different maximum strain positions for different materials.
In Figure 9, the total nonlinear strain of the epoxy composite linear elastic model was observed in EPYY, while in Figure 10 and Figure 11, the total nonlinear strain of carbon fibre composite and Nylon PA66GF composite linear elastic models, respectively, were both observed in EPXY. In conclusion, it can be concluded that reeling is an excellent method to assess the strain on bonded reeling hoses and reeled pipelines. In conclusion, it is important to assess the strain during reeling by considering Accumulated Plastic Strain (APS) which is recommended at 2% according to DNV-OS-F101, which can increase due to the limitation of plastic deformation on the composite materials selected. However, the EPS was considered, which also gives an indication of the behaviour of the material and shows profiles of the strained and unstrained regions. Due to the locus of the yield stress on the hose section being reeled, the hose material has a plastic behaviour observed after reeling. As such, total linear strain and total nonlinear strains were considered.

4.2. Result of Von Mises Stress (VMS)

Based on the same reeling model, the von Mises stress profiles were obtained, as presented in Figure 12a–f and Figure 13g–j. It can be observed that the von Mises has some effect on the hose during the reeling. From Figure 13, it is evident that the linear elastic von Mises stress was maximum, followed by the elastoplastic von Mises stress. Thus, a detailed contour plot study as in Section 4.3 is presented to inundate upon the understanding on the strain-wise behaviour of the hose when reeled. Von Mises stress is a value that is utilized in determining if a specific material will fracture or yield. Historically, Tresca [74] had proposed the maximum stress theory while the von Mises stress was then first proposed by Huber [75] and later re-proposed by von Mises [76] to receive more attention. Other aspects of the von Mises criterion were obtained later as available in literature [34,77,78,79]). In other words, von Mises stress is a measure of the total overall stress acting on the material including its shear stress and the normal stresses in the x and y directions. By considering stress limits, the von Mises stress yields criterion states that if the material under load equals or is greater than material’s yield limit under simple tension load, then the material yields. Mathematically, the von Mises stress is not a square of a sum of stress values squared, but represented as in Equation (2), where V is the von Mises stress; τ x y is the shear stress; σ x is the normal stress acting in x-component and σ y is the normal stress acting in y-component. Thus, the von Mises stress remains positive. By applying this parameter, it becomes challenging to analyze the behaviour of the hose when undergoing tension, compression or torsion. However, the signed von Mises stress, considers both the absolute value and the stress signal; as such, it is considered in this study. With the “signed von Mises” method, this allows the transformation of a fluctuating load cycle into a symmetric cycle, including the rotation load boundary condition considered. This is an extension of the von Mises stress towards the critical plane models, where the damage parameter is a shear stress or normal stress. Thirdly, the signed von Mises stress can be computed using user-defined results. Considering stress in the three directions xyz, dividing the von Mises stress by an absolute value of itself will yield −1 for compression and +1 for tension. Thus, the signed von Mises stress, seqv*, can be represented as Equation (3). However, when the stress is zero from dividing it using the absolute value, the expression for the user defined result changes to account for this factor, as given in Equation (4).
V = σ x 2 − σ x * σ y   +   σ y 2 + 3 * τ x y 2  
seqv * = σ x + σ y + σ z / abs σ x + σ y + σ z  
seqv * = σ x + σ y + σ z + 1 e − 6 / abs σ x + σ y + σ z + 1 e − 6  

4.3. Result of Reeling Time-Step Contour Study

The nonlinear analysis of the reeling operation as carried out in the Finite Element Analysis (FEA) is depicted in the order of the timesteps in Figure 12. A detailed plot of the reeling by time-steps is presented to visualize the strain-wise effect of reeling on the symmetry section of the hose. It is evident that the total strains started to propagate through the hose section as it was tensioned and spooled onto the reeling drum. A contour study on the reeling model was carried out to visualize the strains on the reeled sections of the hose. It was observed that they have relatively similar strains but were not all the same along the axis of strain for EPXX, EPYY, EPZZ, EPXY, EPXZ and EPYZ. These contour strain plots are similar to those presented in Figure 13 on the total strains, and the total nonlinear strains also depict the strain-wise effect from longitudinal loading during the reeling. However, the tensioner (or roller) was used to stretch and align the hoseline, which strains the section along which it applies per time frame. Secondly, there is an Accumulated Plastic Strain (APS) observed in the reeling operation, which also transfers some strain energy onto the reeling drum, as seen in these strain contour plots. Thus, it is necessary to investigate the contact pressure and the accumulated strain energy at these regions on the hoses. Contour profiles for (a) epoxy composite, (b) carbon fibre composite and (c) Nylon PA66-GF glass fibre composite models were analysed as presented. It can be concluded that the materials have different effects on the hose; as such, two models were preferred: the carbon fibre and the nylon PA66GF composite models, as the strains showed better consistency.

4.4. Result of Contact Force Load

As observed in the result profile from the FEM, the reeling hose experiences contact pressure force during the reeling. In this represented model, the material is a Nylon PA66-GF composite reeled pipe on a steel drum. Over long turns of reel, it is likely to lead to early hose failure, thereby reducing the service life. The contact pressure is due to the reaction between the tensioner and the reeling drum, as seen in the model result in Figure 13a,b. During the reeling, the motion of the tensioner as it rolls onto the reeling drum to align it creates an opposite reaction, seen in the reaction force in Figure 13c,d. As this continues, the areas of the hose that are weakened start to deform, and directional deformation starts to propagate in the direction of the composite layer. Considering both the elastic linearity and the elastoplastic models, the later model seems to have an increase in hose deformation, contact pressure and reaction force than the linear elastic model, but this is relative, as it depends on the stress–strain data from experiment.

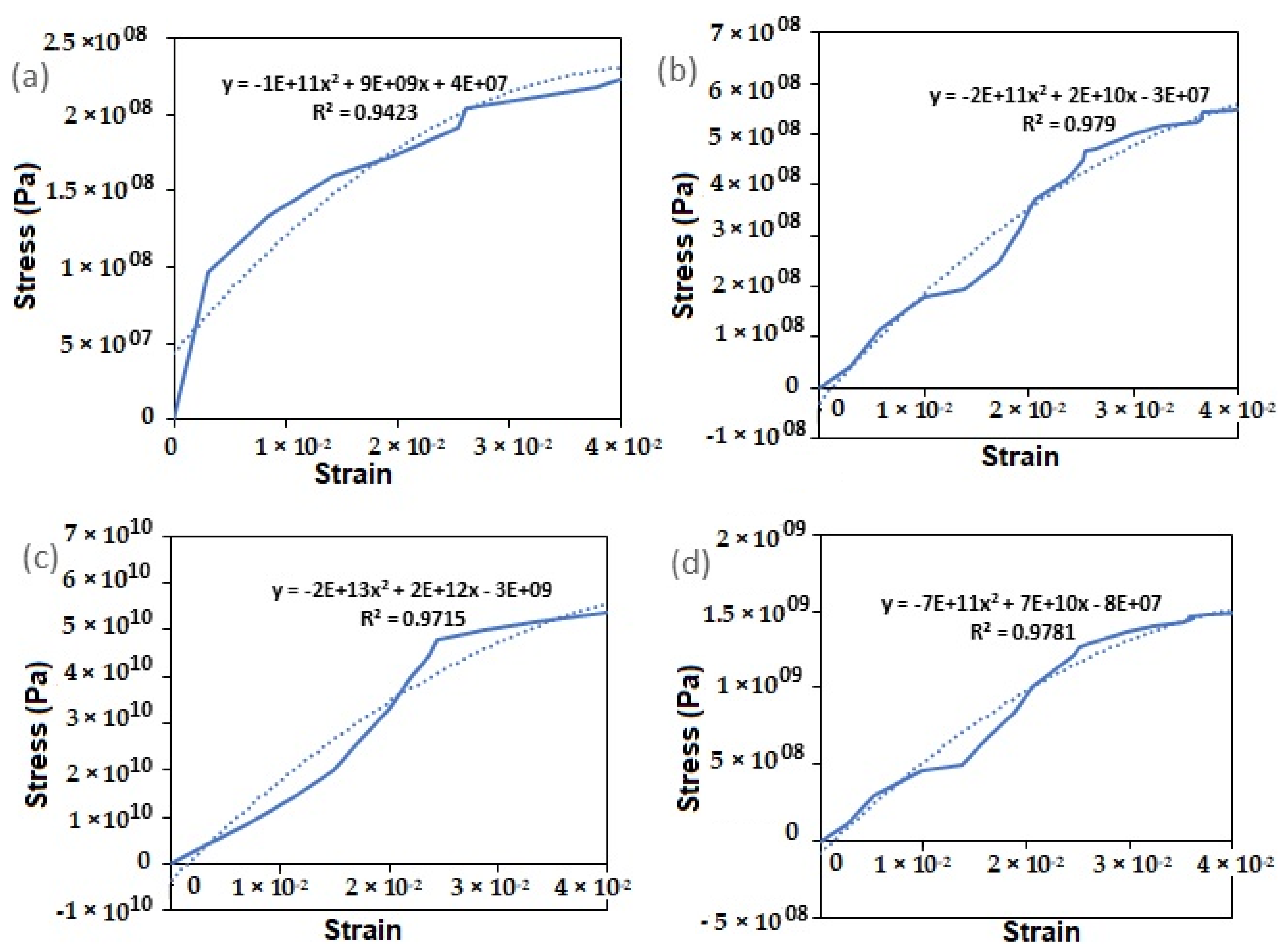
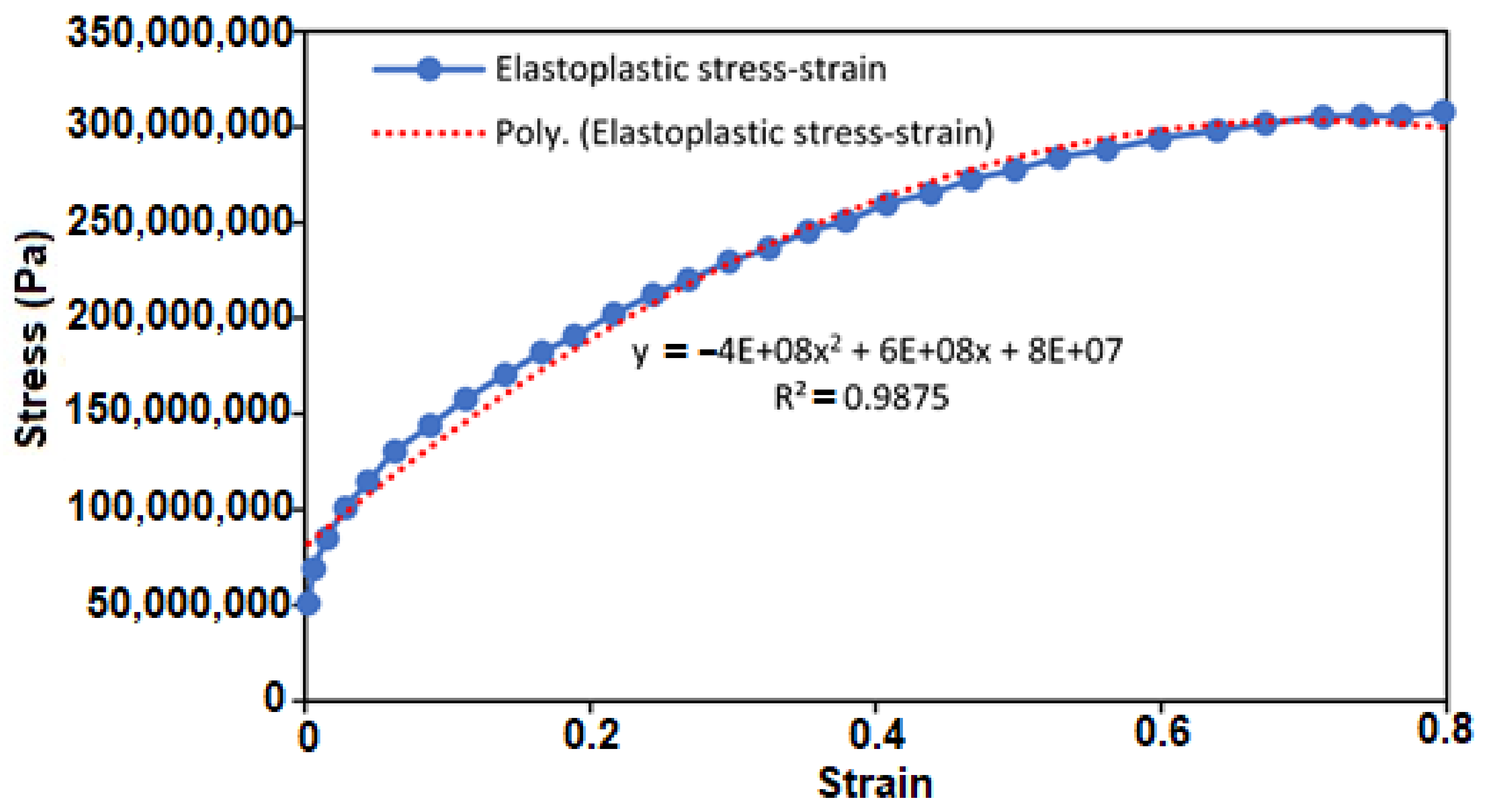
4.5. Result of Stress–Strain Relationship

An important aspect of the study is to investigate the effect of the stress–strain relationship of the material along the principal strain axis. As a result of this, the designers can understand a bit more on the behaviour of the hose material. It should be noted that the stress–strain relationship at any point in the material is the one entered in the finite element program, as is herewith. From Figure 14, it is evident that the materials have different stress–strain relationships exhibited, also along different strain directions. This can also be seen in the stress–strain relationship applied to epoxy composite tubular pipe in Figure 15, with the polynomial curve fitting on the model. As observed in Figure 14a, the elastoplastic material stress–strain behaviour shows early yield, around 2.54 × 10−2, and it goes on until it gets to a plastic limit, which is in comparison to Figure 14b–d because of the elastic property. For Figure 14b–d, the epoxy and the Nylon PA66-GF have similar behaviours, despite that they are different because the latter has higher stress values. In Figure 14c, the stress–strain behaviour shows that it yields at 2.43 × 10−2. From this study, it can be observed that if the reeling is done along the fibre direction of the reeling hose along its X–X direction rather than its transverse direction or in-plane shear directions, it will yield along that direction. As such, failure of reeling hose is also dependent on the angle of orientation of the ply layers of the bonded hoses. However, the covalent bonds in the bonded hose are designed to prevent such failures. This study shows that the material effect of elastoplastic properties in elastomers used in modelling the hoses can also help to increase their elastic behaviour and durability and, thus, increase their capacity, suitability and reeling-ability.

4.6. Discussion of Results

The results of the local study presented provide highly useful information that might be used in future study on the use of tubular pipes in offshore hoses and composite risers in this specific application. Although composite materials offer a higher strength-to-weight ratio than typical steels, the operational conditions in which offshore bonded composite hose is deployed cause a sharp and large increase in stress, followed by a cyclic load during reeling. Owing to its free hanging weight, the pipeline encounters maximum force as the reeling process begins, and as the process continues, the pipeline will sway repeatedly due to wave motion, introducing changing magnitudes of force. The pipeline will be subjected to a cyclic load and hence increased fatigue as a result of a continuous application of variable force from wave motion, which will be unexpected in severity in uncontrolled conditions. Mechanical fatigue demands that the theoretical mechanical life spans for both the structures and materials will eventually decline. A steady loss of mechanical strength in the pipeline’s materials would eventually lead to small micro cracks inside the structure, especially in corrosive environments, which, according to earlier literature, increases the pipeline’s fatigue rate even more. Furthermore, the pipeline’s different composite layering can attach to each other in a variety of ways. This cyclic loading of the pipeline will also introduce possible micro cracking of any applied adhesion layers of the pipeline, implying a possible explanation for layer delamination in service of these pipelines.
In principle, the application of this tubular bending model can be seen in reeling, which requires a reeling drum and a material that goes around it. In the pipe-bending model, two models were compared, namely the linear-elastic and the elasto-plastic models. This study presents visualization profiles using EPS from the reeling operation, as it is important to assess the strain during reeling by considering APS, which is recommended at 2% according to DNV-OS-F101; as such, this model also looks at other plastic strain values and effects on the bending model. The assumption is that it can increase due to the limitation of plastic deformation on the composite materials selected. Furthermore, data generated from simulations using various product fluids within the pipeline could be used to deduce more indications of pipeline collapse. As a result of the increment in material density, the magnitude of mechanical factors increases. Marine risers, bonded hoses and subsea pipes are primarily used to transfer fluids such as oil products. As a result, as the density of the fluid increases, so does the necessity for an operational pressure that can ensure the fluid’s continuous flow. An increase in internal pressure, as well as the weight of the pipeline and the product fluid, will result in an increase in mechanical stress. Increased cyclic loading will increase mechanical fatigue of the composite layering as well as the danger of adhesion between layers, which could result in layer delamination. However, the scope of this research is confined to the reeling of bonded hoses without the presence of fluid, as well as the tension resulting from this reeling process. It has also been demonstrated that during reeling, the tensioner and aligner can exert some contact pressure on the hose’s body as it reels around it in a cyclic motion.
From the discussion based on the analysis of this study, the following observations and recommendations were made:
1.
For the reeling model, the results of Effective Plastic Strain (EPS) presented in Figure 7, Figure 8 and Figure 9 were obtained on the reeling hose using three composite models: epoxy composite, carbon fibre composite and Nylon PA66-GF composite. Additionally, two models were used: the elastoplastic model and the elastic linearity model. Assessing strains on each model using EPS, it is observed that the elastoplastic model had higher strains than the linear elastic model. Additionally, the maximum strain direction observed was the strain along EPXY at 1.73 × 10−1. Along the hoop direction, the material will become more hardened, especially in a homogenised model, than along the longitudinal direction of the material. It is important to assess the strain during reeling by considering Accumulated Plastic Strain (APS), which is recommended at 2% according to DNV-OS-F101, which can increase due to the limitation of plastic deformation on the composite materials selected. However, the EPS was considered, which also gives an indication of the behaviour of the material and shows profiles of the strained and unstrained regions. Due to the locus of the yield stress on the hose section been reeled, the hose material has a plastic behaviour observed after reeling. As such, the total linear strain and total nonlinear strains were considered.
2.
The nonlinear analysis of the reeling operation as carried out in the Finite Element Analysis (FEA) is depicted in the order of the timesteps in Figure 13. It can be observed that the total strains started to propagate through the hose section as it was tensioned and spooled onto the reeling drum. Secondly, there is an accumulated plastic strain (APS) observed in the reeling operation which also transfers some strain energy onto the reeling drum as seen in these strain contour plots. Thus, it is necessary to investigate the contact pressure and the accumulated strain energy at these regions on the hoses. Additionally, it evident that the materials have different effects on the hose, as such two models were preferred—the carbon fibre and the nylon PA66GF composite models, as the strains showed a better consistency. However, further study is recommended on optimizing the models and reeling with unhomogenized hose models. Additionally, more studies on the application of this model and the global response of the reeling hose model are recommended on the effect of the reel drum and the HEV couplings load’s contact with the body of the FPSO.
3.
The internal pressure and external pressure tests are very important aspect of the design of the reeling hoses. It was observed that the higher the pressure, the higher the von Mises stresses, maximum strains and maximum deformations on the reeling hose, as presented in Section 4.2, Section 4.3 and Section 4.4. However, this can be minimised by increasing the reinforcement of the reeling hose or by using lighter materials with a high strength–weight ratio, such as composites, or applying the hose hydrodynamic loads. A detailed study is recommended based on combined loading and the effect of the composite materials in the layers. Additionally, a global analysis on the reeling hose operation is recommended to investigate the effect of effective tension, bending moment, curvature and fluid content in the dynamic analysis of the offshore bonded composite hose.
4.
From this study, it can be observed that if the reeling is done along the fibre direction of the reeling hose along its X–X direction, rather than its transverse direction or in-plane shear directions, it will yield along that direction. As such, failure of the reeling hose is also dependent on the angle of the orientation of the ply layers of the bonded hoses. However, the covalent bonds in the bonded hose are designed to prevent such failures. This study shows that the material effect of elastoplastic properties in elastomers used in modelling the hoses can also help to increase its elastic behaviour and durability, thus increasing its capacity, suitability and reeling ability.
5.
The contact pressure is due to the reaction between the tensioner and the reeling drum, as seen in the model result in Figure 14a,b. During the reeling, the motion of the tensioner as it rolls onto the reeling drum to align it creates an opposite reaction, seen in the reaction force in Figure 14c,d. As this continues, the areas of the hose that are weakened start to deform and directional deformation starts to propagate in the direction of the composite layer. Considering both the elastic linearity and the elastoplastic model, the later seems to have an increase in hose deformation, contact pressure and reaction force than the linear elastic model, but this is relative as it depends on the stress–strain data from experiment. However, further research is recommended on the limit for the layers and on the interfacial stress of the offshore hose model.

5. Conclusions

This study presents an investigation of plastic strain deformation investigation on the effective plastic strain (EPS) of under bending and reeling operations. This study is an application based on an understanding of the material mechanics of pipe structures, plasticity studies, stress analysis and finite element modelling (FEM). The model highlights include the following: Firstly, the determination of Effective Plastic Strain (EPS) of the hose and the implications on the reeling hose. This involved the design of the hose tube with detailed stress profiles. Secondly, the novelty was the response study on the effect of contact pressure leading to the compression load or crush load on the tubular hose that comes from either the load of the tensioner or other reeled sections of the hose while on the reel drum or the vessel load response. Thirdly, there was novelty in the analytical model on the plastic deformation of tubular hoses and stress analysis. Fourthly, some results on stress–strain profiles for the different hose models compared against the elastoplastic hose model.
From the local design analysis, the results obtained in this study provide useful results for understanding the fundamental strain-wise mechanical behaviours during both operational, and static non-operational, conditions and reeling operations. This is important, as this homogenised offshore bonded composite hose is designed for a reeling system, but could be applied for other operations. However, further research is recommended on this investigation to provide similar mechanical data results and trends and carry out the global design with other environmental sea states. In addition, more studies on the local design based on burst case and collapse case, the effect of liner wrinkling, micro-cracking and metal-composite interface can be conducted, similar to the study [29,30]. Lastly, the reeling modelling used in local design in Simscale OpenFE platform with Effective Plastic Strain (EPS) contour profiles obtained from the Finite Element Analysis (FEA) were presented as another strain estimation method like the Accumulated Plastic Strain (APS).

Author Contributions

Conceptualization, C.V.A.; methodology, C.V.A.; software, C.V.A.; validation, C.V.A.; I.A.; E.F.A.; A.K.O.; I.A.J.; A.C.O. and F.W.; formal analysis, C.V.A.; I.A.; E.F.A.; A.K.O.; I.A.J.; A.C.O. and F.W.; investigation, C.V.A.; I.A.; E.F.A.; A.K.O.; I.A.J.; A.C.O. and F.W.; resources, C.V.A.; data curation, C.V.A., writing—original draft preparation, C.V.A.; writing—review and editing, C.V.A.; I.A.; E.F.A.; A.K.O.; I.A.J.; A.C.O. and F.W.; visualization, C.V.A.; I.A.; E.F.A.; A.K.O.; I.A.J.; A.C.O. and F.W.; supervision, C.V.A. and F.W; project administration, C.V.A.; funding acquisition, C.V.A., E.F.A., A.K.O. and F.W. All authors have read and agreed to the published version of the manuscript.

Funding

The Department of Engineering, Lancaster University, UK, and the EPSRC Doctoral Training Centre (DTC) are highly appreciated. In addition, the funding of Overseas Scholarships by Nigeria’s NDDC (Niger Delta Development Commission) is also appreciated, as well as the support of Standards Organisation of Nigeria (SON), F.C.T Abuja, Nigeria. I.A.J. acknowledges the funding support of Yayasan UTP (YUTP) education grant and Ahmadu Bello University (ABU), Zaria. The financial support of TETFUND Nigeria is acknowledged by E.F.A. and A.K.O. In addition, F.W. acknowledges the National Natural Science Foundation of China (NSFC) for supporting Projects 51922064 and 51879143 including this study. The article processing charges (APC) for this article were funded by the 1st Author—C.V.A., with support from MDPI’s Inventions.

Data Availability Statement

The data supporting the reported results cannot be shared at this time, as they have been used in producing more publications on this research.

Acknowledgments

The author acknowledges the technical support from Lancaster University Engineering Department, especially during the COVID-19 pandemic. The authors appreciate the provision of the online software by Simscale, their technical support and the permissions granted by Simscale to adapt model for our study using their online platform is also well acknowledged and duly appreciated. We also appreciate the support of both the journal reviewers and journal editors for their feedback while reviewing this manuscript.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript or in the decision to publish the results.

References

  1. Dawood, A.A. A Study of Pipeline Response during Reel-Lay Installation. Master’s Thesis, Memorial University of Newfoundland, St John’s Newfoundland, NL, Canada, 2014. Available online: https://research.library.mun.ca/8055/1/thesis.pdf (accessed on 18 December 2021).
  2. Palmer, A.C.; King, R.A. Subsea Pipeline Engineering, 2nd ed.; PennWell Corporation: Tulsa, Oklahoma, USA, 2008. [Google Scholar]
  3. Bai, Y.; Bai, Q. Subsea Pipeline and Risers; Elsevier Publishers: Oxford, UK, 2005. [Google Scholar]
  4. Guo, B.; Song, S.; Ghalambor, A.; Lin, T.R.; Chacko, J. Offshore Pipelines; Elsevier Publishers: Oxford, UK, 2005. [Google Scholar]
  5. Amaechi, C.V.; Ye, J.; Hou, X.; Wang, F.-C. Sensitivity Studies on Offshore Submarine Hoses on CALM Buoy with Comparisons for Chinese-Lantern and Lazy-S Configuration OMAE2019-96755. In Proceedings of the 38th International Conference on Ocean, Offshore and Arctic Engineering, Glasgow, Scotland, 9–14 June 2019. [Google Scholar]
  6. Amaechi, C.V.; Wang, F.; Hou, X.; Ye, J. Strength of submarine hoses in Chinese-lantern configuration from hydrodynamic loads on CALM buoy. Ocean. Eng. 2019, 171, 429–442. [Google Scholar] [CrossRef] [Green Version]
  7. Amaechi, C.V.; Wang, F.; Ye, J. Numerical studies on CALM buoy motion responses, and the effect of buoy geometry cum skirt dimensions with its hydrodynamic waves-current interactions. Ocean Eng. 2022, 244, 110378. [Google Scholar] [CrossRef]
  8. Amaechi, C.V.; Wang, F.; Ye, J. Understanding the fluid-structure interaction from wave diffraction forces on CALM buoys: Numerical and analytical solutions. Ships Offshore Struct. 2021, in press. [Google Scholar] [CrossRef]
  9. Amaechi, C.V.; Wang, F.; Ye, J. Numerical Assessment on the Dynamic Behaviour of Submarine Hoses Attached to CALM Buoy Configured as Lazy-S under Water Waves. J. Mar. Sci. Eng. 2021, 9, 1130. [Google Scholar] [CrossRef]
  10. Amaechi, C.V.; Wang, F.; Ye, J. Mathematical Modelling of Bonded Marine Hoses for Single Point Mooring (SPM) Systems, with Catenary Anchor Leg Mooring (CALM) Buoy Application—A Review. J. Mar. Sci. Eng. 2021, 9, 1179. [Google Scholar] [CrossRef]
  11. Amaechi, C.V.; Chesterton, C.; Butler, H.O.; Wang, F.; Ye, J. An Overview on Bonded Marine Hoses for sustainable fluid transfer and (un)loading operations via Floating Offshore Structures (FOS). J. Mar. Sci. Eng. 2021, 9, 1236. [Google Scholar] [CrossRef]
  12. Amaechi, C.V.; Chesterton, C.; Butler, H.O.; Wang, F.; Ye, J. Review on the mechanics and design of marine bonded hoses for CALM buoys. Ocean Eng. J. 2021, 242, 1–32. [Google Scholar] [CrossRef]
  13. Amaechi, C.V.; Wang, F.; Ja’e, I.A.; Aboshio, A.; Odijie, A.C.; Ye, J. A literature review on the technologies of bonded hoses for marine application. Ships Offshore Struct. 2022. under review. [Google Scholar]
  14. Amaechi, C.V. Novel Design, Hydrodynamics and Mechanics of Marine Hoses in Oil/Gas Applications. Ph.D. Thesis, Lancaster University, Lancaster, UK, 2021. [Google Scholar]
  15. Chesterton, C. A Global and Local Analysis of Offshore Composite Material Reeling Pipeline Hose, with FPSO Mounted Reel Drum. Ph.D. Thesis, Lancaster University, Lancaster, UK, 2020. [Google Scholar]
  16. Szczotka, M. Dynamic analysis of offshore pipe laying operation using the reel method. Acta Mech. Sin. 2011, 27, 44–55. [Google Scholar] [CrossRef]
  17. Szczotka, M. Pipe laying simulation with an active reel drive. Ocean Eng. 2010, 37, 539–548. [Google Scholar] [CrossRef]
  18. Ahmetoglu, M.; Altan, T. Tube hydroforming: State-of-the-art and future trends. J. Mater. Process. Technol. 2000, 98, 25–33. [Google Scholar] [CrossRef]
  19. Kyriakides, S.; Corona, E. Mechanics of Offshore Pipelines: Volume 1: Buckling and Collapse; Elsevier Publishers: Oxford, UK, 2007. [Google Scholar]
  20. Yang, H.; Li, H.; Zhang, Z.; Zhan, M.; Liu, J.; Li, G. Advances and Trends on Tube Bending Forming Technologies. Chin. J. Aeronaut. 2012, 25, 1–12. [Google Scholar] [CrossRef] [Green Version]
  21. Lipski, W. Mechanical Lined Pipe—Installation by Reel-Lay. Page 17. 2011. Available online: https://www.yumpu.com/en/document/read/26877695/mechanical-lined-pipe-installation-by-reel-lay-subsea-uk (accessed on 15 November 2020).
  22. Toguyeni, G.A.; Banse, J. Mechanically lined pipe: Installation by reel-lay. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 2012. [Google Scholar] [CrossRef]
  23. Liu, K.X.; Liu, Y.L.; Yang, H.; Zhao, G.Y. Experimental study on cross-section distortion of thin-walled rectangular 3A21 aluminium alloy tube by rotary draw bending. Int. J. Mater. Prod. Technol. 2011, 42, 110–120. [Google Scholar] [CrossRef]
  24. Lu, S.; Fang, J.; Wang, K. Plastic deformation analysis and forming quality prediction of tube NC bending. Chin. J. Aeronaut. 2016, 29, 1436–1444. [Google Scholar] [CrossRef] [Green Version]
  25. McCann, S.; Evans, D.; Bannister, A.; Tan, H. Effects of Reeling on the Mechanical Properties of HFI Welded Pipes. Available online: https://www.pipeline-conference.com/sites/default/files/papers/PTC%202009%201.2%20Mc%20Cann.pdf (accessed on 18 December 2021).
  26. Chen, Y.; Tan, L.B.; Jaiman, R.K.; Sun, X.; Tay, T.E.; Tan, V.B.C. Global-Local Analysis of a Full-Scale Composite Riser During Vortex-Induced Vibration. In Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013. [Google Scholar] [CrossRef]
  27. Wang, C.; Shankar, K.; Morozov, E. Global design and analysis of deep sea FRP composite risers under combined environmental loads. Adv. Compos. Mater. 2017, 26, 79–98. [Google Scholar] [CrossRef]
  28. Wang, C.; Sun, M.; Shankar, K.; Xing, S.; Zhang, L. CFD Simulation of Vortex Induced Vibration for FRP Composite Riser with Different Modeling Methods. Appl. Sci. 2018, 8, 684. [Google Scholar] [CrossRef] [Green Version]
  29. Amaechi, C.V.; Gillett, N.; Odijie, A.C.; Hou, X.; Ye, J. Composite risers for deep waters using a numerical modelling approach. Compos. Struct. 2019, 210, 486–499. [Google Scholar] [CrossRef] [Green Version]
  30. Amaechi, C.V.; Ye, J. Local tailored design of deep water composite risers subjected to burst, collapse and tension loads. Ocean. Eng. 2021, in press. [Google Scholar] [CrossRef]
  31. Amaechi, C.V.; Gillett, N.; Odijie, A.C.; Wang, F.; Hou, X.; Ye, J. Local and Global Design of Composite Risers on Truss SPAR Platform in Deep waters. In Proceedings of the 5th International Conference on Mechanics of Composites, Lisbon, Portugal, 1–4 July 2019; pp. 1–3. [Google Scholar]
  32. Amaechi, C.V.; Ye, J. A numerical modeling approach to composite risers for deep waters. In Proceedings of the International Conference on Composite Structures, Paris, France, 4–7 September 2017. [Google Scholar]
  33. Pham, D.; Sridhar, N.; Qian, X.; Sobey, A.; Achintha, M.; Shenoi, A. A review on design, manufacture and mechanics of composite risers. Ocean. Eng. 2016, 112, 82–96. [Google Scholar] [CrossRef] [Green Version]
  34. Singh, M.; Ahmad, S. Fatigue Life Calculation of Deep Water Composite Production Risers by Rain Flow Cycle Counting Method. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering; Volume 5B: Pipeline and Riser Technology, St. John’s, NL, Canada, 31 May–5 June 2015. [Google Scholar] [CrossRef]
  35. Xu, Y.; Fang, P.; Bai, Y. Mechanical behavior of metallic strip flexible pipes during reeling operation. Mar. Struct. 2021, 77, 102942. [Google Scholar] [CrossRef]
  36. Williams, D. Analysis of Drilling Risers in Harsh and Deepwater Environments. 2010. Available online: https://www.offshore-mag.com/rigs-vessels/article/16763767/analysis-of-drilling-risers-in-harsh-and-deepwater-environments (accessed on 9 April 2021).
  37. Sohrabi, M.; Henderson, G.D.; Tehrani, D.H.; Danesh, A. Visualisation of Oil Recovery by Water Alternating Gas (WAG) Injection Using High Pressure Micromodels—Water-Wet System. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 1–4 October 2000. [Google Scholar] [CrossRef]
  38. Ye, J.; Cai, H.; Liu, L.; Zhai, Z.; Amaechi, C.V.; Wang, Y.; Wan, L.; Yang, D.; Chen, X.; Ye, J. Microscale intrinsic properties of hybrid unidirectional/woven composite laminates: Part I experimental tests. Compos. Struct. 2021, 262, 113369. [Google Scholar] [CrossRef]
  39. Amaechi, C.V.; Odijie, C.; Sotayo, A.; Wang, F.; Hou, X.; Ye, J. Recycling of Renewable Composite Materials in the Offshore Industry. Encycl. Renew. Sustain. Mater. 2019, 2, 583–613. [Google Scholar] [CrossRef]
  40. Amaechi, C.V.; Odijie, C.; Etim, O.; Ye, J. Economic Aspects of Fiber Reinforced Polymer Composite Recycling. Encycl. Renew. Sustain. Mater. 2019, 2, 377–397. [Google Scholar] [CrossRef]
  41. Tang, N.C. Plastic-deformation analysis in tube bending. Int. J. Press. Vessel. Pip. 2000, 77, 751–759. [Google Scholar] [CrossRef]
  42. Popoola, L.T.; Grema, A.S.; Latinwo, K.; Gutti, B.; Balogun, A.S. Corrosion problems during oil and gas production and its mitigation. Int. J. Ind. Chem. 2013, 4, 35. [Google Scholar] [CrossRef] [Green Version]
  43. Raja, P.B.; Sethuraman, M.G. Natural products as corrosion inhibitor for metals in corrosive media—A review. Mater. Lett. 2008, 62, 113–116. [Google Scholar] [CrossRef]
  44. Szczygieł, B.; Kołodziej, M. Composite Ni/Al2O3 coatings and their corrosion resistance. Electrochim. Acta 2005, 50, 4188–4195. [Google Scholar] [CrossRef]
  45. Lassen, T.; Lem, A.I.; Imingen, G. Load response and finite element modelling of bonded offshore loading hoses. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014. [Google Scholar] [CrossRef]
  46. Wu, W.; Zhang, P.; Zeng, X.; Jin, L.; Yao, S.; Luo, A.A. Bendability of the wrought magnesium alloy AM30 tubes using a rotary draw bender. Mater. Sci. Eng. A 2008, 486, 596–601. [Google Scholar] [CrossRef]
  47. Liu, K.X.; Liu, Y.L.; Yang, H. Experimental study on the effect of dies on wall thickness distribution in NC bending of thin-walled rectangular 3A21 aluminum alloy tube. Int. J. Adv. Manuf. Technol. 2013, 68, 1867–1874. [Google Scholar] [CrossRef]
  48. Corner, E. Bredero Shaw’s Complete Coating Assurance Model; World Pipelines: Farnham, UK, 2014; Available online: https://www.worldpipelines.com/product-news/21052014/bredero_shaws_complete_coating_assurance_model/ (accessed on 21 December 2021).
  49. Fang, J.; Lu, S.; Wang, K.; Gu, Q.; Shang, S. Springback behaviors of high strength stainless steel tube after numerical control rotary draw bending. IOP Conf. Ser. Mater. Sci. Eng. 2018, 423, 012184. [Google Scholar] [CrossRef]
  50. Fang, J.; Ouyang, F.; Lu, S.; Wang, K.; Min, X.; Xiao, B. Wall thinning behaviors of high strength 0Cr21Ni6Mn9N tube in numerical control bending considering variation of elastic modulus. Adv. Mech. Eng. 2021, 13, 16878140211021241. [Google Scholar] [CrossRef]
  51. Zhang, X.; Zhao, C.; Du, B.; Chen, D.; Li, Y.; Han, Z. Research on Hydraulic Push-Pull Bending Process of Ultra-Thin-Walled Tubes. Metals 2021, 11, 1932. [Google Scholar] [CrossRef]
  52. Zhang, Z.; Wu, J.; Guo, R.; Wang, M.; Li, F.; Guo, S.; Wang, Y.; Liu, W. A semi-analytical method for the springback prediction of thick-walled 3D tubes. Mater. Des. 2016, 99, 57–67. [Google Scholar] [CrossRef]
  53. Zhao, T.; Hu, Z. Numerical analysis of detaching and wrinkling of mechanically lined pipe during its spooling-on stage to the reel. Theor. Appl. Mech. Lett. 2015, 5, 205–209. [Google Scholar] [CrossRef] [Green Version]
  54. Qian, S.; Bai, Z.H.; Hu, W.T.; Lin, W.; Wang, T.L.; Zhang, J.S. Design and Key Process Simulation of a New Type of Pipe Bending Unit. Int. J. Simul. Model. 2021, 20, 559–570. [Google Scholar] [CrossRef]
  55. Gou, Y.; Shuang, Y.; Zhou, Y.; Mao, F.; Ding, X.; Cai, W.; Zhao, C. Effect of additional axial tension on formability of equal curvature-diameter bending without mandrel for 0Cr18Ni9 stainless steel tube. Mater. Res. Express 2019, 6, 066518. [Google Scholar] [CrossRef]
  56. Bilston, D.; Ruan, D.; Candido, A.; Durandet, Y. Parametric study of the cross-section shape of aluminium tubes in dynamic three-point bending. Thin-Walled Struct. 2019, 136, 315–322. [Google Scholar] [CrossRef]
  57. Cheng, X.; Wang, H.; El-Aty, A.A.; Tao, J.; Wei, W.; Qin, Y.; Gui, X. Cross-section deformation behaviors of a thin-walled rectangular tube of continuous varying radii in the free bending technology. Thin-Walled Struct. 2020, 150, 106670. [Google Scholar] [CrossRef]
  58. Guo, X.; Wei, W.; Xu, Y.; El-Aty, A.A.; Liu, H.; Wang, H.; Luo, X.; Tao, J. Wall thickness distribution of Cu–Al bimetallic tube based on free bending process. Int. J. Mech. Sci. 2019, 150, 12–19. [Google Scholar] [CrossRef]
  59. Wu, J.; Zhang, Z.; Shang, Q.; Li, F.; Wang, Y.; Hui, Y.; Fan, H. A method for investigating the springback behavior of 3D tubes. Int. J. Mech. Sci. 2017, 131, 191–204. [Google Scholar] [CrossRef]
  60. Jian, Z.; Xin, W.; Wenxian, T.; Fang, W.; Baoji, Y. Experimental and numerical buckling analysis of toroidal shell segments under uniform external pressure. Thin-Walled Struct. 2020, 150, 106689. [Google Scholar] [CrossRef]
  61. Li, H.; Yang, H.; Zhang, Z.Y.; Li, G.J.; Liu, N.; Welo, T. Multiple instability-constrained tube bending limits. J. Mater. Process. Technol. 2014, 214, 445–455. [Google Scholar] [CrossRef]
  62. Timoshenko, S.P. LXVI. On the correction for shear of the differential equation for transverse vibrations of prismatic bars. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1921, 41, 744–746. [Google Scholar] [CrossRef] [Green Version]
  63. Timoshenko, S.P.X. On the transverse vibrations of bars of uniform cross-section. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1922, 43, 125–131. [Google Scholar] [CrossRef] [Green Version]
  64. Timoshenko, S.P. Strength of Materials, Part II, 2nd ed.; McGraw Hill Publishers: New York, NY, USA, 1941. [Google Scholar]
  65. Focke, E.S. Reeling of Tight Fit Pipe. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2007. Available online: http://resolver.tudelft.nl/uuid:21348ba3-bce9-4b01-98fd-f1a32fafaaa9 (accessed on 29 November 2020).
  66. Manouchehri, S. A Discussion of Practical Aspects of Reeled Flowline Installation. Available online: http://cyrusogr.com/files/OMAE2012-83649.pdf (accessed on 9 April 2021).
  67. Taams, V.J. The Onset of Pipeline Twist during Reel-Lay Operations. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2016. Available online: http://resolver.tudelft.nl/uuid:9edd02a2-956f-414d-83c8-dae8b928f585 (accessed on 9 April 2021).
  68. Gao, Q.; Zhang, P.; Duan, M.; Yang, X.; Shi, W.; An, C.; Li, Z. Investigation on structural behavior of ring-stiffened composite offshore rubber hose under internal pressure. Appl. Ocean Res. 2018, 79, 7–19. [Google Scholar] [CrossRef]
  69. Amaechi, C.V.; Chesterton, C.; Butler, H.O.; Odijie, C.A.; Gu, Z.; Wang, F.; Hou, X.; Ye, J. Finite element modelling on the mechanical behaviour of Marine Bonded Composite Hose (MBCH) under burst and collapse. J. Mar. Sci. Eng. 2021. under review. [Google Scholar]
  70. Amaechi, C.V.; Wang, F.; Ye, J. Investigation on hydrodynamic characteristics, wave-current interaction, and sensitivity analysis of submarine hoses attached to a CALM buoy. J. Mar. Sci. Eng. 2021. under review. [Google Scholar]
  71. Amaechi, C.V.; Wang, F.; Ye, J. Experimental study on motion characterization of CALM buoy hose system under water waves. J. Mar. Sci. Eng. 2021. under review. [Google Scholar]
  72. API 17K. Specification for Bonded Flexible Pipe, 3rd ed.; American Petroleum Institute (API): Washington, DC, USA, 2017. [Google Scholar]
  73. Simscale. Simscale Documentation. 2021. Available online: https://www.simscale.com/docs/ (accessed on 18 December 2021).
  74. Tresca, H. Sur l’Ecoulement des Corps Solides Soumis a de Fortes Pressions. C. R. Acad. Sci. Paris 1864, 59, 754. [Google Scholar]
  75. Huber, M.T. Właściwa praca odkształcenia jako miara wyteżenia materiału. Czasopismo Techniczne 1904, 22, 38–40, 49–50, 61–62, 80–81. [Google Scholar]
  76. Von Mises, R. Mechanik der Festen Korper im Plastisch Deformablen Zustand. Nachr. Ges. Wiss. Gott. 1913, 1913, 582–592. [Google Scholar]
  77. Dowling, N.E.; Kampe, S.L.; Kral, M.V. Mechanical Behavior of Materials, 5th ed.; Pearson, Prentice Hall: Hoboken, NY, USA, 2019. [Google Scholar]
  78. Hencky, H.Z. Zur Theorie Plasticher Deformationen und der Hierdurch im Material Hervorgerufenen Nachspannungen. Z. Angerw. Math. Mech. 1924, 4, 323. [Google Scholar] [CrossRef]
  79. Taylor, G.I.; Quinney, H. The Plastic Distortion of Metals. Philos. Trans. R. Soc. Lond. 1931, 230, 323–363. [Google Scholar] [CrossRef]
Inventions 07 00009 g001 550
Figure 1. An application of tubular pipe bending using two methods conducted in Lancaster University Engineering Workshop.
Figure 1. An application of tubular pipe bending using two methods conducted in Lancaster University Engineering Workshop.
Inventions 07 00009 g001
Inventions 07 00009 g002 550
Figure 2. Typical example of a reeled system during a bend test for validating reeling capability after coating by Bredero Shaw. (Permission obtained from World Pipelines and Elizabeth Corner. Source: Corner E. [48]).
Figure 2. Typical example of a reeled system during a bend test for validating reeling capability after coating by Bredero Shaw. (Permission obtained from World Pipelines and Elizabeth Corner. Source: Corner E. [48]).
Inventions 07 00009 g002
Inventions 07 00009 g003 550
Figure 3. Plastic bending showing moments.
Figure 3. Plastic bending showing moments.
Inventions 07 00009 g003
Inventions 07 00009 g004 550
Figure 4. Sign conventions for the cylindrical layer of tubular pipe showing force and deformations.
Figure 4. Sign conventions for the cylindrical layer of tubular pipe showing force and deformations.
Inventions 07 00009 g004
Inventions 07 00009 g005 550
Figure 5. The details for the FEA of bending tubular pipe model, in Simscale.
Figure 5. The details for the FEA of bending tubular pipe model, in Simscale.
Inventions 07 00009 g005
Inventions 07 00009 g006 550
Figure 6. Hose-Pipe mechanics analysis in reeling operation on OBCH, (a) before spooling, (b) during spooling, (c) moment diagram during spooling-on in reality and (d) shear force diagram during spooling-on in reality.
Figure 6. Hose-Pipe mechanics analysis in reeling operation on OBCH, (a) before spooling, (b) during spooling, (c) moment diagram during spooling-on in reality and (d) shear force diagram during spooling-on in reality.
Inventions 07 00009 g006
Inventions 07 00009 g007 550
Figure 7. Forces on the (a) hoseline and the reel during spooling-on in reality, (b) hoseline during spooling-on in reality and (c) mechanical system for hose and reel separately for spooling-on.
Figure 7. Forces on the (a) hoseline and the reel during spooling-on in reality, (b) hoseline during spooling-on in reality and (c) mechanical system for hose and reel separately for spooling-on.
Inventions 07 00009 g007
Inventions 07 00009 g008 550
Figure 8. The mesh considered in the finite element modelling of the reeling hose.
Figure 8. The mesh considered in the finite element modelling of the reeling hose.
Inventions 07 00009 g008
Inventions 07 00009 g009 550
Figure 9. The total strain profiles for the reeling hose epoxy composite model. (a) total nonlinear strain of carbon fibre linear elastic model, (b) total linear strain of carbon fibre linear elastic model, (c) total nonlinear strain of epoxy elastoplastic model, (d) total linear strain of epoxy elastoplastic model.
Figure 9. The total strain profiles for the reeling hose epoxy composite model. (a) total nonlinear strain of carbon fibre linear elastic model, (b) total linear strain of carbon fibre linear elastic model, (c) total nonlinear strain of epoxy elastoplastic model, (d) total linear strain of epoxy elastoplastic model.
Inventions 07 00009 g009
Inventions 07 00009 g010 550
Figure 10. The total strain profiles for the reeling hose Carbon fibre composite model, showing (a) total nonlinear strain of carbon fibre linear elastic model, (b) total linear strain of carbon fibre linear elastic model, (c) total nonlinear strain of carbon fibre elastoplastic model, (d) total linear strain of carbon fibre elastoplastic model.
Figure 10. The total strain profiles for the reeling hose Carbon fibre composite model, showing (a) total nonlinear strain of carbon fibre linear elastic model, (b) total linear strain of carbon fibre linear elastic model, (c) total nonlinear strain of carbon fibre elastoplastic model, (d) total linear strain of carbon fibre elastoplastic model.
Inventions 07 00009 g010
Inventions 07 00009 g011 550
Figure 11. The total strain profiles for the reeling hose Nylon PA66GF composite model, showing (a) total nonlinear strain of nylon PA66GF linear elastic model, (b) total linear strain of nylon PA66GF linear elastic model, (c) total nonlinear strain of nylon PA66GF elastoplastic model, (d) total linear strain of nylon PA66GF elastoplastic model.
Figure 11. The total strain profiles for the reeling hose Nylon PA66GF composite model, showing (a) total nonlinear strain of nylon PA66GF linear elastic model, (b) total linear strain of nylon PA66GF linear elastic model, (c) total nonlinear strain of nylon PA66GF elastoplastic model, (d) total linear strain of nylon PA66GF elastoplastic model.
Inventions 07 00009 g011
Inventions 07 00009 g012 550
Figure 12. The stress profiles for the (a) von Mises stress on epoxy composite, (b) von Mises stress (signed) on epoxy composite, (c) von Mises stress on carbon fibre composite, (d) von Mises stress (signed) on carbon fibre composite, (e) von Mises stress on Nylon PA66-GF glass fibre composite models and (f) von Mises stress (signed) on Nylon PA66-GF glass fibre composite models.
Figure 12. The stress profiles for the (a) von Mises stress on epoxy composite, (b) von Mises stress (signed) on epoxy composite, (c) von Mises stress on carbon fibre composite, (d) von Mises stress (signed) on carbon fibre composite, (e) von Mises stress on Nylon PA66-GF glass fibre composite models and (f) von Mises stress (signed) on Nylon PA66-GF glass fibre composite models.
Inventions 07 00009 g012
Inventions 07 00009 g013 550
Figure 13. Contour plots of the reeling hose showing the reaction force, contact pressure, deformation and Von Mises stress from tensioner and reeling hose model, and the material is a Nylon PA66-GF composite reeled pipe on a steel drum. (a) Contact Pressure for linear elastic model, (b) Contact Pressure for elastoplastic model, (c) Reaction force for linear elastic model, (d) Reaction force for elastoplastic model, (e). Deformation for linear elastic model, (f) Deformation for elastoplastic model, (g) Von Mises profile for linear elastic model, (h) Von Mises profile for elastoplastic model, (i) VonMises (signed) profile for linear elastic model and (j) Von Mises (signed) profile for elastoplastic model.
Figure 13. Contour plots of the reeling hose showing the reaction force, contact pressure, deformation and Von Mises stress from tensioner and reeling hose model, and the material is a Nylon PA66-GF composite reeled pipe on a steel drum. (a) Contact Pressure for linear elastic model, (b) Contact Pressure for elastoplastic model, (c) Reaction force for linear elastic model, (d) Reaction force for elastoplastic model, (e). Deformation for linear elastic model, (f) Deformation for elastoplastic model, (g) Von Mises profile for linear elastic model, (h) Von Mises profile for elastoplastic model, (i) VonMises (signed) profile for linear elastic model and (j) Von Mises (signed) profile for elastoplastic model.
Inventions 07 00009 g013
Inventions 07 00009 g014 550
Figure 14. Stress–strain relationships for total strain in XX direction showing (a) elastoplastic material model, (b) epoxy linear elastic model, (c) carbon fibre linear elastic model and (d) Nylon PA66-Glass Fibre linear elastic model.
Figure 14. Stress–strain relationships for total strain in XX direction showing (a) elastoplastic material model, (b) epoxy linear elastic model, (c) carbon fibre linear elastic model and (d) Nylon PA66-Glass Fibre linear elastic model.
Inventions 07 00009 g014
Inventions 07 00009 g015 550
Figure 15. Strain–strain relationship applied to epoxy composite tubular pipe.
Figure 15. Strain–strain relationship applied to epoxy composite tubular pipe.
Inventions 07 00009 g015
Table
Table 1. Parameters for tubular pipe model.
Table 1. Parameters for tubular pipe model.
ParameterValueUnit
Tubular Pipe Outer radius0.025m
Tubular Pipe Inner radius0.02m
Length of Tube model0.45m
Radius of reel0.09m
Outer Reel radius0.11m
Tensioner roller radius0.02m
Table
Table 2. The Mechanical Properties of the Reeling Model Materials.
Table 2. The Mechanical Properties of the Reeling Model Materials.
MaterialDensity (kg/m3)Youngs Modulus (Pa)Bulk Modulus (Pa)Shear Modulus (Pa)Compressive Yield Strength (Pa)Tensile Yield Strength (Pa)Tensile Ultimate Strength (Pa)Poisons Ratio
Resin Polyester *12003 × 1092.7174 × 1091.1398 × 1091.41 × 1081.28 × 1085.18 × 1070.316
Nylon PA66 *11401.06 × 1091.1778 × 1093.9259 × 1082.32 × 1094.31 × 1074.97 × 1070.35
Nylon PA6/6 glass fiber reinforced (PA66-GF) *13606.82 × 1097.5778 × 1092.5259 × 1093.45 × 1071.39 × 1081.49 × 1080.35
Structural Steel *78502 × 10111.6667 × 10117.6923 × 10102.5 × 1082.5 × 1084.6 × 1080.3
Carbon fibre Composite (290GPa) *18102.9 × 10112.45 × 10119 × 1095.7 × 1084.2 × 1096 × 1080.3
Epoxy Composite14002.5 × 1093.16 × 1094.12 × 1097.36 × 1081.23 × 1089.19 × 1080.3
* Material properties data were obtained from MatWeb and Granta Material.
Table
Table 3. Metrics statistics for mesh quality.
Table 3. Metrics statistics for mesh quality.
tetEdgeRatiomin: 1.0376168721694845
max: 3.093679141141022
average: 1.5687727603714354
standard deviation 0.24089263488291165
median: 1.5297991927985433
0-th percentile: 1.0376168721694845
20-th percentile: 1.3834451887266506
40-th percentile: 1.4840930791225821
60-th percentile: 1.5785868300256487
80-th percentile: 1.704422472523748
100-th percentile: 3.093679141141022
triMaxAnglemin: 60.05482321990108
max: 127.35381485025293
average: 75.16684693915764
standard deviation 9.776579039415518
median: 73.29453691831603
0-th percentile: 60.05482321990108
20-th percentile: 66.44694506447732
40-th percentile: 71.02152546319378
60-th percentile: 75.96067124402948
80-th percentile: 83.28559263336597
100-th percentile: 127.35381485025293
triMinAnglemin: 19.35217668366241
max: 59.91366406827127
average: 46.70468441834977
standard deviation 7.28819486436269
median: 47.247565915521015
0-th percentile: 19.35217668366241
20-th percentile: 40.614183026171084
40-th percentile: 45.26696822391534
60-th percentile: 49.251397045870696
80-th percentile: 53.39908813577736
100-th percentile: 59.91366406827127
volumeRatiomin: 1.000000006324029
max: 3.961157286070154
average: 1.2483925373820084
standard deviation 0.2594881050104104
median: 1.1690056215931153
0-th percentile: 1.000000006324029
20-th percentile: 1.046584535039526
40-th percentile: 1.1233096677153573
60-th percentile: 1.2269723611496575
80-th percentile: 1.3949996092464683
100-th percentile: 3.961157286070154
tetAspectRatiomin: 1.0139867699918363
max: 4.118610423840127
average: 1.4166774878493793
standard deviation 0.2220781989410356
median: 1.3715678703595808
0-th percentile: 1.0139867699918363
20-th percentile: 1.2377215653270137
40-th percentile: 1.3283845255084676
60-th percentile: 1.4231277037383703
80-th percentile: 1.5670293674134164
100-th percentile: 4.118610423840127
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Amaechi, C.V.; Adefuye, E.F.; Oyetunji, A.K.; Ja’e, I.A.; Adelusi, I.; Odijie, A.C.; Wang, F. Numerical Study on Plastic Strain Distributions and Mechanical Behaviour of a Tube under Bending. Inventions 2022, 7, 9. https://doi.org/10.3390/inventions7010009

AMA Style

Amaechi CV, Adefuye EF, Oyetunji AK, Ja’e IA, Adelusi I, Odijie AC, Wang F. Numerical Study on Plastic Strain Distributions and Mechanical Behaviour of a Tube under Bending. Inventions. 2022; 7(1):9. https://doi.org/10.3390/inventions7010009

Chicago/Turabian Style

Amaechi, Chiemela Victor, Emmanuel Folarin Adefuye, Abiodun Kolawole Oyetunji, Idris Ahmed Ja’e, Ibitoye Adelusi, Agbomerie Charles Odijie, and Facheng Wang. 2022. "Numerical Study on Plastic Strain Distributions and Mechanical Behaviour of a Tube under Bending" Inventions 7, no. 1: 9. https://doi.org/10.3390/inventions7010009

Article Metrics

Back to TopTop