Fractional Order Active Disturbance Rejection Control for Canned Motor Conical Active Magnetic Bearing-Supported Pumps
Abstract
:1. Introduction
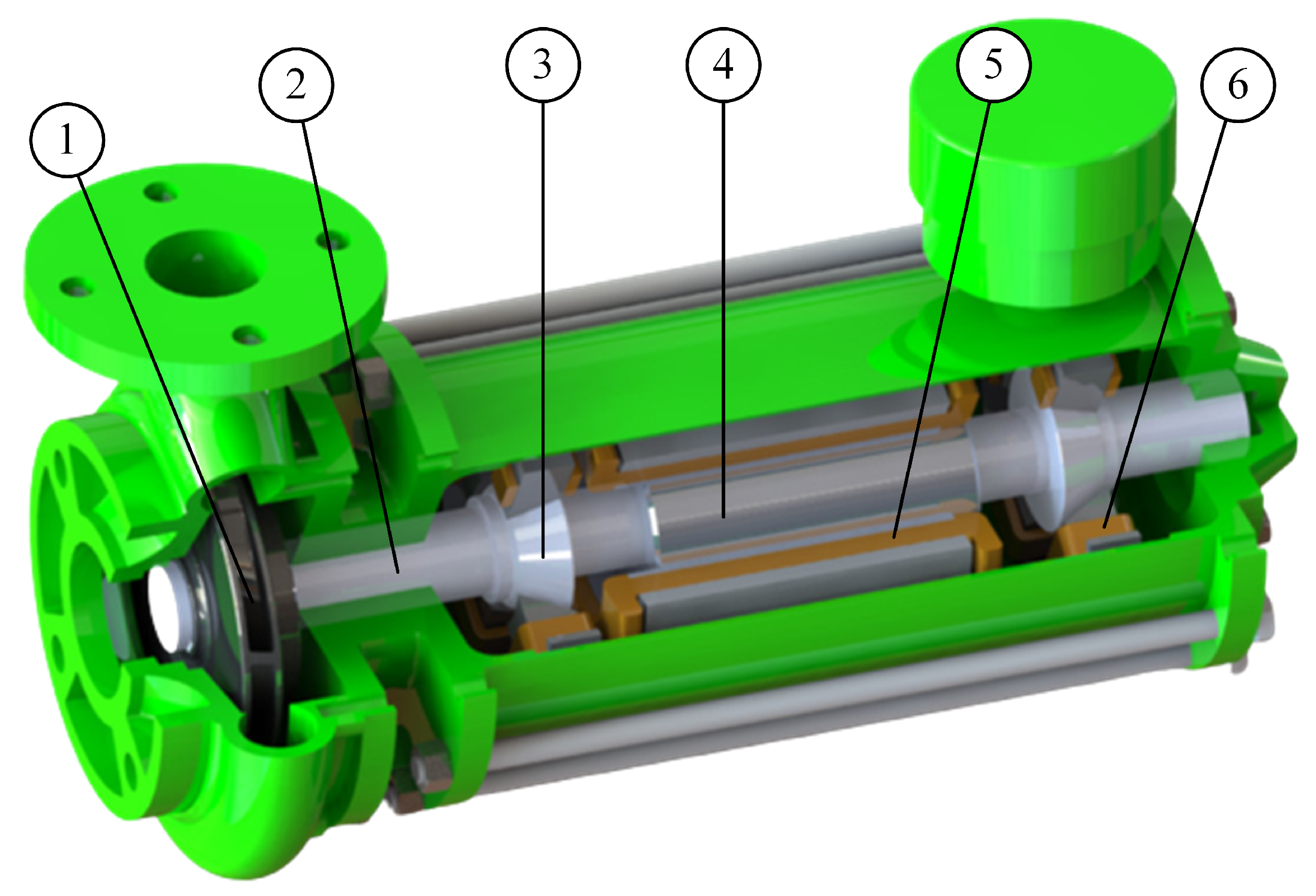
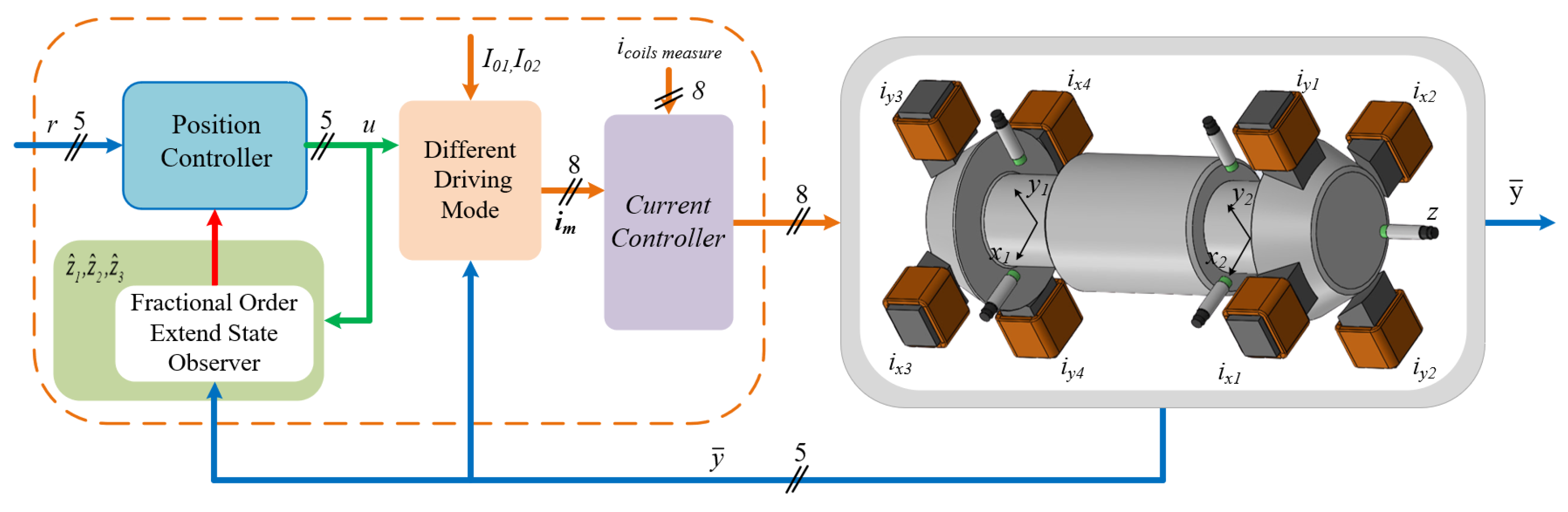
2. System Description and Modeling
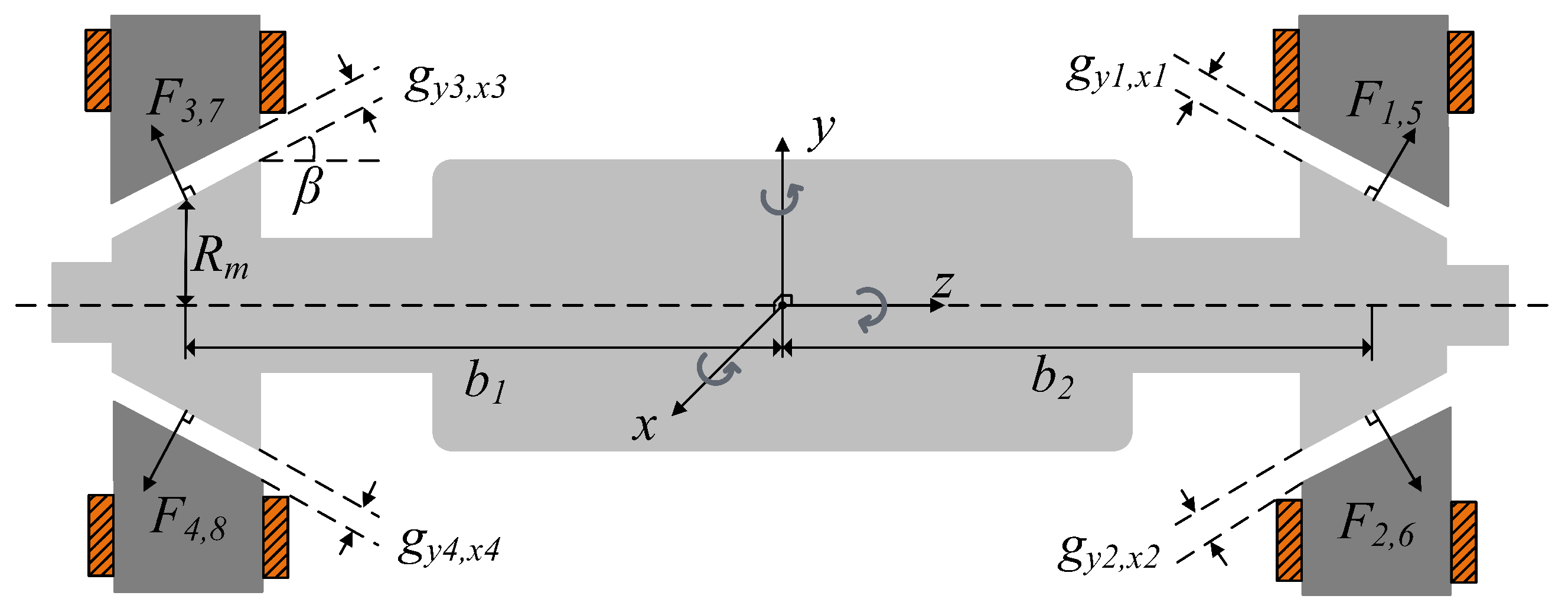
2.1. Fundamental Principle of Rigid Rotor Dynamics
2.2. Conical Active Magnetic Bearing Model
2.2.1. Electromechanical Interaction
2.2.2. Electromagnetic Forces
2.3. Hydrodynamic Forces
2.4. CAMB with Lumped Disturbances
2.5. Driving Current Structure
3. Lumped Disturbances Rejection Control Design
3.1. Preliminaries and Problem Formulation
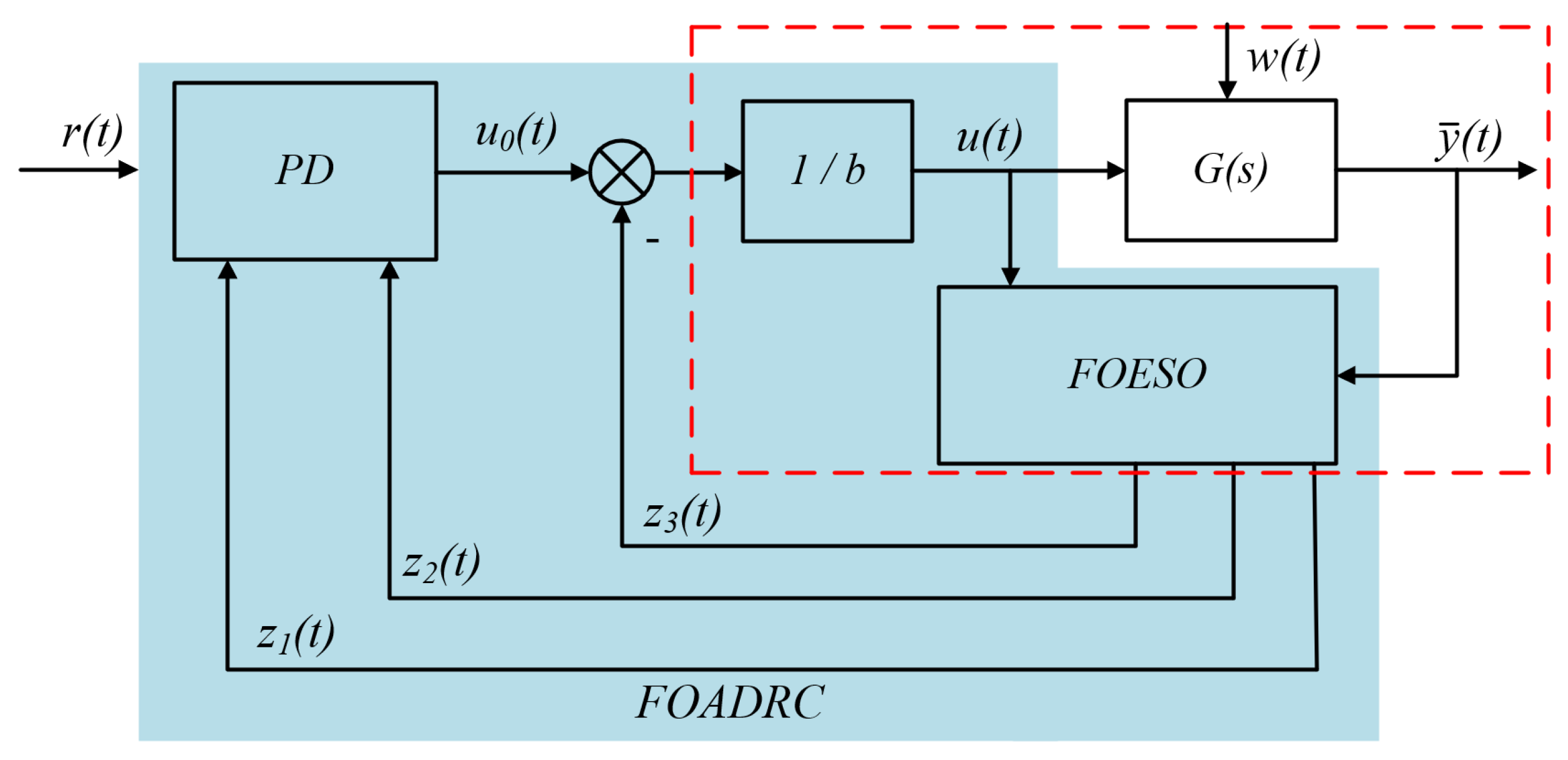
3.2. FOADRC Design
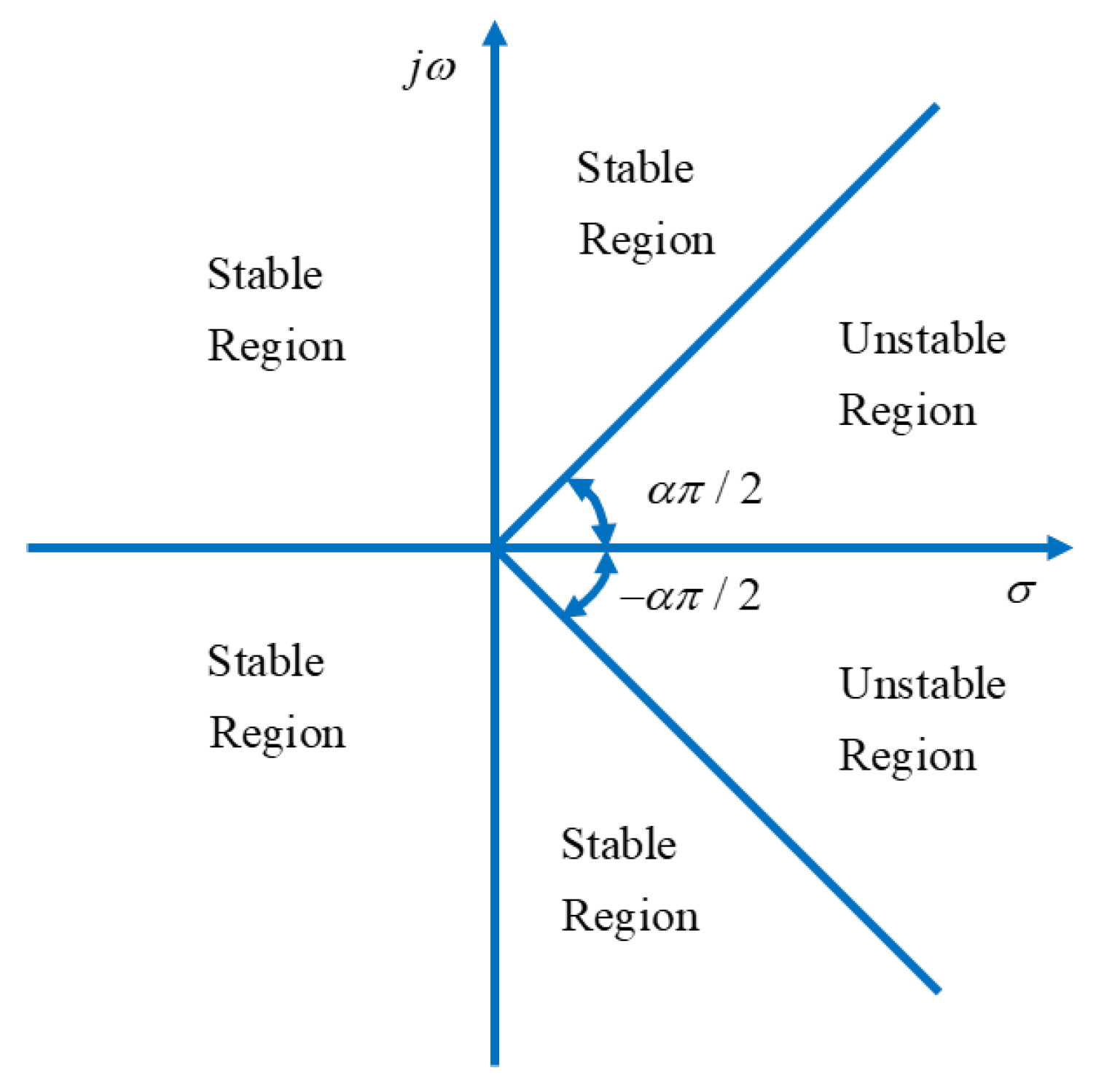
3.3. Stability Analysis and Parameter Tuning
4. Numerical Simulation Study
4.1. Simulation Settings
4.2. Results and Discussion
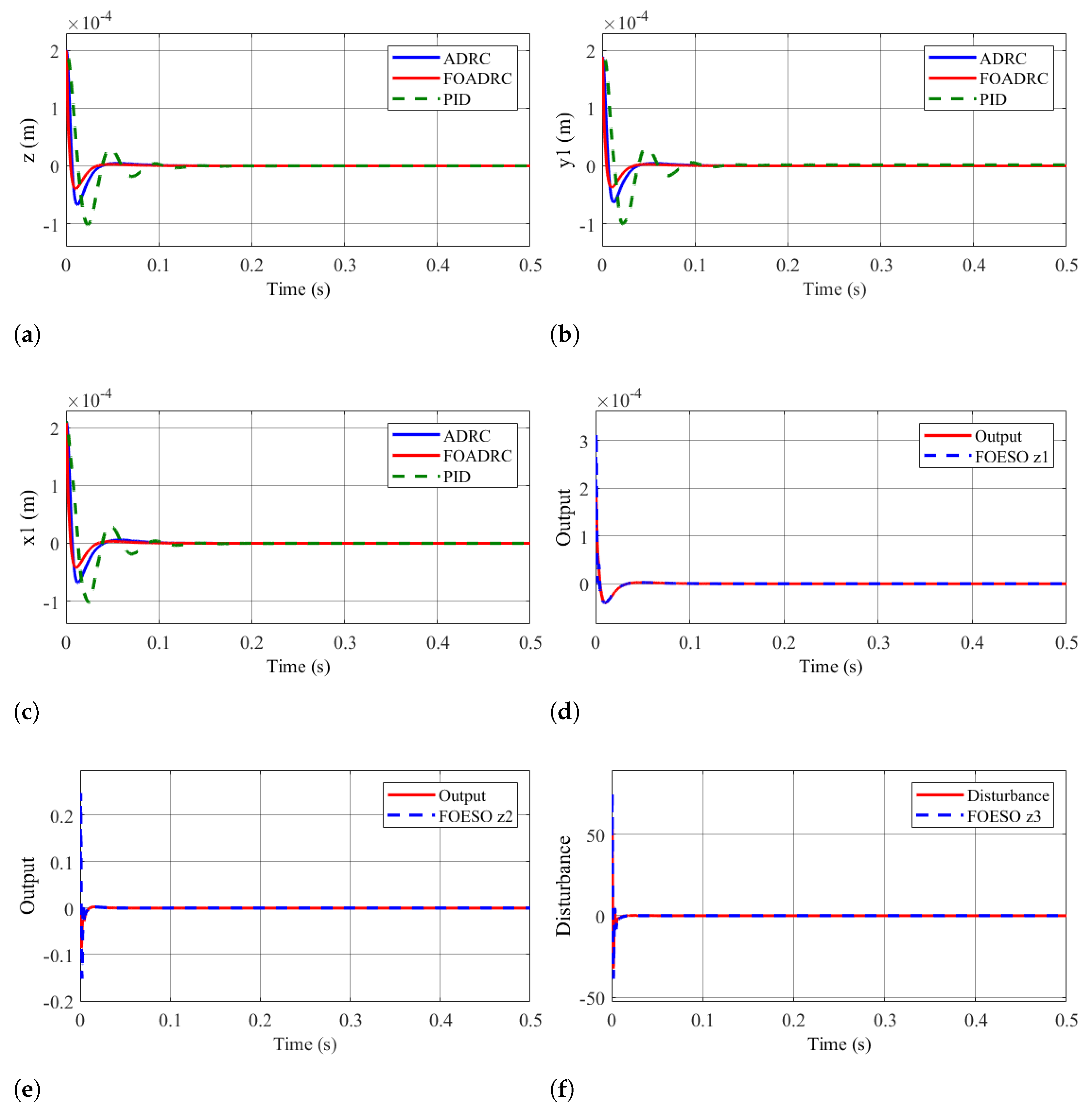
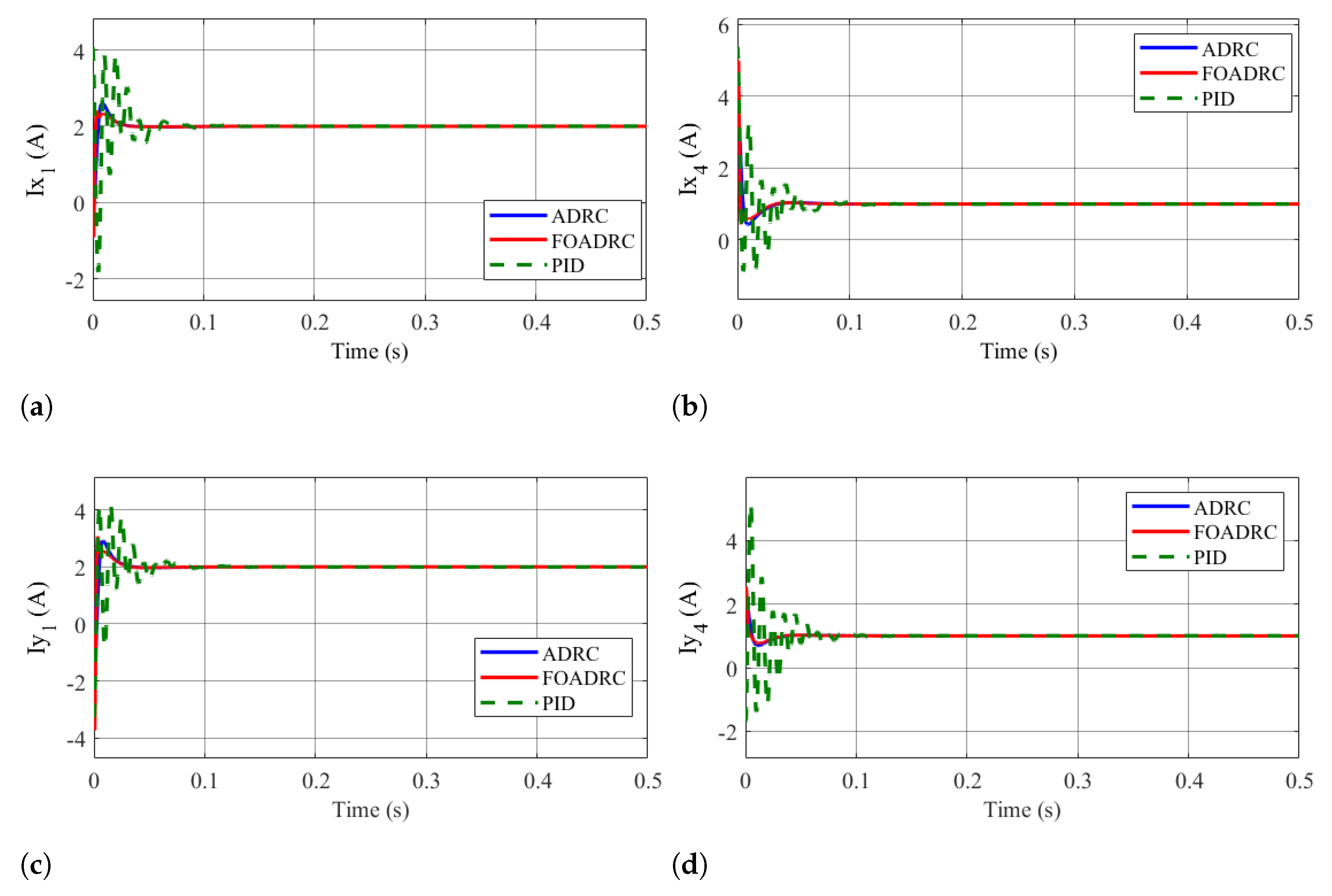
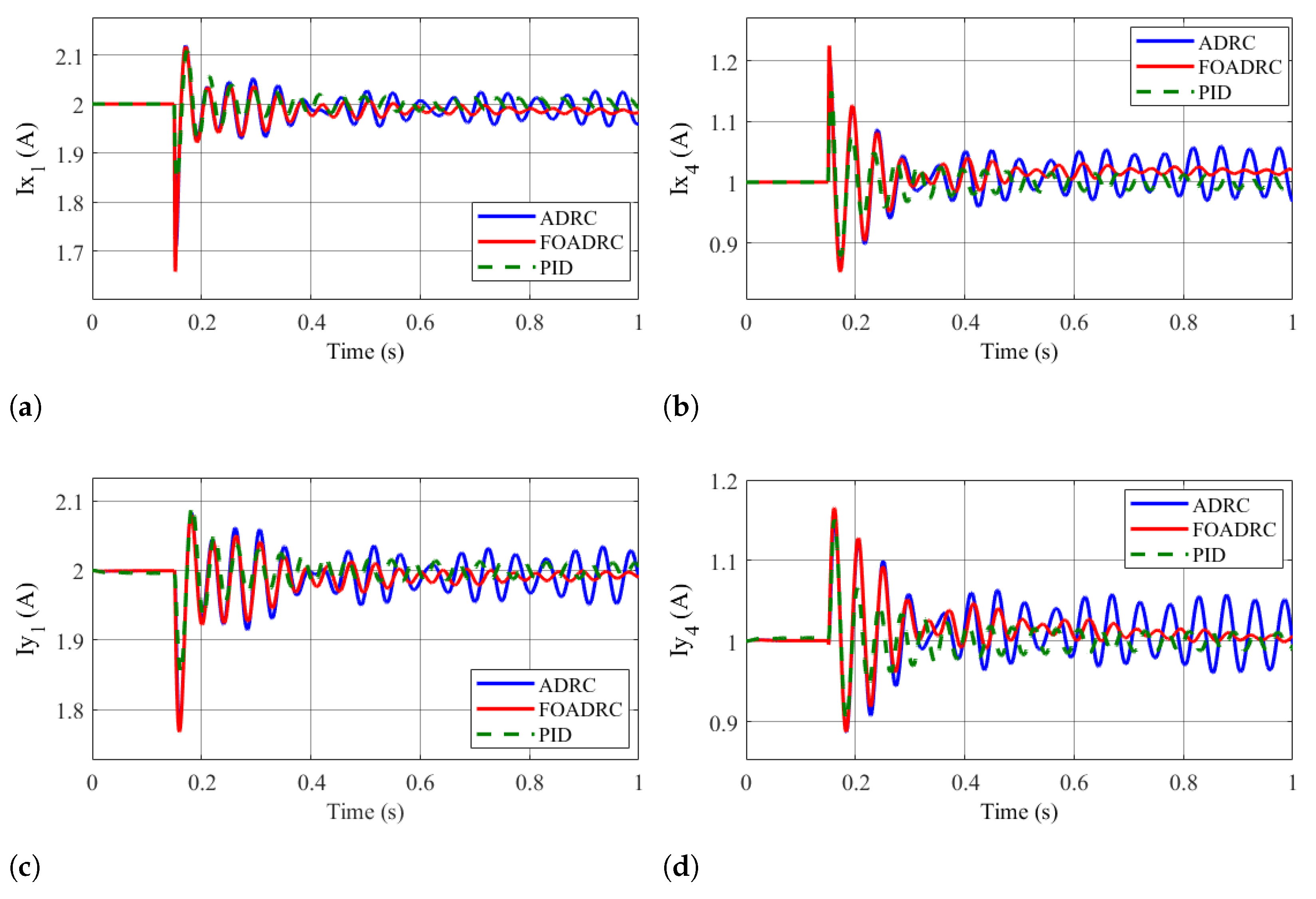
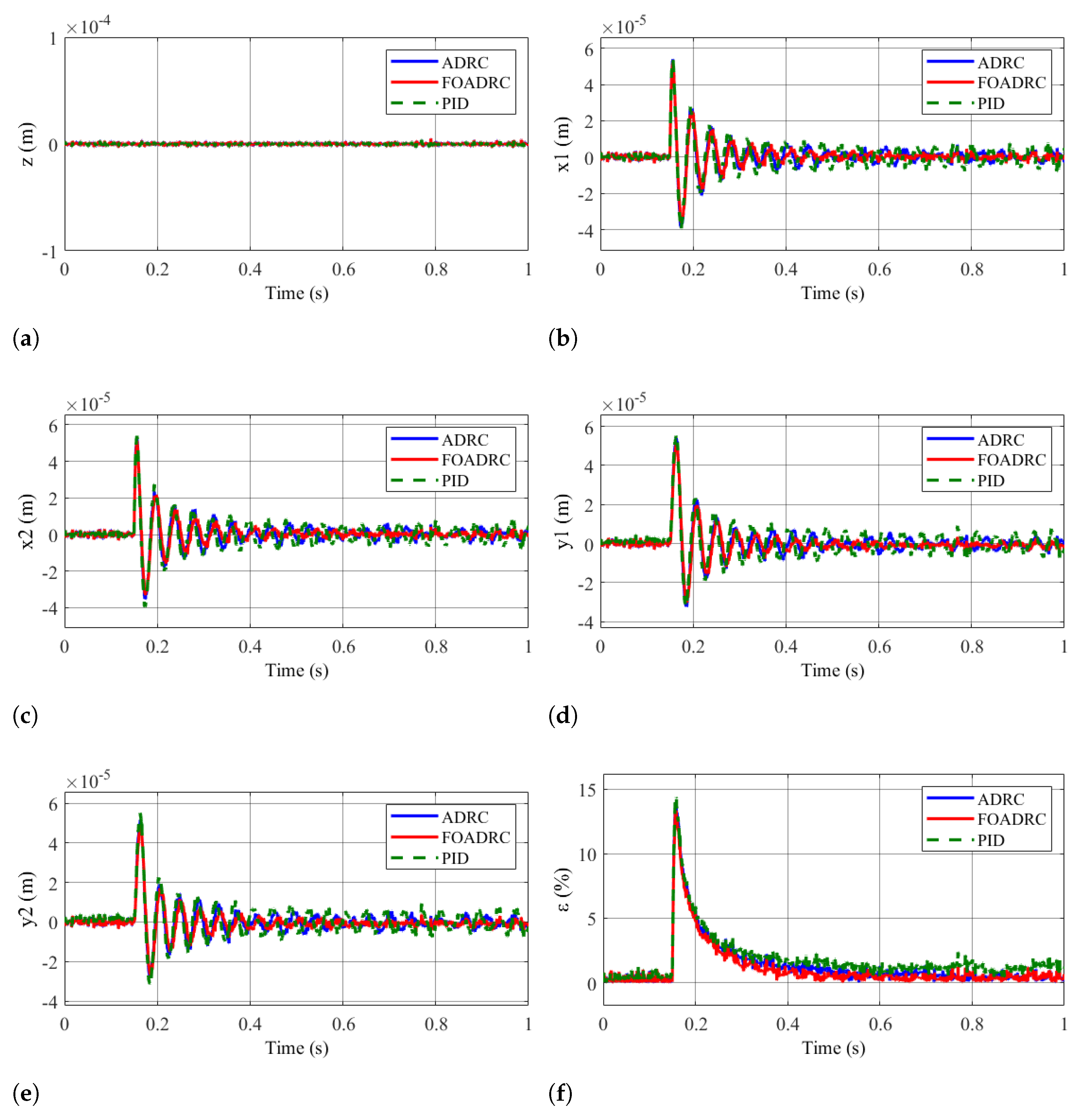
4.2.1. Results of Scenario 1
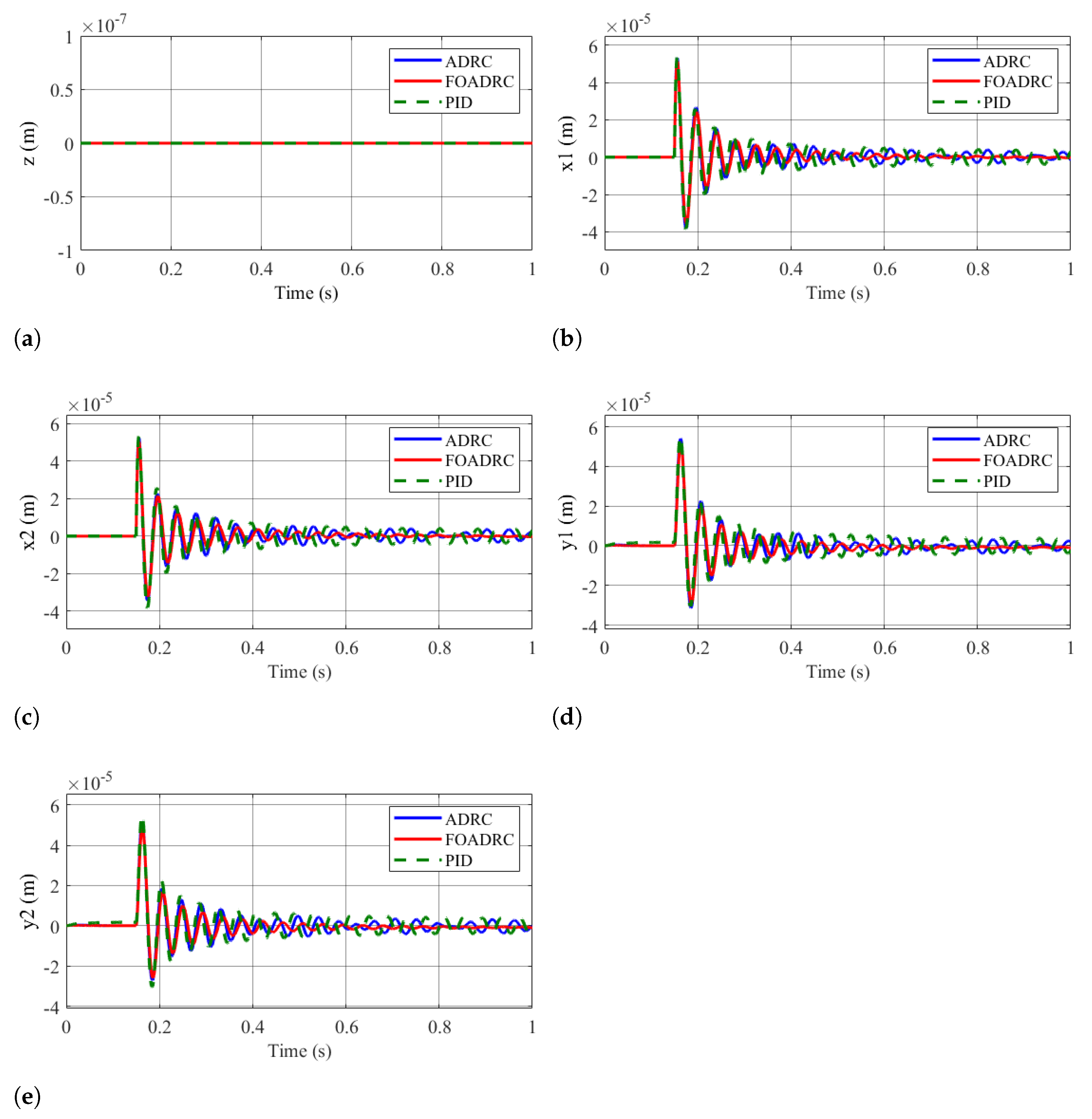
4.2.2. Results of Scenario 2
4.2.3. Results of Scenario 3
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nguyen, D.; Nguyen, L.; Hoang, D. A non-linear control method for active magnetic bearings with bounded input and output. Int. J. Power Electron. Drive Syst. 2020, 11, 2154. [Google Scholar] [CrossRef]
- Nguyen, T. Decoupling Control of a Disc-type Rotor Magnetic Bearing. Int. J. Integr. Eng. 2021, 13, 247–261. [Google Scholar] [CrossRef]
- Nguyen, D.; Nguyen, T.; Nguyen, M.; Nguyen, H. Nonlinear Control of an Active Magnetic Bearing with Output Constraint. Int. J. Electr. Comput. Eng. (IJECE) 2018, 8, 3666–3677. [Google Scholar] [CrossRef]
- Breńkacz, Ł.; Witanowski, Ł.; Drosińska-Komor, M.; Szewczuk-Krypa, N. Research and applications of active bearings: A state-of-the-art review. Mech. Syst. Signal Process. 2021, 151, 107423. [Google Scholar] [CrossRef]
- Li, X.; Palazzolo, A.; Wang, Z. A Combination 5-DOF Active Magnetic Bearing for Energy Storage Flywheels. IEEE Trans. Transp. Electrif. 2021, 7, 2344–2355. [Google Scholar] [CrossRef]
- Chiba, A.; Fukao, T.; Ichikawa, O.; Oshima, M.; Takemoto, M.; Dorrell, D. Magnetic Bearings and Bearingless Drives; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Hantke, A.; Sobotzik, J.; Nordmann, R.; Brodersen, S.; Gröschel, J.; Köhler, B. Integration of Magnetic Bearings in a Canned Motor Pump. IFAC Proc. Vol. 2000, 33, 215–221. [Google Scholar] [CrossRef]
- Allaire, P. Others Design, construction and test of magnetic bearings in an industrial canned motor pump. In Proceedings of the 6th International Pump Users Symposium; Turbomachinery Laboratories, Department of Mechanical Engineering, Texas A&M University: College Station, TX, USA, 1989. [Google Scholar]
- Yamamoto, N.; Takemoto, M.; Ogasawara, S.; Hiragushi, M. Experimental estimation of a 5-axis active control type bearingless canned motor pump. In Proceedings of the 2011 IEEE International Electric Machines And Drives Conference, IEMDC 2011, Niagara Falls, ON, Canada, 15–18 May 2011; pp. 148–153. [Google Scholar]
- Miyamoto, K.; Hiragushi, M.; Takemoto, M.; Ogasawara, S. Verification of a novel 5-axis active control type bearingless canned motor pump utilizing passive magnetic bearing function for high power. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition, ECCE 2014, Pittsburgh, PA, USA, 14–18 September 2014; pp. 2454–2461. [Google Scholar]
- Mohamed, A.; Emad, F. Conical magnetic bearings with radial and thrust control. IEEE Trans. Autom. Control 1992, 37, 1859–1868. [Google Scholar] [CrossRef]
- Lee, C.; Jeong, H. Dynamic modeling and optimal control of cone-shaped active magnetic bearing systems. Control. Eng. Pract. 1996, 4, 1393–1403. [Google Scholar] [CrossRef]
- Jing, Y.; Lie, Y.; Jing, X. Coupled dynamics and control of a rotor-conical magnetic bearing system. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2006, 220, 581–586. [Google Scholar] [CrossRef]
- Huang, S.; Lin, L. Fuzzy modeling and control for conical magnetic bearings using linear matrix inequality. J. Intell. Robot. Syst. Theory Appl. 2003, 37, 209–232. [Google Scholar] [CrossRef]
- Castellanos Molina, L.; Bonfitto, A.; Galluzzi, R. Offset-Free Model Predictive Control for a cone-shaped active magnetic bearing system. Mechatronics 2021, 78, 102612. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Nguyen, D.; Le Vu, M.; Do Trong, H.; Nguyen, D.; Nguyen, T. Active disturbance rejection control-based anti-coupling method for conical magnetic bearings. Acta Polytech. 2022, 62, 479–487. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and Bandwidth-Parameterization based Controller Tuning. Proc. Am. Control. Conf. 2003, 6, 4989–4996. [Google Scholar]
- Atangana, A. Fractional Operators with Constant and Variable Order with Application to Geo-Hydrology; Academic Press: Cambridge, MA, USA, 2017; pp. 79–112. [Google Scholar]
- Lazarević, M.; Rapaić, M.; Šekara, T.; Mladenov, V.; Mastorakis, N. Introduction to fractional calculus with brief historical background. Advanced Topics on Applications of Fractional Calculus on Control Problems, System Stability And Modeling; WSEAS Press: Florence, Italy, 2014; p. 3. [Google Scholar]
- Dang, V.; Le, D.; Nguyen-Thi, V.; Nguyen, D.; Tong, T.; Nguyen, D.; Nguyen, T. Adaptive Control for Multi-Shaft with Web Materials Linkage Systems. Inventions 2021, 6, 76. [Google Scholar] [CrossRef]
- Thi, L.; Van, T.; Nhu, B.; Van, H.; Minh, D.; Danh, H.; Nguyen, T. An Output Observer Integrated Dynamic Surface Control for a Web Handing Section. In Proceedings of the International Conference On Engineering Research And Applications, Thai Nguyen, Vietnam, 1–2 December 2021; pp. 150–157. [Google Scholar]
- Pham, V.; Le, D.; Nguyen, N.; Dang, V.; Nguyen-Thi, V.; Nguyen, D.; Nguyen, T. Backstepping Sliding Mode Control Design for Active Suspension Systems in Half-Car Model. In Proceedings of the International Conference on Engineering Research And Applications, Thai Nguyen, Vietnam, 1–2 December 2022; pp. 281–289. [Google Scholar]
- Le, D.; Nguyen, D.; Le, N.; Nguyen, T. Traction control based on wheel slip tracking of a quarter-vehicle model with high-gain observers. Int. J. Dyn. Control. 2022, 10, 1130–1137. [Google Scholar] [CrossRef]
- Le, D.; Dang, V.; Dinh, B.; Vu, H.; Pham, V.; Nguyen, T. Disturbance Observer-Based Speed Control of Interior Permanent Magnet Synchronous Motors for Electric Vehicles. In Proceedings of the Regional Conference in Mechanical Manufacturing Engineering, Hanoi, Vietnam, 10–12 December 2021; pp. 244–259. [Google Scholar]
- Manh; Le, T.; Huy, D.; Quang, P.; Quang, D.D.; Nguyen, T. Nonlinear Control of Axial Gap Magnetic Bearing Motors: A Disturbance Observer-Based Method. In Proceedings of the International Conference On Engineering Research And Applications, Thai Nguyen, Vietnam, 1–2 December 2021; pp. 675–684. [Google Scholar]
- Thi, H.; Dang, V.; Nguyen, N.; Le, D.; Nguyen, T. A Neural Network-Based Fast Terminal Sliding Mode Controller for Dual-Arm Robots. In Proceedings of the International Conference on Engineering Research And Applications, Thai Nguyen, Vietnam, 1–2 December 2022; pp. 42–52. [Google Scholar]
- Nguyen, D.; Truong, V.; Lam, N. Others Nonlinear control of a 3-DOF robotic arm driven by electro-pneumatic servo systems. Meas. Control. Autom. 2022, 3, 51–59. [Google Scholar]
- Zheng, W.; Luo, Y.; Chen, Y.; Wang, X. Synthesis of fractional order robust controller based on Bode’s ideas. ISA Trans. 2021, 111, 290–301. [Google Scholar] [CrossRef]
- Dang, V.; Nguyen, D.; Tran, T.; Le, D.; Nguyen, T. Model-free hierarchical control with fractional-order sliding surface for multisection web machines. Int. J. Adapt. Control Signal Process. 2022, 1–22. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, G.; Lv, X. A Novel Compound Nonlinear State Error Feedback Super-Twisting Fractional-Order Sliding Mode Control of PMSM Speed Regulation System Based on Extended State Observer. Math. Probl. Eng. 2020, 2020. [Google Scholar] [CrossRef]
- Sondhi, S.; Hote, Y. Fractional Order Controller and its Applications: A Review. Model. Identif. Control/770 Adv. Comput. Sci. Eng. 2012, 4, 118–123. [Google Scholar] [CrossRef]
- Chen, Y.; Petráš, I.; Xue, D. Fractional order control—A tutorial. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 1397–1411. [Google Scholar]
- Gomaa Haroun, A.; Yin-Ya, L. A novel optimized fractional-order hybrid fuzzy intelligent PID controller for interconnected realistic power systems. Trans. Inst. Meas. Control. 2019, 41, 3065–3080. [Google Scholar] [CrossRef]
- Li, D.; Ding, P.; Gao, Z. Fractional active disturbance rejection control. ISA Trans. 2016, 62, 109–119. [Google Scholar] [CrossRef]
- Fareh, R. Control of a single flexible link manipulator using fractional active disturbance rejection control. In Proceedings of the 2019 6th International Conference on Control, Decision and Information Technologies, CoDIT 2019, Paris, France, 23–26 April 2019; pp. 900–905. [Google Scholar]
- Chen, P.; Luo, Y.; Zheng, W.; Gao, Z. A new active disturbance rejection controller design based on fractional extended state observer. In Proceedings of the Chinese Control Conference, CCC, Guangzhou, China, 27–30 July 2019; pp. 4276–4281. [Google Scholar]
- Al-Saggaf, U.; Mehedi, I.; Mansouri, R.; Bettayeb, M. Fractional Order Linear ADRC-Based Controller Design for Heat-Flow Experiment. Math. Probl. Eng. 2021, 2021, 7291420. [Google Scholar] [CrossRef]
- Chen, P.; Luo, Y.; Zheng, W.; Gao, Z.; Chen, Y. Fractional order active disturbance rejection control with the idea of cascaded fractional order integrator equivalence. ISA Trans. 2021, 114, 359–369. [Google Scholar] [CrossRef]
- Song, Y. Control of Nonlinear Systems Via PI, PD and PID: Stability and Performance; CRC Press: Boca Raton, FL, USA, USA, 2018. [Google Scholar]
- Maruyama, Y.; Mizuno, T.; Takasaki, M.; Ishino, Y.; Ishigami, T.; Kameno, H. An application of active magnetic bearing to gyroscopic and inertial sensors. J. Syst. Des. Dyn. 2008, 2, 155–164. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.; Fang, J. A Novel Conical Active Magnetic Bearing with Claw Structure. IEEE Trans. Magn. 2014, 50, 8101108. [Google Scholar]
- Riba Ruiz, J.; Garcia Espinosa, A.; Romeral, L. A computer model for teaching the dynamic behavior of ac contactors. IEEE Trans. Educ. 2010, 53, 248–256. [Google Scholar] [CrossRef] [Green Version]
- Yucel, U. Calculation of Dynamic Coefficients for Fluid Film Journal Bearing. J. Eng. Sci. 2005, 11, 335–343. [Google Scholar]
- Tavares, D.; Almeida, R.; Torres, D. Caputo derivatives of fractional variable order: Numerical approximations. Commun. Nonlinear Sci. Numer. Simul. 2016, 35, 69–87. [Google Scholar] [CrossRef] [Green Version]
- Rivero, M.; Rogosin, S.; Tenreiro Machado, J.; Trujillo, J. Stability of Fractional Order Systems. Math. Probl. Eng. 2013, 2013, 356215. [Google Scholar] [CrossRef] [Green Version]
- Patil, M.; Vyawahare, V.; Bhole, M. A new and simple method to construct root locus of general fractional-order systems. ISA Trans. 2014, 53, 380–390. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Li, D.; Gao, Z.; Wang, C. Tuning method for second-order active disturbance rejection control. In Proceedings of the 30th Chinese Control Conference, CCC 2011, Yantai, China, 22–24 July 2011; pp. 6322–6327. [Google Scholar]


| Symbol | Description | Value |
|---|---|---|
| Radial air gap | 0.45 mm | |
| A | Cross-sectional area | 118 |
| m | Rotor mass | 0.755 |
| Inclined angle | 0.98 | |
| N | Magnetic coils | 82 |
| Diametral moment | kg · m2 | |
| Polar moment | 1.54 × 10−4 kg · m2 | |
| Bias current | 2A | |
| Bias current | 1A | |
| Bearing span | 55 | |
| Bearing span | 55 | |
| Effective radius |
| Symbol | Description | Value |
|---|---|---|
| Fractional order | 0.98 | |
| Time settle | ||
| Controller bandwidth | 60 | |
| Controller gain | 3600 | |
| Controller gain | 120 | |
| Observer bandwidth | 600 | |
| Observer gain | 1800 | |
| Observer gain | 1,080,000 | |
| Observer gain | 216,000,000 |
| Scenario | Controller | Index | ||
|---|---|---|---|---|
| ISE 1 | IAE 2 | ITAE 3 | ||
| 1 | FOADRC | |||
| ADRC | ||||
| PID | ||||
| 2 | FOADRC | |||
| ADRC | ||||
| PID | ||||
| 3 | FOADRC | |||
| ADRC | ||||
| PID | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, D.H.; Ta, T.T.; Vu, L.M.; Dang, V.T.; Nguyen, D.G.; Le, D.T.; Nguyen, D.D.; Nguyen, T.L. Fractional Order Active Disturbance Rejection Control for Canned Motor Conical Active Magnetic Bearing-Supported Pumps. Inventions 2023, 8, 15. https://doi.org/10.3390/inventions8010015
Nguyen DH, Ta TT, Vu LM, Dang VT, Nguyen DG, Le DT, Nguyen DD, Nguyen TL. Fractional Order Active Disturbance Rejection Control for Canned Motor Conical Active Magnetic Bearing-Supported Pumps. Inventions. 2023; 8(1):15. https://doi.org/10.3390/inventions8010015
Chicago/Turabian StyleNguyen, Danh Huy, The Tai Ta, Le Minh Vu, Van Trong Dang, Danh Giang Nguyen, Duc Thinh Le, Duy Dinh Nguyen, and Tung Lam Nguyen. 2023. "Fractional Order Active Disturbance Rejection Control for Canned Motor Conical Active Magnetic Bearing-Supported Pumps" Inventions 8, no. 1: 15. https://doi.org/10.3390/inventions8010015
APA StyleNguyen, D. H., Ta, T. T., Vu, L. M., Dang, V. T., Nguyen, D. G., Le, D. T., Nguyen, D. D., & Nguyen, T. L. (2023). Fractional Order Active Disturbance Rejection Control for Canned Motor Conical Active Magnetic Bearing-Supported Pumps. Inventions, 8(1), 15. https://doi.org/10.3390/inventions8010015










