Heat Transfer Investigation during Condensation on the Horizontal Pipe
Abstract
1. Introduction
- The heat flux is assumed to equal the rate of heat absorption by the coolantwhere is the coolant water mass flow rate, and are the coolant enthalpy rise at the temperature of the coolant at the inlet and outlet of the pipe, and F is the area of the heat exchange surface.
- The heat flux is calculated through direct measurement of the condensate mass flow rate from the heat exchange surfacewhere is the condensate mass flow rate, and is the latent heat of condensation.
- The heat flux is assumed to equal the longitudinal conductive heat flux in the condensing wallwhere k is the thermal conductivity of the wall, and is the temperature gradient.
- The heat flux is calculated according to Newton’s cooling lawwhere is the wall temperature, is the cooling water temperature, and R is the overall thermal resistance.
- The method allows us to determine the heat flux during condensation on various surfaces.
- It allows us to measure the flow of condensate without the need to separate the main one, formed on the experimental model, and the additional one, formed on the setup case.
- The method leads to a decrease in the number of measuring probes.
2. Experimental Procedure
2.1. Gradient Heatmetry
2.2. GHFS Type Selection
- The local heat flux by the GHFS () and HGHFS ().
- The temperature of the copper pipe outer surface () by the L-type thermocouple.
- The temperature difference () between inlet and outlet cooling water by the L-type differential thermocouple.
- The cooling water () and condensate () rate.
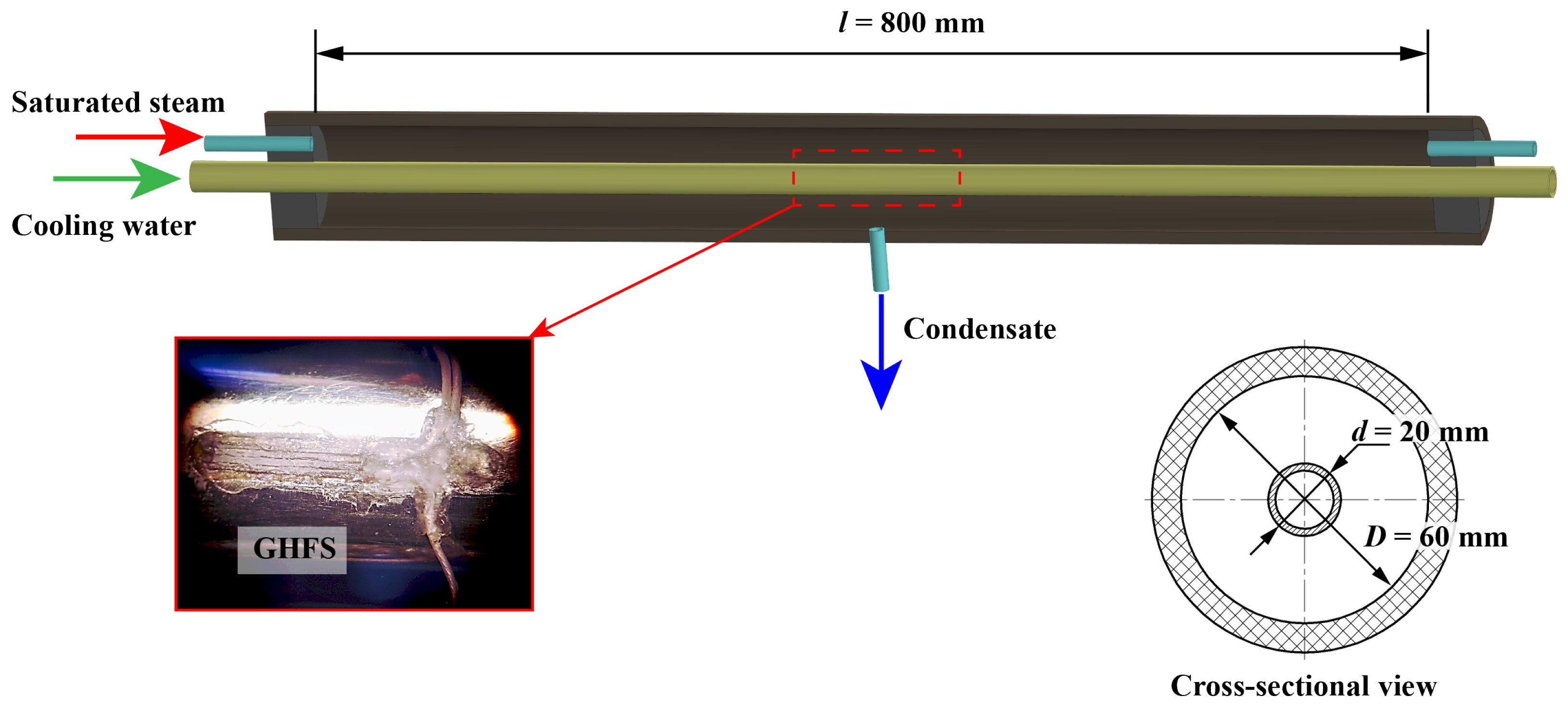
2.3. Experimental Setup
- The pipe material must be exchanged for a less thermal conductivity one. The copper’s high thermal conductivity led to temperature equalization over the pipe surface and increased the model thermal inertia which reduced the information content of the temperature measurement;
- The measuring section length must be increased to hydrodynamic flow stabilization;
- The GHFS cross area should be increased to promote the generated thermoEMF, but it is necessary to minimize GHFS width. The purpose of the study is to determine the heat flux distribution over the horizontal pipe surface, and it is necessary to reduce the azimuthal angle at which the heat flux is averaged;
- To eliminate distortions in the natural condensate flow, it is necessary to minimize the number of GHFS and thermocouples and develop a method for removing wires from the heat exchange surface.
2.4. Uncertainty Analysis
3. Results
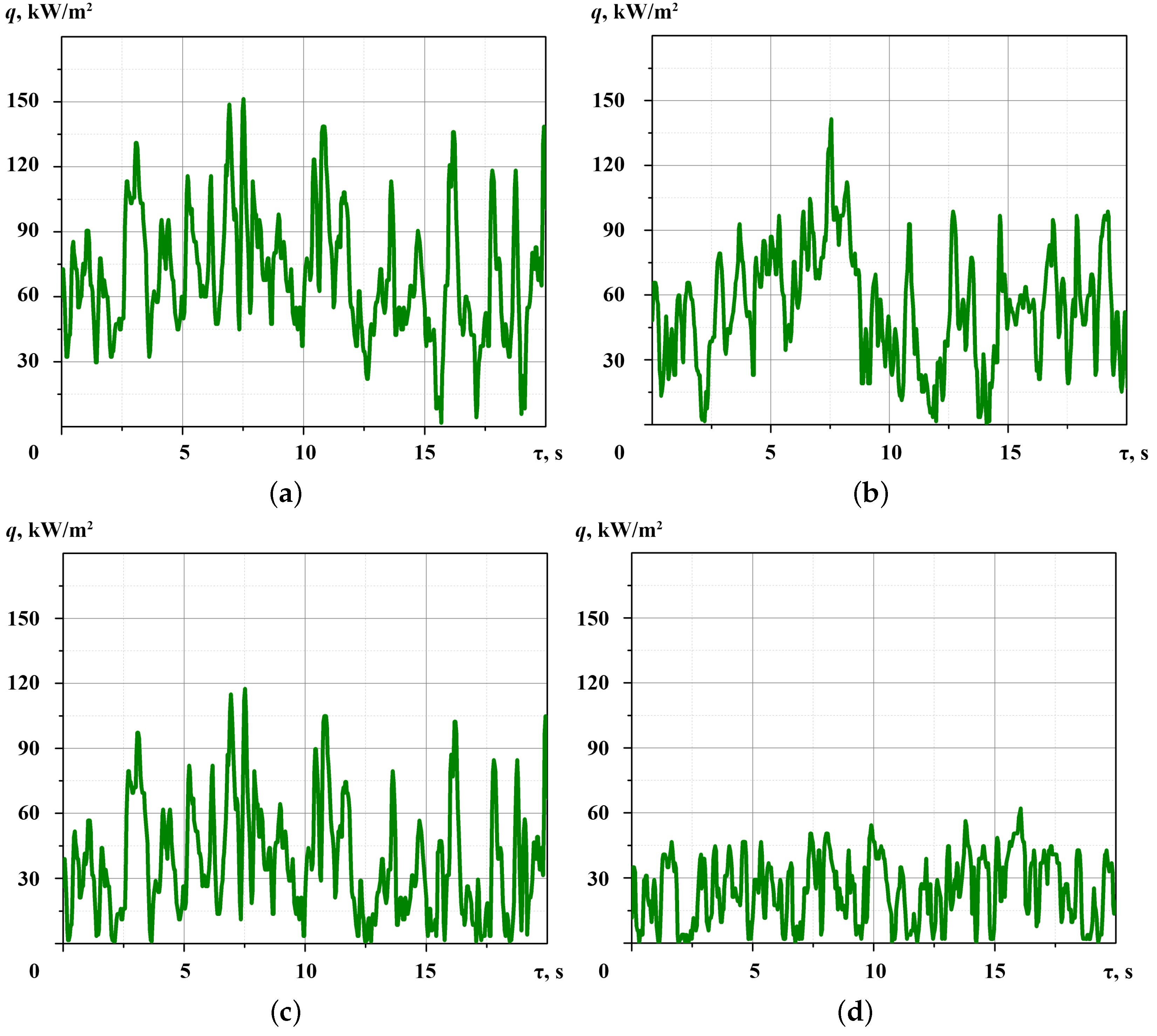
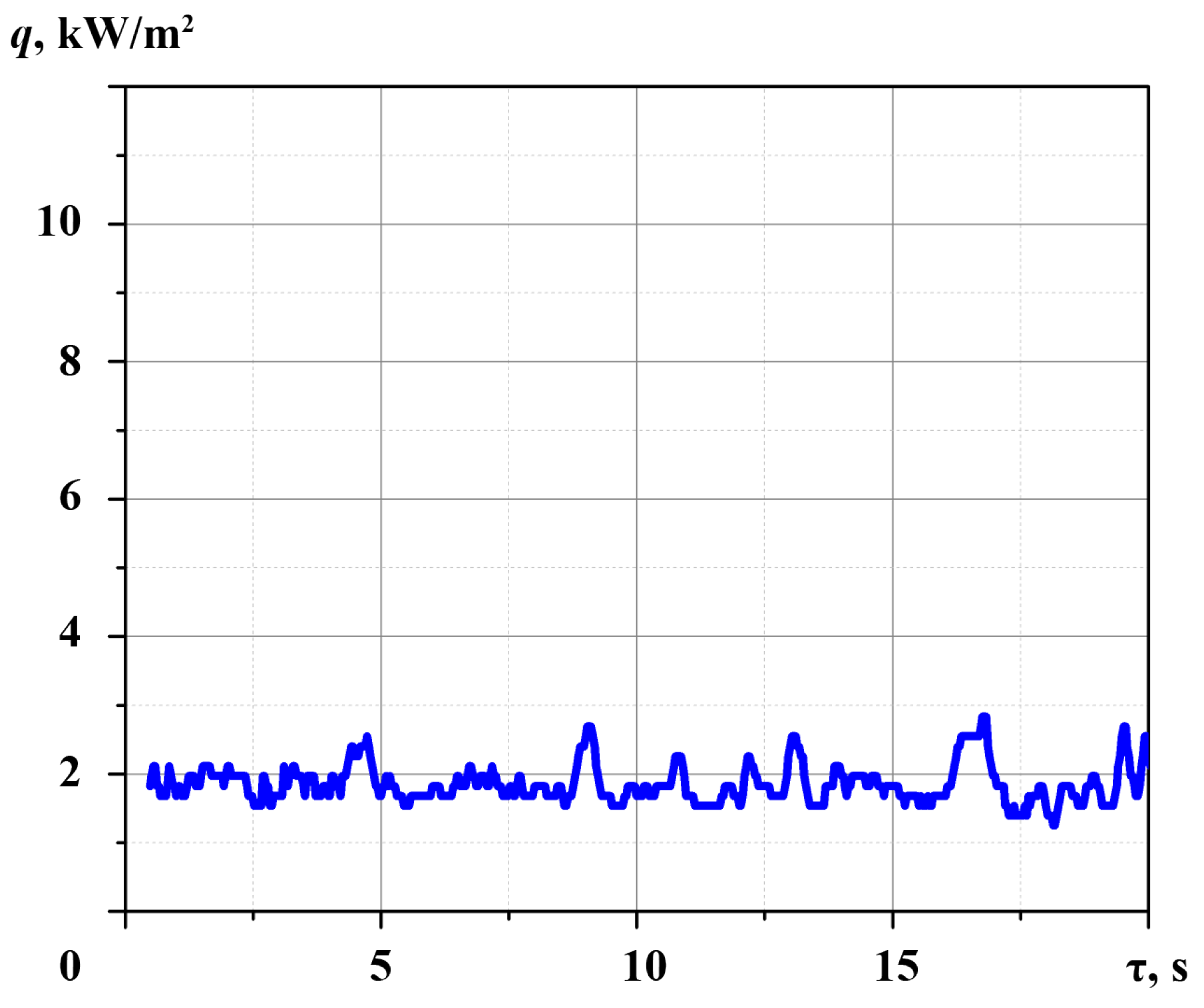
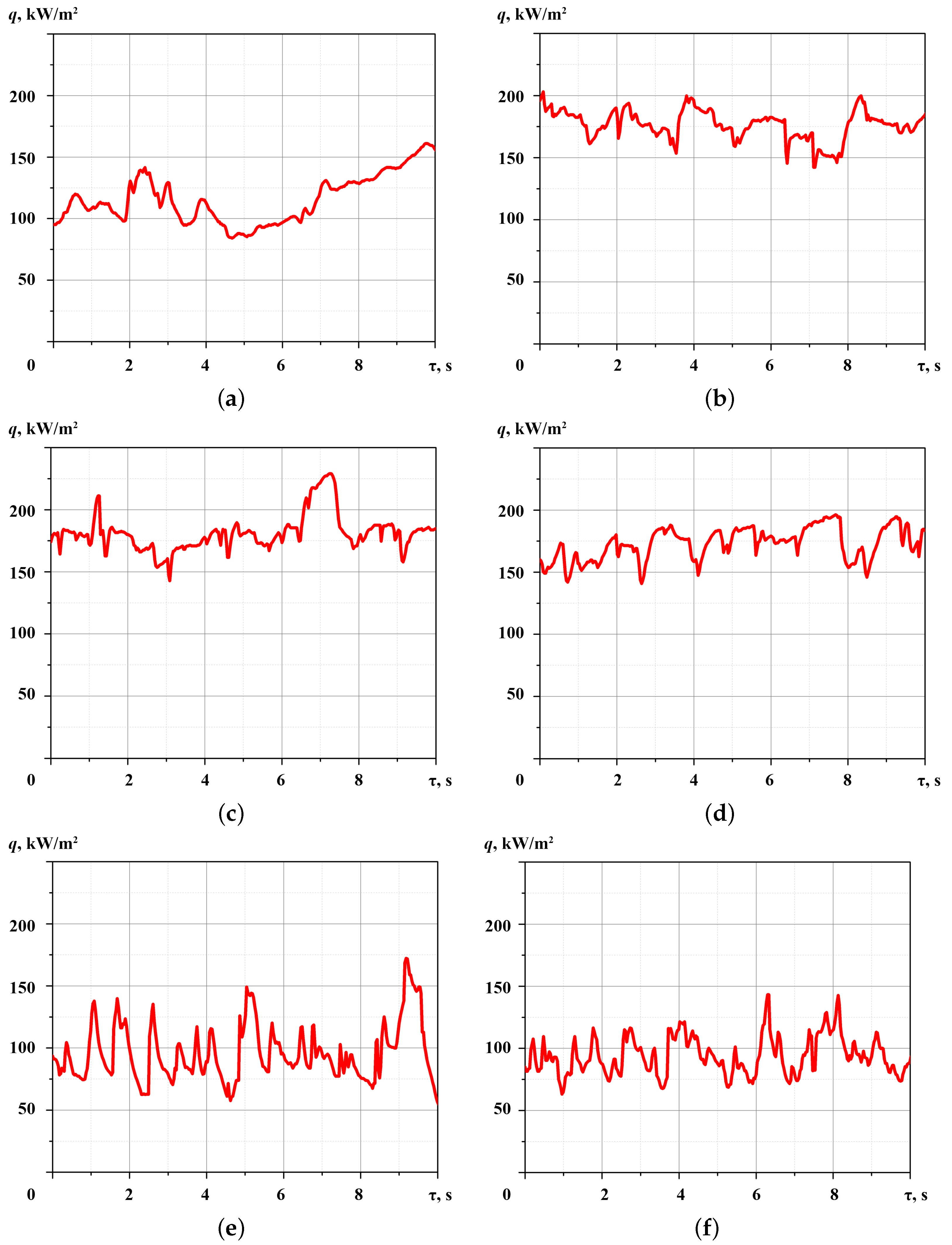
- The experimental conditions do not provide for the organization of film condensation on the surface of a horizontal pipe. According to the fluctuations on the heat flux graphs (Figure 8), the condensate flows down from the pipe surface in the form of separate rivulets. It is necessary to add visual observation of the condensate flow for an explanation of fluctuations in the heat flux recorded using GHFS.
- There is no generally accepted theoretical model for calculating the heat flux during not-filmwise and not-dropwise condensation. Comparison of the results with the Nusselt model for film condensation is irrelevant. Therefore, in continued investigation, the regime conditions should be expanded to achieve film condensation on a horizontal pipe.
4. Discussion
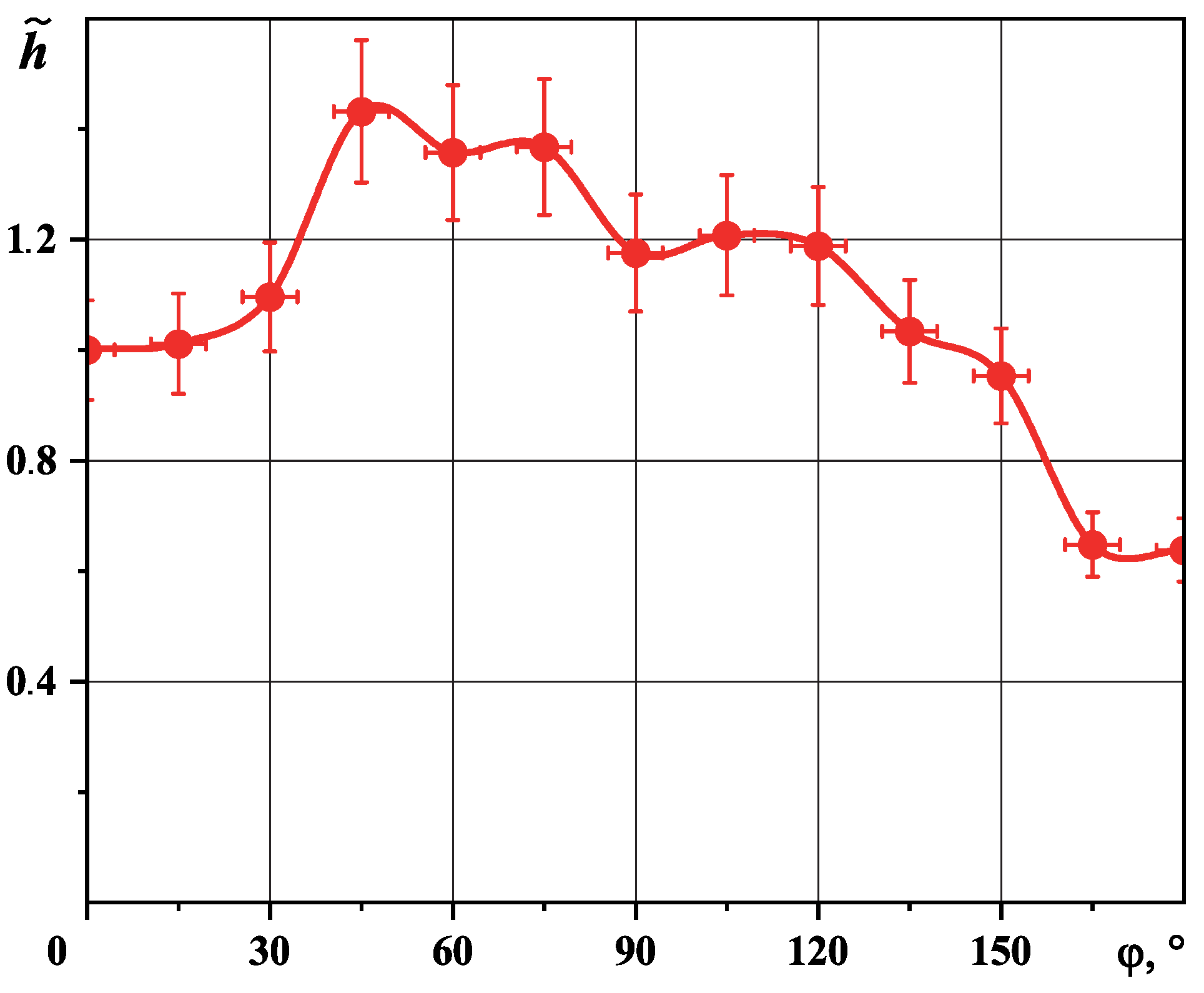
- The experiment result indicates that the HTC maximum corresponds to the region of = 30…75.
- The HTC becomes less than the value on the upper generatrix only in the lower pipe region in the range of = 150…180.
- Theoretically, the HTC is equal to zero on the lower pipe generatrix. However, in practice this is not possible because then the thickness of the condensate film is equal to an infinitely large value. The experiment results indicate HTCs decrease in the lower pipe region which is associated with a sub-bottom zone formation.
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sapozhnikov, S.Z.; Mityakov, V.Y.; Mityakov, A.V.; Gusakov, A.A.; Zainullina, E.R.; Grekov, M.A.; Seroshtanov, V.V.; Bashkatov, A.; Babich, A.Y.; Pavlov, A.V. Gradient Heatmetry Advances. Energies 2020, 13, 6194. [Google Scholar] [CrossRef]
- Li, T.J.; Wang, H.F.; Sang, Z.F. Enhanced Condensation Outside Horizontal Heat Transfer. AIP Conf. Proc. 2010, 1207, 628. [Google Scholar]
- Ji, W.-T.; Zhao, C.-Y.; Zhang, D.-C.; Li, Z.-Y.; He, Y.-L.; Tao, W.-Q. Condensation of R134a outside single horizontal titanium, cupronickel (B10 and B30), stainless steel and copper tubes. Int. J. Heat Mass Transf. 2014, 77, 194–201. [Google Scholar] [CrossRef]
- Tokunaga, A.; Tsuruta, T. Enhancement of condensation heat transfer on a microstructured surface with wettability gradient. Int. J. Heat Mass Transf. 2020, 156, 119839. [Google Scholar] [CrossRef]
- Yao, Y.; Peng, Y.; Wu, X.; Luo, Y.; Yang, X.; Zheng, C.; Chen, J. Dropwise condensation heat transfer of the surface with micro columns. Energy Rep. 2022, 8, 8883–8895. [Google Scholar] [CrossRef]
- Fan, G.; Tong, P.; Sun, Z.; Chen, Y. Development of a new empirical correlation for steam condensation rates in the presence of air outside vertical smooth tube. Ann. Nucl. Energy 2018, 113, 139–146. [Google Scholar] [CrossRef]
- Lee, Y.-G.; Jang, Y.-J.; Choi, D.-J. An experimental study of air–steam condensation on the exterior surface of a vertical tube under natural convection conditions. Int. J. Heat Mass Transf. 2017, 104, 1034–1047. [Google Scholar] [CrossRef]
- Su, J.; Sun, Z.; Ding, M.; Fan, G. Analysis of experiments for the effect of noncondensable gases on steam condensation over a vertical tube external surface under low wall subcooling. Nucl. Eng. Des. 2014, 278, 644–650. [Google Scholar] [CrossRef]
- Kim, J.W.; Lee, Y.G.; Ahn, H.K.; Park, G.C. Condensation heat transfer characteristic in the presence of noncondensable gas on natural convection at high pressure. Nucl. Eng. Des. 2009, 239, 688–698. [Google Scholar] [CrossRef]
- Swartz, M.M.; Yao, S.-C. Experimental study of turbulent natural-convective condensation on a vertical wall with smooth and wavy film interface. Int. J. Heat Mass Transf. 2017, 113, 943–960. [Google Scholar] [CrossRef]
- Tang, G.H.; Hu, H.W.; Zhuang, Z.N.; Tao, W.Q. Film condensation heat transfer on a horizontal tube in presence of a noncondensable gas. Appl. Therm. Eng. 2012, 36, 414–425. [Google Scholar] [CrossRef]
- Cao, B.; Li, Y.; Lu, Y.; Zhou, S.; Bian, H.; Ding, M. Experimental study of air–steam condensation on the influence of tube diameter and inclination angle. Nucl. Eng. Des. 2021, 381, 111357. [Google Scholar] [CrossRef]
- Chen, R.; Zhang, P.; Ma, P.; Tan, B.; Wang, Z.; Zhang, D.; Tian, W.; Qiu, S.; Su, G.H. Experimental investigation of steam-air condensation on containment vessel. Ann. Nucl. Energy 2020, 136, 107030. [Google Scholar] [CrossRef]
- Zhang, J.X.; Wang, L. Experimental study of air accumulation in vapor condensation across horizontal tube. Int. J. Heat Mass Transf. 2017, 112, 676–688. [Google Scholar] [CrossRef]
- Xiao, R.; Miljkovic, N.; Enright, R.; Wang, E.N. Immersion Condensation on Oil-Infused Heterogeneous Surfaces for Enhanced Heat Transfer. Sci. Rep. 2013, 3, 1988. [Google Scholar] [CrossRef] [PubMed]
- Preston, D.J.; Lu, Z.; Song, Y.; Zhao, Y.; Wilke, K.L.; Antao, D.S.; Louis, M.; Wang, N. Transfer Enhancement During Water and Hydrocarbon Condensation on Lubricant Infused Surfaces. Sci. Rep. 2018, 8, 540. [Google Scholar] [CrossRef]
- Preobrazhensky, V.P. Teplotekhnicheskiye Izmereniya i Pribory (Thermotechnical Measurements and Devices); Energy publishing house: Moscow, Russia, 1946; p. 268. [Google Scholar]
- Fulpagare, Y.; Wu, Y.J.; Chang, J.Y.; Wang, C.C. Effect of Non-Condensable gas on condensing performance of HFE7100 With/Without hydrophobic coating. Appl. Therm. Eng. 2022, 213, 118807. [Google Scholar] [CrossRef]
- Gundermanna, M.; Raabb, F.; Raabc, D.; Botsch, T.W. Investigation of the heat transfer coefficient during the condensation of small quantities of water vapour from a mixture with a high proportion of non-condensable gas in a horizontal smooth tube. Int. J. Heat Mass Transf. 2021, 170, 121016. [Google Scholar] [CrossRef]
- Xu, H.; Gu, H.; Sun, Z. Forced convection condensation of steam in the presence of multicomponent noncondensable gases inside a horizontal tube. Int. J. Heat Mass Transf. 2017, 104, 1110–1119. [Google Scholar] [CrossRef]
- Li, G.; Huang, L.; Tao, L. Experimental investigation of refrigerant condensation heat transfer characteristics in the horizontal microfin tubes. Appl. Therm. Eng. 2017, 123, 1484–1493. [Google Scholar] [CrossRef]
- Han, D.; Lee, K.-J. Experimental study on condensation heat transfer enhancement and pressure drop penalty factors in four microfin tubes. Int. J. Heat Mass Transf. 2005, 48, 3804–3816. [Google Scholar] [CrossRef]
- Li, W.; Wang, J.; Guo, Y.; Gu, Z.; Wang, X.; Sun, Z.; Tang, W.; Kukulka, D.J. Two-phase heat transfer of R410A in annuli outside enhanced tubes with micro-fin and dimple. Int. J. Heat Mass Transf. 2021, 175, 121370. [Google Scholar] [CrossRef]
- Wang, Y.; MuShengqiang, X.; Zhang, S. Heat transfer characteristics of steam condensation flow in vacuum horizontal tube. Int. J. Heat Mass Transf. 2017, 108, 128–135. [Google Scholar] [CrossRef]
- Longo, G.A.; Mancin, S.; Righetti, G.; Zilio, C. Saturated vapour condensation of HFC404A inside a 4mm ID horizontal smooth tube: Comparison with the long-term low GWP substitutes HC290 (Propane) and HC1270 (Propylene). Int. J. Heat Mass Transf. 2017, 108, 2088–2099. [Google Scholar] [CrossRef]
- Ölçeroğlu, E.; Hsieh, C.Y.; Rahman, M.M.; Lau, K.K.; McCarthy, M. Full-Field Dynamic Characterization of Superhydrophobic Condensation on Biotemplated Nanostructured Surfaces. Langmuir 2014, 30, 7556–7566. [Google Scholar] [CrossRef]
- Stevens, K.A.; Crockett, J.; Maynes, D.; Iverson, B.D. An Optical-Based Aggregate Approach to Measuring Condensation Heat Transfer. Bull. Am. Phys. Soc. 2017. [Google Scholar]
- Lyulin, Y.; Marchuk, I.; Chikov, S.; Kabov, O. Experimental study of laminar convective condensation of pure vapor inside an inclined circular tube. Microgravity Sci. Technol. 2011 23, 439–445. [CrossRef]
- Janasz, F.; Prasser, H.-M.; Suckow, D.; Mityakov, A. The use of a novel gradient heat flux sensor for characterization of reflux condensation. Nucl. Eng. Des. 2022, 395, 111885. [Google Scholar] [CrossRef]
- Sapozhnikov, S.Z.; Mityakov, V.Y.; Mityakov, A.V.; Babich, A.Y.; Zainullina, E.R. An investigation into film condensation of saturated steam on tube surfaces by a gradient heatmetry. Therm. Eng. 2021, 68, 794–801. [Google Scholar] [CrossRef]
- Mityakov, A.; Babich, A.; Bashkatov, A.; Gusakov, A.; Dymkin, A.; Zainullina, E.; Sapozhnikov, S.; Mityakov, V.; Seroshtanov, V. Investigating heat transfer augmentation using gradient heat flux measurement and PIV method. In Proceedings of the XXXIII Siberian Thermophysical Seminar (STS-33), Novosibirsk, Russia, 6–8 June 2017; p. 02006. [Google Scholar]
- Sapoznikov, S.Z.; Mityakov, V.Y.; Gusakov, A.A.; Pavlov, A.V.; Bobylev, P.G. Gradient heatmetry for boiling of underheated water on spherical surface. In Proceedings of the 3rd Conference on Problems of Thermal Physics and Power Engineering (PTPPE 2020), Moscow, Russia, 19–23 October 2020; Volume 1683, p. 022020. [Google Scholar]
- ISO/IEC Guide 98-1:2009—Uncertainty of Measurement—Part 1: Introduction to the Expression of Uncertainty in Measurement. Available online: www.iso.org/standard (accessed on 3 December 2022).
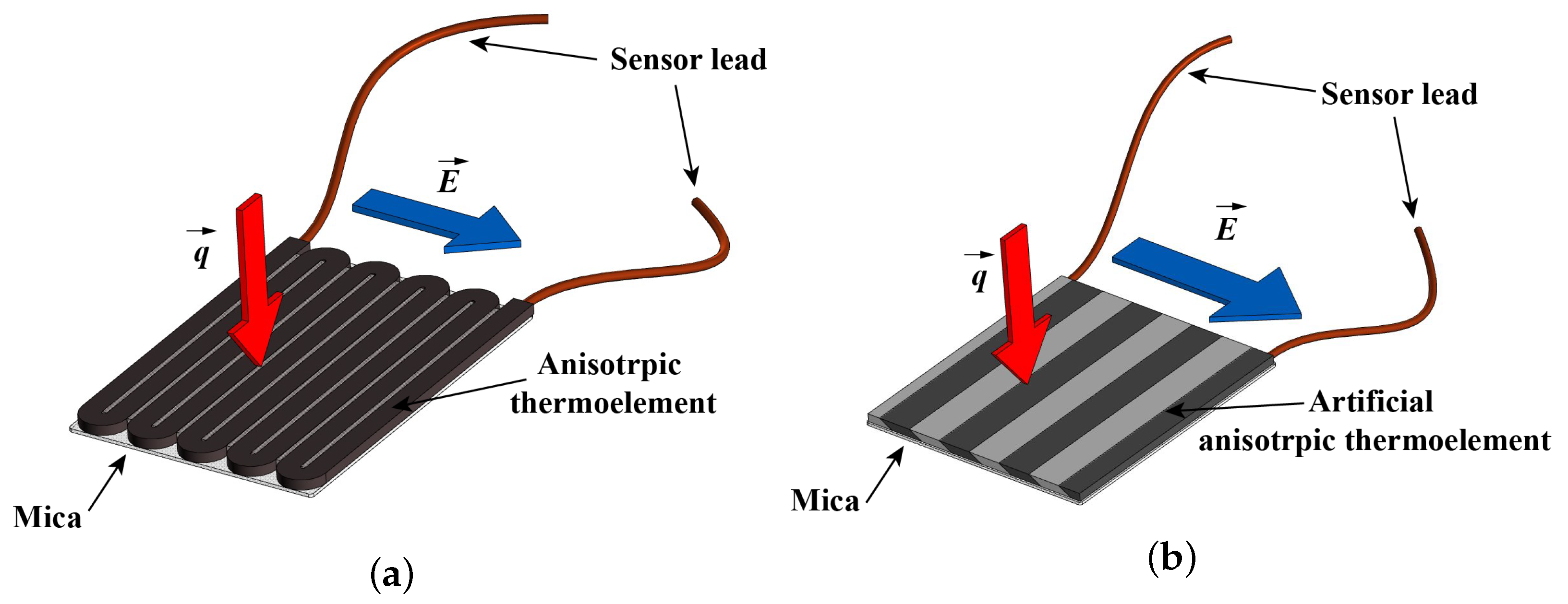





| Sensor Type | Material | Sizes, mm | Volt-Watt Sensitivity S, V/W Depending on Temperature | |
|---|---|---|---|---|
| T = 322 K | T = 372 K | |||
| GHFS | single-crystal bismuth | 3 × 3 × 0.2 | 2810 | 2810 |
| HGHFS | copper–nickel composition | 5 × 5 × 0.2 | 21.5 | 19.3 |
| No | ||||||
|---|---|---|---|---|---|---|
| kW/m | K | g/s | ||||
| 1 | 66.4 | 64.8 | 322 | 1.5 | 120 | 0.34 |
| 2 | 55.9 | 56.6 | 337 | 3.6 | 41 | 0.28 |
| 3 | 34.4 | 35.7 | 354 | 9.0 | 9.6 | 0.17 |
| 4 | 24.8 | 23.7 | 362 | 9.5 | 9.0 | 0.13 |
| 5 | 2.9 | 0 | 372 | 0 | 0 | - |
| Sensor Type | Material | Sizes, mm | Volt–Watt Sensitivity , mV/W |
|---|---|---|---|
| GHFS | single-crystal bismuth | 2.5 × 10 × 0.2 | 2.65 |
| Quantity, | Estimate, | Standard Uncertainty, | Uncertainty Contribution, |
|---|---|---|---|
| E | 9341 V | 35.0 V | 528 W/m |
| 2650 V/W | 67.4 V/W | 3582 W/m | |
| A | 25 × 10 m | 10.7 × 10 m | 605 W/m |
| Quantity, | Estimate, | Standard Uncertainty, | Uncertainty Contribution, |
|---|---|---|---|
| q | 141,060 W/m | 3670 W/m | 142.8 W/(m K) |
| 25.6 K | 1 K | 215.2 W/(m K) |
| , | q, kW/m | T, K |
|---|---|---|
| 0 | 117.57 | 350.0 |
| 15 | 116.32 | 350.5 |
| 30 | 131.13 | 349.6 |
| 45 | 176.41 | 348.9 |
| 60 | 181.13 | 346.9 |
| 75 | 173.34 | 348.2 |
| 90 | 156.86 | 346.9 |
| 105 | 161.15 | 346.9 |
| 120 | 157.94 | 347.0 |
| 135 | 137.93 | 346.9 |
| 150 | 159.04 | 345.5 |
| 165 | 95.73 | 344.1 |
| 180 | 94.23 | 344.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zainullina, E.R.; Mityakov, V.Y. Heat Transfer Investigation during Condensation on the Horizontal Pipe. Inventions 2023, 8, 2. https://doi.org/10.3390/inventions8010002
Zainullina ER, Mityakov VY. Heat Transfer Investigation during Condensation on the Horizontal Pipe. Inventions. 2023; 8(1):2. https://doi.org/10.3390/inventions8010002
Chicago/Turabian StyleZainullina, Elza R., and Vladimir Yu. Mityakov. 2023. "Heat Transfer Investigation during Condensation on the Horizontal Pipe" Inventions 8, no. 1: 2. https://doi.org/10.3390/inventions8010002
APA StyleZainullina, E. R., & Mityakov, V. Y. (2023). Heat Transfer Investigation during Condensation on the Horizontal Pipe. Inventions, 8(1), 2. https://doi.org/10.3390/inventions8010002





