Optimal Siting and Sizing of Electric Vehicle Energy Supplement Infrastructure in Highway Networks
Abstract
:1. Introduction
2. Literature Review
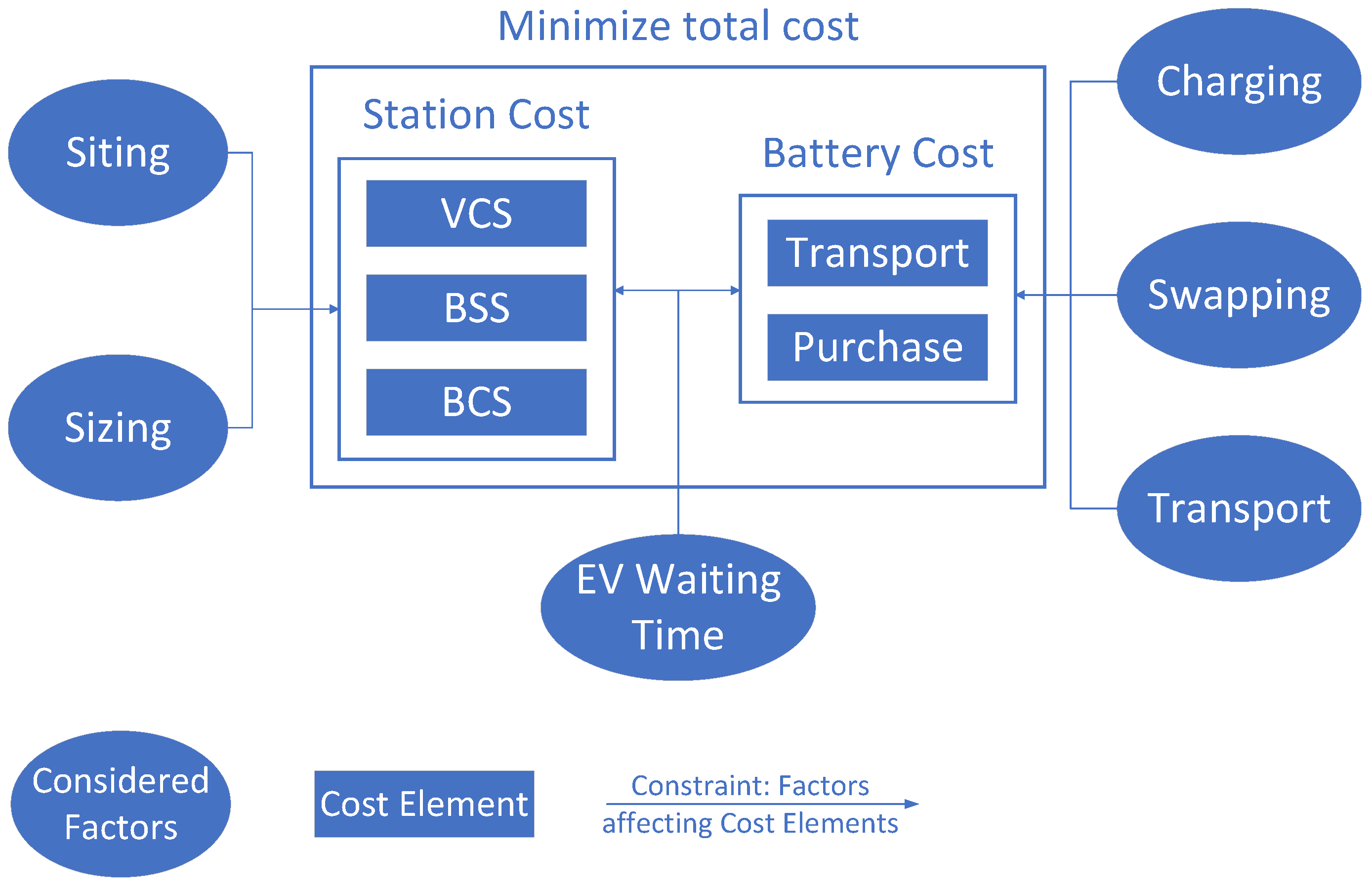
- This study establishes a coupled MILP model to optimize the battery quantity and the planning of VCS, BSS, and BCS while considering battery transportation and the EV battery’s energy supplement behavior (EV charging, EV battery swapping, and battery charging). This is the first study to integrate various charging/swapping station planning approaches with different charging/swapping behaviors.
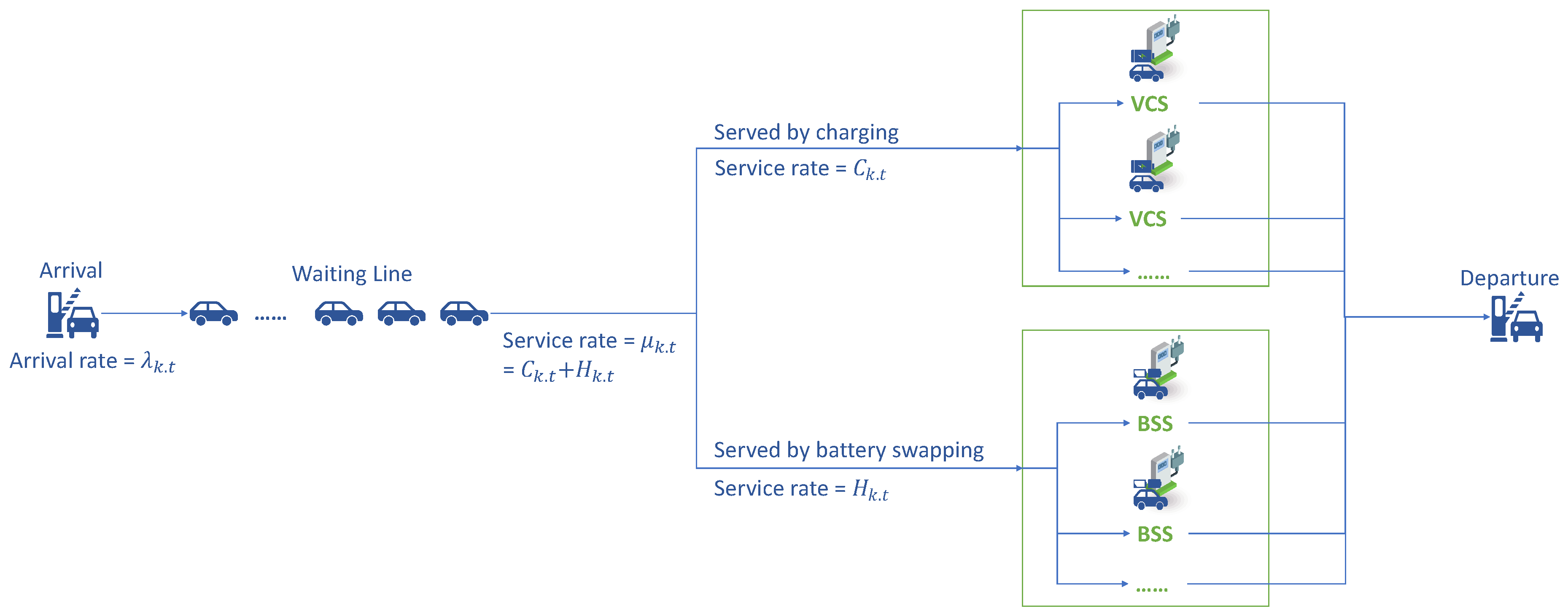
- A chance constraint is set to consider more realistic scenarios regarding the average waiting time for electric vehicle charging.
- This research designs a model based on general traffic flow in a real highway network, which is a more general case compared to buses or taxis in a city road network.
3. Methodology
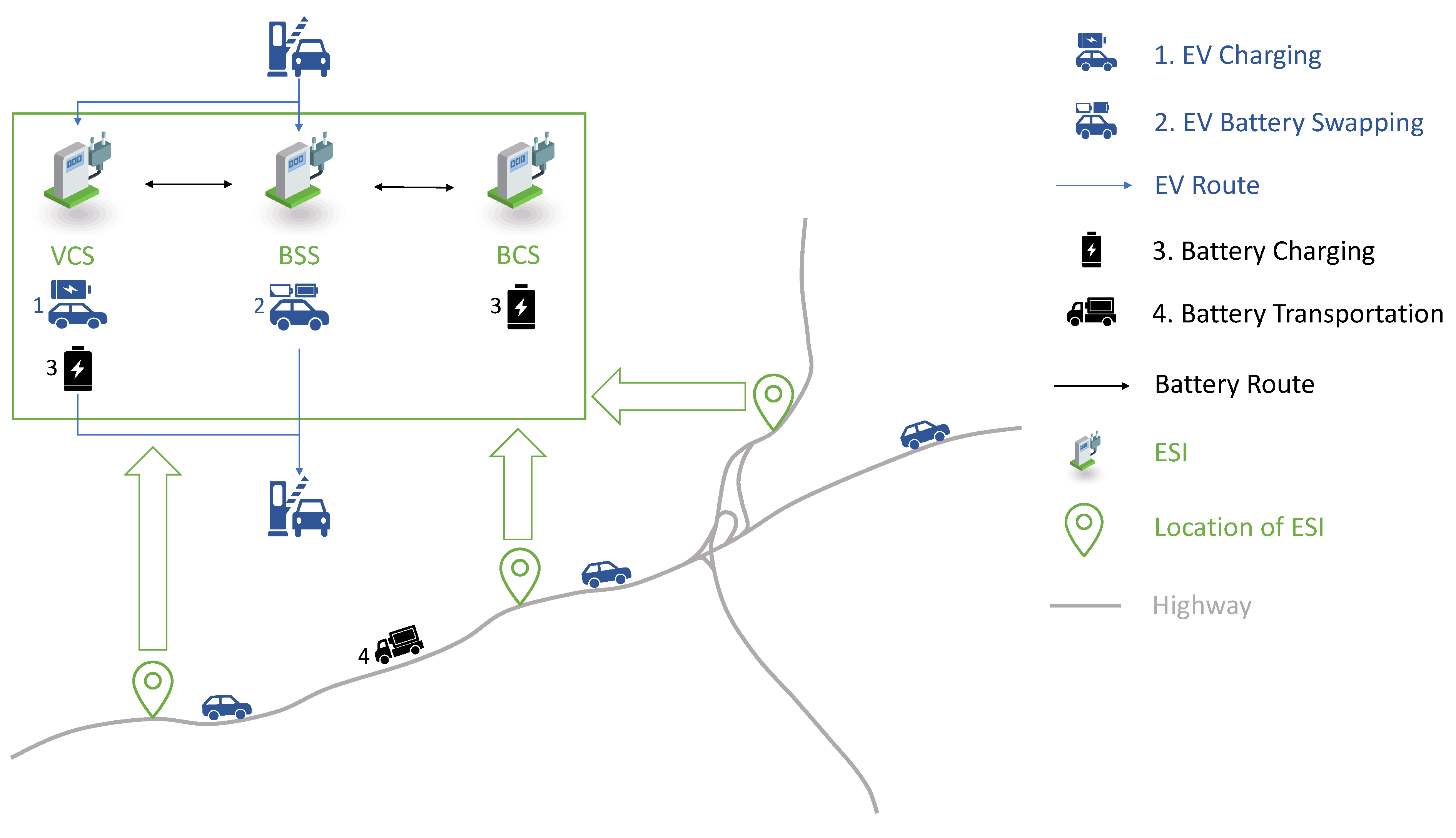
3.1. Research Question Statement
3.2. Parameters and Variables
- (a)
- Parameters
- (b)
- Decision Variables
- (c)
- Auxiliary Variables
3.3. Model
- (a)
- Objective Function
- (b)
- Constraints on Siting and Sizing of Energy Supplement Infrastructure
- (c)
- Constraints on Battery Charging and Transportation
- (d)
- Chance Constraint on EV Average Waiting Time
4. Case Study with Numerical Results
4.1. Parameter Settings
4.2. Planning Results for Energy Supplement Infrastructure
4.3. Effect of Average Waiting Time Tolerance
4.4. Effect of Battery Cost
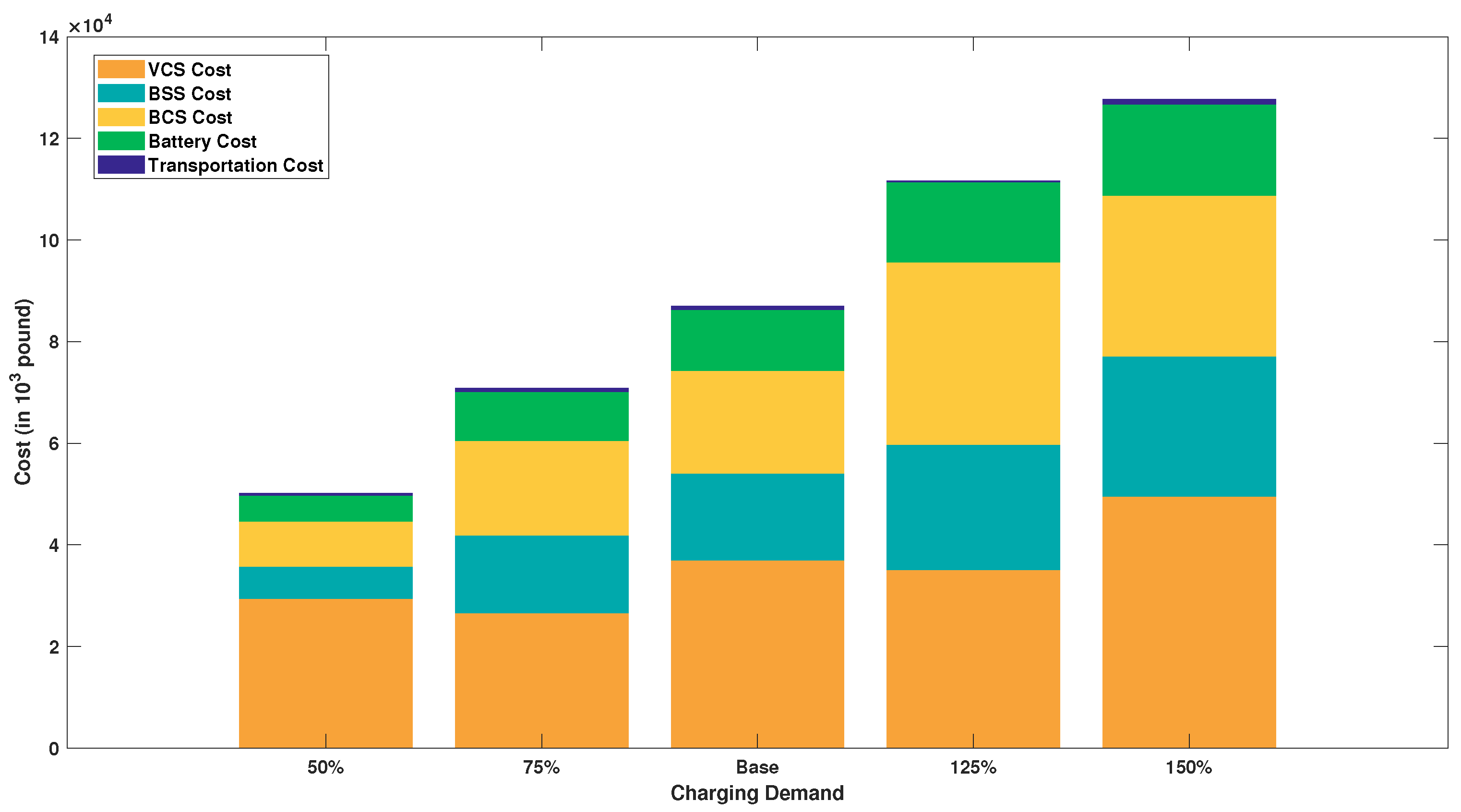
4.5. Effect of Charging Demand
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- UN. The Paris Agreement. Available online: https://www.un.org/en/climatechange/paris-agreement (accessed on 30 July 2023).
- IEA. Electric Vehicles. Available online: https://www.iea.org/energy-system/transport/electric-vehicles (accessed on 30 July 2023).
- GOV.UK. Electric Vehicle Charging Device Statistics: July 2023. Available online: https://www.gov.uk/government/statistics/electric-vehicle-charging-device-statistics-july-2023/electric-vehicle-charging-device-statistics-july-2023 (accessed on 30 July 2023).
- Leijon, J.; Boström, C. Charging Electric Vehicles Today and in the Future. World Electr. Veh. J. 2022, 13, 139. [Google Scholar] [CrossRef]
- Charge, T.F. NIO Ramps Up UK Team for Swap Station Launches. Available online: https://www.fastcharge.email/p/nio-swap-station-uk-launch (accessed on 26 August 2023).
- Hakimi, S.L. Optimum Distribution of Switching Centers in a Communication Network and Some Related Graph Theoretic Problems. Oper. Res. 1965, 13, 462–475. [Google Scholar] [CrossRef]
- Serra, D.; Marianov, V. The p-median problem in a changing network: The case of Barcelona. Locat. Sci. 1998, 6, 383–394. [Google Scholar] [CrossRef]
- Celik Turkoglu, D.; Erol Genevois, M. A comparative survey of service facility location problems. Ann. Oper. Res. 2020, 292, 399–468. [Google Scholar] [CrossRef]
- Jia, L.; Hu, Z.; Song, Y.; Luo, Z. Optimal siting and sizing of electric vehicle charging stations. In Proceedings of the 2012 IEEE International Electric Vehicle Conference, Greenville, SC, USA, 4–8 March 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Uslu, T.; Kaya, O. Location and capacity decisions for electric bus charging stations considering waiting times. Transp. Res. Part D Transp. Environ. 2021, 90, 102645. [Google Scholar] [CrossRef]
- Ma, H.; Pei, W.; Zhang, Q.; Xu, D.; Li, Y. Location of Electric Vehicle Charging Stations Based on Game Theory. World Electr. Veh. J. 2023, 14, 128. [Google Scholar] [CrossRef]
- Jin, Y.; Acquah, M.A.; Seo, M.; Han, S. Optimal Siting and Sizing of EV Charging Station using Stochastic Power Flow Analysis for Voltage Stability. IEEE Trans. Transp. Electrif. 2023, 1. [Google Scholar] [CrossRef]
- Henrique, L.F.; Silva, W.N.; Silva, C.C.A.; Dias, B.H.; Oliveira, L.W.; Almeida, M.C.d. Optimal siting and sizing of distributed energy resources in a Smart Campus. Electr. Power Syst. Res. 2023, 217, 109095. [Google Scholar] [CrossRef]
- Keleshteri, S.F.; Niknam, T.; Ghiasi, M.; Chabok, H. New optimal planning strategy for plug-in electric vehicles charging stations in a coupled power and transportation network. J. Eng. 2023, 2023, e12252. [Google Scholar] [CrossRef]
- Kłos, M.J.; Sierpiński, G. Siting of electric vehicle charging stations method addressing area potential and increasing their accessibility. J. Transp. Geogr. 2023, 109, 103601. [Google Scholar] [CrossRef]
- Kłos, M.J.; Sierpiński, G. Strategy for the Siting of Electric Vehicle Charging Stations for Parcel Delivery Service Providers. Energies 2023, 16, 2553. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, S.; An, J.; Kang, Q. Demand-Side Management Optimization in Electric Vehicles Battery Swapping Service. IEEE Access 2019, 7, 95224–95232. [Google Scholar] [CrossRef]
- Revankar, S.R.; Kalkhambkar, V.N. Grid integration of battery swapping station: A review. J. Energy Storage 2021, 41, 102937. [Google Scholar] [CrossRef]
- Mehrjerdi, H. Resilience oriented vehicle-to-home operation based on battery swapping mechanism. Energy 2021, 218, 119528. [Google Scholar] [CrossRef]
- Lu, T.; Gao, C. A General Model for Optimal Scheduling of Battery Charging and Renewal Network. Power Syst. Technol. 2014, 38, 2700–2707. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhang, Y. Optimal Location of Charging Station of Electric Bus in Battery Replacement Mode. In Smart Innovation, Systems and Technologies, Proceedings of the International Symposium for Intelligent Transportation and Smart City (ITASC) 2017 Proceedings, Shanghai, China, 19–20 May 2017; Zeng, X., Xie, X., Sun, J., Ma, L., Chen, Y., Eds.; Smart Innovation, Systems and Technologies; Springer: Singapore, 2017; pp. 113–125. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, T.; Yao, S.; Soh, C.B.; Wang, P. Distributed Operation Management of Battery Swapping-Charging Systems. IEEE Trans. Smart Grid 2019, 10, 5320–5333. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, X.; Yu, Z.; Zhu, X.; Shi, D. A Monte Carlo Simulation Approach to Evaluate Service Capacities of EV Charging and Battery Swapping Stations. IEEE Trans. Ind. Inform. 2018, 14, 3914–3923. [Google Scholar] [CrossRef]
- Schoenberg, S.; Dressler, F. Planning Ahead for EV: Total Travel Time Optimization for Electric Vehicles. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 3068–3075. [Google Scholar] [CrossRef]
- Xu, P.; Sun, X.; Wang, J.; Li, J.; Zheng, W.; Liu, H. Dynamic pricing at electric vehicle charging stations for waiting time reduction. In Proceedings of the 4th International Conference on Communication and Information Processing, ICCIP ’18, New York, NY, USA, 2–4 November 2018; pp. 204–211. [Google Scholar] [CrossRef]
- Bhat, U.N. An Introduction to Queueing Theory: Modeling and Analysis in Applications; Birkhäuser: Boston, MA, USA, 2008. [Google Scholar] [CrossRef]
- Crouhy, M.; Galai, D.; Mark, R. A comparative analysis of current credit risk models. J. Bank. Financ. 2000, 24, 59–117. [Google Scholar] [CrossRef]
- NationalHighways. WebTRIS—Map View. Available online: https://webtris.highwaysengland.co.uk (accessed on 30 July 2023).



| Parameter | Value | Unit |
|---|---|---|
| N | - | |
| 100 | - | |
| 50 | - | |
| 100 | - | |
| GBP | ||
| GBP | ||
| GBP | ||
| 10 | GBP | |
| r | 30 | mile |
| 2 | hour | |
| hour | ||
| hour | ||
| 0.8 | - | |
| w | 0.0365 | GBP per battery per mile |
| 6 | - | |
| 23 | - |
| Node | Model with Battery Transportation | Model without Battery Transportation | |||||||
|---|---|---|---|---|---|---|---|---|---|
| VCS | BSS | BCS | Battery | VCS | BSS | BCS | Battery | ||
| 1 | 19 | 3 | 0 | 87 | 50 | 1 | 6 | 28 | |
| 2 | 43 | 5 | 80 | 105 | 85 | 4 | 52 | 52 | |
| 3 | 32 | 4 | 77 | 97 | 88 | 1 | 0 | 27 | |
| 4 | 26 | 5 | 0 | 111 | 92 | 6 | 53 | 93 | |
| 5 | 30 | 5 | 99 | 99 | 53 | 5 | 52 | 90 | |
| 6 | 51 | 5 | 60 | 83 | 39 | 6 | 62 | 107 | |
| 7 | 58 | 6 | 68 | 107 | 61 | 7 | 67 | 111 | |
| 8 | 58 | 7 | 97 | 122 | 56 | 8 | 79 | 135 | |
| 9 | 46 | 5 | 71 | 90 | 40 | 6 | 59 | 99 | |
| 10 | 100 | 2 | 0 | 51 | 40 | 6 | 59 | 99 | |
| 11 | 47 | 1 | 0 | 34 | 59 | 2 | 0 | 13 | |
| 12 | 99 | 1 | 0 | 31 | 37 | 5 | 48 | 91 | |
| 13 | 45 | 4 | 78 | 126 | 33 | 5 | 48 | 92 | |
| 14 | 44 | 4 | 0 | 55 | 48 | 4 | 37 | 79 | |
| Total | 698 | 57 | 630 | 1198 | 781 | 66 | 622 | 1116 | |
| Cost | 8.70 × | 9.28 × | |||||||
| Full Battery | Empty Battery | ||||
|---|---|---|---|---|---|
| Time | Route | Number | Time | Route | Number |
| 6 | 64 | 6 | 7 | ||
| 7 | 25 | 6 | 13 | ||
| 7 | 25 | 7 | 15 | ||
| 8 | 48 | 8 | 25 | ||
| 11 | 39 | 8 | 27 | ||
| 11 | 4 | 8 | 4 | ||
| 12 | 21 | 9 | 22 | ||
| 12 | 13 | 9 | 13 | ||
| 12 | 28 | 9 | 7 | ||
| 13 | 30 | 9 | 1 | ||
| 13 | 25 | 9 | 38 | ||
| 14 | 26 | 10 | 25 | ||
| 14 | 22 | 10 | 30 | ||
| 15 | 33 | 10 | 2 | ||
| 15 | 20 | 10 | 3 | ||
| 15 | 14 | 10 | 4 | ||
| 15 | 23 | 10 | 5 | ||
| 15 | 5 | 10 | 14 | ||
| 15 | 13 | 11 | 25 | ||
| 15 | 5 | 11 | 20 | ||
| 16 | 25 | 11 | 10 | ||
| 16 | 1 | 11 | 25 | ||
| 16 | 1 | 12 | 30 | ||
| 17 | 23 | 12 | 28 | ||
| 17 | 23 | 12 | 8 | ||
| 17 | 12 | 12 | 34 | ||
| 17 | 6 | 12 | 13 | ||
| 17 | 10 | 12 | 32 | ||
| 17 | 38 | 13 | 24 | ||
| 18 | 21 | 13 | 1 | ||
| 19 | 18 | 14 | 24 | ||
| 19 | 3 | 14 | 20 | ||
| 19 | 8 | 14 | 33 | ||
| 20 | 69 | 15 | 46 | ||
| 21 | 50 | 15 | 19 | ||
| 21 | 57 | 15 | 3 | ||
| 21 | 3 | 16 | 48 | ||
| 22 | 1 | 16 | 73 | ||
| 22 | 97 | 16 | 1 | ||
| 22 | 2 | 17 | 27 | ||
| 22 | 33 | 17 | 24 | ||
| 22 | 21 | 19 | 37 | ||
| 19 | 11 | ||||
| 19 | 3 | ||||
| 19 | 30 | ||||
| 19 | 45 | ||||
| 19 | 22 | ||||
| 20 | 13 | ||||
| 20 | 59 | ||||
| 20 | 28 | ||||
| 20 | 29 | ||||
| 20 | 4 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, D.; Zhang, H.; Han, B.; Liu, G.; Xue, F.; Lu, S. Optimal Siting and Sizing of Electric Vehicle Energy Supplement Infrastructure in Highway Networks. Inventions 2023, 8, 117. https://doi.org/10.3390/inventions8050117
Jin D, Zhang H, Han B, Liu G, Xue F, Lu S. Optimal Siting and Sizing of Electric Vehicle Energy Supplement Infrastructure in Highway Networks. Inventions. 2023; 8(5):117. https://doi.org/10.3390/inventions8050117
Chicago/Turabian StyleJin, Ding, Huayu Zhang, Bing Han, Gang Liu, Fei Xue, and Shaofeng Lu. 2023. "Optimal Siting and Sizing of Electric Vehicle Energy Supplement Infrastructure in Highway Networks" Inventions 8, no. 5: 117. https://doi.org/10.3390/inventions8050117
APA StyleJin, D., Zhang, H., Han, B., Liu, G., Xue, F., & Lu, S. (2023). Optimal Siting and Sizing of Electric Vehicle Energy Supplement Infrastructure in Highway Networks. Inventions, 8(5), 117. https://doi.org/10.3390/inventions8050117









