Model Problems on Oscillations of Mechanical and Biological Membranes
Abstract
:1. Introduction
2. Materials and Methods
- —equations for voltage fluctuations in a limited telegraph line.
- —equation of damped gas oscillations in a spherical region.
- —vibration equation of a circular membrane.
3. Results
3.1. Spherically Symmetric Cases in Three-Dimensional Space
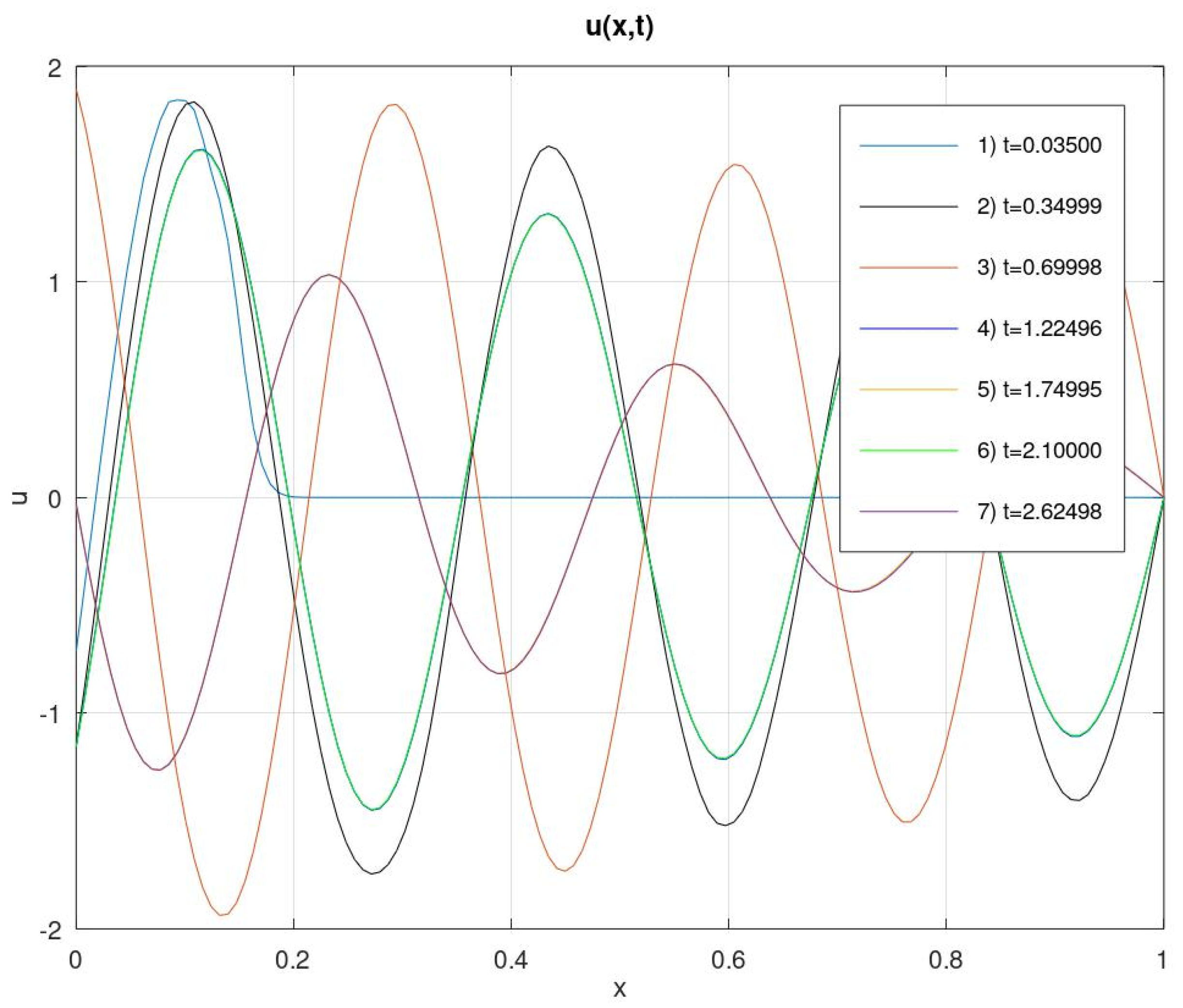
3.2. Oscillations of Circular Membranes
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sorokin, V.M.; Yashchenko, A.K. Oscillations of frameless film membrane stabilized by ampere force in zero-gravity state. Appl. Mech. Tech. Phys. 2013, 54, 27–37. [Google Scholar] [CrossRef]
- Ukhobotov, V.I.; Livanov, N.D. On one problem of controlling a moving cart with elastic rode on it. Bull. SUSU Ser. Math. Mech. Phys. 2021, 13, 22–28. [Google Scholar]
- Volnikov, M.I.; Smogunov, V.V. Mathematical models of dynamics of heterostructures with friction News of higher educational institutions. Volga region. Tech. Sci. 2020, 55, 98–108. [Google Scholar] [CrossRef]
- Aleksandrovich, I.V.; Viktorovich, M.K.; Vitalievich, N.D. Exact solution of differential equation describing free and forced pendulum oscillations with friction in the suspension center. Sci. Tech. Bull. Inf. Technol. Mech. Opt. 2003, 9, 100–105. Available online: https://cyberleninka.ru/article/n/tochnoe-reshenie-differentsialnogo-uravneniya-opisyvayuschego-svobodnye-i-vynuzhdennye-kolebaniya-mayatnika-s-treniem-v-tochke-podvesa (accessed on 3 April 2022).
- Pozhalostin, A.A.; Kuleshov, B.G.; Panshina, A. Oscillations of elastic one-dimensional systems with friction. Eng. J. Sci. Innov. 2013, 12. Available online: http://engjournal.ru/catalog/eng/teormech/1136.html (accessed on 10 June 2023). [CrossRef]
- Varin, V.P.; Petrov, A.G. Mathematical model of human cochlea. Prepr. IAM 2008, 96, 26. [Google Scholar]
- Kulterbaev, K.P.; Islamova, O.V. Oscillations of membranes at different-type random disturbances. In Proceedings of the 2nd All-Russian Scientific Conference, SamSTU, Samara, Russia, 1–3 June 2005; Part 1, Mathematical Models of Mechanics, Strength and Reliability of Structures, Mathematical Modeling and Boundary Value Problems. pp. 179–182. [Google Scholar]
- Muñoz, J.C.; Ruzhansky, M.; Tokmagambetov, N. Acoustic and Shallow Water Wave Propagation with Irregular Dissipation. Funct. Anal. Its Appl. 2019, 53, 153–156. [Google Scholar] [CrossRef]
- Agoshkov, V.I.; Dubovsky, P.B.; Shutyaev, V. Methods of Solving Problems of Mathematical Physics; Fizmatlit: Moscow, Russia, 2002; 320p. [Google Scholar]
- Shubin, M.A. Lectures on Equations of Mathematical Physics; MCCME: Moscow, Russia, 2003; 303p. [Google Scholar]
- Oleinik, O.A. Lectures on Equations with Partial Derivatives; Laboratory of Knowledge: Moscow, Russia, 2020; 261p, ISBN 978-5-00101-703-5. [Google Scholar]
- Hayt, W.H. Engineering Electromagnetics (English), 5th ed.; McGraw-Hill Education: New York, NY, USA, 1989; pp. 382–392. ISBN 0070274061. [Google Scholar]
- Sadiku, M.N.O. Elements of Electromagnetics (English), 1st ed.; Saunders College Publishing: Orlando, FL, USA, 1989; pp. 497–505. ISBN 993013846. [Google Scholar]
- Metzger, G. Transmission Lines with Pulse Excitation (English), 1st ed.; Academic Press: New York, NY, USA, 1969; pp. 1–10. [Google Scholar]
- Marshall, S.V. Electromagnetic Concepts & Applications (English), 2nd ed.; Prentice-Hall: New York, NY, USA, 1987; pp. 369–372. ISBN 0132490048. [Google Scholar]
- Mikhin, E.A.; Drobyshev, A.A. Modeling the dynamics of particle movement above the rectangular membrane surface performing forced oscillations in the gravity field. Bull. Voronezh State Univ. (VSU) Ser. Phys. Math. 2021, 1, 38–46. [Google Scholar]
- Koshlyakov, N.S.; Gliner, E.B.; Smirnov, M.M. Equations in Partial Derivatives of Mathematical Physics. Study Aid for Mechanical-Mathematical Faculties of Universities; Vysshaya Shkola: Moscow, Russia, 1970; 712p. [Google Scholar]
- Ya, A.V. Methods of Mathematical Physics and Special Functions, 2nd ed.; Chief Publishers of Physical and Mathematical Literature: Soviet Union, 1984; 384p. [Google Scholar]
- Kezik, V.I. Forced axisymmetric oscillations of a spherical membrane being an element of the acoustic oscillatory system. Tech. Acoust. 2013, 9. Available online: http://www.ejta.org (accessed on 18 June 2023).
- Mayer, R.V. Numerical method of solving a boundary value problem for an oscillating membrane. Cybern. Program. 2015, 2, 59–67. Available online: https://nbpublish.com/library_read_article.php?id=14454 (accessed on 18 June 2023). [CrossRef]
- Puria, S.; Allen, J.B. Measurements and model of the cat middle ear: Evidence of tympanic membrane acoustic delay. J. Acoust. Soc. Am. 1998, 104, 3463–3481. [Google Scholar] [CrossRef] [PubMed]
- Mikhasev, G.I.; Firsov, M.A.; Sitnikov, V.P. Sitnikov Modeling of free oscillations of the sound-transmitting system of the reconstructed middle ear. Biomechanics 2005, 1, 52–62. Available online: https://cyberleninka.ru/article/n/modelirovanie-svobodnyh-kolebaniy-zvukoprovodyaschey-sistemy-rekonstruirovannogo-srednego-uha (accessed on 14 August 2023).
- Ugarteburu, M.; Withnell, R.H.; Cardoso, L.; Carriero, A.; Richter, C.-P. Mammalian middle ear mechanics: A review. Front. Bioeng. Biotechnol. 2022, 10, 983510. [Google Scholar] [CrossRef]
- Heider, D.T.; van Hemmen, J.L. Effective-Spring Model of Tympanic Response in Archo-saurs. Open J. Biophys. 2019, 9, 21–50. [Google Scholar] [CrossRef]
- Iyoho, A.E.; Ho, K.; Chan, P. The Development of a Tympanic Membrane Model and Probabilistic Dose-Response Risk Assessment of Rupture Because of Blast. Mil. Med. 2020, 185 (Suppl. S1), 234–242. [Google Scholar] [CrossRef]
- Wu, C.; Chen, Y.; Al-Furjan, M.S.H.; Ni, J.; Yang, X. Free vibration model and theoretical solution of the tympanic membrane. Comput. Assist. Surg. 2016, 21 (Suppl. S1), 61–68. [Google Scholar] [CrossRef]
- Fay, J.P.; Puria, S.; Steele, C.R. The discordant eardrum. Biophys. Comput. Biol. 2006, 103, 19743–19748. [Google Scholar] [CrossRef]
- Edgar, A.; Rivas, B.I. Theoretical and computacional analysis of the fixing of ossicular chain. Nova Sci. 2008, 1, 107–117. [Google Scholar] [CrossRef]
- Ahn, T.S.; Baek, M.J.; Lee, D. Experimental measurement of tympanic membrane response for finite element model validation of a human middle ear. SpringerPlus 2013, 2, 527. [Google Scholar] [CrossRef]
- Caminos, L.; Garcia-Manrique, J.; Lima-Rodriguez, A.; Gonzalez-Herrera, A. Analysis of the Mechanical Properties of the Human Tympanic Membrane and Its Influence on the Dynamic Behaviour of the Human Hearing System. Appl. Bionics Biomech. 2018, 2018, 1736957. [Google Scholar] [CrossRef]
- Keefe, D.H. Human middle-ear model with compound eardrum and airway branching in mastoid air cells. J. Acoust. Soc. Am. 2015, 137, 2698–2725. [Google Scholar] [CrossRef]
- Zhang, X.; Guan, X.; Nakmali, D.; Palan, V.; Pineda, M.; Gan, R.Z. Experimental and Modeling Study of Human Tympanic Membrane Motion in the Presence of Middle Ear Liquid. JARO 2014, 15, 867–881. [Google Scholar] [CrossRef] [PubMed]
- Bosyakov, S.M.; Slavashevich, I.L.; Yurkevich, K.S.; Mikhasev, G.I. Finite-element modeling of free oscillations of the reconstructed middle ear during stapedoplasty. Bull. BSU Ser. 1 Phys. Math. Inform. 2016, 1, 101–106. [Google Scholar]
- Bosyakov, S.M.; Yurkevich, K.S.; Mikhasev, G.I.; Petrova, L.G.; Maisyuk, M.M. Evaluation of cartilage transplant thickness for a tympanic membrane when resecting the retraction pocket (finite-element modeling). Math. Inform. 2021, 1, 69–78. [Google Scholar] [CrossRef]
- Leonidovna, S.I.; Ivanovich, M.G. Modeling of free oscillations of the reconstructed middle ear subjected to tympanostapedoplasty and perforation of stapes’ underfoot plate. Bull. NNSU 2011, 4-2, 527–529. Available online: https://cyberleninka.ru/article/n/modelirovanie-svobodnyh-kolebaniy-rekonstruirovannogo-srednego-uha-podvergnutogo-timpanostapedoplastike-i-perforatsii-podnozhnoy (accessed on 14 August 2023).
- Savotchenko, S.E.; Gorlov, A.S. Simulation of wave processes in liquid under the vibrations of the membrane in the tube. Sci. Innov. Technol. 2018, 1, 43–54. (In Russian) [Google Scholar]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kostikov, Y.; Romanenkov, A. Model Problems on Oscillations of Mechanical and Biological Membranes. Inventions 2023, 8, 139. https://doi.org/10.3390/inventions8060139
Kostikov Y, Romanenkov A. Model Problems on Oscillations of Mechanical and Biological Membranes. Inventions. 2023; 8(6):139. https://doi.org/10.3390/inventions8060139
Chicago/Turabian StyleKostikov, Yury, and Aleksandr Romanenkov. 2023. "Model Problems on Oscillations of Mechanical and Biological Membranes" Inventions 8, no. 6: 139. https://doi.org/10.3390/inventions8060139
APA StyleKostikov, Y., & Romanenkov, A. (2023). Model Problems on Oscillations of Mechanical and Biological Membranes. Inventions, 8(6), 139. https://doi.org/10.3390/inventions8060139





