Influence of Density Ratios on Richtmyer–Meshkov Instability with Non-Equilibrium Effects in the Reshock Process
Abstract
:1. Introduction
2. Two-Component Discrete Boltzmann Model
3. Results and Discussions
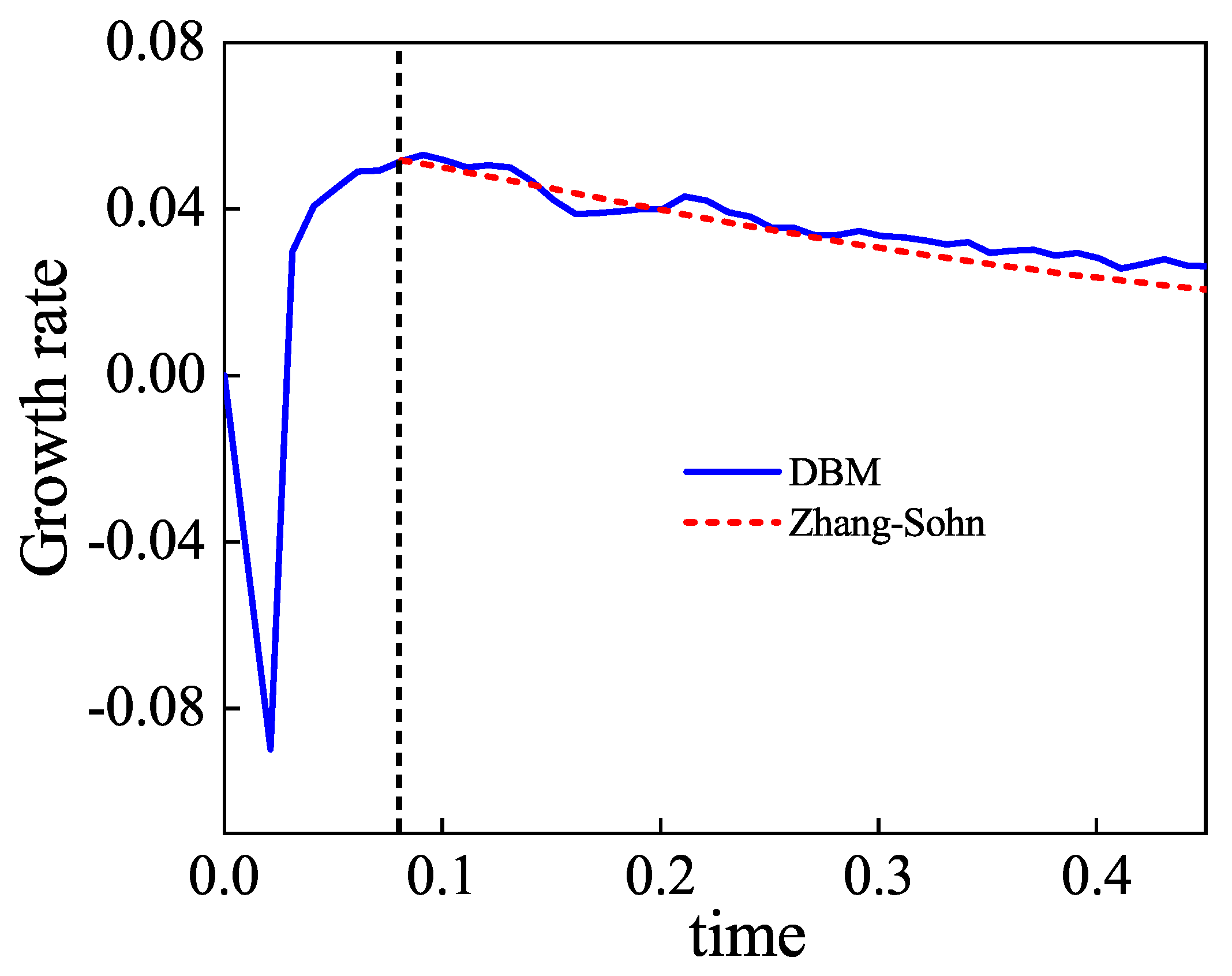
3.1. Verification and Validation
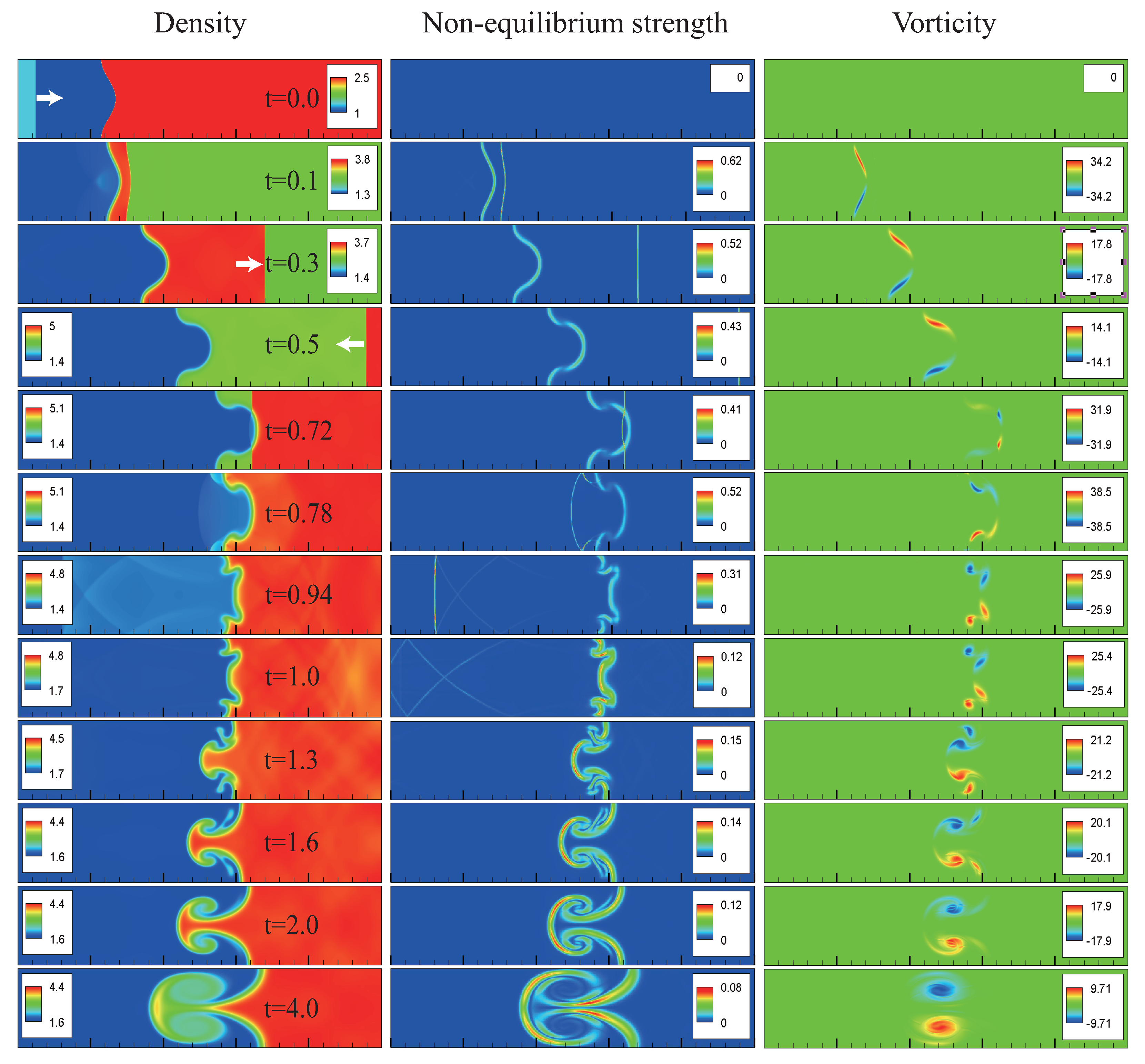
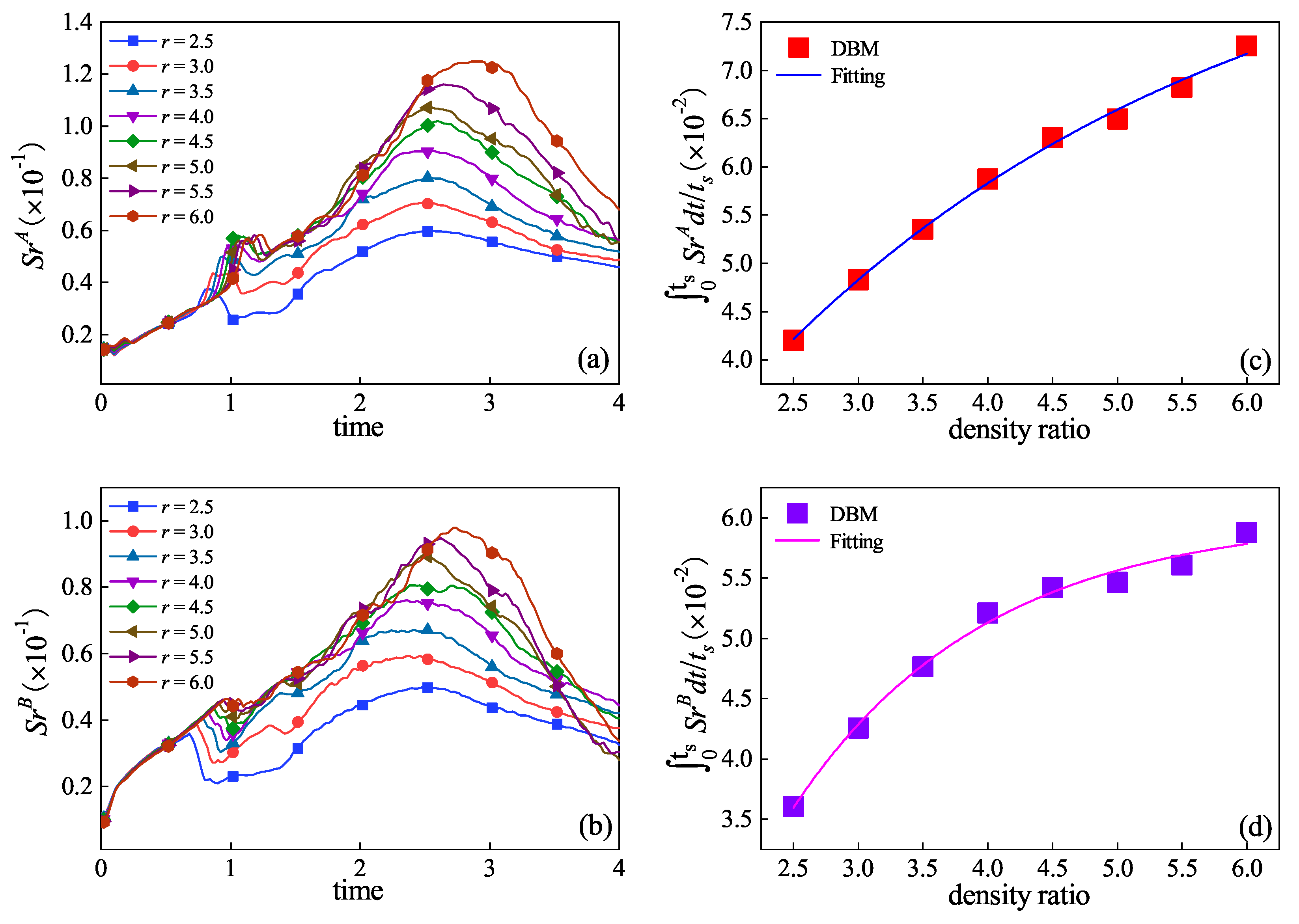
3.2. Hydrodynamic Non-Equilibrium Effects
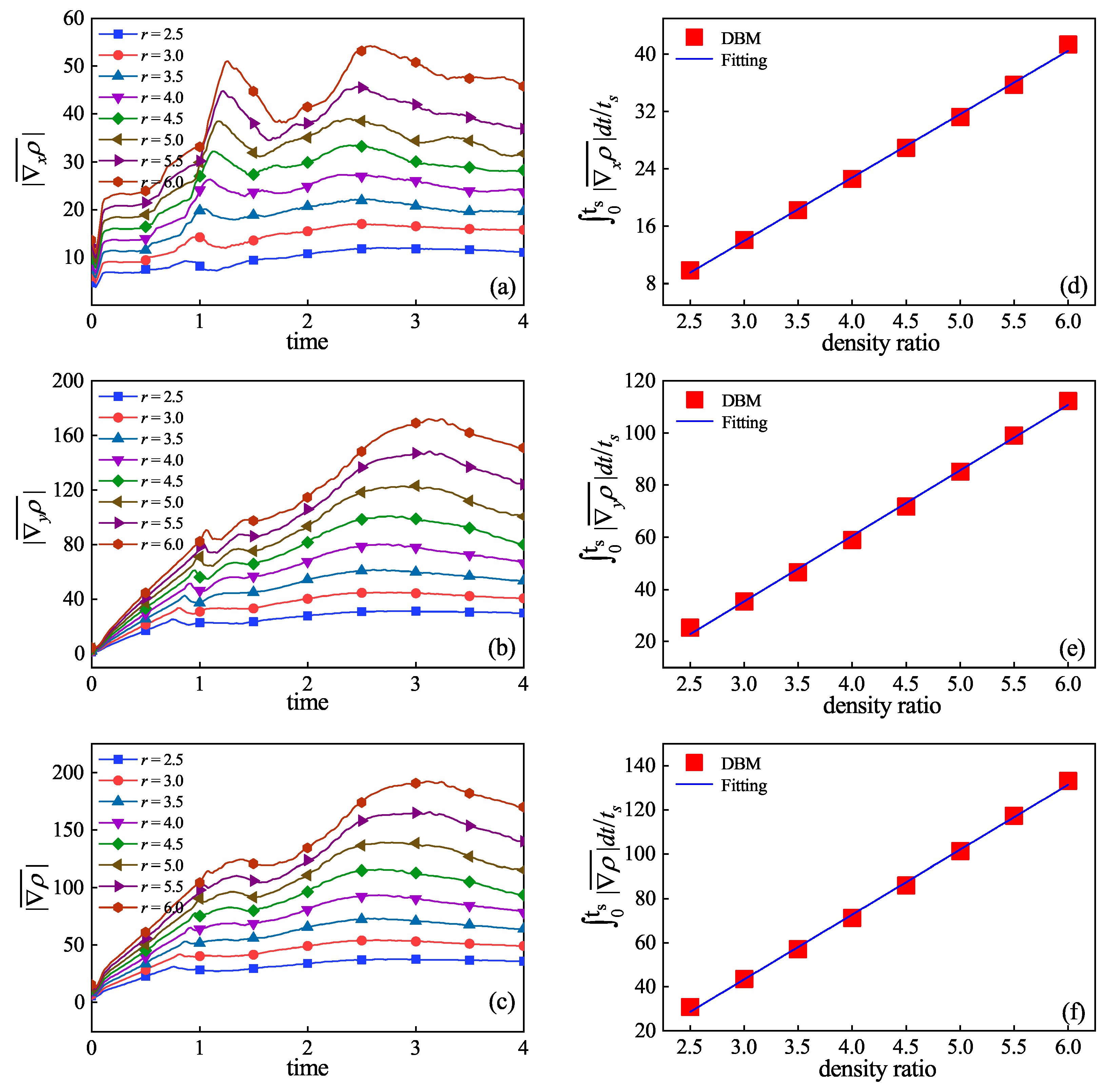
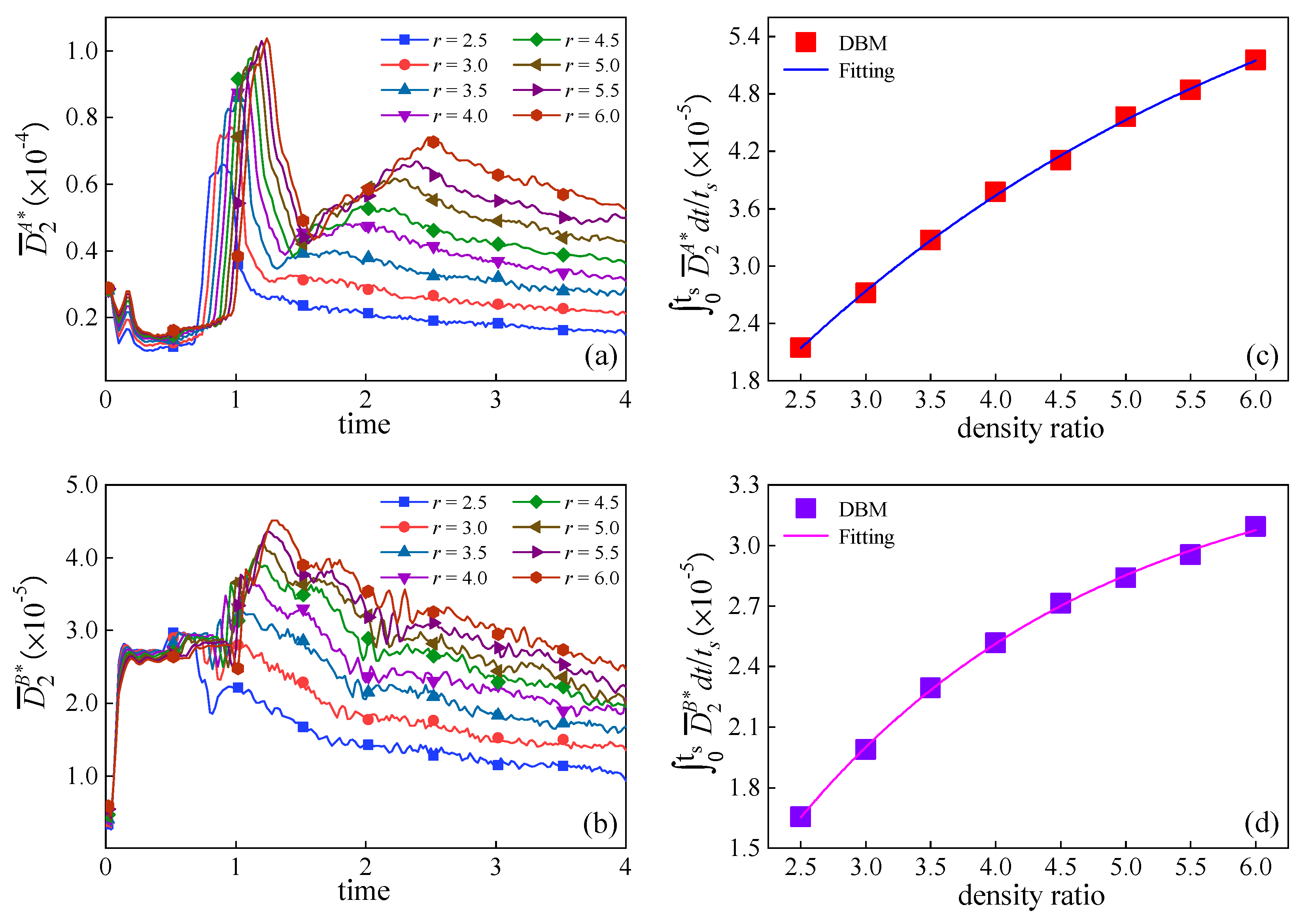
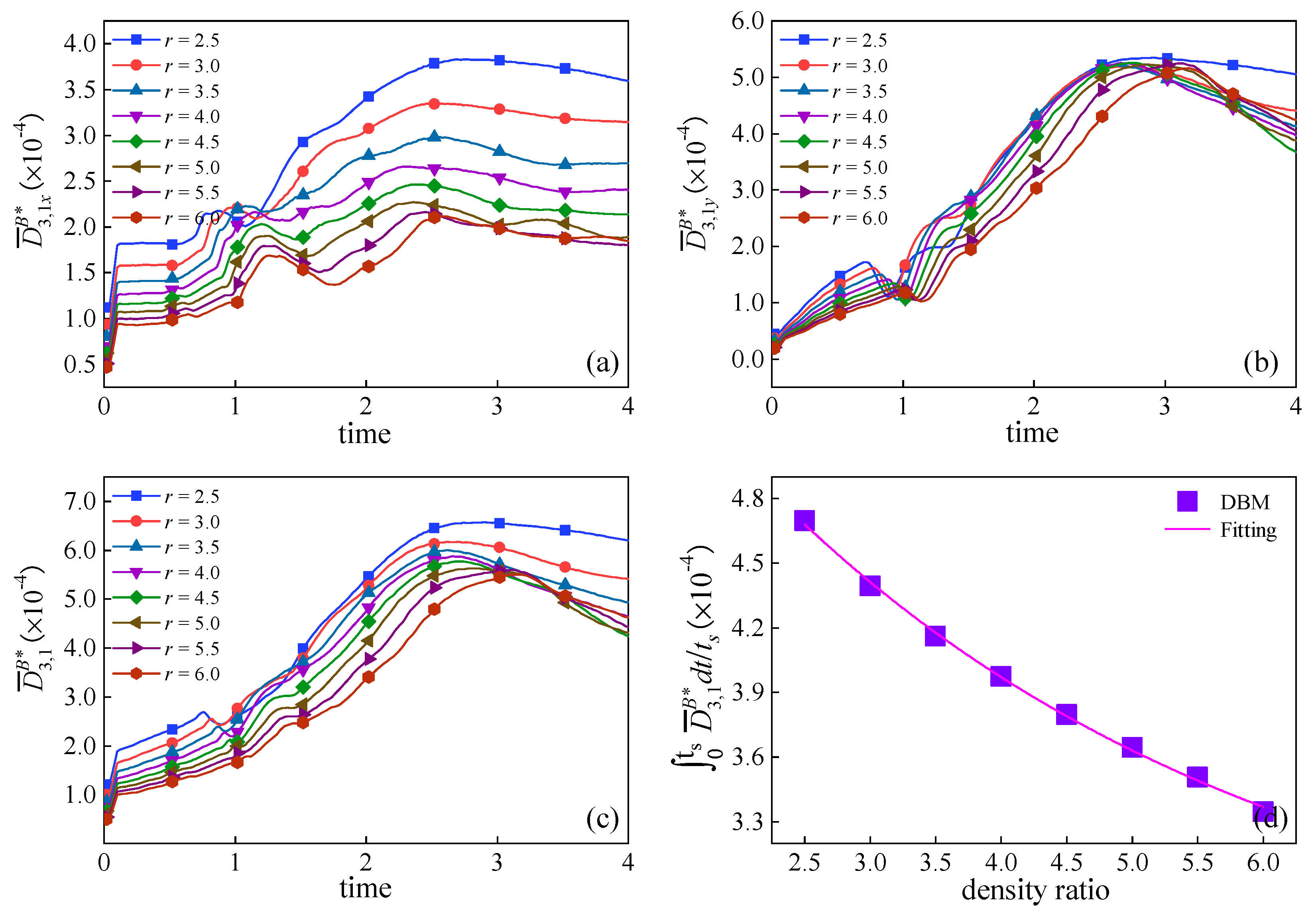
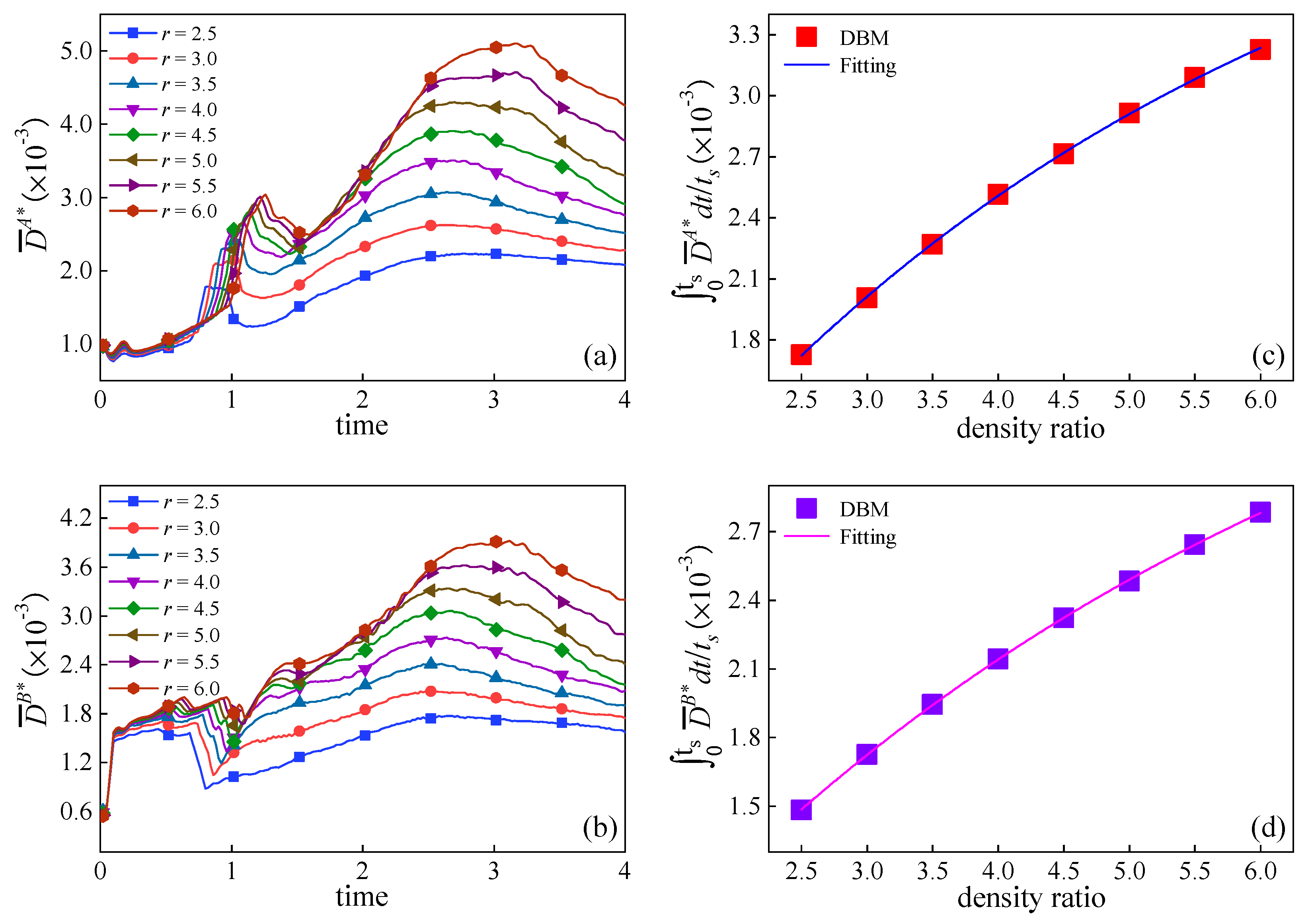
3.3. Thermodynamic Non-Equilibrium Effects
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| chemical species | |
| i | index of discrete velocity |
| discrete (equilibrium) distribution function | |
| t | time |
| space coordinate | |
| discrete velocity | |
| collision term | |
| relaxation time | |
| relaxation parameter | |
| , n | number density |
| , | mass density |
| , | flow velocity |
| , p | pressure |
| molecular mass | |
| , T | temperature |
| , E | internal energy density |
| D | spatial dimension |
| I | extra degrees of freedom |
| an matrix | |
| the inverse matrix of | |
| central kinetic moments of | |
| central kinetic moments of | |
| peculiar velocity | |
| non-organized momentum flux | |
| non-organized energy flux | |
| flux of non-organized momentum flux | |
| flux of non-organized energy flux | |
| total thermodynamic non-equilibrium quantity | |
| average of over the physical system | |
| average of over the physical system | |
| average of over the physical system | |
| average of over the physical system | |
| average of over the physical system | |
| length of the fluid system | |
| width of the fluid system | |
| , , , | size of discrete velocities |
| , , , | parameter of extra degrees of freedom |
| L, M, R | left, middle, and right regions |
| Mach number | |
| perturbation amplitude | |
| k | wave number |
| r | density ratio |
| Atwood number | |
| , | mesh grids |
| , | space step |
| time step | |
| v | amplitude growth |
| post-shock Atwood number | |
| post-shock amplitude | |
| the change of interface velocity | |
| vorticity | |
| average density gradient over the physical system | |
| average density gradient in the x direction over the physical system | |
| average density gradient in the y direction over the physical system | |
| specific heat ratio | |
| heat conductivity | |
| dynamic viscosity coefficient | |
| e | internal energy of the mixing system per unit mass |
Appendix A. Navier–Stokes Equations
Appendix B. Expressions of the Kinetic Moments
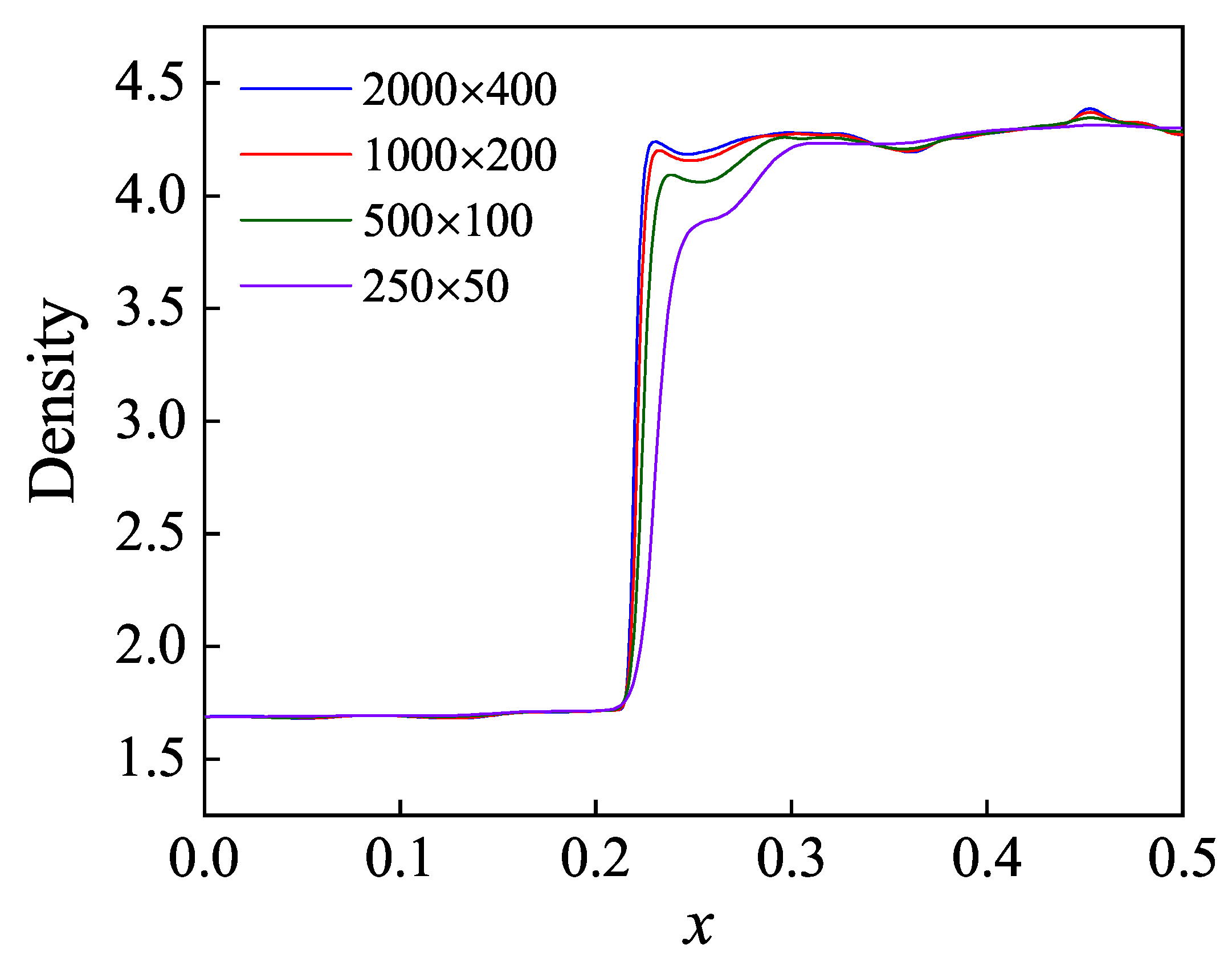
Appendix C. The Verification of Grid Convergence
References
- Richtmyer, R.D. Taylor instability in shock acceleration of compressible fluids. Commun. Pur. Appl. Math. 1960, 13, 297–317. [Google Scholar] [CrossRef]
- Meshkov, E. Instability of the interface of two gases accelerated by a shock wave. Fluid Dynam. 1969, 4, 101–104. [Google Scholar] [CrossRef]
- Brouillette, M. The Richtmyer-Meshkov instability. Annu. Rev. Fluid Mech. 2002, 34, 445–468. [Google Scholar] [CrossRef]
- Poludnenko, A.Y.; Chambers, J.; Ahmed, K.; Gamezo, V.N.; Taylor, B.D. A unified mechanism for unconfined deflagration-to-detonation transition in terrestrial chemical systems and type Ia supernovae. Science 2019, 366, eaau7365. [Google Scholar] [CrossRef] [PubMed]
- Morris, C.; Hopson, J.W.; Goldstone, P. Proton radiography. Los Alamos Sci. 2006, 30, 32. [Google Scholar]
- Yang, J.; Kubota, T.; Zukoski, E.E. A model for characterization of a vortex pair formed by shock passage over a light-gas inhomogeneity. J. Fluid Mech. 1994, 258, 217–244. [Google Scholar] [CrossRef]
- MacPhee, A.; Smalyuk, V.; Landen, O.; Weber, C.; Robey, H.; Alfonso, E.; Baker, K.; Berzak, H.L.; Biener, J.; Bunn, T.; et al. Hydrodynamic instabilities seeded by the X-ray shadow of ICF capsule fill-tubes. Phys. Plasmas 2018, 25, 082702. [Google Scholar] [CrossRef]
- Roycroft, R.; Sauppe, J.P.; Bradley, P.A. Double cylinder target design for study of hydrodynamic instabilities in multi-shell ICF. Phys. Plasmas 2022, 29, 032704. [Google Scholar] [CrossRef]
- Mostert, W.; Wheatley, V.; Samtaney, R.; Pullin, D.I. Effects of magnetic fields on magnetohydrodynamic cylindrical and spherica Richtmyer-Meshkov instability. Phys. Fluids 2015, 27, 104102. [Google Scholar] [CrossRef]
- Attal, N.; Ramaprabhu, P. Numerical investigation of a single-mode chemically reacting Richtmyer-Meshkov instability. Shock Waves 2015, 25, 307–328. [Google Scholar] [CrossRef]
- Valerio, E.; Jourdan, G.; Houas, L.; Zeitoun, D.; Besnard, D. Modeling of Richtmyer-Meshkov instability-induced turbulent mixing in shock-tube experiments. Phys. Fluids 1999, 11, 214–225. [Google Scholar] [CrossRef]
- Guo, X.; Si, T.; Zhai, Z.; Luo, X. Large-amplitude effects on interface perturbation growth in Richtmyer-Meshkov flows with reshock. Phys. Fluids 2022, 34, 082118. [Google Scholar] [CrossRef]
- Cong, Z.; Guo, X.; Si, T.; Luo, X. Experimental and theoretical studies on heavy fluid layers with reshock. Phys. Fluids 2022, 34, 104108. [Google Scholar] [CrossRef]
- Wang, H.; Ding, J.; Si, T.; Luo, X. Richtmyer-Meshkov instability of a single-mode interface with reshock. Acta Aerodyn. Sin. 2022, 40, 33–40. [Google Scholar]
- Guo, X.; Cong, Z.; Si, T.; Luo, X. Shock-tube studies of single-and quasi-single-mode perturbation growth in Richtmyer-Meshkov flows with reshock. J. Fluid Mech. 2022, 941, 65. [Google Scholar] [CrossRef]
- Nagel, S.; Raman, K.; Huntington, C.; MacLaren, S.; Wang, P.; Bender, J.; Prisbrey, S.; Zhou, Y. Experiments on the single-mode Richtmyer-Meshkov instability with reshock at high energy densities. Phys. Plasmas 2022, 29, 032308. [Google Scholar] [CrossRef]
- Rasteiro Dos Santos, M.; Bury, Y.; Jamme, S.; Griffond, J. On the effect of characterised initial conditions on the evolution of the mixing induced by the richtmyer–meshkov instability. Shock Waves 2023, 33, 117–130. [Google Scholar] [CrossRef]
- Ukai, S.; Balakrishnan, K.; Menon, S. Growth rate predictions of single-and multi-mode Richtmyer-Meshkov instability with reshock. Shock Waves 2011, 21, 533–546. [Google Scholar] [CrossRef]
- Tritschler, V.K.; Olson, B.J.; Lele, S.K.; Hickel, S.; Hu, X.; Adams, N.A. On the Richtmyer-Meshkov instability evolving from a deterministic multimode planar interface. J. Fluid Mech. 2014, 755, 429–462. [Google Scholar] [CrossRef]
- Olson, B.J.; Greenough, J.A. Comparison of two-and three-dimensional simulations of miscible Richtmyer-Meshkov instability with multimode initial conditions. Phys. Fluids 2014, 26, 101702. [Google Scholar] [CrossRef]
- Li, H.; He, Z.; Zhang, Y.; Tian, B. On the role of rarefaction/compression waves in Richtmyer-Meshkov instability with reshock. Phys. Fluids 2019, 31, 054102. [Google Scholar] [CrossRef]
- Latini, M.; Schilling, O. A comparison of two-and three-dimensional single-mode reshocked Richtmyer-Meshkov instability growth. Physica D 2020, 401, 132201. [Google Scholar] [CrossRef]
- Bin, Y.; Xiao, M.; Shi, Y.; Zhang, Y.; Chen, S. A new idea to predict reshocked Richtmyer-Meshkov mixing: Constrained large-eddy simulation. J. Fluid Mech. 2021, 918, R1. [Google Scholar] [CrossRef]
- Mohaghar, M.; McFarland, J.; Ranjan, D. Three-dimensional simulations of reshocked inclined Richtmyer-Meshkov instability: Effects of initial perturbations. Phys. Rev. Fluids 2022, 7, 093902. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, S.; Ding, J.; Wang, W.; Luo, X. Molecular dynamics simulation of cylindrical Richtmyer-Meshkov instability. Sci. Chin. Phys. Mech. Astron. 2018, 61, 114712. [Google Scholar] [CrossRef]
- Liu, H.; Yu, B.; Chen, H.; Chen, H.; Zhang, B.; Xu, H.; Liu, H. Contribution of viscosity to the circulation deposition in the Richtmyer–Meshkov instability. J. Fluid Mech. 2020, 895, A10. [Google Scholar] [CrossRef]
- Lin, C.; Xu, A.; Zhang, G.; Li, Y.; Succi, S. Polar-coordinate lattice Boltzmann modeling of compressible flows. Phys. Rev. E 2014, 89, 013307. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Xu, A.; Zhang, G. Collaboration and competition between Richtmyer-Meshkov instability and Rayleigh-Taylor instability. Phys. Fluids 2018, 30, 102105. [Google Scholar] [CrossRef]
- Shan, Y.; Xu, A.; Wang, L.; Zhang, Y. Nonequilibrium kinetics effects in Richtmyer–Meshkov instability and reshock processes. Commun. Theor. Phys. 2023, 75, 115601. [Google Scholar] [CrossRef]
- Xu, A.; Zhang, G.; Gan, Y.; Chen, F.; Yu, X. Lattice Boltzmann modeling and simulation of compressible flows. Front. Phys. 2012, 7, 582–600. [Google Scholar] [CrossRef]
- Xu, A.; Shan, Y.; Chen, F.; Gan, Y.; Lin, C. Progress of mesoscale modeling and investigation of combustion multiphase flow. Acta Aero. Astro. Sin. 2021, 42, 625842. [Google Scholar]
- Benzi, R.; Succi, S.; Vergassola, M. The lattice Boltzmann equation: Theory and applications. Phys. Rep. 1992, 222, 145–197. [Google Scholar] [CrossRef]
- Wei, Y.; Yang, H.; Dou, H.; Lin, Z.; Wang, Z.; Qian, Y. A novel two-dimensional coupled lattice Boltzmann model for thermal incompressible flows. Appl. Math. Comput. 2018, 339, 556–567. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, Y.; Qian, Y. A bounce back-immersed boundary-lattice Boltzmann model for curved boundary. Appl. Math. Model. 2020, 81, 428–440. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, Y.; Qian, Y. A novel thermal lattice Boltzmann model with heat source and its application in incompressible flow. Appl. Math. Model. 2022, 427, 127167. [Google Scholar] [CrossRef]
- Li, Q.; Jiang, J.; Hong, Y.; Du, J. Numerical investigation of thermal management performances in a solar photovoltaic system by using the phase change material coupled with bifurcated fractal fins. J. Energy Storage 2022, 56, 106156. [Google Scholar] [CrossRef]
- Fei, L.; Qin, F.; Zhao, J.; Derome, D.; Carmeliet, J. Lattice boltzmann modelling of isothermal two-component evaporation in porous media. J. Fluid Mec. 2023, 955, 18. [Google Scholar] [CrossRef]
- Li, Q.; Xing, Y.; Huang, R. Equations of state in multiphase lattice Boltzmann method revisited. Phys. Rev. E 2023, 107, 015301. [Google Scholar] [CrossRef]
- Lai, H.; Xu, A.; Zhang, G.; Gan, Y.; Ying, Y.; Succi, S. Nonequilibrium thermohydrodynamic effects on the Rayleigh-Taylor instability in compressible flows. Phys. Rev. E 2016, 94, 023106. [Google Scholar] [CrossRef]
- Lin, C.; Luo, K.; Xu, A.; Gan, Y.; Lai, H. Multiple-relaxation-time discrete Boltzmann modeling of multicomponent mixture with nonequilibrium effects. Phys. Rev. E 2021, 103, 013305. [Google Scholar] [CrossRef]
- Chen, L.; Lai, H.; Lin, C.; Li, D. Specific heat ratio effects of compressible Rayleigh-Taylor instability studied by discrete Boltzmann method. Front. Phys. 2021, 16, 52500. [Google Scholar] [CrossRef]
- Li, Y.; Lai, H.; Lin, C.; Li, D. Influence of the tangential velocity on the compressible Kelvin-Helmholtz instability with nonequilibrium effects. Front. Phys. 2022, 17, 63500. [Google Scholar] [CrossRef]
- Zhang, D.; Xu, A.; Song, J.; Gan, Y.; Zhang, Y.; Li, Y. Specific-heat ratio effects on the interaction between shock wave and heavy-cylindrical bubble: Based on discrete Boltzmann method. arXiv 2023, arXiv:2302.05687. [Google Scholar] [CrossRef]
- Gan, Y.; Xu, A.; Zhang, G.; Succi, S. Discrete Boltzmann modeling of multiphase flows: Hydrodynamic and thermodynamic non-equilibrium effects. Soft Matter 2015, 11, 5336–5345. [Google Scholar] [CrossRef] [PubMed]
- Gan, Y.; Xu, A.; Lai, H.; Li, W.; Sun, G.; Succi, S. Discrete Boltzmann multi-scale modelling of non-equilibrium multiphase flows. J. Fluid Mech. 2022, 951, A8. [Google Scholar] [CrossRef]
- Lin, C.; Luo, K. Discrete Boltzmann modeling of unsteady reactive flows with nonequilibrium effects. Phys. Rev. E 2019, 99, 012142. [Google Scholar] [CrossRef] [PubMed]
- Lombardini, M.; Hill, D.; Pullin, D.; Meiron, D. Atwood ratio dependence of Richtmyer-Meshkov flows under reshock conditions using large-eddy simulations. J. Fluid Mech. 2011, 670, 439–480. [Google Scholar] [CrossRef]
- Zhou, Y.; Cabot, W.H.; Thornber, B. Asymptotic behavior of the mixed mass in Rayleigh-Taylor and Richtmyer-Meshkov instability induced flows. Phys. Plasmas 2016, 23, 052712. [Google Scholar] [CrossRef]
- Chen, Q.; Li, L.; Zhang, Y.; Tian, B. Effects of the Atwood number on the Richtmyer-Meshkov instability in elastic-plastic media. Phys. Rev. E 2019, 99, 053102. [Google Scholar] [CrossRef]
- Liao, S.; Zhang, W.; Chen, H.; Zou, L.; Liu, J.; Zheng, X. Atwood number effects on the instability of a uniform interface driven by a perturbed shockwave. Phys. Rev. E 2019, 99, 013103. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, F.; Luo, X.; Zhai, Z. Effect of Atwood number on convergent Richtmyer-Meshkov instability. Acta Mech. Sin. 2021, 37, 434–446. [Google Scholar] [CrossRef]
- Ren, J.; Culp, D.; Smith, B.; Ma, X. An investigation of the multi-mode Richtmyer-Meshkov instability at a gas/HE interface using Pagosa. Comput. Math. Appl. 2022, 139, 136–151. [Google Scholar] [CrossRef]
- Lin, C.; Xu, A.; Zhang, G.; Li, Y. Double-distribution-function discrete Boltzmann model for combustion. Combust. Flame 2016, 164, 137–151. [Google Scholar] [CrossRef]
- Zhang, H.; Zhuang, F. NND schemes and their applications to numerical simulation of two-and three-dimensional flows. Adv. Appl. Mech. 1991, 29, 193–256. [Google Scholar]
- Lin, C.; Luo, K. Mesoscopic simulation of nonequilibrium detonation with discrete boltzmann method. Combust. Flame 2018, 198, 356–362. [Google Scholar] [CrossRef]
- Succi, S. The Lattice Boltzmann Equation: For Fluid Dynamics and Beyond; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Mohamad, A. Lattice Boltzmann Method; Springer: London, UK, 2001. [Google Scholar]
- Guo, Z.; Shu, C. Lattice Boltzmann Method and Its Application Inengineering; World Scientific: Singapore, 2013. [Google Scholar]
- Gan, Y.; Xu, A.; Zhang, G.; Li, Y. Lattice Boltzmann study on Kelvin-Helmholtz instability: Roles of velocity and density gradients. Phys. Rev. E 2011, 83, 056704. [Google Scholar] [CrossRef] [PubMed]
- Zel’Dovich, Y.B.; Raizer, Y.P. Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena; Publisher Courier Corporation: North Chelmsford, MA, USA, 2002. [Google Scholar]
- Zhang, Q.; Sohn, S.-I. Padé approximation to an interfacial fluid mixing problem. Appl. Math. Lett. 1997, 10, 121–127. [Google Scholar] [CrossRef]
- Frahan, M.T.H.; Movahed, P.; Johnsen, E. Numerical simulations of a shock interacting with successive interfaces using the discontinuous Galerkin method: The multilayered Richtmyer-Meshkov and Rayleigh-Taylor instabilities. Shock Waves 2015, 25, 329–345. [Google Scholar] [CrossRef]
- Jourdan, G.; Houas, L. High-amplitude single-mode perturbation evolution at the Richtmyer-Meshkov instability. Phys. Rev. Lett. 2005, 95, 204502. [Google Scholar] [CrossRef]
- Craxton, R.S.; Anderson, K.S.; Boehly, T.R.; Goncharov, V.N.; Harding, D.R.; Knauer, J.P.; McCrory, R.L.; McKenty, P.W.; Meyerhofer, D.D.; Myatt, J.F.; et al. Direct-drive inertial confinement fusion: A review. Phys. Plasmas 2015, 22, 110501. [Google Scholar] [CrossRef]
- Wright, C.E.; Abarzhi, S.I. Effect of adiabatic index on Richtmyer-Meshkov flows induced by strong shocks. Phys. Fluids 2021, 33, 046109. [Google Scholar] [CrossRef]
- Lindl, J.D.; Amendt, P.; Berger, R.L.; Glendinning, S.G.; Glenzer, S.H.; Haan, S.W.; Kauffman, R.L.; Landen, O.L.; Suter, L.J. The physics basis for ignition using indirect-drive targets on the National Ignition Facility. Phys. Plasmas 2004, 11, 339–491. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, T.; Lin, C.; Li, D.; Lai, H. Influence of Density Ratios on Richtmyer–Meshkov Instability with Non-Equilibrium Effects in the Reshock Process. Inventions 2023, 8, 157. https://doi.org/10.3390/inventions8060157
Yang T, Lin C, Li D, Lai H. Influence of Density Ratios on Richtmyer–Meshkov Instability with Non-Equilibrium Effects in the Reshock Process. Inventions. 2023; 8(6):157. https://doi.org/10.3390/inventions8060157
Chicago/Turabian StyleYang, Tao, Chuandong Lin, Demei Li, and Huilin Lai. 2023. "Influence of Density Ratios on Richtmyer–Meshkov Instability with Non-Equilibrium Effects in the Reshock Process" Inventions 8, no. 6: 157. https://doi.org/10.3390/inventions8060157
APA StyleYang, T., Lin, C., Li, D., & Lai, H. (2023). Influence of Density Ratios on Richtmyer–Meshkov Instability with Non-Equilibrium Effects in the Reshock Process. Inventions, 8(6), 157. https://doi.org/10.3390/inventions8060157






