Enhancing Tractor Stability and Safety through Individual Actuators in Active Suspension
Abstract
:1. Introduction
2. Materials and Methods
2.1. 3D Model of a Tractor for Simulation
2.2. Simulation Conditions and Method
- The tractor was placed on plain ground;
- The ground was tilted in a longitude vector, and the tractor overturned;
- The overturning angle was analyzed when the contact force between the ground and tractor wheels became 0 N.
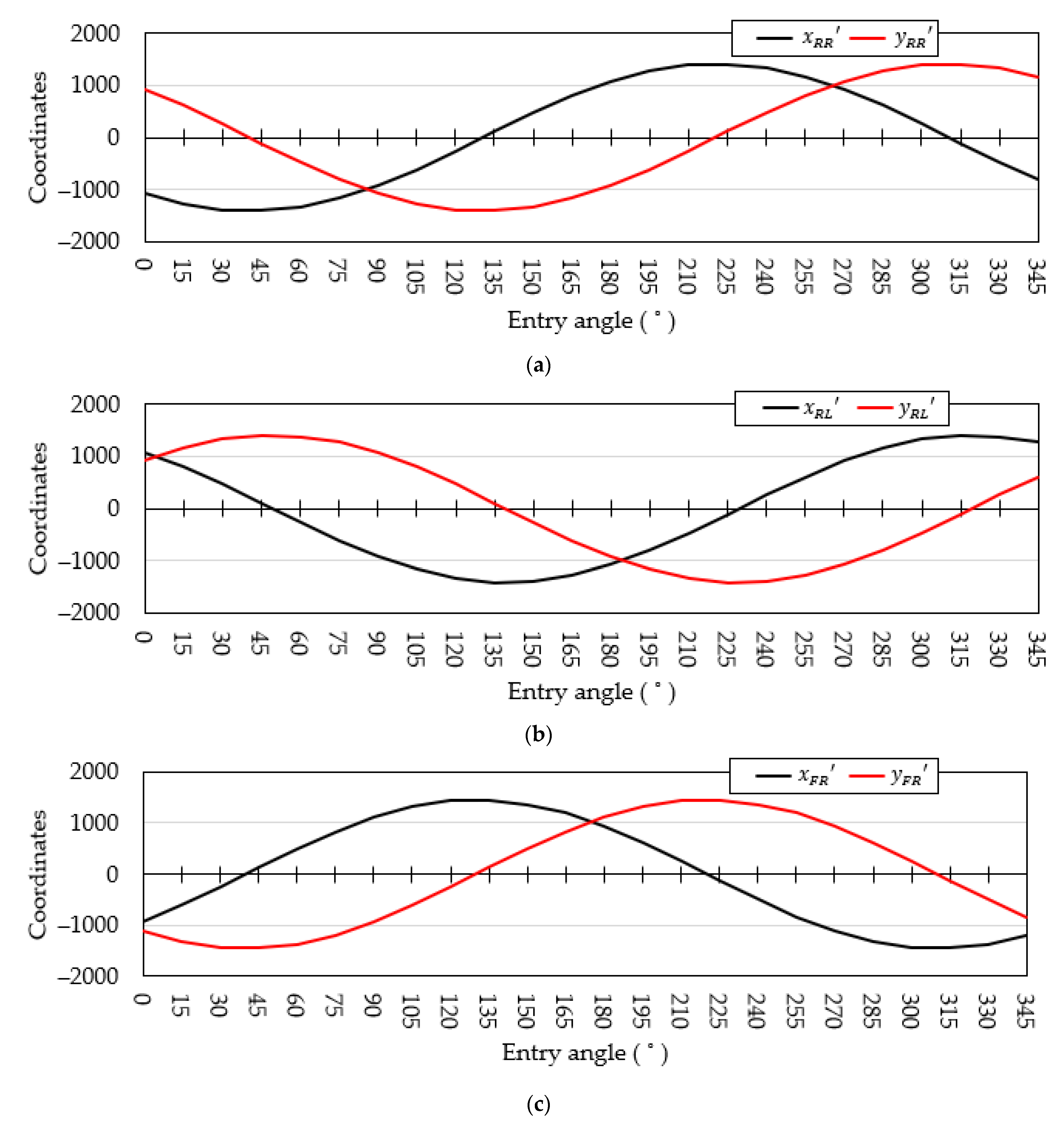
2.3. Mathematical Model of the Tractor Rollover
2.4. Mathematical Model of the Actuator Height
2.5. Hydraulic Actuator Model
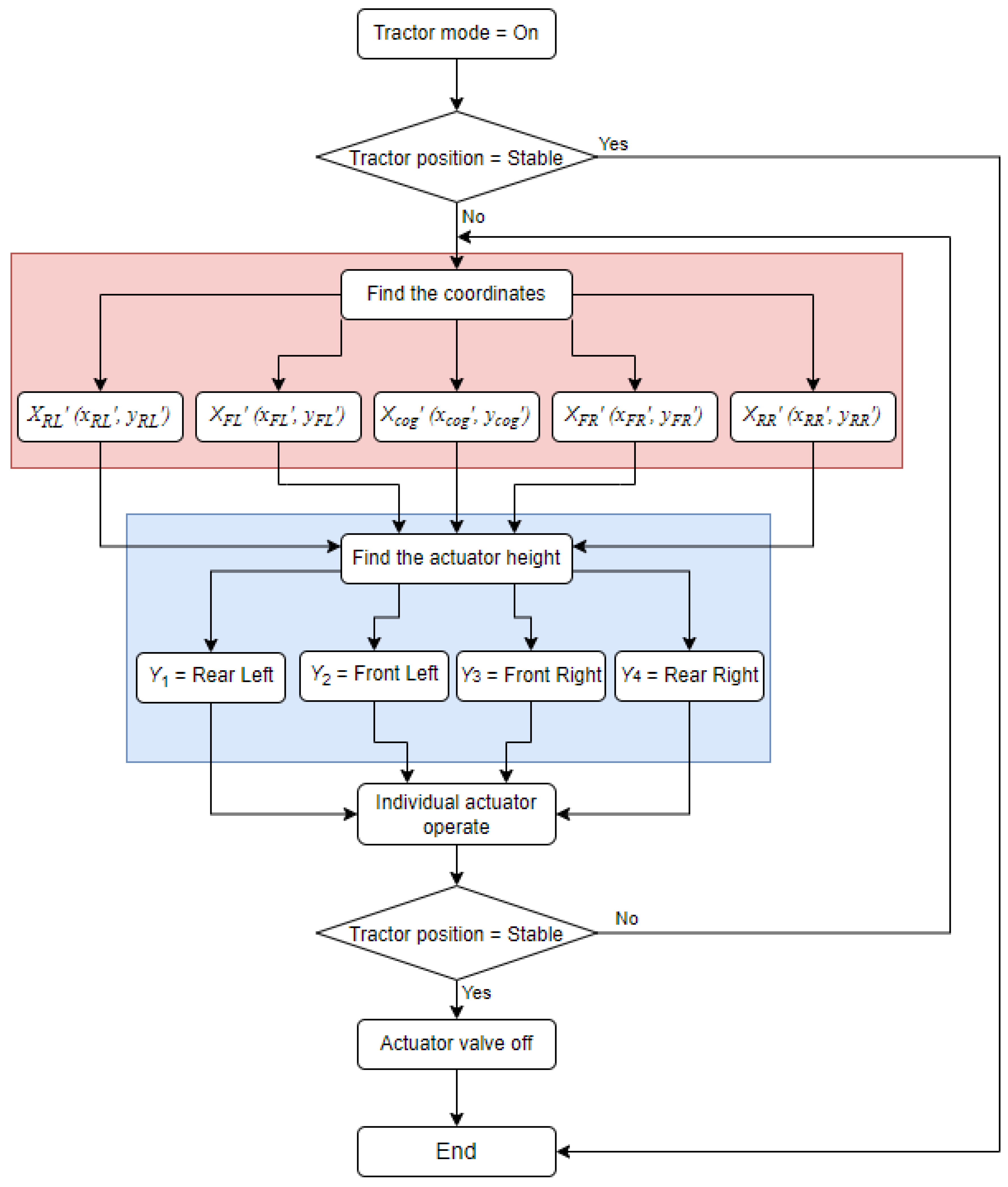
2.6. Development of Tractor Horizontal Attitude Control Logic
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- He, Z.; Song, Z.; Wang, L.; Zhou, X.; Gao, J.; Wang, K.; Yang, M.; Li, Z. Fasting the stabilization response for prevention of tractor rollover using active steering: Controller parameter optimization and real-vehicle dynamic tests. Comput. Electron. Agric. 2023, 204, 107525. [Google Scholar] [CrossRef]
- Kang, S.; Kim, Y.; Park, H.; Kim, Y.; Woo, S.; Uyeh, D.D.; Ha, Y. Rollover Safety and Workable Boundary Suggestion of an Agricultural Platform with Different Attachments. Agriculture 2022, 12, 1148. [Google Scholar] [CrossRef]
- Son, J.; Kim, Y.; Kang, S.; Ha, Y. Enhancing Safety through Optimal Placement of Components in Hydrogen Tractor: Rollover Angle Analysis. Agriculture 2024, 14, 315. [Google Scholar] [CrossRef]
- Jang, M.-K.; Hwang, S.-J.; Nam, J.-S. Simulation Study for Overturning and Rollover Characteristics of a Tractor with an Implement on a Hard Surface. Agronomy 2022, 12, 3093. [Google Scholar] [CrossRef]
- U.S. Bureau of Labor Statistics. Fatal occupational injuries by industry and event or exposure. In Injuries, Illnesses, and Fatalities; U.S. Bureau of Labor Statistics: Washington, DC, USA, 2021. [Google Scholar]
- Antunes, S.M.; Cordeiro, C.; Teixeira, H.M. Analysis of fatal accidents with tractors in the Centre of Portugal: Ten years analysis. Forensic Sci. Int. 2018, 287, 74–80. [Google Scholar] [CrossRef] [PubMed]
- Rondelli, V.; Casazza, C.; Martelli, R. Tractor rollover fatalities, analyzing accident scenario. J. Saf. Res. 2018, 67, 99–106. [Google Scholar] [CrossRef]
- Aysel, A.; Muharrem, K. Trailer-Attached Two-Wheel Tractor (Patpat) Accidents on Roads in Turkey. J. Agric. Fac. Mustafa Kemal Univ. 2018, 23, 165–180. [Google Scholar]
- Moreschi, C.; Da Broi, U.; Cividino, S.R.S.; Gubiani, R.; Pergher, G.; Vello, M.; Rinaldi, F. The Analysis of the Cause-Effect Relation between Tractor Overturns and Traumatic Lesions Suffered by Drivers and Passengers: A Crucial Step in the Reconstruction of Accident Dynamics and the Improvement of Prevention. Agriculture 2017, 7, 97. [Google Scholar] [CrossRef]
- Facchinetti, D.; Santoro, S.; Galli, L.E.; Pessina, D. Agricultural Tractor Roll-Over Related Fatalities in Italy: Results from a 12 years Analysis. Sustainability 2021, 13, 4536. [Google Scholar] [CrossRef]
- Yuya, A.; Masami, M. Theoretical Verification of Driving Force Control System for the Suppression of the Dynamic Pitching Angle of Tractors. Eng. Agric. Environ. Food 2022, 15, 13–23. [Google Scholar]
- Kumar, S.; Kumar, A.; Pranav, P.K. Design and Development of Drop Centre Axle for 2WD Tractor. In Research into Design for a Connected World: Proceedings of ICoRD; Springer: Singapore, 2019; Volume 1, pp. 941–953. [Google Scholar]
- Vita, L.; Gattamelata, D.; Pessina, D. Retrofitting Agricultural Self-Propelled Machines with Roll-Over and Tip-Over Protective Structures. Safety 2021, 7, 46. [Google Scholar] [CrossRef]
- Liu, B.; Bulent, K. SafeDriving: A mobile application for tractor rollover detection and emergency reporting. Comput. Electron. Agric. 2013, 98, 117–120. [Google Scholar] [CrossRef]
- Gonzalez, D.O.; Martin-Gorriz, B.; Berrocal, I.I.; Hernandez, B.M.; Garcia, F.C.; Sanchez, P.M. Development of an automatically deployable roll overprotective structure for agricultural tractors based on hydraulic power: Prototype and first tests. Comput. Electron. Agric. 2016, 124, 46–54. [Google Scholar] [CrossRef]
- Ayers, P.; Khorsandi, F. Reducing tractor rollover fatalities: Progress in ROPS technology. Am. Soc. Agric. Biol. Eng. 2017, 24, 6–7. [Google Scholar]
- Qin, J.; Zhu, Z.; Ji, H.; Zhu, Z.; Li, Z.; Du, Y.; Song, Z.; Mao, E. Simulation of active steering control for the prevention of tractor dynamic rollover on random road surfaces. Biosyst. Eng. 2019, 185, 135–149. [Google Scholar] [CrossRef]
- Gattamelata, D.; Puri, D.; Vita, L.; Fargnoli, M. A Full Assistance System (FAS) for the Safe Use of the Tractor’s Foldable Rollover Protective Structure (FROPS). AgriEngineering 2023, 5, 15. [Google Scholar] [CrossRef]
- Ayers, P.; Khorsandi, F.; Wang, X.; Araujo, G. ROPS designs to protect operators during agricultural tractor rollovers. J. Terramechanics 2018, 75, 49–55. [Google Scholar] [CrossRef]
- Franceschetti, B.; Rondelli, V.; Ciuffoli, A. Comparing the influence of Roll-Over Protective Structure type on tractor lateral stability. Saf. Sci. 2019, 115, 42–50. [Google Scholar] [CrossRef]
- Pascuzzi, S.; Anifantis, A.S.; Santoro, F. The Concept of a Compact Profile Agricultural Tractor Suitable for Use on Specialised Tree Crops. Agriculture 2020, 10, 123. [Google Scholar] [CrossRef]
- Kise, M.; Zhang, Q. Sensor-in-the-loop tractor stability control: Look-ahead attitude prediction and field tests. Comput. Electron. Agric. 2006, 52, 107–118. [Google Scholar] [CrossRef]
- Qin, J.; Wu, A.; Song, Z.; He, Z.; Suh, C.S.; Zhu, Z.; Li, Z. Recovering tractor stability from an intensive rollover with a momentum flywheel and active steering: System formulation and scale-model verification. Comput. Electron. Agric. 2021, 190, 106458–106469. [Google Scholar] [CrossRef]
- Ni, Z.; He, Y. Design and validation of a robust active trailer steering system for multi-trailer articulated heavy vehicles. Veh. Syst. Dyn. 2019, 57, 1545–1571. [Google Scholar] [CrossRef]
- Jia, W.; Zhang, W.; Ma, F.; Wu, L. Attitude Control of Vehicle Based on Series Active Suspensions. Actuator 2023, 12, 67–86. [Google Scholar] [CrossRef]
- Baek, S.M.; Kim, W.S.; Kim, Y.S.; Baek, S.Y.; Kim, Y.J. Development of a simulation model for HMT of a 50 kW class agricultural tractor. Appl. Appl. Sci. 2020, 10, 4064. [Google Scholar] [CrossRef]
- Pawar, N.M.; Velaga, N.R. Modelling the influence of time pressure on reaction time of drivers. Transp. Res. Part F Traffic Psychol. Behav. 2020, 72, 1–22. [Google Scholar] [CrossRef]
- Zheng, E.; Cui, S.; Yang, Y.; Xue, J.; Zhu, Y.; Lin, X. Simulation of the Vibration Characteristics for Agricultural Wheeled Tractor with Implement and Front Axle Hydropneumatic Suspension. Shock Vib. 2019, 2019, 91345312. [Google Scholar] [CrossRef]
- Watanabe, M.; Sakai, K. Identifying tractor overturning scenarios using a driving simulator with a motion system. Biosyst. Eng. 2021, 210, 261–270. [Google Scholar] [CrossRef]
- Gao, J.; Yin, C.; Yuan, G. Warning and active steering rollover prevention control for agricultural wheeled tractor. PLoS ONE 2022, 17, e028021. [Google Scholar] [CrossRef]
- Chowdhury, M.; Islam, M.N.; Iqbal, M.Z.; Islam, S.; Lee, D.H.; Kim, D.G.; Jun, H.J.; Chung, S.O. Analysis of Overturning and Vibration during Field Operation of a Tractor-Mounted 4-Row Radish Collector toward Ensuring User Safety. Machines 2020, 8, 77–91. [Google Scholar] [CrossRef]
- Chowdhury, M.; Ali, M.; Habineza, E.; Reza, M.N.; Kabir, M.S.N.; Lim, S.J.; Choi, I.S.; Chung, S.O. Analysis of Rollover Characteristics of a 12 kW Automatic Onion Transplanter to Reduce Stability Hazards. Agriculture 2023, 13, 652–669. [Google Scholar] [CrossRef]
- Kim, W.S.; Siddique, M.A.A.; Kim, Y.J.; Jung, Y.J.; Baek, S.M.; Baek, S.Y.; Kim, Y.S.; Lim, R.G. Simulation of the Rollover Angle of a Self-Propelled Radish Harvester for Different Load Conditions. Appl. Sci. 2022, 12, 10733–10748. [Google Scholar] [CrossRef]
- Jung, Y.J.; Lim, R.G.; Choi, C.H.; Kim, Y.J. Analysis of Overturning Angle for Radish Harvester. Korean Soc. Agric. Mach. 2019, 1, 458–459. [Google Scholar]

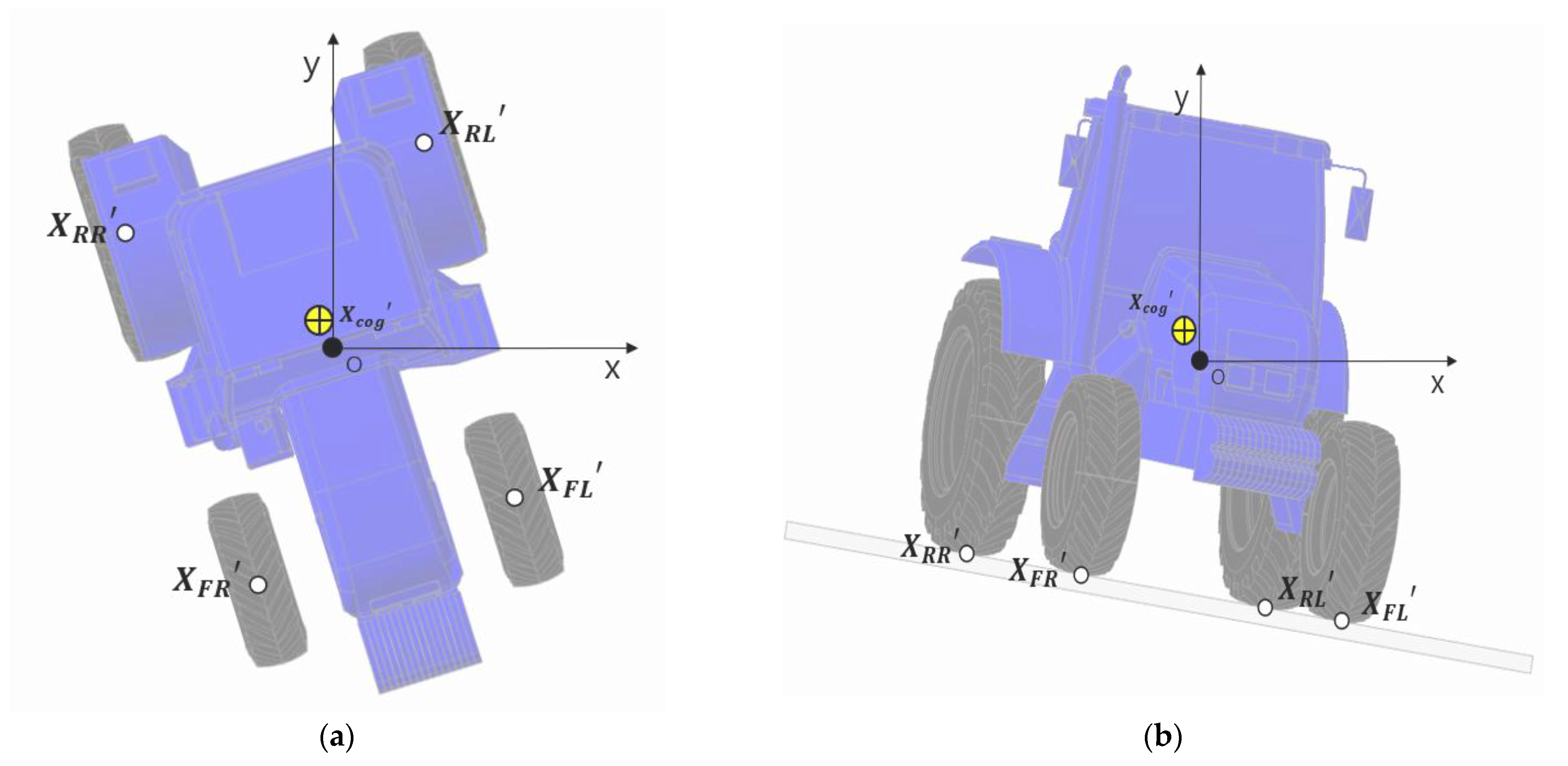
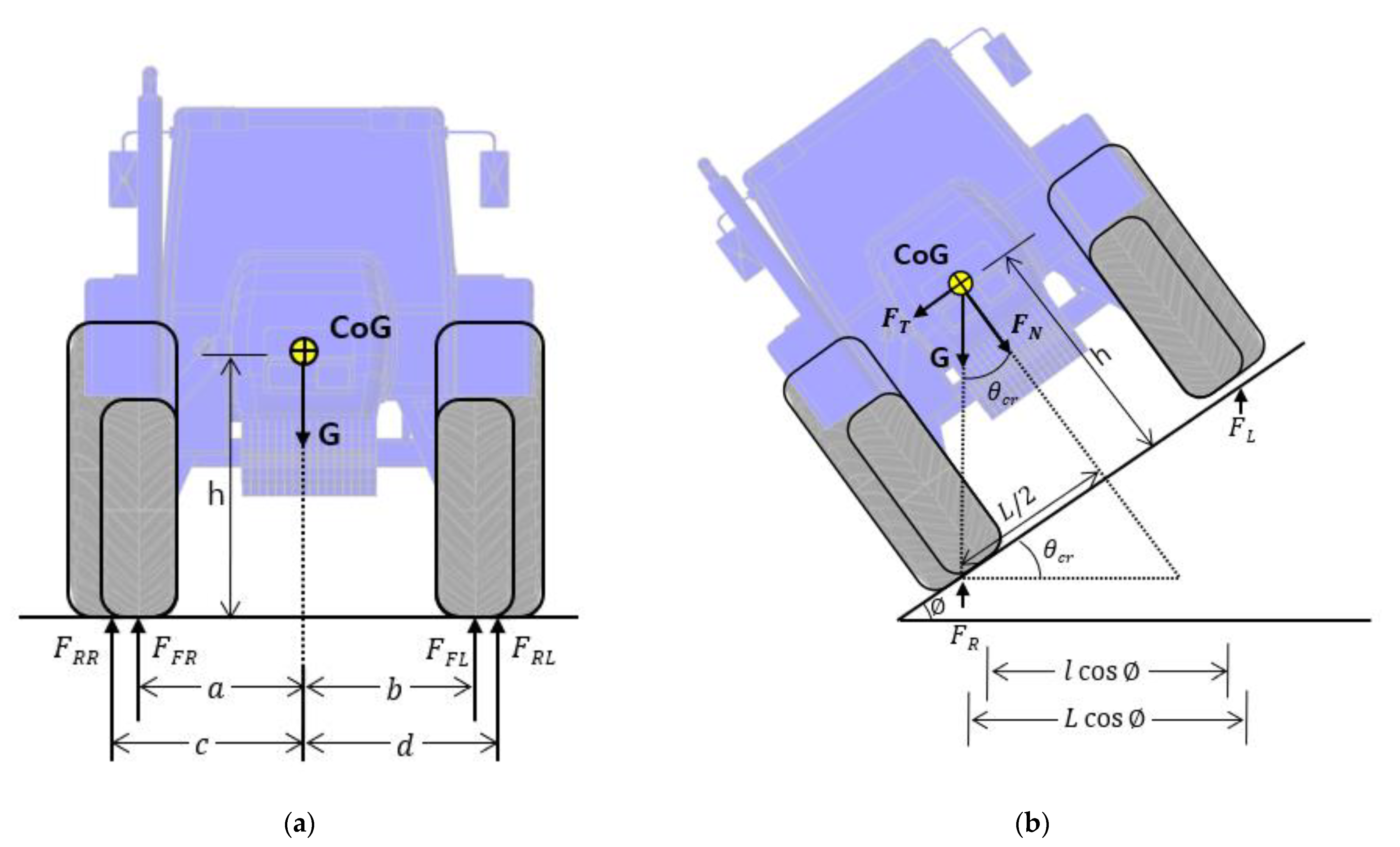
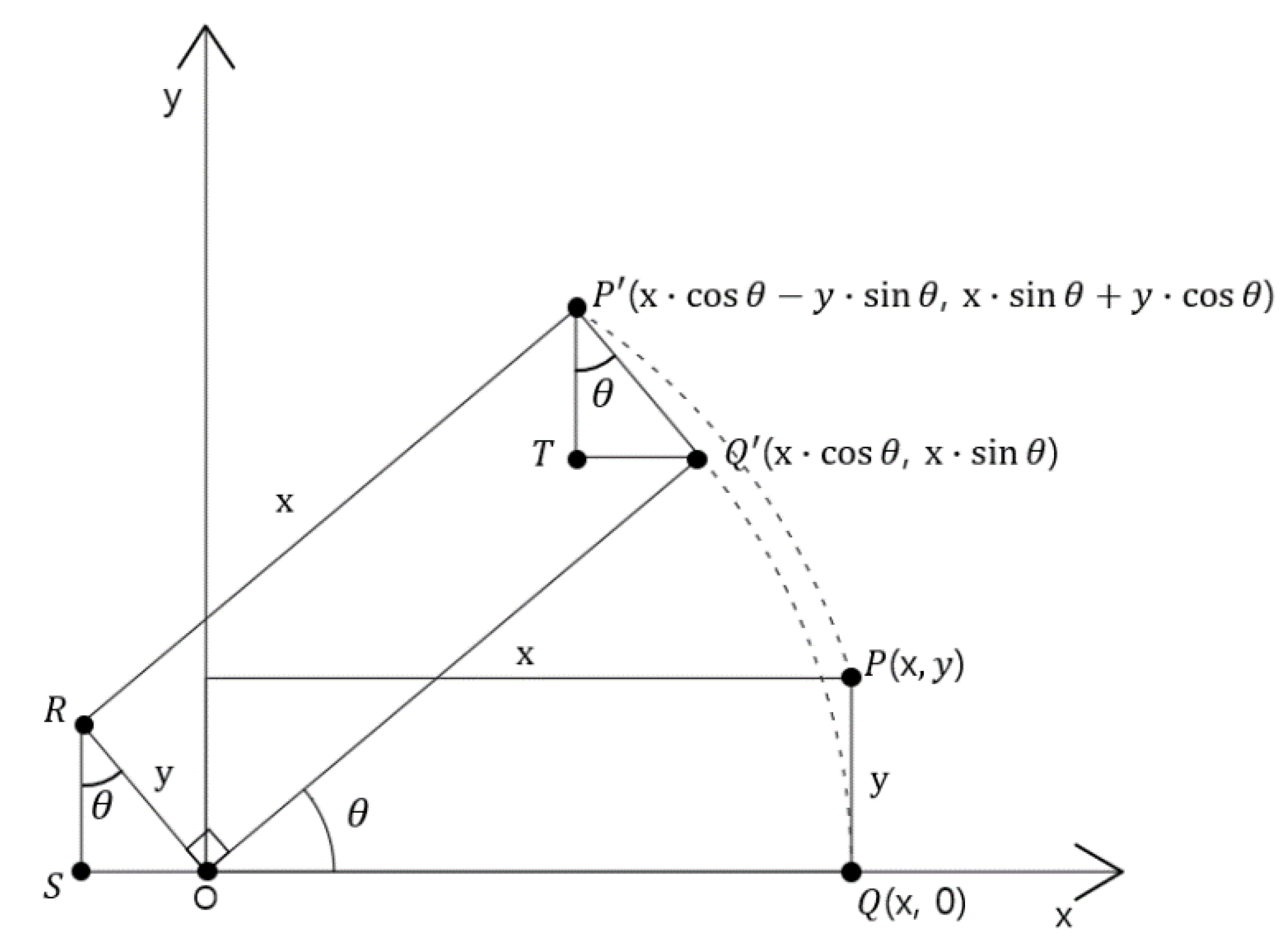

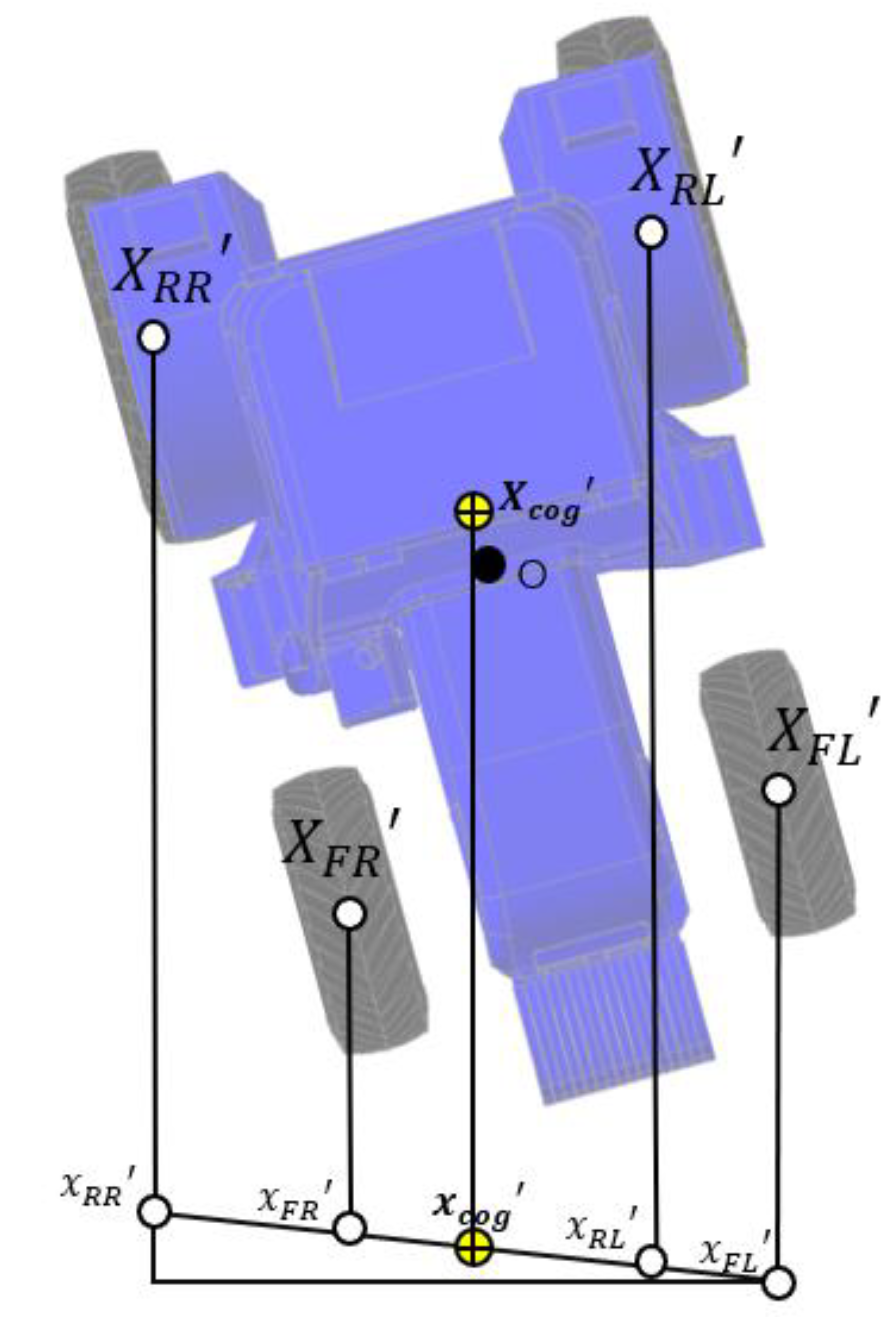





| Parameters | Values |
|---|---|
| Overall width (W) | 2700 mm |
| Overall length (L) | 3200 mm |
| Overall height (H) | 2800 mm |
| Mass of front wheel | 46.32 kg |
| Mass of rear wheel | 100.87 kg |
| Total mass of the tractor | 4494.38 kg |
| Parameters | Values |
|---|---|
| Dynamic friction coefficient | 1.2 |
| Stiffness coefficient | 105 |
| Damping coefficient | 10 |
| Simulation time | 30 s |
| Simulation steps | 1000 |
| Rotate Angle (°) | With the Actuator (°) | Without the Actuator (°) | Relative Change |
|---|---|---|---|
| 0 | 36.92 | 30.98 | 19% |
| 15 | 36.25 | 31.46 | 15% |
| 30 | 38.27 | 33.75 | 13% |
| 45 | 41.85 | 38.75 | 8% |
| 60 | 48.53 | 46.64 | 4% |
| 75 | 45.77 | 42.93 | 7% |
| 90 | 45.29 | 42.19 | 7% |
| 105 | 45.77 | 43.20 | 6% |
| 120 | 48.94 | 46.98 | 4% |
| 135 | 42.46 | 39.08 | 9% |
| 150 | 38.68 | 34.36 | 13% |
| 165 | 36.79 | 32.00 | 15% |
| 180 | 36.86 | 31.52 | 17% |
| 195 | 37.67 | 32.74 | 15% |
| 210 | 39.76 | 35.5 | 12% |
| 225 | 41.85 | 39.29 | 7% |
| 240 | 36.18 | 33.82 | 7% |
| 255 | 33.55 | 30.91 | 9% |
| 270 | 33.41 | 29.98 | 11% |
| 285 | 33.75 | 30.98 | 9% |
| 300 | 36.18 | 33.75 | 7% |
| 315 | 42.05 | 38.27 | 10% |
| 330 | 39.22 | 35.44 | 11% |
| 345 | 36.79 | 32.20 | 14% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Son, J.; Kim, Y.; Kang, S.; Ha, Y. Enhancing Tractor Stability and Safety through Individual Actuators in Active Suspension. Inventions 2024, 9, 29. https://doi.org/10.3390/inventions9020029
Son J, Kim Y, Kang S, Ha Y. Enhancing Tractor Stability and Safety through Individual Actuators in Active Suspension. Inventions. 2024; 9(2):29. https://doi.org/10.3390/inventions9020029
Chicago/Turabian StyleSon, Jinho, Yeongsu Kim, Seokho Kang, and Yushin Ha. 2024. "Enhancing Tractor Stability and Safety through Individual Actuators in Active Suspension" Inventions 9, no. 2: 29. https://doi.org/10.3390/inventions9020029
APA StyleSon, J., Kim, Y., Kang, S., & Ha, Y. (2024). Enhancing Tractor Stability and Safety through Individual Actuators in Active Suspension. Inventions, 9(2), 29. https://doi.org/10.3390/inventions9020029






