Coordinated, Centralized, and Simultaneous Control of Fast Charging Stations and Distributed Energy Resources
Abstract
:1. Introduction
2. Literature Review
Power-Based Control
- The active power () and reactive power () in the PCC of the microgrid in the current cycle ℓ.
- The sum of the maximum active () and reactive () powers that each DER can dispatch in the current cycle ℓ.
- The sum of active () and reactive () powers dispatched by DERs in the current cycle ℓ.
- The active power references () and reactive () desired in the PCC in the next cycle ().
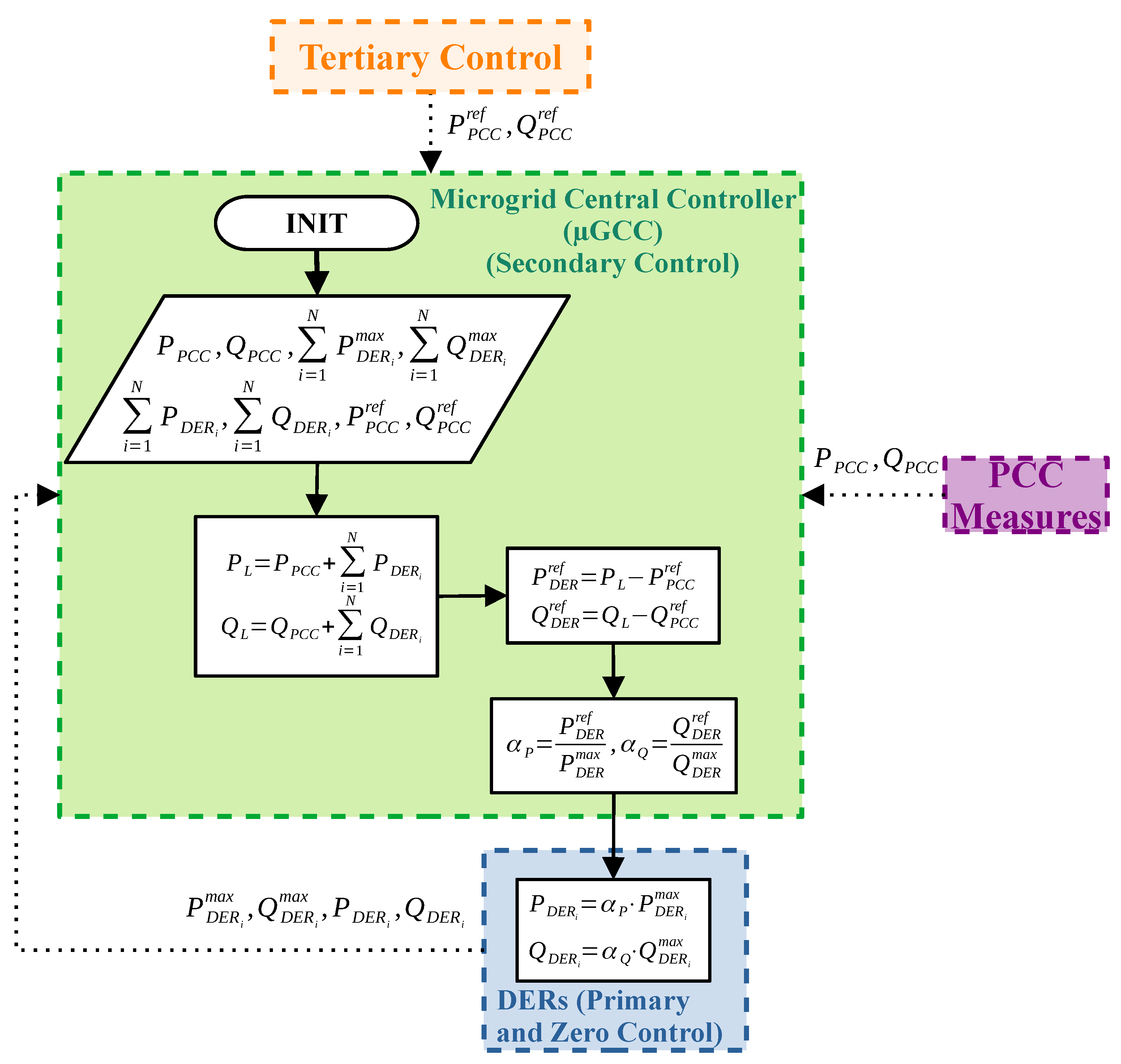
3. Methodology and Methods
3.1. Proposed Power-Based Control Applied to Fast Charging Stations
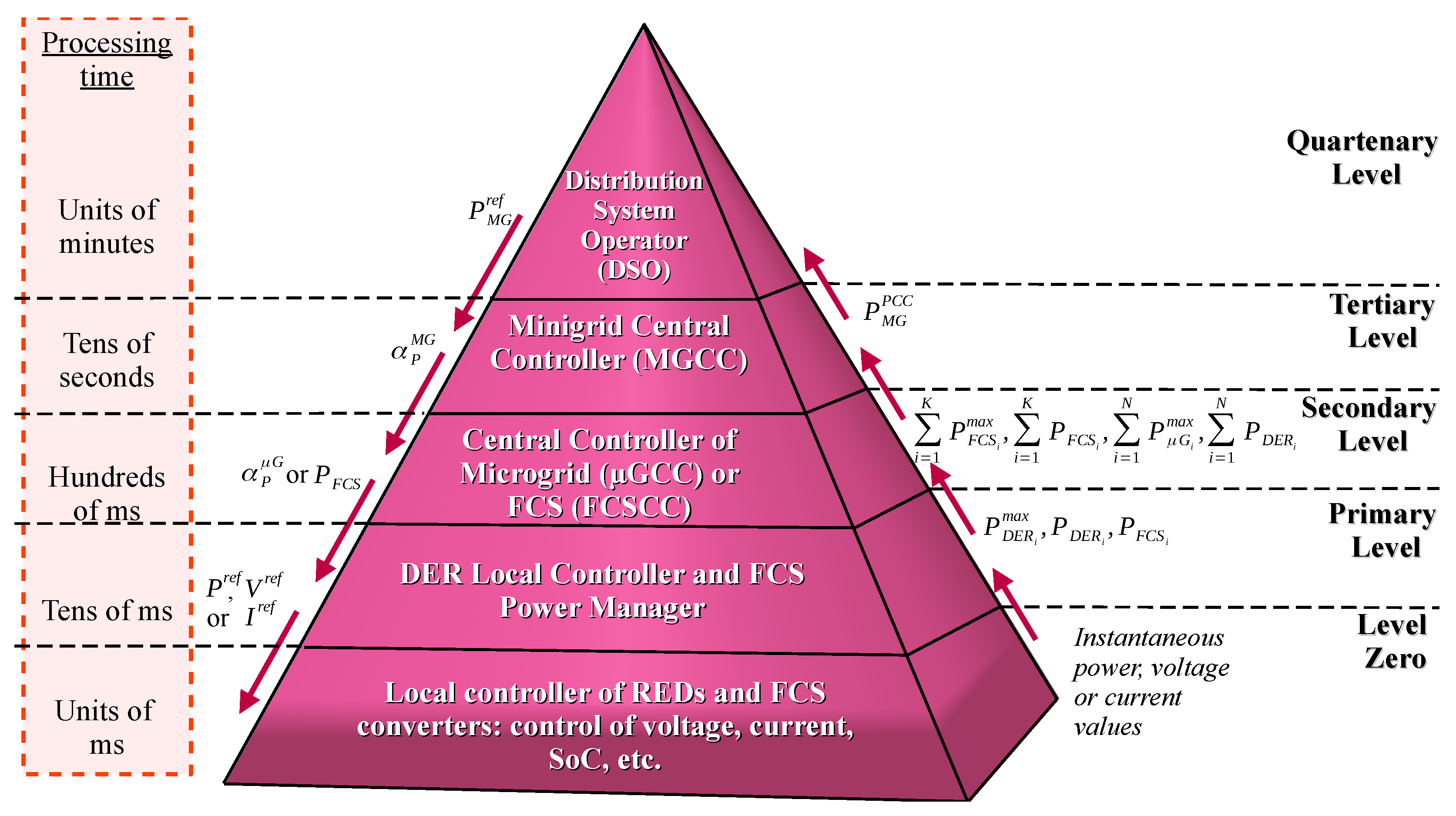
- Quartenary level: Composed of a distribution system operator (DSO). The electric power utility or a control entity that covers a set of minigrids controls the DSO, responsible for determining the power references for the MGCC. With the absence of the DSO, power references can be determined locally by the MGCC based on the integrity of the voltage levels (as in the work of [67]) and grid frequency or based on financial parameters involving energy consumption from the upstream grid.
- Tertiary level: Composed of an MGCC, responsible for controlling the power flow from the MG to the upstream network. Responsible for sharing and processing information from the microgrid central controller (GCC), FCSCC, and DSO. It is responsible for sending the coefficient to the GCC and FCSCC and receives, from the DSO, the desired power reference for the PCC of the MG.
- Secondary level: Composed of the GCC or FCSCC, responsible for controlling the power flow from the microgrid/FCS with the upstream network. It is responsible for sharing and processing information from the MGCC and local controllers of the DER/energy managers of the FCS. Using the coefficient , you must determine your own coefficient and send it to the DERs or FCS energy managers.
- Primary level: Composed of DER local controllers and the FCS energy manager. In the case of the FCS, it may be part of the FCSCC. Responsible for sharing and processing information with GCC/FCSCC and with the DER or FCS converters. It is he who sends the power, current, or voltage references to the DER or FCS converters.
- Level zero: Composed of the local controllers of the DER and FCS converters. They share information with the DER local controller and are responsible for dispatching/absorbing power to the grid.

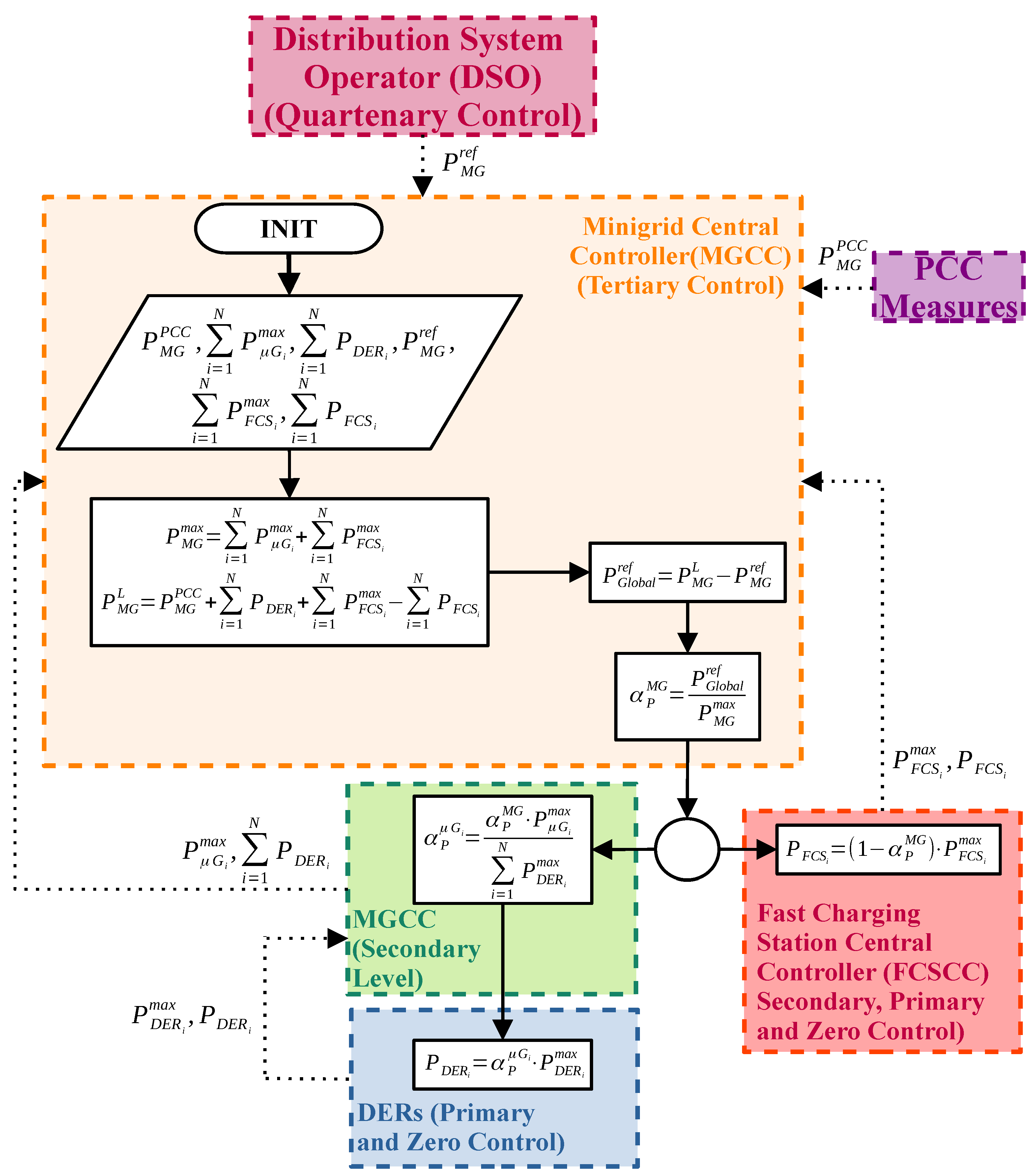
- The active power () in the PCC of the minigrid in the current cycle ℓ. This information is collected locally by MGCC, which is connected to PCC.
- The sum of the maximum active powers () that each microgrid can dispatch in the current cycle ℓ. N is the number of microgrids present in the minigrid. This power is the sum of the maximum powers that DERs can dispatch. This information is sent by GCCs to the MGCC over a low bandwidth (according to the US Federal Communications Commission [69], communication links below 25 Mbps are low-bandwidth links) and long-range communication links;
- The sum of active powers () dispatched by the DERs of the microgrids in the current cycle ℓ. N is the number of microgrids present in the minigrid. This information is sent by the DERs to GCCs through a low-bandwidth communication link, such as the radio data system (RDS). Subsequently, these data are sent to the MGCC through a low-bandwidth and long-range communication link;
- The desired active power reference in the PCC of the minigrid in the next cycle () (). This information is sent by the DSO to the MGCC over a low-bandwidth and long-range communication link;
- The sum of the maximum active powers () that each charging station can absorb in the current cycle ℓ. K is the number of FCSs present in the minigrid. This information is sent by FCSCCs to the MGCC over a low bandwidth and long-range communication link;
- The sum of active powers () absorbed by the charging stations in the current cycle ℓ. K is the number of FCSs present in the minigrid. This information is sent by FCSCCs to the MGCC over a low bandwidth and long-range communication link.
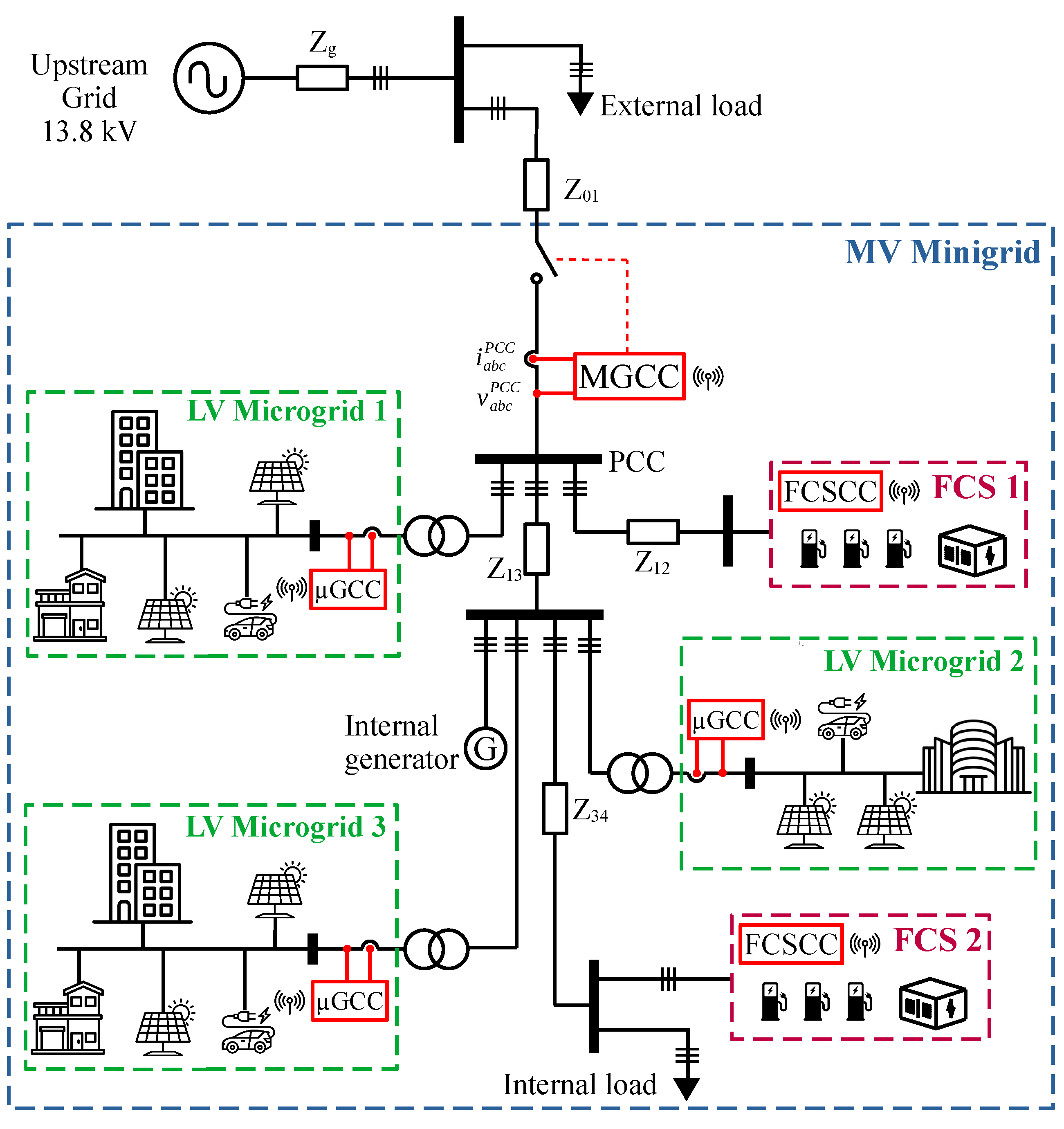
3.2. Minigrid Parameters
3.3. Evaluated Scenarios and Metrics
- Without FCSs: in this condition, there are no FCSs on the grid.
- With FCSs not participating in the proposed control: Charging stations operate as constant loads due to the internal management algorithm at all times. FCSs are not controlled by the MGCC.
- With FCSs participating in the proposed control: charging stations operate as constant loads due to the internal management algorithm. Upon receiving a control command, they start to control the energy demand according to the complement of the coefficient (). Therefore, FCSs are controlled by MGCC.
- Without DERs: in this condition, there is no type of distributed generation on the grid; that is, the grid does not have dispatchable DERs nor non-dispatchable DERs.
- Without dispatchable DERs: All the DERs in the network dispatch all available active power. In this condition, the DERs are not controlled by the MGCC.
- With dispatchable DERs: In this condition, the non-dispatchable DERs dispatch all available active power, and the dispatchable DERs dispatch power according to the index . The MGCC commands dispatchable DERs.
- The non-dispatchable DERs do not have energy storage. Generation from photovoltaic modules is the basis for all energy dispatch;
- The dispatchable DERs have energy storage;
- For dispatchable DERs, it is considered that there is an internal energy-management system that manages the recharging of the batteries based on the generation of the photovoltaic modules. This management will guarantee a fixed installment that can always be dispatched, even at times when there is no generation (e.g., at night). Some works suggest energy-management algorithms for DERs [63,76,77,78].
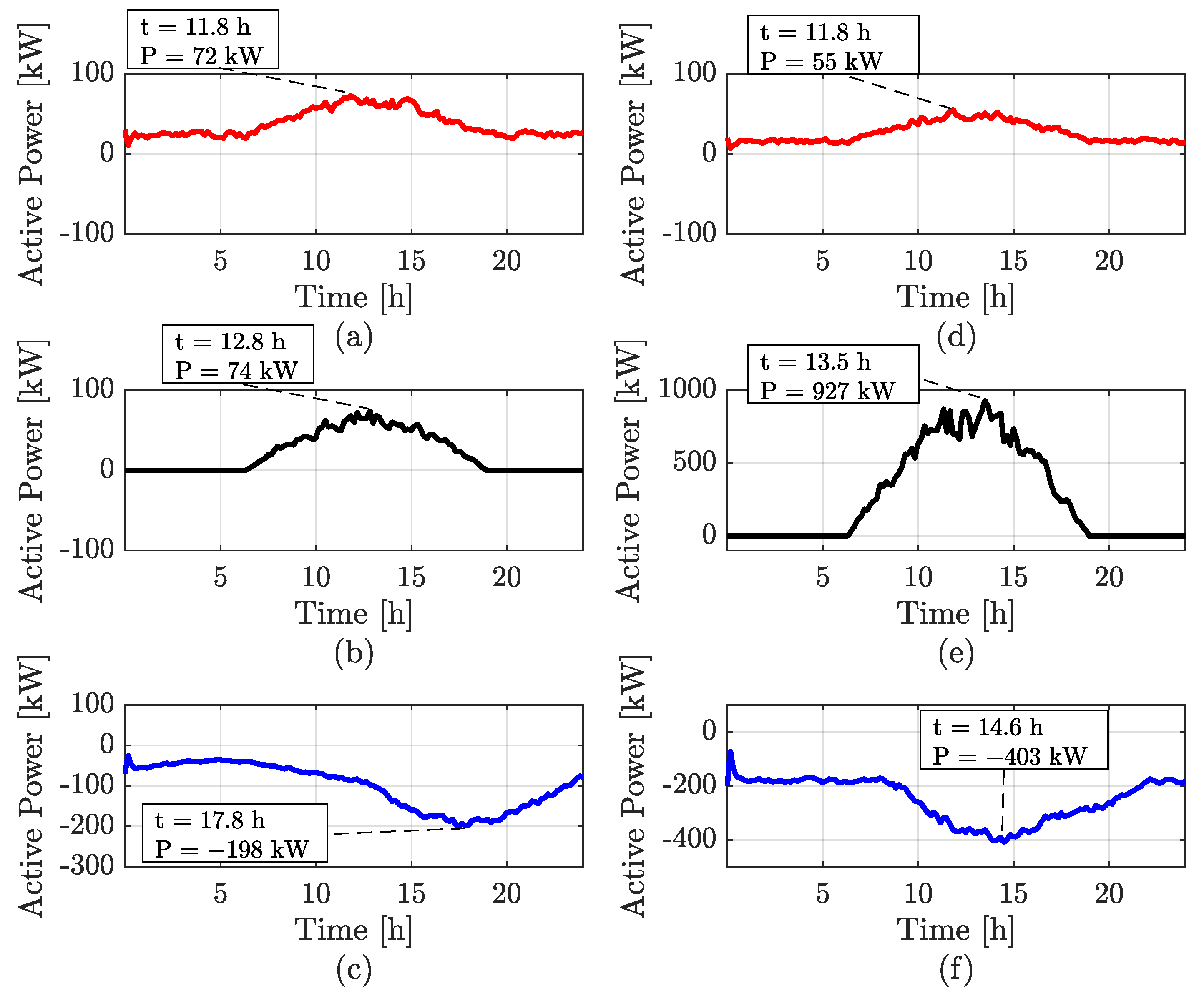
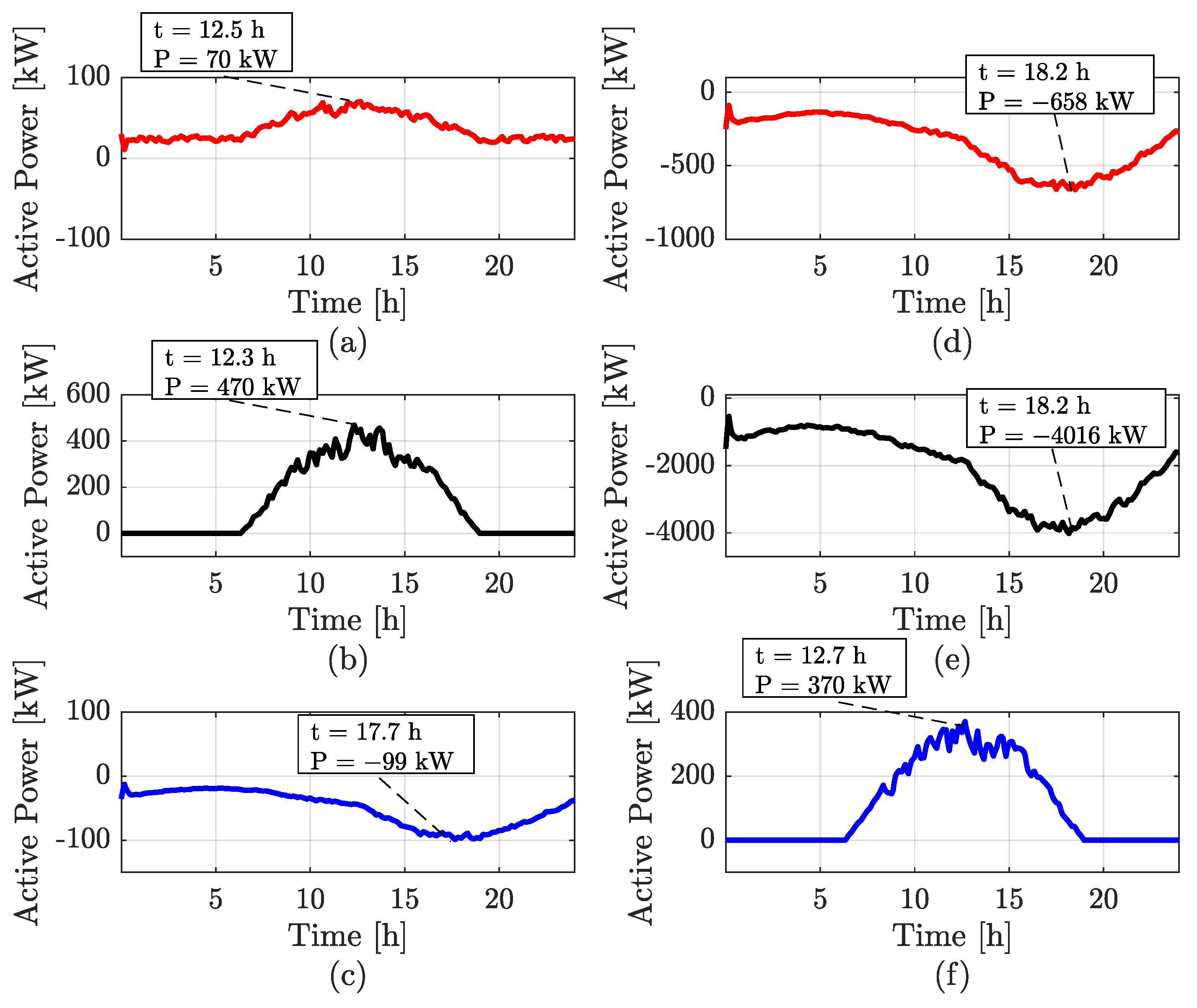
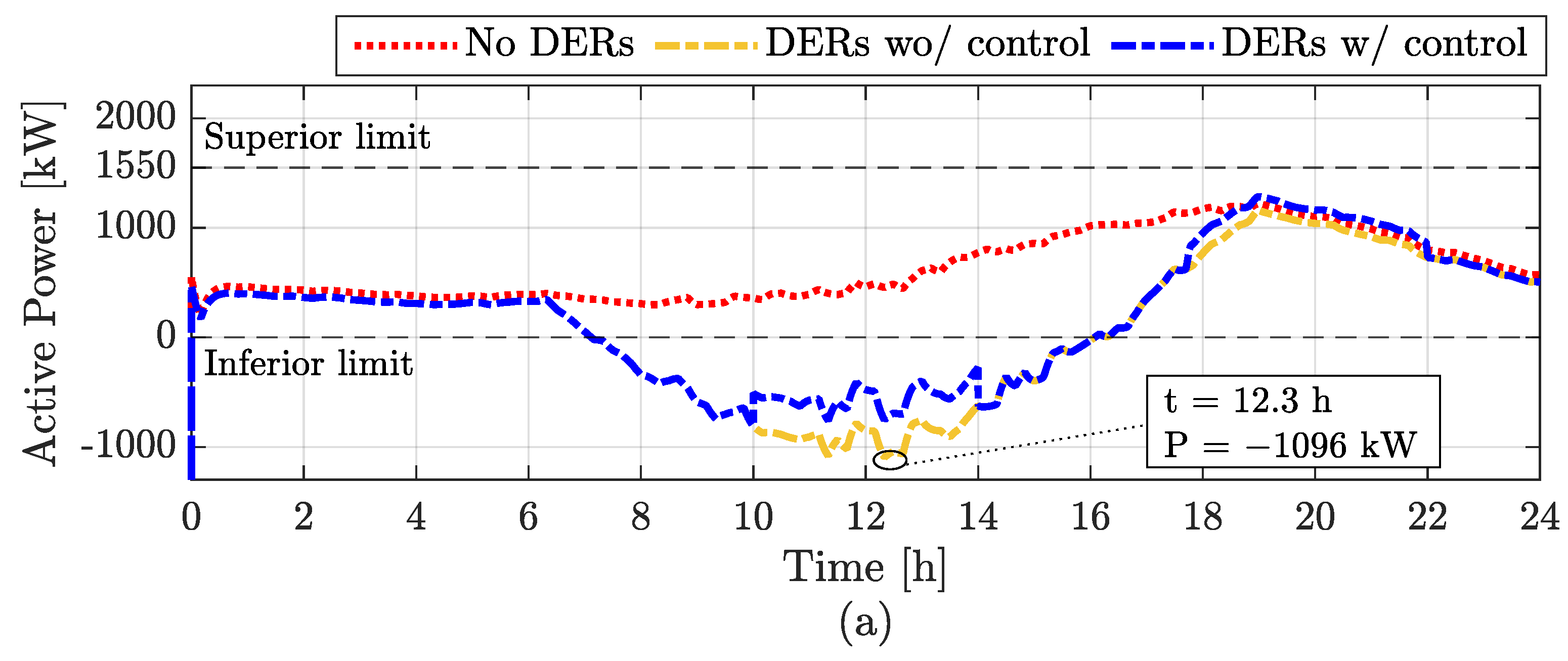
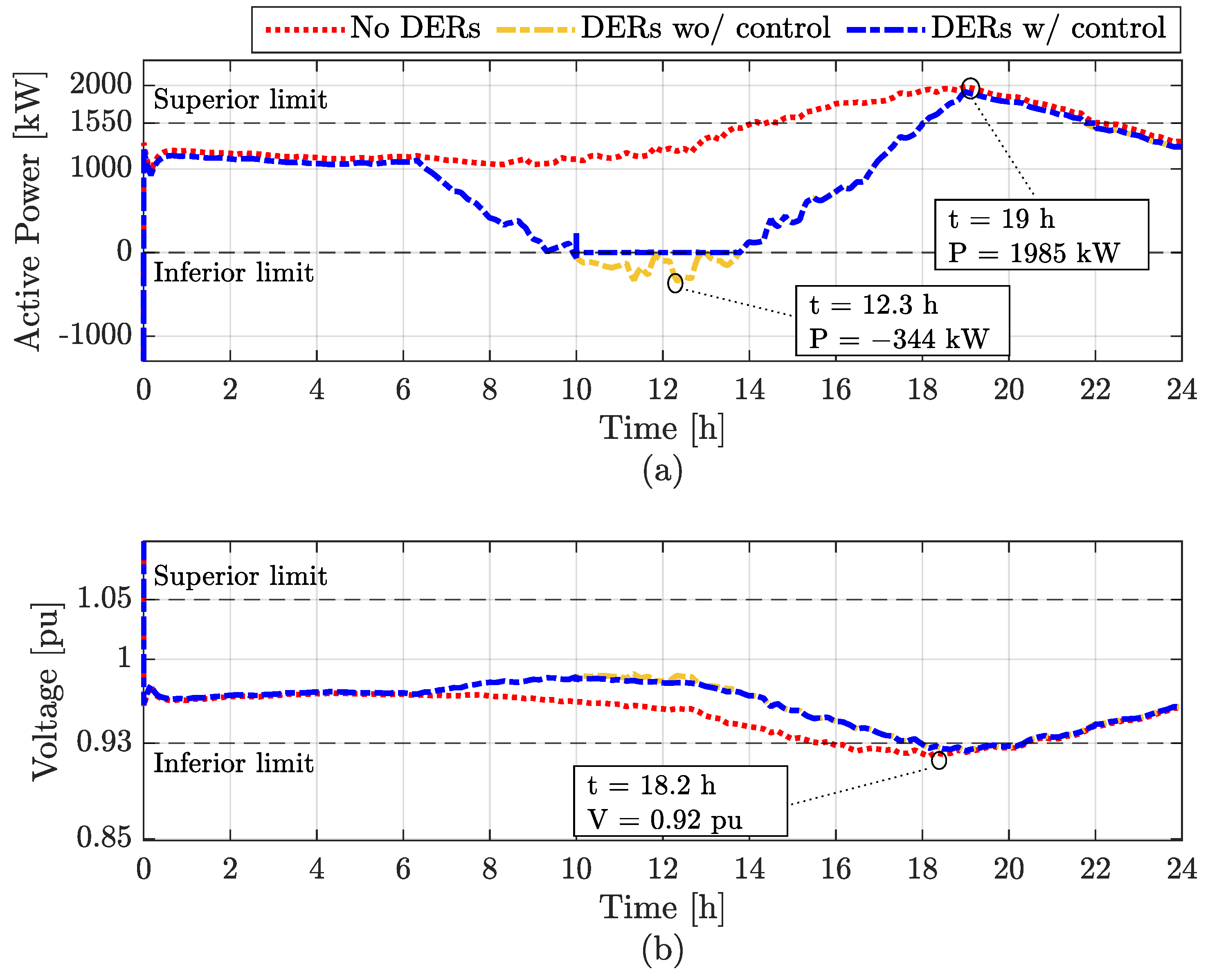
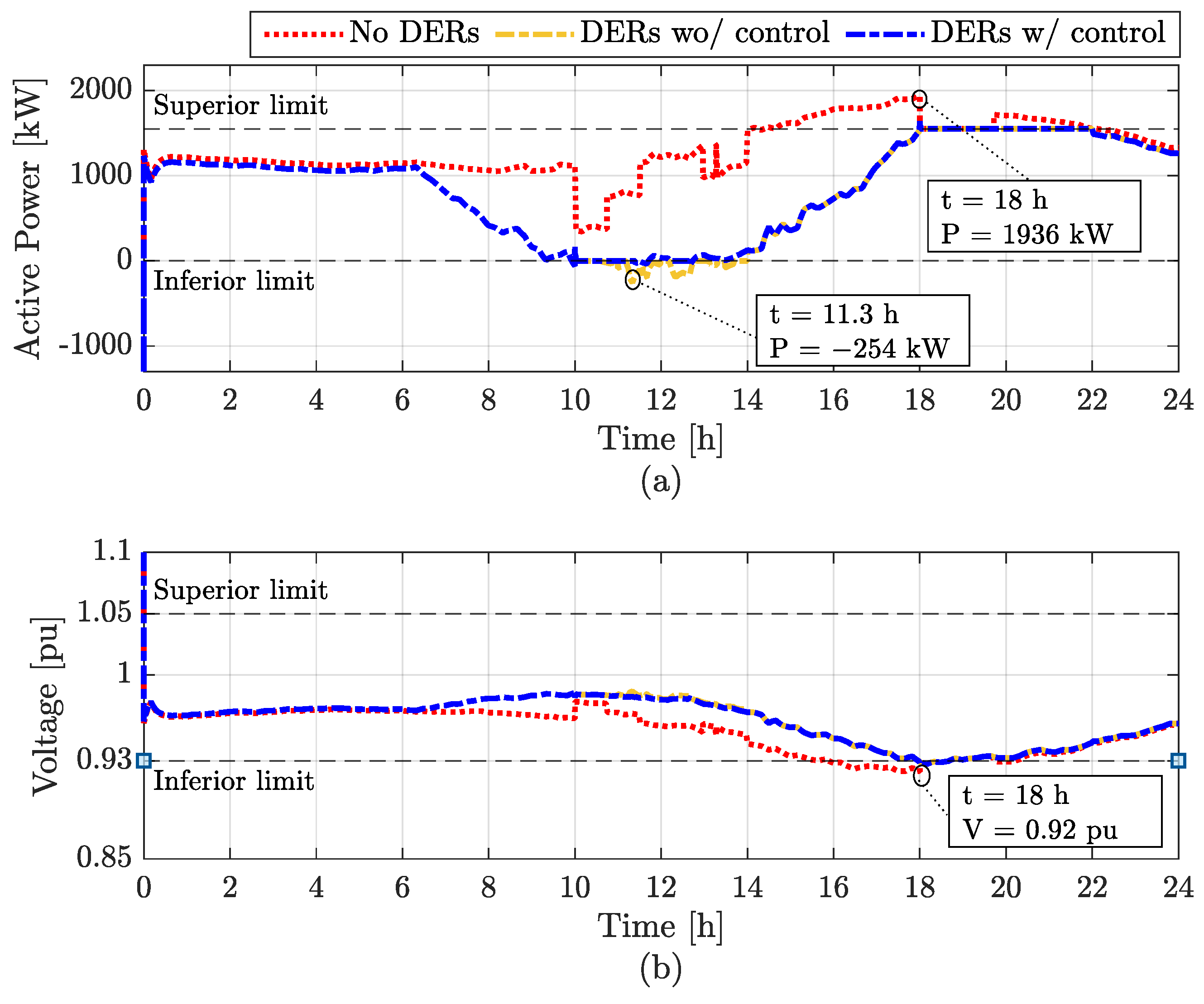
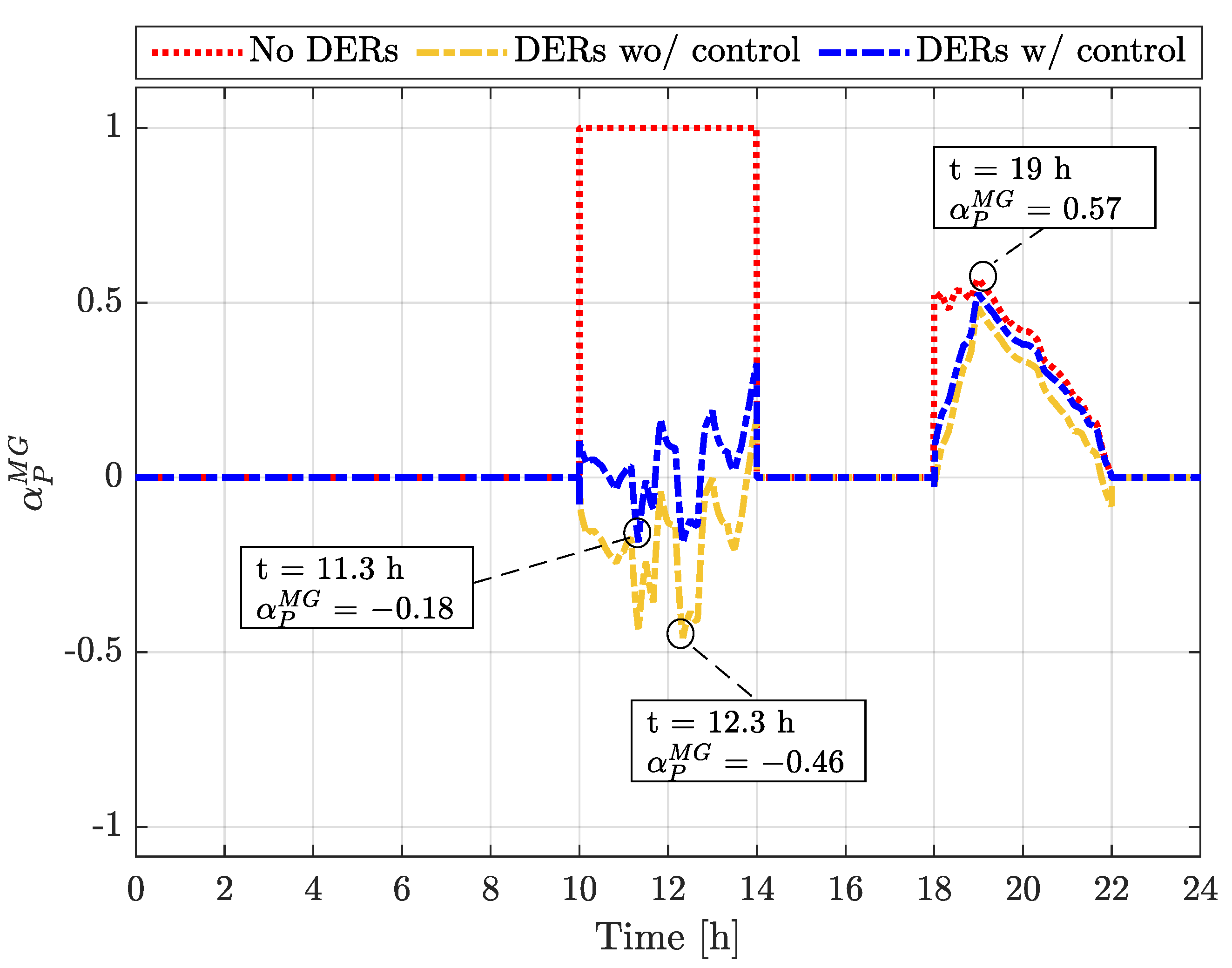
4. Simulation Results
4.1. Scenarios without FCS
4.2. Scenarios with Uncontrolled FCS
4.3. Scenarios with FCS with Control
5. Discussion of Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANEEL | Agência Nacional de Energia Elétrica |
| BESS | battery energy storage system |
| DER | distributed energy resource |
| DSO | distribution system operator |
| EV | electric vehicle |
| FCS | fast charging station |
| FCSCC | fast charging station central controller |
| LV | low voltage |
| MG | minigrid |
| MGCC | minigrid central controller |
| MISO | multiple inputs single output |
| MV | medium voltage |
| PBC | power-based control |
| PCC | point of common coupling |
| PI | proportional-integral |
| PRODIST | Procedimento de Distribuição de Energia Elétrica no Sistema Elétrico Nacional |
| SoC | state of charge |
| G | microgrid |
| GCC | microgrid central controller |
| V2G | vehicle-to-grid |
References
- National Geographic. Air Pollution. 2023. Available online: https://education.nationalgeographic.org/resource/air-pollution/ (accessed on 12 January 2024).
- Air Quality Life Index (AQLI). South Korea Analysis: Air Pollution Cuts Lives Short by More than a Year. 2019. Available online: https://aqli.epic.uchicago.edu/news/south-korea-analysis-air-pollution-cuts-lives-short-by-more-than-a-year/ (accessed on 12 January 2024).
- United States Environmental Protection Agency (EPA). Summary of the Clean Air Act. 2023. Available online: https://www.epa.gov/laws-regulations/summary-clean-air-act (accessed on 13 January 2024).
- European Environment Agency. Emissions of the Main Air Pollutants in Europe. 2023. Available online: https://eea.europa.eu/en/analysis/indicators/emissions-of-the-main-air (accessed on 12 January 2024).
- United States Environmental Protection Agency (EPA). Carbon Pollution from Transportation. 2022. Available online: https://www.epa.gov/transportation-air-pollution-and-climate-change/carbon-pollution-transportation (accessed on 14 January 2024).
- The New York Times. For Electric Car Owners, ‘Range Anxiety’ Gives Way to ‘Charging Time Trauma’. 2017. Available online: https://www.nytimes.com/2017/10/05/automobiles/wheels/electric-cars-charging.html (accessed on 12 January 2024).
- U.S. News & World Report. 11 Reasons People Don’t Buy Electric Cars (and Why They’re Wrong). 2023. Available online: https://cars.usnews.com/cars-trucks/advice/why-people-dont-buy-electric-cars (accessed on 16 January 2024).
- Kantar. Understanding Consumer Attitudes Towards Electric Vehicles. 2023. Available online: https://www.kantar.com/inspiration/research-services/understanding-consumer-attitudes-towards-electric-vehicles-pf (accessed on 16 January 2024).
- Federal Highway Administration—U.S. Departament of Transportation. National Electric Vehicle Infrastructure Formula Program. 2022. Available online: https://www.fhwa.dot.gov/environment/alternative_fuel_corridors/resources/nprm_evcharging_unofficial.pdf (accessed on 17 January 2024).
- Alternative Fuels Data Center. Alternative Fueling Station Counts by State. 2024. Available online: https://afdc.energy.gov/stations/states (accessed on 17 January 2024).
- International Energy Agency (IEA). Trends in Charging Infrastructure. 2023. Available online: https://www.iea.org/reports/global-ev-outlook-2023/trends-in-charging-infrastructure (accessed on 17 January 2024).
- Statista. Estimated Number of Plug-In Electric Vehicles in Use in Selected Countries as of 2022. 2022. Available online: https://www.statista.com/statistics/244292/number-of-electric-vehicles-by-country/ (accessed on 17 January 2024).
- Nafi, I.M.; Tabassum, S.; Hassan, Q.R.; Abid, F. Effect of Electric Vehicle Fast Charging Station on Residential Distribution Network in Bangladesh. In Proceedings of the 2021 5th International Conference on Electrical Engineering and Information Communication Technology (ICEEICT), Dhaka, Bangladesh, 18–20 November 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Alshareef, S.M. Voltage Sag Assessment, Detection, and Classification in Distribution Systems Embedded With Fast Charging Stations. IEEE Access 2023, 11, 89864–89880. [Google Scholar] [CrossRef]
- Tovilović, D.M.; Rajaković, N.L. The simultaneous impact of photovoltaic systems and plug-in electric vehicles on the daily load and voltage profiles and the harmonic voltage distortions in urban distribution systems. Renew. Energy 2015, 76, 454–464. [Google Scholar] [CrossRef]
- Lamedica, R.; Geri, A.; Gatta, F.M.; Sangiovanni, S.; Maccioni, M.; Ruvio, A. Integrating Electric Vehicles in Microgrids: Overview on Hosting Capacity and New Controls. IEEE Trans. Ind. Appl. 2019, 55, 7338–7346. [Google Scholar] [CrossRef]
- Caro, L.M.; Ramos, G.; Rauma, K.; Rodriguez, D.F.C.; Martinez, D.M.; Rehtanz, C. State of Charge Influence on the Harmonic Distortion From Electric Vehicle Charging. IEEE Trans. Ind. Appl. 2021, 57, 2077–2088. [Google Scholar] [CrossRef]
- Chudy, A.; Hołyszko, P.; Mazurek, P. Fast Charging of an Electric Bus Fleet and Its Impact on the Power Quality Based on On-Site Measurements. Energies 2022, 15, 5555. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Hosani, K.A.; Al-Sumaiti, A.S.; Nguyen, T.H.; Jaafari, K.A.A.; Alsawalhi, J.Y.; El Moursi, M.S. Fast Harmonic Rejecting Control Design to Enable Active Support of Charging Stations to Micro-Grids Under Distortion. IEEE Trans. Transp. Electrif. 2023, 9, 4132–4146. [Google Scholar] [CrossRef]
- Steen, D.; Tuan, L.A.; Carlson, O.; Bertling, L. Assessment of Electric Vehicle Charging Scenarios Based on Demographical Data. IEEE Trans. Smart Grid 2012, 3, 1457–1468. [Google Scholar] [CrossRef]
- Awadallah, M.A.; Singh, B.N.; Venkatesh, B. Impact of EV Charger Load on Distribution Network Capacity: A Case Study in Toronto. Can. J. Electr. Comput. Eng. 2016, 39, 268–273. [Google Scholar] [CrossRef]
- Ramadan, H.; Ali, A.; Farkas, C. Assessment of plug-in electric vehicles charging impacts on residential low voltage distribution grid in Hungary. In Proceedings of the 2018 6th International Istanbul Smart Grids and Cities Congress and Fair (ICSG), Istanbul, Turkey, 25–26 April 2018; pp. 105–109. [Google Scholar] [CrossRef]
- Coban, H.H.; Lewicki, W.; Sendek-Matysiak, E.; Łosiewicz, Z.; Drożdż, W.; Miśkiewicz, R. Electric Vehicles and Vehicle–Grid Interaction in the Turkish Electricity System. Energies 2022, 15, 8218. [Google Scholar] [CrossRef]
- European Council—Council of the European Union. Climate Change Summit COP26. 2021. Available online: https://www.consilium.europa.eu/en/policies/climate-change/paris-agreement/cop26/ (accessed on 21 January 2024).
- U.S. Department of Energy. Homeowner’s Guide to the Federal Tax Credit for Solar Photovoltaics. 2023. Available online: https://www.energy.gov/eere/solar/homeowners-guide-federal-tax-credit-solar-photovoltaics (accessed on 21 January 2024).
- Ministério do Desenvolvimento, Indústria, Comércio e Serviços—Brasil. Decreto do Governo Garante Isenção Fiscal Para Semicondutores e Inclui Energia Solar em Benefício. 2023. Available online: https://gov.br/mdic/pt-br/assuntos/noticias/2023/marco/decreto-do-governo-garante-isencao-fiscal-para-semicondutores-e-inclui-energia-solar-em-beneficio (accessed on 21 January 2024).
- Reuters. China Sets 2022 Renewable Power Subsidy at $607 mln. 2021. Available online: https://www.reuters.com/business/energy/china-sets-2022-renewable-power-subsidy-607-mln-2021-11-16/ (accessed on 21 January 2024).
- European Comission. EU Renewable Energy Financing Mechanism. 2023. Available online: https://energy.ec.europa.eu/topics/renewable-energy/financing/eu-renewable-energy-financing-mechanism_en (accessed on 21 January 2024).
- Hossain, E.; Tür, M.R.; Padmanaban, S.; Ay, S.; Khan, I. Analysis and Mitigation of Power Quality Issues in Distributed Generation Systems Using Custom Power Devices. IEEE Access 2018, 6, 16816–16833. [Google Scholar] [CrossRef]
- Zenhom, Z.M.; Aleem, S.H.E.A.; Zobaa, A.F.; Boghdady, T.A. A Comprehensive Review of Renewables and Electric Vehicles Hosting Capacity in Active Distribution Networks. IEEE Access 2024, 12, 3672–3699. [Google Scholar] [CrossRef]
- Falahi, M.; Chou, H.M.; Ehsani, M.; Xie, L.; Butler-Purry, K.L. Potential Power Quality Benefits of Electric Vehicles. IEEE Trans. Sustain. Energy 2013, 4, 1016–1023. [Google Scholar] [CrossRef]
- Pahasa, J.; Ngamroo, I. PHEVs Bidirectional Charging/Discharging and SoC Control for Microgrid Frequency Stabilization Using Multiple MPC. IEEE Trans. Smart Grid 2015, 6, 526–533. [Google Scholar] [CrossRef]
- Bayat, M.; Sheshyekani, K.; Rezazadeh, A. A Unified Framework for Participation of Responsive End-User Devices in Voltage and Frequency Control of the Smart Grid. IEEE Trans. Power Syst. 2015, 30, 1369–1379. [Google Scholar] [CrossRef]
- Weckx, S.; Driesen, J. Load Balancing with EV Chargers and PV Inverters in Unbalanced Distribution Grids. IEEE Trans. Sustain. Energy 2015, 6, 635–643. [Google Scholar] [CrossRef]
- Akhavan-Rezai, E.; Shaaban, M.F.; El-Saadany, E.F.; Karray, F. Managing Demand for Plug-in Electric Vehicles in Unbalanced LV Systems With Photovoltaics. IEEE Trans. Ind. Inform. 2017, 13, 1057–1067. [Google Scholar] [CrossRef]
- Rana, R.; Singh, M.; Mishra, S. Design of Modified Droop Controller for Frequency Support in Microgrid Using Fleet of Electric Vehicles. IEEE Trans. Power Syst. 2017, 32, 3627–3636. [Google Scholar] [CrossRef]
- Datta, U.; Kalam, A.; Shi, J.; Li, J. Electric Vehicle Charging Station for Providing Primary Frequency Control in Microgrid. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 2440–2444. [Google Scholar] [CrossRef]
- Ahmad, F. Analysis of Microgrids for Plug-in Hybrid Electric Vehicles Charging Stations. Ph.D. Thesis, Department of Electrical Engineering, Faculty of Engineering & Technology, Aligarh Muslim University, Aligarh, India, 2019. [Google Scholar]
- Rücker, F.; Merten, M.; Gong, J.; Villafáfila-Robles, R.; Schoeneberger, I.; Sauer, D.U. Evaluation of the Effects of Smart Charging Strategies and Frequency Restoration Reserves Market Participation of an Electric Vehicle. Energies 2020, 13, 3112. [Google Scholar] [CrossRef]
- Da Silva, E.C.; Melgar-Dominguez, O.D.; Romero, R. Simultaneous Distributed Generation and Electric Vehicles Hosting Capacity Assessment in Electric Distribution Systems. IEEE Access 2021, 9, 110927–110939. [Google Scholar] [CrossRef]
- Lai, C.S.; Chen, D.; Xu, X.; Taylor, G.A.; Pisica, I.; Lai, L.L. Operational Challenges to Accommodate High Penetration of Electric Vehicles: A Comparison between UK and China. In Proceedings of the 2021 IEEE 15th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Florence, Italy, 14–16 July 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Kasturi, K.; Nayak, C.; Nayak, M. Photovoltaic and Electric Vehicle-to-Grid Strategies for Peak Load Shifting in Low Voltage Distribution System Under Time of Use Grid Pricing. Iran. J. Sci. Technol. Trans. Electr. Eng. 2021, 45, 789–801. [Google Scholar] [CrossRef]
- Khazali, A.; Rezaei, N.; Saboori, H.; Guerrero, J.M. Using PV systems and parking lots to provide virtual inertia and frequency regulation provision in low inertia grids. Electr. Power Syst. Res. 2022, 207, 107859. [Google Scholar] [CrossRef]
- Kiani, S.; Sheshyekani, K.; Dagdougui, H. An Extended State Space Model for Aggregation of Large-Scale EVs Considering Fast Charging. IEEE Trans. Transp. Electrif. 2023, 9, 1238–1251. [Google Scholar] [CrossRef]
- Morstyn, T.; Hredzak, B.; Agelidis, V.G. Control Strategies for Microgrids With Distributed Energy Storage Systems: An Overview. IEEE Trans. Smart Grid 2018, 9, 3652–3666. [Google Scholar] [CrossRef]
- Gao, X.; De Carne, G.; Andresen, M.; Brüske, S.; Pugliese, S.; Liserre, M. Voltage-Dependent Load-Leveling Approach by Means of Electric Vehicle Fast Charging Stations. IEEE Trans. Transp. Electrif. 2021, 7, 1099–1111. [Google Scholar] [CrossRef]
- Zahedmanesh, A.; Muttaqi, K.M.; Sutanto, D. Active and Reactive Power Control of PEV Fast Charging Stations Using a Consecutive Horizon-Based Energy Management Process. IEEE Trans. Ind. Inform. 2021, 17, 6742–6753. [Google Scholar] [CrossRef]
- Radu, A.T.; Eremia, M.; Toma, L. Use of Battery Storage Systems in EV Ultrafast Charging Stations for Load Spikes Mitigation. Sci. Bull.-Univ. Politeh. Buchar. 2021, 83, 283–294. [Google Scholar]
- Gao, X.; De Carne, G.; Langwasser, M.; Liserre, M. Online Load Control in Medium Voltage Grid by Means of Reactive Power Modification of Fast Charging Station. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Gjelaj, M.; Hashemi, S.; Traeholt, C.; Andersen, P.B. Grid integration of DC fast-charging stations for EVs by using modular li-ion batteries. IET Gener. Transm. Distrib. 2018, 12, 4368–4376. [Google Scholar] [CrossRef]
- Yang, H.; Pan, H.; Luo, F.; Qiu, J.; Deng, Y.; Lai, M.; Dong, Z.Y. Operational Planning of Electric Vehicles for Balancing Wind Power and Load Fluctuations in a Microgrid. IEEE Trans. Sustain. Energy 2017, 8, 592–604. [Google Scholar] [CrossRef]
- Cheng, Q.; Chen, L.; Sun, Q.; Wang, R.; Ma, D.; Qin, D. A smart charging algorithm based on a fast charging station without energy storage system. CSEE J. Power Energy Syst. 2021, 7, 850–861. [Google Scholar] [CrossRef]
- Lymperopoulos, I.; Qureshi, F.A.; Bitlislioglu, A.; Poland, J.; Zanarini, A.; Mercangoez, M.; Jones, C. Ancillary Services Provision Utilizing a Network of Fast-Charging Stations for Electrical Buses. IEEE Trans. Smart Grid 2020, 11, 665–672. [Google Scholar] [CrossRef]
- Yong, J.Y.; Ramachandaramurthy, V.K.; Tan, K.M.; Mithulananthan, N. Bi-directional electric vehicle fast charging station with novel reactive power compensation for voltage regulation. Int. J. Electr. Power Energy Syst. 2015, 64, 300–310. [Google Scholar] [CrossRef]
- Yuan, H.; Wei, G.; Zhu, L.; Zhang, X.; Zhang, H.; Luo, Z.; Hu, J. Optimal scheduling for micro-grid considering EV charging–swapping–storage integrated station. IET Gener. Transm. Distrib. 2020, 14, 1127–1137. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Li, Y.; Gooi, H.B.; Xin, H. Multi-Agent Based Optimal Scheduling and Trading for Multi-Microgrids Integrated With Urban Transportation Networks. IEEE Trans. Power Syst. 2021, 36, 2197–2210. [Google Scholar] [CrossRef]
- Ton, D.; Reilly, J. Microgrid Controller Initiatives: An Overview of R&D by the U.S. Department of Energy. IEEE Power Energy Mag. 2017, 15, 24–31. [Google Scholar] [CrossRef]
- Caldognetto, T.; Buso, S.; Tenti, P.; Brandao, D.I. Power-Based Control of Low-Voltage Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 1056–1066. [Google Scholar] [CrossRef]
- Brandao, D.I.; Caldognetto, T.; Marafão, F.P.; Simões, M.G.; Pomilio, J.A.; Tenti, P. Centralized Control of Distributed Single-Phase Inverters Arbitrarily Connected to Three-Phase Four-Wire Microgrids. IEEE Trans. Smart Grid 2017, 8, 437–446. [Google Scholar] [CrossRef]
- Brandao, D.I.; de Araújo, L.S.; Caldognetto, T.; Pomilio, J.A. Coordinated control of three- and single-phase inverters coexisting in low-voltage microgrids. Appl. Energy 2018, 228, 2050–2060. [Google Scholar] [CrossRef]
- Araujo, L.S.; Brandao, D.I.; Silva, S.M.; Cardoso Filho, B.J. Reactive Power Support in Medium Voltage Networks by Coordinated Control of Distributed Generators in Dispatchable Low-Voltage Microgrid. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; pp. 2603–2608. [Google Scholar] [CrossRef]
- Brandao, D.I.; Araujo, L.S.; Alonso, A.M.S.; dos Reis, G.L.; Liberado, E.V.; Marafão, F.P. Coordinated Control of Distributed Three- and Single-Phase Inverters Connected to Three-Phase Three-Wire Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 3861–3877. [Google Scholar] [CrossRef]
- Brandao, D.I.; Santos, R.P.d.; Silva, W.W.A.G.; Oliveira, T.R.; Donoso-Garcia, P.F. Model-Free Energy Management System for Hybrid Alternating Current/Direct Current Microgrids. IEEE Trans. Ind. Electron. 2021, 68, 3982–3991. [Google Scholar] [CrossRef]
- Ferreira, D.M.; Brandao, D.I.; Bergna-Diaz, G.; Tedeschi, E.; Silva, S.M. Distributed Control Strategy for Low-Voltage Three-Phase Four-Wire Microgrids: Consensus Power-Based Control. IEEE Trans. Smart Grid 2021, 12, 3215–3231. [Google Scholar] [CrossRef]
- Dos Reis, G.; Liberado, E.; Marafão, F.; Sousa, C.; Silva, W.; Brandao, D. Model-Free Power Control for Low-Voltage AC Dispatchable Microgrids with Multiple Points of Connection. Energies 2021, 14, 6390. [Google Scholar] [CrossRef]
- Reis, G.L.; Brandao, D.I.; Oliveira, J.H.; Araujo, L.S.; Cardoso Filho, B.J. Case Study of Single-Controllable Microgrid: A Practical Implementation. Energies 2022, 15, 6400. [Google Scholar] [CrossRef]
- Callegari, J.M.S.; Pereira, H.A.; Brandao, D.I. Voltage Support and Selective Harmonic Current Compensation in Advanced AC Microgrids. IEEE Trans. Ind. Appl. 2023, 59, 4880–4892. [Google Scholar] [CrossRef]
- Soares Callegari, J.M.; Araujo, L.S.; De Lisboa Brandão, D.A.; Cardoso Filho, B.J.; Brandao, D.I. Centralized Strategy Incorporating Multiple Control Actions Applied to Advanced Microgrids. In Proceedings of the 2023 IEEE 8th Southern Power Electronics Conference (SPEC), Florianopolis, Brazil, 26–29 November 2023; pp. 1–7. [Google Scholar] [CrossRef]
- Federal Communications Commission. FCC Finds U.S. Broadband Deployment Not Keeping Pace. 2015. Available online: https://www.fcc.gov/document/fcc-finds-us-broadband-deployment-not-keeping-pace-0 (accessed on 22 January 2024).
- Ramos, G.V.; Parreiras, T.M.; Brandão, D.A.d.L.; Silva, S.M.; Filho, B.d.J.C. A Zero Harmonic Distortion Grid-Forming Converter for Islanded Microgrids. In Proceedings of the 2023 IEEE Industry Applications Society Annual Meeting (IAS), Nashville, TN, USA, 29 October–2 November 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Brandao, D.A.L.; Parreiras, T.M.; Callegari, J.M.S.; Pires, I.A.; Brandao, D.I.; Cardoso Filho, B.D.J. Power-based Control for Microgrids and Extreme Fast Charging Stations with Low-Harmonic Current Content in the Medium Voltage Power Grid. In Proceedings of the 2023 IEEE Transportation Electrification Conference & Expo (ITEC), Detroit, MI, USA, 21–23 June 2023; pp. 1–6. [Google Scholar] [CrossRef]
- TeslaTap. Supercharger Superguide. 2023. Available online: https://teslatap.com/articles/supercharger-superguide/ (accessed on 21 October 2023).
- Induscabos—Condutores Elétricos. Electrical Parameters—Medium Voltage Cables. 2018. Available online: https://www.induscabos.com.br/wp-content/uploads/2018/03/induscabos-parametros-eletricos-cabos-de-media-tensao.pdf (accessed on 21 October 2023).
- Pedrotti, R.F. Simulação Termo Energética de um Supermercado. Master’s Thesis, Energy Engineering, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil, 2015. [Google Scholar]
- Origin. Origin1500 1.5kW Solar System Panel Specifications. 2023. Available online: https://www.originenergy.com.au/wp-content/uploads/Origin1500B_Solar_Panel_Brochure.pdf (accessed on 21 October 2023).
- Newaz, A.; Ospina, J.; Faruque, M.O. Controller Hardware-in-the-Loop Validation of a Graph Search Based Energy Management Strategy for Grid-Connected Distributed Energy Resources. IEEE Trans. Energy Convers. 2020, 35, 520–528. [Google Scholar] [CrossRef]
- Rafique, S.; Hossain, M.J.; Nizami, M.S.H.; Irshad, U.B.; Mukhopadhyay, S.C. Energy Management Systems for Residential Buildings With Electric Vehicles and Distributed Energy Resources. IEEE Access 2021, 9, 46997–47007. [Google Scholar] [CrossRef]
- Ahmad, S.; Shafiullah, M.; Ahmed, C.B.; Alowaifeer, M. A Review of Microgrid Energy Management and Control Strategies. IEEE Access 2023, 11, 21729–21757. [Google Scholar] [CrossRef]
- Agência Nacional de Energia Elétrica. Procedimentos de Distribuição de Energia Elétrica No Sistema Elétrico Nacional—PRODIST—Módulo 8—Qualidade do Fornecimento de Energia Elétrica. 2021. Available online: https://www2.aneel.gov.br/cedoc/aren2021956_2_7.pdf (accessed on 24 October 2023).

| Reference | Voltage Level | Ancillary Service Category | DERs Control | FCSs Control | Control Architecture a |
|---|---|---|---|---|---|
| [18] | low voltage (LV) | Power quality (voltage and frequency disturbances and harmonic injection) | ✗ | ✗ | ✗/✗ |
| [14] | medium voltage (MV) | Power quality (transient voltage disturbances) | ✗ | ✗ | ✗/✗ |
| [46] | MV | Reactive power support (voltage control) | ✗ | ✓ | ✗/C |
| [13] | MV | Power quality (voltage disturbances) | ✗ | ✗ | ✗/✗ |
| [47] | MV | Active/reactive power support (voltage control) | ✗ | ✓ | ✗/C |
| [48] | LV | Active power support (peak shaving) | ✗ | ✓ | ✗/D |
| [49] | MV | Reactive power support (voltage support) | ✗ | ✓ | ✗/D |
| [50] | MV | - | ✗ | ✓ | ✗/D |
| [51] | MV | Active power support (peak shaving) | ✗ | ✓ | ✗/C |
| [52] | LV | - | ✗ | ✓ | ✗/C |
| [53] | MV | Active power support (load shifting) | ✗ | ✓ | ✗/D |
| [54] | MV | Reactive power support (voltage support) | ✗ | ✓ | ✗/D |
| [55] | MV | Active power support (load shifting) | ✗ | ✓ | ✗/C |
| [56] | MV | - | ✓ | ✗ | C/✗ |
| Here | LV/MV | Active power support: peak shaving and valley filling | ✓ | ✓ | C/C |
| Reference | Microgrid Configuration | Migrogrid Control Architecture | Power Quality Compensation | Active Load Control | Sharing Coefficients |
|---|---|---|---|---|---|
| [58] | 1 to 2 wires and low voltage | Centralized | Reactive and load unbalance | ✗ | e |
| [59] | 1 and 3 to 4 wires and low voltage | Centralized | Reactive and load balance | ✗ | , , , , e |
| [60] | 1 and 3 to 4 wires and low voltage | Centralized | Reactive and load balance | ✗ | , , , , , , e |
| [61] | 1 and 3 to 4 wires and low voltage | Centralized | Reactive and load balance | ✗ | , , , , e |
| [62] | 1 and 3 to 4 wires and low voltage | Centralized | Reactive and load balance | ✗ | , , , , , , e |
| [63] | 1 to 2 wire and low voltage | Centralized | Reactive and load unbalance | ✗ | , , , , e |
| [64] | 1 and 3 to 4 wires and low voltage | Distributed | Load balance | ✗ | , , e |
| [65] | 1 and 2 to 4 wires and low voltage | Centralized | Reactive and load balance | ✗ | , , , , e |
| [66] | 1 and 2 to 4 wires and low voltage | Centralized | Reactive and load balance | ✗ | , , , , e |
| [67] | 1 and 3 to 4 wires and low voltage | Centralized/ decentralized | Reactive and load balance | ✗ | , , , , e |
| Here | 3 to 3 wires and medium voltage | Centralized | Load balance | ✓ |
| Grid Element | Internal Elements | Load Profile | Power |
|---|---|---|---|
| LV Microgrid 1 | Non-dispatchable DERs | - | 80 kWp |
| Dispatchable DERs | - | 80 kWp | |
| Load | Residential | 200 kWp | |
| LV Microgrid 2 | Non-dispatchable DERs | - | 900 kWp |
| Dispatchable DERs | - | 60 kWp | |
| Load | Commercial | 450 kWp | |
| LV Microgrid 3 | Non-dispatchable DERs | - | 500 kWp |
| Dispatchable DERs | - | 80 kWp | |
| Load | Residential | 100 kWp | |
| FCS 1 | Chargers | - | 250 kW (3) |
| BESS | - | 750 kW | |
| BESS Energy | - | 646.4 kWh | |
| BESS state of charge (SoC) | - | 20% to 100% | |
| Contracted demand | - | 375 kW | |
| FCS 2 | Chargers | - | 250 kW (3) |
| BESS Power | - | 750 kW | |
| BESS Energy | - | 646.4 kWh | |
| BESS SoC | - | 20% to 100% | |
| Contracted demand | - | 375 kW | |
| Internal load | - | Residential | 670 kWp |
| External load | - | Residential | 4100 kWp |
| Internal generator | - | - | 370 kWp |
| Symbol | Cable Cross-Section () a | Cable Length (km) | Equivalent Resistance () | Equivalent Inductance (mH) |
|---|---|---|---|---|
| 50 | 2.3 | 2.0 | 1.4 | |
| 50 | 1.7 | 1.2 | 0.9 | |
| 50 | 1.8 | 1.3 | 0.9 | |
| 50 | 1.5 | 1.0 | 0.7 | |
| 50 | 2.0 | 1.6 | 1.2 |
| Scenario | FCS? | DERs? | FCS Control? | DERs Control? |
|---|---|---|---|---|
| 1 | ✗ | ✗ | ✗ | ✗ |
| 2 | ✗ | ✓ | ✗ | ✗ |
| 3 | ✗ | ✓ | ✗ | ✓ |
| 4 | ✓ | ✗ | ✗ | ✗ |
| 5 | ✓ | ✓ | ✗ | ✗ |
| 6 | ✓ | ✓ | ✗ | ✓ |
| 7 | ✓ | ✗ | ✓ | ✗ |
| 8 | ✓ | ✓ | ✓ | ✗ |
| 9 | ✓ | ✓ | ✓ | ✓ |
| Activation Periods | Reference Powers (kW) |
|---|---|
| 10 h to 14 h | 0 |
| 18 h to 22 h | 1550 |
| Service Voltage | Reading Voltage Variation Range (RV) in Relation to Reference Voltage (RefV) |
|---|---|
| Proper | |
| Precarious | |
| Critical | or |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brandao, D.A.d.L.; Callegari, J.M.S.; Brandao, D.I.; Pires, I.A. Coordinated, Centralized, and Simultaneous Control of Fast Charging Stations and Distributed Energy Resources. Inventions 2024, 9, 35. https://doi.org/10.3390/inventions9020035
Brandao DAdL, Callegari JMS, Brandao DI, Pires IA. Coordinated, Centralized, and Simultaneous Control of Fast Charging Stations and Distributed Energy Resources. Inventions. 2024; 9(2):35. https://doi.org/10.3390/inventions9020035
Chicago/Turabian StyleBrandao, Dener A. de L., João M. S. Callegari, Danilo I. Brandao, and Igor A. Pires. 2024. "Coordinated, Centralized, and Simultaneous Control of Fast Charging Stations and Distributed Energy Resources" Inventions 9, no. 2: 35. https://doi.org/10.3390/inventions9020035
APA StyleBrandao, D. A. d. L., Callegari, J. M. S., Brandao, D. I., & Pires, I. A. (2024). Coordinated, Centralized, and Simultaneous Control of Fast Charging Stations and Distributed Energy Resources. Inventions, 9(2), 35. https://doi.org/10.3390/inventions9020035







