Repeatability and Validity of Different Methods to Determine the Anaerobic Threshold Through the Maximal Multistage Test in Male Cyclists and Triathletes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Study Design
2.3. Testing Procedures
2.4. Preliminary Trial
2.5. Maximal Multistage Cycling Test (MMCT)
2.6. Constant Load Tests for the Determination of MLSSW
2.7. Statistical Analyses
3. Results
3.1. Repeatability of Anaerobic Thresholds Through MMCTs
3.2. Constant Load Tests
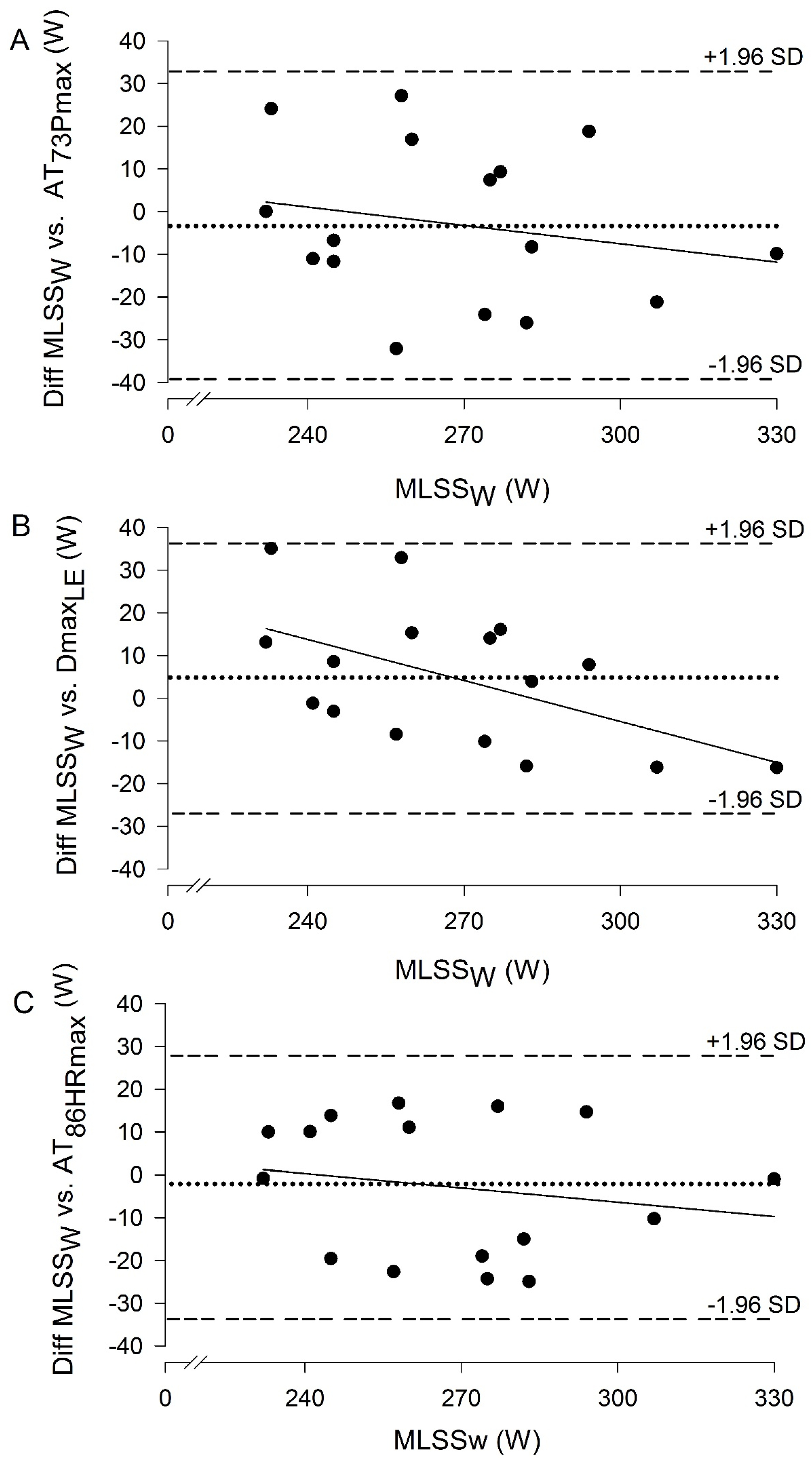
3.3. Validity of Anaerobic Thresholds
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANOVA | Analysis of variance |
| AT | Anaerobic threshold |
| AT73Pmax | The workload corresponding to 73% of the maximal aerobic workout |
| AT86HRmax | The workload associated with the 86% of HRmax |
| CI | Confidence intervals |
| CLT | Constant load tests |
| CV | Coefficient of variation |
| Dmax0.4 | The workload at the maximum perpendicular distance from the straight line between the blood lactate concentration associated with the previous stage to the one that the blood lactate concentration increased ≥0.4mmol·L−1 and final blood lactate concentration data point in the third-order polynomial curve describing the blood lactate concentration kinetics during the maximal multistage cycling test |
| DmaxLE | The workload at the maximum perpendicular distance from the straight line between the blood lactate concentration associated with the minimum lactate equivalent and final blood lactate concentration data point in the third-order polynomial curve describing the blood lactate concentration kinetics during the maximal multistage cycling test |
| ES | Effect size |
| HRmax | Maximal heart rate |
| ICC | Intraclass correlation coefficient |
| [La−] | Blood lactate concentration |
| LEmin | Minimum lactate equivalent |
| LE+1.5mM | The workload corresponding to the minimum lactate equivalent plus 1.5 mmol·L−1 |
| LoA | Limits of agreement method |
| LT1+1.5mM | The workload at 1.5 mmol·L−1 above the blood lactate concentration associated with the lowest stage above which blood lactate concentration increased by ≥0.1 mmol·L−1 in the following stage and ≥0.2 mmol·L−1 in the subsequent stage |
| LT2 | The workload at 1.5 mmol·L−1 in the individual blood lactate concentration vs. workload second-order polynomial curves above the average of the first four blood lactate concentrations values of exercise |
| LT3.5mM | The workloads associated with fixed blood lactate concentration of 3.5 mmol·L−1 |
| LT4mM | The workloads associated with fixed blood lactate concentration of 4 mmol·L−1 |
| MDC | Minimum detectable change |
| MLSSW | Exercise intensity corresponding to the maximal lactate steady state |
| MMCT | Maximal multistage cycling test |
| Pmax | Maximal aerobic workout |
| RPE | Rating of perceived exertion |
| SD | Standard deviation |
| SEE | Standard error of the estimate |
| SEM | Standard error of measurement |
References
- Faria, E.W.; Parker, D.L.; Faria, I.E. The Science of Cycling: Factors Affecting Performance—Part 2. Sports Med. 2005, 35, 313–337. [Google Scholar] [CrossRef]
- O’Toole, M.L.; Douglas, P.S. Applied Physiology of Triathlon. Sports Med. 1995, 19, 251–267. [Google Scholar] [CrossRef]
- Beneke, R.; von Duvillard, S.P. Determination of Maximal Lactate Steady State Response in Selected Sports Events. Med. Sci. Sports Exerc. 1996, 28, 241–246. [Google Scholar] [CrossRef]
- Billat, V.L.; Sirvent, P.; Py, G.; Koralsztein, J.P.; Mercier, J. The Concept of Maximal Lactate Steady State: A Bridge between Biochemistry, Physiology and Sport Science. Sports Med. 2003, 33, 407–426. [Google Scholar] [CrossRef] [PubMed]
- Kilding, A.E.; Jones, A.M. Validity of a Single-Visit Protocol to Estimate the Maximum Lactate Steady State. Med. Sci. Sports Exerc. 2005, 37, 1734–1740. [Google Scholar] [CrossRef]
- Llodio, I.; Garcia-Tabar, I.; Sánchez-Medina, L.; Ibáñez, J.; Gorostiaga, E.M. Estimation of the Maximal Lactate Steady State in Junior Soccer Players. Int. J. Sports Med. 2015, 36, 1142–1148. [Google Scholar] [CrossRef]
- Llodio, I.; Gorostiaga, E.M.; Garcia-Tabar, I.; Granados, C.; Sánchez-Medina, L. Estimation of the Maximal Lactate Steady State in Endurance Runners. Int. J. Sports Med. 2016, 37, 539–546. [Google Scholar] [CrossRef]
- Messias, L.H.D.; Polisel, E.E.C.; Manchado-Gobatto, F.B. Advances of the Reverse Lactate Threshold Test: Non-Invasive Proposal Based on Heart Rate and Effect of Previous Cycling Experience. PLoS ONE 2018, 13, e0194313. [Google Scholar] [CrossRef]
- Sotero, R.C.; Pardono, E.; Campbell, C.S.; Simões, H.G. Indirect Assessment of Lactate Minimum and Maximal Blood Lactate Steady-State Intensity for Physically Active Individuals. J. Strength Cond. Res. 2009, 23, 847–853. [Google Scholar] [CrossRef] [PubMed]
- Sotero, R.C.; Pardono, E.; Landwehr, R.; Campbell, C.S.; Simões, H.G. Blood Glucose Minimum Predicts Maximal Lactate Steady State on Running. Int. J. Sports Med. 2009, 30, 643–646. [Google Scholar] [CrossRef]
- Van Schuylenbergh, R.; Vanden Eynde, B.; Hespel, P. Correlations between Lactate and Ventilatory Thresholds and the Maximal Lactate Steady State in Elite Cyclists. Int. J. Sports Med. 2004, 25, 403–408. [Google Scholar] [CrossRef] [PubMed]
- Harnish, C.R.; Swensen, T.C.; Pate, R.R. Methods for Estimating the Maximal Lactate Steady State in Trained Cyclists. Med. Sci. Sports Exerc. 2001, 33, 1052–1055. [Google Scholar] [CrossRef] [PubMed]
- Leti, T.; Mendelson, M.; Laplaud, D.; Flore, P. Prediction of Maximal Lactate Steady State in Runners with an Incremental Test on the Field. J. Sports Sci. 2012, 30, 609–616. [Google Scholar] [CrossRef]
- Halson, S.L.; Bridge, M.W.; Meeusen, R.; Busschaert, B.; Gleeson, M.; Jones, D.A.; Jeukendrup, A.E. Time Course of Performance Changes and Fatigue Markers during Intensified Training in Trained Cyclists. J. Appl. Physiol. 2002, 93, 947–956. [Google Scholar] [CrossRef] [PubMed]
- Iannetta, D.; Ingram, C.P.; Keir, D.A.; Murias, J.M. Methodological Reconciliation of CP and MLSS and Their Agreement with the Maximal Metabolic Steady State. Med. Sci. Sports Exerc. 2022, 54, 622–632. [Google Scholar] [CrossRef]
- Gorostiaga, E.M.; Garcia-Tabar, I.; Sánchez-Medina, L. Critical power: Over 95 years of “evidence” and “evolution”. Scand. J. Med. Sci. Sports 2022, 32, 1069–1071. [Google Scholar] [CrossRef] [PubMed]
- Iannetta, D.; Inglis, E.C.; Fullerton, C.; Passfield, L.; Murias, J.M. Metabolic and performance-related consequences of exercising at and slightly above MLSS. Scand. J. Med. Sci. Sports 2018, 28, 2481–2493. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Tabar, I.; Gorostiaga, E.M. A “Blood Relationship” Between the Overlooked Minimum Lactate Equivalent and Maximal Lactate Steady State in Trained Runners: Back to the Old Days? Front. Physiol. 2018, 9, 1034. [Google Scholar] [CrossRef]
- Garcia-Tabar, I.; Rampinini, E.; Gorostiaga, E.M. Lactate Equivalent for Maximal Lactate Steady State Determination in Soccer. Res. Q. Exerc. Sport 2019, 90, 678–689. [Google Scholar] [CrossRef] [PubMed]
- Heck, H.; Mader, A.; Hess, G.; Mücke, S.; Müller, R.; Hollmann, W. Justification of the 4-Mmol/l Lactate Threshold. Int. J. Sports Med. 1985, 6, 117–130. [Google Scholar] [CrossRef] [PubMed]
- Bourdon, P. Blood Lactate Transition Thresholds: Concepts and Controversies. In Physiological Tests for Elite Athletes; Gore, C., Ed.; Human Kinetics: Champaign, IL, USA, 2000; pp. 55–65. [Google Scholar]
- Zwingmann, L.; Strütt, S.; Martin, A.; Volmary, P.; Bloch, W.; Wahl, P. Modifications of the Dmax Method in Comparison to the Maximal Lactate Steady State in Young Male Athletes. Physician Sports Med. 2019, 47, 174–181. [Google Scholar] [CrossRef] [PubMed]
- McKay, A.K.A.; Stellingwerff, T.; Smith, E.S.; Martin, D.T.; Mujika, I.; Goosey-Tolfrey, V.L.; Sheppard, J.; Burke, L.M. Defining Training and Performance Caliber: A Participant Classification Framework. Int. J. Sports Physiol. Perform. 2022, 17, 317–331. [Google Scholar] [CrossRef]
- World Medical Association. World Medical Association Declaration of Helsinki: Ethical Principles for Medical Research Involving Human Subjects. JAMA 2013, 310, 2191–2194. [Google Scholar] [CrossRef] [PubMed]
- Denadai, B.S.; Figueira, T.R.; Favaro, O.R.; Gonçalves, M. Effect of the Aerobic Capacity on the Validity of the Anaerobic Threshold for Determination of the Maximal Lactate Steady State in Cycling. Braz. J. Med. Biol. Res. 2004, 37, 1551–1556. [Google Scholar] [CrossRef]
- Hoefelmann, C.P.; Diefenthaeler, F.; Costa, V.P.; de Lucas, R.D.; Shambrook, P.; Guglielmo, L.G. Test-Retest Reliability of Second Lactate Turnpoint Using Two Different Criteria in Competitive Cyclists. Eur. J. Sport Sci. 2015, 15, 265–270. [Google Scholar] [CrossRef]
- Nikooie, R. Determination of Anaerobic Threshold by Monitoring the O2 Pulse Changes in Endurance Cyclists. J. Strength Cond. Res. 2016, 30, 1700–1707. [Google Scholar] [CrossRef] [PubMed]
- Płoszczyca, K.; Jazic, D.; Piotrowicz, Z.; Chalimoniuk, M.; Langfort, J.; Czuba, M. Comparison of Maximal Lactate Steady State with Anaerobic Threshold Determined by Various Methods Based on Graded Exercise Test with 3-Minute Stages in Elite Cyclists. BMC Sports Sci. Med. Rehabil. 2020, 12, 70. [Google Scholar] [CrossRef]
- Roseguini, B.T.; Narro, F.; Oliveira, A.R.; Ribeiro, J.P. Estimation of the Lactate Threshold from Heart Rate Response to Sub-Maximal Exercise: The Pulse Deficit. Int. J. Sports Med. 2007, 28, 463–469. [Google Scholar] [CrossRef]
- Borg, G. Perceived Exertion as an Indicator of Somatic Stress. Scand. J. Rehabil. Med. 1970, 2, 92–98. [Google Scholar] [CrossRef] [PubMed]
- Berg, A.; Jakob, E.; Lehmann, M.; Dickhuth, H.H.; Huber, G.; Keul, J. Aktuelle Aspekte der modernen Ergometrie. Pneumologie 1990, 44, 2–13. [Google Scholar] [PubMed]
- Keul, J.; Berg, A. Energiestoffwechsel und körperliche Leistung. In Zentrale Themen der Sportmedizin, 3rd ed.; Hollmann, W., Ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA; Tokyo, Japan, 1985; pp. 196–244. [Google Scholar]
- Beneke, R.; Hütler, M.; Leithäuser, R.M. Maximal Lactate-Steady-State Independent of Performance. Med. Sci. Sports Exerc. 2000, 32, 1135–1139. [Google Scholar] [CrossRef]
- Beneke, R.; Leithäuser, R.M.; Hütler, M. Dependence of the Maximal Lactate Steady State on the Motor Pattern of Exercise. Br. J. Sports Med. 2001, 35, 192–196. [Google Scholar] [CrossRef] [PubMed]
- Dekerle, J.; Baron, B.; Dupont, L.; Vanvelcenaher, J.; Pelayo, P. Maximal Lactate Steady State, Respiratory Compensation Threshold and Critical Power. Eur. J. Appl. Physiol. 2003, 89, 281–288. [Google Scholar] [CrossRef]
- Snyder, A.C.; Woulfe, T.; Welsh, R.; Foster, C. A Simplified Approach to Estimating the Maximal Lactate Steady State. Int. J. Sports Med. 1994, 15, 27–31. [Google Scholar] [CrossRef] [PubMed]
- Beneke, R. Methodological aspects of maximal lactate steady state implications for performance testing. Eur. J. Appl. Physiol. 2003, 89, 95–99. [Google Scholar] [CrossRef] [PubMed]
- Weir, J.P. Quantifying Test-Retest Reliability Using the Intraclass Correlation Coefficient and the SEM. J. Strength Cond. Res. 2005, 19, 231–240. [Google Scholar] [CrossRef]
- Koo, T.K.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J. Chiropr. Med. 2016, 15, 155–163, Correction in J. Chiropr. Med. 2017, 16, 346. [Google Scholar] [CrossRef] [PubMed]
- Bland, J.M.; Altman, D.G. Statistical Methods for Assessing Agreement Between Two Methods of Clinical Measurement. Lancet 1986, 1, 307–310. [Google Scholar] [CrossRef]
- Hopkins, W.G.; Schabort, E.J.; Hawley, J.A. Reliability of Power in Physical Performance Tests. Sports Med. 2001, 31, 211–234. [Google Scholar] [CrossRef]
- Jamnick, N.A.; Botella, J.; Pyne, D.B.; Bishop, D.J. Manipulating Graded Exercise Test Variables Affects the Validity of the Lactate Threshold and VO2peak. PLoS ONE 2018, 13, e0199794. [Google Scholar] [CrossRef]
- Pallarés, J.G.; Morán-Navarro, R.; Ortega, J.F.; Fernández-Elías, V.E.; Mora-Rodriguez, R. Validity and Reliability of Ventilatory and Blood Lactate Thresholds in Well-Trained Cyclists. PLoS ONE 2016, 11, e0163389. [Google Scholar] [CrossRef] [PubMed]
- Murgatroyd, S.R.; Wylde, L.A.; Cannon, D.T.; Ward, S.A.; Rossiter, H.B. A ‘Ramp-Sprint’ Protocol to Characterise Indices of Aerobic Function and Exercise Intensity Domains in a Single Laboratory Test. Eur. J. Appl. Physiol. 2014, 114, 1863–1874. [Google Scholar] [CrossRef]
- Stratton, E.; O’Brien, B.J.; Harvey, J.; Blitvich, J.; McNicol, A.J.; Janissen, D.; Paton, C.; Knez, W. Treadmill Velocity Best Predicts 5000-m Run Performance. Int. J. Sports Med. 2009, 30, 40–45. [Google Scholar] [CrossRef] [PubMed]
- Weston, S.B.; Gabbett, T.J. Reproducibility of Ventilation of Thresholds in Trained Cyclists during Ramp Cycle Exercise. J. Sci. Med. Sport 2001, 4, 357–366. [Google Scholar] [CrossRef] [PubMed]
- Lucía, A.; Pardo, J.; Durántez, A.; Hoyos, J.; Chicharro, J.L. Physiological Differences Between Professional and Elite Road Cyclists. Int. J. Sports Med. 1998, 19, 342–348. [Google Scholar] [CrossRef] [PubMed]
- Nimmerichter, A.; Williams, C.; Bachl, N.; Eston, R. Evaluation of a Field Test to Assess Performance in Elite Cyclists. Int. J. Sports Med. 2010, 31, 160–166. [Google Scholar] [CrossRef]
- Shrout, P.E.; Fleiss, J.L. Intraclass Correlations: Uses in Assessing Rater Reliability. Psychol. Bull. 1979, 86, 420–428. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.M.; Lee, J.; Chung, C.Y.; Ahn, S.; Sung, K.H.; Kim, T.W.; Lee, H.J.; Park, M.S. Pitfalls and important issues in testing reliability using intraclass correlation coefficients in orthopaedic research. Clin. Orthop. Surg. 2012, 4, 149–155. [Google Scholar] [CrossRef]
- Czuba, M.; Zając, A.; Cholewa, J.; Poprzęcki, S.; Waśkiewicz, Z.; Mikołajec, K. Lactate threshold (D-max method) and maximal lactate steady state in cyclists. J. Hum. Kinet. 2009, 21, 49–56. [Google Scholar] [CrossRef]
- Hauser, T.; Adam, J.; Schulz, H. Comparison of Selected Lactate Threshold Parameters with Maximal Lactate Steady State in Cycling. Int. J. Sports Med. 2014, 35, 517–521. [Google Scholar] [CrossRef] [PubMed]
- Grossl, T.; De Lucas, R.D.; De Souza, K.M.; Guglielmo, L.G.A. Maximal Lactate Steady-State and Anaerobic Thresholds from Different Methods in Cyclists. Eur. J. Sport Sci. 2012, 12, 161–167. [Google Scholar] [CrossRef]
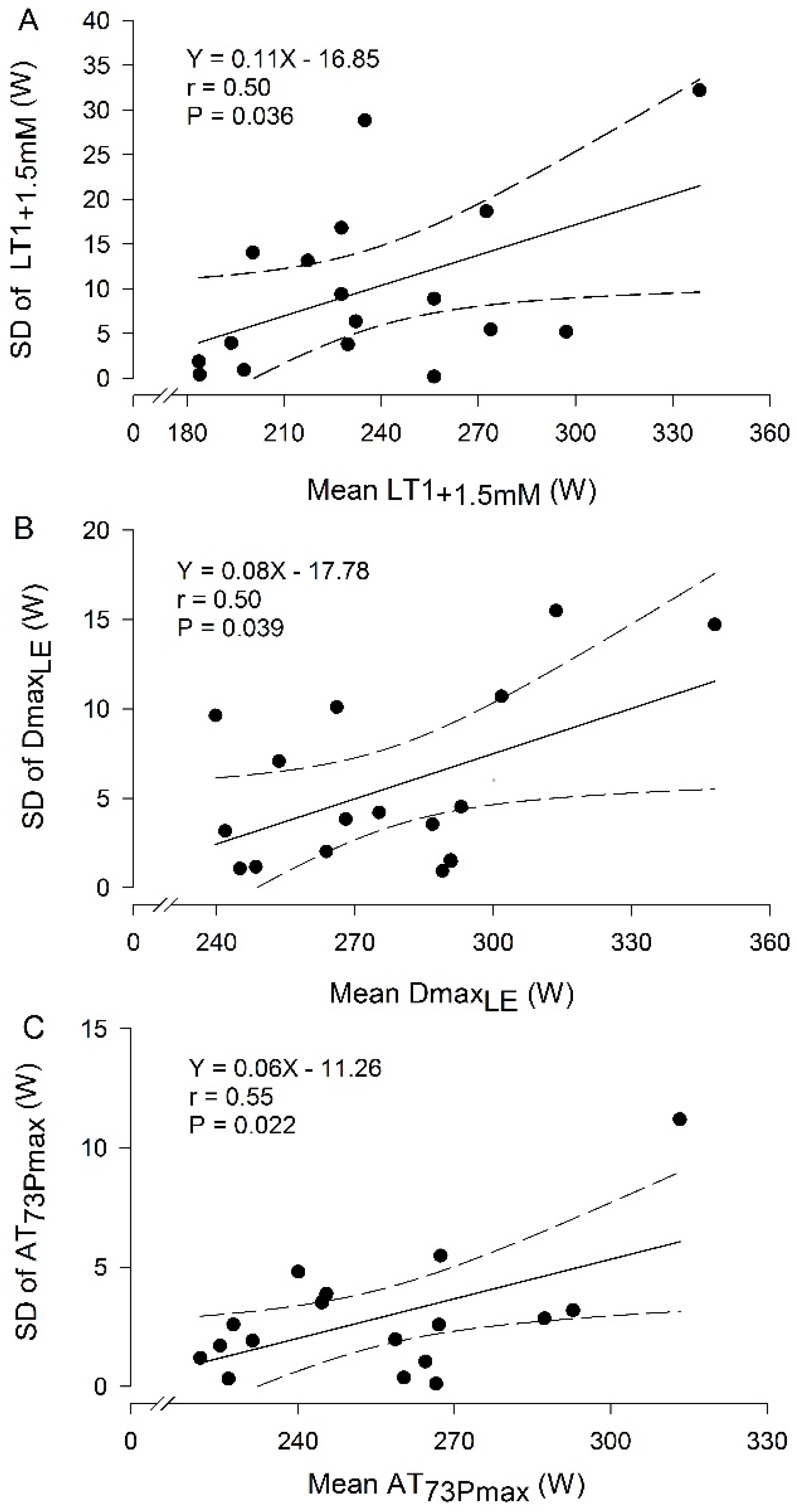
| Mean ± SD | Difference | ICC | Bland Altman | Intra-Subject SD | Intra-Subject CV (%) | SEM | MDC | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MMCT1 | MMCT2 | p | 90% CI | ES | p | r | Bias | LoA | ||||||
| AT73Pmax | Workload (W) | 254 ± 25 | 256 ± 28 | 0.20 | −3.97; 0.52 | 0.310 | <0.001 | 0.986 | 1.72 | −8.67; 12.11 | 1.97 | 1.08 | 3.75 | 10.39 |
| HR (beats·min−1) | 146 ± 10 | 145 ± 8 | 0.66 | −1.66; 2.79 | 0.102 | <0.001 | 0.902 | −0.56 | −10.86; 9.73 | 1.10 | 1.10 | 3.72 | 10.30 | |
| DmaxLE | Workload (W) | 275 ± 27 | 280 ± 31 | 0.02 § | −9.46; −1.99 | 0.618 | <0.001 | 0.972 | 5.73 | −11.56; 23.01 | 4.11 | 1.96 | 6.24 | 17.29 |
| HR (beats·min−1) | 153 ± 10 | 154 ± 8 | 0.52 | −3.79; 1.71 | 0.153 | <0.001 | 0.849 | 1.04 | −11.68; 13.76 | 1.85 | 1.66 | 4.59 | 12.72 | |
| AT86HRmax | Workload (W) | 267 ± 32 | 273 ± 36 | 0.13 | −13.20; 0.66 | 0.365 | <0.001 | 0.954 | 6.27 | −25.78; 38.31 | 5.20 * | 2.94 * | 11.56 | 32.05 |
| HR (beats·min−1) | 151 ± 7 | 152 ± 7 | 0.09 | −2.18; −0.45 | 0.420 | <0.001 | 0.949 | 1.11 | −3.83; 6.05 | 1.45 | 0.94 | 1.78 | 4.94 | |
| LT3.5mM | Workload (W) | 261 ± 36 | 265 ± 34 | 0.29 | −10.01; 2.30 | 0.253 | <0.001 | 0.965 | 3.86 | −24.65; 32.36 | 4.68 * | 3.08 * | 10.28 | 28.50 |
| HR (beats·min−1) | 148 ± 14 | 148 ± 9 | 0.99 | −3.62; 3.69 | 0.004 | <0.001 | 0.798 | −0.04 | −16.95; 16.87 | 3.44 *$ | 3.14 $* | 6.10 | 16.91 | |
| LT2 | Workload (W) | 240 ± 30 | 242 ± 32 | 0.57 | −9.01; 4.55 | 0.132 | <0.001 | 0.958 | 2.23 | −29.17; 33.62 | 3.42 | 3.14 * | 11.32 | 31.39 |
| HR (beats·min−1) | 141 ± 12 | 141 ± 9 | 0.65 | −2.25; 3.90 | 0.108 | <0.001 | 0.812 | −0.82 | −15.03; 13.38 | 2.80 * | 2.41 $* | 5.13 | 14.21 | |
| LT4mM | Workload (W) | 271 ± 39 | 276 ± 36 | 0.29 | −10.80; 2.42 | 0.256 | <0.001 | 0.832 | 4.19 | −26.39; 34.77 | 5.44 * | 3.19 * | 11.03 | 30.58 |
| HR (beats·min−1) | 152 ± 14 | 152 ± 9 | 0.95 | −4.02; 3.75 | 0.014 | <0.001 | 0.793 | 0.13 | −17.87; 18.14 | 3.61 *$† | 3.24 $*† | 6.49 | 18.00 | |
| LE+1.5mM | Workload (W) | 240 ± 32 | 242 ± 32 | 0.46 | −8.97; 3.52 | 0.176 | <0.001 | 0.962 | 2.72 | −26.19; 31.63 | 5.11 * | 3.44 *† | 10.42 | 28.91 |
| HR (beats·min−1) | 141 ± 12 | 141 ± 10 | 0.69 | −2.36; 3.81 | 0.094 | <0.001 | 0.833 | −0.72 | −15.01; 13.57 | 2.60 * | 2.22 $* | 5.15 | 14.29 | |
| Dmax0.4 | Workload (W) | 277 ± 35 | 279 ± 34 | 0.62 | −10.17; 5.59 | 0.117 | <0.001 | 0.954 | 2.29 | −34.18; 38.76 | 7.28 * | 3.70 * | 13.16 | 36.47 |
| HR (beats·min−1) | 153 ± 13 | 154 ± 9 | 0.87 | −4.06; 3.37 | 0.037 | <0.001 | 0.786 | 0.34 | −16.86; 17.55 | 3.39 *$† | 2.80 $*† | 6.21 | 17.20 | |
| LT1+1.5mM | Workload (W) | 235 ± 37 | 238 ± 48 | 0.47 | −11.76; 4.80 | 0.169 | <0.001 | 0.945 | 3.48 | −34.86; 41.82 | 4.95 * | 4.03 *† | 13.83 | 38.34 |
| HR (beats·min−1) | 140 ± 12 | 140 ± 10 | 0.84 | −2.59; 3.30 | 0.049 | <0.001 | 0.810 | −0.36 | −14.00; 13.29 | 2.56 *$† | 2.70 $* | 4.92 | 13.65 | |
| Mean Differences | Pearson | Bland Altman (W) | SEE (W) | ||
|---|---|---|---|---|---|
| p | r | Bias (Mean ± SD) | LoA | ||
| AT73Pmax | 0.001 | 0.94 | −16.6 ± 16.8 | −49.5; 16.2 | 16.8 |
| DmaxLE | 0.295 | 0.95 | 4.7 ± 16.2 | −27.1; 36.4 | 15.7 |
| AT86HRmax | 0.491 | 0.93 | −2.9 ± 16.2 | −34.6; 28.9 | 18.3 |
| LT3.5mM | 0.117 | 0.93 | −9.2 ± 22.1 | −52.4; 34.0 | 18.0 |
| LT2 | <0.001 | 0.94 | −31.4 ± 17.3 | −65.3; 2.4 | 16.4 |
| LT4mM | 0.835 | 0.93 | 1.3 ± 24 | −46.0; 48.6 | 18.7 |
| LE+1.5mM | <0.001 | 0.91 | −31.0 ± 23 | −76.1; 14.1 | 20.7 |
| Dmax0.4 | 0.222 | 0.95 | 5.4 ± 17.0 | −28.0; 38.8 | 15.9 |
| LT1+1.5mM | <0.001 | 0.88 | −38.0 ± 25.6 | −88.2; 12.3 | 23.2 |
| Correction Equation | Bland Altman (W) | ||
|---|---|---|---|
| Bias (Mean ± SD) | LoA | ||
| LT1+1.5mM | Corrected LT1+1.5mM = 33.76 + (0.999 ∗ LT1+1.5mM) | −4.4 ± 25.60 | −54.61; 45.74 |
| LE+1.5mM | Corrected LE+1.5mM = 6.643+(1.089 ∗ LE+1.5mM) | −3.22 ± 24.23 | −50.71; 44.28 |
| LT2 | Corrected LT2 = 4.794+ (1.110 ∗ LT2) | −0.56 ± 18.11 | −36.06; 34.95 |
| LT3.5mM | Corrected LT3.5mM = 34.088+ (0.894 ∗ LT3.5mM) | −2.56 ± 20.49 | −42.71; 37.60 |
| AT73Pmax | Corrected AT73Pmax = −69.893 + (1.332 ∗ AT73Pmax) | −2.98 ± 18.56 | −39.36; 33.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Llodio, I.; Yanci, J.; Usandizaga, M.; Larrea, A.; Iturricastillo, A.; Cámara, J.; Granados, C. Repeatability and Validity of Different Methods to Determine the Anaerobic Threshold Through the Maximal Multistage Test in Male Cyclists and Triathletes. J. Funct. Morphol. Kinesiol. 2025, 10, 9. https://doi.org/10.3390/jfmk10010009
Llodio I, Yanci J, Usandizaga M, Larrea A, Iturricastillo A, Cámara J, Granados C. Repeatability and Validity of Different Methods to Determine the Anaerobic Threshold Through the Maximal Multistage Test in Male Cyclists and Triathletes. Journal of Functional Morphology and Kinesiology. 2025; 10(1):9. https://doi.org/10.3390/jfmk10010009
Chicago/Turabian StyleLlodio, Iñaki, Javier Yanci, Mikel Usandizaga, Auritz Larrea, Aitor Iturricastillo, Jesús Cámara, and Cristina Granados. 2025. "Repeatability and Validity of Different Methods to Determine the Anaerobic Threshold Through the Maximal Multistage Test in Male Cyclists and Triathletes" Journal of Functional Morphology and Kinesiology 10, no. 1: 9. https://doi.org/10.3390/jfmk10010009
APA StyleLlodio, I., Yanci, J., Usandizaga, M., Larrea, A., Iturricastillo, A., Cámara, J., & Granados, C. (2025). Repeatability and Validity of Different Methods to Determine the Anaerobic Threshold Through the Maximal Multistage Test in Male Cyclists and Triathletes. Journal of Functional Morphology and Kinesiology, 10(1), 9. https://doi.org/10.3390/jfmk10010009








