Learning to Cycle: Why Is the Balance Bike More Efficient than the Bicycle with Training Wheels? The Lyapunov’s Answer
Abstract
:1. Introduction
2. Materials and Methods
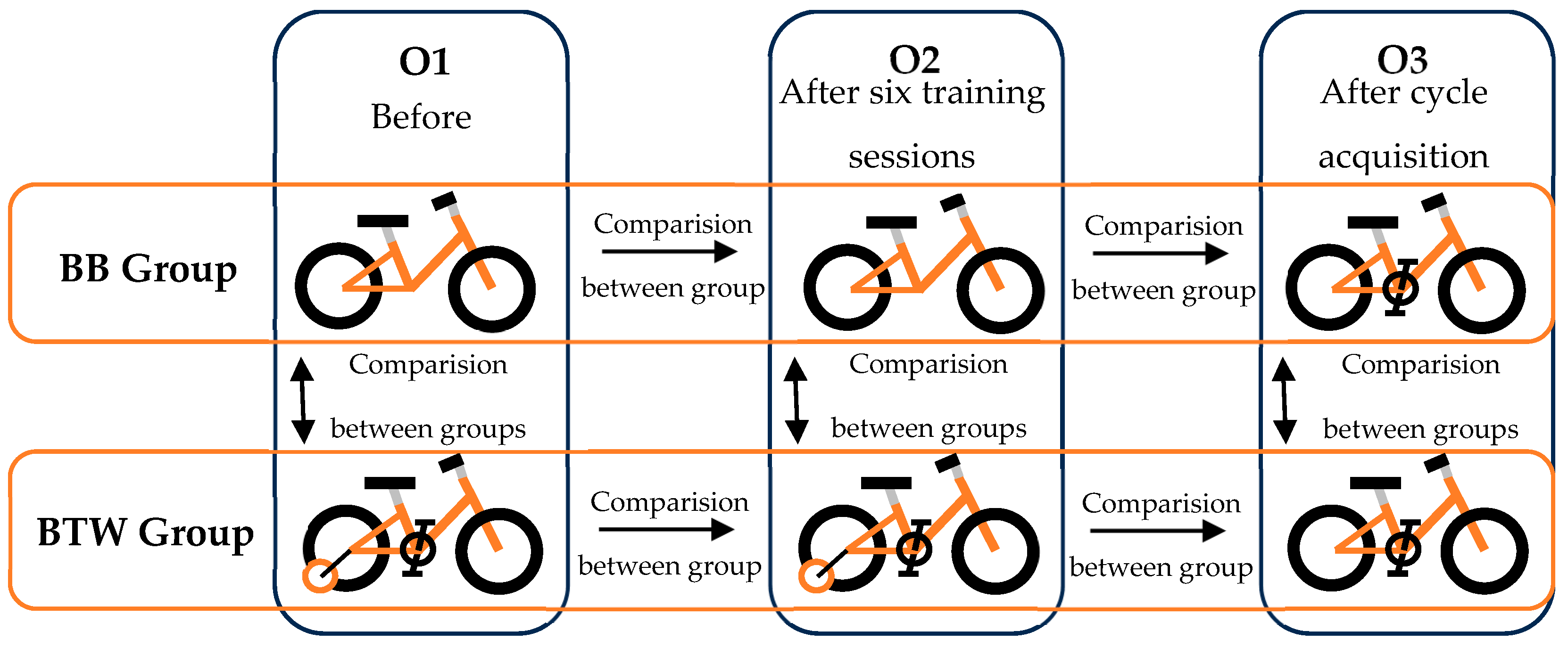
2.1. Study Design
2.2. Participants
2.3. Bicycle Equipment
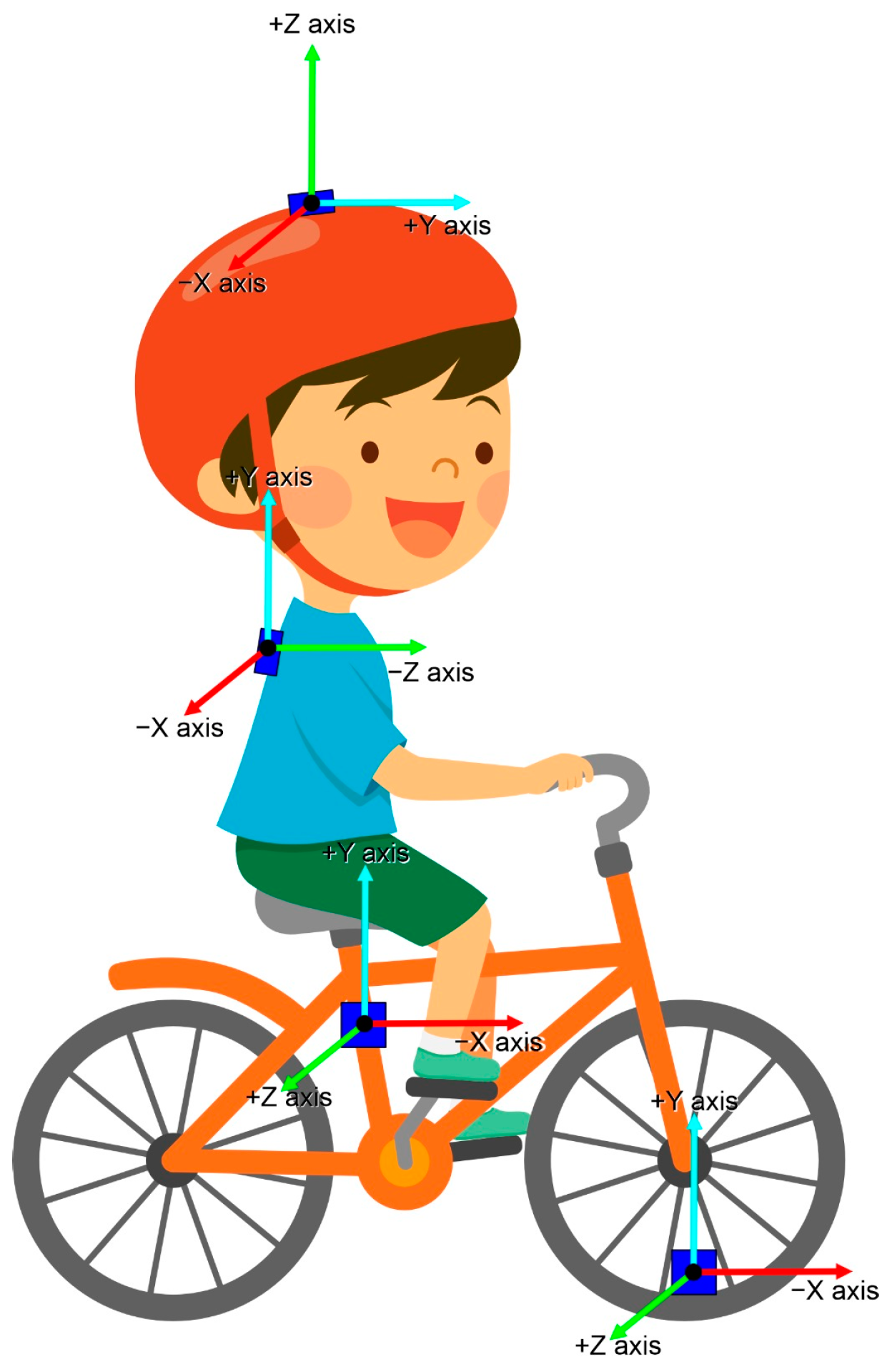
2.4. Data Collection and Protocols
2.5. Data and Statistical Treatment
3. Results
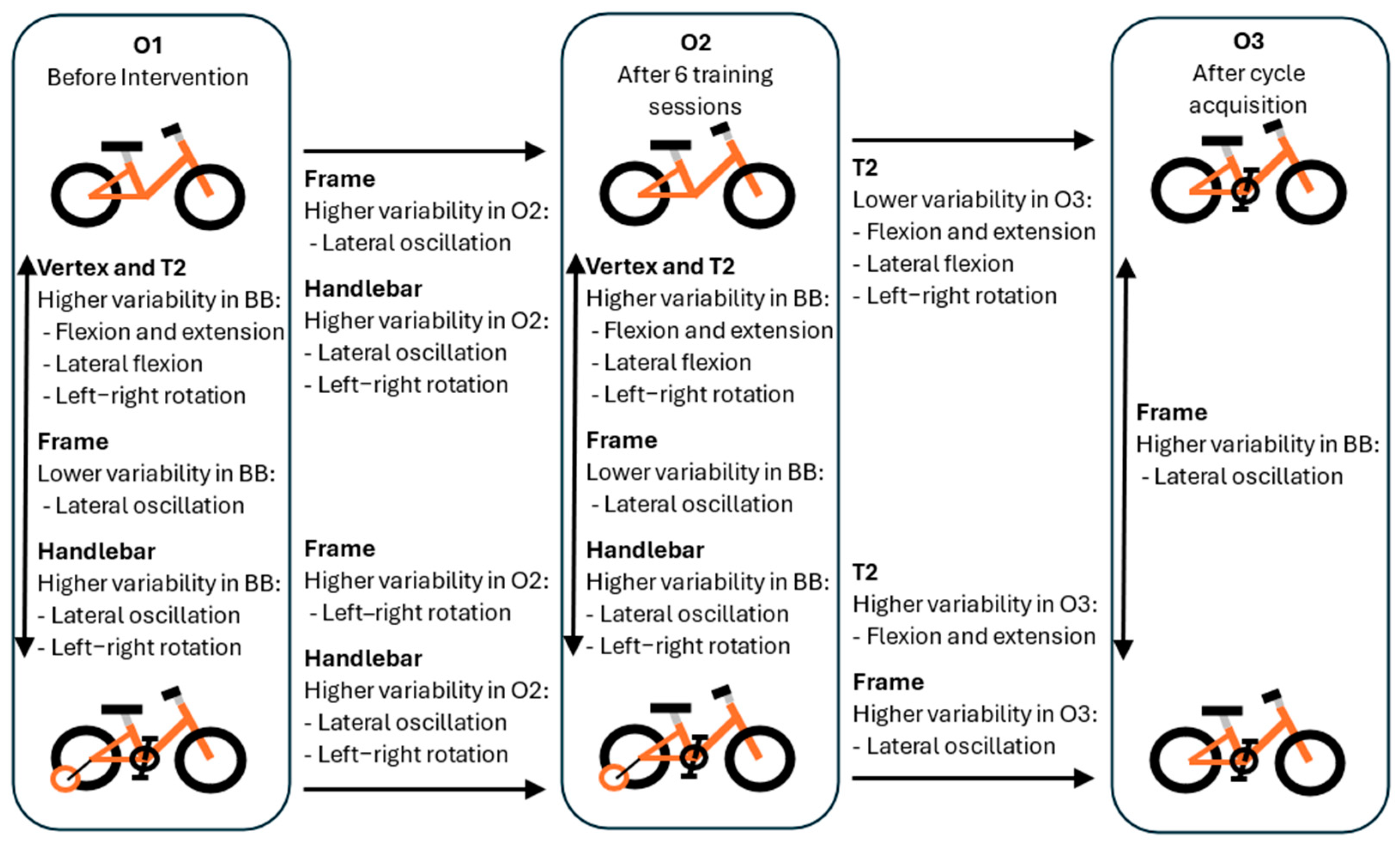
3.1. Comparisons Between Evaluation Moments
3.2. Comparisons Between Groups
3.3. Comparisons to Children That Did Not Acquire the Skill of Cycling Independently
4. Discussion
4.1. Pratical Aplications
4.2. Strengths, Limitations, and Considerations for Future Studies
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hulteen, R.M.; Morgan, P.J.; Barnett, L.M.; Stodden, D.F.; Lubans, D.R. Development of Foundational Movement Skills: A Conceptual Model for Physical Activity Across the Lifespan. Sports Med. 2018, 48, 1533–1540. [Google Scholar] [CrossRef] [PubMed]
- Kavanagh, J.A.; Issartel, J.; Moran, K. Quantifying cycling as a foundational movement skill in early childhood. J. Sci. Med. Sport 2020, 23, 171–175. [Google Scholar] [CrossRef] [PubMed]
- Ramírez-Vélez, R.; García-Hermoso, A.; Agostinis-Sobrinho, C.; Mota, J.; Santos, R.; Correa-Bautista, J.E.; Amaya-Tambo, D.C.; Villa-González, E. Cycling to School and Body Composition, Physical Fitness, and Metabolic Syndrome in Children and Adolescents. J. Pediatr. 2017, 188, 57–63. [Google Scholar] [CrossRef] [PubMed]
- Mercê, C.; Pereira, J.V.; Branco, M.; Catela, D.; Cordovil, R. Training programmes to learn how to ride a bicycle independently for children and youths: A systematic review. Phys. Educ. Sport Pedagog. 2021, 28, 530–545. [Google Scholar] [CrossRef]
- Karabaic, L. Putting the Fun Before the Wonk: Using Bike Fun to Diversify Bike Ridership. 2016. Available online: http://archives.pdx.edu/ds/psu/18207 (accessed on 12 September 2024).
- O’Brien, E.; Pickering, T.; Asmar, R.; Myers, M.; Parati, G.; Staessen, J.; Mengden, T.; Imai, Y.; Waeber, B.; Palatini, P.; et al. Working Group on Blood Pressure Monitoring of the European Society of Hypertension International Protocol for validation of blood pressure measuring devices in adults. Blood Press. Monit. 2002, 7, 3–17. [Google Scholar] [CrossRef]
- Zeuwts, L.; Deconinck, F.; Vansteenkiste, P.; Cardon, G.; Lenoir, M. Understanding the development of bicycling skills in children: A systematic review. Saf. Sci. 2020, 123, 104562. [Google Scholar] [CrossRef]
- Zeuwts, L.; Ducheyne, F.; Vansteenkiste, P.; D’Hondt, E.; Cardon, G.; Lenoir, M. Associations between cycling skill, general motor competence and body mass index in 9-year-old children. Ergonomics 2015, 58, 160–171. [Google Scholar] [CrossRef]
- Mercê, C.; Branco, M.; Catela, D.; Lopes, F.; Cordovil, R. Learning to Cycle: From Training Wheels to Balance Bike. Int. J. Environ. Res. Public Health 2022, 19, 1814. [Google Scholar] [CrossRef]
- Burt, T.L.; Porretta, D.P.; Klein, R.E. Use of Adapted Bicycles on the Learning of Conventional Cycling by Children with Mental Retardation. Educ. Train. Dev. Disabil. 2007, 42, 364–379. [Google Scholar]
- Cain, S.M.; Ulrich, D.A.; Perkins, N.C. Using Measured Bicycle Kinematics to Quantify Increased Skill as a Rider Learns to Ride a Bicycle. In Proceedings of the ASME 2012 5th Annual Dynamic Systems and Control Conference Joint with the JSME 2012 11th Motion and Vibration Conference, Fort Lauderdale, FL, USA, 17–19 October 2012; pp. 195–199. [Google Scholar]
- Ballantine, R.; Grant, R. The Ultimate Bicycle Book; Dorling Kindersley: London, UK, 1992. [Google Scholar]
- Mercê, C.; Davids, K.; Catela, D.; Branco, M.; Correia, V.; Cordovil, R. Learning to cycle: A constraint-led intervention programme using different cycling task constraints. Phys. Educ. Sport Pedagog. 2023, 1–14. [Google Scholar] [CrossRef]
- Newell, K.M.; Mcdonald, P.V. Learning to Coordinate Redundant Biomechanical Degrees of Freedom. In Interlimb Coordination: Neural, Dynamical, and Cognitive Constraints; Swinnen, S., Massion, J., Heuer, H., Casaer, P., Eds.; Academic Press: London, UK, 1994. [Google Scholar]
- Temple, V.A.; Purves, P.L.; Misovic, R.; Lewis, C.J.; DeBoer, C. Barriers and Facilitators for Generalizing Cycling Skills Learned at Camp to Home. Adapt. Phys. Act. Q. 2016, 33, 48–65. [Google Scholar] [CrossRef]
- Hauck, J.; Jeong, I.; Esposito, P.; MacDonald, M.; Hornyak, J.; Argento, A.; Ulrich, D.A. Benefits of Learning to Ride a Two-Wheeled Bicycle for Adolescents with Down Syndrome and Autism Spectrum Disorder. PALAESTRA 2017, 31, 35. [Google Scholar]
- MacDonald, M.; Esposito, P.; Hauck, J.; Jeong, I.; Hornyak, J.; Argento, A.; Ulrich, D.A. Bicycle Training for Youth with Down Syndrome and Autism Spectrum Disorders. Focus Autism Other Dev. Disabil. 2012, 27, 12–21. [Google Scholar] [CrossRef]
- Hawks, Z.; Constantino, J.N.; Weichselbaum, C.; Marrus, N. Accelerating Motor Skill Acquisition for Bicycle Riding in Children with ASD: A Pilot Study. J. Autism Dev. Disord. 2020, 50, 342–348. [Google Scholar] [CrossRef] [PubMed]
- Ulrich, D.A.; Burghardt, A.R.; Lloyd, M.; Tiernan, C.; Hornyak, J.E. Physical activity benefits of learning to ride a two-wheel bicycle for children with Down syndrome: A randomized trial. Phys. Ther. 2011, 91, 1463–1477. [Google Scholar] [CrossRef] [PubMed]
- Shim, A.L.; Norman, S. Incorporating Pedal-less Bicycles into a Pre-K through Third-grade Curriculum to Improve Stability in Children. J. Phys. Educ. Recreat. Danc. 2015, 86, 50–51. [Google Scholar] [CrossRef]
- van Emmerik, R.E.A.; van Wegen, E.E.H. On the Functional Aspects of Variability in Postural Control. Exerc. Sport Sci. Rev. 2002, 30, 177–183. [Google Scholar] [CrossRef]
- Stergiou, N.; Harbourne, R.T.; Cavanaugh, J.T. Optimal Movement Variability: A New Theoretical Perspective for Neurologic Physical Therapy. J. Neurol. Phys. Ther. 2006, 30, 120–129. [Google Scholar] [CrossRef]
- Chow, J.Y.; Davids, K.; Button, C.; Renshaw, I. Nonlinear Pedagogy in Skill Acquisition: An Introduction, 2nd ed.; Routledge: New York, NY, USA, 2022; pp. 1–159. [Google Scholar]
- Latash, M.L.; Scholz, J.P.; Schöner, G. Motor control strategies revealed in the structure of motor variability. Exerc. Sport Sci. Rev. 2002, 30, 26–31. [Google Scholar] [CrossRef]
- Davids, K.; Button, C.; Bennett, S. Dynamics of Skill Acquisition: A Constraints-Led Approach; Human Kinetics: Champaign, IL, USA, 2008; pp. 1–28. [Google Scholar]
- Correia, V.; Carvalho, J.; Araújo, D.; Pereira, E.; Davids, K. Principles of nonlinear pedagogy in sport practice. Phys. Educ. Sport Pedagog. 2019, 24, 117–132. [Google Scholar] [CrossRef]
- Kelso, J.A.S. Dynamic Patterns: The Self-Organization of Brain and Behavior; MIT Press: Cambridge, MA, USA, 1995; pp. 1–28. 334p. [Google Scholar]
- Kelso, S. Coordination Dynamics. In Encyclopedia of Complexity and Systems Science; Meyers, R.A., Ed.; Springer: New York, NY, USA, 2009; pp. 1537–1564. [Google Scholar]
- Newell, K.M. Constraints on the development of coordination. In Motor Development in Children: Aspects of Coordination and Control; Wade, M.G., Whiting, H.T.A., Eds.; Martinus Nijhoff: Dordrecht, The Netherlands, 1986; pp. 341–360. [Google Scholar]
- Button, C.; Seifert, L.; Chow, J.Y.; Araujo, D.; Davids, K. Dynamics of Skill Acquisition: An Ecological Dynamics Approach; Human Kinetics Publishers: Champaign, IL, USA, 2020. [Google Scholar]
- da Costa, C.S.; Batistão, M.V.; Rocha, N.A. Quality and structure of variability in children during motor development: A systematic review. Res. Dev. Disabil. 2013, 34, 2810–2830. [Google Scholar] [CrossRef] [PubMed]
- Webber, C.L.; Marwan, N. (Eds.) Recurrence Quantification Analysis: Theory and Best Practices; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Azami, H.; Rostaghi, M.; Abásolo, D.; Escudero, J. Refined Composite Multiscale Dispersion Entropy and its Application to Biomedical Signals. IEEE Trans. Biomed. Eng. 2017, 64, 2872–2879. [Google Scholar] [CrossRef] [PubMed]
- Yentes, J.M.; Raffalt, P.C. Entropy Analysis in Gait Research: Methodological Considerations and Recommendations. Ann. Biomed. Eng. 2021, 49, 979–990. [Google Scholar] [CrossRef] [PubMed]
- Kędziorek, J.; Błażkiewicz, M. Nonlinear Measures to Evaluate Upright Postural Stability: A Systematic Review. Entropy 2020, 22, 1357. [Google Scholar] [CrossRef]
- Mehdizadeh, S. The largest Lyapunov exponent of gait in young and elderly individuals: A systematic review. Gait Posture 2018, 60, 241–250. [Google Scholar] [CrossRef]
- Harbourne, R.T.; Stergiou, N. Nonlinear analysis of the development of sitting postural control. Dev. Psychobiol. 2003, 42, 368–377. [Google Scholar] [CrossRef]
- Smith, B.A.; Stergiou, N.; Ulrich, B.D. Lyapunov exponent and surrogation analysis of patterns of variability: Profiles in new walkers with and without down syndrome. Mot. Control 2010, 14, 126–142. [Google Scholar] [CrossRef]
- Chow, J.Y.; Davids, K.; Button, C.; Shuttleworth, R.; Renshaw, I.; Araújo, D. The role of nonlinear pedagogy in physical education. Rev. Educ. Res. 2007, 77, 251–278. [Google Scholar] [CrossRef]
- Becker, A.; Jenny, S.E. No Need for Training Wheels: Ideas for Including Balance Bikes in Elementary Physical Education. J. Phys. Educ. Recreat. Danc. 2017, 88, 14–21. [Google Scholar] [CrossRef]
- Norton, K. Standards for Anthropometry Assessment. In Kinanthropometry and Exercise Physiology; Routledge: London, UK, 2018; pp. 68–137. [Google Scholar]
- WHO. WHO Child Growth Standards based on length/height, weight and age. Acta Paediatr. Suppl. 2006, 450, 76–85. [Google Scholar] [CrossRef]
- Luz, C.; Rodrigues, L.P.; Almeida, G.; Cordovil, R. Development and validation of a model of motor competence in children and adolescents. J. Sci. Med. Sport 2016, 19, 568–572. [Google Scholar] [CrossRef] [PubMed]
- Whiteley, A.M.; Whiteley, J. The familiarization study in qualitative research: From theory to practice. Qual. Res. J. 2006, 6, 69–85. [Google Scholar] [CrossRef]
- Mercê, C.; Cordovil, R.; Catela, D.; Galdino, F.; Bernardino, M.; Altenburg, M.; António, G.; Brígida, N.; Branco, M. Learning to Cycle: Is Velocity a Control Parameter for Children’s Cycle Patterns on the Balance Bike? Children 2022, 9, 1937. [Google Scholar] [CrossRef] [PubMed]
- Shurtleff, T.L.; Engsberg, J.R. Changes in Trunk and Head Stability in Children with Cerebral Palsy after Hippotherapy: A Pilot Study. Phys. Occup. Ther. Pediatr. 2010, 30, 150–163. [Google Scholar] [CrossRef] [PubMed]
- Wolter, N.E.; Gordon, K.A.; Campos, J.L.; Vilchez Madrigal, L.D.; Pothier, D.D.; Hughes, C.O.; Papsin, B.C.; Cushing, S.L. BalanCI: Head-Referenced Cochlear Implant Stimulation Improves Balance in Children with Bilateral Cochleovestibular Loss. Audiol. Neurotol. 2020, 25, 60–71. [Google Scholar] [CrossRef]
- Li, Y.; Koldenhoven, R.M.; Liu, T.; Venuti, C.E. Age-related gait development in children with autism spectrum disorder. Gait Posture 2021, 84, 260–266. [Google Scholar] [CrossRef]
- Camomilla, V.; Bergamini, E.; Fantozzi, S.; Vannozzi, G. Trends Supporting the In-Field Use of Wearable Inertial Sensors for Sport Performance Evaluation: A Systematic Review. Sensors 2018, 18, 873. [Google Scholar] [CrossRef]
- Winter, L.; Bellenger, C.; Grimshaw, P.; Crowther, R.G. Analysis of Movement Variability in Cycling: An Exploratory Study. Sensors 2023, 23, 4972. [Google Scholar] [CrossRef]
- Zeng, Z.; Liu, Y.; Hu, X.; Tang, M.; Wang, L. Validity and Reliability of Inertial Measurement Units on Lower Extremity Kinematics During Running: A Systematic Review and Meta-Analysis. Sports Med.-Open 2022, 8, 86. [Google Scholar] [CrossRef]
- Kobsar, D.; Charlton, J.M.; Tse, C.T.F.; Esculier, J.-F.; Graffos, A.; Krowchuk, N.M.; Thatcher, D.; Hunt, M.A. Validity and reliability of wearable inertial sensors in healthy adult walking: A systematic review and meta-analysis. J. NeuroEng. Rehabil. 2020, 17, 62. [Google Scholar] [CrossRef]
- Clemente, F.; Badicu, G.; Hasan, U.; Akyildiz, Z.; Pino Ortega, J.; Silva, R.; Rico-González, M. Validity and reliability of inertial measurement units (IMUs) for jump height estimations: A systematic review. Hum. Mov. 2021, 23, 1–20. [Google Scholar] [CrossRef]
- 9DoF Razor IMU M0 Hookup Guide. Available online: https://learn.sparkfun.com/tutorials/9dof-razor-imu-m0-hookup-guide/all (accessed on 26 November 2024).
- Stins, J.F.; Michielsen, M.E.; Roerdink, M.; Beek, P.J. Sway regularity reflects attentional involvement in postural control: Effects of expertise, vision and cognition. Gait Posture 2009, 30, 106–109. [Google Scholar] [CrossRef]
- Donker, S.F.; Ledebt, A.; Roerdink, M.; Savelsbergh, G.J.P.; Beek, P.J. Children with cerebral palsy exhibit greater and more regular postural sway than typically developing children. Exp. Brain Res. 2008, 184, 363–370. [Google Scholar] [CrossRef] [PubMed]
- Budini, K.; Richards, J.; Cole, T.; Levine, D.; Trede, R.; George, L.S.; Selfe, J. An exploration of the use of Inertial Measurement Units in the assessment of dynamic postural control of the knee and the effect of bracing and taping. Physiother. Pract. Res. 2018, 39, 91–98. [Google Scholar] [CrossRef]
- Allum, J.H.; Carpenter, M.G. A speedy solution for balance and gait analysis: Angular velocity measured at the centre of body mass. Curr. Opin. Neurol. 2005, 18, 15–21. [Google Scholar] [CrossRef]
- Field, A. Discovering Statistics Using IBM SPSS Statistics; SAGE Publications: Thousand Oaks, CA, USA, 2013. [Google Scholar]
- Badihian, S.; Adihian, N.; Yaghini, O. The Effect of Baby Walker on Child Development: A Systematic Review. Iran. J. Child Neurol. 2017, 11, 1–6. [Google Scholar] [PubMed]
- Siegel, A.C.; Burton, R.V. Effects of baby walkers on motor and mental development in human infants. J. Dev. Behav. Pediatr. 1999, 20, 355–361. [Google Scholar] [CrossRef]
- Garrett, M.; McElroy, A.M.; Staines, A. Locomotor milestones and babywalkers: Cross sectional study. BMJ 2002, 324, 1494. [Google Scholar] [CrossRef]
- Chagas, P.S.C.; Fonseca, S.T.; Santos, T.R.T.; Souza, T.R.; Megale, L.; Silva, P.L.; Mancini, M.C. Effects of baby walker use on the development of gait by typically developing toddlers. Gait Posture 2020, 76, 231–237. [Google Scholar] [CrossRef]
- Withagen, R.; de Poel, H.J.; Araújo, D.; Pepping, G.-J. Affordances can invite behavior: Reconsidering the relationship between affordances and agency. New Ideas Psychol. 2012, 30, 250–258. [Google Scholar] [CrossRef]
- Waddington, C.H. The Strategy of the Genes; A Discussion of Some Aspects of Theoretical Biology; Allen & Unwin: London, UK, 1957; p. ix. 262p. [Google Scholar]
- Bernstein, N.A. The Co-Ordination and Regulation of Movements, 1st ed.; Pergamon Press: Oxford, NY, USA, 1967; p. xii. 196p. [Google Scholar]
- Berthouze, L.; Lungarella, M. Motor Skill Acquisition Under Environmental Perturbations: On the Necessity of Alternate Freezing and Freeing of Degrees of Freedom. Adapt. Behav. 2004, 12, 47–64. [Google Scholar] [CrossRef]
- Leech, K.A.; Roemmich, R.T.; Gordon, J.; Reisman, D.S.; Cherry-Allen, K.M. Updates in Motor Learning: Implications for Physical Therapist Practice and Education. Phys. Ther. 2021, 102, pzab250. [Google Scholar] [CrossRef]
- Kafri, M.; Atun-Einy, O. From Motor Learning Theory to Practice: A Scoping Review of Conceptual Frameworks for Applying Knowledge in Motor Learning to Physical Therapist Practice. Phys. Ther. 2019, 99, 1628–1643. [Google Scholar] [CrossRef]
- Mercê, C.; Branco, M.; Catela, D.; Lopes, F.; Rodrigues, L.P.; Cordovil, R. Learning to Cycle: Are Physical Activity and Birth Order Related to the Age of Learning How to Ride a Bicycle? Children 2021, 8, 487. [Google Scholar] [CrossRef]
- Schoen, S.A.; Ferrari, V.; Valdez, A. It’s Not Just about Bicycle Riding: Sensory-Motor, Social and Emotional Benefits for Children with and without Developmental Disabilities. Children 2022, 9, 1224. [Google Scholar] [CrossRef]
- Schedler, S.; Tenelsen, F.; Wich, L.; Muehlbauer, T. Effects of balance training on balance performance in youth: Role of training difficulty. BMC Sports Sci. Med. Rehabil. 2020, 12, 71. [Google Scholar] [CrossRef] [PubMed]
- Blodgett, J.M.; Cooper, R.; Pinto Pereira, S.M.; Hamer, M. Stability of Balance Performance from Childhood to Midlife. Pediatrics 2022, 150, e2021055861. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Yang, J.; Xi, F.; Xu, Z. Relationship between static and dynamic balance in 4-to-5-year-old preschoolers: A cross-sectional study. BMC Pediatr. 2024, 24, 295. [Google Scholar] [CrossRef]
- Moreno, F.J.; Caballero, C.; Barbado, D. Editorial: The role of movement variability in motor control and learning, analysis methods and practical applications. Front. Psychol. 2023, 14, 1260878. [Google Scholar] [CrossRef]
- Getchell, N.; Schott, N.; Brian, A. Motor Development Research: Designs, Analyses, and Future Directions. J. Mot. Learn. Dev. 2020, 8, 410–437. [Google Scholar] [CrossRef]
| Group | IMU | Movement Plane | O1 M ± SD | O2 M ± SD | O3 M ± SD |
|---|---|---|---|---|---|
| BB | Vertex | Sagittal | 58.82 ± 1.45 | 59.27 ± 1.03 | 58.50 ± 1.43 |
| Frontal | 57.85 ± 1.14 | 57.72 ± 0.87 | 56.64 ± 1.26 | ||
| Transverse | 56.51 ± 1.25 | 56.87 ± 1.04 | 55.63 ± 1.71 | ||
| T2 | Sagittal | 59.16 ± 1.51 | 58.48 ± 1.21 | 57.30 ± 0.99 | |
| Frontal | 56.61 ± 1.25 | 56.33 ± 0.77 | 55.39 ± 1.31 | ||
| Transverse | 57.36 ± 0.80 | 57.16 ± 0.65 | 56.18 ± 1.63 | ||
| Bicycle frame | Frontal | 54.32 ± 1.29 | 55.22 ± 0.72 | 55.86 ± 0.94 | |
| Handlebar | Frontal | 55.97 ± 1.08 | 57.33 ± 1.14 | 57.60 ± 1.48 | |
| Transverse | 55.84 ± 1.13 | 57.20 ± 1.14 | 57.72 ± 1.65 | ||
| BTW | Vertex | Sagittal | 56.60 ± 2.13 | 55.39 ± 1.35 | 58.41 ± 1.36 |
| Frontal | 55.18 ± 1.76 | 57.51 ± 1.13 | 56.22 ± 1.98 | ||
| Transverse | 53.91 ± 1.87 | 54.94 ± 1.35 | 54.37 ± 1.45 | ||
| T2 | Sagittal | 56.01 ± 1.82 | 56.28 ± 0.98 | 57.58 ± 0.78 | |
| Frontal | 52.58 ± 2.16 | 53.43 ± 1.21 | 54.55 ± 1.23 | ||
| Transverse | 55.02 ± 1.87 | 55.97 ± 1.70 | 55.79 ± 0.98 | ||
| Bicycle frame | Frontal | 57.52 ± 1.82 | 58.28 ± 1.49 | 55.01 ± 0.47 | |
| Handlebar | Frontal | 53.39 ± 2.12 | 55.35 ± 2.02 | 57.56 ± 1.10 | |
| Transverse | 53.54 ± 2.22 | 55.51 ± 1.66 | 57.68 ± 0.67 |
| Group | IMU | Movement Plane | O1 Versus O2 p, r, Direction Change | O2 Versus O3 p, r, Direction Change |
|---|---|---|---|---|
| BB | Vertex | Sagittal | ns | ns |
| Frontal | ns | ns | ||
| Transverse | ns | ns | ||
| T2 | Sagittal | ns | p = 0.034; r = 0.706; ↓ | |
| Frontal | ns | p = 0.004; r = 0.775; ↓ | ||
| Transverse | ns | p = 0.043; r = 0.682; ↓ | ||
| Bicycle frame | Frontal | p = 0.035; r = 0.588; ↑ | ns | |
| Handlebar | Frontal | p = 0.003; r = 0.748; ↑ | ns | |
| Transverse | p = 0.04; r = 0.576; ↑ | ns | ||
| BTW | Vertex | Sagittal | ns | ns |
| Frontal | ns | ns | ||
| Transverse | p = 0.025; r = 0.640; ↑ | ns | ||
| T2 | Sagittal | ns | p = 0.020; r = 0.790; ↑ | |
| Frontal | ns | ns | ||
| Transverse | ns | ns | ||
| Bicycle frame | Frontal | ns | p = 0.006; r = 0.865; ↑ | |
| Handlebar | Frontal | p = 0.009; r = 0.713; ↑ | ns | |
| Transverse | p = 0.012; r = 0.697; ↑ | ns |
| Groups | IMU | Movement Plane | O1 | O2 | O3 (in TB) |
|---|---|---|---|---|---|
| BB versus BTW | Vertex | Sagittal | p = 0.008; r = 0.541; ↑ | p = 0.001; r = 0.650; ↑ | ns |
| Frontal | p < 0.001; r = 0.689; ↑ | p < 0.001; r = 0.792; ↑ | ns | ||
| Transverse | p = 0.001; r = 0.653; ↑ | p = 0.008; r = 542; ↑ | ns | ||
| T2 | Sagittal | p < 0.001; r = 0.771; ↑ | p < 0.001; r = 0.720; ↑ | ns | |
| Frontal | p < 0.001; r = 0.771; ↑ | p < 0.001; r = 0.833; ↑ | ns | ||
| Transverse | p < 0.001; r = 0.654; ↑ | p = 0.034; r = 0.443; ↑ | ns | ||
| Bicycle frame | Frontal | p < 0.001; r = 0.730; ↓ | p < 0.001; r = 0.814; ↓ | p = 0.048; r = 0.519; ↑ | |
| Handlebar | Frontal | p = 0.001; r = 0.630; ↑ | p = 0.008; r = 0.538; ↑ | ns | |
| Transverse | p = 0.005; r = 0.570; ↑ | p = 0.009; r = 0.530; ↑ | ns |
| BTW Group | IMU | Movement Plane | O1 M ± SD | O2 M ± SD |
|---|---|---|---|---|
| Independent Riders of BTW group | Vertex | Sagittal | 56.72 ± 2.41 | 57.83 ± 1.18 |
| Frontal | 55.08 ± 1.96 | 55.25 ± 1.30 | ||
| Transverse | 54.07 ± 1.92 | 55.51 ± 1.43 | ||
| T2 | Sagittal | 56.14 ± 1.27 | 56.38 ± 1.07 | |
| Frontal | 52.48 ± 2.4 | 53.57 ± 1.37 | ||
| Transverse | 55.04 ± 2.12 | 56.21 ± 1.65 | ||
| Bicycle frame | Frontal | 57.43 ± 1.90 | 58.40 ± 1.66 | |
| Handlebar | Frontal | 53.96 ± 2.00 | 56.32 ± 1.12 | |
| Transverse | 54.18 ± 2.04 | 56.30 ± 0.98 | ||
| Non-Independent Riders of BTW group | Vertex | Sagittal | 56.28 ± 1.43 | 56.65 ± 0.26 |
| Frontal | 55.43 ± 1.39 | 54.09 ± 1.31 | ||
| Transverse | 53.49 ± 2.05 | 55.08 ± 1.29 | ||
| T2 | Sagittal | 55.65 ± 1.00 | 56.02 ± 0.80 | |
| Frontal | 52.84 ± 1.70 | 53.05 ± 0.69 | ||
| Transverse | 54.98 ± 1.37 | 55.30 ± 1.99 | ||
| Bicycle frame | Frontal | 57.78 ± 1.92 | 57.97 ± 1.03 | |
| Handlebar | Frontal | 51.86 ± 1.93 | 52.74 ± 1.45 | |
| Transverse | 51.83 ± 2.04 | 53.41 ± 1.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mercê, C.; Davids, K.; Cordovil, R.; Catela, D.; Branco, M. Learning to Cycle: Why Is the Balance Bike More Efficient than the Bicycle with Training Wheels? The Lyapunov’s Answer. J. Funct. Morphol. Kinesiol. 2024, 9, 266. https://doi.org/10.3390/jfmk9040266
Mercê C, Davids K, Cordovil R, Catela D, Branco M. Learning to Cycle: Why Is the Balance Bike More Efficient than the Bicycle with Training Wheels? The Lyapunov’s Answer. Journal of Functional Morphology and Kinesiology. 2024; 9(4):266. https://doi.org/10.3390/jfmk9040266
Chicago/Turabian StyleMercê, Cristiana, Keith Davids, Rita Cordovil, David Catela, and Marco Branco. 2024. "Learning to Cycle: Why Is the Balance Bike More Efficient than the Bicycle with Training Wheels? The Lyapunov’s Answer" Journal of Functional Morphology and Kinesiology 9, no. 4: 266. https://doi.org/10.3390/jfmk9040266
APA StyleMercê, C., Davids, K., Cordovil, R., Catela, D., & Branco, M. (2024). Learning to Cycle: Why Is the Balance Bike More Efficient than the Bicycle with Training Wheels? The Lyapunov’s Answer. Journal of Functional Morphology and Kinesiology, 9(4), 266. https://doi.org/10.3390/jfmk9040266








