The Geometric Configuration of Lubricant Recesses of the Polymer Sliding Layer of the Bearing
Abstract
:1. Introduction
1.1. Research Objectives
- To evaluate the performance of sliding layer with grease recesses of different geometries under a wide range of working loads;
- To evaluate the influence of frictional properties on the deformation behavior of the sliding layer;
- To evaluate the influence of the presence of lubricant in the recesses designed for it on the deformation behavior of the sliding layer.
1.2. Problem Context
1.2.1. Design Problems of Bridge Bearings
1.2.2. Material Problems of Antifriction Sliding Layers
1.3. Problem Description
2. Materials and Methods
2.1. Materials
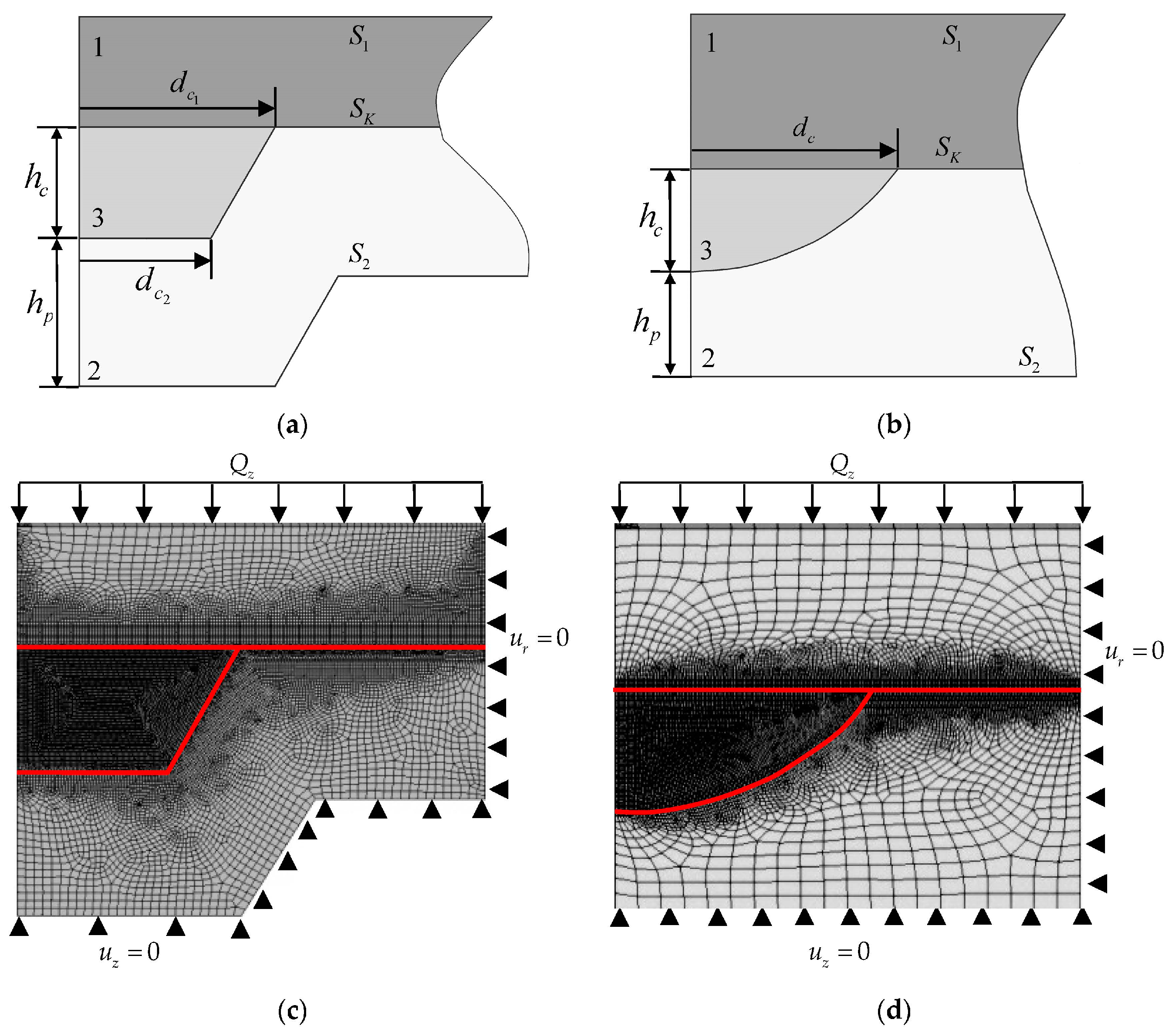
2.2. Model
2.3. Mathematical Boundary and Contact Conditions
- open contact (away from the contact area):
- friction slip:
- for static friction:
- therewith , ,
- for sliding friction:
- therewith , ,
- adhesive contact:
3. Results
4. Discussion
5. Conclusions
- -
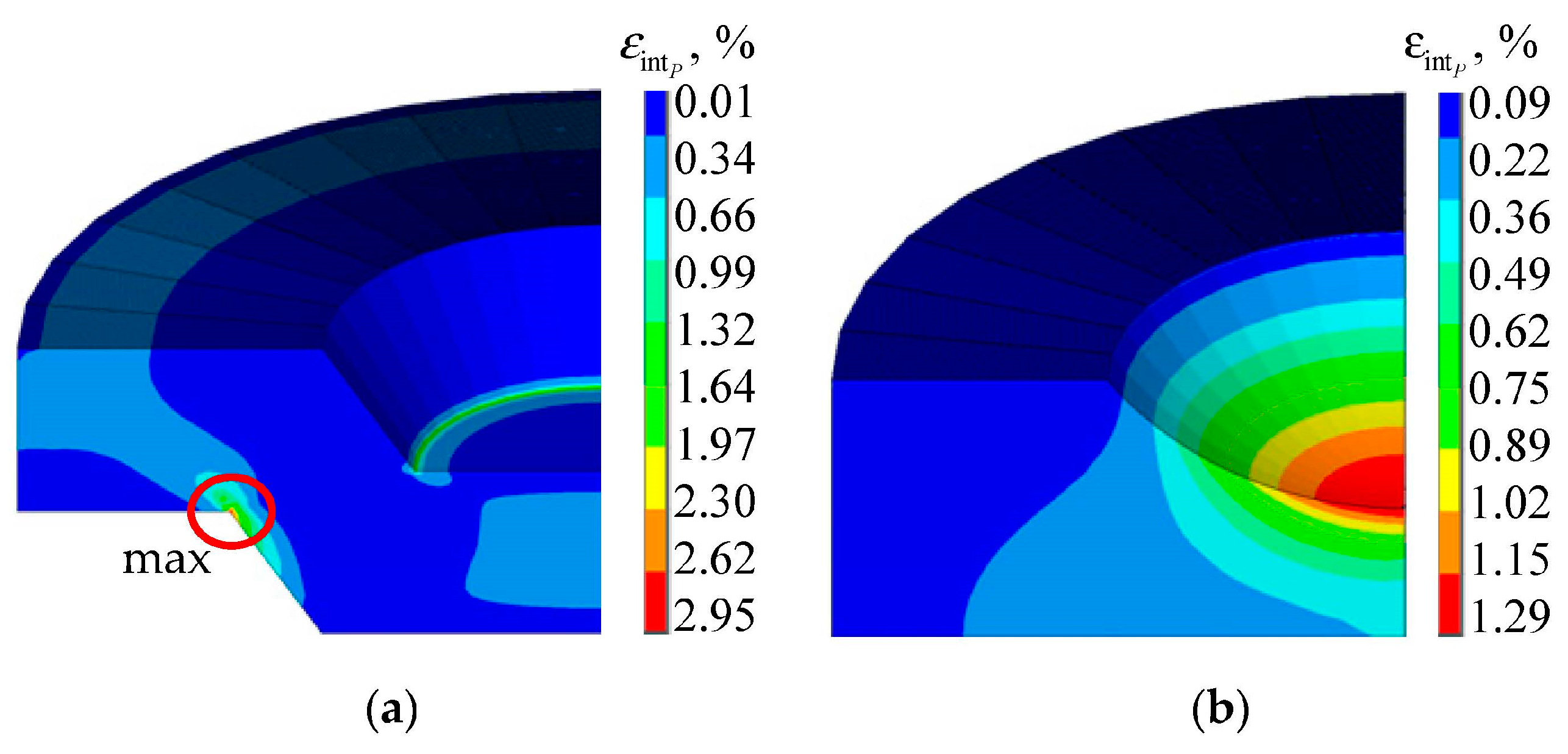
- When the cavities are not lubricated, there are significant changes in the cavity profiles. The annular grooves deform significantly but retain their geometry shape. Spherical cavities completely change their geometry under the action of a steel surface. This effect is observed because there is a void between the spherical notches/groove in the polymer layer and the steel plate, and the polymer deforms greatly under load due to its tendency to fill the void.
- -
- The steel-polymer friction coefficient has no effect on the deformation of the sliding layer (the difference is less than 1%). This effect is observed with and without lubrication in both cavity geometries.
- -
- The friction coefficient obtained experimentally is about six times lower than the reference approximation coefficient.
- -
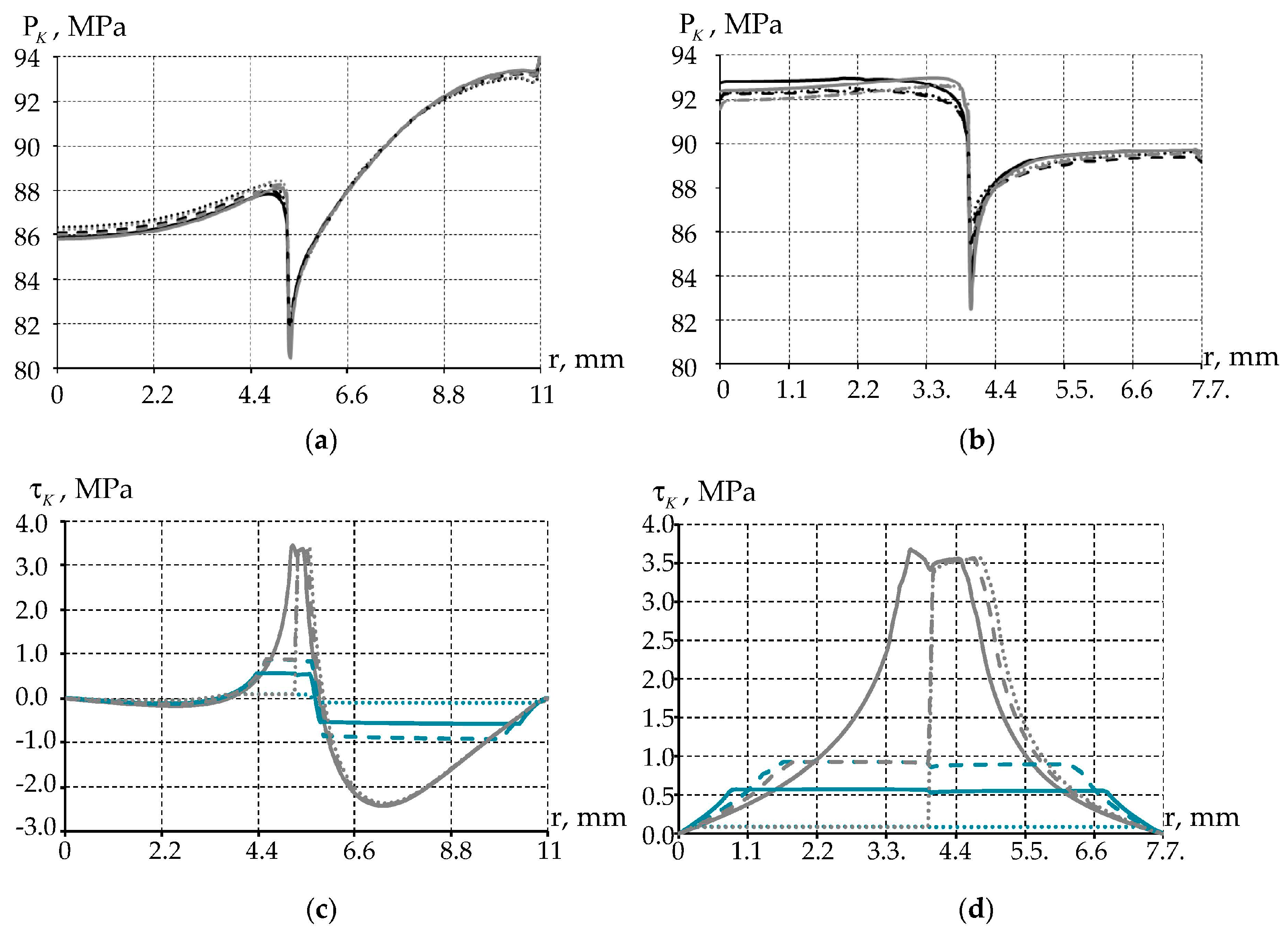
- It has the greatest influence on the tangential contact stress. At the experimental friction coefficient, the tangential contact stress is lower from ~74% to ~97% than at = 0.04, depending on the lubricant friction coefficient. The influence on contact pressure is <1% at almost all positions. And the plastic strain rate becomes <7.2%.
- -
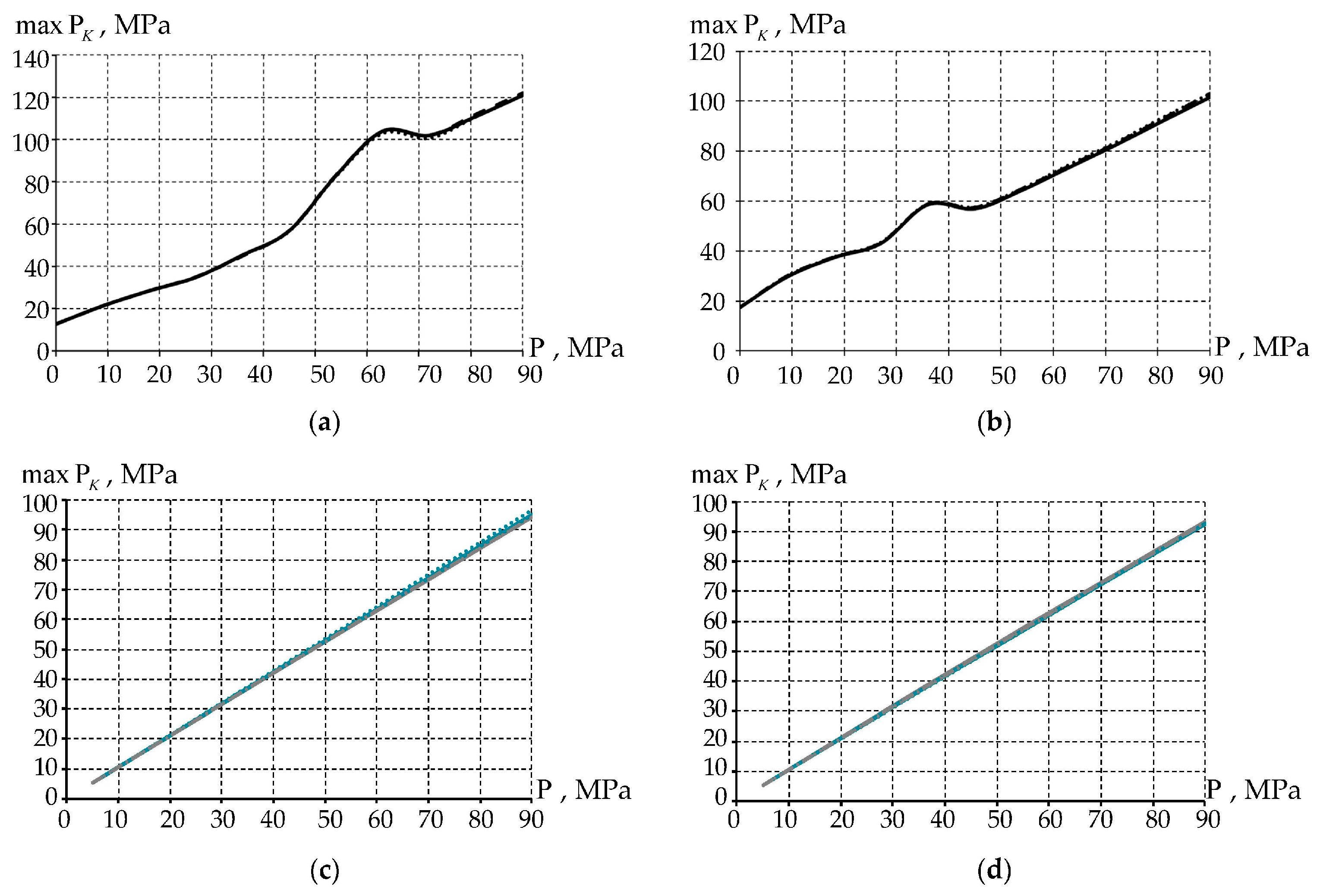
- Annular groove geometry has the greatest influence on plastic deformation intensity. It has the least influence on contact pressure, which is from 1.06% to 1.25% for = 0.04, and from 2.1% to 4.22% for = 0.00631. It has an influence on the contact pressure, which is from 5.35% to 6.28% for = 0.04 and from 4.49% to 5.04% for = 0.00631. Therefore, spherical notches have a number of advantages in comparison with annular grooves.
- -
- A significant influence of the set of friction coefficients of the lubricant and the interlayer on the contact parameters of the central part of the interlayer, with a single cutout for the lubricant, is shown.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tian, Y.; Wang, P.; Wang, M. Pressure Characteristics of Landslide-Generated Waves on Bridge Piers. Water 2023, 15, 3623. [Google Scholar] [CrossRef]
- Cooper, A.H.; Saunders, J.M. Road and bridge construction across gypsum karst in England. Eng. Geol. 2002, 65, 217–223. [Google Scholar] [CrossRef]
- Wang, L.; Yu, L.; Du, X.; Zhang, X.; Li, Z. Seismic Response of a PC Continuous Box Girder Bridge under Extreme Ambient Temperature. Sustainability 2023, 15, 14763. [Google Scholar] [CrossRef]
- Han, D.; Hosamo, H.; Ying, C.; Nie, R. A Comprehensive Review and Analysis of Nanosensors for Structural Health Monitoring in Bridge Maintenance: Innovations, Challenges, and Future Perspectives. Appl. Sci. 2023, 13, 11149. [Google Scholar] [CrossRef]
- Sonbul, O.S.; Rashid, M. Towards the Structural Health Monitoring of Bridges Using Wireless Sensor Networks: A Systematic Study. Sensors 2023, 23, 8468. [Google Scholar] [CrossRef]
- Adamov, A.A.; Kamenskikh, A.A.; Pankova, A.P.; Strukova, V.I. Comparative Analysis of the Work of Bridge Spherical Bearing at Different Antifriction Layer Locations. Lubricants 2022, 10, 207. [Google Scholar] [CrossRef]
- Qian, Y.; Sun, L.; Ai, L.; Zhou, Y.; Li, M. Theoretical Analysis of the Influence of Bearing Plate Position on the Bearing Performance of Soil around the CEP Antipull Force Double Pile. Buildings 2023, 13, 2613. [Google Scholar] [CrossRef]
- Nosov, Y.O.; Kamenskikh, A.A. Influence Analysis of Lubricant Recesses on the Working Capacity of the Bridge Span Spherical Bearing. Lubricants 2022, 10, 283. [Google Scholar] [CrossRef]
- Buckle, I.G.; Built, S.M. Cyclic Shear Energy Absorber. US4499694A, 19 February 1985. [Google Scholar]
- Fyfe, E.R.; Kelly, J.M. System and Apparatus for Limiting the Effect of Vibrations between a Structure and Its Foundation. US5014474A, 14 May 1991. [Google Scholar]
- Fyfe, E.R.; Slater, W.M.; Watson, R.J. Aseismic Bearing for Bridge Structures. US4617769A, 24 February 2004. [Google Scholar]
- Shaferman, I.M.; Gitman, E.M.; Doroshkevich, A.A.; Bukanov, V.V.; Kopytov, A.V.; Bukanova, E.V. Bearing. RU92667U1, 27 March 2010. (In Russian). [Google Scholar]
- Bukanov, V.V.; Ipanov, A.S.; Hatipov, S.A.; Adamov, A.A.; Ostrer, S.G. Bearing. RU146859U1, 20 October 2014. (In Russian). [Google Scholar]
- Zijun, C.; Jinzhao, G.; Yuan, G.; Wanliang, C. High Damping Rubber Bridge Damping Support. CN217419297U, 13 September 2022. [Google Scholar]
- Eggert, H.; Grote, J.; Kauschke, W. Lager im Bauwesen; Ernst & Sohn: Berlin, Germany, 1974. [Google Scholar]
- Shepitko, T.V.; Lutsky, S.Y.; Nak, G.I.; Cherkasov, A.M. Technological Features of Construction and Reconstruction of Geotechnical Structures in the Arctic Zone. Designs 2022, 6, 34. [Google Scholar] [CrossRef]
- Jizhong, Y.; Lie, C.; Kejian, C.; Yingliang, W.; Yinguang, X.; Wanming, Z.; Yongxing, W.; Mingjun, L.; Chengbiao, C.; Yongping, Z.; et al. Method for Improving Seismic Performance of Bridge by Using Beam Body and Energy Dissipation and Seismic Mitigation Bridge Bearing. US10815627B2, 27 October 2020. [Google Scholar]
- Cha, H. Two-Way c.p.s Jack Having Earthquake-Proof Function Using for Intensity Reinforce Mathod for Bridge Bearing and Lifting Method for Structure Using the Same. KR102055925B1, 16 December 2019. [Google Scholar]
- Gupta, P.K.; Ghosh, G.; Kumar, V.; Paramasivam, P.; Dhanasekaran, S. Effectiveness of LRB in Curved Bridge Isolation: A Numerical Study. Appl. Sci. 2022, 12, 11289. [Google Scholar] [CrossRef]
- Ghazal, H.; Mwafy, A. Comparative Performance Evaluation of Retrofit Alternatives for Upgrading Simply Supported Bridges Using 3D Fiber-Based Analysis. Buildings 2023, 13, 1161. [Google Scholar] [CrossRef]
- Moeindarbari, H.; Taghikhany, T. Seismic optimum design of triple friction pendulum bearing subjected to near-fault pulse-like ground motions. Struct. Multidisc. Optim. 2014, 50, 701–716. [Google Scholar] [CrossRef]
- Park, S.K.; Han, K.B. Effects of seismic isolation bearing with sliding mechanism on the response of bridge. Mater. Struct. 2004, 37, 412–421. [Google Scholar] [CrossRef]
- Ningbo, W.; De, Z.; Fanglin, H.; Xinkui, T.; Dongping, L. Bridge bearing capacity evaluation method based on mobile load test. CN110377943B, 25 February 2022. [Google Scholar]
- Orfeo, A.; Tubaldi, E.; McAlorum, J.; Perry, M.; Ahmadi, H.; McDonald, H. Self-Sensing Rubber for Bridge Bearing Monitoring. Sensors 2023, 23, 3150. [Google Scholar] [CrossRef]
- Kim, B.-s. Displacement Gauge for Bridge Bearing and Bridge Bearing with Same. KR102120979B1, 10 June 2020. [Google Scholar]
- Bin, Y.; Ye, X.; Xinmin, Z.; Xingzhong, Z. Elastic Spherical Support for Bridge. CN111472267B, 30 November 2021. [Google Scholar]
- Peel, H.; Luo, S.; Cohn, A.G.; Fuentes, R. Localisation of a mobile robot for bridge bearing inspection. Autom. Constr. 2018, 94, 244–256. [Google Scholar] [CrossRef]
- Deng, Y.; Li, A. Structural Health Monitoring for Suspension Bridges; Springer: Beijing, China, 2019. [Google Scholar]
- Xing, Z.; Jing, L.; Guangyang, L.; Zhi, T.; Fengjing, D. Bridge support capable of being partially replaced and replacement method. CN111321677B, 28 September 2021. [Google Scholar]
- Liu, J.; Liu, L.; He, J.; Zi, D.; Lv, X.; Luo, Q.; Mo, Q.; Lan, Z.; Huang, S.; Li, L. Rapid installation and replacement method of bridge shock insulation rubber support. CN111648254B, 22 October 2021. [Google Scholar]
- Rajczyk, J.; Rajczyk, M.; Lazarev, Y.; Rajczyk, P.; Kirillova, D. Elastomer Bearing Modification for Efficient Design. Lect. Notes Civ. Eng. 2020, 70, 715–726. [Google Scholar]
- Wu, Y.; Wang, H.; Li, A.; Feng, D.; Sha, B.; Zhang, Y. Explicit finite element analysis and experimental verification of a sliding lead rubber bearing. J. Zhejiang Univ. -Sci. A 2017, 18, 363–376. [Google Scholar] [CrossRef]
- Lu, A.-H.; Salabas, E.-L.; Schuth, F. Magnetic nanoparticles: Synthesis, protection, functionalization and application. Angew. Chem. Int. Ed. 2007, 46, 1222–1244. [Google Scholar] [CrossRef]
- Wenhao, W.; Kelvin, W.K.Y. Bone grafts and biomaterials substitutes for bone defect repair: A review. Bioact. Mater. 2017, 2, 224–247. [Google Scholar] [CrossRef]
- Recek, N. Biocompatibility of Plasma-Treated Polymeric Implants. Materials 2019, 12, 240. [Google Scholar] [CrossRef]
- Gould, T.E.; Piland, S.G.; Shin, J.; Hoyle, C.E.; Nazarenko, S. Characterization of mouthguard materials: Physical and mechanical properties of commercialized products. Dent. Mater. 2009, 25, 771–780. [Google Scholar] [CrossRef] [PubMed]
- Forintos, N.; Czigany, T. Multifunctional application of carbon fiber reinforced polymer composites: Electrical properties of the reinforcing carbon fibers—A short review. Compos. Part B Eng. 2019, 162, 331–343. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, L.; Xie, G.; Li, Z.; Chen, H.; Gong, H.; Xu, W.; Guo, D.; Luo, J. A review on tribology of polymer composite coatings. Friction 2021, 9, 429–470. [Google Scholar] [CrossRef]
- Doh, J.; Hur, S.H.; Lee, J. Viscoplastic parameter identification of temperature-dependent mechanical behavior of modified polyphenylene oxide polymers. Polym. Eng. Sci. 2019, 59, E200–E211. [Google Scholar] [CrossRef]
- Dai, W.; Zuo, J.; Liu, D.; Guo, X. Tribological Properties and Seasonal Freezing Damage Evolution of Rotating Spherical Hinge Self-Lubricating Coating. Appl. Sci. 2022, 12, 8329. [Google Scholar] [CrossRef]
- Birleanu, C.; Pustan, M.; Cioaza, M.; Bere, P.; Contiu, G.; Dudescu, M.C.; Filip, D. Tribo-Mechanical Investigation of Glass Fiber Reinforced Polymer Composites under Dry Conditions. Polymers 2023, 15, 2733. [Google Scholar] [CrossRef] [PubMed]
- Adamov, A.; Kamenskikh, A.; Nosov, Y. Analysis of deformation behavior of the antifriction layer part with a spherical recess for lubricant. AIP Conf. Proc. 2021, 2371, 020005. [Google Scholar] [CrossRef]
- Yi, X.-S.; Luo, S.; Zhang, L. Composite Materials Engineering; Springer: Singapore, 2018; Volume 1. [Google Scholar] [CrossRef]
- Kamenskih, A.A.; Trufanov, N.A. Numerical analysis of the stress state of a spherical contact system with an interlayer of antifriction material. Comput. Contin. Mech. 2013, 6, 54–61. [Google Scholar] [CrossRef]
- Ushakov, A.V.; Karpov, I.V.; Fedorov, L.U.; Lepeshev, A.A. Mechanical and tribological properties of complex-modified material based on ultra high molecular weight polyethylene and CuO. J. Frict. Wear 2014, 35, 7–11. [Google Scholar] [CrossRef]
- Kamenskih, A.A.; Trufanov, N.A. Regularities of interactions between elements of a spherical contact unit with an antifriction polymeric interlayer. J. Frict. Wear 2015, 36, 170–176. [Google Scholar] [CrossRef]
- Adamov, A.A.; Kamenskikh, A.A.; Nosov, Y.O. Deformational behavior of the flat sliding layer of the spherical bearing. Int. J. Civ. Eng. Technol. (IJCIET) 2019, 10, 99–107. [Google Scholar]
- Guerrero-Vaca, G.; Rodríguez-Alabanda, O. Analysis of Wear Phenomena Produced by Erosion with Abrasive Particles against Fluoropolymeric Coatings. Polymers 2022, 14, 4617. [Google Scholar] [CrossRef] [PubMed]
- Nosov, Y.O.; Kamenskikh, A.A. Experimental study of the rheology of grease by the example of ciatim-221 and identification of its behavior model. Lubricants 2023, 11, 295. [Google Scholar] [CrossRef]
- Stolbova, O.S.; Tihomirova, K.A. Two methods for calculating the stress-strain state of shape memory alloy constructions taking into account tension–compression asymmetry. PNRPU Mech. Bull. 2020, 1, 109–125. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Liu, X.; Liu, J.; Wu, M.; Huang, Y. Tailoring Interfacial Adhesion between PBAT Matrix and PTFE-Modified Microcrystalline Cellulose Additive for Advanced Composites. Polymers 2022, 14, 1973. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Yao, Z.; Du, H.; Song, J.; Jin, Z.; Xu, W. Wettability and Frictional Studies of PEEK Composites against Co-Cr Alloys with Surface Textures. Polymers 2023, 15, 4006. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.-S.; Zhou, Y.; Li, J.; Ye, H.; Chen, F.; Zhao, Y.; Pan, Q.; Xu, J. All-Organic PTFE Coated PVDF Composite Film Exhibiting Low Conduction Loss and High Breakdown Strength for Energy Storage Applications. Polymers 2023, 15, 1305. [Google Scholar] [CrossRef]
- Liang, X.; Wu, P.; Lan, L.; Wang, Y.; Ning, Y.; Wang, Y.; Qin, Y. Effect of Polytetrafluoroethylene (PTFE) Content on the Properties of Ni-Cu-P-PTFE Composite Coatings. Materials 2023, 16, 1966. [Google Scholar] [CrossRef]
- Mei, S.; Zhou, C.; Hu, Z.; Xiao, Z.; Zheng, Q.; Chai, X. Preparation of a Ni-P-nanoPTFE Composite Coating on the Surface of GCr15 Steel for Spinning Rings via a Defoamer and Transition Layer and Its Wear and Corrosion Resistance. Materials 2023, 16, 4427. [Google Scholar] [CrossRef]
- Qi, Y.; Sun, B.; Zhang, Y.; Gao, G.; Zhang, P.; Zheng, X. Tribological Properties of Nano-ZrO2 and PEEK Reinforced PTFE Composites Based on Molecular Dynamics. Lubricants 2023, 11, 194. [Google Scholar] [CrossRef]
- Trajkovski, A.; Novak, N.; Pustavrh, J.; Kalin, M.; Majdič, F. Performance of Polymer Composites Lubricated with Glycerol and Water as Green Lubricants. Appl. Sci. 2023, 13, 7413. [Google Scholar] [CrossRef]
- Han, O.; Kwark, J.-W.; Lee, J.-W.; Han, W.-J. Analytical Study on the Frictional Behavior of Sliding Surfaces Depending on Ceramic Friction Materials. Appl. Sci. 2023, 13, 234. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, L.; Lu, K.; Gao, B. Study of Cyclic Plasticity and Creep Ratchet Behavior of PTFE. Appl. Sci. 2023, 13, 10039. [Google Scholar] [CrossRef]
- Johansson, P.; Marklund, P.; Björling, M.; Shi, Y. Effect of Oxygen and Moisture on the Friction and Wear of Carbon Fiber-Reinforced Polymers. Lubricants 2023, 11, 412. [Google Scholar] [CrossRef]






| Measurement Time | Diameter , mm | Thickness, mm | Height , mm | Hardness HB |
|---|---|---|---|---|
| Before testing | 103.46–103.50 | 10.58 | 2.73 | 409 |
| After testing | 103.62–104.75 | 10.48 | 2.63 | 482 |
| Reduced specimens after turning of tested specimens | 97.9–98.0 | 4.84 | 1.0–1.3 | 292 |
| After testing of reduced specimens | 99.0–99.1 | 4.80 | 0.3–0.5 | 308 |
| Def. and Cont. Parameters | Spherical Notches | Annular Groove | ||||
|---|---|---|---|---|---|---|
| = 0.01 | = 0.001 | = 0.01 | = 0.001 | |||
| = 0.04 | ||||||
| , % | 0.0146 | 0.0142 | 0.0132 | 0.0300 | 0.0306 | 0.0308 |
| , MPa | 93.1728 | 92.9666 | 92.9777 | 94.1679 | 94.1340 | 94.1499 |
| , MPa | 3.6580 | 3.5557 | 3.5580 | 3.4420 | 3.3670 | 3.3775 |
| = 0.00631 (for load at 90 MPa) | ||||||
| , % | 0.0136 | 0.0140 | 0.0127 | 0.0301 | 0.0302 | 0.0301 |
| , MPa | 92.4102 | 92.5528 | 92.6018 | 95.0633 | 94.5439 | 96.6795 |
| , MPa | 0.5827 | 0.9254 | 0.0926 | 0.5575 | 0.8810 | 0.0886 |
| Comparison model with different friction coefficient | ||||||
| , % | 7.1825 | 1.5261 | 3.6684 | 0.1809 | 1.4626 | 2.3531 |
| , % | 0.8185 | 0.4451 | 0.4043 | 0.9508 | 0.4354 | 2.6868 |
| , % | 84.071 | 73.9743 | 97.3974 | 83.8030 | 73.8355 | 97.3761 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bogdanova, A.P.; Kamenskikh, A.A.; Nosov, Y.O. The Geometric Configuration of Lubricant Recesses of the Polymer Sliding Layer of the Bearing. Designs 2023, 7, 144. https://doi.org/10.3390/designs7060144
Bogdanova AP, Kamenskikh AA, Nosov YO. The Geometric Configuration of Lubricant Recesses of the Polymer Sliding Layer of the Bearing. Designs. 2023; 7(6):144. https://doi.org/10.3390/designs7060144
Chicago/Turabian StyleBogdanova, Anastasia P., Anna A. Kamenskikh, and Yuriy O. Nosov. 2023. "The Geometric Configuration of Lubricant Recesses of the Polymer Sliding Layer of the Bearing" Designs 7, no. 6: 144. https://doi.org/10.3390/designs7060144
APA StyleBogdanova, A. P., Kamenskikh, A. A., & Nosov, Y. O. (2023). The Geometric Configuration of Lubricant Recesses of the Polymer Sliding Layer of the Bearing. Designs, 7(6), 144. https://doi.org/10.3390/designs7060144






