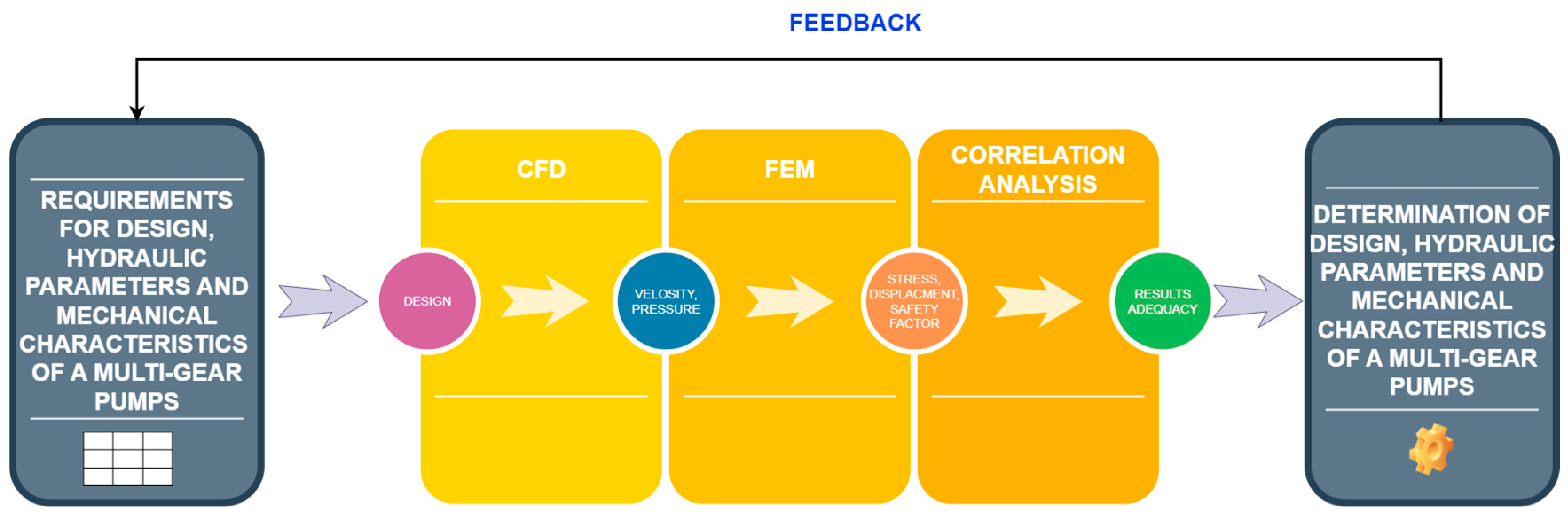
CFD-FEM Analysis for Functionality Prediction of Multi-Gear Pumps

Abstract

A comprehensive model for evaluating the functionality of a multi-gear pump has been developed. The integrated model for assessing the functionality of a multi-gear pump contains a computational fluid dynamics analysis (CFD) model combined with a finite element method (FEM)-based strength model. Two submodels were linked: a CFD submodel to evaluate the internal pressure distribution of the pump and a structural FEM submodel to calculate the stresses and structural displacements of the pump due to fluid pressure. Finite element analysis in SolidWorks 2016 was used to evaluate the strength of the gear joints of the pump gears. As the pressure of the working fluid increases from 6 to 20 MPa, a linear increase in Mises stresses is observed. At the shaft, these stresses increase to 226.2 MPa, and at the tooth mouths, they reach a maximum value of 205.5 MPa. With the increase in torque on the drive shaft from 100 to 500 N·m, there is a significant increase in Mises stresses localized in the contact zones of the shaft with the drive gear. Analysis of the data obtained showed that the displacements caused by the pressure of the working fluid are insignificant compared to the displacements arising under the action of torque. With increasing pressure and torque, there is a tendency to decrease the safety factor, which indicates a decrease in the safety factor of the design of the multi-gear pump. The safety factor is not provided at a torque of 400–500 N·m. The simulation results are confirmed by correlation analysis. The average approximation error is 5–7%.

1. Introduction

Gear pumps are a type of positive displacement pump widely used in various industries and engineering for pumping liquids [1]. The principle of operation of a gear pump is based on the rotation of gears in association with each other [2]. Due to the meshing of the gears, closed cavities are formed that capture the liquid from the suction side and transfer it to the discharge side [3]. The advantages of gear pumps are their high capacity and uniform liquid delivery without pulsations [4]. Gear pumps are also characterized by high efficiency [5]. Gear pumps have a simple and reliable design and can operate at various temperatures and pressures [6].

There are many designs of gear pumps that contain two, three, or more driven gears [7,8,9].

The design of a multi-gear pump, like any positive displacement hydraulic machine, consists of three main tasks [10]:

(1)

Calculation of geometric and energy parameters;

(2)

Development of design measures aimed at increasing the efficiency, uniformity of delivery, life, and serviceability of the pump;

(3)

Calculation of the strength of individual parts of the hydraulic machine design.

The uniformity of the delivery and the serviceability of the gear pump are determined by means of CFD analysis. In works [11,12,13], the authors presented modeling of computational fluid dynamics of flow processes in the external gear pump. Here, the main pump flow characteristics are determined, particularly the flow rate as a function of pressure and the flow rate as a function of velocity.

Works [14,15,16,17] describe the behavior of fluid flow in the meshing zone, pressure decomposition taking into account internal fluid leaks, and prediction of flow turbulence and cavitation.

The calculation of gear meshing of a gear pump is one of the key stages in the design and manufacture of this type of equipment. It allows for evaluating the functionality of the pump under given operating conditions and preventing premature failure due to gear tooth failure.

Work on strength calculation of gear meshes considers the distribution of the stress–strain state of spur gears depending on the change in the shape of the gear tooth [18], the geometric dimensions of the gear tooth [19,20], and the angle in the interdental space [21].

There are also works [22,23,24] on determining the stress state of the gear joint depending on the choice of material.

Despite the long existence of gear pump design, it is difficult to find many studies on the joint use of CFD and FEM methods. The authors of [25] presented a CFD-FEM approach to determine the hydraulic structure and vibroacoustics of a gear pump.

There are almost no studies of multi-gear pumps with four or more gears.

The multi-gear pump provides high performance, reduces gear load, and improves the efficiency of fluid transfer efficiency.

This article proposes a new design of a pinion pump with four positioned idler gears around the driving gear in the center of the gear joint [26]. This can make the delivery more uniform, reduce pulsations, equalize radial loads, and reduce stresses occurring on the gear surfaces.

Before developing a prototype of a multi-gear pump in metal, it is necessary to verify its functionality. For this purpose, simulation modeling techniques such as CFD and FEM are proposed.

The paper aims to develop an integrated CFD/FEM analysis model to predict the functionality of a multi-gear pump.

2. Materials and Methods

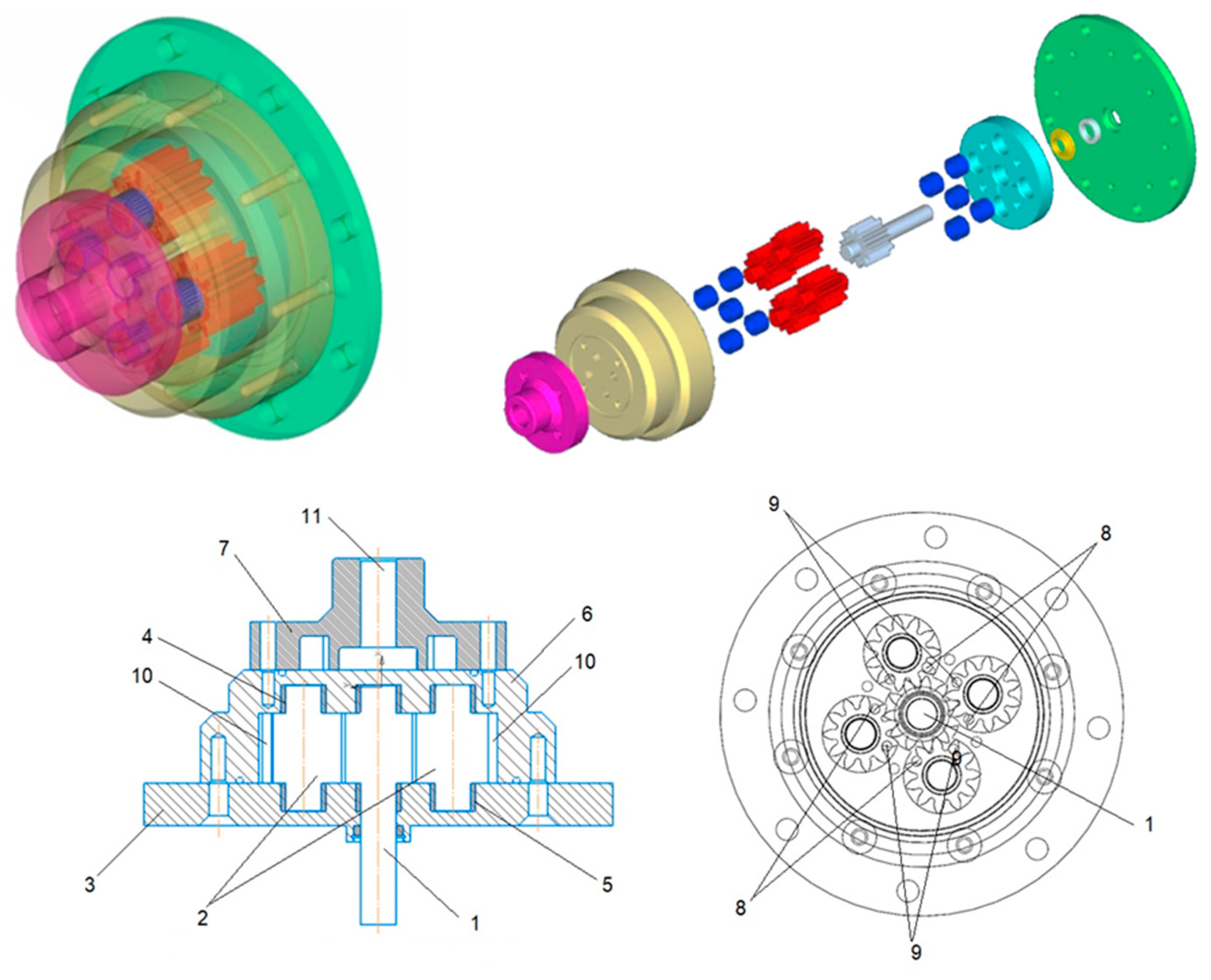
2.1. Object of Study

The design of the five-pinion pump is shown in Figure 1.

When rotating, the driving pinion engages with the driven pinions, thereby causing them to rotate. When the drive gear rotates clockwise, the liquid is sucked through the side openings in the top cover (not shown in the drawing), and then, through the holes (8) in the pump casing, enters the working chambers (10) of the pump. When the idler gears rotate, the fluid is carried by the troughs of the teeth into the discharge cavity, where it is displaced through openings (9) in the pump casing and, further, combining into a common flow in the manifold, is displaced through an opening (11) into the discharge line. The working chambers (10) of the driven gears are separated from each other by special segments made in the pump casing.

2.2. Geometric and Energy Parameters of the Multi-Gear Pump

The geometric and energy parameters of the multistage pump are presented in

Table 1. Geometric and energy parameters of the multi-gear pump.

№	Parameter Name	Designation	Measurement Unit	Value
Geometric parameters
1	Tooth module	m	mm	5
2	Number of gear teeth	z	-	11
3	Dividing diameter of the gear	d	mm	55
4	Diameter of the circumference of the gear projections	df	mm
5	Center distance	a	mm	55
6	Gear width	b	mm	50
7	Working capacity	q	m3	275
Energy parameters
8	Revolutions	n	r/min	1000
9	Productivity	Q	m3/s	0.00458
10	Discharge pressure	Pd	MPa	up to 16
11	Suction pressure	Ps	MPa	0.5
12	Dynamic viscosity coefficient	µ	Pa·s	0.00861

.

2.3. Simulation Model for CFD Analysis

The feeding of the proposed design of a multi-pinion pump should be considered uniform, because the moments of suction and discharge of liquid are displaced in time due to the gear fact that the teeth at the time of meshing have different positions, and the degree of the opening of inlet and outlet ports is different (Figure 2).

The study of the process of fluid flow in a multi-pinion pump was performed in the program complex SolidWorks 2016. For the numerical experiment, a pump simulation model was built, which includes the calculation area enclosed between the casing (1), bottom cover (2), and gears (3) (Figure 2).

The peculiarity is that the rotation of the gears has to be taken into account in the calculation. For this purpose, the model additionally introduced elements of rotation in the form of cylinders with a diameter of 65 mm and height of 50 mm, i.e., a volume approximately equal to the volume of the calculation area of each gear. During assembly, it is necessary to make the rotation elements transparent, and in the initial data of the task, this element should be added to the project as an additional rotation area and specify the number of revolutions n. Analyzing the previous results, we take n = 1000 rpm [28].

The boundary conditions are chosen as follows:

(1)

Volume flow rate of liquid at the entry Q = 0.00458 m³/s (inlet orifices 5);

(2)

Total inlet pressure P = 1 MPa (inlet orifices 5);

(3)

Full pressure at the outlet P = 10 MPa (outlet orifices 6) (Figure 2).

(4)

The calculation takes into account the physical properties of the VMGZ hydraulic oil (all-season thickened hydraulic oil) [28].

After selecting the global targets (total pressure, fluid velocity) and constructing the grid in automatic mode with the minimum grid cell size (level 7), the hydraulic calculation was performed. The grid is shown in Figure 3.

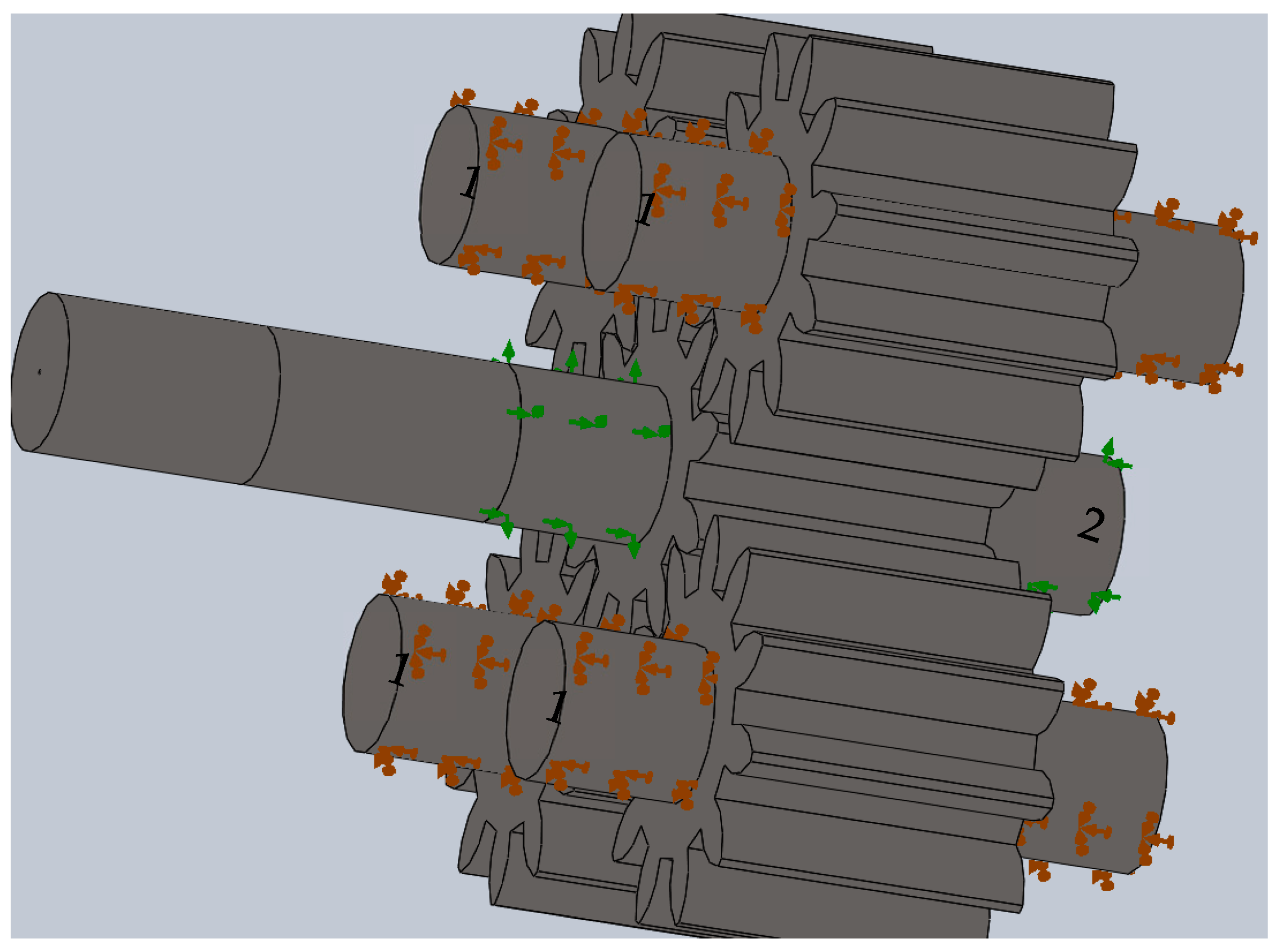
2.4. Stages of FEM Analysis

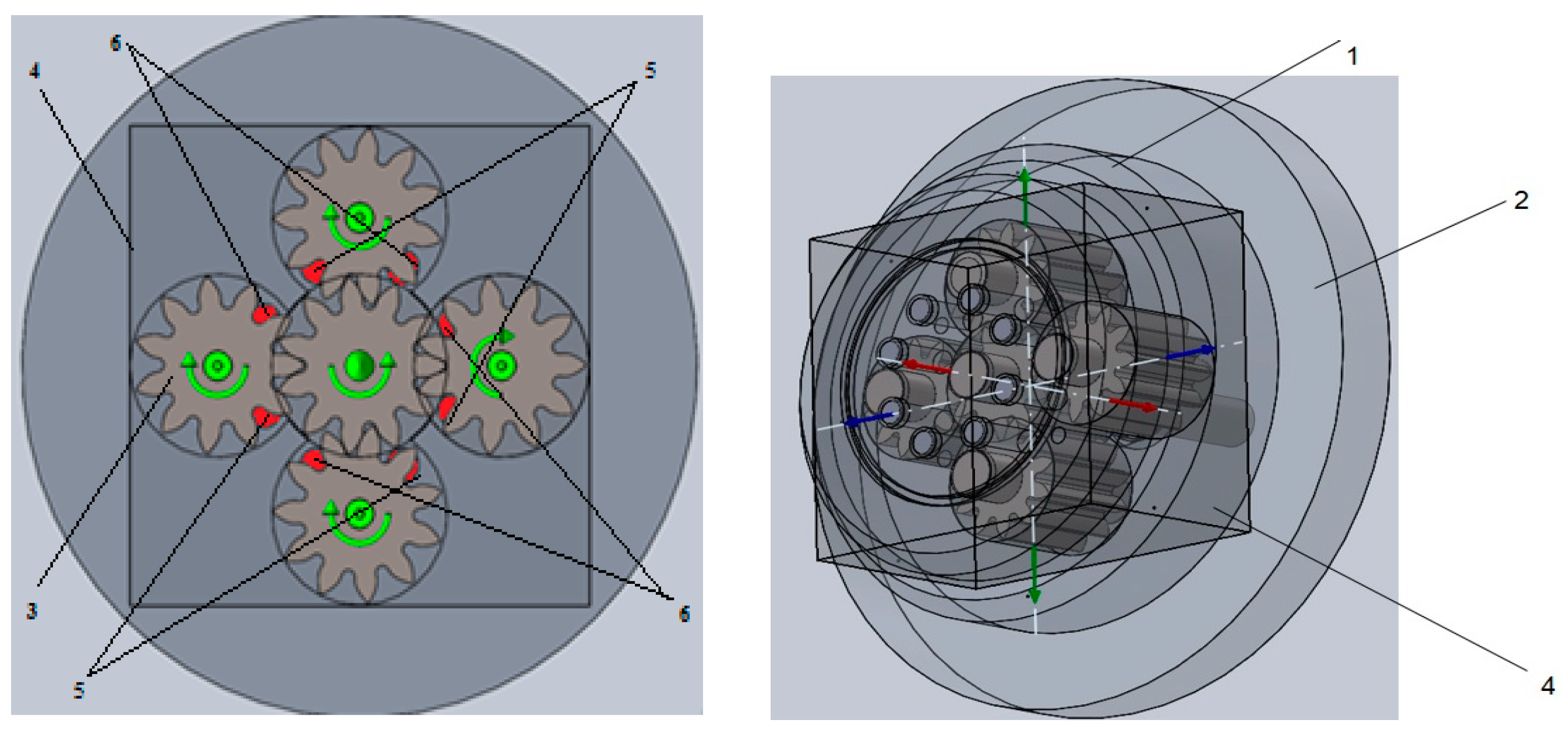
2.4.1. Creation of a Simulation Model

A simulation model was created that consists of one master gear and four slave gears (Figure 4).

The material of gears is carbon steel 30XGSA (GOST 4543-2016). Material properties are given in

Table 2. Physical and mechanical properties of carbon steel 30XGSA.

Material	Yield Stress	Linear Expansion Coefficient	Modulus of Elasticity	Poisson’s Ratio	Density
Steel 30XGSA	760 MPa	12.3 × 10−6 1/°C	211 GPa	0.3	7850 kg/m3

.

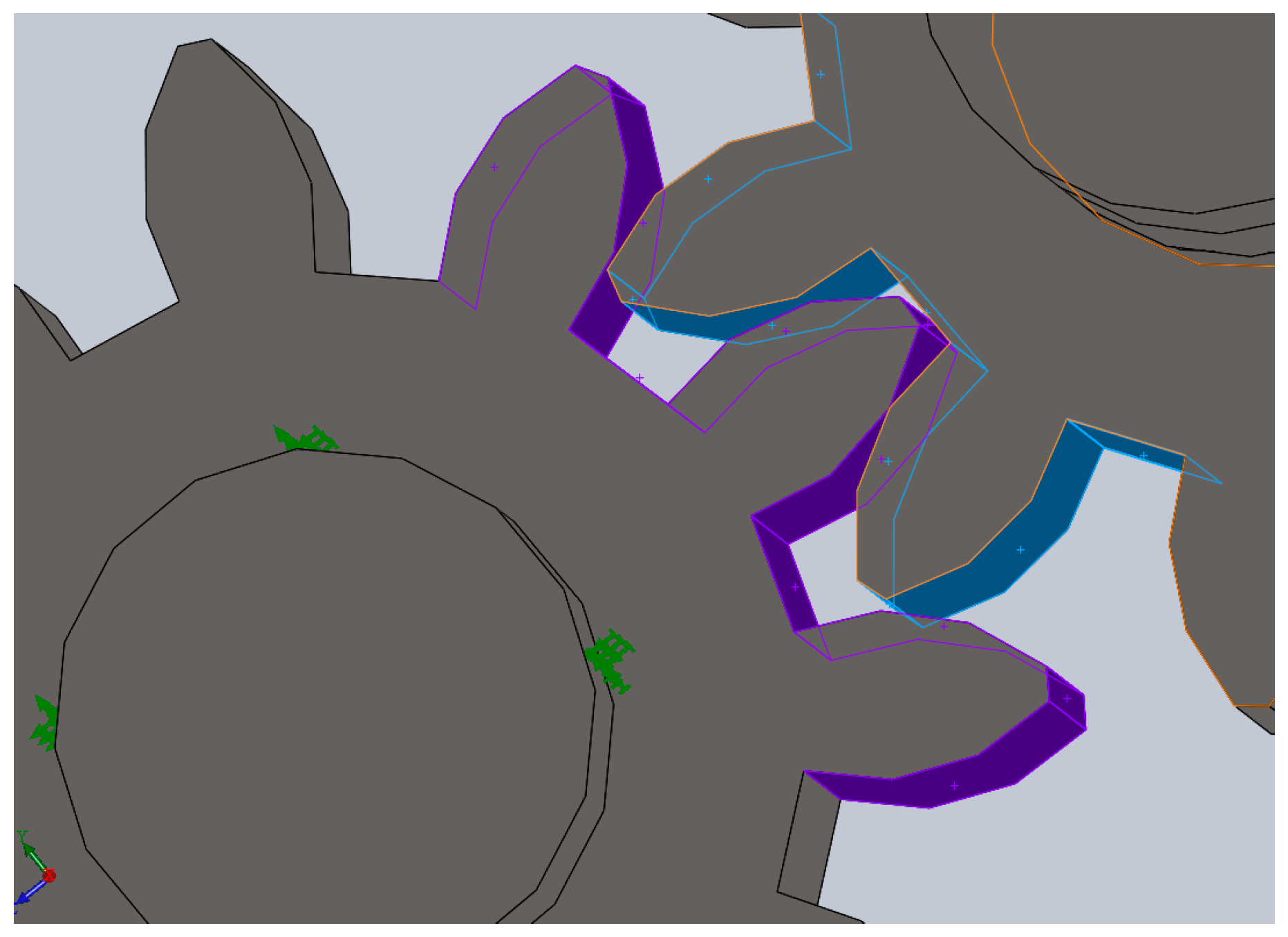
2.4.2. Establishing Contact in a Gear Mesh

The “Connections” tab defines a global contact that specifies the connectivity of the simulation model elements. With this type of contact, all parts work as one unit.

Being geometrically different parts, they share a common finite-element mesh. In addition to the global contact, sets of contacts are defined in which parts can move relative to each other and take friction into account when contact occurs. For this problem, the sets of contacts between the faces of the teeth entering the mesh are defined (Figure 5). The friction coefficient f = 0.1.

2.4.3. Selecting the Type of Fixture

In the “Fixture” tab, it is necessary to specify how the elements of the simulation model will be fixed relative to each other and to the coordinate system. Taking into account the operating principle of the pump, the “Fixed Geometry” fastening type was selected to fasten the supports of the driven gears (1), which eliminates movement of the supports along the Y and Z axes. For the driving gear, which drives the driven gears into rotation, under the action of the applied torque, the second type of fixture was selected for the supports—the “Hinge”. This type of fixture is used to eliminate the movement of the supports along the Y and Z axes and allows rotation only around its axis. For the drive pinion, the mounting type “Fixed joint” was selected (Figure 6).

2.4.4. Torque Setting

The torque M applied to the drive shaft is specified as the load. To determine the range of variable torque values, we use the following formula [29]:

$$M={\displaystyle \frac{N}{2\pi ·n}},$$

(1)

where N—power of the pumping station, W; n—rotation frequency, rpm.

Based on the technical parameters of the pumping station manufactured for conducting full-scale experiments N = 18.5 kW.

The rotation frequency is regulated by a frequency converter in the range from 400 to 1450 rpm. Therefore, using Formula (1), the range of variable values of torque M is within the limits from 121 to 446 N·m. For a better perception of the parameters under study, we will take the range of torque values from 100 to 500 N·m.

The fluid pressure acting on the discharge side is also taken into account (Figure 7).

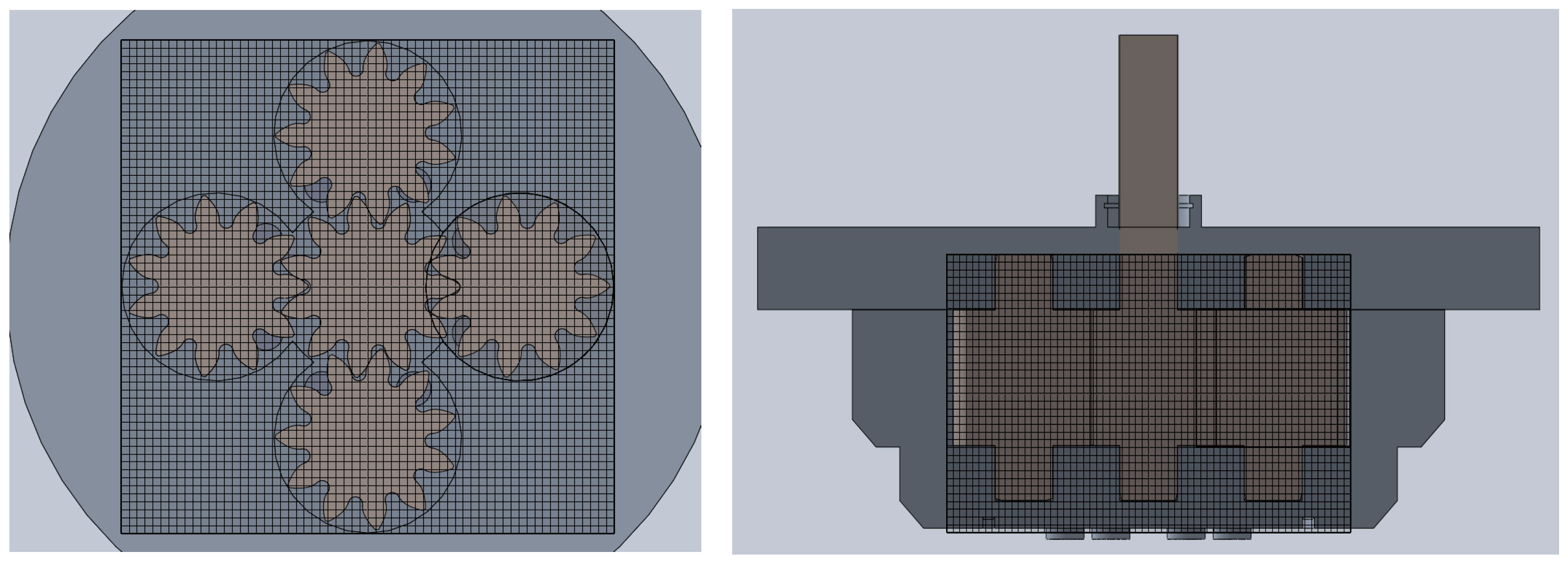
2.4.5. Grid Creation

For a more accurate calculation, the mesh has a minimum size (1.3 mm) at the meshing points of the teeth; in the least-loaded parts of the gear, the size of the finite elements of the mesh is larger and is automatically determined when a high-quality mesh is selected (Figure 8).

2.4.6. Input Data for Strength Calculation

In the study, two series of experiments were carried out using simulation modeling in SolidWorks 2016 (

Table 3. Input data for strength calculation.

№ Experience	Discharge Pressure P, MPa	Torque on Shaft M, N·m
Series 1
1	6	200
2	8
3	10
4	12
5	14
6	16
7	18
8	20
Series 2
9	12	100
10		150
11		200
12		250
13		300
14		350
15		400
16		500

). In the first series, injection pressure P = var, shaft torque M = const. In the second series, shaft torque M = var, injection pressure P = const.

The initial data for the calculation are presented in Table 3. According to research [30], the recommended speed n = 900–1000 rpm. The range of varying pressure values is chosen based on the technical characteristics of gear pumps; the working pressure should be no more than 20 MPa. Consequently, the first series of experiments were conducted at M = 200 N·m. For the second series of experiments, P = 12 MPa (const) was taken.

2.5. Determining the Adequacy of the Data Obtained

This article proposes to use an integrated approach in the modeling of the technological and strength parameters of a multi-gear pump followed by mathematical verification of the results obtained for the determination of design, hydraulic parameters, and mechanical characteristics of multi-gear pumps (Figure 9).

To verify the relationship between fluid injection pressure stresses and torque, correlation analysis [30] is used with the preparation of third- and second-order regression equations and the verification of their adequacy.

The third-order regression equation has the following form [31]:

$$Y=A+BX+C{X}^2+D{X}^3$$

(2)

The second-order regression equation has the following form [32]:

$$Y=A+BX+C{X}^2$$

(3)

where A, B, C, D—regression coefficients; X—variable value.

The correlation coefficient is determined by the formula [33]:

$$r_{xy}={\displaystyle \frac{\sum (x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\sum {(x_i-\overline{x})}^2\sum {(y_i-\overline{y})}^2}}}$$

(4)

where x_i—factor; $\overline{x}$—arithmetic mean value x_i; y_i—response; $\overline{y}$—arithmetic mean value y_i.

The multiple correlation index is determined by the following formula [34]:

$$R=\sqrt{1-{\displaystyle \frac{\sum {(y_i-y_x)}^2}{\sum {(y_i-\overline{y})}^2}}}$$

(5)

where y_x—response value.

The quality of the regression equation is assessed using the absolute approximation error [35,36]:

$$\overline{A}={\displaystyle \frac{\sum _{i=1}^n\frac{\left|y_i-y_x\right|}{y_i}}{n}}·100\%$$

(6)

where n—sample volume.

The significance of the regression equation is determined by Fisher’s F-criterion using the formula [37]:

$$F={\displaystyle \frac{r_{xy}^2}{1-r_{xy}^2}}{\displaystyle \frac{n-m-1}{m}}$$

(7)

where m—number of factors affecting the response.

3. Results and Discussion

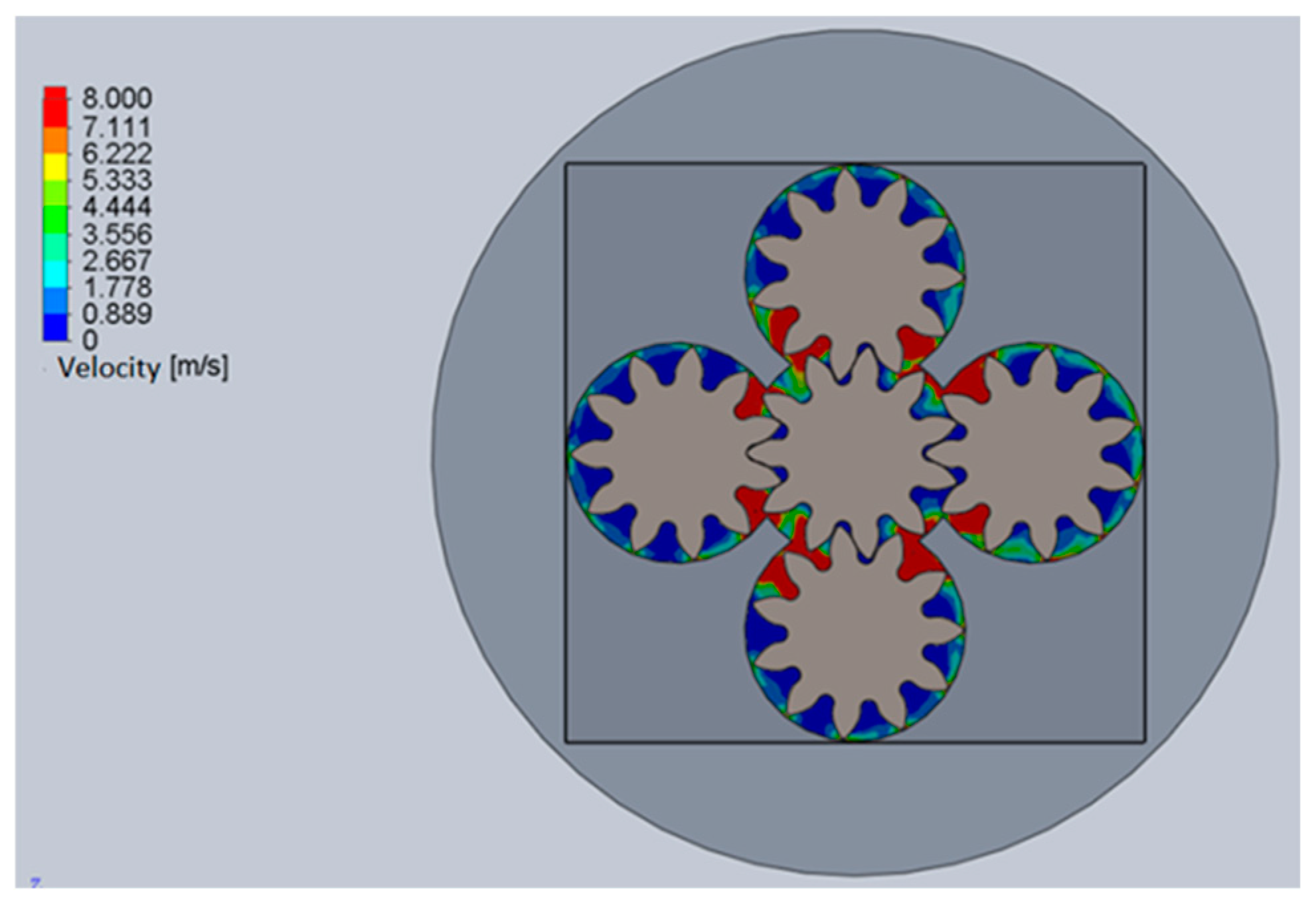
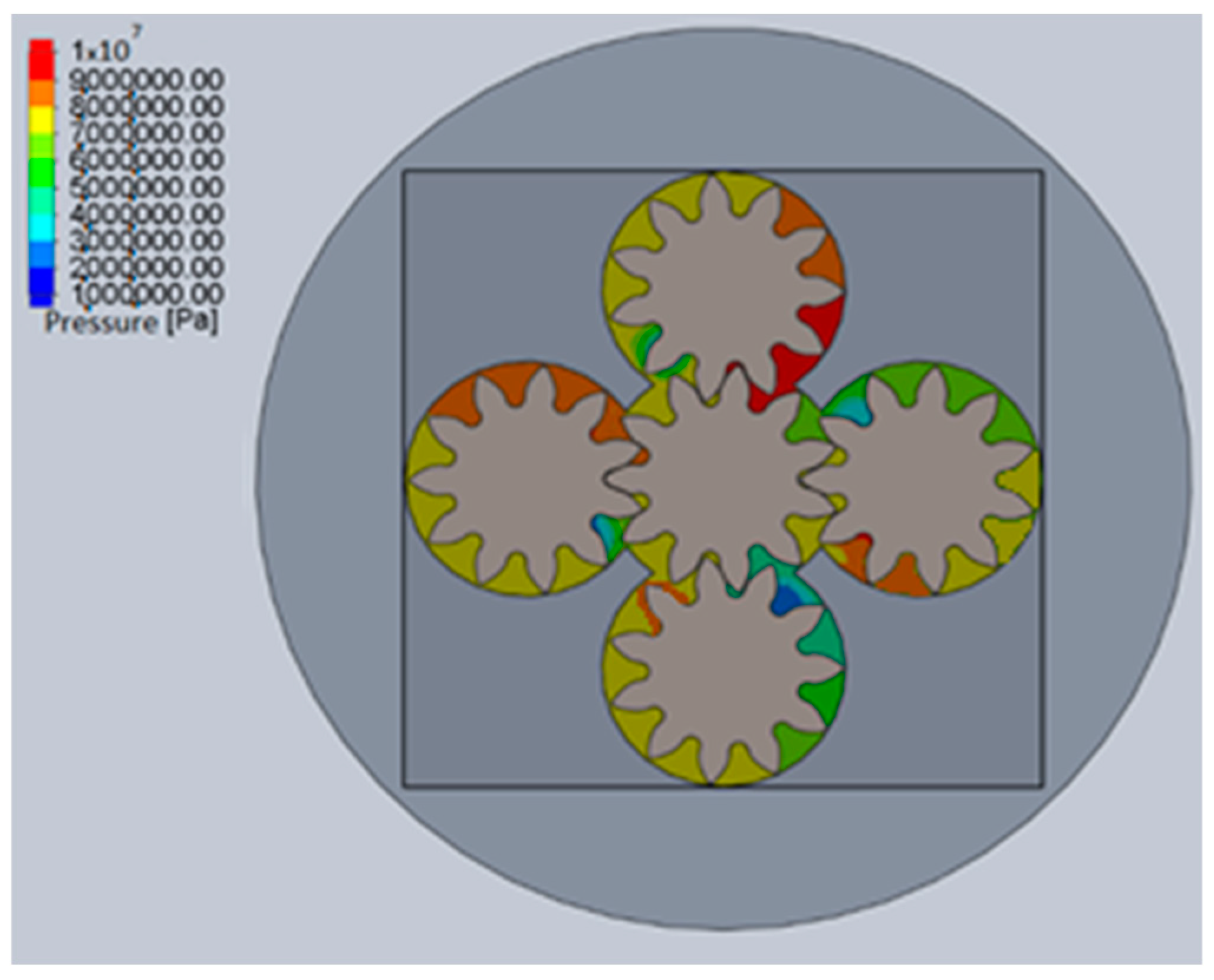
3.1. Computational Fluid Dynamics Analysis

The results of the CFD analysis are presented in Figure 10 and Figure 11 in the form of epicures of changes in the hydraulic parameters of the fluid flow in the gear pump.

Analysis of the results allows us to note the following:

–

The liquid velocity reaches the highest values (up to 8 m/s) in places of suction and discharge of liquid, caused by the change in geometric parameters of the design, for example, when liquid enters the working chamber of the pump through a narrower inlet hole with a diameter of 8 mm. The further movement of liquid in the troughs of the teeth from the inlet to the outlet holes is characterized by a decrease in velocity and reaches minimum values at the teeth legs. Between the body and the teeth of gears on the outer arc, velocity is 1.5–2.5 m/s, and in some places 5 m/s.

–

On the pressure change curve, areas of low pressure are marked in blue, characterizing the process of suction of the liquid. Here, the pressure value is 1 MPa. The red color represents areas of high pressure, where the pressure value varies in the range of 9–10 MPa, and characterizes the liquid injection into the pressure line. The distribution of pressure values in the working chambers of the driven gears is different, which is due to the different degrees of opening of the input and outlet openings. It is worth noting the presence of high pressure (10 MPa) in the gear meshes of the multi-gear pump, which can lead to fluid locking and jamming of the pump. To avoid this process, grooves must be provided to drain the locked liquid in the gear hydraulic machine.

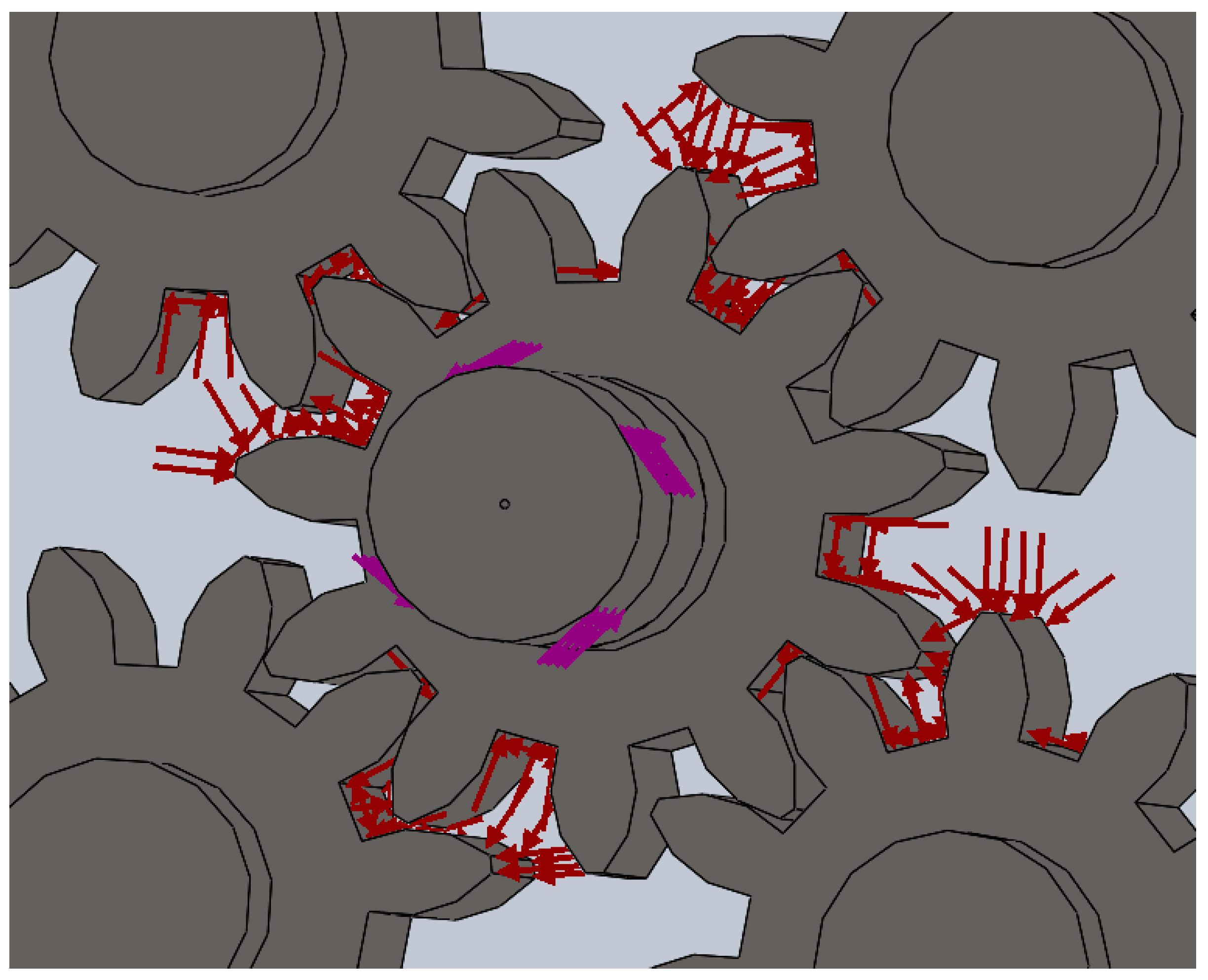
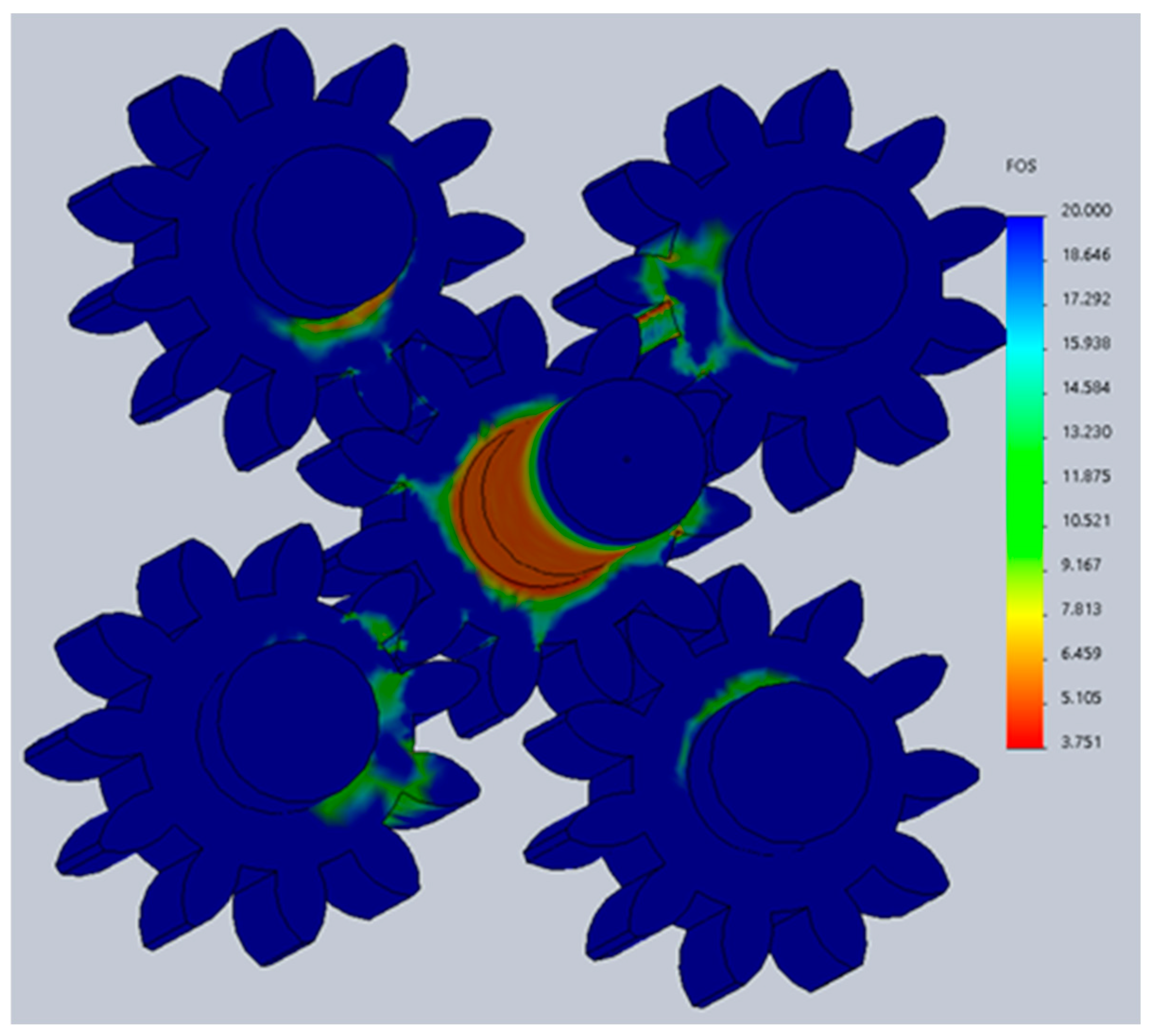
3.2. Finite Element Method Analysis

The results of the FEM analysis are summarized in Figure 12, Figure 13 and Figure 14.

The results of the calculation of the stress–strain state of the gear mesh allow us to determine the most stressed places of the structure, namely the place of connection of the drive shaft with the driving gear. The highest Mises stresses occur here but do not exceed the yield strength of the material (Figure 12a). The gear tooth feet also experience high stresses at the moment of engagement and when the liquid is forced into the pump discharge ports (Figure 12b). Since the shaft experiences the highest loads during the transfer of mechanical rotational energy, the maximum displacements will occur directly at the point of torque application (Figure 13). However, as the results show, the value of displacements is insignificant and amounts to 0.006–0.18 mm.

The results of the safety factor [38] calculation also allow us to note the most stressed zones of the structure mentioned above. In this case, the safety factor is quite high and is 3.75 (Figure 14).

In general, the analysis of the obtained results is represented by the dependence of the maximum stresses, displacements, and safety factor for the shaft and gear teeth on the discharge pressure and torque in Figure 15, which allows us to draw the following conclusions.

The Mises stresses occurring on the shaft when the working fluid pressure changes in the range from 6 to 20 MPa increase with decreasing intensity in the range from 144.2 to 226.2 MPa (Figure 15a). At the tooth legs, the stresses increase with increasing intensity in the range from 50.9 to 250.5 MPa (Figure 15b). The values obtained do not exceed the yield strength of 30XGSA steel, which can reach values of 600–2000 MPa. Therefore, the working pressure generated by the pump can have higher values. However, it should be noted that a significant increase in pressure causes an increase in fluid leakage, which negatively affects the volumetric efficiency of the hydraulic machine.

When the torque on the drive shaft increases from 100 to 500 N·m, the Mises stresses concentrated at the joints of the shaft with the drive gear increase with decreasing intensity in the range from 108.9 to 519.6 MPa (Figure 15c). In the tooth feet, the resulting stresses have lower values compared to the shaft and decrease in the range from 135.2 to 88.6 MPa (Figure 15d).

The calculated safety factor k_s for this pump design limits the maximum shaft torque to 350 N·m. With these torque values (100 to 500 N·m) and safety factor (more 1.5), the design of the multi-gear pump is efficient and safe.

The resulting displacements due to the pressure of the working fluid pressure are insignificant.

Maximum displacement values for the shaft reach 0.072 mm and for the teeth reach 0.018 mm at P = 20 MPa (Figure 15a,b). They are mainly caused by the action of the torque applied to the shaft. Therefore, with a change in torque in the range from 100 to 450 N·m, displacements increase with decreasing intensity on the shaft from 0.035 to 0.18 mm, and on gear teeth decrease from 0.01 to 0.004 mm (Figure 15c,d).

The value of the safety factor (k_s) decreases from 4.3 to 2.5 with increasing pressure and from 4.7 to 1.2 with increasing torque on the shaft (Figure 15). According to [36], the value of ks for structural steels is 1.4–1.7; therefore, the maximum torque value for the considered pump design is limited to 350 N·m.

3.3. Determination of Dependence Between Investigated Strength Parameters

The main parameter for determining the strength of the shaft and gear joint of a five-gear pump is the equivalent stresses. In this connection, the dependences of equivalent stresses on the injection pressure and torque for these elements were established (Figure 16 and Figure 17).

To check the adequacy of the obtained mathematical dependences of equivalent stresses on the mode parameters of the multistage pump, the coefficient of determination (R²), absolute approximation error (A), and Fisher’s criterion (F) were determined, the values of which are shown in Figure 16 and Figure 17.

When the value of R is close to 1, the regression equation better describes the actual data and the factors have a stronger influence on the result. The approximation error within 5–7% indicates a good fit of the trend equation to the original data. Since F > Fcr (5.32), the coefficient of determination (and in general the trend equation) is statistically significant.

4. Conclusions

In general, the results analysis of the obtained allows us to draw the following conclusions.

(1)

As a result of CFD analysis, the character of the pump liquid flow in the working chamber is established; the distribution diagrams of the liquid velocity and pressure in the pump were determined. The maximum velocity values occur in the places of inlet and outlet holes in the pump casing and reach 8 m/s. In the existing gap between the casing and the gear teeth, the velocity value reaches 5 m/s. The pump pressure distribution curve allows us to determine the change in pressure from the suction area (low-pressure area) to the discharge area (high-pressure area). It should be noted that the amount of pressure of the liquid located in the cavities between the teeth is different in all four gears, which is due to the unequal degree of opening of the inlet and outlet ports. When the outlet pressure was from 6 to 20 MPa, it was found that the pressure distribution diagram has the same form, which suggests the possibility of the five-gear pump operating at high-pressure values.

(2)

As a result of the FEM analysis, the most-loaded elements in the gear engagement of the pump were determined: the junction of the shaft with the drive gear and the gear teeth involved in the engagement. With an increase in torque, the stresses on the shaft increase and reach a maximum value of 519.6 MPa at a torque of M = 500 N·m. The magnitude of the stresses on the gear teeth decreases from 135.2 to 75.5 MPa. When the pressure increases to 20 MPa, the magnitude of the stresses on the gear teeth, on the contrary, has greater values (250.5 MPa) compared to the shaft (226.2 MPa).

(3)

The selected material is 30XGSA steel, suitable for the manufacture of gearing elements since the stress values resulting from various loads do not exceed its yield strength.

(4)

Based on the results of calculating the safety factor k_s for this pump design, the maximum possible torque on the shaft M = 350 N·m is determined.

(5)

Mathematical models for the dependence of equivalent voltages on the technological parameters of a five-stage pump are adequate, and the approximation accuracy is within 5–7%.

This study has some limitations since the calculation did not take into account the leakage of working fluid in the existing gaps between the housing and the gear teeth, between the bottom cover, the housing, and the ends of the gears, which is a separate scientific task with the possibility of developing a sealing system for tightness and determining the volumetric efficiency of the structure.

It is also planned to conduct field experiments on an experimental sample of a five-cylinder pump to verify its operability, obtain performance characteristics, and validate the results.