Mitigating Settlement and Enhancing Bearing Capacity of Adjacent Strip Footings Using Sheet Pile Walls: An Experimental Approach
Abstract
:1. Introduction
The Failure Mechanism and Sheet Pile Wall Effects
2. The Experimental Program
2.1. Scale Selection and Scale Effects
2.2. Experimental Setup and Test Parameters
2.3. Soil Preparation and Characterization
2.4. Test Tank and Loading Procedure
2.5. Procedure for the Testing Model’s Operation
3. Results and Discussion
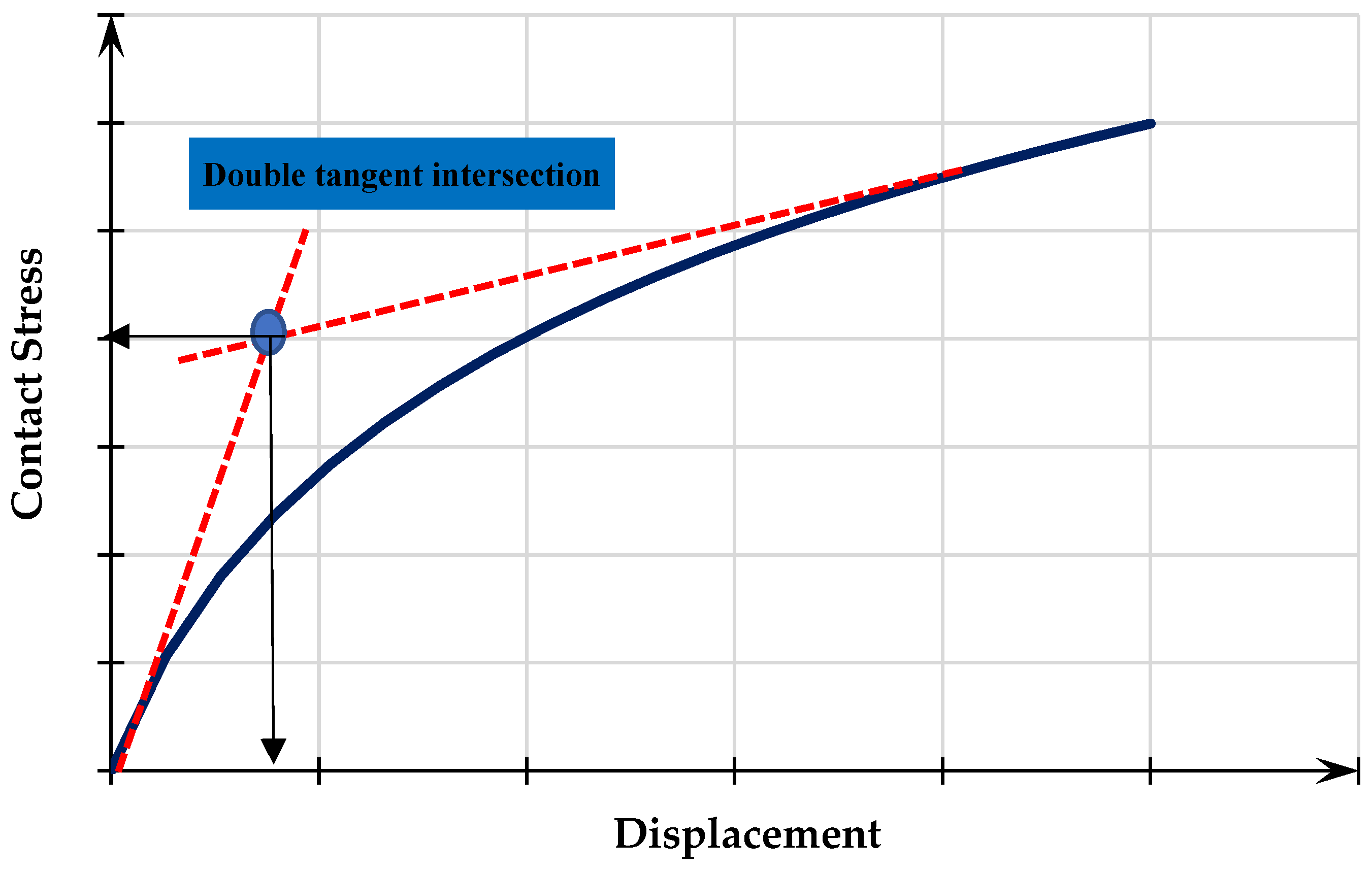
3.1. Settlement Behavior of Single-Strip Footing
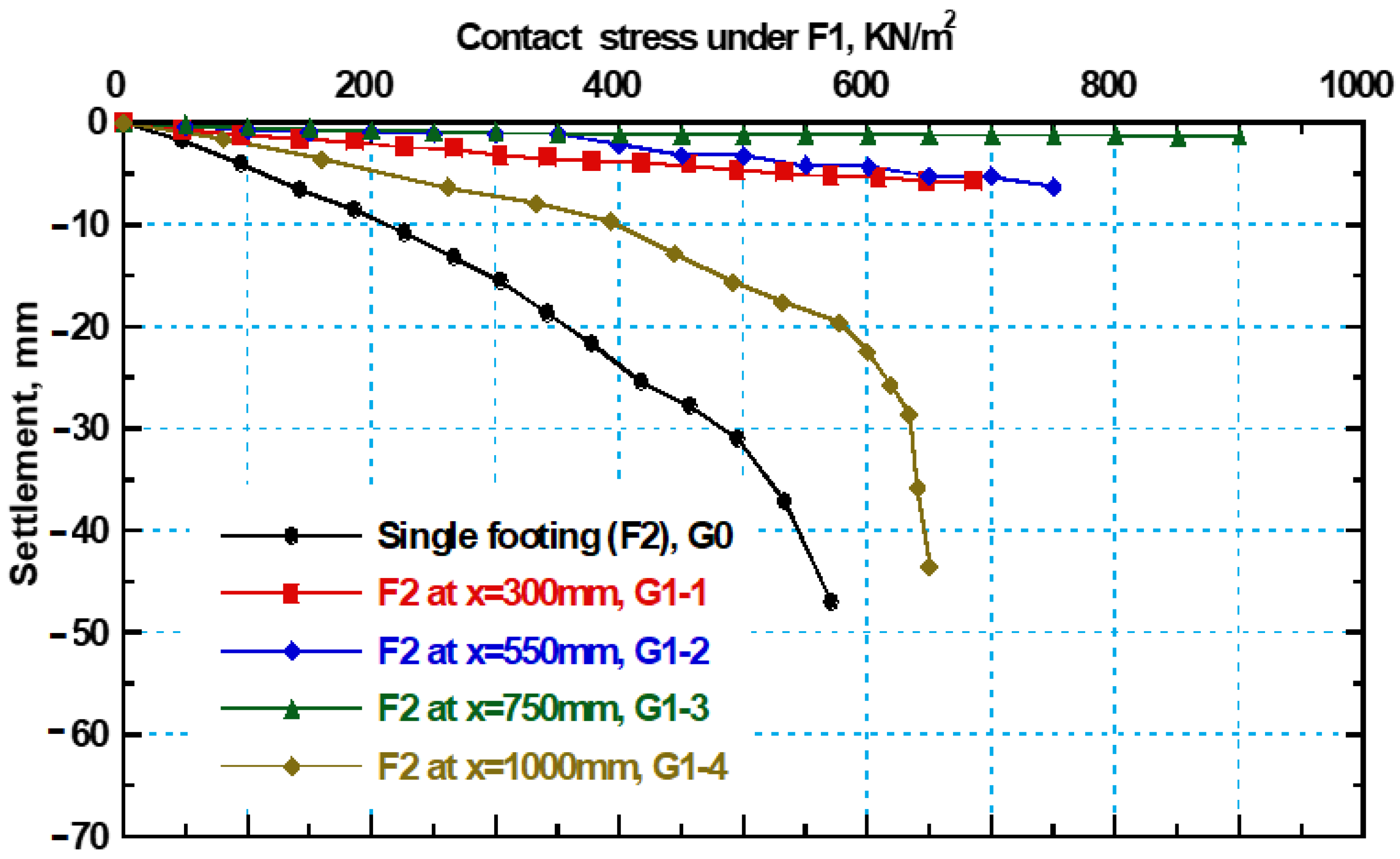
3.2. Settlement Behavior of Interfering New Strip Footings
3.3. Settlement Behavior of Existing Strip Footing with Changing the Center-to-Center Distance Between the New and Old Footings
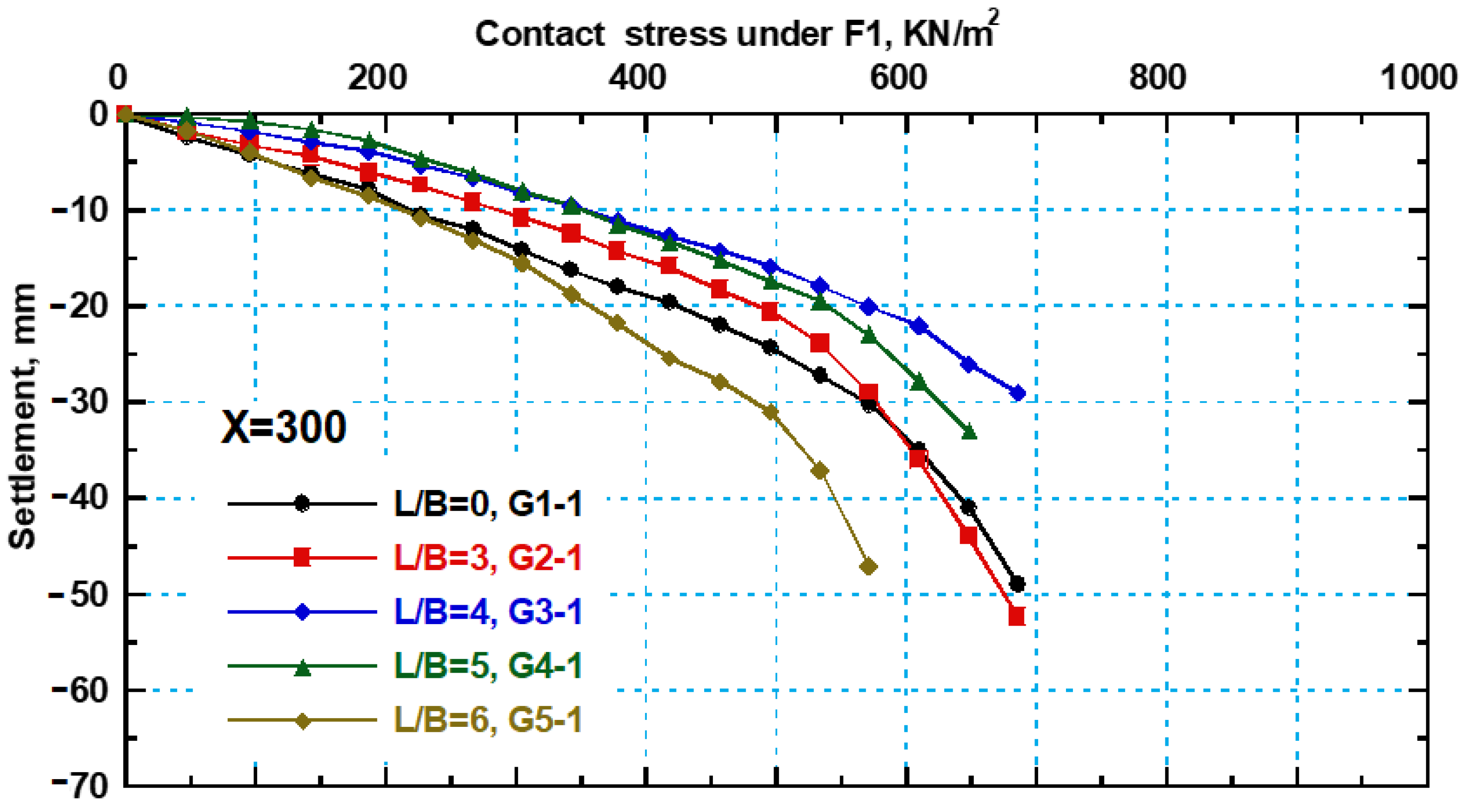
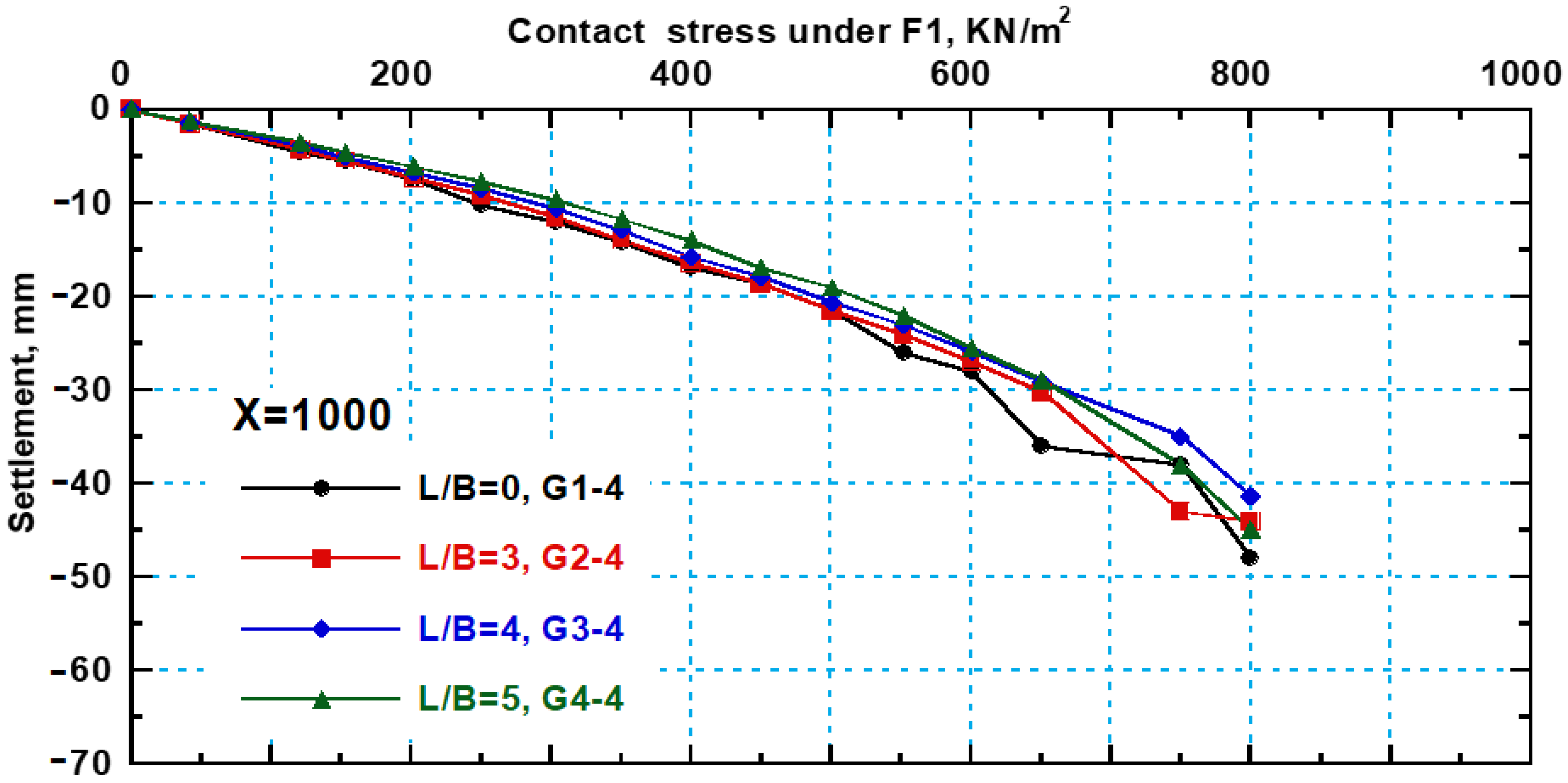
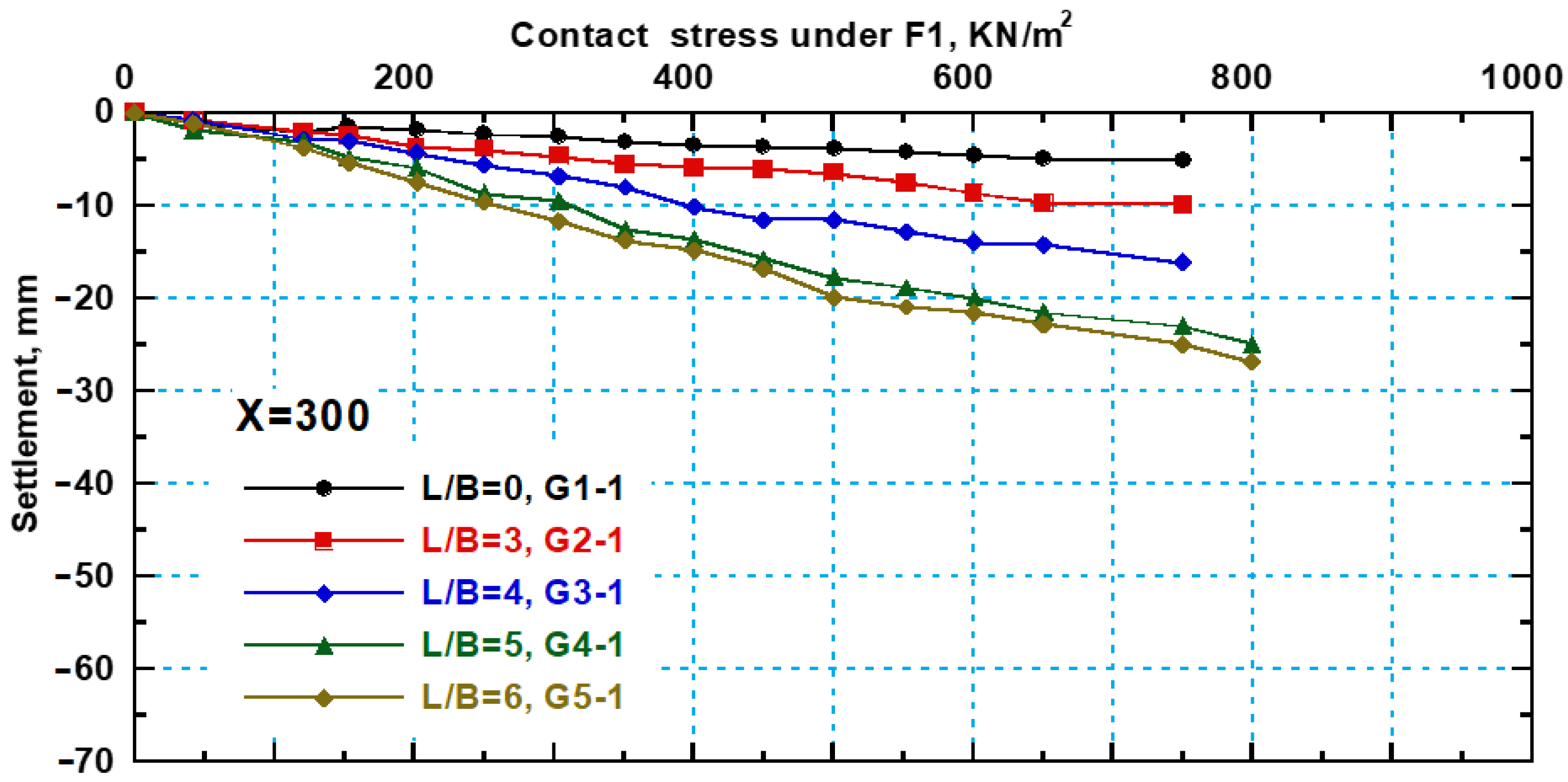
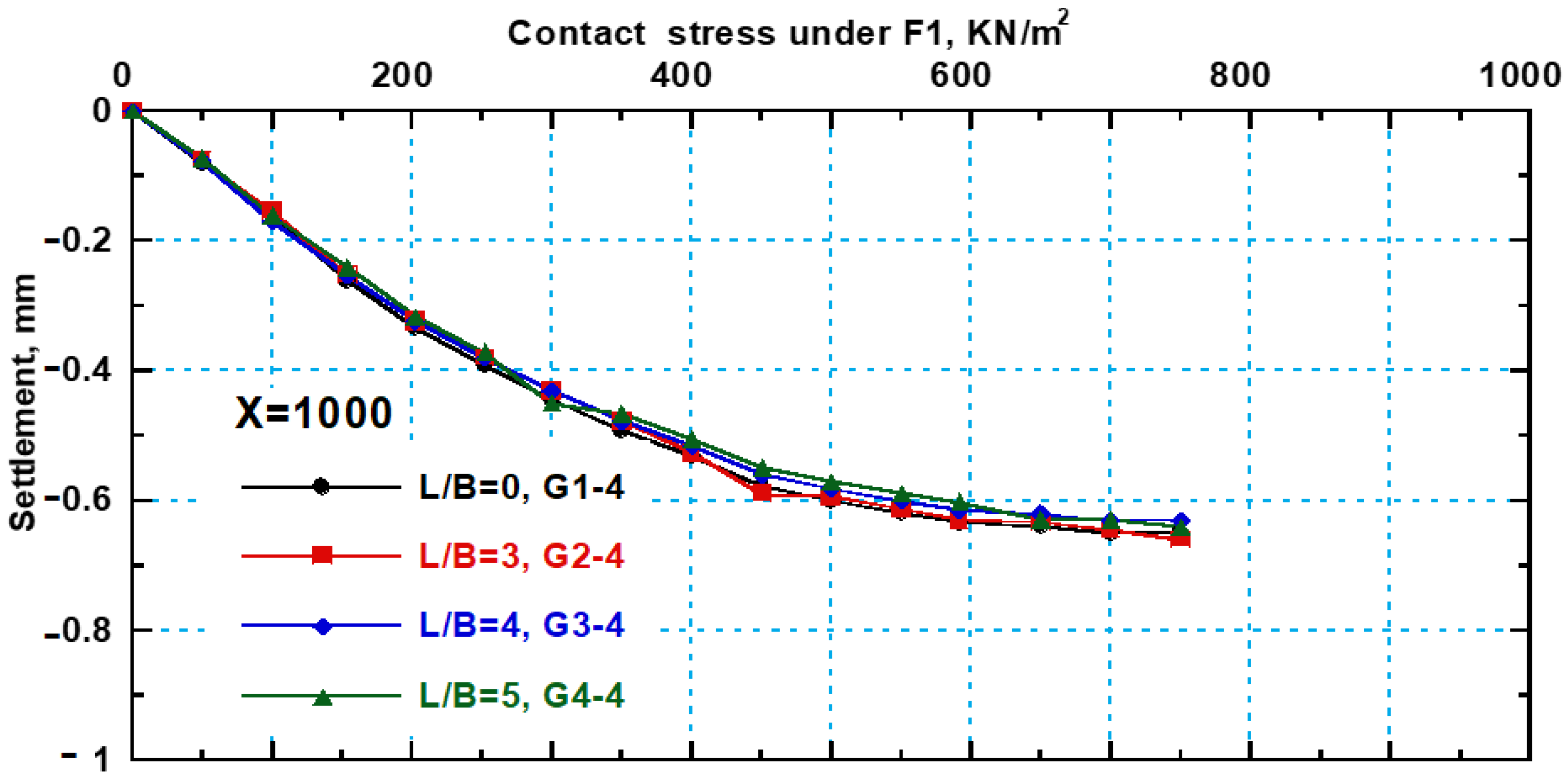
3.4. Settlement Behavior of Interfering New Strip Footings with SPW
3.5. Settlement Behavior of Existing Strip Footing with Different SPW Lengths
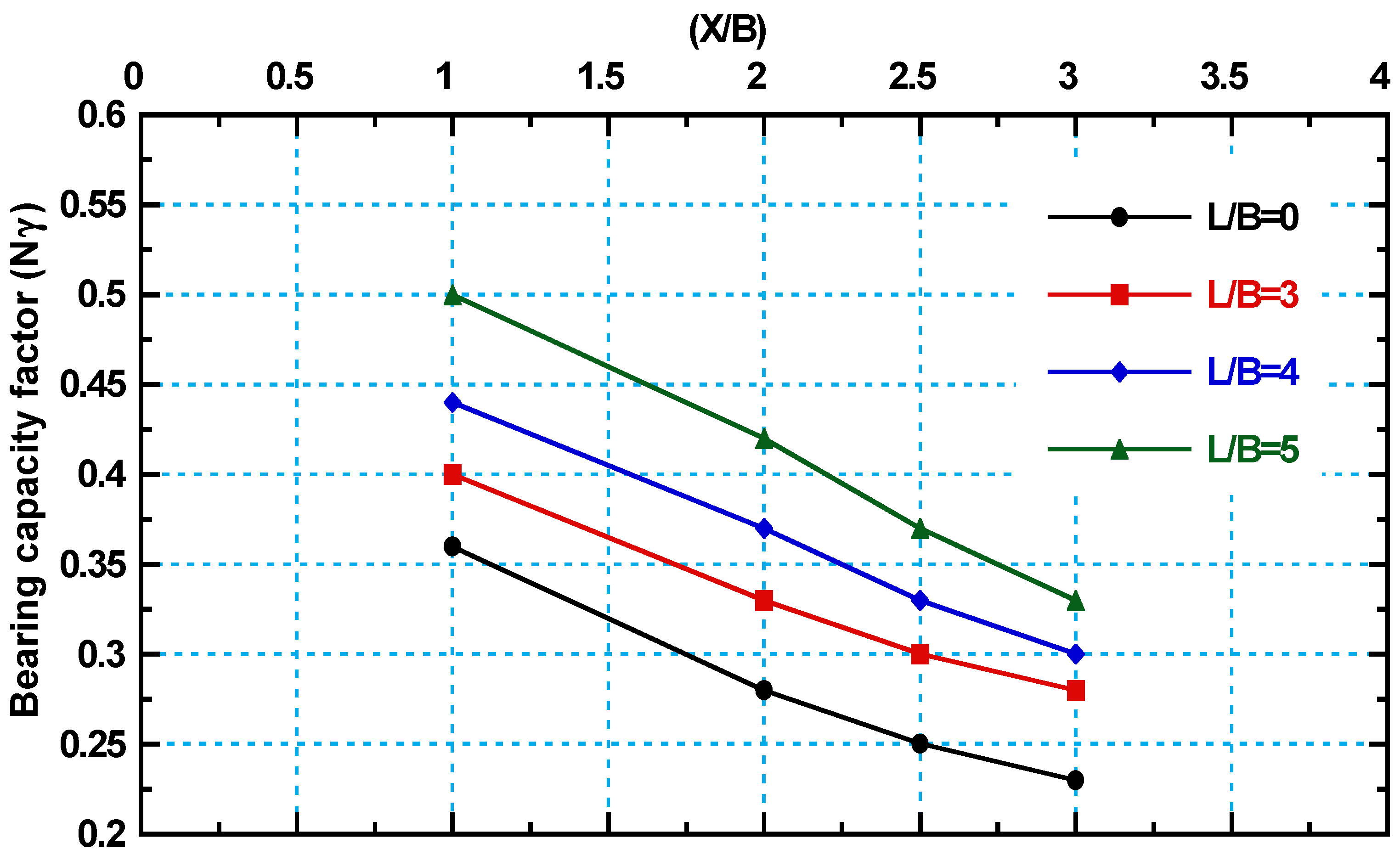
3.6. Effect of Changing the Center-to-Center Distance Between the Two Footings on the Bearing Capacity Factor of Strip Footing
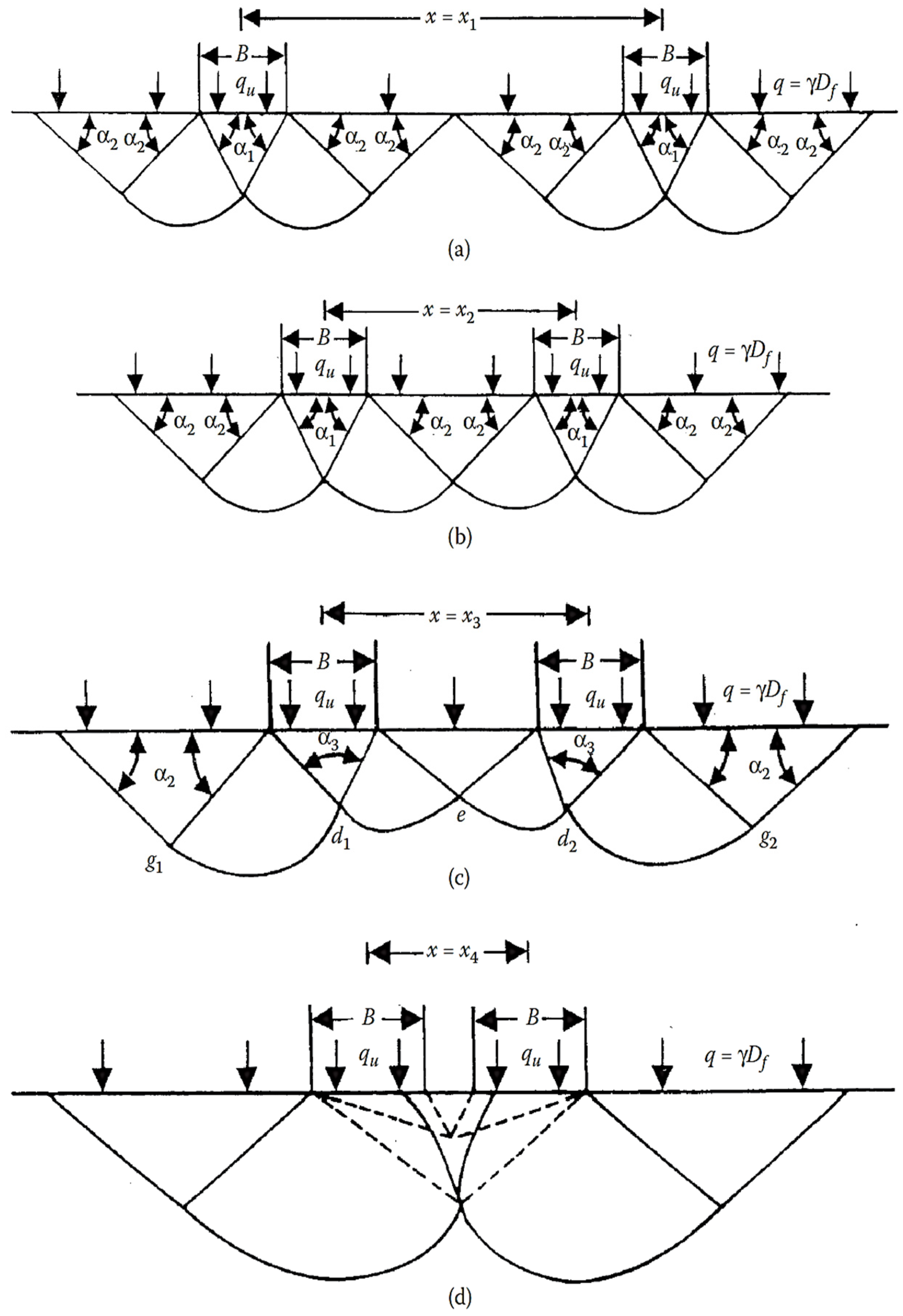
3.7. The Failure Mechanism from Experimental Results Under Two Adjacent Foundations at Different Values for the Distance X Between the Two Footings
4. Practical Implementation Based on Research Findings
5. Conclusions
- The new footing (F1) settlement decreases, and the applied stress increases as the distance (X) between footings decreases. At X = B, the new and old footings act as a single foundation with a width of 2B, enhancing fixation and increasing bearing capacity due to improved load distribution and reduced differential settlement.
- The maximum reduction for the settlement of (F1) is found at (X = 300 mm) and reached 40% compared with single footing at stress = 400 kN/m2.
- Also, the applied stress at (F1) is found to be increased with decreasing distance between footings—it is increased by 53% at distance (X = 300 mm) compared with single footing.
- The settlement of the old footing is increased when decreasing the distance X and the maximum increase in the old footing settlement is found at X = B.
- The settlement of the old footing is increased with a high ratio reached 96% and 89% at X = 300 mm and 550 mm, while, when using distance X = 1000 mm, the settlement is increased with a small ratio reached 47% compared to single footing.
- The new footing (F1) settlement decreased with a ratio reaching 23% when Ls/B is 3. Then, the settlement is found to decrease gradually with increasing Ls/B ratio; it decreases by 36%, 45%, and 48% when Ls/B is 4, 5, and 6, respectively, compared to the footing without sheet piles (Ls/B = 0).
- While the settlement of the old footing (F2) is found to be decreased when using SPW, the reduction ratio of settlement is increased gradually with increasing sheet pile length until sheet pile length (Ls/B) = 5, the settlement reduction in (F2) becomes almost constant.
- The settlement of the old footing (F2) decreases by 47%, 67%, and 77% at Ls/B = 3, 4, and 5, respectively, and the stress is 500 kN/m2 compared to the settlement at Ls/B = 0.
- This study highlights the effectiveness of SPWs in improving foundation behavior, reducing settlement, and enhancing bearing capacity, especially in densely built environments with limited foundation spacing. The results suggest that an SPW length-to-footing width ratio (Ls/B) between 4 and 5 is optimal for minimizing settlement and improving stability, with only a slight difference in effectiveness between these two ratios.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chenari, R.; Mohafezatkar, A. Adjacent building induced settlement reduction in residential constructions. Forensic Approach Anal. Geohazard Probl. 2010, 169. [Google Scholar] [CrossRef]
- Eltohamy, A.; Zidan, A. Performance of interfering strip footings resting on reinforced sand under uniform and non-uniform load-experimental and numerical study. J. Am. Sci. 2013, 9, 421–430. [Google Scholar]
- Stuart, J.G. Interference between foundations, with special reference to surface footings in sand. Geotechnique 1962, 12, 15–22. [Google Scholar]
- Eslami, A.; Afshar, D.; Moghadasi, H.; Akbarimehr, D. Numerical and experimental investigations of interference effect of adjacent buildings on sand and fill deposits. Int. J. Civ. Eng. 2023, 22, 723–738. [Google Scholar] [CrossRef]
- Ghosh, P.; Sharma, A. Interference effect of two nearby strip footings on layered soil: Theory of elasticity approach. Acta Geotech. 2010, 5, 189–198. [Google Scholar]
- Selvadurai, A.P.S.; Rabbaa, S.A.A. Some experimental studies concerning the contact stresses beneath interfering rigid strip foundations resting on a granular stratum. Can. Geotech. J. 1983, 20, 406–415. [Google Scholar]
- Das, B.M.; Larbi-Cherif, S. Bearing capacity of two closely-spaced shallow foundations on sand. Soils. Found. 1983, 23, 1–7. [Google Scholar]
- Hanna, A.M. Bearing capacity of foundations on a weak sand layer overlying a strong deposit. Can. Geotech. J. 1983, 19, 392–396. [Google Scholar]
- Basha, A.; Zakaria, M.; El-Nimr, M.; Abo-Raya, M. Performance analysis of axially loaded secant pile wall embedded in sand: An experimental investigation. Arab. J. Sci. Eng. 2023, 48, 13005–13029. [Google Scholar]
- Basha, A.M.; Zakaria, M.H.; El-Nimr, M.T.; Abo-Raya, M.M. Predicting the maximum axial capacity of secant pile walls embedded in sandy soil. Geotech. Geol. Eng. 2024, 24, 3373–3400. [Google Scholar]
- Ozpolat, A.; Aksoy, H.S. The effect of distance between sheet pile and foundation on bearing capacity of Foundation. Adv. Civ. Eng. 2022, 2022, 7338718. [Google Scholar] [CrossRef]
- Jayamohan, J.; Vimal, A.; Rajeev, K.P. Behaviour of strip footing resting on reinforced foundation bed with underground void. Indian J. Geosynth. Ground Improv. 2022, 9, 25–29. [Google Scholar]
- Basha, A.; Elsiragy, M. Effect of sheet pile driving on geotechnical behavior of adjacent building in sand: Numerical study. Civ. Eng. J. 2019, 5, 1726–1737. [Google Scholar]
- Salamatpoor, S.; Jafarian, Y.; Hajiannia, A. Bearing capacity and uneven settlement of consecutively constructed adjacent footings rested on saturated sand using model tests. Int. J. Civ. Eng. 2019, 17, 737–749. [Google Scholar]
- Alwalan, M.F. Interaction of closely spaced shallow foundations on sands and clays: A review. J. Adv. Eng. Res. Sci. 2018, 5, 101–110. [Google Scholar]
- Denver, H.; Kellezi, L. Modelling of earth pressure from nearby strip footings on a free & anchored sheet pile wall. In Proceedings of the 17th Nordic Geotechical Meeting Challenges in Nordic Geotechniqes, Reykjavik, Iceland, 25–28 March 2016; pp. 913–921. [Google Scholar]
- Debnath, A.; Pal, S. Influence of surcharge strip loads on the behavior of cantilever sheet pile walls: A numerical study. J. Eng. Res. 2023, 11, 100029. [Google Scholar]
- Singh, A.; Chatterjee, K. Influence of soil type on static response of cantilever sheet pile walls under surcharge loading: A numerical study. Arab. J. Geosci. 2020, 13, 138. [Google Scholar]
- Kumar, J.; Ghosh, P. Ultimate bearing capacity of two interfering rough strip footings. Int. J. Geomech. 2007, 7, 53–62. [Google Scholar] [CrossRef]
- Pusadkar, S.; Bhatkar, T. Behaviour of raft foundation with inclined skirt using PLAXIS 2D. In Proceedings of theIndian Geotechnical Conference, Roorkee, India, 22–24 December 2013; Volume 3. [Google Scholar]
- Mowafe, Y.; Eltohamy, A.; Mohamed, A. Performance of cantilever sheet pile supporting excavation adjacent to strip footing. In Proceedings of the 2nd International Conference on Geotechnique, Construction Materials and Environment, Kuala Lumpur, Malaysia, 14–16 November 2012. [Google Scholar]
- Kumar, J.; Bhoi, M.K. Interference of two closely spaced strip footings on sand using model tests. J. Geotech. Geoenvironmental Eng. 2009, 135, 595–604. [Google Scholar]
- Das, B.M.; Puri, V.K.; Neo, B.K. Interference effects between two surface footings on layered soil. Transp. Res. Rec. 1993, 34–40. Available online: https://trid.trb.org/View/384534 (accessed on 1 January 2025).
- Stuart, J.; Hanna, T. Groups of deep foundations, a theoretical and experimental investigation. In Proceedings of the 5th International Conference on Soil Mechanics and Foundation Engineering, Paris, France, 17–22 July 1961; pp. 149–153. [Google Scholar]
- Terzaghi, K. Theoretical Soil Mechanics; Wiley: New York, NY, USA, 1943. [Google Scholar] [CrossRef]
- Das, B. Shallow Foundations: Bearing Capacity and Settlement; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Xu, J.; Zheng, L.; Yu, Z.; Li, Y.; Cai, G. Effects of bending stiffness and interface roughness on tunnel-embedded wall interaction. Tunn. Undergr. Space Technol. 2025, 155, 106209. [Google Scholar]
- ASTM. Standard Test Method for Particle-Size Analysis of Soils (ASTM D422-63); ASTM International: West Conshohocken, PA, USA, 2007. [Google Scholar]
- ASTM, D. 3–9; Standard Test Method for Direct Shear Test of Soils under Consolidated Drained Conditions. ASTM International: West Conshohocken, PA, USA, 2011.
- Aamer, F.; Azzam, W.; Farouk, A.; Nasr, A.; Nazir, A. Utilization of blade anchor for improving the uplift capacity of pile in sand: Model study. Ocean Eng. 2023, 278, 114435. [Google Scholar] [CrossRef]
- Azzam, W.; Elwakil, A. Model study on the performance of single-finned pile in sand under tension loads. Int. J. Geomech. 2017, 17, 4016072. [Google Scholar] [CrossRef]
- Nasr, A.M.A.; Azzam, W.R. Behaviour of eccentrically loaded strip footings resting on sand. Int. J. Phys. Model. Geotech. 2017, 17, 177–194. [Google Scholar] [CrossRef]
- El Sawwaf, M.; Nazir, A. Behavior of eccentrically loaded small-scale ring footings resting on reinforced layered soil. J. Geotech. Geoenvironmental Eng. 2012, 138, 376–384. [Google Scholar] [CrossRef]
- Vinod, P.; Bhaskar, A.; Sreehari, S. Behaviour of a square model footing on loose sand reinforced with braided coir rope. Geotext. Geomembr. 2009, 27, 464–474. [Google Scholar] [CrossRef]
- Hataf, N.; Fatolahzadeh, A. An experimental and numerical study on the bearing capacity of circular and ring footings on rehabilitated sand slopes with geogrid. J. Rehabil. Civ. Eng. 2019, 7, 174–185. [Google Scholar]
- Mansur, C.; Kaufman, R. Pile tests, low-sill structures, old river, La. J. Soil Mech. Found. Div. 1956, 82, 1071–1079. [Google Scholar] [CrossRef]
- Xu, J.; Franza, A.; Marshall, A.M.; Losacco, N.; Boldini, D. Tunnel–framed building interaction: Comparison between raft and separate footing foundations. Géotechnique 2021, 71, 631–644. [Google Scholar] [CrossRef]
- Azzam, W. Utilization of confined cell for improving the machine foundation behavious. J. GeoEng. 2017, 10, 17–23. [Google Scholar]
- Franza, A.; Losacco, N.; Ledesma, A.; Viggiani, G.M.; Jimenez, R. Protecting surface and buried structures from tunnelling using pile walls: A prediction model. Can. Geotech. J. 2021, 58, 1590–1602. [Google Scholar] [CrossRef]
- Xu, J.; Zheng, L.; Song, G.; Zhang, D.; Sheil, B.; Marshall, A.M. Effects of embedded walls on tunnelling-induced sandy ground displacements: A numerical investigation. Géotechnique 2024, 21, 1–14. [Google Scholar]
- Song, G.; Xu, J.; Marshall, A.M. Numerical study on the effect of protective wall depth in reducing structure deformations caused by tunnelling. Comput. Geotech. 2023, 158, 105374. [Google Scholar]





| Parameter | Similarity Law | Constants of Similarity (Prototype: Model) |
|---|---|---|
| Strain (ε) | Cε | 1 |
| Geometrical Scale (L) | CG | 4 |
| Deformation (δ) | Cδ = CG | 4 |
| Young’s Modulus (E_s) | CEs | 1 |
| Flexural Rigidity (E_sI) | CEI = CEs * CG4 | 256 |
| Stress (ϐ) | Cβ = CEs | 1 |
| Poisson’s Ratio (υ) | Cυ | 1 |
| Density (ρ) | Cρ | 1 |
| Mass (m) | Cm = Cρ * CG3 | 64 |
| Concentrated Load (P) | Cp = Cβ * CG2 | 16 |
| Linear Load (W) | Cw = Cβ * CG | 4 |
| Moment (M) | CM = Cβ * CG3 | 64 |
| Series | Test No. | Distance Between Footings, X | Length of the Sheet Pile, Ls | New Strip Footing (F1) | Old Strip Footing (F2) | Notes | ||
|---|---|---|---|---|---|---|---|---|
| Contact Stress | Strip Footing ID | Contact Stress | Strip Footing ID | |||||
| (mm) | (mm) | kN/m2 | kN/m2 | |||||
| G0 | G0-0 | NA | NA | NA | NA | Increase 50 kN/m2 in stages until failure | FO | Benchmark test |
| G1 | G1-1 | 300 | 0.00 | Increase 50 kN/m2 in stages until failure | FN 30-0 | 100 | FO 30-0 | |
| G1-2 | 550 | 0.00 | FN 55-0 | FO 55-0 | ||||
| G1-3 | 750 | 0.00 | FN 75-0 | FO 75-0 | ||||
| G1-4 | 1000 | 0.00 | FN 100-0 | FO 100-0 | ||||
| G2 | G2-1 | 300 | 750 | FN 30-75 | FO 30-75 | |||
| G2-4 | 1000 | 750 | FN 100-75 | FO 100-75 | ||||
| G3 | G3-1 | 300 | 1000 | FN 30-100 | FO 30-100 | |||
| G3-4 | 1000 | 1000 | FN 100-100 | FO 100-100 | ||||
| G4 | G4-1 | 300 | 1250 | FN 30-125 | FO 30-125 | |||
| G4-4 | 1000 | 1250 | FN 100-125 | FO 100-125 | ||||
| G5 | G5-1 | 300 | 1500 | FN 30-150 | FO 30-150 | |||
| Sand Characteristics | Unit | Test Results |
|---|---|---|
| Average median size, D50 | mm | 0.41 |
| Average effective size, D10 | mm | 0.145 |
| Average D30 | mm | 0.255 |
| Average D60 | mm | 0.523 |
| Uniformity coefficient, Cu | --- | 3.631 |
| Curvature coefficient, Cc | --- | 0.848 |
| Max. dry density, γd max | kN/m3 | 18.20 |
| Min. dry density, γd min | kN/m3 | 15.60 |
| Maximum void ratio, emax | --- | 0.70 |
| Minimum void ratio, emin | --- | 0.46 |
| Max. friction angle, φmax | (ᵒ) | 42.9 |
| Min. friction angle, φmim | (ᵒ) | 30 |
| Specific gravity, Gs | --- | 2.66 |
| Classification (USCS) | --- | SP |
| Dense Sand Properties | ||
| Density | kN/m3 | 17.62 |
| Void ratio, efield | --- | 0.508 |
| Relative density, Dr | (%) | 80.00 |
| Internal friction angle | (ᵒ) | 39.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basha, A.M.; Akal, A.Y.; Zakaria, M.H. Mitigating Settlement and Enhancing Bearing Capacity of Adjacent Strip Footings Using Sheet Pile Walls: An Experimental Approach. Infrastructures 2025, 10, 83. https://doi.org/10.3390/infrastructures10040083
Basha AM, Akal AY, Zakaria MH. Mitigating Settlement and Enhancing Bearing Capacity of Adjacent Strip Footings Using Sheet Pile Walls: An Experimental Approach. Infrastructures. 2025; 10(4):83. https://doi.org/10.3390/infrastructures10040083
Chicago/Turabian StyleBasha, Ali M., Ahmed Yousry Akal, and Mohamed H. Zakaria. 2025. "Mitigating Settlement and Enhancing Bearing Capacity of Adjacent Strip Footings Using Sheet Pile Walls: An Experimental Approach" Infrastructures 10, no. 4: 83. https://doi.org/10.3390/infrastructures10040083
APA StyleBasha, A. M., Akal, A. Y., & Zakaria, M. H. (2025). Mitigating Settlement and Enhancing Bearing Capacity of Adjacent Strip Footings Using Sheet Pile Walls: An Experimental Approach. Infrastructures, 10(4), 83. https://doi.org/10.3390/infrastructures10040083