A Probabilistic Approach to the Spatial Variability of Ground Properties in the Design of Urban Deep Excavation
Abstract
:1. Introduction
2. Risk and Probabilistic Analysis in the Geotechnical Context
3. Benchmark Problem and Methods
3.1. Benchmark Problem
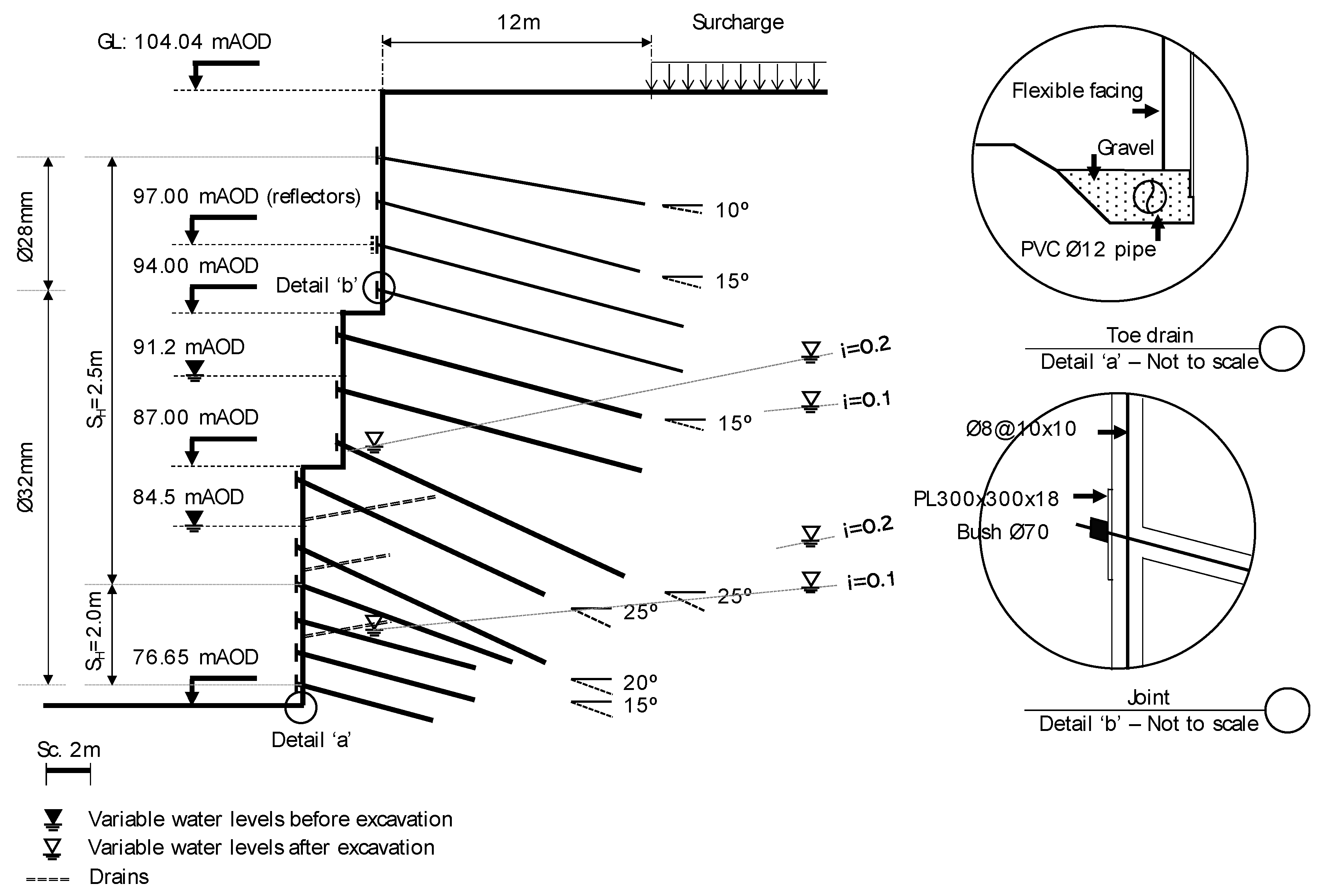
3.1.1. Materials
3.1.2. Plaxis 2D Model
3.2. Probabilistic Framework
3.2.1. Design Scenario 1
3.2.2. Design Scenario 2
3.3. Ultimate and Serviceability Limit States
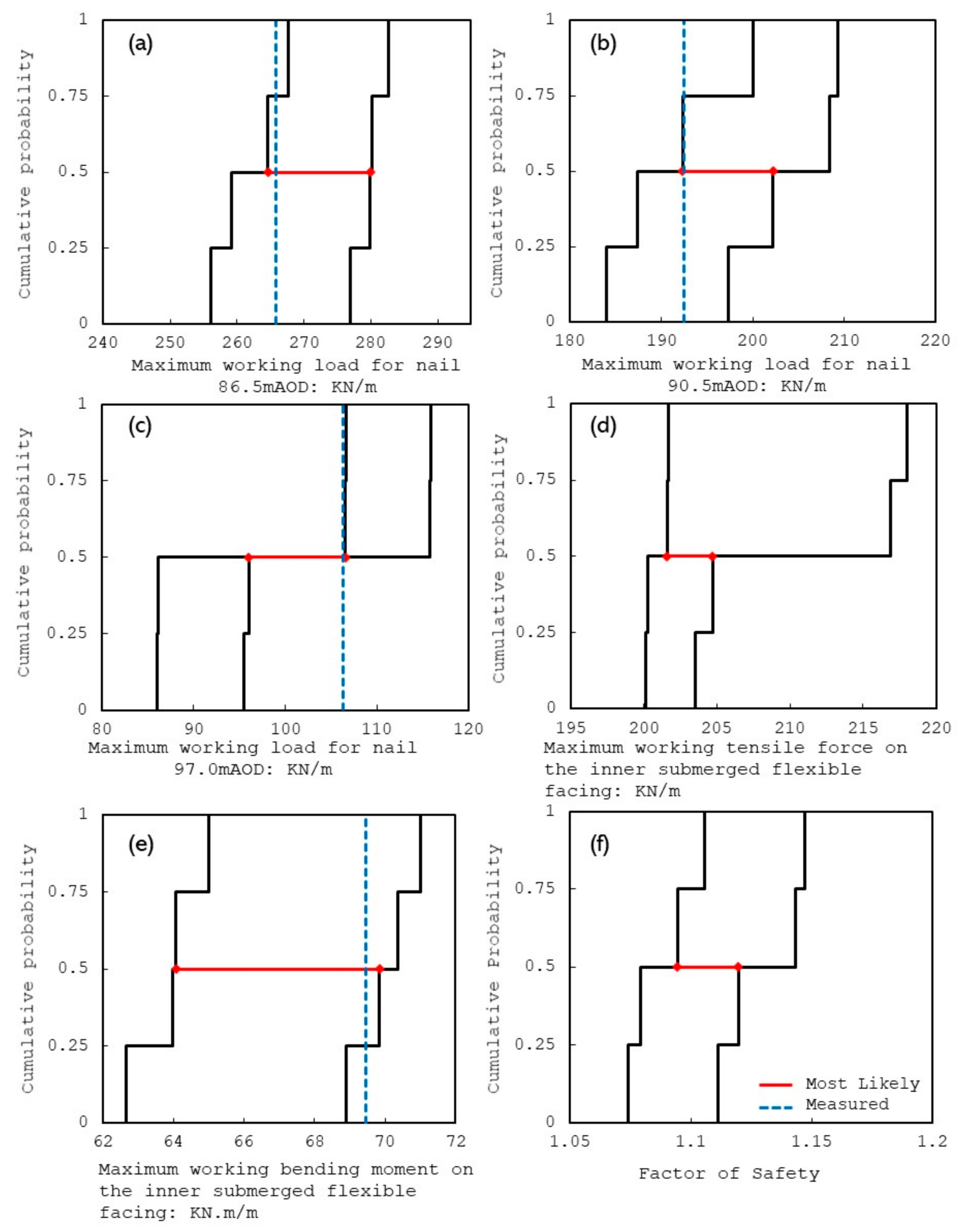
3.3.1. Serviceability of Flexible Facing
3.3.2. Bending Moments along Flexible Facing
3.3.3. Axial Mobilized Force in Soil Nails
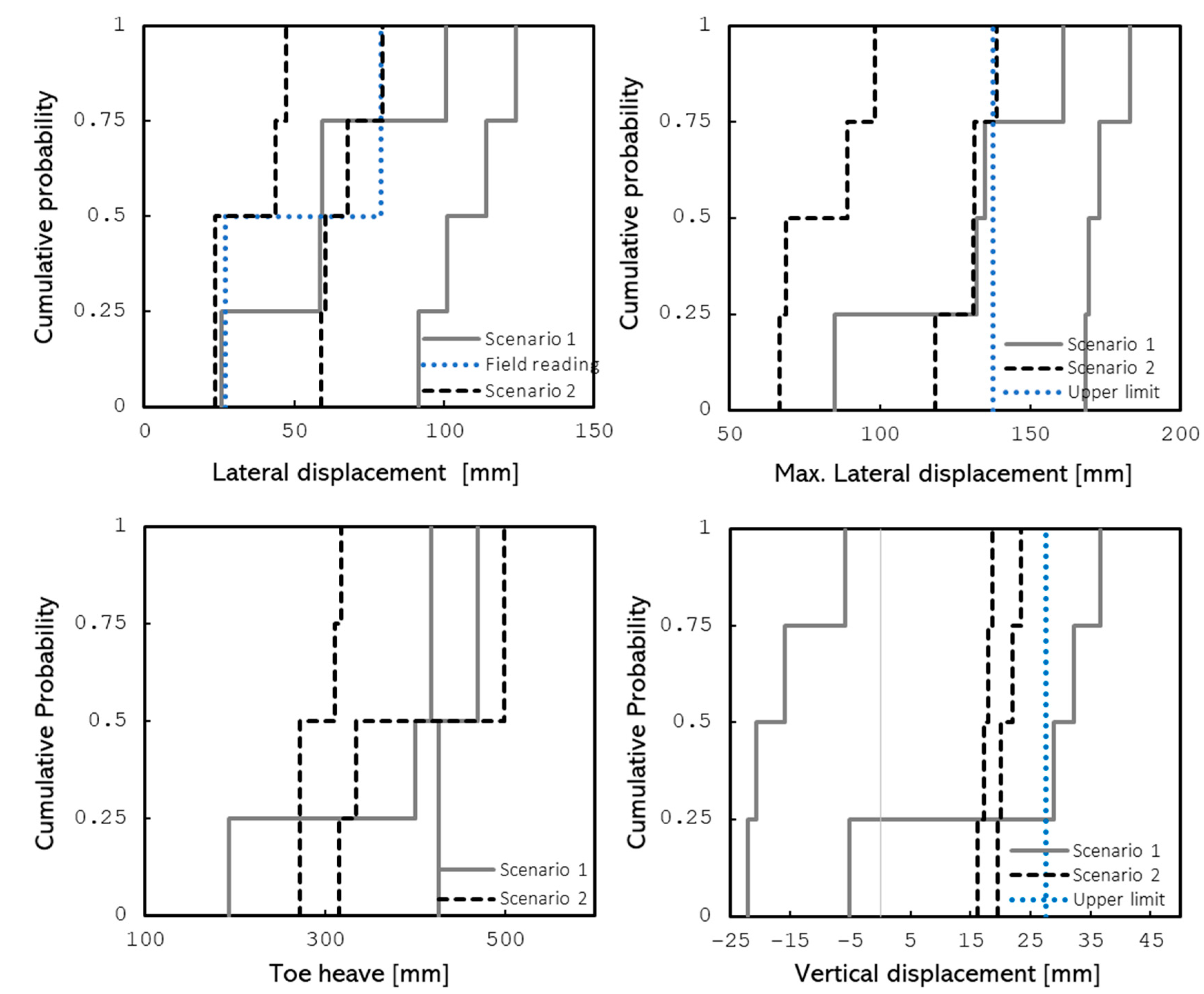
3.3.4. Lateral and Vertical Displacements
4. Results
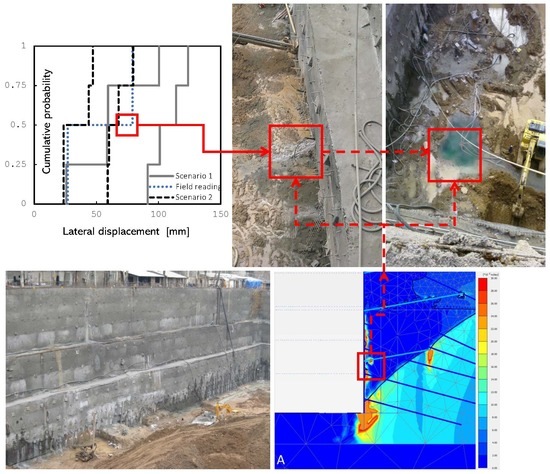
4.1. Design Scenario 1: Stochastically Dependent Variables
4.2. Design Scenario 2: Stochastically Independent Variables
Implications of Seepage
- -
- Lower-bound water level and upper-bound cohesion (representing dry season with maximum cementation) yielded the maximum factor of safety among the deterministic models.
- -
- Figure 8 shows the variation of the maximum bending moment on the inner wall (i.e., submerged) for the eight modelling scenarios. Solid lines represent the FE-predicted values, whereas the dashed line infers the designed mean bending moment according to the FHWA-IF-99-015 (1999) recommendations. Bending moment values derived from the FHWA formulation match those of the upper-bound RS values and as such are of reasonably good credibility.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- UN. World Population Prospects: The 2012 Revision; UN Technical Report; UN: New York, NY, USA, 2013. [Google Scholar]
- The London Borough of Camden. Camden Planning Guidance CPG 4: Basements and Lightwells; The London Borough of Camden: London, UK, 2011.
- Assadi-Langroudi, A.; Theron, E. Gaps in particulate maters: Formation, mechanisms, implications. In Proceedings of the 17th African Regional Conference on Soil Mechanics and Geotechnical Engineering, Cape Town, South Africa, 7–9 October 2019; Geotechnical Division, South African Institute of Civil Engineers: Cape Town, South Africa, 2019. [Google Scholar]
- Assadi-Langroudi, A.; Jefferson, I. Constraints in using site-won calcareous clayey silt (loam) as fill materials. In XVI ECSMGE Geotechnical Engineering for Infrastructure and Development; ICE Institution of Civil Engineers Publishing: London, UK, 2015; pp. 1947–1952. [Google Scholar]
- Soil Nail Walls Reference Manual; FHWA-NHI-14-007; US Department of Transportation, Federal Highway Administration: Washington, DC, USA, 2015.
- Duncan, J.M. Factors of safety and reliability in geotechnical engineering. J. Geotech. Geoenviron. Eng. 2000, 126, 307–316. [Google Scholar] [CrossRef]
- Wong, F.S. First Order Second Moment Method. Comput. Struct. 1985, 20, 779–791. [Google Scholar] [CrossRef]
- Kunstmann, H.; Kinzelbach, W.; Siegfried, T. Conditional first order second moment method and its application to the quantification of uncertainty in groundwater modelling. Water Resour. Res. 2002, 38, 1–14. [Google Scholar] [CrossRef]
- Du, H.; He, W.; Sun, D.; Fang, Y.; Liu, H.; Zhang, X.; Cheng, Z. Monte Carlo simulation of magnetic properties of irregular Fe islands on Pb/Si(111) substrate based on the scanning tunneling microscopy image. Appl. Phys. Lett. 2010, 96, 1–3. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Fenton, G.A. Three dimensional seepage through spatially random soil. J. Geotech. Geoenviron. Eng. 1997, 123, 153–160. [Google Scholar] [CrossRef]
- Goldsworthy, J.S.; Jaksa, M.B.; Fenton, G.A.; Griffiths, D.V.; Kaggwa, W.S.; Poulos, H.S. Measuring the risk of geotechnical site investigations. In Probabilistic Applications in Geotechnical Engineering; ASCE: Denver, CO, USA, 2007; pp. 1–12. [Google Scholar]
- Jiang, S.H.; Li, D.Q.; Cao, Z.J.; Zhou, C.B.; Phoon, K.K. Efficient system reliability analysis of slope stability in spatially variable soils using Monte Carlo simulation. J. Geotech. Geoenviron. Eng. 2014, 141, 1–13. [Google Scholar] [CrossRef]
- Tonon, F.; Mammino, A. A random set approach to the uncertainties in rock engineering and tunnel lining design. In Proceedings of the ISRM International Symposium on Prediction and Performance in Rock Mechanics and Rock Engineering (EUROCK ‘96), Torino, Italy, 2–5 September 1996; Volume 2, pp. 861–868. [Google Scholar]
- Tonon, F.; Bernardini, A.; Mammino, A. Determination of parameters range in rock engineering by means of Random Set Theory. Reliab. Eng. Syst. Saf. 2000, 70, 241–261. [Google Scholar] [CrossRef]
- Tonon, F.; Bernardini, A.; Mammino, A. Reliability analysis of rock mass response by means of Random Set Theory. Reliab. Eng. Syst. Saf. 2000, 70, 263–282. [Google Scholar] [CrossRef]
- Schweiger, H.F.; Peschl, G.M. Basic Concepts and Applications of Random Sets in Geotechnical Engineering. In CISM International Centre for Mechanical Sciences; Griffiths, D.V., Fenton, G.A., Eds.; Springer: Berlin/Heidelberg, Germany, 1975; Volume 491, pp. 113–126. [Google Scholar]
- Assadi, A.; Yasrobi, S.; Nasrollahi, N. A comparison between the lateral deformation monitoring data and the output of the FE predicting models of soil nail walls based on case study. In Proceedings of the 62th Canadian Geotechnical Conference and 10th Joint CGS/IAH-CNC Groundwater Conference, Halifax, NS, Canada, 20–24 September 2009. [Google Scholar]
- Nasekhian, A.; Schweiger, H.F. Random Set Finite Element method application to tunnelling. In Proceedings of the 4th International Workshop on Reliable Engineering Computing, Singapore, 3–5 March 2010. [Google Scholar]
- BS 8006-2:2011+A1:2017. Code of Practice for Strengthened/Reinforced Soils, Soil Nail Design; British Standards Institution: London, UK, 2011.
- Schikora, K.; Ostermeier, B. Two-dimensional calculation model in tunnelling verification by measurement results and by spatial calculation. In Proceedings of the 6th International Conference on Numerical Methods in Geomechanics, Innsbruck, Austria, 11–15 April 1988; Volume 3, pp. 1499–1530. [Google Scholar]
- US Department of Transportation, Federal Highway Administration. Geotechnical Engineering Circular No. 4: Ground Anchors and Anchored Systems; FHWA-IF-99-015; US Department of Transportation: Washington, DC, USA, 1999.
- Phear, A.; Dew, C.; Ozsoy, N.I.; Wharmby, N.J.; Judge, J.; Barley, A.D. Soil Nailing—Best Practice Guidance C637D; Construction Industry Research and Information Association CIRIA Publications: London, UK, 2005. [Google Scholar]
- BS 8002:1994. Code of Practice for Earth Retaining Structures; BSI: London, UK, 1994.





| Layer | Soil Type | Depth: m | Ψ: ° | ϕ′: ° | C’: kPa | γ: kN/m3 | E: kPa | ν | Kh: m/s | Kv: m/s |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Made Ground | 0.0–1.2 | 01 | 20 | 10 | 17 | 9800 | 0.4 | 1.0 × 10−4 | 1.0 × 10−8 |
| 2 | Silty clayey sand | 1.2–4.2 | 14 | 28 | 20 | 18 | 24,500 | 0.3 | 1.2 × 10−4 | 1.2 × 10−8 |
| 3 | Alluvium | 4.2–9.2 | 14 | 28 | 25 | 18 | 24,500 | 0.35 | 3.1 × 10−4 | 3.1 × 10−8 |
| 4 | Silty clayey sand | 9.2–18.2 | 14 | 34 | 20 | 18 | 34,300 | 0.3 | 4.2 × 10−7 | 4.2 × 10−7 |
| 5 | Clay | 18.2–21.2 | 0 | 25 | 35 | 19 | 34,300 | 0.4 | 1.9 × 10−7 | 3.28 × 10−8 |
| 6 | Gravelly sandy clay | 21.2–29.2 | 14 | 30 | 25 | 19 | 49,000 | 0.3 | 1.31 × 10−7 | 4.36 × 10−6 |
| 7 | Silty clayey gravel | 29.2–35.0 | 14 | 36 | 20 | 19 | 58,800 | 0.3 | 3.6 × 10−9 | 1.0 × 10−9 |
| Material | Eeq: kPa | Sh: m | Ddh: m | EI: kN·m−2·m−1 | EA: kN·m−1 | Model |
|---|---|---|---|---|---|---|
| Nail elements (top nine rows) | 2.10 × 108 | 2.50 | 0.08 | 1.38 × 102 | 3.81 × 105 | Elastoplastic |
| Nail elements (lower four rows) | 2.10 × 108 | 2.00 | 0.08 | 1.72 × 102 | 4.79 × 105 | Elastoplastic |
| Reinforced shotcrete facing | - | - | - | 2.50 × 103 | 3.00 × 106 | Elastic |
| Dataset | C’: kPa | WL: mAOD | I | |
|---|---|---|---|---|
| Scenario 1 | Set 1 | 20~24 | 79.75~86 | |
| Set 2 | 22~26 | 85~88 | ||
| Scenario 2 | Set 1 | 79.75~86 | 0.1~0.15 | |
| Set 2 | 85~88 | 0.15~0.2 |
| Diameter: mm | Distance from Crest: m | Horizontal Spacing: m | Vertical Spacing: m | Maximum Normal Force: kN/m | Failure Load: kN/m | |
|---|---|---|---|---|---|---|
| D | H | Sh | Sv | Tmax | Tf | |
| Nail 8 | 28 | 21.5 | 2.5 | 2.25 | 265.8 | 255.4 |
| Nail 6 | 32 | 16.2 | 2.5 | 2 | 192.46 | 333.6 |
| Nail 3 | 32 | 9.68 | 2.5 | 2.5 | 106.37 | 333.6 |
| : mm | 41.1 | 45.9 | 49.0 | 55.2 | 58.2 | 64.8 | 69.2 | 76.5 |
| –1.2 | –0.9 | –0.7 | –0.3 | –0.1 | 0.2 | 0.5 | 0.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herridge, J.B.; Tsiminis, K.; Winzen, J.; Assadi-Langroudi, A.; McHugh, M.; Ghadr, S.; Donyavi, S. A Probabilistic Approach to the Spatial Variability of Ground Properties in the Design of Urban Deep Excavation. Infrastructures 2019, 4, 51. https://doi.org/10.3390/infrastructures4030051
Herridge JB, Tsiminis K, Winzen J, Assadi-Langroudi A, McHugh M, Ghadr S, Donyavi S. A Probabilistic Approach to the Spatial Variability of Ground Properties in the Design of Urban Deep Excavation. Infrastructures. 2019; 4(3):51. https://doi.org/10.3390/infrastructures4030051
Chicago/Turabian StyleHerridge, Jacob B., Konstantinos Tsiminis, Jonas Winzen, Arya Assadi-Langroudi, Michael McHugh, Soheil Ghadr, and Sohrab Donyavi. 2019. "A Probabilistic Approach to the Spatial Variability of Ground Properties in the Design of Urban Deep Excavation" Infrastructures 4, no. 3: 51. https://doi.org/10.3390/infrastructures4030051
APA StyleHerridge, J. B., Tsiminis, K., Winzen, J., Assadi-Langroudi, A., McHugh, M., Ghadr, S., & Donyavi, S. (2019). A Probabilistic Approach to the Spatial Variability of Ground Properties in the Design of Urban Deep Excavation. Infrastructures, 4(3), 51. https://doi.org/10.3390/infrastructures4030051