Modelling and Characterizing a Concrete Gravity Dam for Fragility Analysis

Abstract

Most gravity dams have been designed and built during the past century with methods of analysis that are now considered inadequate. In recent decades, knowledge of seismology, structural dynamics and earthquake engineering has greatly evolved, leading to the evaluation of existing dams to ensure public safety. This study proposes a methodology for the proper modelling and characterisation of the uncertainties to assess the seismic vulnerability of a dam-type structure. This study also includes all the required analyses and verifications of the numerical model prior to performing a seismic fragility analysis and generating the corresponding fragility curves. The procedure presented herein also makes it possible to account for the uncertainties associated with the modelling parameters as well as the randomness in the seismic solicitation. The methodology was applied to a case study dam in Eastern Canada, whose vulnerability was assessed against seismic events with characteristics established by the current safety guidelines.

1. Introduction

Most gravity dams have been in operation for 30 to 50 years, and were built with the knowledge and technologies of the time. Certainly, concrete gravity dams are designed to remain operational under normal conditions, to sustain minimal damage under infrequent operative conditions and to prevent total loss of the reservoir under extreme events such as seismic actions. The importance of the behaviour of the dam under seismic loading then arises, given the human fatalities and the economic losses that can occur as a result. In recent decades, the knowledge of seismic engineering has evolved considerably, making it necessary to reassess the stability of dams under seismic loading.

Methods for analysing the structural response of a dam–reservoir–foundation system rely on deterministic or probabilistic approaches. Deterministic methods are often considered too safe, or even unsafe in some cases, because they neglect the different sources of uncertainty and because of the use of extreme load cases with very low probabilities of occurrence [1,2,3]. Procedures that provide a more rational way of assessing the safety of concrete gravity dams are required to establish priorities. Moreover, a probabilistic approach is required to manage the various sources of uncertainty that may impact the dam performance and decisions related thereto [1]. Within this probabilistic framework, a fragility analysis is a promising alternative, particularly suited to study the seismic vulnerability of structures and to estimate the level of damage likely to be caused by seismic events.

The implementation of fragility curves in the domain of dams is a relatively new practice. To the best of the authors’ knowledge, the first study in the field was carried out by Ellingwood and Tekie [4]. Four limit states were considered in the seismic fragility analyses, and non-linear temporal dynamic analysis were performed including the dam–reservoir–foundation (DRF) interaction effects. Samples of the model were obtained using the method of Latin hypercube sampling (LHS) and were coupled with twelve historical accelerograms. These samples were analysed for six levels of seismic intensity, by calibrating the acceleration time compared to the spectral acceleration measured at the pitch period, to obtain the fragility curves. This study reveals that in all cases the log-normal model of fragility fit the results of the simulation very well. In the same manner, Mirzahosseinkashani and Ghaemian [5] and Ghanaat et al. [6,7] applied the same methodology proposed by Ellingwood and Tekie [4] and performed non-linear analysis to assess the vulnerability of a case study dam considering finite element models with different degrees of complexity. Similarly, the work performed by Lupoi and Callari [8] presents a probabilistic seismic assessment method able to manage the physical complexity of the DRF system and the uncertainties regarding structural data and external actions. The fragility curves were obtained via a standard Monte Carlo simulation procedure, and no probability was assumed to represent the fragility curves. Further studies on the subject were performed by Zhong and Lin [9], where considering the ground motion and material uncertainties, 180 non-linear seismic analyses were performed, based on which typical seismic damage modes were obtained. This research used samples obtained by thirty Monte Carlo simulations and six levels of seismic intensity.

The most recent studies were from Bernier et al. [10,11], Hariri-Ardebili and Saouma [12], Lallemant et al. [13] and Segura et al. [14]. In the first two studies [10,11], the finite element method is used to model a single block of a case study dam considering DRF interaction. Uncertainties in the ground motions and modelling parameters are included, and an LHS technique is used to propagate these sources of uncertainty. The fragility curves are developed using non-linear time-history analysis to evaluate two limit states: sliding at the dam base and at lift-joints. In the fist paper of Bernier et al. [10], the uncertainty related to the spatial variation of angle of friction is included in the fragility analysis through the incorporation of random fields modelling. In their second paper [11] the same methodology is used together with the conditional spectrum method to select ground motion times series. Hariri-Ardebili and Saouma [12] explored the development of seismic fragility curves for gravity dams with and without vertical ground motion. The derived fragility curves using scaled records were compared with those from probabilistic seismic demand analysis, showing acceptable consistency between the two methods. Similarly, the study performed by Lallemant et al. [13] provides a synthesis of the most commonly used methods for fitting fragility curves and highlights some of their significant limitations. Finally, in the study by Segura et al. [14], a similar model of the case study dam in Bernier et al. [10,11] is used to develop up-to-date fragility curves for the sliding limit states using a record selection method based on the generalised conditional intensity measure approach. These fragility functions are then combined with the recently developed regional hazard data to evaluate the annual risk, which is measured in terms of the unconditional probability of limit state exceedance. Further and more exhaustive information can be found in the state-of-the-art review of seismic fragility applied to concrete dams by Hariri-Ardebili and Saouma [15].

These studies show that the most reliable methods should be implemented where dam safety is concerned. Undoubtedly, one of the best methods for analysing gravity dams is non-linear dynamic time history analysis [16]. However, sampling techniques must be used in order to minimise the cost of the non-linear finite element analyses required to develop the fragility functions. While these previous studies have mainly focused on the methodology to develop fragility curves, they provide limited guidelines regarding the modelling and characterisation of concrete gravity dams for such analysis. Moreover, the simplifications regarding the modelling assumptions can lead to the improper evaluation of the seismic response of the dam. Among these simplifications, of note are the use of a very general or wide range of parameters due to the lack of rigorous material properties characterisation, the consideration of linear or unverified numerical models, the lack of a soil–fluid–structure interaction, the assumption of a massless foundation and the inadequate use of border conditions to describe the physical behaviour of the structure. In light of the abovementioned limitations, the main objective of this paper is to present a case study dam to illustrate a systematic methodology for modelling the DRF system and characterisation of the uncertainties associated with this type of structure to perform a seismic fragility analysis. Accordingly, the major contributions of this paper, in order of presentation, can be listed as follows: (i) the development, calibration and validation of a nonlinear finite element model (FEM) of a dam-type structure; (ii) the presentation of a procedure for applying static and dynamic loading in the DRF system, including the detailed deconvolution of the ground motion records; (iii) the design of experiments to generate samples of the system to perform a probabilistic analysis; (iv) the provision of insight into the parameters relevant for the uncertainty modelling and determination of their distributions; (v) illustration of the procedure for selection and scaling of the seismic input and (vi) the presentation of a fragility framework to generate fragility curves and assess the expected seismic performance under extreme events. The proposed methodology was applied to a case study structure in Eastern Canada.

2. Finite Element Model of the Case Study Dam

The present study is focused on a case-study concrete gravity dam spillway structure. The case study dam was built in the 1970s, has a length of 1638 m, a maximum height of 44.2 m and consists of three structures: west dike structure, bottom outlet spillway structure and main dam. This study is particularly interested in the bottom outlet spillway structure, the characteristics of which are summariSed in

Table 1. Main characteristics of the case study dam’s bottom outlet spillway.

Soil foundation	Diorite rock, gneiss, granite, hybrid
Max. height	29.3 m
Crest length	192.6 m
Max. width	28.8 m
Crest width	12.2 m
Drain	Drained with injection curtain

, and one of its blocks is considered representative of the structure. This block is a concrete gravity-type monolith, and its main geometric features and general configuration are shown in Figure 1.

2.1. Model Configuration and Mesh Considerations

The numerical model must adequately represent dynamic behaviour to minimise the epistemic uncertainties related to the modelling assumptions. The model was developed using the computer software LS-Dyna [17], following the recommendation of Noble [18] and the United States Bureau of Reclamation (USBR) [19]. The dimensions and meshing of the foundation and the reservoir in the finite element model were defined consistent with the recommendations of USBR [19], where the extent of the foundation is defined as a function of the block height H and the foundation mesh element sizes are, in general, controlled by seismic requirements. In the same manner, the reservoir is modelled with the same length as the foundation and a constant depth. The elements are sufficiently small to ensure the adequate transmission of the soil movement through the water. Further details are provided in Section 2.1.2 and Section 2.1.3. Figure 2 presents the main features of the finite element model. To reduce the computational burden, an explicit time integration method [20] was used within LS-Dyna with single-point-of-integration hexahedral elements to estimate the seismic response of the dam.

2.1.1. Block-6

Due to the presence of contraction joints, the interaction between the blocks of the bottom outlet spillway structure is not significant enough to justify the realisation of a complex 3D model. Thus, only block-6 was modelled with 10,000 elements and a linear elastic material to model the concrete behaviour. The nonlinearities are introduced later on in the model in the form of contact surfaces between the dam system components. Some elements such as drainage galleries were not taken into account since their influences on the global behaviour of the structure are not significant.

2.1.2. Foundation

Part of the foundation was modelled to account for its inertia, flexibility and damping given that the structure–foundation interaction elongates the periods of vibration and provides an additional energy dissipation mechanism. The extent of the foundation was defined as a function of the block height H (25–28 m) [19]. Its length in the upstream–downstream direction is 160 m (6H), and its depth is 80 m (3H). The foundation mesh element sizes are generally controlled by seismic requirements. Consequently, the maximum element size depends on the foundation material properties and on the frequencies of the structure [19]. There should be no fewer than 10 elements per wavelength, and every attempt should be made to maintain uniform elements. The wavelength of interest is given by:

$$w={\displaystyle \frac{\sqrt{{\displaystyle \frac{E_{rock}}{2(1+{\nu }_{rock}){\rho }_{rock}}}}}{f_0}},$$

(1)

where w is the wavelength, $E_{rock}, {\nu }_{rock} \mathrm{and} {\rho }_{rock}$ are the modulus of elasticity, the Poisson coefficient and the density of the foundation, respectively, and $f_0$ is the fundamental frequency of the structure–reservoir–foundation system. Considering from preliminary analysis that a system’s fundamental frequency is approximately 10 Hz, the maximum foundation element dimension was fixed at 20 m. To limit the number of elements in the model, the foundation width was identical to that of the block-6, and the size of the elements was progressively increased, as shown in Figure 2. The final model of the foundation comprised 57,300 elements.

2.1.3. Reservoir

To account for the interaction between the reservoir and the structure, part of the reservoir was modelled with fluid elements having the physical properties of water. The reservoir was modelled on the same length as the foundation, had a constant depth of 21.94 m, and possessed 6500 elements. The compressibility of water was considered in order to adequately model the propagation of pressure waves in the reservoir, whereas the viscous effect was neglected since it had no influence in the fluid–structure interaction. The elements must be sufficiently small (<15 m) to ensure the adequate transmission of the soil movement through the water [19]. This condition is widely respected in the present model since the maximum dimension of a reservoir element remained less than 2 m. The elements of the reservoir were modelled using a Lagrangian formulation and NULL material in LS-Dyna that has no shear stiffness and no yield strength and behaves in a fluid-like manner. The NULL material is associated with an equation of state, and as recommended by Noble [18], a linear polynomial relation was used, where the pressure P applied to one element is given by:

$$P=K\left({\displaystyle \frac{\rho }{{\rho }_0}}-1\right),$$

(2)

where K is the water isostatic modulus of elasticity equal to 2.18 GPa, $\rho$ is the water density at time t during the analysis, and ${\rho }_0$ is the initial water density.

2.2. Boundary Conditions and Contact Interfaces

In this study, as recommended by several studies [19,21] and detailed below, the loads were applied in two phases: a dynamic relaxation phase for static loads and a dynamic phase for the seismic loads. The boundary conditions were different depending on the loading phase. During the dynamic relaxation phase, a symmetric boundary condition was applied in the bottom and downstream–upstream faces, where the normal displacements were zero to simulate the constraints of the model in the space. In the dynamic phase, symmetric boundary conditions were removed, and the reactions obtained from the dynamic relaxation phase were also applied on the boundary faces for equilibrium. Additionally, non-reflective boundaries were added on the bottom, downstream and upstream faces of the model to account for the radiation damping and to dissipate the energy trapped in the foundation due to the finite length of the model (i.e., to simulate a semi-infinite behaviour). In addition, horizontal and vertical displacements were restricted at the bottom edges of the foundation to prevent rigid body movements of the model during dynamic analyses.

Regarding the contact surfaces between the different components of the system, sliding contact with zero friction was used to model the block–reservoir interface. For the reservoir–foundation interface, tied contact was applied, except near the upstream face of the block, where sliding contact with zero friction was used to maintain the reservoir load during the sliding of the block. Preliminary linear analyses—detailed further below—identified the block–foundation interface at the base of the block as high-tensile-stress areas, and therefore where cracking and sliding are likely to occur. Consequently, the model nonlinearity was constrained to these areas only, using tiebreak contact elements with a tension-shear failure criterion. The finite element code assumes the contact surface is broken when the following criterion is satisfied:

$${\left({\displaystyle \frac{|{\sigma }_n|}{NFLS}}\right)}^2+{\left({\displaystyle \frac{|{\sigma }_s|}{SFLS}}\right)}^2\ge 1,$$

(3)

where ${\sigma }_n$ and ${\sigma }_s$ are the normal and shear stress, respectively, $NFLS$ is the tensile strength, and $SFLS$ is the cohesion. As long as the failure criterion is not reached, the tensile-compressive and shear stresses are transmitted at the contact level. If the normal stress is in compression, the first term of Equation (3) is not considered, and only cohesion is taken into account. In addition, no resistance is mobilised by friction before breaking the contact. Once the failure criterion is reached, only the friction contributes to the resistance of the contact.

2.3. Damping and Hourglassing Control

Energy dissipation within a complex dam–reservoir–foundation model may occur from a number of mechanisms. One major source is the use of nonreflecting boundary conditions; otherwise, too much energy could be trapped within the foundation domain. Another energy dissipation mechanism comes from the interaction of the dam with the reservoir through the generation of elastic waves in the reservoir. This phenomenon is known as radiation damping, which is considered in the model by also using a nonreflecting boundary condition in the upstream face of the reservoir. Regarding the block structure, to consider structural damping and potential nonlinear behaviour, a viscous damping of ${\xi }_{concrete}=1.5\%$ was associated with the concrete material. For the foundation, and as recommended by the USBR [19], a viscous damping of $\xi =5\%$ was also associated with the rock material.

The largest disadvantage of single-point integration elements is the need to control the zero energy modes that can arise, known as hourglassing modes [22]. The hourglass control method used in this study is the stiffness method, where a small elastic stiffness capable of stopping the formation of the anomalous modes but having a negligible effect on the stable global modes was added to the model. The hourglass modes control methods must be calibrated so that the energy associated with these modes remains less than 10% of the internal energy of the system and optimally less than 5% [23]. By setting the hourglassing parameters according to the recommendations of the USBR [23] in LS-Dyna, these parasitic modes were eliminated from the model, and the hourglassing energy criterion was always respected.

2.4. Validation of the Numerical Model

Dynamic Behavior

To evaluate the accuracy of the FEM, the dynamic properties of the block–reservoir–foundation system were compared to the results obtained from existing models of the structure developed by the case study dam owners. The validation of the dynamic characteristics was based on the fundamental period of the system and global damping. Because of the type of element used to model the reservoir in the LS-Dyna model, a modal analysis could not be performed. Therefore, a free vibration test was simulated to estimate the fundamental period and the damping of the system. Considering gravity loads only, a force was applied at the crest of the block in the upstream–downstream direction, and then suddenly withdrawn. The recorded horizontal displacement time series of a node at the crest of the block was then used to estimate the fundamental period of the system through the calculation of the Fourier spectrum. The global damping was approximated using the logarithmic decrement:

$$\xi ={\displaystyle \frac{1}{2\pi m}}ln\left({\displaystyle \frac{u_n}{u_{n+m}}}\right),$$

(4)

where $u_n$ is the displacement measured at a given time and $u_{n+m}$ is the displacement measured m cycles later. The damping was calculated as the average value using the first representative peak (peak n) and m numbers of cycles afterward.

To match the dynamic characteristics of the model, the material properties were selected as the calibration parameters. A first model, which will be referred to as model M0, was generated with initial material properties identical to those adopted by the dam owners and the typical viscous damping values used to calibrate numerical models using dynamic tests on an undamaged dam [24]. The material properties used for the M0 model are summarised in

Table 2. Material properties of the M0 model.

Elasticity modulus	$E_{rock}=40$ GPa, $E_{concrete}=21.4$ GPa
Damping	${\xi }_{rock}=5\%$, ${\xi }_{concrete}=1.5\%$
Density	${\rho }_{rock}=2600$ kg/m${}^3$, ${\rho }_{concrete}=2300$ kg/m${}^3$
Poisson coefficient	${\nu }_{rock}=0.3$, ${\nu }_{concrete}=0.164$
Reservoir	Westergaard added mass

. This model was used to estimate the difference between the fundamental period of the system and the target value of $T_{1,target}=0.096\mathrm{s}$, obtained by the dam owners.

Figure 3 shows the displacement time series of a crest node during the free vibration test simulation conducted with the M0 model. The fundamental period of the system with the M0 model was $T_{1,M0}=0.110$ s and presented a difference of 14.7% compared to the target period. The overestimation of the fundamental period relative to the reference model could be explained by the excessive flexibility of the foundation. Indeed, unlike the model considered by the dam owners, the mass of the foundation was considered together with the absorbing boundary conditions. According to the USBR [19], these border conditions—while more realistic—may introduce additional flexibility to the foundation. Therefore, a second model M1 was tested to confirm this hypothesis, whose rock modulus of elasticity was increased to $E_{rock}=50\mathrm{GPa}$ according to the ASTM D4394-04 [25] for rock foundation sites.

Table 3. Dynamic properties of the finite element model (FEM).

Model	Fundamental Period (s)	Damping (%)
Reference	0.096	5.50
LS-Dyna M1	0.106	2.88
LS-Dyna M0	0.110	3.19

provides a comparison of the dynamic properties obtained with the different models. By adapting the value of the foundation modulus of elasticity, it was possible to match the target value of the natural period and highlight the impact of this parameter on the dynamic behaviour of the studied system and therefore on the seismic response. Regarding the damping of the system, it matches well with the forced-vibration test performed by Proulx and Paultre [24] on undamaged dam-type structures. Nevertheless, given the unavailability of in situ experimental results, the exact natural period of the system and its damping remain unknown. Consequently, as part of the probabilistic framework conducted here, the dynamic properties of the structure will be varied by defining the concrete damping and the concrete and foundation modulus of elasticity as random variables.

3. Loads

The loads considered in this study are summarised in

Table 4. Load conditions.

Load	Details
Self-weight - Plot-6	${\rho }_{concrete}=2300$ kg/m${}^3$
Reservoir weight	Reservoir level = MOL
Upstream hydrostatic thrust	Reservoir level = MOL
Uplift	Concrete–rock contact Reservoir level = MOL Drain efficiency: between 0% and 70%
Hydrodynamic load	Automatic with fluid elements Reservoir level = MOL
Horizontal seismic load	Representative accelerograms
Vertical seismic load	Representative accelerograms

MOL: maximum operating level.

. Loads resulting from ice thrust, sediment surge and thermal gradient were neglected, considering they would not affect the overall behaviour of the system under seismic actions. Only one loading case was considered to analyse the seismic response of the case study structure, which included the self-weight of the block, the hydrostatic and hydrodynamic loads exerted by the reservoir on the block, the uplift pressures at the concrete–rock contact and the horizontal and vertical seismic loads.

3.1. Static and Dynamic Loads

The weight of the block was integrated in all the analyses, and it was determined directly by LS-Dyna as well as the reservoir and the hydrostatic load. For all the analyses, the maximum operating level (MOL) of the reservoir was considered (i.e., a constant reservoir elevation of 21.94 m with respect to the downstream base of block-6). Even if the foundation is associated with a mass, its self-weight was not taken into account in the calculations to avoid settlement during the analysis. Concerning the uplift loads, they were only applied at the concrete–rock contact, and they were calculated at each node of the structure base according to the prescribed expressions by the United States army corps of engineers (USACE) [26].

The dynamic loads considered in the analysis comprised the seismic load in the horizontal (upstream–downstream) and vertical directions. In addition, the model of the reservoir with fluid elements made it possible to automatically account for the hydrodynamic thrust due to the seismic shocks. The dynamic effects on the uplift distribution were neglected, assuming that the uplift profile would remain constant during seismic loading [19,26].

3.2. Application of Static and Dynamic Loads

The application of gravity and static loads in an explicit analysis can produce unexpected results if the load is applied too quickly, because the solution may diverge. To avoid this problem, as previously mentioned, the static loads were applied during a dynamic relaxation phase, and the seismic loads were applied in a dynamic analysis phase. The dynamic relaxation then reduced the nodal velocity at each time step, which is equivalent to a highly damped dynamic analysis [22]. Within the context of this study, the application of the gravity and statics loads took a total duration of 8 s. The self-weight of the dam was applied progressively from 0 to 4 s, whereas the weight of the reservoir and uplift pressures were applied gradually, after the self-weight, between 4 and 8 s. At the end of the dynamic relaxation phase, the reaction forces at each node belonging to the foundation faces were recorded to be used in the next phase to maintain a quasistatic state of the model.

Regarding the dynamic phase, the most straightforward method for applying ground motions to finite element models is to apply accelerations at the base [19]. In contrast, earthquake motion cannot be specified directly at the model truncations, as this would render any absorbing boundary ineffective [27]. Instead, effective earthquake forces were computed from the earthquake excitation and applied either directly at the absorbing boundaries. Given the presence of an absorbing boundary condition during the dynamic phase, it is necessary to use nodal forces instead of base accelerations at the same location as a non-reflecting boundary condition. The seismic time series were applied as a stress time series using the following expressions:

$$\begin{array}{cc}\hfill {\sigma }_h& = 2{\rho }_{rock}{v}_h\sqrt{{\displaystyle \frac{E_{rock}}{2{\rho }_{rock}(1+{\nu }_{rock})}}},\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill {\sigma }_v& = 2{\rho }_{rock}{v}_v\sqrt{{\displaystyle \frac{E_{rock}(1-{\nu }_{rock})}{{\rho }_{rock}(1+{\nu }_{rock})(1-2{\nu }_{rock})}}},\hfill \end{array}$$

(6)

where ${\sigma }_h$ is the horizontal stress time series, ${\rho }_{rock}$ is the foundation density, $v_h$ is the horizontal ground velocity (obtained by integration of the horizontal acceleration), ${\sigma }_v$ is the vertical stress time series, $v_v$ is the vertical ground velocity (obtained by integration of the vertical acceleration) and $E_{rock}$ and ${\nu }_{rock}$ are the modulus of elasticity and the Poisson coefficient of the foundation, respectively. Since the non-reflecting boundary condition and earthquake ground motions were to be applied at the same location, care was taken to ensure that the nodal forces applied were of the proper magnitude to ensure that the incident waves propagating through the foundation medium produced the proper excitation at the base of the structure [27].

3.3. Deconvolution of the Ground Motions

Given that the foundation mass and inertia effect were considered in the analysis, ground motions needed to be deconvolved. Deconvolution methods allow for the adjustment of the amplitude and frequency contents of a seismic ground motion applied at the base of the foundation to achieve the desired target acceleration time series at the structure–foundation interface. Following the method proposed by Sooch and Bagchi [28] and presented in Figure 4, the ground motion was initially applied at the base of the foundation, and it was assumed to be the same as the free-field ground acceleration. The acceleration time series at the top surface (i.e., block–foundation interface) was then estimated by solving the wave propagation problem using the finite element model. This estimated or reproduced ground motion at a reference point on the block–foundation interface was then compared to the original free-field ground motion after transforming both signals into the frequency domain using Fourier analysis. The synthesised and free-field signals at the top of the foundation were then compared in the frequency domain, and a correction factor for each frequency was computed. The modified ground motion was then transformed back into the time domain, and the wave propagation analysis for the foundation system was repeated iteratively with the modified ground motion applied at the base of the foundation. This procedure was repeated until the difference between the spectra of the output and the target ground motion was less than 5% over the range of periods of interest ($0.2T_1-2T_1$) and 10% elsewhere. As shown in Figure 5, the comparison of the acceleration response spectra further confirms the effectiveness of the deconvolution.

4. Uncertainty Modelling

Each parameter of the analysis was defined either as a fixed value or as a random variable associated with a probability density function (PDF). The preliminary analyses carried out in the finite element model showed that some parameters (e.g., moduli of elasticity) had to be defined as random variables in order to account for the uncertainty about the estimated value. The lack of knowledge relative to the parameters quantifying the resistance of the structure, loading conditions and seismic input were considered in this study. All the parameters considered as random variables and their associated PDFs are listed in

Table 5. Uncertain parameters.

Modelling Parameter	Probability Distribution	Distribution Parameter		Units
Directionality factor	Uniform	$L=0.5$	$U=0.8$	-
Concrete damping	Log-Normal	$\lambda =-2.99$	$\zeta =0.35$	%
Concrete–concrete cohesion	Uniform	$L=0.5$	$U=2.5$	MPa
Concrete–rock cohesion	Uniform	$L=0.1$	$U=1.5$	MPa
Concrete–concrete angle of friction	Uniform	$L=45$	$U=55$	${}^{\circ }$
Concrete–rock angle of friction	Uniform	$L=30$	$U=45$	${}^{\circ }$
Concrete–concrete tensile strength	Uniform	$L=0.3$	$U=2.3$	MPa
Concrete–rock tensile strength	Uniform	$L=0.05$	$U=0.8$	MPa
Concrete elasticity modulus	Uniform	$L=18.5$	$U=26.9$	MPa
Rock elasticity modulus	Uniform	$L=40$	$U=50$	MPa
Drain efficiency	Uniform	$L=0$	$U=70$	%

, while all the material properties considered constant throughout the analysis are summarised in

Table 6. Sample’s constant parameters.

Material Properties	Constant Value
Concrete density	2300 kg/m${}^3$
Rock density	2600 kg/m${}^3$
Concrete Poisson’s coefficient	0.164
Rock Poisson’s coefficient	0.300
Foundation damping	5%

. The 11 uncertain parameters listed in Table 5 were sampled using Latin hypercube sampling (LHS) to generate $N=22$ model samples to propagate sources of uncertainty in the fragility analysis. When using an LHS experimental design, the minimum number of design runs required for optimally spaced design points is typically at least twice the number of parameters considered [29,30]. This sampling method was chosen because of its ability to efficiently generate representative samples by dividing the range of possible values for each variable into N equiprobable intervals.

4.1. Material Properties

To test the accuracy of the finite element model, it was necessary to specify the densities, moduli of elasticity, damping and Poisson coefficients of the concrete and foundation material (Table 2). However, these values were re-evaluated here for estimation of the impact of their uncertainty on the dynamic behaviour of the structure.

4.1.1. Modulus of Elasticity

As already pointed out, the seismic response of the system changes according to the value of the concrete and foundation modulus of elasticity. It is therefore appropriate to define these parameters as a random variables, especially given the lack of empirical or experimental data to calibrate them accurately. From a series of tests carried out at the dam site, it was determined that the concrete static modulus of elasticity could be associated with extreme values between 14.8 and 21.5 GPa. As recommended by [26,31], the concrete modulus of elasticity is amplified by 25% in the presence of dynamic loadings. Therefore, the extreme values of the modulus of elasticity were 18.5–26.9 GPa. Regarding the foundation, because no test was carried out to characterise the modulus of elasticity, the values adopted in models M0 and M1 (40–50 GPa) were considered herein as the extreme values of the uniform distribution associated with this variable.

4.1.2. Damping

The concrete damping is difficult to estimate, especially since the possible cracking of the structure under the effect of the seismic load will cause additional energy dissipation. Given that the concrete is associated with an elastic linear behaviour in the numerical model, the increase in damping with cracking is not automatically taken into account. The average damping should therefore be increased with respect to the 1.5% value obtained from an experimental test for relatively small vibrations [24] and used during model verification to anticipate cracking of the structure and the nonlinear mechanisms that can develop during an earthquake. As proposed by Ghanaat et al. [6], for the concrete damping, a log-normal distribution with a median of 5% and a standard deviation of 0.35 was adopted. Taking these values into account, the system damping was estimated with the free-decay method, and it was verified that the total system damping remained under 7% [32]. With respect to the foundation damping, given that the knowledge on this parameter is limited, the viscous damping of the foundation was assumed to be 5% for all samples [19].

4.1.3. Shear and Tensile Strength

In the absence of sufficient data, a uniform PDF was also used to describe the parameters characterising the shear and tensile strength. For determining the shear and tensile strength parameters at the rock–concrete contact and based on the construction plan of the dam, the foundation rock at the dam site was determined to be composed of diorite, gneiss and granite. The maximum and minimum values for the cohesion and the angle of friction were estimated from literature test results for the same type of rock foundation [33]. As a result, a range of values of 0.1–1.5 MPa and 30–45° were assigned to the uniform PDF for the cohesion and the angle of friction, respectively. Similarly, for the tensile strength, the adopted extreme values varied between 0.05 and 0.8 MPa.

4.2. Load Parameters

4.2.1. Drain Efficiency

The efficiency of the drainage system is defined by the proportion of the flow that can be captured by this system to reduce the hydraulic load. To account for the uncertainties in the uplift pressures, the drain efficiency was defined as a random variable with a uniform PDF. From previous studies of the dam owners at the base of block-6 and using the extreme values of a water column height to calculate the uplift load, it was concluded that the drains allow for a decrease in the uplift pressures between 15% and 75%, while the USBR [19] recommends limiting the effectiveness of the drains to 67%. Consequently, the efficiency of the drain system was sampled by considering values between 0% and 70% to also include the undrained case.

4.2.2. Directionality Factor

The directionality factor $f_{h/v}$ is defined as the ratio of the vertical to the horizontal peak ground acceleration (PGA), as expressed by Equation (7):

$${\mathrm{PGA}}_v=f_{h/v}{\mathrm{PGA}}_h,$$

(7)

where ${\mathrm{PGA}}_v$ and ${\mathrm{PGA}}_h$ represent the peak accelerations in the vertical and horizontal directions, respectively. Traditionally, this factor is assumed to be equal to 2/3, but its value can vary greatly, having a significant influence on the response of the structure. In fact, from the available recorded ground motions, it can be seen that this ratio generally varies between 0.3 and 1.0 depending on the magnitude, the epicentral distance, the tectonic environment and the spectral period [34,35,36]. Due to the lack of seismic data at the dam site, the range of values was slightly reduced to 0.5–0.8.

4.3. Ground Motions

To perform the fragility analysis for assessing the seismic vulnerability of the case-study structure, a representative set of ground motion time series (GMTS) that efficiently depicts the aleatory uncertainty was needed. Each of the 22 samples generated with the LHS procedure was randomly coupled with a seismic event. Thus, 22 ground motion time series in the vertical and horizontal direction were selected.

4.3.1. Levels of Seismic Intensity

The response of each sample was analysed for several levels of seismic intensity through an incremental dynamic analysis (IDA). Most of the studies found in the literature concerning seismic fragility assessment for gravity-dam-type structures use the peak ground acceleration (PGA) or the spectral acceleration at fundamental period of the structure as the seismic intensity measure [10,14,15]. Nevertheless, given that the fundamental period depends on the concrete and foundation modulus of elasticity, defined herein as random variables, the spectral acceleration at the fundamental period varies according to the sample considered for the analysis. Therefore, in this study, the PGA in the horizontal direction was chosen to characterise the seismic solicitation at seven target intensity levels: ${\mathrm{PGA}}_{target}=\{0.1g,0.2g,0.25g,0.3g,0.4g,0.5g,0.7g\}$ to efficiently cover return periods corresponding to 200–20,000 years. Thus, the 22 selected horizontal accelerograms were scaled according to these seven intensity levels, while the vertical accelerograms were scaled taking into account the directionality factor associated with the sample in question.

Due to the limited availability of strong ground motion records for the considered region, synthetic accelerograms developed by Atkinson [37] for Eastern Canada were used. The accelerograms were simulated for the following cases: magnitude 6 and epicentral distances between 10 and 15 km and between 20 and 30 km, and magnitude 7 and epicentral distances of 15–25 km and 50–70 km. For each of these four sets, three random components of the earthquake were simulated at 15 random locations around the epicentre. Seismic solicitations were then selected considering accelerograms from the four sets.

4.3.2. Selection and Scaling of Accelerograms

Current seismic guidelines for dimensioning recommend the use of seismic events compatible with the uniform hazard spectrum (UHS) for the studied site. The UHS provided by the Geological Survey of Canada (GSC) at the dam site for soil type A ($VS30\ge 1500$ m/s), referred to as the target spectrum, was used for this study, and it is shown in Figure 6a. Taking into consideration the different simulated sets of accelerograms in terms of magnitude and epicentral distance, GMTS were selected for soil type A, keeping those whose response spectrum closely matched the target spectrum. For that purpose, the method proposed by Atkinson [37] was used to compare the shape of the response spectra of the target and the selected ground motion over the range of periods of interest, $T\in [0,1]\mathrm{s}$. Finally, the 22 accelerograms presenting the smallest values of the standard deviation within the considered range of periods were selected. Each simulated record, with initial ${\mathrm{PGA}}_h$, was then multiplied by the factor ${\mathrm{PGA}}_{target}/{\mathrm{PGA}}_h$ to match the peak ground acceleration at each intensity level. Figure 6b shows the selected horizontal accelerograms for the seismic intensity level $\mathrm{PGA}=0.23g$, corresponding to the UHS PGA. It is possible to note in this figure that the spectra are relatively well dispersed, which will allows for the representation of the random nature of the seismic solicitation.

Each horizontal accelerogram is associated with a vertical accelerogram from the two remaining simulated components, and the one with the closest response spectrum to the UHS was kept. Following the same procedure as the horizontal component, in addition to the directionality factor $f_{h/v}$ associated with the sample, the vertical acceleration values were multiplied by the factor $f_{h/v}\times {\mathrm{PGA}}_{target}/{\mathrm{PGA}}_h$.

5. Fragility Analysis

With the FE model and the uncertainty characterisation presented above, it was possible to perform a fragility analysis to evaluate the vulnerability of the case study dam. Fragility analysis is a technique for assessing and displaying, in probabilistic terms, the capability of an engineered system to withstand a specified event [3]. In other words, as presented in Equation (8), the fragility $P_f\left(y\right)$ defines the conditional probability that a system reaches a structural limit state (LS) for a given ground motion intensity measure (IM):

$$P_f\left(y\right)=Pr\left[LS\right|IM=y].$$

(8)

In this equation, y is the demand variable that defines the ground motion intensity. Two fundamental steps are needed before performing the fragility analysis: the (i) identification of all limit states relevant to the system performance and (ii) rational assessment of all sources of uncertainty likely to affect the response of the structure, as described in the previous section.

5.1. Limit States: Preliminary Analyses and Nonlinearities

Before initiating fragility analyses, a series of preliminary linear analyses were conducted. The objective was to determine where tensile stresses are likely to appear in order to limit the nonlinearities to those places only and to identify the typical damage modes that could lead to the potential collapse of dams after a seismic event. Linear analyses were conducted on the 22 samples assuming a peak ground acceleration of $\mathrm{PGA}=0.25g$—the highest seismic intensity level studied near the PGA of the target spectrum. All samples developed tensile stresses at the upstream and downstream foot during seismic loading, varying between $0.25$ and $4.1\mathrm{MPa}$. Figure 7a illustrates the development of tensile stresses at the upstream and downstream foot. Similarly, tensile stresses were also identified on several samples at the upstream or downstream faces of the block, as shown in Figure 7b, but given that no specific area could be identified, only the block–foundation contact at the base of the block was modified to introduce contact elements with a shear-tension failure criterion, as detailed above.

In the same manner, the results from these analyses identified sliding as the critical failure mode for the case-study dam, and other failure modes would only occur after sliding was already observed. As a consequence, the only damage state contemplated in this study was sliding at the concrete–rock interface. Each limit state, presented in

Table 7. Limit states.

Limit State	Displacement (mm)
LS0—Minor damage	Incipient sliding
LS1—Moderate damage	25
LS2—Severe damage	50

, was defined based on the damage states proposed in Tekie and Ellingwood [38].

5.2. Fragility Curves

Within this 7-intensity-level IDA framework, 22 samples of the finite element model were generated with LHS and were paired with the 22 sets of ground motion records selected as explained in Section 4.3.2. Nonlinear dynamic analyses were performed for the 22 samples at each considered intensity level, resulting in a total of 154 analyses. From each simulation, the maximum relative base displacement was computed.

Table 8. Incremental dynamic analysis (IDA) results—Fraction of samples exceeding the limit state. PGA: peak ground acceleration.

Limit State	Seismic Intensity Levels—PGA (g)
	0.1	0.2	0.25	0.3	0.4	0.5	0.7
LS0	0/22	2/22	5/22	10/22	15/22	17/22	20/22
LS1	0/22	0/22	1/22	3/22	6/22	10/22	19/22
LS2	0/22	0/22	0/22	0/22	3/22	5/22	11/22

summarises the results of the IDA analyses in terms of the fraction of the number of samples where sliding exceeded the limit state divided by the total number of samples. The results from Table 8 (i.e., the seven fragility point estimates) allow the development of fragility curves for the three considered limit states.

A well-known mathematical equation was then fitted to these fragility estimates in order to develop fragility curves for the considered limit states. The log-normal cumulative distribution function (CDF), together with the least square estimate fitting technique, was found to be adequate for depicting the fragility of the three considered limit states, as given by:

$$P_f=\mathsf{\Phi }\left({\displaystyle \frac{lny/m_R}{{\beta }_R}}\right),$$

(9)

where y is the PGA level, and $m_R$ and ${\beta }_R$ are the median capacity and the logarithmic standard deviation of the log-normal CDF, respectively. The parameters $m_R$ and ${\beta }_R$ of the log-normal CDF are synthesised in

Table 9. Fragility curve parameters.

Limit State	Log-Normal Parameters
	${\mathit{m}}_{\mathit{R}}$ (g)	${\mathit{\beta }}_{\mathit{R}}$
LS0	0.336	0.456
LS1	0.499	0.374
LS2	0.698	0.454

, and the corresponding fragility curves are shown in Figure 8. Further details on the fragility analysis procedure can be found in [10].

6. Expected Seismic Performance

For structures of special importance, such as dams and nuclear power plants, it is typical to consider the high confidence low probability of failure (HCLPF) criteria. This notion represents the level for which the probability of exceedance of a limit state is sufficiently low to consider that it will not be reached throughout the life of the structure [39] and usually corresponds to a probability of less than 5%. Accordingly, to evaluate the expected seismic performance of the case-study structure for the HCLPF level, the spectral acceleration for each limit state was extracted from the fragility curves for a probability of exceedance of 5%. Moreover, given that the PGA at the dam site for seismic events with a return period of 2475 could be computed, the expected seismic performance of the structure for events with these characteristics, usually used in the safety guidelines for dimensioning and verification, could also be estimated. Considering a ${\mathrm{PGA}}_{target}=0.23g$ from the UHS, the probability of exceedance was extracted from the fragility curves for each limit state.

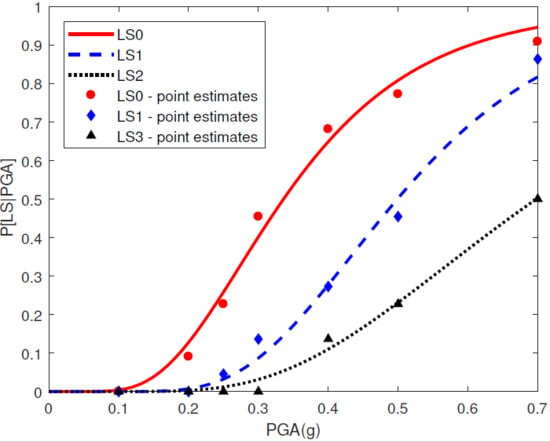
The results presented in

Table 10. Expected seismic performance results. HCLPF: high confidence low probability of failure.

Limit State	PGA for HCLPF	PGA${}_{\mathbf{target}}$
LS0	0.16g	20%
LS1	0.27g	2%
LS2	0.33g	0.7%

show that the sliding at the concrete–rock interface of block-6 could be initiated for a PGA greater than 0.16g. Additionally, the sliding remained low (<25 mm) for PGA values below 0.27g, while it is unlikely to reach such a level of damage during an earthquake with a return period of 2475 years. Finally, the probability of reaching a severe damage limit state that could lead to the loss of control of the reservoir becomes significant when the PGA reaches values close to 0.33g.

7. Conclusions

The main objective of this study was to assess the seismic vulnerability of a dam-type structure through a fragility framework and to present all the required analyses and verifications of the numerical model prior to obtaining the fragility curves. The methodology was applied to the bottom outlet spillway structure of the case study dam and more particularly to block-6 of the latter. For that purpose, a finite element model of the block–reservoir–foundation system was developed to describe the real behaviour of the structure as closely as possible. Following the results of the preliminary analyses, the study of the fragility of the system was restricted to a single damage state related to the sliding at the base of the block. Fragility curves were generated, taking into account the results of nonlinear dynamic analyses that were calculated with the structure samples obtained with LHS and coupled to GMTS, describing the seismic scenario at the dam site.

The methodology proposed herein makes it possible to account for the uncertainties associated with the modelling parameters as well as the randomness in the seismic solicitation. The results obtained from the fragility curves indicate that the probability of observing an incipient sliding at the base of the block, when solicited with PGA values used by the current guidelines for dimensioning and verification, is 20%. In contrast, it is unlikely that more severe damage to the structure for this intensity level will be observed.