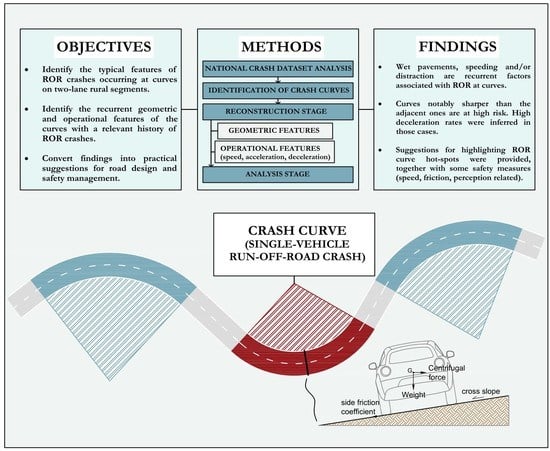
Geometric and Operational Features of Horizontal Curves with Specific Regard to Skidding Proneness
Abstract
:1. Introduction
- Road design consistency, which is intrinsically related to the drivers’ expectations.
- What are the typical features of ROR crashes occurring at curves on rural roads, in particular two-way two-lane rural segments?
- What are the recurrent road geometric and operational characteristics of segments including the highlighted curves with a relevant history of ROR crashes?
- Which of the previously highlighted aspects can be useful, and in which way, from a road safety management perspective?
2. Materials and Methods
2.1. Selection of Road Sites Based on Their Run-Off-Road Crash History
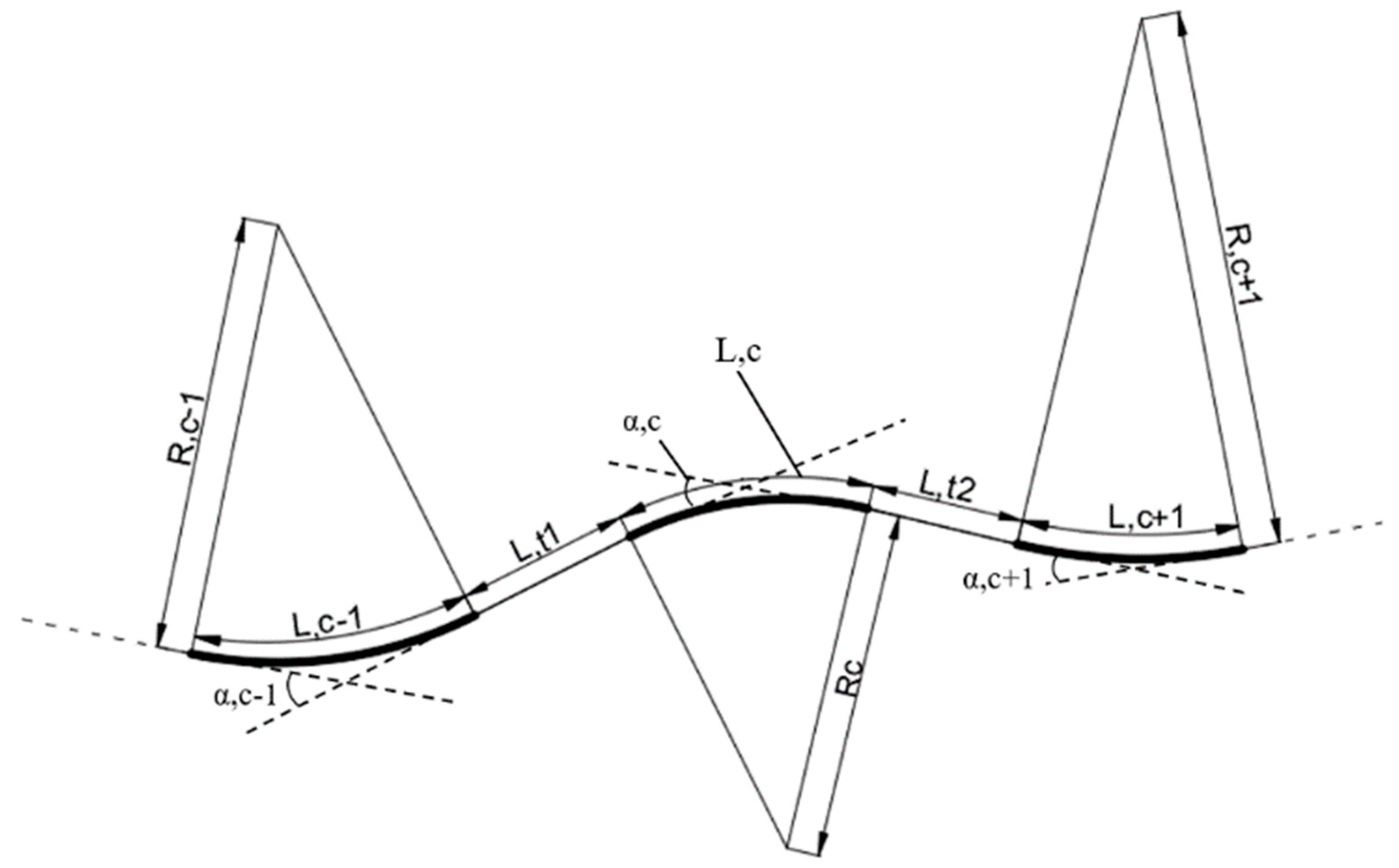
2.2. Geometric Characteristics of the Selected Road Sites
- Radius (“R,c”) of the curve (“C”) at which more than one ROR FI crash has occurred;
- Length of the above defined curve (“L,c”)
- Radius (“R,c+1”) and length (“L,c+1”) of the curve (“C+1”) following the curve “C”;
- Radius (“R,c-1”) and length (“L,c-1”) of the curve (“C-1”) previous to the curve “C”;
- Length (“L,t1) of the tangent (“T1”) included between the curves “C” and “C-1”; and
- Length (“L,t2”) of the tangent (“T2”) included between the curves “C” and “C+1”.
2.3. Operational Characteristics of the Selected Road Sites
2.3.1. Inferred Operating Speeds
2.3.2. Inferred Design Speeds
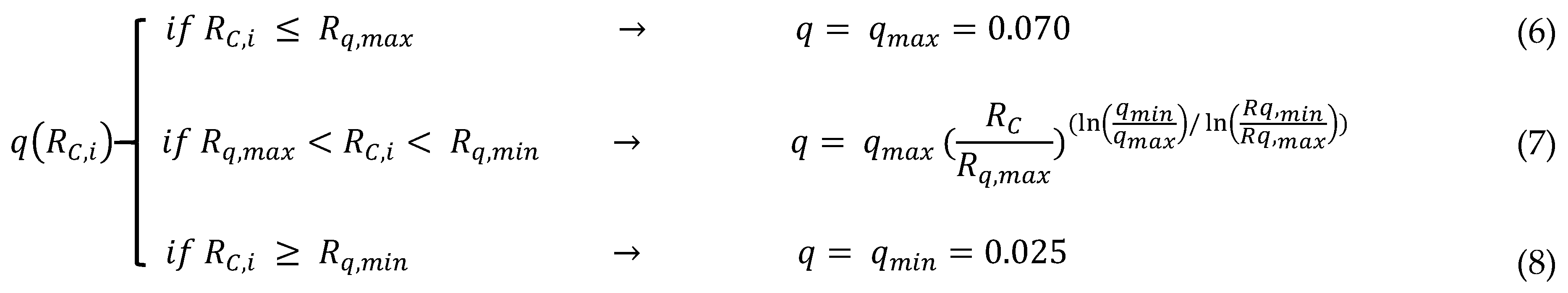
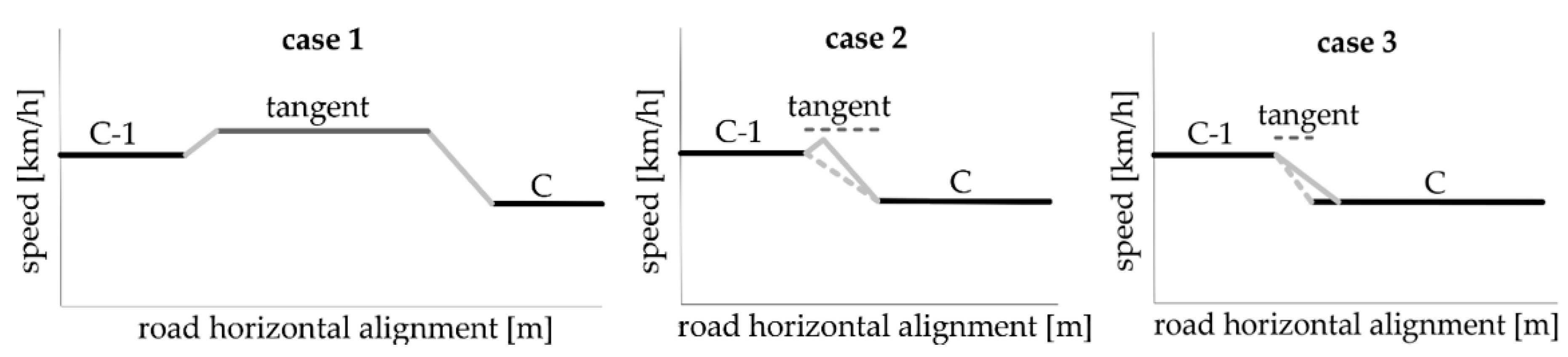
2.3.3. Acceleration Rates
- The tangent before the crash curve C can include both the previous curve-to-tangent acceleration length and the tangent-to-curve C acceleration/deceleration length;
- The tangent before the curve C is not long enough to include both the previous curve-to-tangent acceleration length and the tangent-to-curve C acceleration/deceleration length; and
- The tangent before the curve C is so short that it cannot even include the tangent-to-curve C acceleration/deceleration length.
2.4. Safety Measures of Selected Road Sites
3. Results and Discussion
3.1. Typical Features of Run-Off-Road Fatal+Injury Crashes
3.2. Typical Features of Road Segments Including Curves with Notable History of ROR FI Crashes
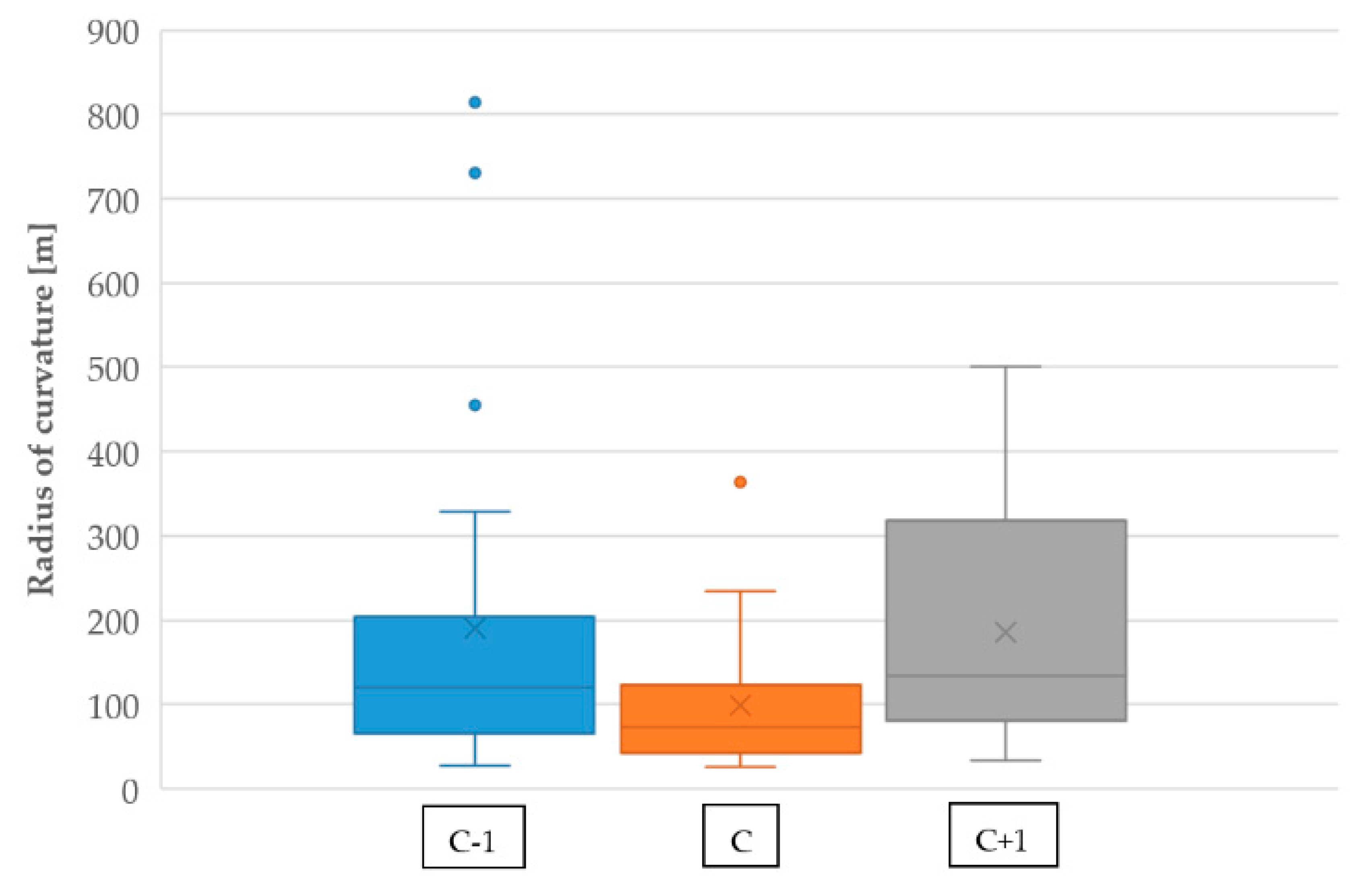
3.2.1. Geometric Characteristics
3.2.2. Operational Characteristics
- In eight cases, the length of the tangents included between the crash and adjacent curves were sufficient for both acceleration from the previous curve and further deceleration to the considered curve, with the AR/DR rates computed through Equations (11) and (12) (case 1, Figure 2).
- In seven cases, both the previous and following tangent lengths were insufficient (based on Equation (13) for a proper deceleration computed through Equation (12) to occur, and assumed to possibly occur on tangents only (an experimentally verified usual condition [48]). In cases of insufficient tangent length (case 3, Figure 2), the deceleration rate was computed through Equation (14).
- In all other cases, the length of tangents between the crash curve and the adjacent curves were not sufficient for both acceleration from the previous curve and deceleration to the crash curve to occur (case 2, Figure 2). Hence, in this case, only the deceleration from the previous curve was computed (hypothesis of no acceleration).
3.2.3. Predicted Safety Characteristics
3.3. Practical Implications for Road Safety Management
3.3.1. Recurrent Features Useful for Road Safety Management
- The ratio between the curve radius and the radius of the adjacent curves (average between the previous and the following curves, since the road type is two-way operated). In this study, by excluding the adjacent curves on which the ROR FI crashes occurred, the average ratio between the crash curve radius and the average adjacent curve radius (on which ROR FI crashes did not occur) was equal to 0.59 and the 85th percentile of the distribution of ratios for the crash curves was 0.76. Hence, for road safety management purposes, two-way two-lane rural curves withcould be targeted for further investigation while conducting campaigns dedicated to preventing ROR FI crashes on two-way two-lane rural road curves. The choice between the two values proposed (the mean and the 85th percentile) may depend on the capability for planning further investigations (e.g., inspections) at curves. The CMF (Equation (16) [12]), which has been demonstrated to have the capability to highlight ROR FI crash sites, only depends on the CCR. Hence, a suggested measure based on the difference in CMFs would have been redundant, having already provided the above described relation in Equation (17).
- The difference between the operating speed and design speed in dry conditions. In dry conditions, an inferred operating speed significantly close to the maximum inferred design speed (average margin of −3.7 km/h) was found to be associated with ROR FI crashes at curves. In Figure 6, Equation (3) (85th inferred operating speed) and Equation (10) (max. inferred design speed) are solved. Given the findings from this study, the radii of curvature for which the 85th operating speed is greater or closer than the maximum inferred design speed could be targeted for further investigation. In this case, the threshold can be set to around 250 m (close to the intersection between the two curves in Figure 6 and roughly corresponding to the same average margin found in this study). This indication is more conservative than using the conventional 85th-design speed margin of +10 km/h [23,27] as a threshold, which would correspond to curves with a radius of less than around 150 m, as based on Figure 6.
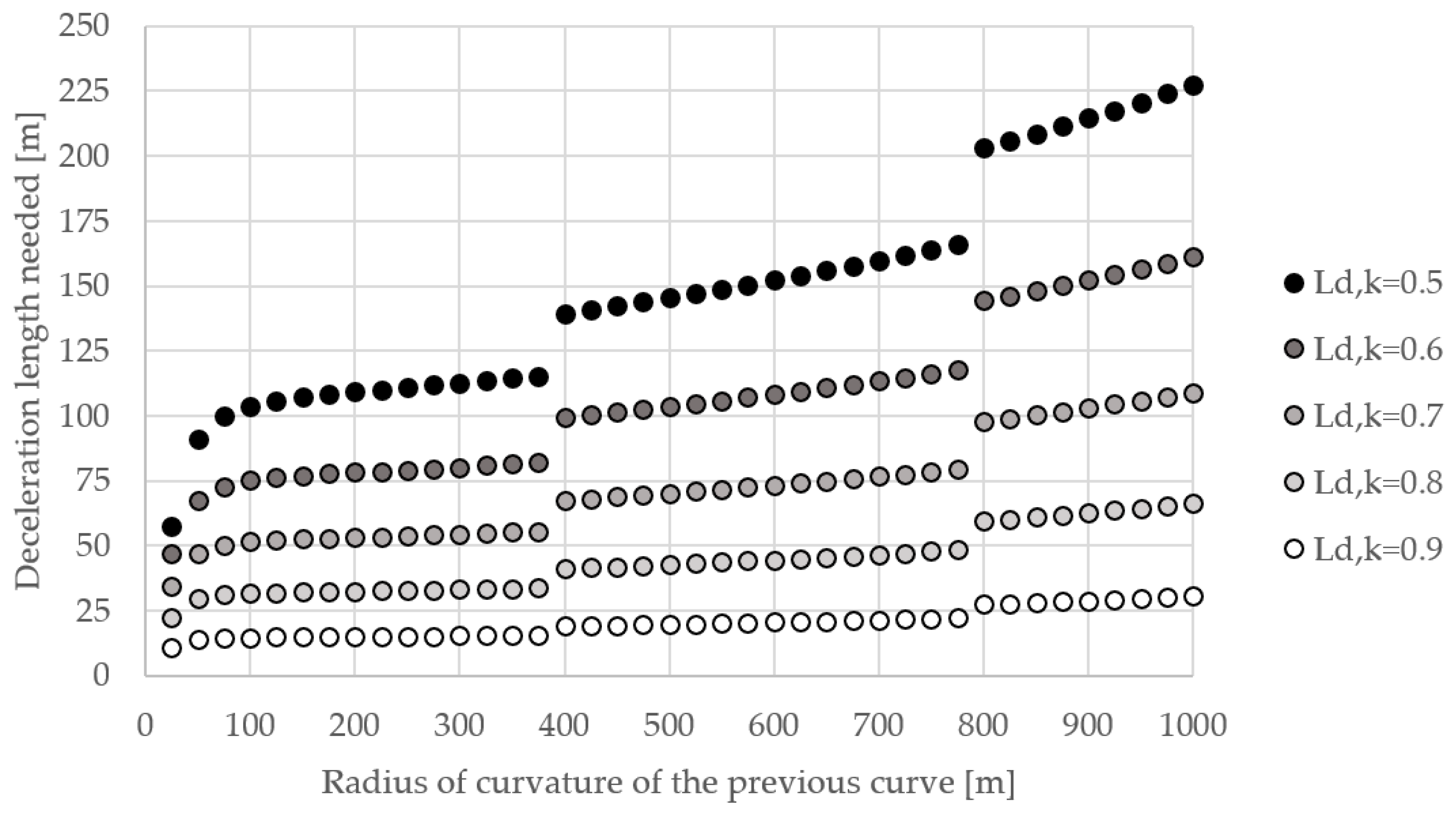
- Deceleration rates. High inferred deceleration rates were found to be associated with ROR FI crash curves. This clearly points out that the length of the tangent included between two subsequent curves (with largely different radii) plays a crucial role. Hence, if the tangent length does not allow a deceleration compatible with Equation (12) (i.e., the tangent is shorter), then tangents before curves with a radius of curvature sharper than the previous ones should be targeted for further investigation. A practice-ready abacus is graphically depicted in Figure 7 and provides the minimum length of the tangent set as equal to the minimum deceleration length needed from the previous curve (with larger radius) to the following curve (with sharper radius). This can be used starting from the radius of the previous curve and by reading the value of the necessary tangent length for different k values (ratio between the radii of the following and previous curve). Tangents that do not satisfy this minimum criterion should be targeted for further investigation during the network screening stage.
- Longitudinal slope. This was highlighted as a critical factor for ROR FI crashes at curves: the average slope was 4.0% in the study sample. This suggests that, as expected, curves on steep slopes should certainly be targeted for further investigation. No further detailed indications are provided in this study since the vertical alignment was considered to a minor extent, given the available data sources and the need for accurate data.
3.3.2. Remarks for Safety Countermeasures on Similar Sites
- Perceptual measures. It was extensively shown how the mis-perception of the crash curve or the drivers’ distraction could have played an important role in the analyzed crashes. Hence, measures such as curve delineation, warning signs, and sequential flashing beacons can effectively reduce crashes [53] by acting on the drivers’ perceptual mechanism.
- Physical improvements. It is paramount that one of the most frequent ROR FI crash mechanisms is the loss of friction (i.e., when the friction demanded exceeds the available friction [9,10]). A design friction coefficient varying with speed was assumed in the calculations made throughout the paper, since no direct measurements were available. However, considering drivers travelling at the inferred 85th operating speeds in sharp radii curves (higher than then maximum inferred design speeds, see Figure 6 for R shorter than about 225 m), the friction used is higher than the friction computed in the case of design speed. The actual friction used can be computed through the following equation (obtained by rearranging Equation (5), where q = qmax = 0.07 due to the assumed sharp radii):The cross friction coefficients used (light grey dashed line in Figure 8) were significantly higher than the design cross friction coefficients in wet conditions (black dashed line in Figure 8). In fact, a threshold for indicating an unacceptable design condition could be a difference between the used and design cross friction coefficients of more than 0.04 [23,27]. This means that treatments for improving skid resistance should be implemented where there is noticeable evidence that this condition could occur, especially in the case of sharp radii. Another solution could be an increase in the cross slope (superelevation) up to 10% (as suggested in particular cases, e.g., in [31]). In this case, no skid resistance treatments are needed (that is, still assuming the design cross slope is valid) and can be applied to radii of curvature roughly down to 300 m (see black solid line in Figure 8) where q = 0.10 is reached. However, a similar treatment should be considered with extreme cautiousness, especially in the presence of notable vertical grades and possible icy pavements. In fact, the compound slope is often limited by design guidelines, thus resulting in the unfeasibility of implementing cross slopes equal to 10%. Finally, considering the implementation of both increased superelevation and skid resistance treatments does not dramatically reduce the need for increased available friction, especially for very sharp radii (compare dashed light grey line with dashed grey line in Figure 8).
4. Conclusions
- There were some recurrent features in the ROR FI crash dataset analyzed. In particular, a typical ROR FI crash is an injury light vehicle crash that occurs to adult drivers (aged between 30–64) in the afternoon, on wet pavements, with speeding and/or distraction as a contributory factor.
- Typically, curves with a relevant history of ROR FI crashes have significantly smaller radii of curvature than the adjacent ones. This finding was associated with possible distraction and great deceleration rates, based on the data exploration. In fact, crashes in which distraction was a contributory factor were associated with crash curves having a notably smaller radius than the previous one. Moreover, several crash curves require high deceleration rates, thus also implying insufficient tangent lengths before curves. Nevertheless, in dry conditions, the 85th inferred operating speeds are comparable with the inferred design speeds that meet the curve equilibrium, while they are higher in wet conditions.
- Some suggestions for road safety management and safety interventions (i.e., reducing speeds, improving perception and skid resistance) are provided based on the findings. The suggestions for targeting specific ranges of radii of curvature, ratios between the curve radius and the average adjacent radii, and previous tangent lengths may be useful in targeting two-way two-lane rural road curves for further investigation (e.g., while attempting to reduce the ROR crash type).
Concluding Remarks on Strengths and Limitations
Author Contributions
Funding
Conflicts of Interest
References
- Liu, C.; Ye, T.J. Run-off-Road Crashes: An on-Scene Perspective; Report No. DOT HS-811 500; United States Department of Transportation, National Highway Traffic Safety Administration: Washington, DC, USA, 2011.
- Wegman, F. Analyzing road design risk factors for run-off-road crashes in the Netherlands with crash prediction models. J. Saf. Res. 2014, 49, 121.e1–127. [Google Scholar]
- Federal Highway Administration. US Department of Transportation. Roadway Departure Safety. Available online: https://safety.fhwa.dot.gov/roadway_dept/ (accessed on 24 November 2019).
- Adminaite, D.; Jost, G.; Stipdonk, H.; Ward, H. Reducing Deaths in Single Vehicle Collisions; PIN Flash Report 32; European Transport Safety Council (ETSC): Brussel, Belgium, 2017. [Google Scholar]
- Colonna, P.; Intini, P.; Berloco, N.; Ranieri, V. Integrated American-European protocol for safety interventions on existing two-lane rural roads. Eur. Transp. Res. Rev. 2018, 10, 5. [Google Scholar] [CrossRef]
- Davidse, R.J.; Doumen, M.J.A.; van Duijvenvoorde, K.; Louwerse, W.J.R. Bermongevallen in Zeeland: Karakteristieken en oplossingsrichtingen (Run-off-Road Crashes in the Province of Zeeland: Characteristics and Possible Solutions); SWOV: Leidschendam, The Netherlands, 2011. [Google Scholar]
- Istituto Nazionale di Statistica, ISTAT, Italy. Rilevazione degli Incidenti Stradali con Lesioni a Persone: Microdati ad Uso Pubblico. Available online: https://www.istat.it/it/archivio/87539 (accessed on 17 November 2019).
- Elvik, R. International transferability of accident modification functions for horizontal curves. Accid. Anal. Prev. 2013, 59, 487–496. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lamm, R.; Choueiri, E.M.; Mailaender, T. Side friction demand versus side friction assumed for curve design on two-lane rural highways. Transp. Res. Rec. 1991, 1303, 11–21. [Google Scholar]
- Colonna, P.; Berloco, N.; Intini, P.; Perruccio, A.; Ranieri, V. Evaluating skidding risk of a road layout for all types of vehicles. Transp. Res. Rec. 2016, 2591, 94–102. [Google Scholar] [CrossRef]
- Elvik, R. The more (sharp) curves, the lower the risk. Accid. Anal. Prev. 2019, 133, 105322. [Google Scholar] [CrossRef]
- Gooch, J.P.; Gayah, V.V.; Donnell, E.T. Quantifying the safety effects of horizontal curves on two-way, two-lane rural roads. Accid. Anal. Prev. 2016, 92, 71–81. [Google Scholar] [CrossRef]
- Intini, P.; Berloco, N.; Colonna, P.; Ottersland Granås, S.; Olaussen Ryeng, E. Influence of Road Geometric Design Consistency on Familiar and Unfamiliar Drivers’ Performances: Crash-Based Analysis. Transp. Res. Rec. 2019. [Google Scholar] [CrossRef]
- Roque, C.; Cardoso, J.L. Investigating the relationship between run-off-the-road crash frequency and traffic flow through different functional forms. Accid. Anal. Prev. 2014, 63, 121–132. [Google Scholar] [CrossRef] [Green Version]
- Gong, L.; Fan, W.D. Modeling single-vehicle run-off-road crash severity in rural areas: Accounting for unobserved heterogeneity and age difference. Accid. Anal. Prev. 2017, 101, 124–134. [Google Scholar] [CrossRef]
- Claros, B.; Edara, P.; Sun, C. Site-specific safety analysis of diverging diamond interchange ramp terminals. Transp. Res. Rec. 2016, 2556, 20–28. [Google Scholar] [CrossRef] [Green Version]
- Intini, P.; Colonna, P.; Berloco, N.; Ranieri, V.; Ryeng, E. The relationships between familiarity and road accidents: Some case studies. In Transport Infrastructure and Systems, Proceedings of the AIIT International Congress on Transport Infrastructure and Systems, Rome, Italy, 10–12 April 2017; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Intini, P.; Berloco, N.; Colonna, P.; Ranieri, V.; Ryeng, E. Exploring the relationships between drivers’ familiarity and two-lane rural road accidents. A multi-level study. Accid. Anal. Prev. 2018, 111, 280–296. [Google Scholar] [CrossRef] [PubMed]
- American Association of State Highway and Transportation Officials. Highway Safety Manual, 1st ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2010. [Google Scholar]
- Directive 2008/96/EC of the European Parliament and of the Council of 19 November 2008 on road infrastructure safety management. OJL 2008, 319, 59–67.
- La Torre, F.; Domenichini, L.; Corsi, F.; Fanfani, F. Transferability of the Highway Safety Manual Freeway Model to the Italian Motorway Network. Transp. Res. Rec. J. Transp. Res. Board 2014, 2435, 61–71. [Google Scholar] [CrossRef]
- Shin, H.S.; Dadvar, S.; Lee, Y.J. Results and lessons from local calibration process of the highway safety manual for the state of Maryland. Transp. Res. Rec. 2015, 2515, 104–114. [Google Scholar] [CrossRef]
- Lamm, R.; Psarianos, B.; Choueiri, E.M.; Soilemezoglou, G. A practical safety approach to highway geometric design. In International Case Studies: Germany, Greece, Lebanon, and the United States, Proceedings of theInternational Symposium on Highway. Geometric Design Practices, Boston, MA, USA, 30 August–1 September 1995; Transportation Research Board: Washington DC, USA, 1995. [Google Scholar]
- Marchionna, A.; Perco, P. Operating speed-profile prediction model for two-lane rural roads in the Italian context. Adv. Transp. Stud. 2008, 14, 57–68. [Google Scholar]
- Crisman, B.; Marchionna, A.; Perco, P.; Roberti, R. Operating speed prediction model for two-lane rural roads. In Proceedings of the 3rd International Symposium on Highway Geometric Design, Chicago, IL, USA, 29 June–1 July 2005. [Google Scholar]
- Santagata, F.A. (Ed.) Strade: Teoria e Tecnica delle Costruzioni Stradali; Pearson Education: Milano, Italy, 2016. [Google Scholar]
- Lamm, R.; Psarianos, B.; Mailaender, T. Highway Design and Traffic Safety Engineering Handbook; Mc Graw-Hill: New York, NY, USA, 1999. [Google Scholar]
- Lamm, R.; Choueiri, E.M.; Goyal, P.B.; Mailaender, T. Design Friction Factors of Different Countries Versus Actual Pavement Friction Inventories. Transp. Res. Rec. 1990, 1260, 135–146. [Google Scholar]
- Ministero delle Infrastrutture e dei Trasporti. Norme Funzionali e Geometriche per la Costruzione delle Strade; Decreto Ministeriale 6792; Ministero delle Infrastrutture e dei Trasporti: Rome, Italy, 2001.
- American Association of State Highway and Transportation Officials. A Policy on Geometric Design of Highways and Streets; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2001. [Google Scholar]
- Queensland Government (Australia), Department of Transport and Main Roads (DTMR). Road Planning and Design Manual, 2nd ed.; Queensland Government (Australia), Department of Transport and Main Roads (DTMR): Queensland, Australia, 2013.
- Eboli, L.; Mazzulla, G.; Pungillo, G. Combining speed and acceleration to define car users’ safe or unsafe driving behaviour. Transp. Res. Part C Emerg. Technol. 2016, 68, 113–125. [Google Scholar] [CrossRef]
- Juga, I.; Nurmi, P.; Hippi, M. Statistical modelling of wintertime road surface friction. Meteorol. Appl. 2013, 20, 318–329. [Google Scholar]
- Harwood, D.W.; Council, F.M.; Hauer, E.; Hughes, W.E.; Vogt, A. Prediction of the Expected Safety Performance of Rural Two-Lane Highways; No. FHWA-RD-99-207, MRI 4584-09, Technical Report; Federal Highway Administration: McLean, VA, USA, 2000.
- McLaughlin, S.B.; Hankey, J.M.; Klauer, S.G.; Dingus, T.A. Contributing Factors to Run-off-Road Crashes and near-Crashes; Report No. DOT HS 811 079; United States Department of Transportation, National Highway Traffic Safety Administration: Washington, DC, USA, 2009.
- Liu, C.; Subramanian, R. Factors Related to Fatal Single-Vehicle Run-off-Road Crashes; Report No. DOT HS-811 232; United States Department of Transportation, National Highway Traffic Safety Administration: Washington, DC, USA, 2009.
- Preusser, D.F.; Williams, A.F.; Ulmer, R.G. Analysis of fatal motorcycle crashes: Crash typing. Accid. Anal. Prev. 1995, 27, 845–851. [Google Scholar] [CrossRef]
- Peng, Y.; Boyle, L.N. Commercial driver factors in run-off-road crashes. Transp. Res. Rec. 2012, 2281, 128–132. [Google Scholar] [CrossRef]
- Davis, G.A.; Davuluri, S.U.J.A.Y.; Pei, J. Speed as a risk factor in serious run-off-road crashes: Bayesian case-control analysis with case speed uncertainty. J. Transp. Stat. 2006, 9, 17. [Google Scholar]
- Fitzpatrick, K.; Wooldridge, M.D.; Tsimhoni, O.; Collins, J.M.; Green, P.; Bauer, K.; Parma, K.D.M.; Koppa, R.; Harwood, D.W.; Anderson, I.; et al. Alternative Design Consistency Rating Methods for Two-Lane Rural Highways; No. 21 FHWA-RD-99-172; Federal Highway Administration: McLean, VA, USA, 2000.
- Torbic, D.J.; Harwood, D.W.; Gilmore, D.K.; Pfefer, R.; Neuman, T.R.; Slack, K.L.; Hardy, K.K. Guidance for Implementation of the AASHTO Strategic Highway Safety Plan, Volume 7: A Guide for Reducing Collisions on Horizontal Curves; No. Project G17-18 (3) FY’00; Transportation Research Board: Washington DC, USA, 2004. [Google Scholar]
- Charlton, S.G.; Starkey, N.J. Driving without awareness: The effects of practice and automaticity on attention and driving. Transp. Res. Part F Traffic Psychol. Behav. 2011, 14, 456–471. [Google Scholar] [CrossRef]
- Oviedo-Trespalacios, O.; Haque, M.M.; King, M.; Washington, S. Effects of road infrastructure and traffic complexity in speed adaptation behaviour of distracted drivers. Accid. Anal. Prev. 2019, 101, 67–77. [Google Scholar] [CrossRef]
- Camacho-Torregrosa, F.J.; Pérez-Zuriaga, A.M.; Campoy-Ungría, J.M.; García-García, A. New geometric design consistency model based on operating speed profiles for road safety evaluation. Accid. Anal. Prev. 2013, 61, 33–42. [Google Scholar] [CrossRef]
- Hassan, Y. Highway design consistency: Refining the state of knowledge and practice. Transp. Res. Rec. 2004, 1881, 63–71. [Google Scholar] [CrossRef]
- Lamm, R.; Guenther, A.K.; Choueiri, E.M. Safety module for highway geometric design. Transp. Res. Rec. 1995, 1512, 7–15. [Google Scholar]
- Lamm, R.; Choueiri, E.M.; Mailaender, T. Comparison of operating speeds on dry and wet pavements of two-lane rural highways. Transp. Res. Rec. 1990, 1280, 199–207. [Google Scholar]
- Figueroa Medina, A.M.; Tarko, A.P. Speed changes in the vicinity of horizontal curves on two-lane rural roads. J. Transp. Eng. 2007, 133, 215–222. [Google Scholar] [CrossRef]
- Fitzpatrick, K.; Elefteriadou, L.; Harwood, D.W.; Collins, J.M.; McFadden, J.; Anderson, I.B.; Krammes, R.A.; Irizarry, N.; Parma, K.D.; Bauer, K.M.; et al. Speed Prediction for Two-Lane Rural Highways; Report No. FHWA-RD-99-171; Federal Highway Administration: McLean, VA, USA, 2000.
- Findley, D.J.; Hummer, J.E.; Rasdorf, W.; Zegeer, C.V.; Fowler, T.J. Modeling the impact of spatial relationships on horizontal curve safety. Accid. Anal. Prev. 2012, 45, 296–304. [Google Scholar] [CrossRef]
- Montella, A. Safety evaluation of curve delineation improvements: Empirical Bayes observational before-and-after study. Transp. Res. Rec. 2009, 2103, 69–79. [Google Scholar] [CrossRef]
- Jeong-Gyu, K. Changes of speed and safety by automated speed enforcement systems. IATSS Res. 2002, 26, 38–44. [Google Scholar]
- Montella, A.; Galante, F.; Mauriello, F.; Pariota, L. Low-cost measures for reducing speeds at curves on two-lane rural highways. Transp. Res. Rec. 2015, 2472, 142–154. [Google Scholar] [CrossRef]
- Das, S.; Sun, X. Association knowledge for fatal run-off-road crashes by Multiple Correspondence Analysis. IATSS Res. 2016, 39, 146–155. [Google Scholar] [CrossRef] [Green Version]
- Intini, P.; Berloco, N.; Binetti, R.; Fonzone, A.; Ranieri, V.; Colonna, P. Transferred versus local Safety Performance Functions: A geographical analysis considering two European case studies. Saf. Sci. 2019, 120, 906–921. [Google Scholar] [CrossRef]
- Lee, J.; Mannering, F. Impact of roadside features on the frequency and severity of run-off-roadway accidents: An empirical analysis. Accid. Anal. Prev. 2002, 34, 149–161. [Google Scholar] [CrossRef]
- Colonna, P.; Intini, P.; Berloco, N.; Ranieri, V. Connecting Rural Road Design to Automated Vehicles: The Concept of Safe Speed to Overcome Human Errors. In International Conference on Applied Human Factors and Ergonomics; Springer: Cham, Germany, 2017; pp. 571–582. [Google Scholar]
- Intini, P.; Colonna, P.; Berloco, N.; Ranieri, V. Rethinking the main road design concepts for future Automated Vehicles Native Roads. Eur. Transp. 2019, 73, 3. [Google Scholar]
- Colonna, P.; Berloco, N.; Intini, P.; Ranieri, V. The method of the friction diagram: New developments and possible applications. In Transport Infrastructure and Systems, Proceedings of the AIIT International Congress on Transport Infrastructure and Systems, Rome, Italy, 10–12 April 2017; CRC Press: Boca Raton, FL, USA, 2017; p. 309. [Google Scholar]
- De Cerio, D.; Valenzuela, J. Provisioning vehicular services and communications based on a bluetooth sensor network deployment. Sensors 2015, 15, 12765–12781. [Google Scholar] [CrossRef] [Green Version]




| Crash Features | Classes of the Crash Features | |||
|---|---|---|---|---|
| Period of the day | Morning | Afternoon | Evening | Night |
| Per crash | 21 (0.30) | 34 (0.49) | 6 (0.09) | 8 (0.12) |
| Per curve site | ||||
| (most frequent class per site) 1 | 3 (0.10) | 10 (0.33) | 0 (0.00) | 3 (0.10) |
| (most frequent together with others) 2 | 14 (0.47) | 21 (0.7) | 4 (0.13) | 5 (0.17) |
| Pavement conditions | Dry | Wet | Icy | |
| Per crash | 29 (0.42) | 38 (0.55) | 2 (0.03) | |
| Per curve site | ||||
| (most frequent class per site) 1 | 9 (0.30) | 12 (0.40) | 0 (0.00) | |
| (most frequent together with others) 2 | 17 (0.57) | 20 (0.67) | 2 (0.07) | |
| Vehicle | Auto | Motorcycle | Heavy vehicle | |
| Per crash | 47 (0.68) | 14 (0.20) | 8 (0.12) | |
| Per curve site | ||||
| (most frequent class per site) 1 | 16 (0.53) | 4 (0.13) | 1 (0.03) | |
| (most frequent together with others) 2 | 25 (0.83) | 8 (0.27) | 6 (0.20) | |
| Contributory factor | Speeding | Distraction | Avoiding strike | Missing |
| Per crash | 29 (0.42) | 29 (0.42) | 5 (0.07) | 6 (0.09) |
| Per curve site | ||||
| (most frequent class per site) 1 | 8 (0.27) | 8 (0.27) | 2 (0.07) | 0 (0.00) |
| (most frequent together with others) 2 | 15 (0.50) | 20 (0.67) | 3 (0.10) | 4 (0.13) |
| Driver age | Young: 18–29 | Adult: 30–64 | Over 65 | Missing |
| Per crash | 15 (0.22) | 46 (0.67) | 7 (0.10) | 1 (0.01) |
| Per curve site | ||||
| (most frequent class per site) 1 | 2 (0.50) | 14 (0.67) | 0 (0.10) | 0 (0.00) |
| (most frequent together with others) 2 | 10 (0.33) | 28 (0.93) | 5 (0.17) | 1 (0.03) |
| Crash Curve Geometric Features | Descriptive Statistics | |||
|---|---|---|---|---|
| Mean | St. Dev. | Maximum | Minimum | |
| Radius of curvature Rc [m] | 112.3 | 86.9 | 364.0 | 26.0 |
| Length of the curve Lc [m] | 93.7 | 79.3 | 302.0 | 24.0 |
| CCR ratio–curve C [gon/km] | 924.6 | 607.2 | 2448.5 | 174.9 |
| Length of adjacent tangent 1 [m] | 151.7 | 212.3 | 1193.0 | 9.0 |
| Curve road width [m] | 7.5 | 1.2 | 9.5 | 4.5 |
| Curve average longitudinal slope [%] | 4.0 | 2.8 | 12.0 | 0.0 |
| Mean radius of adjacent curves 1 [m] | 190.9 | 160.3 | 814.0 | 26.0 |
| Mean length of adjacent curves 1 [m] | 82.9 | 63.3 | 299.0 | 7.0 |
| CCR ratio—adjacent curves 1 [gon/km] | 618.5 | 534.8 | 2448.5 | 78.2 |
| Curve Operational Features | Descriptive Statistics | |||
|---|---|---|---|---|
| Mean | St. Dev. | Max. | Min. | |
| Dry inferred maximum design speed—curve C [km/h] 1 | 65.5 | 20.2 | 104.6 | 38.2 |
| Wet inferred maximum design speed—curve C [km/h] 2 | 54.3 | 15.6 | 89.1 | 33.4 |
| Icy inferred maximum design speed—curve C [km/h] 3 | 44.4 | 20.1 | 58.6 | 30.1 |
| Dry inferred max. design speed—adjacent curves 4 [km/h]1 | 77.5 | 23.8 | 135.4 | 39.4 |
| Wet inferred max. design speed—adjacent curves 4 [km/h]2 | 65.0 | 19.2 | 110.7 | 31.4 |
| Icy inferred max. design speed—adjacent curves 4 [km/h]3 | 53.8 | 22.0 | 85.0 | 33.8 |
| Dry 85th—max. design speed difference: curve C [km/h]1 | −3.5 | 7.2 | 2.4 | −21.9 |
| Wet 85th—max. design speed difference: curve C [km/h] 2 | 7.9 | 4.5 | 11.7 | −6.5 |
| Icy 85th—max. design speed difference: curve C [km/h] 3 | 16.0 | 1.8 | 17.2 | 14.7 |
| Dry 85th—max. design speed diff.: adjacent curves 4 [km/h] 1 | −8.0 | 12.1 | 2.4 | −46.8 |
| Wet 85th—max. design speed diff.: adjacent curves 4 [km/h] 2 | 4.5 | 8.2 | 11.7 | −22.0 |
| Icy 85th—max. design speed diff.: adjacent curves 4 [km/h] 3 | 13.6 | 11.2 | 20.0 | −3.2 |
| Deceleration in approaching curve C—both directions [m/s2] 5 | −1.6 | 2.0 | -0.4 | −9.7 |
| Acceleration in approaching curve C—both directions [m/s2] 6 | 2.2 | - | - | - |
| Discordant deceleration/acceleration in approaching curve C in the two different directions [m/s2] 7 | 0.3 | 2.4 | 2.4 | −2.0 |
| Crash curve Predicted Safety Characteristics | Descriptive Statistics | |||
|---|---|---|---|---|
| Mean | St. Dev. | Max | Min. | |
| Crash Modification Factor—curve C—Equation (15) [-] | 8.6 | 7.8 | 36.3 | 1.2 |
| Crash Modification Factor—adjacent curves 1—Equation (15) [-] | 7.3 | 8.6 | 39.6 | 1.1 |
| Crash Modification Factor—curve C—Equation (16) [-] | 6.5 | 8.1 | 39.5 | 1.4 |
| Crash Modification Factor—adjacent curves 1—Equation (16) [-] | 4.3 | 6.8 | 39.5 | 1.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Intini, P.; Berloco, N.; Ranieri, V.; Colonna, P. Geometric and Operational Features of Horizontal Curves with Specific Regard to Skidding Proneness. Infrastructures 2020, 5, 3. https://doi.org/10.3390/infrastructures5010003
Intini P, Berloco N, Ranieri V, Colonna P. Geometric and Operational Features of Horizontal Curves with Specific Regard to Skidding Proneness. Infrastructures. 2020; 5(1):3. https://doi.org/10.3390/infrastructures5010003
Chicago/Turabian StyleIntini, Paolo, Nicola Berloco, Vittorio Ranieri, and Pasquale Colonna. 2020. "Geometric and Operational Features of Horizontal Curves with Specific Regard to Skidding Proneness" Infrastructures 5, no. 1: 3. https://doi.org/10.3390/infrastructures5010003
APA StyleIntini, P., Berloco, N., Ranieri, V., & Colonna, P. (2020). Geometric and Operational Features of Horizontal Curves with Specific Regard to Skidding Proneness. Infrastructures, 5(1), 3. https://doi.org/10.3390/infrastructures5010003